Jackknife empirical likelihood of error variance in partially linear varying-coefficient errors-in-variables models

Abstract

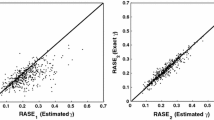
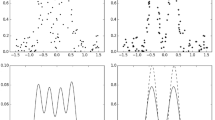
For the partially linear varying-coefficient model when the parametric covariates are measured with additive errors, the estimator of the error variance is defined based on residuals of the model. At the same time, we construct Jackknife estimator as well as Jackknife empirical likelihood statistic of the error variance. Under both the response variables and their associated covariates form a stationary $\alpha$-mixing sequence, we prove that the proposed estimators and Jackknife empirical likelihood statistic are asymptotic normality and asymptotic $\chi ^2$ distribution, respectively. Numerical simulations are carried out to assess the performance of the proposed method.

Appendix

In this section, we give some preliminary Lemmas, which have been used in Section 5. Let $\{X_i, i\ge 1\}$ be a stationary sequence of $\alpha$-mixing random variables with the mixing coefficients $\{\alpha (k)\}$.

Lemma 6.1

(Liebscher (2001), Proposition 5.1) Assume that $EX_i=0$ and $|X_i|\le S<\infty$ a.s. $(i=1,2,\cdots ,n)$. Then for n, $m\in \mathbb {N}$, $0<m\le n/2$ and $\epsilon >0$, $P(|\sum _{i=1}^nX_i|>\epsilon )\le 4\exp \{-\frac{\epsilon ^2}{16}(nm^{-1}D_m+\frac{1}{3}\epsilon Sm)^{-1}\}+32\frac{S}{\epsilon }n\alpha (m),$ where $D_m=\max _{1\le j\le 2m}Var(\sum _{i=1}^jX_i)$.

Lemma 6.2

(Yang (2007), Theorem 2.2)

• (i) Let $r>2,~\delta >0,~EX_i=0$ and $E|X_i|^{r+\delta }<\infty$. Suppose that $\lambda >r(r+\delta )/(2\delta )$ and $\alpha (n)=O(n^{-\lambda })$. Then for any $\epsilon >0$, there exists a positive constant $C:=C(\epsilon ,r,\delta ,\lambda )$ such that $E\max _{1\le m\le n}|\sum _{i=1}^mX_i|^r\le C\{n^\epsilon \sum _{i=1}^nE|X_i|^r+(\sum _{i=1}^n\Vert X_i\Vert _{r+\delta }^2)^{r/2}\}.$

• (ii) If $EX_i=0$ and $E|X_i|^{2+\delta }<\infty$ for some $\delta >0$, then $E(\sum _{i=1}^nX_i)^2\le \{1+16\sum _{l=1}^n\alpha ^{\frac{\delta }{2+\delta }}(l)\}\sum _{i=1}^n\Vert X_i\Vert _{2+\delta }^2$.

Lemma 6.3

(Lin and Lu (1996), Theorem 3.2.1) Suppose that $EX_1\!=\!0,~~E|X_1|^{2+\delta }\!<\!\infty$ for some $\delta \!>\!0$ and $\sum _{n=1}^{\infty }\alpha ^{\delta /(2+\delta )}(n)\!<\!\infty$. Then $\sigma ^2\!:=\!EX_1^2+2\sum _{j=2}^\infty EX_1X_j<\infty$ and, if $\sigma \ne 0$, $\frac{S_n}{\sigma \sqrt{n}}\mathop {\rightarrow }\limits ^\mathcal{{D}}N(0,1).$

Lemma 6.4

(Miller (1974), Lemma 2.1) For a nonsingular matrix A, and vectors U and V, we have $(A+UV^\tau )^{-1}=A^{-1}-\frac{(A^{-1}U)(V^\tau A^{-1})}{1+V^\tau A^{-1}U}$.

Lemma 6.5

(Shao (1993), Corollary 1) Let $EX_i=0$ and $\sup _i E|X_i|^r<\infty$ for some $r>1$. Suppose that $\alpha (n)=O(\log ^{-\psi }n)$ for some $\psi >r/(r-1)$. Then $n^{-1}\sum _{i=1}^n X_i=o(1)~~a.s$.

Lemma 6.6

Suppose (A1)–(A3), (A5) and (A6) are satisfied, then

$$\begin{aligned} \sup _{t\in \Omega }\Big |\frac{1}{n}D_t^\tau \omega _tD_t-f(t)\Gamma (t)\otimes \Big ( \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad \mu _2 \end{array}\Big )\Big | =O_p(c_n), \end{aligned}$$

(6.1)

$$\begin{aligned} \sup _{t\in \Omega }\Big |\frac{1}{n}D_t^\tau \omega _t\mathbf X -f(t)\Phi (t)\otimes \Big ( \begin{array}{c} 1 \\ 0 \end{array} \Big )\Big | =O_p(c_n). \end{aligned}$$

(6.2)

Proof

We only prove (6.1) here, because (6.2) can be proved similarly. Write

$$\begin{aligned} D_t^\tau \omega _tD_t&= \left( \! \begin{array}{ccc} W_1,&{}\ldots ,&{} W_n \\ \frac{T_1-t}{h}W_1,&{}\ldots ,&{} \frac{T_n-t}{h}W_n \end{array} \!\right) \!\left( \! \begin{array}{ccc} K_h(T_1\!-\!t) &{} &{} \\ &{}\ddots &{} \\ &{} &{} K_h(T_n\!-\!t) \end{array} \!\right) \!\left( \! \begin{array}{ccc} W_1^\tau &{} \frac{T_1\!-\!t}{h}W_1^\tau \\ \vdots &{} \vdots \\ W_n^\tau &{} \frac{T_n\!-\!t}{h}W_n^\tau \end{array}\right) \nonumber \\&=\left( \begin{array}{llll} \sum _{i=1}^nW_iW_i^\tau K_h(T_i-t) &{}\quad \sum _{i=1}^nW_iW_i^\tau \frac{T_i-t}{h}K_h(T_i-t) \\ \sum _{i=1}^nW_iW_i^\tau \frac{T_i-t}{h}K_h(T_i-t) &{}\quad \sum _{i=1}^nW_iW_i^\tau \Big (\frac{T_i-t}{h}\Big )^2K_h(T_i-t) \end{array} \right) . \end{aligned}$$

(6.3)

Here, we only give the proof of

$$\begin{aligned} \sup _{t\in \Omega }\Big |\frac{1}{n}\sum _{i=1}^nW_iW_i^\tau K_h(T_i-t)-f(t)\Gamma (t) \Big |=O_p(c_n). \end{aligned}$$

(6.4)

We divide $\Omega$ into subintervals $\{\Delta _l\}$ ($l=1,2,\cdots ,l_n$) with length $r_n=h\sqrt{\frac{\log n}{nh}}$, and the center of $\Delta _l$ is at $t_l$. Then the total number of the subintervals satisfies $l_n=O(r_n^{-1})$. Then

$$\begin{aligned}&\sup _{t\in \Omega }\Big |\frac{1}{n}\sum _{i=1}^nW_iW_i^\tau K_h(T_i-t)-f(t)\Gamma (t)\Big | \\&\quad \le \max _{1\le l\le l_n}\sup _{t\in \Delta _l}\Big |\frac{1}{n}\sum _{i=1}^nW_iW_i^\tau K_h(T_i-t)-\frac{1}{n}\sum _{i=1}^nW_iW_i^\tau K_h(T_i-t_l)\Big | \\&\qquad +\,\max _{1\le l\le l_n}\Big |\frac{1}{n}\sum _{i=1}^nW_iW_i^\tau K_h(T_i-t_l)-f(t_l)\Gamma (t_l)\Big |\\&\qquad +\,\max _{1\le l\le l_n}\sup _{t\in \Delta _l}\Big |f(t_l)\Gamma (t_l)-f(t)\Gamma (t)\Big | \\&\quad :=I_1+I_2+I_3. \end{aligned}$$

Therefore, to prove (6.4), it is sufficient to show that $I_k=O_p(c_n),~~k=1,2,3$.

Using the Lipschitz continuity of $K(\cdot )$, we have $|K_h(T_i-t)-K_h(T_i-t_l)|\le \frac{C_1}{h^2}|t-t_l|I(|T_i-t_l|\le C_2h)\le \frac{C_1 r_n}{h^2}I(|T_i-t_l|\le C_2h).$ Therefore, the $(k_1,k_2)$ component in $I_1$, $1\le k_1\le k_2\le p$, can be written as

$$\begin{aligned}&\max _{1\le l\le l_n}\sup _{t\in \Delta _l}\Bigg |\frac{1}{n}\sum _{i=1}^nW_{ik_1}W_{ik_2}[K_h(T_i-t)-K_h(T_i-t_l)]\Bigg | \\&\quad \le \frac{C_1 r_n}{nh^2}\max _{1\le l\le l_n}\Bigg |\sum _{i=1}^n|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h) \\&\qquad -\,\sum _{i=1}^nE|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h)\Bigg | \\&\qquad +\,\frac{C_1 r_n}{nh^2}\max _{1\le l\le l_n}\sum _{i=1}^nE|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h):=I_{11}+I_{12}. \end{aligned}$$

For $I_{11}$, applying Lemmas 6.1 and 6.2 we have

$$\begin{aligned}&P\Big (\frac{C_1 r_n}{h^2}\max _{1\le l\le l_n}\Big |\frac{1}{n}\sum _{i=1}^n[|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h) \\&\qquad \qquad -E|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h)]\Big |\ge C_0\sqrt{\frac{\log n}{nh}}\Big ) \\&\le \sum _{l=1}^{l_n}\Big \{4\exp \Big [\frac{-\frac{1}{16}C_0^2nh\log n n^{-2/\delta }}{\frac{n}{m}D_m+\frac{1}{3}C_0\sqrt{nh\log n }n^{-1/\delta }C_1m}\Big ]+32\frac{C_1}{C_0\sqrt{nh\log n}n^{-1/\delta }}n\alpha (m)\Big \}, \end{aligned}$$

where $D_m=\max _{1\le j\le 2m}E(h\sum _{i=1}^j[|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h) -E|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h)])^2 n^{-2/\delta } \le \frac{C_2mh}{n^{2/\delta }}$. Taking $m=[\frac{n^{1-1/\delta }h}{C_0\sqrt{nh\log n}}]$, we have

$$\begin{aligned}&P\Big (\max _{1\le l\le l_n}\Big |\frac{1}{n}\sum _{i=1}^n[|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h) \nonumber \\&\qquad \qquad -E|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h)]\Big |\ge C_0\sqrt{\frac{\log n}{nh}}\Big ) \nonumber \\&\le l_n\Big \{\frac{4}{n}+C_1\frac{C_1n^{1+1/\delta }}{\sqrt{nh\log n}}\alpha (m)\Big \}\le \frac{C_0}{n}l_n\rightarrow 0. \end{aligned}$$

(6.5)

On the other hand, we have $E|W_{ik_1}W_{ik_2}|I(|T_i-t_l|\le C_2h)=O(h).$ Therefore $I_{12}=O(\sqrt{\frac{\log n}{nh}}).$ Together with (6.5), one can derive $I_1=O_p(C_n).$ One can rewrite $I_2$ as

$$\begin{aligned} I_2\le&\max _{1\le l\le l_n}\Big |\frac{1}{n}\sum _{i=1}^n[W_iW_i^\tau -\Gamma (T_i)]K_h(T_i-t_l)\Big | \\&\qquad \qquad +\max _{1\le l\le l_n}\Big |\frac{1}{n}\sum _{i=1}^n\Gamma (T_i)K_h(T_i-t_l)-E\Gamma (T_i)K_h(T_i-t_l)\Big | \\&+\max _{1\le l\le l_n}|E\Gamma (T_i)K_h(T_i-t_l)-f(t_l)\Gamma (t_l)|:=I_{21}+I_{22}+I_{23}. \end{aligned}$$

By the same technique used in proving (6.5), we have $I_{21}=O_p\left( \sqrt{\frac{\log n}{nh}}\right)$, $I_{22}=O_p\left( \sqrt{\frac{\log n}{nh}}\right) .$ Using Taylor’s expansion, we have $I_{23}=O(h^2).$ From (A1), we have

$$\begin{aligned} I_3=\max _{1\le l\le l_n}\sup _{t\in \Delta _l}|f(t_l)\Gamma (t_l)-f(t)\Gamma (t)|\le C_1r_n^2+C_2r_n=O\Big (\sqrt{\frac{\log n}{nh}}\Big ). \end{aligned}$$

Thus, (6.4) is proved, which completes the proof of this lemma. $\square$

Lemma 6.7

Suppose (A1)–(A3), (A5) and (A6) are satisfied, then $\frac{1}{n}\sum _{i=1}^n\tilde{\xi _i}\tilde{\xi _i}^\tau \mathop {\rightarrow }\limits ^\mathrm{P} \Sigma _e+EX_1X_1^\tau -E[\Phi ^\tau (T_1)\Gamma ^{-1}(T_1)\Phi (T_1)].$

Proof

From the definition $\tilde{\xi _i}^\tau =\xi _i^\tau -S_i{\varvec{\xi }}$ and (1.1), we have

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n\tilde{\xi _i}\tilde{\xi _i}^\tau&=\frac{1}{n}\sum _{i=1}^n(X_i^\tau -S_i\mathbf X )^\tau (X_i^\tau -S_i\mathbf X ) +\frac{1}{n}\sum _{i=1}^n(e_i^\tau -S_i\mathbf e )^\tau (X_i^\tau -S_i\mathbf X ) \nonumber \\&\quad \ +\frac{1}{n}\sum _{i=1}^n(X_i^\tau -S_i\mathbf X )^\tau (e_i^\tau -S_i\mathbf e ) +\frac{1}{n}\sum _{i=1}^n(e_i^\tau -S_i\mathbf e )^\tau (e_i^\tau -S_i\mathbf e ), \end{aligned}$$

where $S_i=(W_i^\tau ,~0)(D_{T_i}^\tau \omega _{T_i}D_{T_i})^{-1}D_{T_i}^\tau \omega _{T_i}$. By (6.1) and (6.2) in Lemma 6.6, we have

$$\begin{aligned} S_i\mathbf X&=(W_i^\tau ,~0)(D_{T_i}^\tau \omega _{T_i}D_{T_i})^{-1}D_{T_i}^\tau \omega _{T_i}\mathbf X \nonumber \\&=(W_i^\tau ,~0)\Big \{[nf(T_i)\Gamma (T_i)]^{-1}\otimes \frac{1}{\mu _2} \Big ( \begin{array}{cc} 1 &{}\quad 0\\ 0 &{}\quad \mu _2 \end{array}\Big ) \Big \}\nonumber \\ {}&\quad \ \times \Big \{ n\Phi (T_i)f(T_i)\otimes \Big ( \begin{array}{c} 1 \\ 0 \end{array} \Big )\{1+O_p(c_n)\} \Big \} \nonumber \\&=(W_i^\tau ,~0)\Big \{[nf(T_i)\Gamma (T_i)]^{-1}[n\Phi (T_i)f(T_i)]\otimes \frac{1}{\mu _2} \Big (\begin{array}{cc} 1 &{}\quad 0\\ 0 &{}\quad \mu _2 \end{array}\Big ) \Big ( \begin{array}{c} 1 \\ 0 \end{array} \Big )\{1\!+\!O_p(c_n)\} \Big \} \nonumber \\&=(W_i^\tau ,~0)\Big \{\Gamma ^{-1}(T_i)\Phi (T_i)\otimes \frac{1}{\mu _2} \Big (\begin{array}{c} 1 \\ 0 \end{array} \Big )\{1+O_p(c_n)\} \Big \} \nonumber \\&=W_i^\tau \Gamma ^{-1}(T_i)\Phi (T_i)\{1+O_p(c_n)\}. \end{aligned}$$

(6.6)

Similarly, using the approaches above and those in the proof of (6.1) and (6.2), we have

$$\begin{aligned} S_i\mathbf e =W_i^\tau \Gamma ^{-1}(T_i)E(W_ie_i^\tau |T_i)\{1+O_p(c_n)\}=0. \end{aligned}$$

(6.7)

From (6.6) and using Lemma 6.5, it follows that

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n(X_i^\tau -S_i\mathbf X )^\tau (X_i^\tau -S_i\mathbf X ) \mathop {\rightarrow }\limits ^\mathrm{P} EX_1X_1^\tau -E[\Phi ^\tau (T_1)\Gamma ^{-1}(T_1)\Phi (T_1)]. \end{aligned}$$

Similarly $\frac{1}{n}\sum _{i=1}^n(e_i^\tau -S_i\mathbf e )^\tau (X_i^\tau -S_i\mathbf X ) =\frac{1}{n}\sum _{i=1}^ne_i (X_i^\tau -W_i^\tau \Gamma ^{-1}(T_i)\Phi (T_i))\{1+O_p(c_n)\} \mathop {\rightarrow }\limits ^\mathrm{P} 0.$ According to (6.7), we have $\frac{1}{n}\sum _{i=1}^n(e_i^\tau -S_i\mathbf e )^\tau (e_i^\tau -S_i\mathbf e ) =\frac{1}{n}\sum _{i=1}^ne_ie_i^\tau \mathop {\rightarrow }\limits ^\mathrm{a.s.} \Sigma _e.$ Thus the conclusion is proved. $\square$

Lemma 6.8

Suppose (A1)–(A6) are satisfied, then $\sum _{i=1}^n\tilde{\xi _i}\tilde{M}_i=o_p(\sqrt{n}),$ where $\tilde{M}_i=M_i-S_iM$ and $M_i=W_i^\tau a(T_i)$.

Proof

According to the definition, we have

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n\tilde{\xi _i}\tilde{M}_i =\frac{1}{n}\sum _{i=1}^n(X_i^\tau -S_i\mathbf X )^\tau (M_i^\tau -S_iM) +\frac{1}{n}\sum _{i=1}^n(e_i^\tau -S_i\mathbf e )^\tau (M_i^\tau -S_iM). \end{aligned}$$

(6.8)

Note that $D_t^\tau \omega _tM =\Big (\begin{array}{ccc} \sum _{i=1}^nW_iW^\tau _i a(T_i) K_h(T_i-t) \\ \sum _{i=1}^nW_iW^\tau _i a(T_i) \frac{T_i-t}{h}K_h(T_i-t) \end{array}\Big ).$ Using the similar techniques in the proof of Lemma 6.6, one can easily check that $D_t^\tau \omega _tM=n\Gamma (t)f(t) a(t)\otimes \Big (\begin{array}{c} 1 \\ 0 \end{array} \Big )\{1+O_p(c_n)\}.$ Therefore $S_iM=W_i^\tau a(T_i)\{1+O_p(c_n)\}$, furthermore,

$$\begin{aligned} \tilde{M}_i=M_i-S_iM=W_i^\tau a(T_i)O_p(c_n). \end{aligned}$$

(6.9)

Then, from (6.6) and law of large numbers for stationary $\alpha$-mixing sequences, one can obtain

$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^n(X_i^\tau -S_i\mathbf X )^\tau (M_i^\tau -S_iM) \nonumber \\&\quad =\frac{1}{n}\sum _{i=1}^n[X_i^\tau -W_i^\tau \Gamma ^{-1}(T_i)\Phi (T_i) -W_i^\tau \Gamma ^{-1}(T_i)\Phi (T_i)O_p(c_n)]^\tau W_i^\tau a(T_i)O_p(c_n) \nonumber \\&\quad =\frac{1}{n}\sum _{i=1}^nX_iW_i^t a(T_i)O_p(c_n) -\frac{1}{n}\sum _{i=1}^n\Phi ^\tau (T_i)\Gamma ^{-1}(T_i)W_iW_i^\tau a(T_i)O_p(c_n) \nonumber \\&\qquad -\,\frac{1}{n}\sum _{i=1}^n\Phi ^\tau (T_i)\Gamma ^{-1}(T_i)W_iW_i^\tau a(T_i)O_p(c_n^2) \nonumber \\&\quad =E[\Phi ^\tau (T_1) a(T_1)]O_p(c_n^2). \end{aligned}$$

(6.10)

Similarly with (6.7), we have $\frac{1}{n}\sum _{i=1}^n(e_i^\tau -S_i\mathbf e )^\tau (M_i^\tau -S_iM) \mathop {\rightarrow }\limits ^\mathrm{P} 0,$ which, together with (6.8) and (6.10), yields that $\sum _{i=1}^n\tilde{\xi }_i\tilde{M}_i=O_p(nc_n^2)=o_p(\sqrt{n}).$ $\square$

Lemma 6.9

• (i) Suppose (A1)–(A6) are satisfied, then

  $$\begin{aligned} \sqrt{n}(\hat{\beta }_n-\beta )\mathop {\rightarrow }\limits ^\mathcal{{D}} N(0,\Sigma _1^{-1}\Sigma _2\Sigma _1^{-1}), \end{aligned}$$

  where $\Sigma _1=E(X_1X_1^\tau )-E[\Phi ^\tau (T_1)\Gamma ^{-1}(T_1)\Phi (T_1)]$, $\Phi (T_1)=E(W_1X_1^\tau |T_1)$, $\Gamma (T_1)=E(W_1W_1^\tau |T_1)$ $\Sigma _2=\lim _{n\rightarrow \infty }Var\{\frac{1}{\sqrt{n}}\sum _{i=1}^n[\xi _i-\Psi ^\tau (T_i)\Gamma ^{-1}(T_i)W_i][\epsilon _i-e_i^\tau \beta ]\}$. Further, $\hat{\Sigma }_1^{-1}\hat{\Sigma }_2\hat{\Sigma }_1^{-1}$ is a consistent estimator of $\Sigma _1^{-1}\Sigma _2\Sigma _1^{-1}$, where $\hat{\Sigma }_1=\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }_i^\tau -\Sigma _e,$ $\hat{\Sigma }_2=\frac{1}{n}\Big \{\sum _{i=1}^n [\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)]+\Sigma _e\hat{\beta }_n\Big \}^{\otimes 2},$ here $C^{\otimes 2}$ means $CC^\tau$.

• (ii) Suppose (A1)–(A6) are satisfied, then $\sqrt{n}(\hat{\beta }_J-\beta )=\sqrt{n}(\hat{\beta }_n-\beta )+o_p(1)$.

Proof

(i) Let $\sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }^\tau _i-n\Sigma _e=A$, then $\hat{\beta }_n=A^{-1}\sum _{i=1}^n\tilde{\xi }_i\tilde{Y}^\tau _i$. Write

$$\begin{aligned} \hat{\beta }_n-\beta =A^{-1}n\Sigma _e\beta +A^{-1}\sum _{i=1}^n\tilde{\xi }_i(\tilde{Y}^\tau _i-\tilde{\xi }_i^\tau \beta ). \end{aligned}$$

(6.11)

From Lemma 6.7, we have $A^{-1}=O(\frac{1}{n})$. According to the definition and (1.1), we write

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i(\tilde{Y}^\tau _i-\tilde{\xi }_i^\tau \beta )&=\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i(M_i-S_iM) +\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i(\epsilon _i-S_i\epsilon )\nonumber \\&\quad \ -\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i(e_i^\tau -S_i\mathbf e ^\tau )\beta . \end{aligned}$$

(6.12)

From (6.6) and (6.7), we have

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i(e_i^\tau -S_i\mathbf e ^\tau )\beta =\frac{1}{n}\sum _{i=1}^n[\xi _i-\Phi ^\tau (T_i)\Gamma ^{-1}(T_i)W_i]e_i^\tau \beta +o_p\Big (\frac{1}{\sqrt{n}}\Big ). \end{aligned}$$

(6.13)

Similar to the proof of (6.2) in Lemma 6.6, one can easily check that $D_t^\tau \omega _t\epsilon =n\mathbf 1 _{2q}\otimes \Big (\begin{array}{c} 1 \\ 0 \end{array} \Big )O_p\Big (\sqrt{\frac{\log n}{nh}}\Big ).$ Together with (6.1), (A1) and (A2), we have

$$\begin{aligned} S_i\epsilon&=(W_i^\tau ,~~0)(D_{T_i}^\tau \omega _{T_i}D_{T_i})^{-1}D_{T_i}\omega _{T_i}\epsilon \nonumber \\&=(W_i^\tau ,~~0)\Big \{[nf(T_i)\Gamma (T_i)]^{-1}\otimes \frac{1}{\mu _2} \Big ( \begin{array}{cc} \mu _2 &{} 0 \\ 0 &{} 1 \end{array}\Big ) \Big \}\Big \{n\mathbf 1 _{2q}\otimes \Big ( \begin{array}{c} 1 \\ 0 \end{array}\Big ) \Big \}O_p\Big (\sqrt{\frac{\log n}{nh}}\Big ) \nonumber \\&=W_i^\tau \mathbf 1 _{q}[f(T_i)\Gamma (T_i)]^{-1}O_p\Big (\sqrt{\frac{\log n}{nh}}\Big ) =W_i^\tau \mathbf 1 _{q} O_p\Big (\sqrt{\frac{\log n}{nh}}\Big ). \end{aligned}$$

(6.14)

Therefore

$$\begin{aligned} \sum _{i=1}^n\tilde{\xi }_i(\epsilon _i-S_i\epsilon )&=\sum _{i=1}^ne_i\epsilon _i+\sum _{i=1}^n(X_i-\Phi ^\tau (T_i)\Gamma ^{-1}(T_i)W_i)\epsilon _i+o_p(\sqrt{n}) \nonumber \\&=\sum _{i=1}^n(\xi _i-\Phi ^\tau (T_i)\Gamma ^{-1}(T_i)W_i)\epsilon _i+o_p(\sqrt{n}). \end{aligned}$$

(6.15)

Combining (6.11)–(6.15) and Lemma 6.8, we have

$$\begin{aligned} \sqrt{n}(\hat{\beta }_n\!-\!\beta )\!=\!\Big (\frac{A}{n}\Big )^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^n \Big \{\Sigma _e\beta \!+[\xi _i\!-\!\Phi ^\tau (T_i)\Gamma ^{-1}(T_i)W_i][\epsilon _i\!-\!e^\tau \beta ]\Big \}\!+\!o_p(1). \end{aligned}$$

Let $\eta _i=\Sigma _e\beta +[\xi _i-\Phi ^\tau (T_i)\Gamma ^{-1}(T_i)W_i][\epsilon _i-e^\tau \beta ]$. Obviously, $\{\eta _i,i\ge 1\}$ is an $\alpha$-mixing sequence with $E\eta _i=0$ and $E|\eta _i|^\delta <\infty$ for $\delta >4$. Applying Lemma 6.3, one can complete the proof of (i).

(ii) To prove $\sqrt{n}(\hat{\beta }_J-\beta )=\sqrt{n}(\hat{\beta }_n-\beta )+o_p(1)$, it is sufficient to prove $\hat{\beta }_J=\hat{\beta }_n+o_p(\frac{1}{\sqrt{n}})$.

Note that $\hat{\beta }_J=\hat{\beta }_n+\frac{n-1}{n}\sum _{i=1}^n(\hat{\beta }_n-\hat{\beta }_{n,-i}).$ Therefore, we only need to prove that

$$\begin{aligned} \sqrt{n}\sum _{i=1}^n(\hat{\beta }_n-\hat{\beta }_{n,-i})=o_p(1). \end{aligned}$$

(6.16)

From the definition,

$$\begin{aligned} \hat{\beta }_n-\hat{\beta }_{n,-i}\!=\!\left[ \sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }_i^\tau -n\Sigma _e\right] ^{-1}\sum _{i=1}^n\tilde{\xi }_i\tilde{Y}_i \!-\!\left[ \sum _{j\ne i}^n\tilde{\xi }_j\tilde{\xi }_j^\tau \!-\!(n-1)\Sigma _e\right] ^{-1}\sum _{j\ne i}^n\tilde{\xi }_j\tilde{Y}_j. \end{aligned}$$

Using the fact [see Theorem 11.2.3 in Golub and Van Loan (1996)] $(A+B)^{-1}=A^{-1}-A^{-1}BA^{-1}-A^{-1}B\sum _{k=1}^{\infty }C^kA^{-1},$ where A is a nonsingular matrix, and $C=-A^{-1}B$. We write

$$\begin{aligned}&\left[ \sum _{j\ne i}\tilde{\xi }_j\tilde{\xi }_j^\tau -(n-1)\Sigma _e\right] ^{-1} \nonumber \\&\quad =\,\left[ \sum _{j\ne i}\tilde{\xi }_j\tilde{\xi }_j^\tau -n\Sigma _e\right] ^{-1} \!-\!\left[ \sum _{j\ne i}\tilde{\xi }_j\tilde{\xi }_j^\tau \!-\!n\Sigma _e\right] ^{-1}\Sigma _e \left[ \sum _{j\ne i}\tilde{\xi }_j\tilde{\xi }_j^\tau \!-\!n\Sigma _e\right] ^{-1}\!-\!D, \end{aligned}$$

(6.17)

where $D=A^{-1}B\sum _{k=1}^{\infty }C^kA^{-1}, A=[\sum _{j\ne i}\tilde{\xi }_j\tilde{\xi }_j^\tau -n\Sigma _e], B=\Sigma _e, C=-A^{-1}B$.

Applying Lemma 6.4, we write

$$\begin{aligned}&\left[ \sum _{j\ne i}\tilde{\xi }_j\tilde{\xi }_j^\tau -n\Sigma _e\right] ^{-1} =\left[ \sum _{j=1}^n\tilde{\xi }_j\tilde{\xi }_j^\tau -n\Sigma _e-\tilde{\xi }_i\tilde{\xi }_i^\tau \right] ^{-1} \nonumber \\&\quad =\, \left[ \sum _{j=1}^n\tilde{\xi }_j\tilde{\xi }_j^\tau -n\Sigma _e\right] ^{-1} +\frac{[\sum _{j=1}^n\tilde{\xi }_j\tilde{\xi }_j^\tau -n\Sigma _e]^{-1}\tilde{\xi }_i\tilde{\xi }_i^\tau [\sum _{j=1}^n\tilde{\xi }_j\tilde{\xi }_j^\tau -n\Sigma _e]^{-1}}{1-\tilde{\xi }_i^\tau [\sum _{j=1}^n\tilde{\xi }_j\tilde{\xi }_j^\tau -n\Sigma _e]^{-1}\tilde{\xi }_i}. \end{aligned}$$

(6.18)

Let $A=[\sum _{j=1}^n\tilde{\xi }_j\tilde{\xi }_j^\tau -n\Sigma _e]$, the same as in the proof of Lemma 6.9 (i). Then combining (6.17), (6.18) and the definitions of $\hat{\beta }_n$ and $\hat{\beta }_{n,-i}$ and noting that $\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]=0$, we write

$$\begin{aligned}&\sum _{i=1}^n(\hat{\beta }_n-\hat{\beta }_{n,-i}) \nonumber \\&=A^{-1}\sum _{i=1}^n\frac{v_i\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n}{1-v_i} -A^{-1}\sum _{i=1}^n\frac{r_i[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]}{(1-v_i)^2} \nonumber \\&~~~~-A^{-1}\Sigma _eA^{-1}\sum _{i=1}^n\frac{\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n}{1-v_i} -A^{-1}\sum _{i=1}^n\frac{v_i}{1-v_i}\Sigma _e\hat{\beta }_n \nonumber \\&~~~~ +A^{-1}\Sigma _eA^{-1}\sum _{i=1}^n\frac{1}{1-v_i}\Sigma _e\hat{\beta }_n \nonumber \\&~~~~+A^{-1}\sum _{i=1}^nr_i\frac{\Sigma _e\hat{\beta }_n}{(1-v_i)^2} +A^{-1}\sum _{i=1}^n\frac{\tilde{\xi }_i\tilde{\xi }_i^\tau A^{-1}\Sigma _e\hat{\beta }_n}{1-v_i} +D\sum _{i=1}^n\sum _{j\ne i}\tilde{\xi }_j\tilde{Y}_j \nonumber \\&:=A^{-1}\sum _{i=1}^7I_i+D\sum _{i=1}^n\sum _{j\ne i}\tilde{\xi }_j\tilde{Y}_j, \end{aligned}$$

(6.19)

where $v_i=\tilde{\xi }_i^\tau A^{-1}\tilde{\xi }_i$, $r_i=\tilde{\xi }_i^\tau A^{-1}\Sigma _e A^{-1}\tilde{\xi }_i$. By Lemma 6.7 and (A3), we have $v_i=O_p(n^{-1})$ and $r_i=O_p(n^{-2})$. Therefore, to prove (6.16), it is sufficient to prove that

$$\begin{aligned} I_i=o_p(\sqrt{n}),~~i=1,2,\cdots ,7~~\text{ and }~~ D\sum _{i=1}^n\sum _{j\ne i}\tilde{\xi }_j\tilde{Y}_j=o_p(\frac{1}{\sqrt{n}}). \end{aligned}$$

First, we deal with $I_1$. Since

$$\begin{aligned}&\Bigg |\sum _{i=1}^n\frac{v_i}{1-v_i}[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]\Bigg |\le \sqrt{n}(\max _{1\le i\le n}v_i^2)^{1/2} \\&\qquad \qquad \Bigg (\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]^2\Bigg )^{1/2}, \end{aligned}$$

to prove the desired result, one needs only to show that

$$\begin{aligned} \Bigg (\max _{1\le i\le n}v_i^2\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]^2\Bigg )^{1/2}=o_p(1). \end{aligned}$$

In fact, from $\max _{1\le i\le n}|v_i|=o(n^{-3/4})~a.s.$ by the proof of Lemma 3 in Owen (1990), and Lemma 6.11, it follows that $\frac{1}{\sqrt{n}}I_1=o_p(1).$ Similarly $\frac{1}{\sqrt{n}}I_2=o_p(1)$, $\frac{1}{\sqrt{n}}I_3=o_p(1).$

Meanwhile, $\Vert \frac{1}{\sqrt{n}}I_{n4}\Vert =\frac{n}{\sqrt{n}}O_p(\frac{1}{n})\rightarrow 0.$ Similarly, we have

$$\begin{aligned} \frac{1}{\sqrt{n}}I_5=o_p(1),~ \frac{1}{\sqrt{n}}I_6=o_p(1),~ \frac{1}{\sqrt{n}}I_7=o_p(1). \end{aligned}$$

Recall the definition of A, B, C, D and Lemma 6.7, we have $A^{-1}=O(\frac{1}{n})$, $C=O(\frac{1}{n})$ and

$$\begin{aligned} D=A^{-1}B(CA^{-1}+C^2A^{-1}+C^3A^{-1}+\cdots ) =\frac{1}{n^3}+\frac{1}{n^4}+\cdots =O\Big (\frac{1}{n^3}\Big ). \end{aligned}$$

Therefore, by (A3), one can easily obtain that $\sqrt{n}D\sum _{i=1}^n\sum _{j\ne i}^n\tilde{\xi }_j\tilde{Y}_j=\sqrt{n}O\Big (\frac{1}{n^3}\Big )n^2O_p(1)\rightarrow 0.$ $\square$

Lemma 6.10

Suppose (A3) and (A6) are satisfied, then $\frac{1}{n}\sum _{i=1}^n\epsilon _iW_{ik}\!=\!o(n^{-1/4})~~a.s.$ for $1\le k\le p$.

Proof

Following the proof of Lemma 2 in Hong and Cheng (1994) under the independent case, using Lemmas 6.1 and 6.2, it is not difficult to prove this lemma. $\square$

Lemma 6.11

Suppose (A1)–(A3), (A5) and (A6) are satisfied, then $\frac{1}{n}\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n] [\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]^\tau \mathop {\rightarrow }\limits ^\mathrm{P} \Sigma _3$ and $\max _{1\le i\le n}\Vert \hat{\beta }_n-\hat{\beta }_{n,-i}\Vert =O_p(n^{-1})$, where $\Sigma _3=(\Sigma _1+\Sigma _e)(\sigma ^2+\beta ^\tau \Sigma _e\beta )-\Sigma _e\beta \beta ^\tau \Sigma _e$.

Proof

(i) Write

$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n] [\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]^\tau \nonumber \\&\quad =\,\frac{1}{n}\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }^\tau \beta )][\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }^\tau \beta )]^\tau +\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }_i^\tau (\hat{\beta }_n-\beta )(\hat{\beta }_n-\beta )^\tau \tilde{\xi }_i\tilde{\xi }_i^\tau \nonumber \\&\qquad +\,\frac{1}{n}\sum _{i=1}^n\Sigma _e\hat{\beta }_n\hat{\beta }_n^\tau \Sigma _e -\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \beta )\tilde{\xi }_i^\tau \tilde{\xi }_i^\tau (\hat{\beta }_n-\beta )\nonumber \\&\qquad +\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \beta )\hat{\beta }_n^\tau \Sigma _e -frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }_i^\tau (\hat{\beta }_n-\beta )\hat{\beta }_n^\tau \Sigma _e \nonumber \\&\qquad -\,\frac{1}{n}\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \beta )\tilde{\xi }_i^\tau \tilde{\xi }_i^\tau (\hat{\beta }_n-\beta )]^\tau +\frac{1}{n}\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \beta )\hat{\beta }_n^\tau \Sigma _e]^\tau \nonumber \\&\qquad -\,\frac{1}{n}\sum _{i=1}^n[\tilde{\xi }_i\tilde{\xi }_i^\tau (\hat{\beta }_n-\beta )\hat{\beta }_n^\tau \Sigma _e]^\tau . \end{aligned}$$

(6.20)

First, we evaluate the cross terms. By Lemmas 6.9 and 6.5, (A2) and (A3), we have

$$\begin{aligned} \Bigg \Vert \frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }_i^\tau (\hat{\beta }_n-\beta )\hat{\beta }_n^\tau \Sigma _e\Bigg \Vert =\Bigg \Vert \frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }_i^\tau \Bigg \Vert \Bigg \Vert \hat{\beta }_n-\beta \Bigg \Vert \Bigg \Vert \hat{\beta }_n^\tau \Sigma _e\Bigg \Vert =O_p(n^{-1/2})\rightarrow 0. \end{aligned}$$

Similarly $\Vert \frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \beta )\tilde{\xi }_i^\tau \tilde{\xi }_i^\tau (\hat{\beta }_n-\beta )\Vert \mathop {\rightarrow }\limits ^\mathrm{P}0.$ Note that $\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]=0$, with Lemma 6.7 we have

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \beta )\hat{\beta }_n^\tau \Sigma _e&=-\Sigma _e\hat{\beta }_n\hat{\beta }_n^\tau \Sigma _e+\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }_i^\tau (\hat{\beta }_n-\beta )\hat{\beta }_n^\tau \Sigma _e \\&=-\Sigma _e\hat{\beta }_n\hat{\beta }_n^\tau \Sigma _e\!+\!(\Sigma _e\!+\!\Sigma _1)(\hat{\beta }_n\!-\! \beta )\hat{\beta }_n^\tau \Sigma _e \mathop {\rightarrow }\limits ^\mathrm{P} \!-\!\Sigma _e\beta \beta ^\tau \Sigma _e. \end{aligned}$$

Therefore, one can write (6.20) as

$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n] \tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]^\tau \nonumber \\&\quad =\frac{1}{n}\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }^\tau \beta )][\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }^\tau \beta )]^\tau +\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }_i^\tau (\hat{\beta }_n-\beta )(\hat{\beta }_n-\beta )^\tau \tilde{\xi }_i\tilde{\xi }_i^\tau \nonumber \\&\qquad +\,\frac{1}{n}\sum _{i=1}^n\Sigma _e\hat{\beta }_n\hat{\beta }_n^\tau \Sigma _e-2\Sigma _e\beta \beta ^\tau \Sigma _e \nonumber \\&\quad :=H_1+H_2+H_3-2\Sigma _e\beta \beta ^\tau \Sigma _e. \end{aligned}$$

On applying Lemma 6.5 and (6.6) we have

$$\begin{aligned} H_1&=\frac{1}{n}\sum _{i=1}^n\tilde{\xi }_i\tilde{\xi }_i^\tau (\epsilon _i-e_i^\tau \beta )^2 =\frac{1}{n}\sum _{i=1}^n(X_i^\tau -W_i^\tau \Gamma ^{-1}(T_i)\Phi (T_i) \\&\qquad \qquad (1+O_p(c_n))+e_i^\tau )^2(\epsilon _i-e_i^\tau \beta )^2 \nonumber \\ \mathop {\rightarrow }\limits ^\mathrm{P}&E[X_1^\tau -W_1^\tau \Gamma ^{-1}(T_1)\Phi (T_1)+e_1^\tau ]^2(\epsilon _1-e_1^\tau \beta )^2 =(\sigma ^2+\beta ^\tau \Sigma _e\beta )(\Sigma _1+\Sigma _e). \end{aligned}$$

With $\max _{1\le i\le n}\Vert \tilde{\xi }_i\Vert =o(n^{1/{2\delta }})$, $\Vert \hat{\beta }_n-\hat{\beta }\Vert =O_p(n^{-1/2})$, and Lemma 6.7, one can derive that $H_2\rightarrow 0$, $H_3\rightarrow \Sigma _e\beta \beta ^\tau \Sigma _e.$ Hence, the first conclusion is verified.

Similar to the derivation of (6.19), one can write

$$\begin{aligned} \hat{\beta }_n-\hat{\beta }_{n,-i}&=A^{-1}\frac{\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n}{1-v_i}-A^{-1}\frac{v_i}{1-v_i}\Sigma _e\hat{\beta }_n \\&\ \quad -A^{-1}\Sigma _eA^{-1}\frac{\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n}{1-v_i} \nonumber \\&\quad \ +A^{-1}\Sigma _eA^{-1}\frac{\Sigma _e\hat{\beta }_n}{1-v_i} +A^{-1}\frac{\tilde{\xi }_i\tilde{\xi }_i^\tau A^{-1}\Sigma _e\hat{\beta }_n}{1-v_i} \\&\quad \ -A^{-1}r_i\frac{\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n}{(1-v_i)^2} \nonumber \\&\quad \ +A^{-1}r_i\frac{\Sigma _e\hat{\beta }_n}{(1-v_i)^2} +D\sum _{j\ne i}\tilde{\xi }_j\tilde{Y}_j :=\sum _{k=1}^8a_{ki}, \end{aligned}$$

where $v_i=\tilde{\xi }_i^\tau A^{-1}\tilde{\xi }_i$, $r_i=\tilde{\xi }_i^\tau A^{-1}\Sigma _e A^{-1}\tilde{\xi }_i$. Then, it is sufficient to show that

$$\begin{aligned} \max _{1\le i\le n}\Vert a_{ki}\Vert =O_p(n^{-1}),~~k=1,2,\cdots ,8. \end{aligned}$$

For $a_{1i}$, since $E[\tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n]=0$, $E\Vert \tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n\Vert ^\delta <\infty$ and $\max _{1\le i\le n}|v_i|=o(n^{-3/4})~~a.s.$, we have $\max _{1\le i\le n}\Vert \tilde{\xi }_i(\tilde{Y}_i-\tilde{\xi }_i^\tau \hat{\beta }_n)+\Sigma _e\hat{\beta }_n\Vert =O_p(1)$. Therefore, $\max _{1\le i\le n}\Vert a_{1i}\Vert =O_p(n^{-1}).$ It is easy to see that

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^na_{i3}^2 \!=\!\frac{1}{n}\sum _{i=1}^n[\tilde{\xi }_i(\tilde{Y}_i\!-\!\tilde{\xi }_i^\tau \hat{\beta }_n)\!+\! \Sigma _e\hat{\beta }_n] [\tilde{\xi }_i(\tilde{Y}_i\!-\!\tilde{\xi }_i^\tau \hat{\beta }_n)\!+\!\Sigma _e\hat{\beta }_n]^\tau O(n^{-4}) \!=\!O(n^{-4}), \end{aligned}$$

which implies $\frac{n^2\max _{1\le i\le n}\Vert a_{i3}\Vert }{\sqrt{n}}\rightarrow 0$. Then $\max _{1\le i\le n}\Vert a_{i3}\Vert =o_p(n^{-3/2}).$ Similarly, $\max _{1\le i\le n}\Vert a_{6i}\Vert =o_p(n^{-3/2}).$

From $\max _{1\le i\le n}|v_i|\!=\!o(1)~a.s.$, $\max _{1\le i\le n}|r_i|\!=\!o(n^{-1})~a.s.$ and $\max _{1\le i\le n}\Vert \tilde{\xi }_i\Vert =o(n^{1/{2\delta }})~~a.s.$, it is easy to show that $\max _{1\le i\le n}\Vert a_{2i}\Vert =o(n^{-1})$, $\max _{1\le i\le n}\Vert a_{4i}\Vert =O(n^{-2})$, $\max _{1\le i\le n}\Vert a_{5i}\Vert =o(n^{-1})$, $\max _{1\le i\le n}\Vert a_{7i}\Vert =o(n^{-2})$, $\max _{1\le i\le n}\Vert a_{8i}\Vert =o(n^{-1})$.

Then the proof of the second conclusion is completed. $\square$