Single-index composite quantile regression with heteroscedasticity and general error distributions

Abstract

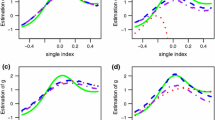
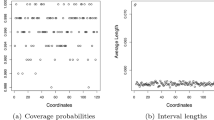
It is known that composite quantile regression (CQR) could be much more efficient and sometimes arbitrarily more efficient than the least squares estimator. Based on CQR method, we propose a weighted CQR (WCQR) method for single-index models with heteroscedasticity and general error distributions. Because of the use of weights, the estimation bias is eliminated asymptotically. By comparing asymptotic relative efficiency, WCQR estimation outperforms the CQR estimation and least squares estimation. The simulation studies and a real data application are conducted to illustrate the finite sample performance of the proposed methods.

Appendix

To prove main results in this paper, the following technical conditions are imposed.

C1. :

The kernel $K(\cdot )$ is a symmetric density function with finite support.

C2. :

The density function of $X^{T}\upgamma$ is positive and uniformly continuous for $\upgamma$ in a neighborhood of 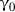. Further the density of is continuous and bounded away from 0 and $\infty$ on its support.

C3. :

The function $g_{0}(\cdot )$ has a continuous and bounded second derivative.

C4. :

Assume that the model error $\varepsilon$ has a positive density $f(\cdot )$.

C5. :

The conditional variance $\sigma (\cdot )$ is positive and continuous.

Remark 4

Conditions C1-C4 are standard conditions, which are commonly used in single-index regression model, see Wu et al. (2010). And condition C5 is also assumed in Sun et al. (2013).

Lemma 1

Let $(X_{1},Y_{1}),\cdots ,(X_{n},Y_{n})$ be independent and identically distributed random vectors, where the $Y_{i}$ are scalar random variables. Further assume that $E|y|^{s}<\infty$, and $\sup _{x}\int |y|^{s}f(x,y)dy<\infty$, where $f(\cdot ,\cdot )$ denotes the joint density of $(X,Y)$. Let $K$ be a bounded positive function with a bounded support, satisfying a Lipschitz condition. Given that $n^{2\varepsilon -1}h\rightarrow \infty$ for some $\varepsilon <1-s^{-1}$, then

$$\begin{aligned} \sup _{x}\left| \frac{1}{n}\sum _{i=1}^{n}\left\{ K_{h}(X_{i}-x)Y_{i}-E(K_{h}(X_{i}-x)Y_{i})\right\} \right| =O_{p}\left( \left[ \frac{\log (1/h)}{nh}\right] ^{1/2}\right) . \end{aligned}$$

Proof

This follows immediately from the result obtained by Mack and Silverman (1982). $\square$

Proof of Theorem 1

Note that

where is a local linear estimator of $g_{0}(\cdot )$ when the index coefficient is known. By Theorem 3.1 in Sun et al. (2013), we have

and can be shown $o_{p}(1)$. The details are given below.

For given $u$, for notational simplicity, we write $\sum _{k=1}^{q}w_k\hat{a}_{\hat{\upgamma }k}\triangleq \hat{g}(u;h,\hat{\upgamma })$; $\hat{b}_{\hat{\upgamma }}\triangleq \hat{g}'(u;h,\hat{\upgamma })$; and which are the solutions of the following minimization problems, respectively,

$$\begin{aligned} \min _{(a_{1},\ldots ,a_{q},b)}\sum _{k=1}^{q}\sum _{i=1}^{n}\rho _{\tau _{k}}\left\{ Y_{i}-a_{k}-b\Big (X_{i}^{T}\hat{\upgamma }-u\Big )\right\} K\left( \frac{X_{i}^{T}\hat{\upgamma }-u}{h}\right) , \end{aligned}$$

Denote

where $e_{k}$ is a q-vector with 1 on the kth position and 0 elsewhere. Further, write $K_{i}^{*}=K\left( \frac{X_{i}^{T}\hat{\upgamma }-u}{h}\right)$, , $\eta _{i,k}=I(\varepsilon _{i}\le c_{k})-\tau _{k}$, , , where and .

Let , where $\Delta _{i,k}=\{Z_{i,k}^{*}\}^{T}\theta ^{*}/\sqrt{nh}$. Then, $\bar{\theta }^{*}$ is also the minimizer of

By applying the identity (Knight 1998)

$$\begin{aligned} \rho _{\tau }(x-y)-\rho _{\tau }(x)=y\left\{ I(x\le 0)-\tau \right\} +\int _{0}^{y}\left\{ I(x\le z)-I(x\le 0)\right\} dz, \end{aligned}$$

we have

where $W_{n}^{*}=\frac{1}{\sqrt{nh}}\sum _{k=1}^{q}\sum _{i=1}^{n}\eta _{i,k}^{*}(u)Z_{i,k}^{*}K_{i}^{*}$ and

Since $B_{n,k}^{*}(\theta ^{*})$ is a summation of i.i.d. random variables of the kernel form, it follows by Lemma 1 that

$$\begin{aligned} B_{n,k}^{*}(\theta ^{*})=E[B_{n,k}^{*}(\theta ^{*})]+O_{p}\left( \log ^{1/2}(1/h)/\sqrt{nh}\right) . \end{aligned}$$

The conditional expectation of $\sum _{k=1}^{q}B_{n,k}^{*}(\theta ^{*})$ can be calculated as

Then,

$$\begin{aligned} L_{n}^{*}(\theta ^{*})&=(W_{n}^{*})^{T}\theta ^{*}+\sum _{k=1}^{q}E[B_{n,k}^{*}(\theta ^{*})]+O_{p}\left( \log ^{1/2}(1/h)/\sqrt{nh}\right) \\&=(W_{n}^{*})^{T}\theta ^{*}+\sum _{k=1}^{q}E\left\{ E[B_{n,k}^{*}(\theta ^{*})|U_0]\right\} +O_{p}\left( \log ^{1/2}(1/h)/\sqrt{nh}\right) \\&=(W_{n}^{*})^{T}\theta ^{*}+\frac{1}{2}(\theta ^{*})^{T}E[S_{n}^{*}]\theta ^{*}+O_{p}\left( \log ^{1/2}(1/h)/\sqrt{nh}\right) . \end{aligned}$$

It can be shown that $E[S_{n}^{*}]=\frac{f_{U_{0}}(u)}{\sigma (u)}S^{*}+O(h^{2})$, where

$$\begin{aligned} S^{*}=\left( \begin{array}{cc} C &{} 0\\ 0 &{} c\mu _{2} \end{array} \right) . \end{aligned}$$

where $C$ is a $q\times q$ diagonal matrix with $C_{jj}=f(c_{j})$. Therefore, we can write $L_{n}^{*}(\theta ^{*})$ as

$$\begin{aligned} L_{n}^{*}(\theta ^{*})=(W_{n}^{*})^{T}\theta ^{*}+\frac{1}{2}\frac{f_{U_{0}}(u)}{\sigma (u)}(\theta ^{*})^{T}S^{*}\theta ^{*}+O_{p}\left( \log ^{1/2}(1/h)/\sqrt{nh}\right) . \end{aligned}$$

By applying the convexity lemma (Pollard 1991) and the quadratic approximation lemma (Fan and Gijbels 1996), the minimizer of $L_{n}^{*}(\theta ^{*})$ can be expressed as

$$\begin{aligned} \bar{\theta }^{*}=-\frac{\sigma (u)}{f_{U_{0}}(u)}\{S^{*}\}^{-1}W_{n}^{*}+o_{p}(1). \end{aligned}$$

$\bar{\theta }^{**}$ can be shown similarly as

$$\begin{aligned} \bar{\theta }^{**}=-\frac{\sigma (u)}{f_{U_{0}}(u)}\{S^{**}\}^{-1}W_{n}^{**}+o_{p}(1), \end{aligned}$$

where $S^{**}=S^{*}$ and $W_{n}^{**}=\frac{1}{\sqrt{nh}}\sum _{k=1}^{q}\sum _{i=1}^{n}\eta _{i,k}^{**}(u)Z_{i,k}^{**}K_{i}^{**}$. Thus, we can obtain

$$\begin{aligned} \bar{\theta }^{*}-\bar{\theta }^{**}&=-\frac{\sigma (u)}{f_{U_{0}}(u)}\{S^{*}\}^{-1}(W_{n}^{*}-W_{n}^{**})+o_{p}(1)\\&=-\frac{\sigma (u)}{f_{U_{0}}(u)}\{S^{*}\}^{-1}\frac{1}{\sqrt{nh}}\sum _{k=1}^{q}\sum _{i=1}^{n}\left\{ \eta _{i,k}^{*}(u)Z_{i,k}^{*}K_{i}^{*}\!-\!\eta _{i,k}^{**}(u)Z_{i,k}^{**}K_{i}^{**}\right\} \!+\!o_{p}(1)\\&=-\frac{\sigma (u)}{f_{U_{0}}(u)}\{S^{*}\}^{-1}\frac{1}{\sqrt{nh}}\sum _{k=1}^{q}\sum _{i=1}^{n}\eta _{i,k}^{*}(u)\left\{ Z_{i,k}^{*}K_{i}^{*}-Z_{i,k}^{**}K_{i}^{**}\right\} +o_{p}(1).\\ \end{aligned}$$

The last equality is due to the fact that ,

$$\begin{aligned}&E\{(\bar{\theta }^{*}-\bar{\theta }^{**})(\bar{\theta }^{*}-\bar{\theta }^{**})^{T}\}\\&\quad \le -rf_{U_{0}}^{-2}(u)\{S^{*}\}^{-1}h^{-1}E\{(\eta _{i,k}^{*}(u))^{2}(Z_{i,k}^{*}K_{i}^{*}-Z_{i,k}^{**}K_{i}^{**})(Z_{i,k}^{*}K_{i}^{*}\nonumber \\&\qquad -Z_{i,k}^{**}K_{i}^{**})^{T}\}(\{S^{*}\}^{-1})^{T}\\&\quad = O(h^{-1}E[(Z_{i,k}^{*}K_{i}^{*}-Z_{i,k}^{**}K_{i}^{**})(Z_{i,k}^{*}K_{i}^{*}-Z_{i,k}^{**}K_{i}^{**})^{T}])\\&\quad = o(1), \end{aligned}$$

which also implies $E(\bar{\theta }^{*}-\bar{\theta }^{**})=o(1)$. Thus, $\bar{\theta }^{*}-\bar{\theta }^{**}=E(\bar{\theta }^{*}-\bar{\theta }^{**})+o_{p}(1)=o_{p}(1)$ according to its first and second term. Therefore $\bar{\theta }^{*}-\bar{\theta }^{**}=o_{p}(1)$. Then, we can obtain . This completes the proof. $\square$

Proof of Theorem 2

For given X,

by the Taylor theorem, . Thus, Theorem 2 is the result of Theorem 1.

Proof of Theorem 3

The proof is similar to that of Theorem 3.1 of Sun et al. (2013). $\square$

Proof of Theorem 4

Write and given $(\hat{a}_{1j},\ldots ,\hat{a}_{qj},\hat{b}_{j})$, note that $\hat{\upgamma }^{*}$ minimizes the following

$$\begin{aligned} \sum _{j=1}^{n}\sum _{k=1}^{q}\sum _{i=1}^{n}\rho _{\tau _{k}}\left\{ Y_{i}-\hat{a}_{kj}-\hat{b}_{j}(X_{i}-X_{j})^{T}\upgamma \right\} \omega _{ij}. \end{aligned}$$

Then, $\hat{\upgamma }^{*}$ is also the minimizer of

where .

By applying the identity (Knight 1998), we can rewrite $L_{n}^{*}(\upgamma ^{*})$ as follows:

where

Firstly, we consider the conditional expectation of $L_{2n}(\upgamma ^{*})$,

In the following, we consider $L_{2n1}(\upgamma ^{*})$ and $L_{2n2}(\upgamma ^{*})$,

$$\begin{aligned} L_{2n1}(\upgamma ^{*})=\frac{1}{2}(\upgamma ^{*})^{T}cS\upgamma ^{*}+o_p(1). \end{aligned}$$

Next consider $L_{2n2}(\upgamma ^{*})$, note that

and by the result $\bar{\theta }^{**}=-\frac{\sigma (u)}{f_{U_{0}}(u)}\{S^{*}\}^{-1}W_{n}^{**}+o_{p}(1)$, we can obtain

It is easy to obtain that , thus

Then,

where . It follows by the convexity lemma (Pollard 1991) that the quadratic approximation to $L_{n}(\upgamma ^{*})$ holds uniformly for $\upgamma ^{*}$ in any compact set $\Theta$. Thus, it follows that

$$\begin{aligned} \hat{\upgamma }^{*}=-\frac{1}{c}S^{-1}W_{n}+o_{p}(1). \end{aligned}$$

By the Cramér-Wald theorem and the Central Limit Theorem for $W_{n}$ holds and $Var(W_{n})\rightarrow \sum _{k=1}^{q}\sum _{k'=1}^{q}\tau _{kk'}S$. This completes the proof. $\square$