Abstract
In this paper, we will tackle the issue of accounting for skewness and potentially severe excess kurtosis of the empirical distribution of a random variable of interest by adjusting a parent leptokurtic distribution, using orthogonal polynomials. We will show that the polynomial shape adapter that allows the transformation from a given parent to a target distribution is a linear combination of the orthogonal polynomials associated to the former with coefficients depending on the difference between the moments of these two distributions. A recent work (Zoia, Commun Stat Theory Methods 39(1):52–64, 2010) has shown how to adjust the normal density by using Hermite polynomials but this application is suitable only for series with moderate kurtosis (lower than 5). This is why we provide two other parent distributions, the logistic and the hyperbolic secant which, once polynomially adjusted, can be used to reshape series with higher degrees of kurtosis. We will apply these results for modelling heavy-tailed and skewed distributions of financial asset returns by using both the conditional and unconditional approaches. We empirically demonstrate the advantages of using the polynomially adapted distributions in place of popular alternatives.





Similar content being viewed by others
Notes
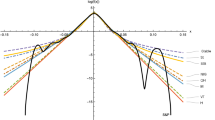
We have checked that the coefficients lie inside the relevant region shown in Fig. 1.
Nyblom’s test (Nyblom 1989) is finalized for detecting possible changes in parameters when the observations are obtained sequentially in time. The null hypothesis of constancy of parameters over time is tested against the alternative of a martingale specification for the parameter variation. The test turns out to be based on cumulative sums of the score function (the derivative of the log-likelihod) whose limiting behavior is a standard Brownian bridge under the null.
References
Bagnato L, De Capitani L, Punzo A (2013) Testing serial independence via density-based measures of divergence. Methodol Comput Appl Probab 19:1–15
Box GE, Tiao GC (1962) A further look at robustness via bayes’s theorem. Biometrika 49:419–432
Bronshtein IN, Semendyayev KA, Musiol G, Mühlig H (2007) Handbook of mathematics. Springer, Berlin
Chihara TS (1978) An introduction to orthogonal polynomials. Gordon & Breach, New York
Curto JD, Pinto JC, Tavares GN (2009) Modeling stock markets’ volatility using garch models with normal, student’st and stable paretian distributions. Stat Pap 50(2):311–321
Engle RF (1982) Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation. Econom J Econom Soc 50:987–1007
Faliva M, Zoia M, Poti V (2013) Orthogonal polynomials for tailoring density functions to excess kurtosis, asymmetry and dependence. Commun Stat Theory Methods. doi:10.1080/03610926.2013.818698
Feller W (1974) Introduction to probability theory and its applications, vol II POD. Wiley, New York
Fernández C, Steel MF (1998) On bayesian modeling of fat tails and skewness. J Am Stat Assoc 93(441):359–371
Fischer MJ (2010) Generalized tukey-type distributions with application to financial and teletraffic data. Stat Pap 51(1):41–56
Fischer MJ (2013) Generalized hyperbolic secant distribution—with application to finance. Springer, Berlin
Francq C (2011) GARCH models: structure, statistical inference and financial applications. Wiley, Chichester
Gallant AR, Tauchen G (1989) Seminonparametric estimation of conditionally constrained heterogeneous processes: asset pricing applications. Econom J Econom Soc 406:1091–1120
Gallant AR, Tauchen G (1993) A nonparametric approach to nonlinear time series analysis: estimation and simulation. In: Brillinger D, Caines P, Geweke J, Parzen E, Rosenblatt M, Taqqu MS (eds) New directions in time series analysis. Part II. Springer, New York, pp 71–92
Granger C, Maasoumi E, Racine J (2004) A dependence metric for possibly nonlinear processes. J Time Ser Anal 25(5):649–669
Handcock MS, Morris M (1999) Relative distribution methods in the social sciences (statistics for social science and behavorial sciences). Springer, New York
Hansen B (1994) Autoregressive conditional density estimation. Int Econom Rev 35(3):705–730
Maasoumi E, Racine J (2002) Entropy and predictability of stock market returns. J Econom 107(1–2):291–312
McDonald JB (1991) Parametric models for partially adaptive estimation with skewed and leptokurtic residuals. Econom Lett 37(3):273–278
McDonald JB, Newey WK (1988) Partially adaptive estimation of regression models via the generalized t distribution. Econom Theory 4(03):428–457
Mills TC, Markellos RN (2008) The econometric modelling of financial time series. Cambridge University Press, Cambridge
Nyblom J (1989) Testing for the constancy of parameters over time. J Am Stat Assoc 84(405):223–230
Palmitesta P, Provasi C (2004) Garch-type models with generalized secant hyperbolic innovations. Stud Nonlinear Dyn Econom 8(2):106–122
Papoulis A, Maradudin A (1963) The fourier integral and its applications. Phys Today 16:70–72
Provost S, Jiang M (2011) Orthogonal polynomial density estimates: alternative representation and degree selection. World Acad Sci Eng Technol 5:1074–1081
Provost SB (2005) Moment-based density approximants. Math J 9(4):727–756
R Core Team (2013) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna
Rachev ST, Hoechstoetter M, Fabozzi FJ, Focardi SM et al. (2010). Probability and statistics for finance, vol 176. Wiley
Shuangzhe L, Chris H (2006) On estimation in conditional heteroskedastic time series models under non-normal distributions. Stat Pap 49(3):455–469
Szegö, G. (1967). Orthongonal polynomials, vol 23. AMS Bookstore
Szegö GP (2004) Risk measures for the 21st century. Wiley, New York
Zoia MG (2010) Tailoring the gaussian law for excess kurtosis and skewness by hermite polynomials. Commun Stat Theory Methods 39(1):52–64
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The probability density function of the hyperbolic secant is
where \(a\) and \(b\) are parameters. By choosing these parameters so that the first two central moments of the variable \(x\) are zero and one, respectively, we get the density function of the normalized hyperbolic secant, that is
Bearing in mind that the characteristic function of \(\text {sech}(x)\) is \(\pi \text {sech} \left( \displaystyle \frac{\pi t}{2} \right) \) and the time scaling property of the Fourier integrals (see Papoulis and Maradudin 1963) we conclude that the characteristic function of (49) is \(\text {sech}(it)\) which, likewise the Gaussian case, has the same functional form as the density to within a scalar factor. Expanding \(\text {sech}(it)\) about \(t=0\), yields
The coefficients of the expansion at stake, which are the Eulero numbers \(E_{r}\), provide the moments of this density. The first even Eulero numbers are
By taking the square of (49) we get the logistic density, that is
Normalizing, we eventually get the density of a zero-mean and unit-variance variable, that is
Upon noting that the characteristic function of the random variable \(y\) with density (50) is
and bearing in mind the time scaling property of the Fourier integrals, we conclude that the characteristic function corresponding to (51) is given by
Expansion of the characteristic function (52) about \(t=0\) eventually yields to find out the moments. Referring to Feller (1974), the moments can be expressed in closed form as follows
where \(\Gamma (\cdot )\) is the gamma function and \(\xi (r)=\sum _{j=1}^{\infty }j^{-r}\) is the Riemann zeta function. Upon noting that \(\Gamma (r+1)=r!\) and that
simple computations provide the moments of the said distribution.
Rights and permissions
About this article
Cite this article
Bagnato, L., Potì, V. & Zoia, M.G. The role of orthogonal polynomials in adjusting hyperpolic secant and logistic distributions to analyse financial asset returns. Stat Papers 56, 1205–1234 (2015). https://doi.org/10.1007/s00362-014-0633-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00362-014-0633-3