A thermodynamic-based approach to model the entry into metabolic depression by mammals and birds

Abstract

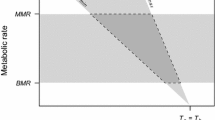
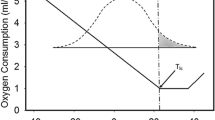
For decades, there was an intense debate in relation to the mechanism behind the entry into metabolic depression (EMD) of mammals and birds. The fulcrum of the argument was whether the depression of metabolic rate ($\dot{W}$) was caused by the drop in body temperature, the so-called “Q₁₀ effect”, or whether it was caused by a metabolic downregulation. One present-day model of this process is a qualitative (textual) description: the initial step of EDM would be a downregulation in $\dot{W}$ from the value maintaining euthermia at a given ambient temperature to the basal metabolic rate of the animal and, then, Q₁₀ effect would take over and drop $\dot{W}$ to its lower levels. Despite widely accepted, this qualitative description still misses a theoretical analysis. Here, we transpose the descriptive model to a formal quantitative one and analyze it under necessary thermodynamic conditions of a system. We, then, compare the results of the formal model to empirical data of EMD by mammals and birds. The comparisons indicate that the metabolic evolution in the course of the entry phase does not follow the descriptive model. Instead, as proposed by alternate models, EMD is a downregulated process as a whole until a new equilibrium T_b is attained.

Appendices

Appendix 1

Thermodynamical compatibility of Ty

The pair {${\dot{W}}_{\mathrm{B}}$, T_x} is inherently compatible from a thermodynamic standpoint. This will become clear shortly. Because of this, the pair {${\dot{W}}_{\mathrm{B}}$, T_y} cannot represent another solution (equilibrium point) of the system unless the thermal conductance had changed, and such a change would preclude Q₁₀ computations correctly (see “Relaxing assumptions #1 and #6: another intermediate body temperature landmark—T_y”). However, we can relax the condition of equilibrium and consider that the system undergoes a series of quasi-static transitions between its states, without changes in thermal conductance. This means that despite ever-changing, the temperature of the system is a reliable measurement.

Under these assumptions, using Eq. (3c), we rewrite Eq. (2) as

$$\frac{\mathrm{d}{T}_{b}}{\mathrm{d}t}=\gamma \cdot \left[\dot{W}-{\dot{W}}_{\mathrm{E}}\cdot \frac{\left({T}_{\mathrm{b}}-{T}_{\mathrm{A}}\right)}{\left({T}_{\mathrm{E}}-{T}_{\mathrm{A}}\right)}\right].$$

Therefore, when ${\dot{W}=\dot{W}}_{\mathrm{B}}$ and T_b = T_y, using Eq. (4b) we obtain

$$\frac{\mathrm{d}{T}_{b}}{\mathrm{d}t}{|}_{{T}_{y}}=\gamma \cdot {\dot{W}}_{\mathrm{B}}\left[1-\frac{\left({T}_{y}-{T}_{\mathrm{A}}\right)}{\left({T}_{x}-{T}_{\mathrm{A}}\right)}\right].$$

(11)

Equation (11) can then be used to compute the expected rate of change in body temperature when the pair {${\dot{W}}_{\mathrm{B}}$, T_y} occurs. Such an expected ratio is thermodynamically correct due to the quasi-static assumption presented above. Because of this and the constancy of the thermal conductance also assumed, Q₁₀ computations would make sense even with an ever-changing body temperature.

Therefore, the ratio between the expected $\frac{\mathrm{d}{T}_{\mathrm{b}}}{\mathrm{d}t}{|}_{{T}_{y}}$ (Eq. (A1)) and the one observed experimentally gives an index of the thermodynamic adequacy to compute Q₁₀ values. In other words, this is a direct comparison between the model and the actual behavior of the animal when it crosses the T_y temperature. Values close to 1 indicate such adequacy. On the other hand, values not close to 1 indicate that the system is not following a dynamic compatible with the assumption of the pair {${\dot{W}}_{\mathrm{B}}$, T_y}.

If we use T_y = T_x in Eq. (A1), it can be seen that $\frac{\mathrm{d}{T}_{\mathrm{b}}}{\mathrm{d}t}{|}_{{T}_{x}}=0$ and the system is in internal equilibrium. This gives the correctness of using the pair {${\dot{W}}_{\mathrm{B}}$, T_x} which would be exactly the end of the first phase of EMD.

The mixed model for analytical solution

Consider that the energy input to the system is negligible in face of energy loss as heat, leading to a cooling process. For a Newtonian cooling, Eq. (2) becomes

$$\frac{\mathrm{d}{T}_{\mathrm{b}}}{\mathrm{d}t}=-\gamma \cdot X\cdot \left({T}_{\mathrm{b}}-{T}_{\mathrm{A}}\right).$$

(12)

Considering Eq. (12), Eq. (7) becomes

$$\mathrm{d}t=\frac{-\mathrm{d}{T}_{\mathrm{b}}}{\gamma \cdot X\cdot \left({T}_{\mathrm{b}}-{T}_{\mathrm{A}}\right)}.$$

(13)

Strictly speaking, in a Newtonian cooling process, there is no energy input to the system and then, obviously, the total metabolic demand during the cooling would be zero (a useless result for the analysis). To make a comparison between the numerical solution of Eq. (9) and an analytical one, we mixed Eq. (14) with metabolic rate dictated by temperature effects (as in Eq. (9)) but without functioning as an energy input to the system. The cooling process will lead to ${T}_{\mathrm{b}}={T}_{\mathrm{A}}$, and we write the variable $\tau$ as

$$\tau =\left({T}_{\mathrm{b}}-{T}_{\mathrm{A}}\right)\cdot \mathrm{ln}q\leftrightarrow \frac{\mathrm{d}\tau }{\mathrm{d}{T}_{\mathrm{b}}}=\mathrm{ln}q.$$

(14)

Then, from Eqs. (12) and (13), we can re-express Eq. (9) as the so-called exponential integral:

$${\tilde{W }}^{\mathrm{N}}=-\frac{\left({T}_{\mathrm{E}}-{T}_{\mathrm{A}}\right)}{\gamma }\cdot {q}^{\left({T}_{\mathrm{A}}-{T}_{\mathrm{E}}\right)}\cdot \underset{{\tau }_{0}}{\overset{{\tau }_{1}}{\int }}\frac{{\mathrm{e}}^{\tau }}{\tau }\mathrm{d}\tau =-\frac{\left({T}_{\mathrm{E}}-{T}_{\mathrm{A}}\right)}{\gamma }\cdot {q}^{\left({T}_{\mathrm{A}}-{T}_{\mathrm{E}}\right)}\cdot \left(\mathrm{ln}\frac{{\tau }_{1}}{{\tau }_{0}}+\sum_{n=1}^{\infty }\frac{{\tau }_{1}^{n}-{\tau }_{0}^{n}}{n\cdot n!}\right),$$

(15)

where the superscript “N” is to indicate that this total metabolic demand was computed as if “a Newtonian cooling process”. If we plot the analytical solution of Eq. (15) and the numerical integration of Eq. (9), we can see that the two equations have very similar behaviors. Figure 2 illustrates this.

Appendix B

The plots in Fig. 8 suggest that thermal conductance X changes during EMD, and that such changes are a linear function of metabolic rate $\dot{W}$ within a range of the process. Therefore, let us assume this linear relationship:

$$X={X}_{0}+K\cdot \dot{W,}$$

(16)

where X₀ is a constant of minimal thermal conductance and K is the rate of change in X due to $\dot{W}$. We shall show that Eq. (16) leads to contradictions, implying that to assume thermal conductance computations during EMD as true values is incorrect.

For the sake of notation, we use ΔT instead of (T_b − T_A). The subscript “E”, as stated before, refers to euthermic conditions. From Eqs. (2) and (16), one obtains

$$\Delta T=\frac{\dot{W}}{{X}_{0}+K\cdot \dot{W}}.$$

(17)

Thus, if $\dot{W}$ = 0, ΔT = 0 (as expected), and, as $\dot{W}$ increases:

$$\Delta T\to \frac{1}{K}.$$

(18)

Consequently, given the limiting of euthermic conditions:

$$K=\frac{1}{\Delta {T}_{\mathrm{E}}}$$

(19)

In addition,

$${X}_{\mathrm{E}}={X}_{0}+\frac{{\dot{W}}_{\mathrm{E}}}{\Delta {T}_{\mathrm{E}}}.$$

(20)

The euthermic steady-state condition demands

$${\dot{W}}_{\mathrm{E}}-{X}_{\mathrm{E}}\cdot \Delta {T}_{\mathrm{E}}=0.$$

(21)

Inserting (20) in (21):

$${X}_{0}\cdot \Delta {T}_{\mathrm{E}}=0$$

(22)

which poses a problem in Eq. (16), since, then, ${X}_{0}=0$. One could envisage two possible ways to circumvent such a problem, although none of them can be true solutions as it will be demonstrated.

${X}_{0}=0$

Assuming ${X}_{0}=0$, Eq. (16) becomes

$$\varvec{X}=\varvec{K}\cdot \dot{\varvec{W}}$$

(23)

Thus, the quasi-static condition of $\frac{\mathrm{d}{T}_{\mathrm{b}}}{\mathrm{d}t}=0$ during EMD now implies

$$\varvec1-{\varvec{K}}\cdot {\varvec{\Delta T}}=\varvec{0}$$

(24)

or:

$$K=\frac{1}{\Delta T}.$$

(25)

However, since ΔT is changing during EMD, Eq. (25) implies that K is not a constant as previously assumed (Eq. (16) or (23)). In other words, the linear relationship between X and $\dot{W}$ observed in Fig. 8 evidences the absence of quasi-static conditions of the system, as the R values in Table 2 also show, or, given a non-constant K, a closed-control loop of body temperature regulation.

${X}_{\mathrm{total}}={X}_{0}+K\cdot \dot{W}$

This assumption is quite similar to Eq. (16), but we shall now write the euthermic thermal conductance as

$${X}_{\mathrm{E}}={X}_{0}+K\cdot {\dot{W}}_{\mathrm{E}}$$

(26)

Considering that X_E is usually computed as the slope of the (linear) relationship of metabolic rate and T_A below the critical lower temperature of the thermoneutral zone (see Fig. 1), Eq. (16) must be a constant irrespectively to T_A below such a critical temperature. However, euthermic metabolic rate ${\dot{W}}_{\mathrm{E}}$ increases as T_A falls, and, thus, as in the previous section, K cannot be a constant as supposed (Eq. (16) or (23)).