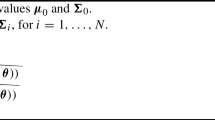Clustering Longitudinal Data for Growth Curve Modelling by Gibbs Sampler and Information Criterion

Abstract

Clustering longitudinal data for growth curve modelling is considered in this paper, where we aim to optimally estimate the underpinning unknown group partition matrix. Instead of following the conventional soft clustering approach, which assumes the columns of the partition matrix to have i.i.d. multinomial or categorical prior distributions and uses a regression model with the response following a finite mixture distribution to estimate the posterior distribution of the partition matrix, we propose an iterative partition and regression procedure to find the best partition matrix and the associated best growth curve regression model for each identified cluster. We show that the best partition matrix is the one minimizing a recently developed empirical Bayes information criterion (eBIC), which, due to the involved combinatorial explosion, is difficult to compute via enumerating all candidate partition matrices. Thus, we develop a Gibbs sampling method to generate a Markov chain of candidate partition matrices that has its equilibrium probability distribution equal the one induced from eBIC. We further show that the best partition matrix, given a priori the number of latent clusters, can be consistently estimated and is computationally scalable based on this Markov chain. The number of latent clusters is also best estimated by minimizing eBIC. The proposed iterative clustering and regression method is assessed by a comprehensive simulation study before being applied to two real-world growth curve modelling examples involving longitudinal data clustering.

1 Introduction

Longitudinal data consist of measurements taken repeatedly on each of the sample units in observation, with the typical feature, especially in clinical settings, that both the time points and the number of measurements observed at each time point stay the same across all sample units. In cases of both the number of measurements and the time points do not stay the same, we call the observed data unbalanced; otherwise, we call them balanced data. Only balanced longitudinal data are considered in this paper. Analysis of longitudinal data needs to take into account the correlations among observations from the same sample unit and/or the same time point. Linear and nonlinear random effects regression models are commonly used to incorporate these correlations, cf. Davidian and Giltinan (1995); Vonesh and Chinchilli (1997); Verbeke and Molenberghs (2000); Fitzmaurice et al. (2004).

Longitudinal data analysis may be better performed under a data clustering framework. Namely, observations from those sample units belonging to the same cluster are more similar to each other than to that from other clusters. Thus, separate models should be used for longitudinal data analysis for data coming from different clusters. The problem is the cluster membership label for each sample unit is often unknown, and so is the number of clusters in the data. Therefore, it becomes necessary to perform longitudinal data clustering in such situations. Gaffney and Smyth (2003) studied longitudinal data clustering using a mixture random effects regression model, while James and Sugar (2003) discussed a functional data clustering approach. Celeux et al. (2005) applied a mixture linear mixed effects model to cluster gene microarray expression profiles. Pfeifer (2004) discussed the clustering analysis by semi-parametric linear mixed effects regression model. Booth et al. (2008) studied longitudinal data clustering based on a multi-level linear mixed effects model.

Most model-based longitudinal data clustering methods are processed in two steps. In the first step, the number of clusters is assumed given, following which the cluster labels (i.e., the partition matrix) of the sample units are optimally estimated by a maximum likelihood alike principle or Bayesian method. In the second step, the number of clusters is optimally estimated by a model selection criterion. McNicholas (2016) provides a comprehensive review of finite mixture model based clustering (MBC) including clustering longitudinal data. Teuling et al. (2021) provides a tutorial on a selection of methods for longitudinal clustering, including group-based trajectory modeling (GBTM), growth mixture modeling (GMM), and k-means based modelling for longitudinal data clustering (KML, cf. Genolini and Falissard, 2010; Genolini et al. 2015). In this paper, we will compare our proposed method with MBC and KML where we use the adjusted Rand index (ARI) proposed by Hubert and Arabie (1985) to evaluate the performance.

In the course of longitudinal data clustering by MBC, covariance matrix of observations from an individual sample unit can be computationally intractable when these observations are high-dimensional. Banfield and Raftery (1993); Celeux and Govaert (1995); Fraley and Raftery (2002) proposed a family of reduced covariance structure models by using eigen-decomposition of group covariance matrices to tackle the high-dimensionality complication. The methods have been implemented in the mclust package in R (R Core Team, 2023). Bouveyron et al. (2007) focused on Gaussian mixture models for high-dimensional data clustering resulting in a clustering method based on the Expectation-Maximization (EM) algorithm, which was further developed by McNicholas and Murphy (2008) using a mixture factor model and extended by McNicholas and Murphy (2010) for longitudinal data clustering. A review on model-based clustering of high-dimensional data is Bouveyron and Brunet-Saumard (2014). Despite these developments, computational challenges still remain, e.g., EM algorithm in non-Gaussian data clustering, when applying them to high-dimensional longitudinal data clustering.

Growth curve model (GCM) is a general regression model shown to be effective for modelling balanced longitudinal data, especially when the data dimension is high. Therefore, advantages of using GCM should be exploited when performing balanced longitudinal data clustering. Pan (1991) discussed the GCM for longitudinal data that follow a class of elliptic symmetric distributions including multivariate normal and multivariate T distributions, and obtained a likelihood ratio test criterion for testing the model parameters. Lee (1988) studied the GCM estimation with special covariance structure such as the uniform one and the sequential one. There are at least three benefits of using GCM for balanced longitudinal data. Firstly, GCM is a parametric model with the statistical inference results often enjoying nice large-sample properties. Secondly, GCM is operating friendly in most applications since the formulations involved are often of closed forms. Thirdly, parameters in GCM are often low-dimensional although the data may be high-dimensional. More details can be found in Section 3.

When applying GCM to cluster balanced longitudinal data, both the group partition matrix in the model and the number of clusters are unknown and need to be optimally estimated together with estimating the regression coefficient parameters in GCM. Most methods in literature for this estimation assume that columns of the partition matrix are i.i.d. a priori random vectors so that the estimation becomes based on a mixture GCM. Then the EM algorithm and Bayesian sampling are mostly used to estimate the joint posterior distribution of the partition matrix and the true number of clusters. In most such cases, Markov chain Monte Carlo (MCMC) is needed to implement the involved Bayesian sampling, which can be computationally very intensive, and also difficult to interpret and assess the results, cf. Diebolt and Robert (2005); Escobar and West (1995) and a recent overview of Bayesian cluster analysis by Wade (2023). Assuming i.i.d. columns of the partition matrix may reduce the clustering efficacy because the membership of a data point most likely depends on the response and covariate values of this data point.

In this paper, we treat the columns of the partition matrix as non-random latent vectors instead, and estimate it for optimal clustering also by MCMC but do not need prior distribution specification for the partition matrix and the number of clusters. Specifically, we develop a Gibbs sampler to generate a Markov chain of candidate partition matrices where the number of clusters for the data is fixed first, from which the true partition matrix is consistently estimated based on the resultant sampling frequency distribution of the generated Markov chain. It can be shown that the partition matrix estimate, together with the estimates of the model parameters, converges to that maximizing the global log-likelihood function or equivalently minimizing the empirical Bayesian information criterion (eBIC) developed in Qian et al. (2019). Next, we propose to use the eBIC to determine the best number of clusters involved. Our proposed method is abbreviated to GCM-Gibbs-eBIC, which will be shown to be effective and efficient to cluster the balanced longitudinal data and estimate the resultant GCMs. The clustering results include optimal estimates of the true number of clusters and the true partition matrix, which are easy to interpret to practitioners.

The rest of this paper is organized as follows. In Section 2, a synthetic growth curve dataset is generated to form three true clusters and then analyzed by MBC and KML to see how well the true clusters can be recovered. The purpose of this is to provide a motivation for developing the GCM-Gibbs-eBIC method. In Section 3, GCM regression and Gibbs sampler are briefly reviewed before introducing the GCM clustering framework and the information criteria for clustering and regression. In Section 4, we develop a streamlined procedure to optimally estimate the model parameters, the partition matrix, and the number of clusters in balanced longitudinal data clustering under the established framework. The simulation study and real data applications are presented in Section 5 and Section 6, respectively. Finally, conclusions as well as directions for further research are discussed in Sections 7.

2 Motivating Example

Motivation for developing the GCM-Gibbs-eBIC comes from performing growth curve data clustering on a synthetic dataset by the current MBC and KML methods.

2.1 Generating Synthetic Data

The synthetic dataset is constructed based on the growth curve structure learned from the schizophrenia dataset that was analyzed in Gibbons and Hedeker (1994). This dataset comes from a National Institute of Mental Health (NIMH) study where the inpatient multidimensional psychiatric scale 79 (IMPS79) score (ranging from 1 to 7, with 1 for normal and 7 for most severe) was recorded for each of the 312 inpatients in weeks 0, 1, 3, and 6, respectively. A detailed analysis of the real schizophrenia data will be presented in Section 6.2, where we can see the IMPS79 trajectory for each inpatient follows a quadratic polynomial growth curve subject to normal random error. Namely, for each inpatient

$$\text {IMPS79}(\textbf{t})=(\textbf{1}, \textbf{t},\textbf{t}^2)(\beta _0,\beta _1,\beta _2)^\top +\varvec{\varepsilon },\quad \text {where}\, \textbf{t}=(0,1,3,6)^\top \,\text {and}\, \varvec{\varepsilon }\sim N_4(\textbf{0}_4, \mathbf {\Sigma }_{4\times 4}).$$

Here $N_4(\textbf{0}, \mathbf {\Sigma })$ is a 4-D normal distribution with mean $\textbf{0}$ and variance $\mathbf {\Sigma }$. Using the above growth curve structure, we generate 180 synthetic IMPS79 trajectories, formed as a $4\times 180$ matrix $\textbf{Y} \equiv \textbf{Y}_{4\times 180}$ being generated from the GCM: $\textbf{Y}_{4\times 180}=\textbf{X}_{4\times 3}\textbf{B}_{3\times 3}\textbf{Z}_{3\times 180}+\mathbf {\mathcal {E}}_{4\times 180}$, where $\mathbf {\mathcal {E}}_{4\times 180}$ has a matrix normal distribution $N_{4,180}(\textbf{0}_{4\times 180},\mathbf { \Sigma }_{4\times 4}, \textbf{I}_{180\times 180})$ and

$$\begin{aligned} \textbf{X}=\left[ \begin{array}{ccc} 1 &{} 0 &{} 0\\ 1 &{}1 &{}1 \\ 1&{}3 &{}9 \\ 1 &{}6 &{}36 \\ \end{array}\right] , \textbf{B}=\left[ \begin{array}{ccc} 5.89 &{} 5.26 &{} 5.53 \\ -0.23 &{} -1.78 &{}0.04\\ 0.04 &{} 0.21 &{}-0.09 \\ \end{array}\right] ,\, \textbf{Z}=\left[ \begin{array}{ccc} \textbf{1}_{50}^{\top } &{} 0 &{} 0 \\ 0 &{} \textbf{1}_{60}^{\top} &{} 0 \\ 0 &{} 0 &{} \textbf{1}_{70}^{\top } \\ \end{array} \right] ,\, \mathbf {\Sigma }=\left[ \begin{array}{cccc} 1.38 &{} 0.56 &{} 0.35 &{}0.25\\ 0.56 &{}2.21 &{}0.41 &{}0.25\\ 0.35 &{}0.41 &{} 0.79 &{}0.39\\ 0.25 &{}0.25 &{}0.39&{}1.3\\ \end{array}\!\right] \!. \end{aligned}$$

It can be seen that $\textbf{Y}_{4\times 180}$ consists of three column blocks or clusters, of size 50, 60, and 70 columns respectively, and the three columns of $\textbf{XB}$ are the mean values of these three clusters. Since $\textbf{X}=(\textbf{1}, \textbf{t},\textbf{t}^2)$, $\textbf{XB}$ as a quadratic vector function of $\textbf{t}$ gives the mean trajectory curves of the three clusters of $\textbf{Y}$. The 180 generated trajectories and the corresponding three cluster mean trajectories $\textbf{X}_{4\times 3}\textbf{B}_{3\times 3}$, are displayed in Fig. 1a and b, respectively.

Fig. 1

(a) 180 individual synthetic IMPS79 trajectories, and (b) the 3 cluster means

2.2 MBC and KML Clustering Results

We first use MBC to cluster $\textbf{Y}$ by assuming quadratic mean cluster trajectories based on Fig. 1 but not using the true partition information. This can be done using the R package mclust, by which the number of clusters is correctly estimated to be 3 achieving the smallest Bayesian information criterion (BIC) value of 1315.9. The confusion matrix, ARI value, and mis-clustering rate (MCR) of the MBC outcome are displayed in the left panel of Table 1, showing the result is pretty good but has room to be improved. It should be mentioned that the model complexity term in BIC for MBC often underestimates the clustering wholeness so that the number of clusters tends to be overestimated when the data are more variable, cf. Qian et al. (2016b, 2019) and references therein. This was verified when we multiplied $\mathbf {\Sigma }$ by a factor larger than 1.2. For the current synthetic data, when we fix the number of clusters at 4, MBC gives the second smallest BIC value of 1326.0, bigger than the smallest 1315.9 by less than 1%. The confusion matrix, ARI value, and MCR of the latter MBC outcome are displayed in the right panel of Table 1.

Table 1 Confusion matrices and clustering performance under MBC

Next, we use KML, introduced in Genolini and Falissard (2010) and Genolini et al. (2015), to cluster the synthetic data. The R packages kml and kml3d are employed which incorrectly estimate the number of clusters to be 2. The associated confusion matrix, ARI, and MCR are displayed in Table 2 left panel, showing the performance is poor. When fixing the number of clusters as 3, KML gives better result as shown in Table 2 right panel which is still poorer than that in Table 1 left panel.

Table 2 Confusion matrices and clustering performance under KML

The above clustering results suggest MBC-BIC tends to give better clustering results than KML. But the penalty term in BIC tends to underestimate the clustering complexity so that overclustering data is possible. This motivates us to develop GCM-Gibbs-eBIC to improve the clustering performance.

3 GCM Regression and Gibbs Sampler for Clustering

Growth curve model (GCM) is a multivariate analysis of variance (MANOVA) model, or general regression model, which is useful especially for investigating growth problems in short time series in biology, economics, epidemiology, and medical research (Lee & Geisser, 1975). Also, the GCM is one of the fundamental tools for dealing with longitudinal data, especially with serial correlation (Jones, 1993) as well as repeated measurements (Laird et al., 1987). Early works on GCM are reviewed in Rao (1972), some of which are still applicable in practice at this time. In this section, we review more recent studies on GCM. We also provide a brief review on MCMC and particularly on Gibbs sampler which plays an important role on facilitating the computing involved in GCM clustering analysis.

3.1 GCM Regression and Its Parameter Estimation

According to Pan and Fang (2002), a growth curve model (GCM) is defined as:

$$\begin{aligned} \textbf{Y}_{p\times n}=\textbf{X}_{p\times l}\textbf{B}_{l\times r}\mathbf {Z}_{r\times n}+\mathbf {\mathcal {E}}_{p\times n}, \end{aligned}$$

(1)

where $\textbf{Y}_{p\times n}\equiv \textbf{Y}$ is a $p\times n$ response data matrix; $\textbf{X}_{p\times l}\equiv \textbf{X}$ and $\textbf{Z}_{r\times n}\equiv \textbf{Z}$ are known within- and between-design matrices of ranks $l<p$ and $r<n$, respectively; $\textbf{Z}$ is also named group partition matrix because each column of $\textbf{Z}$ has one element equal 1 and the rest equal 0; the regression coefficient matrix $\textbf{B}_{l\times r}\equiv \textbf{B}$ is unknown and to be estimated. Moreover, columns of the error matrix $\mathbf {\mathcal {E}}_{p\times n}\equiv \mathbf {\mathcal {E}}$ are independent, each following a p-variate normal distribution with $\textbf{0}$ mean vector and common unknown covariance matrix $\mathbf {\Sigma }>0$. That is, we say $\mathbf {\mathcal {E}} \thicksim N_{p,n}(\textbf{0}_{p\times n},\mathbf {\Sigma }, \textbf{I}_n)$. Hence, $\textbf{Y}\thicksim N_{p,n}(\textbf{XBZ},\mathbf {\Sigma }, \textbf{I}_n)$. Namely, $\textbf{Y}_{p\times n}$ follows a matrix normal distribution with mean $\textbf{XBZ}$ and common unknown covariance matrix $\mathbf {\Sigma }>0$, and columns of $\textbf{Y}_{p\times n}$ are independent p-variate normal random vectors.

According to model Eq. 1, $\textbf{Y}$ can be regarded as the set of n independent observations of a $p\times 1$ vector response variable $\textbf{y}$ from n sample units, and $\textbf{y}\thicksim N_p ( \textbf{XBz}, \mathbf {\Sigma })$ with $\textbf{z}$ being a between-design $r\times 1$ vector. Denoting $\textbf{Y}=(\textbf{y}_1,\ldots , \textbf{y}_n)$, we may treat $\textbf{y}_i=(y_i(t_1),\ldots , y_i(t_p))^\top$ as the p realizations, for sample unit i, from, e.g., a response function

$$y_i(t)=b_{0}+b_{1}t+\cdots +b_{l-1}t^{l-1}+\varepsilon _i(t)\; \quad \text {with}\;\, t=t_1,\ldots , t_p,$$

where $(\varepsilon _i(t_1), \ldots , \varepsilon _i(t_p))^\top \!\equiv \! \varvec{\varepsilon }_i$ is deemed as the column-i of $\mathbf {\mathcal {E}}=(\varvec{\varepsilon }_1, \ldots , \varvec{\varepsilon }_n)$, and $\textbf{b}\equiv (b_0,b_1,\ldots \!,b_{l-1})^\top =\textbf{Bz}$ is certain column of $\textbf{B}$ determined by $\textbf{z}$. In this case, the j-th row of the within-design matrix $\textbf{X}$ is $\textbf{x}_j^\top =(1, t_j, \ldots , t_j^{l-1})$, the observation of the l covariates $(1,t, \ldots , t^{l-1})$ at time $t=t_j$ which does not change across all sample units. In general, $\textbf{X}$ is determined by l covariates in $y_i(t)$ of the form

$$y_i(t)=b_{0}+b_{1}x_1(t)+\cdots +b_{l-1}x_{l-1}(t)+\varepsilon _i(t)\; \quad \text {at}\, p\, \text {times of}\, t:\;\, t_1,\ldots , t_p,$$

where the covariate functions $x_1(t), \ldots \!, x_{l-1}(t)$ do not change across all n sample units. In this paper, we consider the scenario where the n sample units belong to r different clusters and each cluster has its own coefficient vector corresponding to $\textbf{b}$. The r such coefficient vectors constitute $\textbf{B}$ which is rewritten as $\textbf{B}=(\textbf{b}_1,\ldots , \textbf{b}_r)$. Then the between-design matrix $\textbf{Z}$ may be set as a partition matrix to specify the membership of each sample unit. Namely, we set $\textbf{Z}=(\textbf{z}_1, \ldots , \textbf{z}_n)$ with $\textbf{z}_i=(z_{1i},\ldots , z_{ri})^\top$, where $z_{ki}=1$ if sample unit i belongs to cluster k and $z_{ki}=0$ otherwise, with $k=1,\ldots , r$ and $i=1,\ldots , n$. Note that in longitudinal data clustering, both $\textbf{B}$ and $\textbf{Z}$ are unknown and to be estimated. When $\textbf{Z}$ is given, (Pan & Fang, 2002) investigated the estimation of $\textbf{B}$ and $\mathbf {\Sigma }$ under GCM Eq. 1, and proved that, when $\mathbf {\mathcal {E} }\thicksim N_{p,n}(\textbf{0}_{n\times p},\mathbf {\Sigma }, \textbf{I}_n)$ and $n>p+r$ with both $\textbf{X}$ and $\textbf{Z}$ being of full rank, the maximum likelihood estimators (MLEs) of $\textbf{B}$ and $\mathbf {\Sigma }$ uniquely exist and are

$$\begin{aligned} \hat{\textbf{B}}=(\textbf{X}^\top \textbf{S}^{-1} \textbf{X})^{-1} \textbf{X}^\top \textbf{S}^{-1} \textbf{Y}\textbf{Z}^\top (\textbf{Z}\textbf{Z}^\top )^{-1} \;\;\text {and}\;\; \hat{\mathbf {\Sigma }}=\frac{1}{n}(\textbf{Y}-\textbf{X}\hat{\textbf{B}}\textbf{Z})(\textbf{Y}-\textbf{X}\hat{\textbf{B}}\textbf{Z})^\top \end{aligned}$$

(2)

respectively, where $\textbf{S}=\textbf{Y}(\textbf{I}_n-\textbf{P}_{\textbf{Z}})\textbf{Y}^\top$ and $\textbf{P}_{\textbf{Z}}=\textbf{Z}^\top (\textbf{Z}\textbf{Z}^\top )^{-1}\textbf{Z}$.

3.2 Gibbs Sampler

Clustering the data satisfying GCM Eq. 1 is equivalent to estimating or specifying the partition matrix $\textbf{Z}_{r\times n}$, which is computationally infeasible even when n is moderately large. We propose to estimate $\textbf{Z}_{r\times n}$ by stochastic sampling and search together with the maximum global likelihood method in a regression-clustering setting. We find Gibbs sampler (Geman & Geman, 1984; Casella & George, 1992) is especially powerful for stochastic search in a high-dimensional point space, e.g., that spanned by $\textbf{Z}_{r\times n}$. To better understand this property which will be detailed in Section 4, we briefly describe Gibbs sampler here.

Gibbs sampler is for generating random vectors indirectly from a multivariate probability distribution where a direct generation is often very difficult if not impossible. Suppose we aim to generate a random vector $\textbf{V}=(V_1, \ldots , V_n)^\top$ from a multivariate probability distribution $F(\textbf{v})$. Suppose $F(\textbf{v})$ is very complicated and difficult to be simulated directly. But for each $k=1, \ldots , n$, the conditional distribution of $V_k$ given $\textbf{v}_{-k} =\textbf{v}_{-k}\equiv (v_1,\ldots , v_{k-1}, v_{k+1},\ldots , v_n)^\top \equiv (\textbf{v}_{1:(k-1)}^\top , \textbf{v}_{(k+1):n}^\top )^\top$, denoted as $F(v_k|\textbf{v}_{-k})$, is presumably easy to simulate. Here we define $\textbf{v}_{a:b}=\emptyset$ if $a>b$, otherwise $\textbf{v}_{a:b}=(v_a, v_{a+1}, \ldots , v_b)^\top$. Then Gibbs sampler for generating $M_1$ samples of $\textbf{V}$ is given by the following algorithm:

Algorithm 1 Gibbs sampler

$1^\circ$:

Arbitrarily generate an initial vector $\textbf{v}^{(0)}=(v_1^{(0)}, \ldots , v_n^{(0)})^\top$ from the support of $F(\textbf{v})$.

$2^\circ$:

For $m=1,\ldots , M_0, M_0+1, \ldots , M_0+M_1$ with pre-specified burn-in and post-burn-in numbers $M_0$ and $M_1$, generate $\textbf{v}^{(m)}=(v_1^{(m)}, \ldots , v_n^{(m)})^\top$ as following

$2.1^\circ$:

Generate $v_1^{(m)}$ from $F(v_1|\textbf{v}_{2:n}^{(m-1)})$.

$2.2^\circ$:

For $k=2,\ldots , n-1$, generate $v_k^{(m)}$ from $F(v_k|\textbf{v}_{1:(k-1)}^{(m)}, \textbf{v}_{(k+1):n}^{(m-1)})$.

$2.3^\circ$:

Generate $v_n^{(m)}$ from $F(v_n|\textbf{v}_{1:(n-1)}^{(m)})$.

$3^\circ$:

Deliver $\textbf{v}^{(M_0+1)}, \ldots , \textbf{v}^{(M_0+M_1)}$ as the $M_1$ samples from $F(\textbf{v})$.

The samples $\textbf{v}^{(M_0+1)}, \ldots , \textbf{v}^{(M_0+M_1)}$ generated by Gibbs sampler are in fact a Markov chain. When $F(\textbf{v})$ is multivariate discrete having a finite sample space, it is shown in Arnold (1993) that $\textbf{v}^{(m)}$ converges to $F(\textbf{v})$ in distribution as $m\rightarrow \infty$, or equivalently, the generated Markov chain has $F(\textbf{v})$ as its unique stationary distribution. Hence, when $M_0$ is sufficiently large, $\textbf{v}^{(M_0+1)}, \ldots , \textbf{v}^{(M_0+M_1)}$ can be regarded as ergodic samples from $F(\textbf{v})$.

3.3 GCM Clustering-Regression and Information Criterion

The parameter estimators $\hat{\textbf{B}}$ and $\hat{\mathbf {\Sigma }}$ given in Eq. 2 depend on the specification of the partition matrix $\textbf{Z}$, thus being incomputable when $\textbf{Z}$ is unknown. Pan et al. (2020) developed a mixture model approach to estimate $\textbf{B}$, $\mathbf {\Sigma }$ and $\textbf{Z}$ jointly, where columns of $\textbf{Z}$ are assumed to be i.i.d. random vectors each following a categorical distribution (i.e., a multinomial distribution of size 1) with unknown category probabilities and given number of categories (i.e., clusters). The optimal number of clusters is then estimated using an information criterion such as the Akaike Information Criterion (AIC) (Akaike, 1973) or BIC (Schwarz, 1978). A drawback of using an approach of mixture model with a non-informative prior distribution for $\textbf{Z}$ is that effects of the response and covariates on the category probabilities are not taken into account at the modelling stage, cf. Hennig (2000). Consequently, the regression analysis between $\textbf{Y}$ and $\textbf{X}$, and the clustering among the sample units seem to proceed separately without informing each other in the mixture model approach. In this paper, we propose to estimate $\textbf{B}$, $\mathbf {\Sigma }$, and $\textbf{Z}$ by an iterative regression and clustering method maximizing global log-likelihood or equivalently minimizing an information criterion.

Using the GCM setup in Section 3.1, when $\textbf{Z}$ and r are specified, we know the n sample units are deemed to fall into r clusters, denoted as

$$\{1, 2, \ldots , n\}=\mathcal {C}_1\cup \mathcal {C}_2\cdots \cup \mathcal {C}_r=\bigcup _{k=1}^r\mathcal {C}_k,$$

and the number of sample units in $\mathcal {C}_k$ equals $|\mathcal {C}_k|=\sum _{i=1}^nz_{ki}$, the number of 1’s in row k of $\textbf{Z}$. In this situation, the GCM model Eq. 1 is equivalent to the following r multivariate linear regression models jointly

$$\textbf{y}_i=\textbf{X}_{p\times l}\textbf{b}_k+\varvec{\varepsilon }_i,\quad \text {with}\, \varvec{\varepsilon }_i \sim N(\textbf{0},\mathbf {\Sigma }),\, \text {sample unit}\, i\in \mathcal {C}_k,\, \text {and}\, k=1,\ldots , r,$$

or equivalently

$$\textbf{Y}_{\mathcal {C}_k}=\textbf{X}_{p\times l}\textbf{b}_k\textbf{1}^\top _{|\mathcal {C}_k|}+\mathbf {\mathcal {E}}_{\mathcal {C}_k},\quad k=1,\ldots ,r$$

where $\textbf{Y}_{\mathcal {C}_k}$ is the column subset of $\textbf{Y}$ indexed by those sample units in $\mathcal {C}_k$, $\mathcal {E}_{\mathcal {C}_k}$ is similarly defined, and $\textbf{1}_{|\mathcal {C}_k|}$ is a $|\mathcal {C}_k|\times 1$ vector of 1’s. The log-likelihood function for the data $\mathbf {(Y,X, Z)}$ can be found to be

$$\begin{aligned} \ell (\textbf{Y}_{p\times n}|\textbf{Z}_{r\times n},\textbf{X},\textbf{B},\mathbf {\Sigma }) = -\frac{pn}{2}\log (2\pi )- \frac{n}{2}\log \left( |\mathbf {\Sigma }|\right) -\frac{1}{2}\text {tr}\left[ \mathbf {\Sigma }^{-1}(\textbf{Y}\!-\!\textbf{XBZ})(\textbf{Y}\!-\!\textbf{XBZ})^\top \right] \end{aligned}$$

(3)

with which the MLE $(\hat{\textbf{B}}(\textbf{Z}), \hat{\mathbf {\Sigma }}(\textbf{Z}))$ of $(\textbf{B}, \mathbf {\Sigma })$ can be computed by Eq. 2 for given $\textbf{Z}$ and r. It seems that the best clustering of the n sample units would be found by maximizing $\ell (\textbf{Y}_{p\times n}|\textbf{Z}_{r\times n},\textbf{X},\hat{\textbf{B}}(\textbf{Z}),\hat{\mathbf {\Sigma }}(\textbf{Z}))$ over all candidate values of $\textbf{Z}$ and r. However, the maximum value of $\ell (\textbf{Y}_{p\times n}|\textbf{Z}_{r\times n},\textbf{X},\hat{\textbf{B}}(\textbf{Z}),\hat{\mathbf {\Sigma }}(\textbf{Z}))$ is $+\infty$, achieved at $\textbf{Z}=\textbf{I}_n$ and $r=n$, where the GCM Eq. 1 becomes saturated and has perfect fit of the data. Therefore, one is not able to optimally partition the n sample units by the maximum likelihood method. This difficulty can be resolved by using an information criterion to determine the best partition of the sample units represented by their respective longitudinal observations.

Many information criteria are derived as estimators of the Kullback-Leibler information divergence between a fitted GCM and the true GCM characterizing the data, which can be formulated in the form of a model selection criterion (SC)

$$\begin{aligned} \text {SC}(\textbf{Z}_{r\times n}, r)=-\ell (\textbf{Y}_{p\times n}|\textbf{Z}_{r\times n},\textbf{X},\hat{\textbf{B}}(\textbf{Z}_{r\times n}),\hat{\mathbf {\Sigma }}(\textbf{Z}_{r\times n}))+C(\textbf{Z}_{r\times n},r), \end{aligned}$$

(4)

where $C(\textbf{Z},r)\equiv C(\textbf{Z}_{r\times n},r)>0$ measures the intrinsic complexity of $(\textbf{Z}, \textbf{B}, \mathbf {\Sigma })$. It is ready to see that many commonly used model selection criteria, such as AIC, BIC, HQC (Hannan & Quinn, 1979), and empirical BIC (eBIC) (Qian et al., 2019), are of the form Eq. 4 in GCM setting. Specifically, $C(\textbf{Z},r)$ in these cases equals:

$$\begin{aligned}{} & {} \text {AIC:}\qquad C(\textbf{Z},r) = lr+0.5p(p+1)\\{} & {} \text {BIC:}\quad C(\textbf{Z},r) = 0.5[lr+0.5p(p+1)]\log n\\{} & {} \text {HQC:}\quad C(\textbf{Z},r) = 0.5[lr+0.5p(p+1)]\log \log n\\{} & {} \text {eBIC:}\quad C(\textbf{Z},r) = \xi _{1}\log S(n,r)+\xi _{2}[lr+0.5p(p+1)](\log n)^{\xi _{3}} \end{aligned}$$

where $0\le \xi _1\le 1$, $\xi _2\ge 0.5$ and $\xi _3\ge 1$ are tuning parameters; and

$$S(n,r)=\frac{1}{r!}\sum _{k=1}^r (-1)^{r-k} {r\atopwithdelims ()k} k^{n}$$

is the Stirling number of the second kind which equals the number of possible ways to partition n data points into r clusters (Tomescu, 1985; Qian et al., 2016b). Note that AIC and BIC can be obtained from eBIC by setting $(\xi _1,\xi _2,\xi _3)=(0,1,0)$ and (0,0.5,1), respectively. For the purpose of finding the best partition of the set of sample units, AIC, BIC, and HQC tend to have the involved $C(\textbf{Z},r)$ being too small to penalize over-partition, while eBIC has the capacity to properly penalize the partition complexity so that clustering can be more accurately performed. The main reason is that eBIC is derived by using information from the probability distribution of the observed data given $(\textbf{Z},r)$ and the combinatorial complexity in determining the partition matrix $\textbf{Z}$, and applying the maximum global likelihood principle, cf. Qian et al. (2019). This returns S(n, r) as the dominant term in $C(\textbf{Z},r)$ of eBIC, which does not appear in $C(\textbf{Z},r)$ for other SCs. Due to asymptotic analysis nature involved in the derivation, eBIC inevitably contains the tuning parameters $(\xi _1,\xi _2, \xi _3)$ to weigh relative importance of different parts in its $C(\textbf{Z},r)$, which is the same as in many penalized likelihood alike information criteria. Consequently, one needs to utilize subject domain information and data-informed approach to properly set these tuning parameters in any real data analysis scenario, although it does not impact the asymptotic optimal properties of eBIC. For example, due to the dominant role of S(n, r) in eBIC, we should never set $\xi _1=0$. Empirical studies in Sections 5 and 6 show that setting $\xi _1=1$ gives more powerful clustering performance than setting $\xi _1=0$. Based on the simulation study in Section 5, we suggest $\xi _1=1, \xi _2=0.5$ and $\xi _3=1$ for eBIC and call it eBIC2.

From the above discussions, we proceed with GCM clustering-regression by the following iterative hierarchical procedure based on $SC(\textbf{Z},r)$ and the result in Eq. 2:

Algorithm 2 Iterative hierarchical GCM clustering and regression

$1^\circ$:

Run $r=1,2, \ldots$ until R, a pre-specified maximum number of latent clusters .

$2^\circ$:

For each given r, repeat the following until a partition matrix $\textbf{Z}_{r\times n}$ that exactly or stochastically minimizes $\text {SC}(\textbf{Z},r)$ of Eq. 4 is found.

$2.1^\circ$:

For each candidate $\textbf{Z}$ matrix, estimate $\textbf{B}$ and $\mathbf {\Sigma }$ by maximizing the log-likelihood function $\ell (\textbf{Y}_{p\times n}|\textbf{Z}_{r\times n},\textbf{X},\textbf{B},\mathbf {\Sigma })$ given by Eq. 3.

$2.2^\circ$:

Compute $\text {SC}(\textbf{Z},r)$ for the given $\textbf{Z}$.

$2.3^\circ$:

Find the estimate $\hat{\textbf{Z}}(r)$ of $\textbf{Z}$ that minimizes the sequence of computed $\text {SC}(\textbf{Z},r)$ values for the given r. Namely

$$\hat{\textbf{Z}}(r)=\underset{{\, all\, \textbf{Z}\, given\, r}}{\arg \!\min } \{SC(\textbf{Z},r)\}.$$

$3^\circ$:

Deliver the resultant list $(\hat{\textbf{Z}}(r),r)$ values and the associated lists $\ell (\textbf{Y}_{p\times n}|\hat{\textbf{Z}}(r),\textbf{X},\hat{\textbf{B}},\hat{\mathbf {\Sigma }})$ and $\text {SC}(\hat{\textbf{Z}}(r),r)$ values. The optimal number of clusters for partitioning the sample units is given by

$$\hat{r}=\underset{r=1,\ldots , R}{\arg \!\min }\ \{SC(\hat{\textbf{Z}}(r),r)\}.$$

Note the number of possible values that $\textbf{Z}$ can take when r is given is S(n, r), the Stirling number of the second kind which is of exponential order $O(r^n)$. Thus, step $2.3^\circ$ in Algorithm 2 is not scalable. A computationally feasible implementation of Algorithm 2 is detailed in the following section.

4 Implementing GCM Clustering and Regression by Gibbs Sampler and Information Criterion

Implementing steps $2.1^\circ$ and $2.2^\circ$ of Algorithm 2 for a given partition matrix $\textbf{Z}_{r\times n}$ is straightforward based on the result in Section 3.1 and Eq. 4. But as explained above it is challenging to implement step $2.3^\circ$ when the number of sample units n is not small. Hence, we will focus on step $2.3^\circ$ and step $3^\circ$ in this section.

4.1 An Equivalent Representation $\textbf{v}$ for the Partition Matrix

Recall that the partition matrix $\textbf{Z}=(z_{ki})_{r\times n}$ with $z_{ki}=1$ if sample unit i belongs to cluster $\mathcal {C}_k$, and $z_{ki}=0$ otherwise; $k=1,\ldots , r$; $i=1,\ldots ,n$. Namely, each column of $\textbf{Z}$ has one and only one element that equals 1, and the rest of the column equal 0. For example, if

$$\begin{aligned} \textbf{Z}= \left[ \begin{array}{cccccccccc} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0\\ 1 &{} 1 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 1 &{} 1 &{} 1\\ \end{array} \right] , \end{aligned}$$

(5)

it means sample units 1, 2, and 3 belong to cluster $\mathcal {C}_2$; sample units 4, 5, and 6 belong to $\mathcal {C}_1$, and sample units 7, 8, 9, and 10 belong to $\mathcal {C}_3$. The partition matrix $\textbf{Z}$ can be equivalently expressed by an $n\times 1$ latent partition vector $\textbf{v}=(v_1, \ldots , v_n)^\top$, where $v_i=k$ if sample unit i belongs to cluster $\mathcal {C}_k$ ($k=1,\ldots , r;\; i=1,\ldots , n$). For $\textbf{Z}$ given by Eq. 5, it is easy to see that $\textbf{v}=(2,2,2,1,1,1,3,3,3,3)^\top$. Now step $2.3^\circ$ of Algorithm 2 can be replaced by finding the optimal partition vector $\hat{\textbf{v}}(r)$ for given r as

$$\begin{aligned} \hat{\textbf{v}}(r)\equiv \hat{\textbf{Z}}(r)=\underset{\text {all}\,\textbf{v}\,\text {given}\,r}{\text {argmin}}\{\text {SC}(\textbf{v},r)\}. \end{aligned}$$

(6)

Also step $3^\circ$ of Algorithm 2 can be replaced by finding the optimal number of clusters as

$$\begin{aligned} \hat{r}=\underset{r=1,\ldots , R}{\text {argmin}}\, \{\text {SC}(\hat{\textbf{v}}(r),r)\}. \end{aligned}$$

(7)

4.2 A Gibbs Sampler for MCMC Simulation of v

Finding $\hat{\textbf{v}}(r)$ for given r by enumerating all candidate values of $\textbf{v}$ is not computationally scalable with n because there are $r^n$ candidate values to be evaluated in Eq. 6 for given r. On the other hand, define the following probability mass function (pmf) over $\{1, \ldots , r\}^n\equiv [1:r]^n$, the domain of $\textbf{v}$:

$$\begin{aligned} P_{\text {SC},r}(\textbf{v})\equiv P_{\text {SC},r}(v_1,\ldots ,v_n)=\frac{e^{-\text {SC}(\textbf{v},r)}}{\sum _{\textbf{v}^\prime \in [1:r]^n}e^{-\text {SC}(\textbf{v}^\prime ,r)}}, \quad \textbf{v}\in [1:r]^n. \end{aligned}$$

(8)

Then it is easy to see that

$$\begin{aligned} \hat{\textbf{v}}(r)=\underset{\textbf{v}\in [1:r]^n}{\arg \!\max }\, \{P_{\text {SC},r}(\textbf{v})\}. \end{aligned}$$

(9)

If one is able to randomly generate candidates of $\textbf{v}$ from $P_{\text {SC},r}(\textbf{v})$, then $\hat{\textbf{v}}(r)$ has the highest probability to appear in the generated candidates, and tends to appear early rather than late. This provides insight on finding $\hat{\textbf{v}}(r)$ by a stochastic search method that is computationally scalable with n. Note that the vector $\tilde{\textbf{v}}(r)$ that minimizes $\text {SC}(\textbf{v},r)$ over the generated $\textbf{v}$ candidates has the highest $P_{\text {SC},r}(\textbf{v})$ value over the generated $\textbf{v}$ candidates as well. Under certain regularity conditions, it can be shown by the law of large numbers that $\tilde{\textbf{v}}(r)$ and $P_{\text {SC},r}(\tilde{\textbf{v}}(r))$ converge to $\hat{\textbf{v}}(r)$ and $P_{\text {SC},r}(\hat{\textbf{v}}(r))$ with probability 1, respectively, when the number of randomly generated $\textbf{v}$ vectors is sufficiently large.

Since $P_{\text {SC},r}(\textbf{v})$ is a multivariate discrete pmf having an intractable denominator, it is natural to use Gibbs sampler to generate random samples from $P_{\text {SC},r}(\textbf{v})$. By Algorithm 1 in Section 3.2 this involves generating random numbers from each conditional pmf $P_{\text {SC},r}(v_i|\textbf{v}_{-i})$, $i=1,\ldots ,n$, which is

$$\begin{aligned} P_{\text {SC},r}(v_i|\textbf{v}_{-i})&=\frac{P_{\text {SC},r}(\textbf{v}_{1:(i-1)}^\top ,v_i, \textbf{v}_{(i+1):n}^\top )}{\sum _{k=1}^{r} P_{\text {SC},r}(\textbf{v}_{1:(i-1)}^\top ,k,\textbf{v}_{(i+1):n}^\top )}\nonumber \\&=\frac{e^{-\text {SC}(\textbf{v},r)}}{\sum _{k=1}^r e^{-\text {SC}\left( (\textbf{v}_{1:(i-1)}^\top ,k,\textbf{v}_{(i+1):n}^\top )^\top ,r\right) }}, \,\; v_i\!=\!1,\ldots ,r. \end{aligned}$$

(10)

It is easy to see that each $P_{\text {SC},r}(v_i|\textbf{v}_{-i})$ is an r-category size-1 multinomial pmf, and does not involve computing the denominator of $P_{\text {SC},r}(\textbf{v})$ which is of combinatorial complexity. Therefore, instead of using all possible $\textbf{Z}$ matrices or $\textbf{v}$ vectors as the partition candidates for implementing steps $2.1^\circ$ to $2.3^\circ$ of Algorithm 2, we generate a sample of $M_1$ partition candidates from $P_{\text {SC},r}(\textbf{v})$ by Gibbs sampler as following:

Algorithm 3 Gibbs sampling partition candidates for given r

$1^\circ$:

Arbitrarily generate an initial candidate of the partition vector: $\textbf{v}^{(0)}=(v_1^{(0)},\ldots , v_n^{(0)})^\top$ from $[1:r]^n$. Compute $\text {SC}(\textbf{v}^{(0)},r)$.

$2^\circ$:

For $m=1,\ldots , M_0, M_0+1,\ldots , M_0+M_1$ with pre-specified burn-in and post-burn-in numbers $M_0$ and $M_1$, generate $\textbf{v}^{(m)}=(v_1^{(m)},\ldots , v_n^{(m)})^\top$ as follows:

$2.1^\circ$:

Generate $v_1^{(m)}$ from conditional pmf $P_{\text {SC},r}(v_1|\textbf{v}_{2:n}^{(m-1)})$. Also compute

$$\text {SC}\left( \left( v_1^{(m)},\textbf{v}_{2:n}^{(m-1)\top }\right) ^\top ,r\right) .$$

$2.2^\circ$:

For $i=2,\ldots , n-1$, generate $v_i^{(m)}$ from $P_{\text {SC},r}\left( v_i| (\textbf{v}_{1:(i-1)}^{(m)\top },\textbf{v}_{(i+1):n}^{(m-1)\top })^\top \right)$. Also compute

$$\text {SC}\left( \left( \textbf{v}_{1:i}^{(m)\top },\textbf{v}_{(i+1):n}^{(m-1)\top }\right) ^\top ,r\right) .$$

$2.3^\circ$:

Generate $v_n^{(m)}$ from $P_{\text {SC},r}\left( v_n|\textbf{v}_{1:(n-1)}^{(m)}\right)$. Also compute $\text {SC}\left( (v_1^{(m)},\ldots , v_n^{(m)})^\top ,r\right) =\text {SC}(\textbf{v}^{(m)},r)$.

$3^\circ$:

Deliver $\textbf{v}^{(M_0+1)}, \ldots , \textbf{v}^{(M_0+M_1)}$ as the $M_1$ random samples from $P_{\text {SC},r}(\textbf{v})$. Return the list of computed values of $\text {SC}(\textbf{v},r)$ as well.

Once $\textbf{v}^{(M_0+1)}, \ldots , \textbf{v}^{(M_0+M_1)}$ have been generated, it is easy to find an optimal partition vector as

$$\begin{aligned} \tilde{\textbf{v}}(r)=\underset{M_0+1\le m\le M_0+M_1}{\arg \!\min }\ \{\text {SC}(\textbf{v}^{(m)},r)\} =\underset{M_0+1\le m\le M_0+M_1}{\arg \!\max }\ \{P_{\text {SC},r}(\textbf{v}^{(m)})\} \end{aligned}$$

(11)

and use $\tilde{\textbf{v}}(r)$ to approximate $\hat{\textbf{v}}(r)$. By the limit theorem on ergodic Markov chains, it can be shown that $\lim _{M_1\rightarrow \infty } \tilde{\textbf{v}}(r)=\hat{\textbf{v}}(r)$ almost surely under regularity conditions. Accordingly, $\hat{\textbf{Z}}(r)$ in Algorithm 2 can be approximated to any desired accuracy by $\tilde{\textbf{Z}}(r)$ corresponding to $\tilde{\textbf{v}}(r)$ if $M_1$ is set to be sufficiently large.

It can be seen from Algorithm 3 that the computing complexity for $\tilde{\textbf{Z}}(r)$ is of order $O((M_0+M_1)n^2)$, in contrast to the exponential $O(r^n)$ complexity for computing $\hat{\textbf{Z}}(r)$. However, $O((M_0+M_1)n^2)$ can still be forbiddingly large if n or $M_0+M_1$ is really large. This prompts us to approximate $\hat{\textbf{Z}}(r)$ by the following alternative method based on the results from Algorithm 3:

Let $\textbf{V}$ denote an $n\times M_1$ matrix collecting the generated samples of $\textbf{v}$, i.e.,

$$\begin{aligned} \textbf{V}=\left( \textbf{v}^{(M_0+1)}, \ldots , \textbf{v}^{(M_0+M_1)}\right) = \left[ \begin{array}{cccc} v_1^{(M_0+1)} &{} v_1^{(M_0+2)} &{} \cdots &{} v_1^{(M_0+M_1)} \\ v_2^{(M_0+1)} &{} v_2^{(M_0+2)} &{} \cdots &{} v_2^{(M_0+M_1)} \\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ v_n^{(M_0+1)} &{} v_n^{(M_0+2)} &{} \cdots &{} v_n^{(M_0+M_1)}\\ \end{array} \right] . \end{aligned}$$

(12)

Denote $f_i(k)=M_1^{-1}\sum _{m=M_0+1}^{M_0+M_1}I(v_i^{(m)}=k)$ for $k=1,\ldots ,r$ and $i=1,\ldots ,n$ where $I(\cdot )$ is an indicator function. Hence $f_i(k)$ is the proportion of $v_i^{(m)}$’s equal to k, giving a measure of the likelihood of assigning sample unit i to cluster $\mathcal {C}_k$. Namely, $\{f_i(1),\ldots , f_i(r)\}$ is an empirical pmf of the ith row of $\textbf{V}$ in Eq. 12. In other words, latent membership of unit i is estimated by the mode of this empirical pmf, denoted as $\check{k}(i)$. That is, for $i=1,\ldots , n$,

$$\begin{aligned} \check{k}(i)=\underset{k=1,\ldots ,r}{\arg \!\max }\, \{f_i(k)\}\;\; \Longleftrightarrow \;\; f_i(\check{k}(i))=\max \{f_i(1),\ldots ,f_i(r)\}. \end{aligned}$$

(13)

Then by the majority rule, we shall cluster sample unit i to cluster $\mathcal {C}_{\check{k}(i)}$. Denote $\check{\textbf{v}}(r)=(\check{k}(1),\ldots ,\check{k}(n))^\top$ and find its equivalent representation $\check{\textbf{Z}}(r)$, which describes the aforementioned alternative method for approximating $\hat{\textbf{Z}}(r)$. Note that in most MCMC cases $M_0$, referenced as the burn-in period, should be tuned so that the underlying Markov chain achieves equilibrium from $M_0$ on. But in our case of estimating the partition matrix $\textbf{Z}(r)$, determining an approximate value for $M_0$ is not critical, because the optimizer $\tilde{\textbf{Z}}(r)$ cannot get worse when being determined on a larger candidate space that includes the first $M_0$ burn-in generated $\textbf{v}$ vectors, cf. Qian (1999); Qian and Zhao (2007); Qian et al. (2016a, 2019) for the detailed reasoning. Therefore, we set $M_0\le 10$ here to only ensure numerical stability of computations. Simulation study in Section 5 confirms that setting $M_0\le 10$ is sufficient.

On the other hand, we tune the value of $M_1$ according to the standard errors of $f_i(k)$’s. Note that a conservative upper bound for the standard error of $f_i(k)$ is $\text {s.e.}(f_i(k))=\sqrt{M_1^{-1}f_i(k)(1-f_i(k))}\le (4M_1)^{-1/2}.$ If we want $\text {s.e.}(f_i(k))\le \delta$ for a desired accuracy $\delta$, then $M_1\ge (4\delta ^2)^{-1}$ is needed. For example, $M_1\ge 100$ is needed if $\delta =0.05$. Since our aim is not to estimate the true proportion value associated with $f_i(k)$ but to use $f_i(k)$ to cluster sample unit i, there is no need to set a very stringent value for $\delta$. Rather, a $\delta$ value being able to give a clear-cut clustering of the n sample units would be sufficient for achieving our aim. This implies that whether the generated Markov chain of $\textbf{v}$ has achieved equilibrium or not is not critical for selecting a good value of $M_1$ that ensures clear-cut clustering.

4.3 Determine the Optimal Number of Clusters

To close the whole data clustering process, we still need to determine the optimal number of clusters $\hat{r}$. This can be readily done based on the model selection criterion $SC(\textbf{v},r)$ introduced in Section 3.3. Specifically, by Eq. 7, $\hat{r}=\underset{r=1,\ldots , R}{\arg \!\min }\, \{\text {SC}(\hat{\textbf{v}}(r),r)\}$. Since $\hat{\textbf{v}}(r)$ can be best estimated by $\tilde{\textbf{v}}(r)$ or $\check{\textbf{v}}(r)$ as shown in Section 4.2, we will estimate $\hat{r}$ by

$$\begin{aligned} \tilde{r}=\underset{r=1,\ldots ,R}{\arg \!\min }\,\{\text {SC}(\tilde{\textbf{v}}(r),r)\}\quad \text {or} \quad \check{r}=\underset{r=1,\ldots ,R}{\arg \!\min }\,\{\text {SC}(\check{\textbf{v}}(r),r)\}, \end{aligned}$$

(14)

which differ little between them in all cases studied in this paper. Once $\tilde{r}$ or $\check{r}$ is obtained, we will use either $\tilde{\textbf{v}}(\tilde{r})$ (i.e., $\tilde{\textbf{Z}}(\tilde{r})$) or $\check{\textbf{v}}(\check{r})$ (i.e., $\check{\textbf{Z}}(\check{r})$) to cluster all the n sample units. Again, $\tilde{\textbf{Z}}(\tilde{r})$ and $\check{\textbf{Z}}(\check{r})$ differ little from each other in all cases studied in this paper.

As discussed in Section 3.3, the second kind Stirling number S(n, r) appearing in eBIC but not other SCs plays the dominant role in representing the partition complexity properly. We expect eBIC would give the overall best clustering result. This will be confirmed in Sections 5 and 6.

Finally, GCM Eq. 1 need be re-fitted to the data based on $\tilde{\textbf{Z}}(\tilde{r})$ or $\check{\textbf{Z}}(\check{r})$, where the MLE $\hat{\textbf{B}}(\tilde{\textbf{Z}}(\tilde{r}))$ (or $\hat{\textbf{B}}(\check{\textbf{Z}}(\check{r}))$) and $\hat{\mathbf {\Sigma }}(\tilde{\textbf{Z}}(\tilde{r}))$ (or $\hat{\mathbf {\Sigma }}(\check{\textbf{Z}}(\check{r}))$) of $\textbf{B}$ and $\mathbf {\Sigma }$ can be computed, respectively.

5 Simulation Study

5.1 Re-analyze the Motivating Example by GCM-Gibbs-eBIC

Now we apply the developed GCM-Gibbs-eBIC clustering method to re-analyze the synthetic IMPS79 data generated for the motivating example. Same as in Section 2, we assume the synthetic data follows the GCM of Eq. 1 with unknown partition matrix $\textbf{Z}$, unknown cluster number r, and unknown matrix parameters $\textbf{B}$ and $\mathbf {\Sigma }$. We also assume the within-design matrix $\textbf{X}\equiv \textbf{X}_{4\times 3}$ is the one specified in Section 2.1, implying the mean response vector $\textbf{X}_{4\times 3}\textbf{b}_k$ of cluster k follows a quadratic polynomial curve with $l=3$ coefficients in $\textbf{b}_k$ to be estimated. To see how different information selection criterion (SC) affects the clustering performance, we choose four different settings for $(\xi _1, \xi _2,\xi _3)$: (0,1,0) giving AIC; (0,0.5,1) giving BIC; (0,0.5,2) denoted eBIC1; and (1,0.5,1) denoted eBIC2. The clustering process proceeds to generate $M_1=200$ partition vectors of $\textbf{v}$ by Gibbs sampler via Algorithms 2 and 3, so that the Monte Carlo error of $f_i(k)$ defined after Eq. 12 is at most 3.54%. The clustering results are summarized in Table 3 first, from which we see eBIC1 and eBIC2 correctly estimate the true number of clusters to be 3, while AIC and BIC all overestimate the true number of clusters. Also eBIC1 for $r=4$ is 1327.625, slightly bigger than 1327.270—eBIC1 for $r=3$. The optimal clustering by using GCM-Gibbs-eBIC2 has the highest ARI of 0.8514, while the associated confusion matrix is displayed in Table 4 with a mis-clustering rate (MCR) of 5%. These results are significantly better than those based on MBC-BIC and KML that are summarized in Tables 1 and 2.

Table 3 SC values in using GCM-Gibbs-eBIC for clustering the synthetic IMPS79 data

Table 4 Confusion matrix for clustering the synthetic IMPS79 data by GCM-Gibbs-eBIC2

Based on the final clustering result using GCM-Gibbs-eBIC2, the parameters $\textbf{B}$ and $\mathbf {\Sigma }$ have the MLEs as follows:

$$\begin{aligned}{} & {} \hat{\textbf{B}}= \left[ \begin{array}{ccc} 5.9379 &{} 5.3666 &{} 5.6024\\ -0.1757 &{}-1.9075 &{}-0.0086\\ 0.0333 &{} 0.2265 &{}-0.0847 \\ \end{array} \right] ,\qquad \hat{\mathbf {\Sigma }}= \left[ \begin{array}{cccc} 1.3824 &{} 0.4275 &{} 0.3441 &{} 0.2753\\ 0.4275 &{} 2.4074 &{}0.2802 &{}0.1685\\ 0.3441 &{} 0.2802 &{} 0.6958 &{} 0.2874\\ 0.2753&{}0.1685 &{}0.2874 &{} 1.0558\\ \end{array} \right] . \end{aligned}$$

Differences between $(\hat{\textbf{B}}, \hat{\mathbf {\Sigma }})$ and the true $(\mathbf {(B}, \mathbf {\Sigma })$ value can be assessed by measures:

$$\begin{aligned} \texttt {edu.dis}(\hat{\textbf{B}})= & {} \sqrt{(\text {vec}(\textbf{B})-\text {vec}(\hat{\textbf{B}}))^\top (\text {vec}(\textbf{B})-\text {vec}(\hat{\textbf{B}}))};\\ \texttt {edu.dis}(\hat{\mathbf {\Sigma }})= & {} \sqrt{(\text {vec}(\mathbf {\Sigma })-\text {vec}(\hat{\mathbf {\Sigma }}))^\top (\text {vec}(\mathbf {\Sigma })-\text {vec}(\hat{\mathbf {\Sigma }}))};\\ F\texttt {-norm}({\hat{\textbf{B}}})= & {} \sqrt{\frac{\text {tr}((\textbf{B}-\hat{\textbf{B}})(\textbf{B}-\hat{\textbf{B}})^\top )}{\text {tr}(\textbf{BB}^\top )}};\\ F\texttt {-norm}({\hat{\mathbf {\Sigma }}})= & {} \sqrt{\frac{\text {tr}((\mathbf {\Sigma }-\hat{\mathbf {\Sigma }})(\mathbf {\Sigma }-\hat{\mathbf {\Sigma }})^\top )}{ \text {tr}(\mathbf {\Sigma \Sigma }^\top )}}, \end{aligned}$$

giving edu.dis($\hat{\textbf{B}}$)=0.202, F-norm($\hat{\textbf{B}}$)=0.021, edu.dis($\hat{\mathbf {\Sigma }}$)=0.459, and F-norm($\hat{\mathbf {\Sigma }}$)=0.139.

Finally, we find the fitted mean cluster IMPS79 trajectories obtained from GCM-Gibbs-eBIC2 are very close to the true mean cluster trajectories for the synthetic IMPS79 data, cf. Fig. 2. Note that the fitted mean trajectories are obtained from fitting the assumed quadratic polynomial regression curves. Other regression functions, e.g., cubic splines and kernel regression functions, can also be used. This is beyond the scope of this paper.

Fig. 2

True mean cluster trajectory curves (red) vs. the corresponding fitted ones (blue) based on GCM-Gibbs-eBIC for the synthetic IMPS79 data

5.2 Simulation Study of Experiment Data

In this section, we assess the finite sample performance of Algorithms 2 and 3 for GCM longitudinal data clustering by Gibbs sampler and information criterion SC (focusing on eBIC to simplify the presentation, i.e., on GCM-Gibbs-eBIC2 with $(\xi _1,\xi _2,\xi _3)=(1,0.5,1)$). Also the model-based clustering methods MBC (McNicholas, 2016) and KML (Genolini & Falissard, 2010) are used and the results are compared with that from GCM-Gibbs-eBIC2.

Simulated datasets are used in the assessment. While many ways exist for generating datasets for simulation study, the way we use in this paper is determined by four factors: sample size (ss) of each dataset ($n=60, 150$, or 600); number of clusters in each dataset ($r=2$ or 3); partition pattern (pp) in the form of ratios of cluster sample sizes (css); and mean response growth curve (mrgc) of form $E[y_i(t)]=b_{0k}+b_{1k}t+b_{2k}t^2+b_{3k}t^3$ for any unit i in cluster k (with $t=1,2,3,4$ and $k=1,\ldots , r$ and given $\textbf{b}_k\equiv (b_{0k}, b_{1k}, b_{2k}, b_{3k})^\top$) for each dataset. Note $E[y_i(t)]$ is a polynomial function of t determined by the value of $\textbf{b}_k$’s. In the simulation study, we use three mrgc types (qc for quadratic and cubic curves in $r=2$ clusters; lqc for linear, quadratic, and cubic curves in $r=3$ clusters; and ccc for cubic curves in all $r=3$ clusters) specified by $\textbf{B}=(\textbf{b}_1,\ldots ,\textbf{b}_r)$:

$$\begin{aligned} \textbf{B}_{{\texttt {qc}}}\!=\!\!\left[ \! \begin{array}{cc} 0 &{} 30\\ 22 &{} -28\\ -2.2 &{} 8.8\\ 0 &{} -0.6\\ \end{array}\!\!\right] \!,\qquad \textbf{B}_{{\texttt {lqc}}}\!=\!\!\left[ \!\! \begin{array}{ccc} 3.89 &{} 0 &{} 10 \\ 7.42 &{} 16.13 &{} -8 \\ 0 &{} -1.34 &{} 6 \\ 0 &{} 0 &{} -0.6\\ \end{array}\!\right] \!, \qquad \textbf{B}_{{\texttt {ccc}}}\!=\!\!\left[ \! \begin{array}{ccc} 15 &{} 5 &{} 5\\ -7 &{}-2 &{}-8 \\ 5.3 &{} 4.2 &{} 6 \\ -0.5 &{}-0.4 &{}-0.6 \\ \end{array}\!\right] . \end{aligned}$$

The mean growth curves determined by $\textbf{B}_{{\texttt {qc}}}, \textbf{B}_{{\texttt {lqc}}}$ and $\textbf{B}_{{\texttt {ccc}}}$ are shown in Fig. 3.

Fig. 3

Mean response curves determined by $\textbf{B}_{{\texttt {qc}}}$ (a), $\textbf{B}_{{\texttt {lqc}}}$ (b), and $\textbf{B}_{{\texttt {ccc}}}$ (c)

Table 5 Description of the 18 simulation studies. Each study has a name of format $S_{{\texttt {ss}, \texttt {mrgc}, \texttt {pp}}}$, where ss = Small for $n=60$, or Medium for $n=150$, or Large for $n=600$; mrgc type = qc, or lqc, or ccc; and pp has css type 1:1, or 2:3, or 1:1:1, or 4:5:6

Regarding the partition pattern (pp), css ratios 4:5:6, for example, specify the data are partitioned into three segments (clusters) with the first, second, and third segments containing 4/15, 5/15, and 6/15 proportion of the data points, respectively. The partition matrix Z can be accordingly specified once the sample size (ss) n and the css ratios are given.

The aforementioned four factors result in 18 specifications displayed in Table 5. For each specification, we randomly generate 100 datasets according to GCM Eq. 1, where $\textbf{X}$ is a $4\times 4$ matrix (i.e., $p=l=4$) with its row t equal to $(1,t, t^2, t^3)$ (where $t=1,2,3,4$) and $\mathbf {\Sigma }$ is set to equal

$$\begin{aligned} \mathbf {\Sigma }=\left[ \begin{array}{cccc} 8 &{} 3.2 &{} 4.8 &{}3.2\\ 3.2 &{}4.8 &{}3.2 &{}4.8\\ 4.8 &{} 3.2 &{} 8 &{}4.8\\ 3.2 &{}4.8 &{}4.8 &{}6.4\\ \end{array} \right] \end{aligned}$$

for all the 18 specifications.

Table 6 Mean performance of parameter estimates and clustering for experiments $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$ (row 1), $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ (row 2), and $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ (row 3) by the GCM-Gibbs-eBIC2 method

Fig. 4

Grouped box plots of the mis.rate (i.e., MCR), $\texttt {edu.dis}(\hat{\textbf{B}})$ and $\texttt {edu.dis}(\hat{\mathbf {\Sigma }})$ values from the clustering and regression results for the 100 iterated datasets by using GCM-Gibbs-eBIC2 for experiment $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$, and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$, respectively

For each of the 18 simulation studies, we pretend that its true specifications were not given, and proceed to perform data clustering and parameter estimation by Algorithms 2 and 3 for each of the 100 simulated datasets, where we set $R=6$, $M_0=50$, and $M_1=200$. Note that the number of clusters selected by GCM-Gibbs-eBIC2 from each simulated dataset always equals the underlying true cluster number in our simulation studies. Thus, the relevant results will not be reported here.

In the rest of this section, we use our proposed GCM-Gibbs-eBIC2 method and the MBC and KML clustering methods to cluster the $18\times 100=1800$ simulated datasets from the 18 simulation studies described in Table 5 and compare the results. To keep a reasonable length of the paper, we present just the summarized results of three simulation studies: $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$ in this section. The results for simulation studies $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {1:1:1}}}$ are presented in Appendix. Results for the other 12 simulation studies are exceptionally good, and thus will not be presented here. The R code for one of the 18 simulation studies is provided in Supplementary Material.

The clustering results are summarized in tables and figures as follows:

• 1. Table 6 gives the mean performance of parameter estimates $(\hat{\textbf{B}}, \hat{\mathbf {\Sigma }})$ and clustering, regarding mean edu.dis, mean F-norm, and mean mis.rate (i.e., MCR), in experiments $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$, each with 100 replicated datasets, by the GCM-Gibbs-eBIC2 method.

• 2. Figure 4 gives three grouped box-plots of the mis.rate (i.e. MCR), $\texttt {edu.dis}(\hat{\textbf{B}})$ and $\texttt {edu.dis}(\hat{\mathbf {\Sigma }})$ values that are computed from the GCM-Gibbs-eBIC2 clustering and regression results for the 100 iterated datasets in experiment $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$, respectively.

• 3. Table 7 displays the respective clustering mean MCR performance and its standard error by GCM-Gibbs-eBIC2 (abbrevated to Gibbs), MBC and KML for experiments $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$, each with 100 replicated datasets.

• 4. Figure 5 provides 3 plots of fitted response mean growth curves (determined by the average $\hat{\textbf{B}}$ value computed from the 100 iterated datasets for each experiment) versus their underpinning true mean curves for experiments $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$.

Table 7 Clustering performance, in terms of mMCR and the associated standard error (SD), obtained by using GCM-Gibbs-eBIC2, MBC and KML for experiments $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$, and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$, each involving the 100 iterated datasets

Fig. 5

Plots of the fitted response mean growth curves (dotted) by the GCM-Gibbs-eBIC2 method compared to their underpinning true mean curves (solid). The three clusters in each experiment are labelled by squares, triangles, and bullets, respectively

Table 6 shows that the GCM-Gibbs-eBIC2 method works well and particularly the mean mis.rate (i.e., mMCR) is low in all cases.

Figure 4 gives grouped box plots of mis.rate (i.e., MCR), $\texttt {edu.dis}(\hat{\textbf{B}})$ and $\texttt {edu.dis}(\hat{\mathbf {\Sigma }})$ obtained from the clustering and regression results for the 100 iterated datasets by using GCM-Gibbs-eBIC2 for experiment $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$, respectively. It conforms to what is seen in Table 6 but provides extra information on the variability of the results.

The average estimates of parameters $\textbf{B}$ and $\mathbf {\Sigma }$ by GCM-Gibbs-eBIC2 from the 100 replicated datasets for experiment $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$ are

$$\begin{aligned}{} & {} \bar{\hat{\textbf{B}}}_{{\texttt {ccc}}}= \left( \begin{array}{ccc} 14.329 &{} 5.375 &{} 4.916\\ -6.639 &{}-2.621 &{}-7.701\\ 5.168 &{} 4.408 &{}5.842 \\ -0.483 &{}-0.423 &{}-0.577\\ \end{array} \right) ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \bar{\hat{\mathbf {\Sigma }}}_{{\texttt {ccc}}}= \left( \begin{array}{cccc} 8.069 &{} 3.412 &{} 5.005 &{} 3.450\\ 3.412 &{} 4.789 &{}3.416 &{}4.891\\ 5.005 &{} 3.416 &{} 7.821 &{} 4.944\\ 3.450 &{}4.891 &{}4.944 &{} 6.463\\ \end{array} \right) . \end{aligned}$$

The average estimators of parameters $\textbf{B}$ and $\mathbf {\Sigma }$ by GCM-Gibbs-eBIC2 from the 100 replicated datasets for experiment $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ are

$$\begin{aligned}{} & {} \bar{\hat{\textbf{B}}}_{{\texttt {ccc}}}= \left( \begin{array}{ccc} 14.645 &{} 4.613 &{} 4.956\\ -6.529 &{}-1.908 &{}-8.104\\ 5.091 &{} 4.197 &{}6.034 \\ -0.472 &{}-0.402 &{}-0.605\\ \end{array} \right) ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \bar{\hat{\mathbf {\Sigma }}}_{{\texttt {ccc}}}= \left( \begin{array}{cccc} 7.264 &{} 2.652 &{} 4.197 &{} 2.678\\ 2.652 &{} 4.215 &{}2.611 &{}4.168\\ 4.197 &{} 2.611 &{} 7.169 &{} 4.099\\ 2.678 &{}4.168 &{}4.099 &{} 5.608\\ \end{array} \right) . \end{aligned}$$

The average estimators of parameters $\textbf{B}$ and $\mathbf {\Sigma }$ by GCM-Gibbs-eBIC2 from the 100 replicated datasets for experiment $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$ are

$$\begin{aligned}{} & {} \bar{\hat{\textbf{B}}}_{{\texttt {ccc}}}= \left( \begin{array}{ccc} 14.939 &{} 4.429 &{} 4.908\\ -6.944 &{}-1.498 &{}-8.022\\ 5.283 &{} 4.024 &{}6.001 \\ -0.498 &{}-0.379 &{}-0.510\\ \end{array} \right) ,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \bar{\hat{\mathbf {\Sigma }}}_{{\texttt {ccc}}}= \left( \begin{array}{cccc} 7.293 &{} 2.604 &{} 4.267 &{}2.702 \\ 2.604 &{}4.184 &{}2.580 &{}4.193\\ 4.267 &{} 2.580 &{}7.352 &{}4.131 \\ 2.702 &{}4.193 &{}4.131 &{}5.701\\ \end{array} \right) . \end{aligned}$$

Table 7 summarizes the clustering results, in terms of mMCR and the associated standard error (SD), obtained by using GCM-Gibbs-eBIC2, MBC, and KML for experiments $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$, and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$, each involving the 100 iterated datasets.

Figure 5 displays the fitted response mean growth curves (determined by the average $\hat{\textbf{B}}$ value computed from using GCM-Gibbs-eBIC2 to the 100 iterated datasets for each experiment) in comparison with their underpinning true mean curves for the three experiments $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$. From Fig. 5, we see the fitted curves are sufficiently close to the ground truth in experiments $S_{{\texttt {S},\texttt {ccc},\texttt {4:5:6}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {4:5:6}}}$, and $S_{{\texttt {L},\texttt {ccc},\texttt {4:5:6}}}$.

In summary, the tables and figures presented in this section show that the proposed GCM-Gibbs-eBIC2 is capable of performing regression and clustering for growth curve longitudinal data with excellent results. In addition, the proposed method is efficient in parameter estimation and clustering, and computationally scalable with sample size n.

6 Clustering for Two Real Datasets

In this section, we use two real examples to illustrate the application of the proposed GCM-Gibbs-eBIC method for longitudinal data regression and clustering. The first example concerns the tooth data, which has been analyzed in Potthoff and Roy (1964); Lee and Geisser (1975); Rao (1987); Lee (1988), etc. The second example considers the schizophrenia data which were obtained from a collaborative study conducted by the National Institute of Mental Health (NIMH) on the treatment and change in severity of schizophrenia. The data were analyzed in Gibbons and Hedeker (1994).

6.1 Cluster the Tooth Data

In the first example, tooth measurements (mm) are available from 11 girls and 16 boys at the ages of 8, 10, 12, and 14, as shown in Fig. 6. The purpose is to investigate whether gender can effectively cluster the tooth measurements and whether all the tooth measurements can be better partitioned into a number of clusters.

Fig. 6

Left: Observed tooth measurement profiles for each of the 27 children. Right: Mean tooth measurements for respective boy and girl groups

Fig. 7

Performance of clustering tooth measurements under MBC, KML, and KML(2)

Since observations of each individual were collected every 2 years at the same time interval, it is natural to use the GCM Eq. 1 to model the data. Rao (1987) set the design matrices $\textbf{X}$ and $\textbf{Z}$ as the following:

$$\begin{aligned}{} & {} \textbf{X}= \left[ \begin{array}{cc} 1 &{} -3 \\ 1 &{} -1 \\ 1 &{} 1 \\ 1 &{} 3 \end{array} \right] ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \textbf{Z}= \left[ \begin{array}{cc} \textbf{1}_{11}^\top &{} 0 \\ 0 &{} \textbf{1}_{16}^\top \end{array} \right] . \end{aligned}$$

From Fig. 6 we see the above partition matrix $\textbf{Z}$, determined according to the boy and girl groups, does not divide the tooth measurements into two clusters very well. This suggests that better clustering result may be obtained by finding a different partition matrix and applying it to the tooth measurements.

First, we use MBC-BIC and KML methods to perform clustering on the tooth data, and the results are displayed in Fig. 7a, showing that cluster 2 contains only five individual profiles which do not seem to separate from the other cluster well. By default setting, KML partitions the children’s profiles into three clusters, more likely an overclustering (see Fig. 7b). KML can also be performed by forcing the number of underlying clusters to 2, which gives a bit better clustering result (see Fig. 7c).

Now we use the proposed GCM-Gibbs-eBIC method to cluster the data. We set $M_0=50$, $M_1=200$, and $r\le 4$ in Gibbs sampler, and use four variants of eBIC to select the best number of clusters: BIC with $(\xi _1, \xi _2, \xi _3)=(0,0.5,1)$, eBIC1 with $(\xi _1, \xi _2, \xi _3)=(0,0.5,2)$, eBIC2 with $(\xi _1, \xi _2, \xi _3)=(1,0.5,1)$, and eBIC3 with $(\xi _1, \xi _2, \xi _3)=(0,1,1)$. Results of selecting the number of clusters by these four eBIC variants together with GCM-Gibbs are displayed in Table 8 and Fig. 8, from which we see eBIC2 selects $\check{r}=2$ as the optimal number of clusters and the other three select $\check{r}=4$ as the optimal number of clusters.

Table 8 Results of clustering the tooth data by GCM-Gibbs and four variants of eBIC

Fig. 8

Left: Fitted profiles of the 27 children’s tooth measurements under GCM-Gibbs-eBIC2. Right: The corresponding mean profile curves for the 2 clusters

The optimal partition vector $\check{\textbf{v}}(2)$ found by GCM-Gibbs-eBIC2 is

$$\check{\textbf{v}}(2)=(1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 2, 1, 2, 1, 1, 1, 2, 1, 1, 2, 2, 2, 1),$$

which mismatches the gender composition by 44.4%; see Table 9. This high mismatch rate together with the strong clustering performance displayed in Fig. 8 suggests that gender is not a right classifier for classifying the tooth measurements studied in this example. On the other hand, the partition matrix obtained from using GCM-Gibbs-eBIC2 is shown to perform best in dividing the 27 children tooth measurements into two clusters.

Finally, estimates of $(\textbf{B},\mathbf {\Sigma })$ under the GCM-Gibbs-eBIC2 clustering are found to be

$$\begin{aligned}{} & {} \hat{\textbf{B}}= \left( \begin{array}{cc} 22.3614 &{} 26.2467 \\ 0.5802 &{} 0.8174 \end{array} \right) ,\qquad \hat{\mathbf {\Sigma }}= \left( \begin{array}{cccc} 5.2903 &{} 1.5414 &{} 3.3254 &{} 2.5888\\ 1.5414 &{} 1.5511 &{} 0.8443 &{} 1.3648\\ 3.3254 &{} 0.8443 &{} 4.9164 &{} 3.1669\\ 2.5888 &{}1.3648 &{}3.1669 &{} 4.5249 \end{array} \right) . \end{aligned}$$

6.2 Cluster the Schizophrenia Data

The real schizophrenia dataset contains IMPS79 scores for 312 schizophrenia inpatients each at weeks 0, 1, 3, and 6, respectively. The observed IMPS79 trajectories for the 312 inpatients are given in Fig. 9, showing they are typical growth curve longitudinal data and cannot be well clustered according to whether the inpatients take drug or placebo treatment. Thus, our objective here is to cluster these trajectories by GCM-Gibbs-eBIC, MBC-BIC, and KML, and compare the results.

Table 9 Confusion matrix between $\check{\textbf{v}}(2)$ and the partition by gender

Fig. 9

Observed profiles of IMPS79 scores for all 312 inpatients (those impatient taking drug treatment are colored black, and those for taking placebo are colored blue)

By using MBC-BIC, the schizophrenia data are partitioned into two clusters shown in Fig. 10, from which we see the two clusters are imbalanced and do not separate themselves well. By using KML, the schizophrenia data are partitioned into two clusters shown in Fig. 11, from which we see there is little difference between the two clusters. Therefore, neither MBC-BIC and KML provides satisfactory clustering results.

Fig. 10

Clustering results under MBC-BIC

Fig. 11

Clustering results under KML

Now we consider using variants of GCM-Gibbs-eBIC to cluster the schizophrenia data. Although it is recommended to use GCM-Gibbs-eBIC2 in Section 3.3, we still want to confirm this default setting gives better results than the other variants. From Fig. 9, it seems reasonable to assume that the mean IMPS79 trajectory for each inpatient is a first degree ($l=2$) or second degree ($l=3$) polynomial function of time t ($t=0,1,3$, and 6 in the data). Thus, the design matrix $\textbf{X}$ for GCM Eq. 1 is

$$\begin{aligned} \textbf{X}=\left[ \begin{array}{cc} 1 &{} 0 \\ 1 &{} 1 \\ 1 &{} 3 \\ 1 &{} 6 \end{array} \right] \; \text {for}\, l=2; \quad \text {or}\quad \textbf{X}=\left[ \begin{array}{ccc} 1 &{} 0 &{} 0\\ 1 &{} 1 &{} 1 \\ 1 &{} 3 &{} 9\\ 1 &{} 6 &{} 36\\ \end{array} \right] \; \text {for}\, l=3. \end{aligned}$$

Suppose the individuals may be partitioned into up to six clusters, i.e., $r\le R=6$. The setup by l and r creates 10 clustering scenarios, for each of which we apply the proposed GCM-Gibbs-eBIC method with four variants of eBIC to perform data clustering, where $M_0=10$ and $M_1=1000$ are used in the Gibbs sampler. Results of BIC, eBIC1, eBIC2, and eBIC3 values for each clustering scenario are displayed in Table 10.

Table 10 Values of BIC, eBIC1, eBIC2, and eBIC3 for clustering the schizophrenia data

Fig. 12

Six estimated mean IMPS79 trajectories obtained by GCM-Gibbs-BIC

From Table 10, we see the optimal cluster number $\check{r}$ equals 6 with $l=2$ (i.e., the mean response curve for each cluster is linear) under criteria BIC, eBIC1, and eBIC3, while $\check{r}=2$ when $l=3$ (i.e., the mean response curve for each cluster is quadratic) under criterion eBIC2. Clearly GCM-Gibbs-eBIC2 gives the most parsimonious result because dividing all observed IMPS79 score trajectories into six clusters seems overclustering, cf. Fig. 12 which displays the six fitted mean IMPS79 trajectories of the six clusters determined by GCM-Gibbs-BIC. It can be seen from Fig. 12 that some of the six mean trajectories are not very different from each other and should be merged.

The estimates of $(\textbf{B},\mathbf {\Sigma })$ obtained from using GCM-Gibbs-BIC are found to be

$$\begin{aligned}{} & {} \hat{\textbf{B}}= \left( \begin{array}{cccccc} 5.7147 &{} 5.7344 &{}4.4229 &{}5.8455&{}4.3275 &{}5.5782\\ -0.4639 &{} -0.6417&{}-0.1037&{}-0.0425&{}-0.4039 &{}-0.2064 \end{array} \right) ,\\{} & {} \hat{\mathbf {\Sigma }}= \left( \begin{array}{cccc} 0.3247 &{} 0.0082&{} 0.0027&{} -0.094\\ 0.0082&{} 1.0661&{} 0.6696&{} 0.2034\\ 0.0027&{} 0.6696&{} 1.1936&{} 0.2451\\ -0.094&{} 0.2034&{} 0.2451&{} 0.2909 \end{array} \right) . \end{aligned}$$

Before going to show how GCM-Gibbs-eBIC2 also returns the best clustering result, we show how the GCM-Gibbs-BIC result can be improved by incorporating the inpatients’ treatment information (i.e., drug or placebo). The last column in Table 11 summarizes the clustering of the 312 inpatients into six clusters (labelled Type 1 to Type 6) by using GCM-Gibbs-BIC. Numbers of inpatients taking active treatment “drug” and inactive treatment “placebo” in each cluster are listed in columns 2 and 3, respectively, in Table 11. In Table 11, there is also a column named “drug/placebo,” which is the ratio of column 2 and column 3. One can use the overall drug/placebo ratio (248/64=3.875) as a threshold to merge the Type 1 to 6 clusters into two new clusters named New type 1 and New type 2, respectively. Specifically, New type 1 combines Type 3 and Type 4 clusters, and New type 2 combines the other four clusters. The confusion matrix comparing the new clustering result with the one from clustering by “drug” and “placebo” is given in Table 12, with a mis-clustering rate (MCR) of 0.301, showing that these two clustering methods are the very different ones. But GCM-Gibbs-BIC incorporating inpatients’ treatment information does improve the clustering performance over GCM-Gibbs-BIC, cf. Figs. 12 and 13a that give the mean IMPS79 score trajectories for New type 1 and New type 2.

Table 11 Classification of the schizophrenia inpatients by cluster type (obtained from GCM-Gibbs-BIC) and treatment type

Table 12 Clustering the inpatients by GCM-Gibbs-BIC-treatment and by only treatment

Now we show that the best clustering result obtained from using GCM-Gibbs-eBIC2, given in Table 10, is even better. Note the model $\check{r}=2$ with $l=3$ is selected under GCM-Gibbs-eBIC2 with the two mean IMPS79 trajectories for the two clusters being displayed in Fig. 13b. Comparing Fig. 13a with b, we see the two mean IMPS79 trajectories obtained from GCM-Gibbs-BIC-treatment are not well separated at the beginning week, while the two mean IMPS79 trajectories obtained from GCM-Gibbs-eBIC2 are well separated across all weeks.

Fig. 13

Fitted mean IMPS79 trajectories for the two clusters

Fig. 14

IMPS79 trajectories for the two clusters determined by GCM-Gibbs-eBIC2

We also plot in Fig. 14 the IMPS79 trajectories of all inpatients in the two clusters determined by GCM-Gibbs-eBIC2. Figure 14 shows that IMPS79 values of patients in cluster 1 are relatively stable, indicating that conditions of the inpatients in this cluster are relatively stable. On the other hand, IMPS79 values in cluster 2 show a downward trend, indicating that conditions of this group of inpatients are improving. Inpatients in cluster 1 include those taking drug and those taking placebo. But their common characteristic is that their IMPS79 values do not change much. In cluster 2, inpatients who take drug or placebo have a common characteristic of downward trend in IMPS79. It indicates that their conditions are improving. Further, the estimates of $(\textbf{B},\mathbf {\Sigma })$ under the GCM-Gibbs-eBIC2 are found to be

$$\begin{aligned}{} & {} \hat{\textbf{B}}= \left( \begin{array}{cc} 5.3639 &{} 5.2555 \\ -0.2234&{} -0.7694\\ 0.0199 &{} 0.0438 \end{array} \right) ,\qquad \hat{\mathbf {\Sigma }}= \left( \begin{array}{cccc} 0.7344 &{} 0.3877&{} 0.3111&{} 0.1185\\ 0.3877&{} 1.2769&{} 0.7928&{} 0.4019\\ 0.3111&{} 0.7928&{} 1.287&{} 0.4059\\ 0.1185&{} 0.4019&{} 0.4059&{} 0.6209 \end{array} \right) . \end{aligned}$$

Finally, Table 13 compares the clustering result of the 312 inpatients by GCM-Gibbs-eBIC2 and that by treatment, with the misclustering ratio (MCR) being 0.385. This again confirms that the treatment factor is not a good classifier for clustering the IMPS79 trajectories.

Table 13 Comparison of the GCM-Gibbs-eBIC2 clustering and the drug/placebo clustering results

7 Discussion

In this paper, we develop a new method for clustering longitudinal data under the growth curve model setting. Clustering longitudinal data is computationally challenging when the sample size is large, due to the associated “curse of dimensionality” or “combinatorial explosion” (Bellman, 1957). The current methods in literature for clustering longitudinal data mostly use soft clustering approach by assuming an i.i.d. prior categorical probability distribution for the unknown partition vector (i.e., the vector of unit label for all sample units). These methods are not able to efficiently use the effect of the covariate design matrix on the response growth curve during clustering. Moreover, the Bayesian clustering results are sometimes difficult to interpret and justify.

In our proposed GCM-Gibbs-eBIC method, we treat the partition matrix as unknown latent data, and our major contributions are as follows: (i) a sampling probability distribution for the partition matrix is induced based on an information criterion; (ii) using Gibbs sampler to generate a Markov chain of manageable size of possible realizations of the partition matrix with the induced sampling distribution of the partition matrix being the stationary distribution, so that the best partition matrix can be identified, with sampling probability 1 in the limit, via stochastic search on the generated Markov chain; (iii) determining the best number of clusters by a partition information based selection criterion including AIC, BIC, and eBIC, etc.  as its special cases. Both the simulation study and the real data examples presented in the paper demonstrate that the proposed method is capable of clustering the longitudinal data, in a computationally feasible way, to maximize the likelihood of capturing the true partition.

The developed GCM-Gibbs-eBIC method has potential to be extended to other settings of longitudinal data clustering. First, it can be extended to generalized linear model based longitudinal data clustering where the probability distribution of the response variable is not Gaussian and the data are not necessarily balanced. Second, regression variable selection and longitudinal data clustering can be tackled jointly and by stochastic search and stochastic optimization. Third, longitudinal data clustering can be performed in a functional data analysis framework (Ramsay & Silverman, 1997) when the longitudinal dimension is high, where each observed response trajectory can be smoothed by a curve before proceeding with clustering. Research on these extensions is currently in progress.

Appendix

1.1 Simulation Results of $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {1:1:1}}}$

Results of simulation studies $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {1:1:1}}}$ are given below.

Table 14 Mean performance of parameter estimates and clustering for experiments $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$ and $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$ by the GCM-Gibbs-eBIC2 method

Fig. 15

Grouped box plots of the mis.rate (i.e., MCR), $\texttt {edu.dis}(\hat{\textbf{B}})$ and $\texttt {edu.dis}(\hat{\mathbf {\Sigma }})$ values from the clustering and regression results for the 100 iterated datasets by using GCM-Gibbs-eBIC2 for experiment $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$, and $S_{{\texttt {L},\texttt {ccc},\texttt {1:1:1}}}$, respectively

Table 15 Clustering performance, in terms of mMCR and the associated standard error given in the parentheses, obtained by using GCM-Gibbs-eBIC2, MBC, and KML for experiments $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {1:1:1}}}$, each involving the 100 iterated datasets

Fig. 16

Plots of the fitted response mean growth curves (dotted) by the GCM-Gibbs-eBIC2 method compared to their underpinning true mean curves (solid). The three clusters in each experiment are labelled by squares, triangles, and bullets, respectively

• 1. Table 14 gives the mean performance of parameter estimates $(\hat{\textbf{B}}, \hat{\mathbf {\Sigma }})$ and clustering, regarding mean edu.dis, mean F-norm, and mean mis.rate, in experiments $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{\texttt {M},\texttt {ccc},\texttt {1:1:1}}$ and $S_{\texttt {L},\texttt {ccc},\texttt {1:1:1}}$, each with 100 replicated datasets, by the GCM-Gibbs-eBIC2 method. This is followed with the values $\bar{\hat{\textbf{B}}}_{\texttt {ccc}}$ and $\bar{\hat{\mathbf {\Sigma }}}_{\texttt {ccc}}$ obtained as the average of $\hat{\textbf{B}}$ and $\hat{\mathbf {\Sigma }}$ in the three experiments, respectively.

• 2. Figure 15 gives 3 grouped box-plots of the mis.rate (i.e. MCR), $\texttt {edu.dis}(\hat{\textbf{B}})$ and $\texttt {edu.dis}(\hat{\mathbf {\Sigma }})$ values that are computed from GCM-Gibbs-eBIC2 clustering results for the 100 iterated datasets in experiment $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {1:1:1}}}$.

• 3. Table 15 displays the clustering mean performance and the respective standard errors by GCM-Gibbs-eBIC2, MBC and KML for experiments $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {1:1:1}}}$, each with the 100 replicated datasets.

• 4. Figure 16 provides three plots of fitted response mean growth curves (determined by the average $\hat{\textbf{B}}$ value computed from the 100 iterated datasets for each experiment) versus their underpinning true mean curves for experiments $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$, $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$ and $S_{{\texttt {L},\texttt {ccc},\texttt {1:1:1}}}$.

In $S_{{\texttt {S},\texttt {ccc},\texttt {1:1:1}}}$:

$$\begin{aligned}{} & {} \bar{\hat{\textbf{B}}}_{\texttt {ccc}}= \left( \begin{array}{ccc} 14.133 &{} 5.599 &{} 5.353\\ -6.010 &{}-2.451 &{}-8.201\\ 4.848 &{} 4.315 &{}6.102 \\ -0.437 &{}-0.411 &{}-0.613\\ \end{array} \right) ,\qquad \bar{\hat{\mathbf {\Sigma }}}_{\texttt {ccc}}= \left( \begin{array}{cccc} 8.615 &{} 3.899 &{} 5.573 &{} 3.907\\ 3.899 &{} 5.155 &{}3.949 &{}5.294\\ 5.573 &{} 3.949 &{} 8.472 &{} 5.512\\ 3.907 &{}5.294 &{}5.512 &{} 6.949\\ \end{array} \right) . \end{aligned}$$

In $S_{{\texttt {M},\texttt {ccc},\texttt {1:1:1}}}$:

$$\begin{aligned}{} & {} \bar{\hat{\textbf{B}}}_{\texttt {ccc}}= \left( \begin{array}{ccc} 14.808 &{} 5.278 &{} 4.679\\ -6.519 &{}-2.602 &{}-7.624\\ 5.049 &{} 4.507 &{}5.827 \\ -0.464 &{}-0.443 &{}-0.577\\ \end{array} \right) ,\qquad \bar{\hat{\mathbf {\Sigma }}}_{\texttt {ccc}}= \left( \begin{array}{cccc} 7.253 &{} 2.672 &{} 4.231 &{} 2.742\\ 2.672 &{} 4.262 &{}2.645 &{}4.237\\ 4.231 &{} 2.645 &{} 7.196 &{} 4.148\\ 2.742 &{}4.237 &{}4.148 &{} 5.686\\ \end{array} \right) . \end{aligned}$$

In $S_{{\texttt {L},\texttt {ccc},\texttt {1:1:1}}}$:

$$\begin{aligned}{} & {} \bar{\hat{\textbf{B}}}_{\texttt {ccc}}= \left[ \begin{array}{ccc} 15.156 &{} 4.491 &{} 5.012\\ -7.052 &{}-1.379 &{}-8.099\\ 5.303 &{} 3.966 &{}6.045 \\ -0.499 &{}-0.371 &{}-0.606\\ \end{array} \right] ,\qquad \bar{\hat{\mathbf {\Sigma }}}_{\texttt {ccc}}= \left[ \begin{array}{cccc} 7.292 &{} 2.638 &{} 4.334 &{} 2.768\\ 2.638 &{} 4.233 &{}2.648 &{}4.256\\ 4.334 &{} 2.648 &{} 7.423 &{} 4.197\\ 2.768 &{}4.256 &{}4.197 &{} 5.762\\ \end{array} \right] . \end{aligned}$$