Polarized Classification Tree Models: Theory and Computational Aspects

Abstract

In this paper, a new approach in classification models, called Polarized Classification Tree model, is introduced. From a methodological perspective, a new index of polarization to measure the goodness of splits in the growth of a classification tree is proposed. The new introduced measure tackles weaknesses of the classical ones used in classification trees (Gini and Information Gain), because it does not only measure the impurity but it also reflects the distribution of each covariate in the node, i.e., employing more discriminating covariates to split the data at each node. From a computational prospective, a new algorithm is proposed and implemented employing the new proposed measure in the growth of a tree. In order to show how our proposal works, a simulation exercise has been carried out. The results obtained in the simulation framework suggest that our proposal significantly outperforms impurity measures commonly adopted in classification tree modeling. Moreover, the empirical evidence on real data shows that Polarized Classification Tree models are competitive and sometimes better with respect to classical classification tree models.

1 Introduction

Classification trees are non-parametric predictive methods obtained by recursively partitioning the data space and fitting a simple prediction model within each partition (Breiman et al. 1984).

The idea is to divide the entire X-space into rectangles such that each rectangle is as homogeneous or pure as possible in terms of the dependent variable (binary or categorical), thus containing points that belong to just one class (Shneiderman 1992).

As decision tree models are simple and easy interpretable models able to obtain good predictive performance, they are of interest in many recent works in literature (see for example Aria et al. 2018, Iorio et al. 2019, Nerini and Ghattas 2007 and D’Ambrosio et al. 2017).

One of the main distinctive element of a classification tree model is how the splitting rule is chosen for the units belonging to a group, which corresponds to a node of the tree, and how an index of impurity is selected to measure the variability of the response values in a node of the tree.

The main used splitting rules are the Gini index, introduced in the CART algorithm proposed in Breiman et al. (1984), and the Information Gain, employed in the C4.5 algorithm (Quinlan 2014). Other different splitting criteria have been proposed in literature as alternatives to these two ones. A faster alternative to the Gini index is proposed in Mola and Siciliano (1997) employing the predictability index τ of Goodman and Kruskal (1979) as a splitting rule. In Ciampi et al. (1987), Clark and Pregibon (2017), and Quinlan (2014), the likelihood is used as splitting criterion, while the mean posterior improvement (MPI) is used as an alternative to the Gini rule in Taylor and Silverman (1993). Statistical tests are also introduced as splitting criteria in Loh and Shin (1997) and Loh and Vanichsetakul (1988). Different splitting criteria are combined with a weighted sum in Shih (1999). A more recent work (see D’Ambrosio and Tutore 2011) proposes a new splitting criterion based on a weighted Gini impurity measure. Mola and Siciliano (1992) introduces a two-stage approach to find the best split as to optimize a predictability function. On this approach is based the splitting rule proposed by Tutore et al. (2007), which introduce an instrumental variable called Partial Predictability Trees. In Cieslak et al. (2012), the Hellinger distance is used as splitting rules, and this method is shown to be very efficient for imbalanced datasets but works only for binary target variables. See Fayyad and Irani (1992), Buntine and Niblett (1992), and Loh and Shin (1997) for a comparison of different splitting rules. Despite many different splitting rules have been proposed in literature, the most used in application problems are still the Information Gain and the Gini index and they are also used in literature as benchmark to compare the performance of new proposed splitting rules, see for example Chandra et al. (2010) and Zhang and Jiang (2012).

In this paper, a new measure of goodness of a split, based on an extension of polarization indices introduced by Esteban and Ray (1994), is proposed for classification tree modeling.

The contribution of the paper is twofold: from a methodological perspective, a new multidimensional polarization measure is proposed; in terms of computation, a new algorithm for classification tree models is derived which the authors call Polarized Classification Tree. The new measure, based on polarization, tackles weaknesses of the classical measures used in classification trees (e.g., Gini index and Information Gain) by reflecting the distribution of each covariate in the node.

The rest of the paper is structured as follows: Section 2 describes impurity and polarization measures; Section 3 shows our methodological proposal; Section 4 integrates the new measure inside decision tree algorithm. Sections 5 and 6 report the empirical evidences obtained on simulated and real datasets respectively. Conclusions and further ideas for research are summarized in Section 7.

2 Impurity and Polarization Measures

In the literature on classification trees (see Mingers 1989), it is recognized that splitting rules based on the impurity measures (i.e., the Gini impurity index, the Information Gain) suffer from some weaknesses. Firstly, impurity measures are equivalent one to one another and they are also equivalent to random splits, in terms of the accuracy of the resulting model, see Mingers (1989). Secondly, impurity measures do not take into account the distribution of the features, but only the pureness of the descendant nodes in terms of the target variable and this fact could lead to an high dependence on the data at hand, see Aluja-Banet (2003). The algorithms proposed in classification tree analytics tend to select the same variables for the splitting in different nodes, especially when these variables could be splitted in a variety of ways, making it difficult to draw conclusions about the tree structure.

As explained in previous section, the problem of finding an efficient splitting rules has been considered in different research papers. The aim of our contribution is to propose a new class of measures to evaluate the goodness of a split which tackles the previous mentioned weaknesses. In order to consider both the impurity and distribution of the features in the growth of the tree, our idea is to replace the impurity measure with a polarization index.

Polarization measures, introduced in Esteban and Ray (1994), Foster and Wolfson (1992), and Wolfson (1994), are typically adopted in the socio-economic context to measure inequality in income distribution. In Esteban and Ray (1994) and Duclos et al. (2004), the authors provide an axiomatic definition for the class of polarization measures and a characterization theorem. In Esteban and Ray (1994), polarization is viewed as a clustering of an observed variable (typically ordinal) around an arbitrary number of local means, while in Duclos et al. (2004), a definition of income polarization is proposed considering a continuous variable. In Esteban and Ray (1994) and Duclos et al. (2004), the results of polarization measures are related to one variable; thus, they can be considered univariate approaches.

In Zhang and Kanbur (2001), a multidimensional measure of polarization is proposed which considers within-groups inequality to capture internal heterogeneity and between-groups inequality to measure external heterogeneity. The index is composed by the ratio of the between groups and the within groups inequality.

In Gigliarano and Mosler (2008), a general class of indices of multivariate polarization is derived starting from a matrix $\mathbb {X}$ of size N × K, where N is the total number of individuals with their endowments classified in K attributes. The class of indices can be written as follows: $P(\mathbb {X})=\zeta (B(\mathbb {X}),W(\mathbb {X}),S(\mathbb {X}))$ where B and W reflect the measure of between and within groups inequality respectively and S takes into account the size of each group. In details, B and W can be chosen among different multivariate inequality indices present in literature, e.g., Tsui (1995) and Maasoumi (1986), and they can be applied only to variables that are transferable among individuals. ζ is a function $\mathbb {R}^{3} \rightarrow \mathbb {R}$ increasing on B and S and decreasing on W. Gigliarano and Mosler (2008) discuss the possibility of extending the discrete version of the axioms proposed in Esteban and Ray (1994) to their proposed measure, stating also some properties of the measure.

Our idea is to define a multidimensional polarization measure, which considers one continuous variable when groups are exogenously defined coupled with a generalization of the continuous version of the axioms defined in Duclos et al. (2004), opportunely adapted for our measure, as described in Section 3 and proved in the Appendix.

3 A New Impurity Measure of Polarization for Classification Analytic

Our measure of polarization is evaluated measuring the homogeneity/heterogeneity of the population with the use of variability between and within groups.

The new proposed index is a function of four inputs:

$$ P(\mathbb{X})=\zeta(B,W,\mathbf{p},M) $$

(1)

where B and W are the variability between and within groups respectively, p = (p₁,...,p_M) is the vector describing the proportion of elements in each group, and M is the number of groups. Since we would like to introduce a measure which treats variables coming from different contexts (not only transferable variable), a measure of variability instead of inequality is introduced, thus making our proposal different from the one in Gigliarano and Mosler (2008).

Following the intuition on polarization, $P(\mathbb {X})$ is high for large values of B (i.e., the groups strongly differ from each other), for small values of W (i.e., the elements of the groups are homogeneous), for large values of ${\max \limits } \{p_{j}\}$, and for small values of M (i.e., the population is divided into few groups with an unbalanced proportion of elements in one single group).

On the other hand, we expect $P(\mathbb {X})$ to take small values when the population is divided into numerous balanced groups with small variability between groups B and high variability within groups W.

Suppose that there are M groups exogenously defined, and that each observation is classified into one group through the use of a categorical variable with M levels. Let n_j be the number of individuals in the j^th group, N the total number of observations in the population, and $p_{j}=\frac {n_{j}}{N}$ the proportion of population in the j^th group. Let f_j be the probability density function of the interesting feature x in the j^th group with expected value μ_j; the expected value of the global distribution f of the population is μ.

We set the following assumptions:

Assumption 1

M > 1

Assumption 2

p_j > 0 ∀j ∈ 1,...,M

Assumption 3

{supp(f_j)}_j= 1,...,M are connected and

{supp(f_i)}∩{supp(f_j)} = ∅ for i,j = 1,…,M with i≠j.

Assumption 4

${\int \limits }_{supp(f_{j})} f_{j} dx =1$.

Assumptions 1 and 2 exclude trivial cases, respectively a unique group for the entire population and the existence of empty groups.

Assumption 3 directly refers to the basic definition proposed in Duclos et al. (2004) for the axiomatic theory of polarization measures. From an empirical point of view, Assumption 3 translates the idea that the M groups of the original population are separated such that there is no uncertainty about the belonging of a single element to a certain group. As for the original definition of polarization measures, also in the case of multidimensional polarization measures, this assumption is not always verify in real application problems.

Assumption 4 requires that the functions f_j are probability densities; this assumption is necessary to provide an axiomatic definition of the polarization measure as pointed out in the Appendix.

Our polarization measure is defined as follows.

Definition 3.1

Given a population $\mathbb {X}$ and M groups, the polarization is:

$$ P(B,W,\textbf{p},M)=\eta(B,W) \cdot \psi(\textbf{p},M) $$

(2)

where

$$ \eta(B,W)=\frac{B}{B+W}=1-\frac{W}{B+W} $$

(3)

with

$$ B=\sum\limits_{j=1}^{M} (\mu_{j}-\mu)^{2} \qquad $$

(4)

and

$$ \qquad W= \sum\limits_{j=1}^{M} {\int}_{\text{supp}\{f_{j}\}} (x-\mu_{j})^{2} f_{j}(x) dx $$

(5)

and

$$ \psi(\mathbf{p},M)=\frac{\max_{j=1,...,M}{(p_{j})}- \frac{1}{N}}{\frac{N-2}{N}} $$

(6)

The measure proposed in Definition 3.1 is the product of two components: η(B,W) accounts for the variability between and within groups, while ψ(p,M) considers the number of the groups and their cardinality.

The measure P is normalized and takes values in the interval [0,1] as proved in the following proposition.

Proposition 3.2

Given a population $\mathbb {X}$ and M groups, P(B,W,p,M) ∈ [0,1].

Proof

Considering Definition 3.1, the measure

P(B,W,p,M) is the product of the two components η(B,W) and ψ(p,M).

The quantity η(B,W) is defined as a ratio of the non-negative variability measures B and W, see Eq. 3; by construction η(B,W) ≤ 1. Moreover, the variability B is strictly positive, and using Assumptions 1 and 3 at least one of the elements in the sum defining B is strictly positive. So we have η(B,W) ∈ (0,1].

The quantity ψ(p,M) is a non-negative ratio; the minimum value is achieved when $\max \limits _{j=1,...,M}{(p_{j})} = \frac {1}{N}$ so that ψ(p,M) = 0. The maximum value is obtained when M = 2 and $\max \limits _{j=1,...,M}{(p_{j})} = \frac {N-1}{N}$; in this case ψ(p,M) = 1. In general, ψ(p,M) ∈ [0,1].

As a consequence P(B,W,p,M) = η(B,W) ⋅ ψ(p,M) ∈ [0,1] and the proposition is proved. □

The following Corollary holds.

Corollary 3.3

The maximum and minimum values for P(B,W,p,M) are respectively equal to 1 and 0 .

Proof

Trivial from Property 3.2. □

We note that P(B,W,p,M) = 0 if and only if ψ(p,M) = 0, or equivalently $\max \limits _{j=1,...,M}{(p_{j})} = \frac {1}{N}$. The condition is verified exclusively when M = N; considering Assumption 2, this is the case where each group contains one single element of the original population supporting the intuition of absence of polarization.

On the other hand, note that P(B,W,p,M) = 1 if and only if η(B,W) = 1 and ψ(p,M) = 1. The condition on η(B,W) requires W = 0 while ψ(p,M) = 1 is equivalent to the case of M = 2 and one of the groups containing N − 1 elements. In other words, the maximum polarization is achieved when the number of groups is minimum, the original population except for one element belongs to one single group and the variance within groups is null such that the groups show maximum internal homogeneity.

Moreover, we should underline that the proposed measure is invariant for any permutation of the vector p; intuitively the polarization of a population does not depend on the order in which we take the groups into account. We provide the axiomatic base for multidimensional polarization measures as a generalization of the axioms proposed by Duclos et al. (2004).

Axiom 3.4

For any number of groups and any distribution of observations into the groups, a global squeeze (as defined in Duclos et al. (2004)) can not modify the polarization.

Axiom 3.4 requires the polarization measure to be invariant with respect to a global reduction of the variance of the population.

Axiom 3.5

If the population is divided symmetrically into three groups, each one composed of a basic density with the same root and mutually disjoint supports, then a symmetric squeeze of the side densities can not reduce polarization.

Axiom 3.5 requires the polarization measure to increase when the variability within groups W decreases. Note that the values of B, p, and M are invariant with respect to the transformation described.

Axiom 3.6

Consider a symmetric distributed population divided into four groups, each one composed of a basic density with the same root and mutually disjoint supports. Slide the two middle densities to the side (keeping all supports disjointed). Then polarization must increase.

Axiom 3.6 requires the polarization measure to increase when the variability between groups B increases, when W, p, and M are given.

Axiom 3.7

If P_F ≥ P_G and q is a non-negative integer value, then P_qF ≥ P_qG, where qF and qG represent population scaling of F and G respectively.

Axiom 3.7 describes a transformation that changes the sample size of the population with no consequences on the proportion of individuals in each group.

In the Appendix, we prove that our proposal respects all four axioms, thus can be classified as a multidimensional polarization measure.

4 Polarized Classification tree

In this section, we show how the multidimensional polarization measure introduced in Section 3 can be used in classification tree models as a new measure of goodness of a split in the growth of a classification tree.

The new approach, which the authors call Polarized Classification Tree (PCT), has been implemented in R software. In Breiman et al. (1984), a split is defined as “good” if it generates “purer” descendant nodes then the goodness of a split criterion can be summarized from an impurity measure.

In our proposal, a split is good if descendant nodes are more polarized, i.e., the polarization inside two sub-nodes is maximum. In order to evaluate the polarization in one sub-node as in 1, we consider:

• The function ψ(p,M) which takes into account, the “pureness” of the sub-node. A sub-node is “purer” if one class of the target variable is more represented with respect to the others and the polarization is higher.

• The function η(B,W) which measures homogeneity and heterogeneity among groups. η(B,W), and consequently the polarization, is higher if the groups are “well characterized” by the variable X, selecting a split that obtains sub-nodes where the variable clearly discriminates well between different groups.

To clarify how our measure works with respect to the indices used in the literature, a toy example is described.

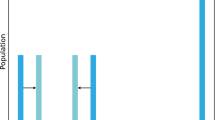
As shown in Fig. 1, two explanatory variables X₁ and X₂ are considered. The target variable Y assumes three possible values a, b, and c, corresponding to three different groups. Figure 1 shows the distribution of the two explanatory variables in the three groups determined by Y.

Fig. 1

Distributions of two explanatory variables for a three-class target variable

In this example, the three groups are well distinguishable in both the distributions of X₁ and X₂, but it is evident that X₂ has an higher discriminatory power compared to X₁.

The four best splits, in terms of pureness of the descendant nodes, are as follows: splits 1 and 3, dividing group a from b and c respectively; splits 2 and 4, dividing a and b from c, as shown in Fig. 1. When evaluating the goodness of these possible splits, Gini and information Gain criteria can not discriminate; indeed, when the tree is estimated on the training set, all the considered splits generate the same situation of impurity in the descendant nodes, thus making impossible to discriminate between the different splits.

When evaluating the goodness of the splits using our polarization measure, the distribution of the explanatory variables in the groups is taken into account. The goodness is higher for splits 3 and 4 with respect to splits 1 and 2, because the groups are more “characterized” by variable X₂, thus leading to selecting a split on X₂ rather than on X₁.

Since classification trees can treat both numerical and categorical variables, we will extend the measure introduced in Section 3 to deal with categorical variables.

Consider a categorical variable X which assumes I different values, e.g., X ∈{1,...,I} and suppose that there are M groups exogenously defined and each observation is assigned to a group.

Let n_ij be the number of observations taking value in the i^th category and assigned to the j^th group, n_i⋅ be the number of observations taking value in the i^th category, and n_⋅j be the number of observations assigned to the j^th group.

The polarization index can be written as in Eq. 2: P(B,W,p,M) = η(B,W) ⋅ ψ(p,M) where $W=\frac {N}{2}-\frac {1}{2} {\sum }_{j=1}^{M} \frac {1}{n_{\cdot j}}{\sum }_{i=1}^{I} n_{ij}^{2}$ and B = M.

Assumptions on the polarization index are described in Section 3. We note that the theoretical definition of the measure requires that M > 1. Obviously this assumption can not always be satisfied in the computational stage when a pure node is obtained at some step. To handle this case, we set P(B,W,p,M) = 1 when M = 1. In addition, some clarification has to be done on Assumption 3; from an empirical point of view, this assumption reflects the idea that observing the distribution of a covariate, we are able to clearly discriminate among the groups defined in the target variable. Of course, in real application problems, this assumption is not always satisfied. We show, in the empirical evaluation on both simulated and real datasets, that the relaxation of this hypothesis does not invalidate the performance of the proposed measure as splitting criteria.

Algorithm 1 shows the procedure used to build the PCT model. Let S be the set of all possible splits defined on the training set T. For each possible split, s ∈ S, all samples can be divided into sub-node ${t_{L}^{s}}$ the condition s is satisfied, otherwise ${t_{R}^{s}}$. The best split s^∗ is identified maximizing the polarization in the two sub-nodes. The growing procedure is stopped in one node if the node is pure in terms of target variable or if other stopping conditions are met (i.e., the number of samples in the node is less than a fixed threshold). Following the same procedure adopted in CART model, when the tree is built, the most representative class in each final node is assigned to that final node.

In the next sections we show how the proposed method works on different simulated and real datasets. Results obtained using the PCT model are compared to the ones obtained using the Gini index and the Information Gain measure as splitting rule, which are procedures most used as benchmark to compare new proposed splitting rules, as already underlined in Section 1.

5 Empirical Evaluation on Simulated Data

In order to show how our new impurity measure works inside PCT, this section reports the empirical results achieved on different simulated datasets. The performance of the PCT algorithm is compared with respect to the classification tree based on different splitting criteria. In particular, the polarization splitting criteria are compared to the Gini impurity index and the Information Gain in terms of the area under the ROC curve (AUC) value. The results reported in the rest of the paper are based on a cross-validation exercise and expressed in terms of out of sample performance.

The simulation framework considered in this paper is inspired by the paper of Loh and Shin (1997) where different impurity measures are compared for classification tree modeling. The data are sampled from four pairs of distributions that are represented by the solid density curves represented in Fig. 2, where each distribution represents the covariate of a group G_i defined by the associated target variable. N(μ,σ²) is a normal distribution with mean μ and variance σ², T2(μ) is a t-distribution with 2 degrees of freedom centered at μ, and Chisq(ν) is a chi-square distribution with ν degrees of freedom. The 100 observations of the two groups represented by the target variable Y are sampled respectively from the first and from the second distribution as shown in Fig. 2.

Fig. 2

Simulation and representation of the different class populations used for the classifier comparison

Results obtained by the three classification models under comparison are expressed in terms of the AUC value. Averaged AUC values (i.e., mean (AUC)) and the corresponding confidence intervals at 95% (i.e., CI (AUC)) for each simulated dataset obtained using Monte Carlo simulation with 100 iterations are reported in Table 1.

Table 1 Confidence intervals for AUC values obtained through a 100 iteration Monte Carlo procedure to compare the performance of classifiers on different simulated datasets

In the reported examples, AUC values obtained for PCT are better with respect to the classical splitting methods based on the Gini index and Information gain, as shown in Table 1. In all cases, the confidence intervals for the AUC derived using the polarization splitting criteria do not intersect those obtained using the Gini index and Information gain. For each simulated dataset, a De Long test (DeLong et al. 1988) is performed to compare obtained results, in terms of AUC, among PCT and trees employing respectively the Gini index and the Information Gain. In Table 2, the average p value of the De Long test obtained along the 100 simulations for each dataset is shown. We also applied a one side Wilcoxon test to compare the AUC values obtained with PCT and decision trees employing Gini and Information Gain; in both cases, obtained p values for all the datasets are lower than 0.05, showing that AUC values obtained with PCT are significantly higher.

Table 2 Average obtained p value of the De Long test to compare the AUC values of PCT against trees employing Gini index and Information Gain

On the basis of the results at hand, the polarization measure introduced in this paper shows a statistical significant superiority with respect to the other considered splitting criteria in terms of predictive performance observing the obtained AUC values.

6 Empirical Evaluation on Real Data

The performance of the splitting criteria under comparison is evaluated on 18 different real datasets. The considered datasets come from the UCI repository (Dua and Graff 2017).

In order to have a complete comparison among classifiers, different datasets characterized by binary or multiple class target variables are considered. The datasets are made up of categorical and/or numerical explanatory variables. In Table 3, different information on the datasets are reported: sample size (Samples), total number of variables (Var), number of categorical (Cat) and numerical (Num) variables, number of classes in the target variable (Num Class), and the normalized Shannon entropy (Balance). The normalized Shannon entropy is evaluated on the target variable to measure the level of imbalance of each dataset (i.e., the value is equal to 0 if the dataset is totally unbalanced and equal to 1 if the samples are equi-distributed among the classes). See Appendix B for more details on the datasets.

Table 3 Dataset descriptions

A 10-fold cross-validation procedure for the datasets reported in Table 3 is performed to evaluate the different approaches under comparison. All the classifiers are trained and evaluated on the same 10-fold. In addition, the same stopping condition is used for all the models, i.e., the minimum number of observations inside a node is set at 10% of the number of observations in the training set.

As suggested in Demsar (2006), since datasets are different, the evaluated performance metrics can not be compared directly, but for each dataset, the metrics are used to rank the classifiers. On the basis of the AUC, each classifiers is ranked assigning value 1 to the best one, considering the mean value between two ranks if the classifiers perform equally. A Dunn test with Bonferroni correction is then applied to compare the obtained rankings with confidence at 95%. Table 4 shows the ranking of each model registered on the datasets. The Polarized Classification Tree works better with respect to Gini and Information Gain assuming different kinds of target variables (i.e., banknotes authentication and glass). We note that classification trees based on the Gini index and Information Gain are superior in terms of performance for only two datasets each.

Table 4 Mean rank values for AUC for each classifier

A Dunn test with Bonferroni correction shows a significant difference between obtained results for PCT and Gini index (the adjust p value is equal to 0.03), while no differences are present between Information Gain and the other two splitting methods. Hence, we can affirm that PCT is competitive and sometimes better with respect to the most two used splitting rules (i.e., Gini index and Information Gain) and can be considered as a valid alternative to be employed and compared when looking for the model that better suits the data at hand. It can be noticed that PCT model obtains good performance when dataset covariates are mainly numerical, as they perform better or equal to the other methods (see for example banknotes, glass, or breast coimbra). Obtained results suggest instead that the balancing of the target variable and the presence of multiclass target variable do not influence the performance of the introduced method.

7 Conclusions

This paper introduces a new index of polarization to measure the goodness of a split in the growth of a classification tree. Definition and properties of the new multidimensional polarization index are described in detail in the paper and proved in the Appendix.

The new measure tackles weaknesses of the classical measures used in classification tree modeling, taking into account the distribution of each covariate in the node. From a computational point of view, the new measure proposed is evaluated inside a classification tree model and implemented in R software and is available from the authors upon request.

The results obtained in the simulation framework suggest that our proposal significantly outperforms classical impurity measure commonly adopted in classification tree modeling (i.e., Gini and Information Gain).

The performance registered running Polarized Classification Tree models on real data extracted from the UCI repository confirms the competitiveness of our methodological approach. More precisely, the empirical evidence at hand shows that Polarized Classification Tree models are competitive and sometimes better with respect to classification tree models based on Gini or Information Gain.

A further analysis on this topic should compare the introduced Polarized Classification Trees with other splitting measures present in literature and to include this new splitting measure in ensemble three modeling (e.g., random forest).

Appendices

Appendix A

Let f be a basic density, as defined in Duclos et al. (2004), i.e., an unnormalized, symmetric and unimodal function, with compact support.

Some transformations can be performed on these functions s:

• λ-squeeze, with λ ∈ (0, 1) $f^{\lambda }=\frac {1}{\lambda } f\left (\frac {x-(1-\lambda )\mu }{\lambda }\right )$ where μ is the mean of f.

• δ-slide, δ > 0 g(x) = f(x ± δ)

• population rescaling of a non-negative integer qg(x) = qf(x)

• income rescaling to a new mean $\mu ^{\prime }$$g(x)=\frac {\mu }{\mu ^{\prime }}f(\frac {x\mu }{\mu ^{\prime }})$

These transformations preserve symmetry and unimodality and the resulting transformed function is still a basic density.

On the basis of the Hypotheses 1–4, stated in Section 3, we prove that the index introduced in this paper verifies the axiomatic definition of polarization given in Section 3.

Some preliminary observations are needed for the proof. Let f be a density function of a continuous. Suppose that suppf = [a,b] and μ is the expected value of the population.

Let f^λ be the squeeze of f with λ ∈ (0, 1), then:

Observation A.1

The support of f^λ is as follows: suppf^λ = [λa + (1 − λ)μ,λb +(1 − λ)μ] ⊂ [a,b]

Observation A.2

${\int \limits }_{\lambda a+(1-\lambda )\mu }^{\lambda b+(1-\lambda )\mu } \frac {1}{\lambda } f(\frac {x-(1-\lambda )\mu }{\lambda }) dx = {{\int \limits }_{a}^{b}} f(x) dx = 1$

Observation A.3

$\mu ^{\prime }= {\int \limits }_{\lambda a+(1-\lambda )\mu }^{\lambda b+(1-\lambda )\mu } x \frac {1}{\lambda }f(\frac {x-(1-\lambda )\mu }{\lambda }) dx={{\int \limits }_{a}^{b}} (\lambda y+(1-\lambda )\mu ) f(y) dy= \\ =\lambda \mu +(1-\lambda )\mu =\mu$

Observation A.4

$V(f^{\lambda }) = {\int \limits }_{\lambda a+(1-\lambda )\mu }^{\lambda b+(1-\lambda )\mu } (x-\mu )^{2} \frac {1}{\lambda }f(\frac {x-(1-\lambda )\mu }{\lambda }) dx= \\ =\lambda ^{2}{{\int \limits }_{a}^{b}} (y-\mu )^{2} f(y) dy=\lambda ^{2}V(f)$

Axiom 1

Let f_j be the density function of each group j = 1,...,M. Since by assumption the f_j have disjoint supports, we can define the global distribution as $f=\frac {1}{M}\left (f_{1}+...+f_{M}\right )$. A global squeeze on the entire population is defined as:

$$ \begin{array}{ll} f^{\lambda}&=\frac{1}{M \lambda} f \left( \frac{x-(1-\lambda)\mu}{\lambda}\right)= \frac{1}{M\lambda}f_{1}\left( \frac{x-(1-\lambda)\mu}{\lambda}\right)+...+\frac{1}{M \lambda}f_{M} \left( \frac{x-(1-\lambda)\mu}{\lambda}\right)=\\ &=\frac{1}{M}\left( f_{1}^{\lambda}+...+f_{M}^{\lambda}\right) \end{array} $$

If supp(f_j) = [a_j,b_j], then $\mathit {supp}(f_{j}^{\lambda })=[\lambda a_{j}+(1-\lambda )\mu ,\lambda b_{j}+(1-\lambda )\mu ]$ (for Observation A.1). The mean of each group is defined as follows: $\mu _{j}={\int \limits }_{a_{j}}^{b_{j}} xf_{j}(x) dx$. The mean of each group after the squeeze becomes $\mu _{j}^{\prime }=\frac {1}{\lambda } {\int \limits }_{\lambda a_{j}+(1-\lambda )\mu }^{\lambda b_{j}+(1-\lambda )\mu } xf_{j}(\frac {x+(1-\lambda )\mu }{\lambda }) dx ={\int \limits }_{a_{j}}^{b_{j}} (\lambda y +(1-\lambda )\mu )f_{j}(y) dy =\lambda {\int \limits }_{a_{j}}^{b_{j}} y f_{j}(y) dy+(1-\lambda )\mu {\int \limits }_{a_{j}}^{b_{j}} f_{j}(y) dy=\lambda \mu _{j}+(1-\lambda )\mu$. So we can evaluate the variability between groups after the squeeze as follows: $B^{\prime }={\sum }_{j} (\mu _{j}^{\prime }-\mu )^{2}={\sum }_{j} (\lambda \mu _{j} +(1-\lambda )\mu -\mu )^{2}={\sum }_{j} (\lambda \mu _{j} -\lambda \mu )^{2} =\lambda ^{2} B$. The variability within groups after the squeeze becomes $W^{\prime }={\sum }_{j} \frac {1}{\lambda } {\int \limits }_{\lambda a_{j}+(1-\lambda )\mu }^{\lambda b_{j}+(1-\lambda )\mu } (x-\mu _{j}^{\prime })^{2} f_{j} \left (\frac {x+(1-\lambda )\mu }{\lambda }\right ) dx=\\ {\sum }_{j}{\int \limits }_{a_{j}}^{b_{j}}(\lambda y+(1-\lambda )\mu -\lambda \mu _{j}-(1-\lambda )\mu )^{2}f_{j}(y) dy=\\ {\sum }_{j}{\int \limits }_{a_{j}}^{b_{j}}\lambda ^{2} (y-\mu _{j})^{2} f_{j}(y) dy=\lambda ^{2}W$. So the polarization becomes $P(B^{\prime },W^{\prime },\mathbf {p},M)=\frac {B^{\prime }}{B^{\prime }+W^{\prime }}\cdot \psi (\mathbf {p},M)=\frac {\lambda ^{2}B}{\lambda ^{2}B+\lambda ^{2}W}\cdot \psi (\mathbf {p},M)=P(B,W,\mathbf {p},M)$. Axiom 1 is proved .

Axiom 2

Let f₁,f₂,f₃ be three basic densities of the population corresponding to three different groups and P the total polarization value. The global distribution is completely symmetric, so groups 1 and 3 have the same population and group 2 is exactly midway between them. If we operate the same squeeze to f₁ and f₃, we can prove that the polarization value is not decreasing.

First, it is possible to observe that as the squeeze is performed on f₁ and f₃ separately, the expected values μ₁ and μ₃ do not change (for Observation A.4). $P(B,W,\mathbf {p},M)=\frac {B}{B+W}\cdot \psi (\mathbf {p},M)$ where $W={\sum }_{j=1}^{3} {\int \limits }_{\text {supp} f_{j}} (x-\mu _{j})^{2} f_{j}(x) dx$ and $P^{\prime }(B,W^{\prime },\mathbf {p},M)=\frac {B}{B+W^{\prime }}\cdot \psi (\mathbf {p},M)$ where $W^{\prime }= K_{2}{\int \limits }_{\text {supp} f_{2}} (x-\mu _{2})^{2} f_{2}(x) dx+\lambda ^{2}\left (K_{1}{\int \limits }_{\text {supp} f_{1}} (x-\mu _{1})^{2} f_{1}(x) dx \\ +K_{3}{\int \limits }_{\text {supp} f_{3}} (x-\mu _{3})^{2} f_{3}(x) dx\right )<W. \\$ So we can conclude that $P^{\prime }(B,W^{\prime },\mathbf {p},M) \geq P(B,W,\mathbf {p},M)$.

Axiom 3

Let f₁,f₂,f₃,f₄ be four basic densities referred to four different groups, with mutually disjoint supports, and let the distribution of the entire population be completely symmetric. A symmetric slide of f₂ and f₃ to the side must increase the polarization.

Before the slide: $P(B,W,\mathbf {p},M)=\left (1-\frac {W}{B+W}\right )\cdot \psi (\mathbf {p},M)$ where $B={\sum }_{j=1}^{4} (\mu _{j}-\mu )^{2}=(\mu _{1}-\mu )^{2}+(\mu _{2}-\mu )^{2}+(\mu _{3}-\mu )^{2}+(\mu _{4}-\mu )^{2}$ After the slide, because of the symmetry of the transformation, the global mean μ does not change while the means of f₂ and f₃ become respectively μ₂ − δ and μ₃ + δ. So we obtain the following: $B^{\prime }= (\mu _{1}-\mu )^{2}+(\mu _{2}-\delta -\mu )^{2}+(\mu _{3}+\delta -\mu )^{2}+(\mu _{4}-\mu )^{2}\\ =(\mu _{1}-\mu )^{2}+(\mu _{2}-\mu )^{2}+\delta (\delta -2\mu _{2}+2\mu ) \\ +(\mu _{3}-\mu )^{2}+\delta (\delta +2\mu _{3}-2\mu )+(\mu _{4}-\mu )^{2}$ where δ(δ − 2μ₂ + 2μ) > 0 and δ(δ + 2μ₃ − 2μ) > 0 under the hypothesis that μ₂ < μ and μ₃ > μ and $B^{\prime }>B$. Thus, we obtain that $P^{\prime }(B^{\prime },W,\mathbf {p},M)>P(B,W,\mathbf {p},M)$.

Axiom 4

Considering two different distributions referred to the same population, the function η(B,W) is not affected by the scaling transformation of the two distributions.

So if P_F(B_F,W_F,p_F,M) > P_G(B_G,W_G,p_G,M),

then $\frac {\max \limits _{j}{{p_{j}^{F}}}- \frac {1}{N}}{\frac {N-2}{N}}>\frac {\max \limits _{j}{{p_{j}^{G}}}- \frac {1}{N}}{\frac {N-2}{N}}$.

Then we can trivially show that P_qF(B_qF,W_qF,p_qF,M) > P_qG(B_qG,W_qG,p_qG,M) with q a non-negative integer value. Indeed: $\frac {\max \limits _{j}{p_{j}^{qF}}- \frac {1}{qN}}{\frac {qN-2}{qN}}>\frac {\max \limits _{j}{p_{j}^{qG}}- \frac {1}{qN}}{\frac {qN-2}{qN}}$. We conclude that the measure proposed is a multidimensional polarization measure.

Appendix B

The performance of the splitting criteria under comparison is evaluated on 18 different real datasets, coming from the UCI repository (Dua and Graff 2017). In this section, detailed information on each dataset are reported.

Banknote authentication

Data were extracted from images that were taken from genuine and forged banknote-like specimens. For digitization, an industrial camera usually used for print inspection was used. The final images have 400 × 400 pixels. Due to the object lens and distance to the investigated object, gray-scale pictures with a resolution of about 660 dpi were gained. Wavelet Transform tool was used to extract features from images.

Breast

The dataset contains information about samples that arrive periodically as Dr. Wolberg reports his clinical cases. The database therefore reflects this chronological grouping of the data and contains 8 groups of patients.

Breast cancer

This is one of three domains provided by the Oncology Institute that has repeatedly appeared in the machine learning literature (see also lymphography and primary-tumor). It contains clinical informations about patient with breast cancer. This data set includes 201 instances of one class and 85 instances of another class. The instances are described by 9 attributes, some of which are linear and some are nominal.

Breast coimbra

The dataset contains clinical features that were observed or measured for 64 patients with breast cancer and 52 healthy controls. There are 10 predictors, all quantitative, and a binary dependent variable, indicating the presence or absence of breast cancer. The predictors are anthropometric data and parameters which can be gathered in routine blood analysis. Prediction models based on these predictors, if accurate, can potentially be used as a biomarker of breast cancer.

Car

Car Evaluation Database was derived from a simple hierarchical decision model originally developed for the demonstration of DEX, as described in Bohanec and Rajkovic (1990). The model evaluates cars according to the following concept structure: car acceptability is estimate by overall price (that is divided in buying price and price of the maintenance) and technical characteristics detailed as confort (number of doors, capacity in terms of persons to carry and size of luggage boot) and safety.

CRX

This dataset contains informations that concerns credit card applications. All attribute names and values have been changed to meaningless symbols to protect confidentiality of the data. This dataset is interesting because there is a good mix of attributes: continuous, nominal with small numbers of values, and nominal with larger numbers of values. There are also a few missing values.

Fertility

A total of 100 volunteers provide a semen sample analyzed according to the WHO 2010 criteria. Sperm concentration is related to socio-demographic data, environmental factors, health status, and life habits

Glass

This data are from USA Forensic Science Service; it contains 6 types of glass defined in terms of their oxide content (i.e., Na, Fe, K). The study of classification of types of glass was motivated by criminological investigation.

Haberman

The dataset contains cases from a study that was conducted between 1958 and 1970 at the University of Chicago’s Billings Hospital on the survival of patients who had undergone surgery for breast cancer.

Hepatitis

This dataset contains medical information about a group of 155 people with acute and chronic hepatitis, initially studied by Peter B. Gregory of the Stanford University School of Medicine. Among these 155 patients, 33 died and 122 survived, and for each of them, 19 variables, such as age, sex, and the results of standard biochemical measurements, are collected. The aim of the dataset is to discover whether the data could be combined in a model that could predict a patient’s chance of survival. See Diaconis and Efron (1983).

Horse colic

This dataset contains health information about horses in order to predict whether or not a horse can survive, based upon past medical conditions.

Krkp

The Chess Endgame Database for White King and Rook against Black King (KRK) contains information on chess end game, where a pawn on a7 is one square away from queening. The main aim is to predict the outcome of the chess endgames; thus, the target variable contains two possible values: White-can-win (“won”) and White-cannot-win (“nowin”).

Lymph

This is one of three domains provided by the Oncology Institute that has repeatedly appeared in the machine learning literature. The aim of this dataset is to make a lymphatic diseases diagnosis observing different information extracted through medical imaging techniques; four different diagnoses are possible: normal, arched, deformed, displaced.

Post-operative

Because hypothermia is a significant concern after surgery, in this dataset, different attributes which correspond roughly to body temperature measurements are collected from 87 different patients. The aim of this dataset is to determine where patients in postoperative recovery area should be sent to next. In particular, three different decisions can be taken: I (patient sent to intensive care unit), S (patient prepared to go home), and A (patient sent to general hospital floor).

Scale

In this dataset, results of a psychological experiment are collected observing tips of 625 patients. Four attributes are collected for each sample: the left weight, the left distance, the right weight, and the right distance. Each example is then classified as having the balance scale tip to the right, tip to the left, or be balanced.

Sonar

This dataset is composed by 208 sonar signals bounced off a metal cylinder or a roughly cylindrical rock. For each signal, we have a set of 60 numbers in the range 0.0 to 1.0, representing the energy within a particular frequency band, integrated over a certain period of time. The integration aperture for higher frequencies occurs later in time, since these frequencies are transmitted later during the chirp. The target variable associated with each record contains the letter “R” if the signal is bounced off a rock and “M” if it is bounced off a mine (metal cylinder).

Spectheart

Diagnosing of cardiac single proton emission computed tomography (SPECT) images are described in the dataset. The database of 80 SPECT image sets (patients) was processed to extract features that summarize the original SPECT images. As a result, 44 continuous feature patterns were created for each patient and then each pattern was further processed to obtain 22 binary feature patterns. Each of the patients is classified into two categories: normal and abnormal, contained in the target variable.

Wine

The wine dataset contains the results of a chemical analysis performed on three different types of wines grown in a specific area of Italy. A total of 178 samples are analyzed and 13 different attributes are recorded for each sample. The target variable is a three classes categorical variable representing the analyzed type of wine.