Abstract
Imagine that the judgments of some individuals on some issues are aggregated into collective judgments. Social deliberation about the issues prior to aggregation can lead to improved judgments, at both the individual and the collective level. In this paper I argue that the epistemic justification for a social deliberation design depends on the chosen judgment aggregation rule, and vice versa. This claim consists of two parts. First, the epistemic superiority of one deliberation design over another or over the absence of any deliberation depends on which procedure is subsequently used to aggregate individual judgments. Second, the epistemic superiority of one aggregation procedure over another depends on how the preceding social deliberation was designed. In short, the choice of deliberation design and of aggregation rule are intertwined. This claim is substantiated by two models. Both models display a tragic rise in competence: social deliberation raises individual competence while reducing collective competence. Here, individual and social epistemology come interestingly apart.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
People routinely disagree about what is the case, or what consequences their actions will bring about. Opponents of universal basic income might believe it will hurt the economy by disincentivizing work, while proponents could argue that it would bolster the economy by empowering people to pursue careers where they add the most value. Almost all climate scientists view human carbon emissions as a driver of climate change, while the deniers cast doubt on this consensus. Securities analysts routinely disagree about the prospects of the companies they cover.
Disagreement can be productive. In a scientific field, disagreement leads researchers to explore different solutions to a problem, resulting in a more efficient allocation of resources (Kitcher 1990; Goldman and Shaked 1991; Muldoon and Weisberg 2009; De Langhe 2014). Even in more mundane argumentative exchanges, disagreement can propel the participants into an exhaustive search for reasons to support their case, thereby allowing for more thoroughly considered standpoints (Mercier and Sperber 2017). Despite our disagreements, however, we sometimes need to arrive at collective decisions. Collective decisions about economic or environmental policy cannot be delayed forever. Hedge funds could not offer competitive performance if they restricted their trades to those that no analyst would disagree with. In the absence of a consensus, then, how should individual opinions be aggregated towards a collective judgment? The answer depends largely on one’s normative scope.
In this paper I focus on opinions that concern matters of fact. Moreover, my discussion is concerned with the epistemic adequacy of these collective opinions. In the philosophical literature on improving collective opinion formation, we can broadly distinguish deliberative approaches from aggregative approaches to collective opinion improvement. These approaches map onto the two stages where one might intervene in a typical collective opinion formation process: the deliberation stage and the aggregation stage. When a group needs to reach a collective judgment on an issue, the group members may choose to deliberate about it with each other. They enter this social deliberation with their pre-deliberative opinions, and leave it with updated post-deliberative opinions. These post-deliberative opinions are then aggregated towards a collective opinion, for instance by taking a majority vote. To make a better collective opinion more likely, then, we could either structure the social deliberation process to improve the post-deliberative opinions, or choose a better aggregation procedure to pool the post-deliberative opinions.
Deliberation designs and judgment aggregation rules have often been justified in isolation from each other. For instance, the literature on ‘crowd wisdom’ has promoted deliberation designs with little or no social interaction, as it warned against detrimental epistemic effects of group communication. Surowiecki (2005) concludes that collective wisdom arises when individuals make up their own minds, independently from conformity pressures exerted during social deliberation. Similarly, Sunstein (2006) enumerates a variety of potential sources of deliberation failure, such as amplification of cognitive errors, the common-knowledge effect, informational cascades, and group polarization, before concluding that “[p]rediction markets have significant advantages over deliberative processes, and in many contexts they might supplement or even replace those processes” (p. 209). In the same vein, Solomon (2006) appeals to the literature on groupthink to caution against unfettered deliberation. She challenges the “widespread and largely unquestioned” faith in the practice of rational deliberation among political philosophers and philosophers of science alike (p. 28), invoking empirical studies that show group deliberation to reduce the quality of collective decisions.
More recent research has suggested that the wisdom of crowds can benefit from social influence: when test subjects are given the opportunity to revise their independent initial opinion in light of the revealed opinions of others, the central tendency of the group moves closer towards the truth (Lorenz et al. 2011, 2015; Becker et al. 2017). Yet when individuals are exposed to social influence prior to forming their own opinion, collective competence may be harmed even if individual competence is increased (Frey and van de Rijt 2020). Accordingly, the latter authors conclude that “teams should seek to prevent the natural inclination of individuals to conform to previously expressed opinions” (p. 11). The focus here is exclusively on the epistemic effects of social deliberation. Incorporating the insight that properties of social deliberation could threaten the veracity of emerging collective opinions, many have investigated the conditions under which this is likely to occur. For example, Zollman (2007, 2010) uses computational modeling to show that a high degree of connectivity could lead a simulated group of scientists to converge on a suboptimal theory. In Hahn et al. (2018), a wide variety of social network topologies is examined to determine the effects of network structure on the accuracy of a collective opinion.
Even this small sample of the literature suggests a wide array of possible interventions that might make a more accurate collective opinion more likely: inhibiting social deliberation, reducing the amount of communication, modifying the communication structure, eliciting independent opinions to provide a ‘wise anchor’ around which the subsequent discussion can converge, and so on. Invariably, these results hold with respect to some or another measure for collective competence, and relative to some procedure that determines what the collective opinion is.
In the epistemic social choice literature, the epistemic interdependence of properties of social deliberation and desiderata for aggregation rules has begun to receive more attention. For instance, Pivato (2019) has criticized axiomatic and probabilistic justifications for epistemic social choice rules, arguing that aggregation rules should be matched to the opinion formation processes that give rise to the judgments to be aggregated. Taking up this challenge, Kao et al. (2018) develops and validates new aggregation rules to counteract individual estimation bias and social influence. Taking a different approach, Bright et al. (2018) ground their choice of aggregation rule for scientific collaborations in existing norms for scientific publishing.
Despite these recent developments in the literature on opinion aggregation, the epistemic interdependence of deliberative norms and aggregation rules remains underappreciated in the normative reflection on social deliberation. As a result, a strict separation between, on the one hand, the effects of deliberative norms on pre-deliberative opinions and, on the other hand, their effects on the epistemic adequacy of collective opinions, is rarely maintained. Typically, some aggregation method is assumed to be appropriate for pooling post-deliberative opinions, after which the resulting collective opinion is assessed on its epistemic adequacy. In many cases these choices reflect popular practices and therefore seem uncontroversial for a discussion where the focus is on deliberation designs simpliciter.
Unfortunately, when effects on opinion profiles are conflated with effects on the collective competence, we lose sight of the potential of aggregation rules to counteract deliberative failures and successes alike. After all, social influence, network topology, opinion diversity, and other such factors do not benefit or harm the collective wisdom just by themselves, they do so when matched with particular judgment aggregation rules. For this reason, any epistemically normative claim that relates constraints on social deliberation to the participants’ collective competence is aggregation-rule-dependent.
My main argument for this point of view will be presented in the context of two models. Both models show how a seemingly desirable deliberation design, when paired with an uncontroversial and popular aggregation rule, can be expected to bring about ‘tragic competence raising’. That is, it improves the individual competence of group members but reduces the competence of the group. Although my examples are idealized, they illustrate a general principle with wide applicability: the epistemic effects of social deliberation and procedures for aggregating post-deliberative opinions are inevitably intertwined.
The paper is structured as follows. In the second section, I characterize aggregation rules and epistemic norms for social deliberation. The third section lays out a simple probabilistic model of social deliberation for a binary classification task. In this model, it turns out that a deliberative norm that improves the competence of each deliberator is recommendable relative to one aggregation rule but ill-advised relative to another. In the fourth section, I show that the same result can be obtained for a numerical estimation problem. Moreover, here I present a mathematical characterization of the general fundamental tension between preserving independence and raising individual competence. Tragically, social deliberation might improve individual competence at the price of introducing correlations among the judgments of the group members, resulting in a worse collective competence. In the final section, the limitations and implications of these results are discussed.
2 Aggregation rules and deliberative norms
The general claim of this paper is that epistemic norms for social deliberation and judgment aggregation should be considered integrally. More precisely, the epistemic evaluation of social deliberation designs depends on a prior choice of judgment aggregation rule and vice versa. Before illustrating this claim, I shall briefly introduce the notions of judgment aggregation rule and social deliberation design, and explain the epistemic criterion used for ranking them.
2.1 Ranking opinion aggregation rules
Judgment aggregation can occur at any stage of social deliberation. For instance, the outcome from an initial round of judgment aggregation could form the starting point for group deliberation. Most often, however, judgment aggregation follows social deliberation.
There is a good reason for this: we almost always need to appeal to a particular aggregation procedure to obtain a collective judgment from social deliberation. Indeed, the only scenario in which the collective judgment does not saliently depend on the choice of aggregation rule is one where the group has reached a consensus. However, that is only in virtue of an implicitly accepted constraint on candidate aggregation rules called unanimity preservation, that is, the condition that “[i]f all individuals hold the same attitudes towards all propositions, then these unanimously held attitudes are the group attitudes” (List and Pettit 2011, p. 55).
I take a judgment aggregation rule to be a function that maps a set of individual attitudes to a single collective attitude. My scope will be constrained to the doxastic attitude of ‘belief’, interchangeably referred to as ‘estimate’, ‘opinion’, or ‘judgment’. Collective opinion formation consists of two phases. In the first, deliberative phase, the participants discuss their individual judgments as well as their reasons for them. In the second, aggregative phase, their post-deliberative judgments are aggregated according to some rule.
This analytic distinction between social deliberation and judgment aggregation is not always so clear in practice. Social deliberation can involve forms of negotiation where participants make compromises with the aim to arrive at sufficiently similar post-deliberative judgments. Indeed, such maneuvers might be critical to winning a majority vote or reaching a consensus. When social deliberation and aggregation are thus intertwined, their epistemic effects are all the more strongly connected. Yet under the idealization that social deliberation and judgment aggregation can be strictly separated, the interdependence of the epistemic effects of deliberation designs and aggregation rules does not disappear.
Normatively speaking, the recommendability of an aggregation rule must be assessed relative to some value that we seek to realize. In this paper, I am only concerned with the epistemic fitness of aggregation rules. Specifically, I evaluate one rule as preferable over another if the collective judgments it produces are more likely to be accurate. As such, I adopt a broadly externalist perspective from which the capacity to reliably produce accurate judgments takes priority over, say, an agent’s introspective awareness of the reasons that justify those judgments.
None of this should be taken to suggest that there are no desirable non-epistemic or epistemologically internalist objectives that aggregation procedures should be designed to achieve. A more democratic aggregation rule could promote group member engagement and better legitimize collective decisions, even if it were epistemically inferior to a less democratic rule. In order to focus on the epistemic aspects of collective opinion formation, however, I set such non-epistemic values aside. Only the epistemic adequacy of the collective judgment resulting from aggregating individual judgments will determine the ranking of different judgment aggregation rules.
2.2 Evaluating social deliberation designs
One of the main purposes of social deliberation is to enable the formation of better judgments through dialogue. The participants can share information, raise questions, pose challenges, gauge each other’s interests and competences, direct attention to different issues, et cetera. Some dialogues may continue into perpetuity. However, if a collective judgment has to be reached in finite time, then social deliberation must eventually come to an end. At that point, it is desirable that the outcome of social deliberation meets our standards for epistemic adequacy.
Since there are endless possibilities for deliberating together, a deliberation designer faces a multitude of choices: who should participate, which topics should be discussed, how should participants communicate with each other, what rules should be followed, and so on. Assuming that the deliberation designer is primarily interested in the epistemic adequacy the deliberation outcomes, what norms should her choices adhere to?
Some general norms for epistemic adequacy, or epistemic norms for short, are widely acknowledged and violations of such norms are easy to recognize. Examples of conspicuous violations of epistemic norm include adopting logically inconsistent beliefs or failing to calibrate one’s beliefs to relevant empirical findings. Epistemic norms are justified if following their precepts helps us avoid making erroneous judgments. Put differently, epistemic norms can be evaluated on their ability to facilitate the formation of judgments that meet some standard of epistemic adequacy.
The normative scope of this paper only covers the accuracy of the collective judgment. From this perspective, epistemic norms for social deliberation are to be evaluated on how well they support the formation of accurate collective judgments. Moreover, this normative standard can be applied broadly to any constraint on social deliberation that a deliberation design imposes.
Throughout this paper, the accuracy of the collective judgment will be the criterion for epistemically ranking social deliberation designs. It may be tempting to think of features of social deliberation as desirable in and of themselves. For instance, we might want deliberators to keep an open mind. Such features might well tend to benefit the epistemic adequacy of the deliberators’ individual judgments. However, the collective epistemic benefits of such features are unavoidably aggregation-rule-dependent, or so I will argue.
3 A binary classification problem
In this section I describe a simple model to demonstrate the interdependence of deliberation designs and aggregation rules. We consider two aggregation rules, the dictatorship rule and the majority rule. For each aggregation rule, we consider (i) the non-deliberation design that marks the absence of social deliberation prior to judgment aggregation, (ii) two different deliberation designs where individuals deliberate together.
Suppose that we wanted to rank aggregation rules based on the probability that the group judgments that they give us are correct. For the following model, it is shown that the majority rule may then perform better in the absence of social deliberation, while the dictatorship rule could perform better in its presence. Furthermore, it is demonstrated that the epistemic ranking of deliberation designs can be aggregation-rule-dependent as well.
3.1 The model
Consider a group of deliberators tasked with estimating whether some numerical quantity, such as the number of asbestos fibers per liter of air in a building, exceeds a given regulatory limit. Assume that these estimates can take only one of two values: ‘safe’ if it is deemed below the limit, and ‘unsafe’ otherwise. A deliberator can thus err in two different ways: she might judge a safe building to be unsafe, or judge the building safe when it is not. We shall assume that avoiding each type of error is equally difficult.
Because of the assumption that both types of error are equally likely, we can build up the model with a single variable that encodes correctness. We represent each individual i’s judgment as a Bernoulli random variable \(X_{i}\) that takes either of two values, correct (1) or incorrect (0). So, \(P\left( X_{i}=1\right) \) represents i’s probability of producing a correct safety assessment. To denote the event that a variable takes a particular value, I add this number in superscript. For instance, \(X_{i}^{1}\) is equivalent to \(X_{i}=1\).
A few more assumptions are made about the deliberators. In realistic decision-making scenarios the judgments of deliberators typically fail to be probabilistically independent, due to the presence of common causes. Such common causes include non-deliberative causes, such as the state of the world that the deliberators are attempting to match (e.g., the actual number of asbestos fibers in the building), or any number of confusing, helpful, or misleading environmental and evidential factors that exert their influence on the deliberators. Likewise, it may include deliberative causes, that is, those causes that come about as a result of one’s choice of deliberation design.
In order to preserve independence, we can conditionalize on these common causes (Dietrich and Spiekermann 2021). This makes it possible to represent the deliberators as conditionally independent Bernoulli random variables. For simplicity, I also assume conditional identical distribution. That is, everyone has the same conditional competence. By implication, the deliberators are interchangeable and their judgments are also unconditionally identically distributed, that is, for any two individuals i and \(i'\), \(P\left( X_{i}^{1}\right) =P\left( X_{i'}^{1}\right) \).
The epistemic performance of a given deliberation design can vary depending on causes that are external to it. In order to evaluate the effects of deliberation designs, then, we separate deliberative causes from non-deliberative ones. Let variable U denote all non-deliberative common causes of individual judgments for a type of decision problem. Then for any two individuals i and \(i'\) prior to deliberation, \(P(X_{i}^{1}|U)=P(X_{i}^{1}|X_{i'}^{1},U)\). For some values u the probability of a correct individual judgment \(P(X_{i}^{1}|u)\) might be high, signaling that it is relatively easy to infer the correct answer from the commonly available evidence. For other values it might be low, indicating instead that the problem is difficult. The available evidence may be confusing, insufficient, or misleading, or inferring the correct answer from the evidence might require some skill that none of the group members possess.
For each instance u of U, let us call the correctness probability \(P\left( X_{i}^{1}\mid u\right) \) the difficulty level of u. That is, for any correctness probability p there is a subset of the range of U consisting of all u with difficulty level p. While there can be many difficulty levels, we will focus on two events: the event E (for ‘easy’) that \(p>\frac{1}{2}\), and the event \(\lnot E\) (for ‘difficult’) that \(p<\frac{1}{2}\). For the sake of simplicity, we ignore the (zero-probability) event that the difficulty level is exactly \(\frac{1}{2}\). In other words, the set of values u of U is partitioned into those of some difficulty level above \(\frac{1}{2}\) and those of some difficulty level below \(\frac{1}{2}\). We will assume that individual judgments are conditionally i.i.d., regardless of whether we conditionalize on E or \(\lnot E\). Both of these events are assumed to have a non-zero probability.
The collective opinion will be determined by either the dictatorship rule or the majority rule. The dictatorship rule takes the post-deliberative judgment of one single individual as the collective judgment, and a correct dictatorship judgment is denoted by \(X_{d}^{1}\). Since all deliberators are interchangeable, the probability of a correct dictatorship judgment equals the probability of a correct judgment from any arbitrary individual. In contrast, the majority rule outputs the majority verdict of the deliberators, and a correct majority judgment will be denoted by \(X_{maj}^{1}\). These rules are then ranked by their probability of producing a correct collective opinion.
3.2 The non-deliberation design
In the non-deliberation design the deliberators do not affect each other’s judgments. Let us now evaluate how the dictatorship rule stacks up against the majority rule. The unconditional probability of a correct dictatorship judgment in the non-deliberation design is given by the probability-weighted average competence,
How does this compare to the performance of the majority rule? Let the total number of correct votes be denoted by the random variable \(X=\sum _{i=1}^{n}X_{i}\) that takes some value s equal to the number of ones in the series up to n. By the law of total probability,
Because \(X_{1},...,X_{n}\) are independent and identically distributed given any u, X is a binomial variable given any u.
Let \(X_{maj}^{1}=\underset{s>\frac{n}{2}}{\bigcup }X^{s}\) denote a correct majority judgment. Since \(P\left( X_{i}^{1}|E\right) >\frac{1}{2}\), the Condorcet Jury Theorem implies that \(P\left( X_{maj}^{1}|E\right) \) monotonically increases in the (odd) group size n and approaches 1. The opposite holds for \(P\left( X_{maj}^{1}|\lnot E\right) \): since \(P\left( X_{i}^{1}|\lnot E\right) <\frac{1}{2}\), the probability of a correct majority monotonically decreases in the (odd) group size n, converging to zero. This implies that the unconditional probability of a correct majority judgment \(P\left( X_{maj}^{1}\right) \) tends to \(P\left( E\right) \) as the (odd) group size increases.
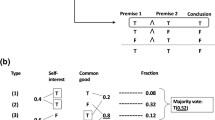
Meanwhile, from Eq. (1) it follows that the probability of a correct individual judgment ranges between \(P\left( X_{i}^{1}|E\right) \) and \(P\left( X_{i}^{1}|\lnot E\right) \). Since all individuals are interchangeable, the same is true for the judgment of a randomly selected dictator. For instance, assume that \(P\left( X_{i}^{1}|E\right) =0.6\) and \(P\left( X_{i}^{1}|\lnot E\right) =0.4\). Then the dictatorship competence \(P\left( X_{d}^{1}\right) \) is bounded by the interval \(\left[ 0.4,0.6\right] \). Figure 1 shows that whether the majority rule outperforms or underperforms the dictatorship rule depends on the probability that the problem is easy.Footnote 1
For \(P\left( E\right) <\frac{1}{2}\), majority competence underperforms dictatorship competence, while for \(P\left( E\right) >\frac{1}{2}\) majority competence is greater.Footnote 2
In order to make intuitive sense of this phenomenon, recall that the classic Condorcet Jury theorem rests of two conditions: individual competence and probabilistic independence. If the problem is difficult or misleading enough, each individual’s competence falls below \(\frac{1}{2}\). It is then unsurprising that the majority performs even worse than any single individual. One might attempt to avoid this outcome by means of boosting individual competence. However, the two conditions of competence and independence are rarely jointly satisfied. Hence, a competence-boosting deliberation phase could introduce probabilistic dependencies that also result in a loss of collective competence. This is a well-known trade-off, sometimes called the ‘fundamental tension’ between independence and competence (Dietrich and Spiekermann 2021). In section (4) I present a formal characterization of this tension.
A more modest version of Condorcet Jury Theorem relativizes the assumption of individual competence to some reference class of decision problems for which the common causes are not misleading. If individuals are most likely to form incorrect judgments, the majority judgment is even more likely to be wrong. Hence, the epistemic ranking of the two considered aggregation rules above depends on the probability that the problem to be solved is sufficiently easy. Hence, the importance of ensuring that common causes are not misleading depends on the chosen aggregation rule. Although we have only discussed non-deliberative common causes so far, the next subsection will apply the same reasoning to argue for the interdependence of aggregation rules and deliberation designs.
3.3 The deliberation designs
I will now show that the epistemic ranking of two aggregation rules, the dictatorship rule and the majority rule, sometimes depends on the chosen deliberation design. Suppose public group deliberation is introduced to increase the probability that the collective judgment is correct. The deliberation design influences how group members reason among each other by imposing some set of norms or constraints that generate deliberative common causes of the individuals’ judgments. I will understand these deliberative common causes to be the totality of what has been publicly communicated during deliberation. Let variable V denote all possible deliberative common causes, and v denote an instance of V. Assuming that a group can choose from a countable set of deliberation designs, let variable \(V_{j}\) be the partition of the range of V where the deliberation design of v is of type \(j\in \mathbb {{\mathbb {N}}}\).
In contrast to the non-deliberation design, conditioning on non-deliberative common causes is no longer enough to make individual judgment probabilistically independent. Instead, they are assumed probabilistically independent and identically distributed only conditional on all common causes, including deliberative ones. That is, for any two individuals i and \(i'\) and all designs j, \(P\left( X_{i}^{1}\mid U,V_{j}\right) =P\left( X_{i}^{1}\mid X_{i'}^{1},U,V_{j}\right) \).Footnote 3
The impact of some combination of deliberative and non-deliberative common causes \(\left( u,v\right) \) on individual competence can be positive, zero, or negative. I do not assume that the impacts of deliberative and non-deliberative common causes are probabilistically independent. Hence, I define a partition over the set \(W=U\times V\) whose elements are ordered pairs \(\left( u,v\right) \), with the following indicator function:
For each design j, there is a set of deliberative common causes instantiating it, \(V_{j}\), and a set of possible non-deliberative common causes U. The random variable \(W_{j}\) then expresses the competence impact of j in a certain context and
where the competence impact result \(r\in \left\{ -,0,+\right\} \). In other words, for all agents the individual competence increases in the event that \(W_{j}^{+}\), decreases if \(W_{j}^{-}\), and remains identical for \(W_{j}^{0}\).
By the law of total probability, the conditional probability of a correct individual judgment given any deliberation design j equals the probability-weighted average
Assume that individual judgments are probabilistically independent and identically distributed when conditionalized on any competence impact of the implemented deliberation design. The probability of a correct majority judgment can then be expressed straightforwardly by substituting \(X_{maj}^{1}\) for \(X_{i}^{1}\) in Equation (4) to obtain \(P\left( X_{maj}^{1}\mid V_{j}\right) =\sum _{r}P\left( X_{maj}^{1}\mid W_{j}^{r}\right) P\left( W_{j}^{r}\right) .\) Moreover, we can express the probability of a correct majority judgment in terms of the probability of a correct individual judgment. Let the sum of correct judgments from a group of n deliberators be denoted by random variable \(X=\sum _{i=1}^{n}X_{i}\). Assuming that \(X_{1},...,X_{n}\) are independent identically distributed Bernoulli variables conditional on any value of the competence impact \(W_{j}\), X has a binomial distribution. Let \(m=\lfloor \frac{n}{2}+1\rfloor \) denote the smallest number of judgments required for a majority in a finite group. Since the conditional probability of the number of correct judgments is based on the cumulative binomial distribution, we know that
where \(p_{V_{j}}=P\left( X_{i}^{1}\mid V_{j}\right) \).
As we saw in the previous subsection, the dictatorship rule outperformed the majority rule when the non-deliberative common causes were misleading. There is ample evidence that social deliberation tends to make majority judgments less accurate if the commonly available evidence is misleading (cf. Lu et al. 2012). One might thus expect that an interdependence of deliberation design and aggregation rule again hinges on the probability of encountering misleading common evidence. However, it suffices that social deliberation itself sometimes reduces individual competence to a certain extent.
Consider two deliberation designs, (1) and (2), with the following probability distributions:
We can see that the two deliberation designs are equally likely to improve individual competence, yet (1) has a larger probability of reducing individual competence than (2) does. Assume further that the conditional probabilities for correct individual judgments are the following:
So while (1) poses a larger risk of reducing individual competence, it yields a correct individual judgment whenever its effect is beneficial with certainty, unlike (2).
How do the majority rule and the dictatorship rule compare with respect to their epistemic performance, between the different deliberation designs? For any design j, Equation (4) gives the probability-weighted average competence of the dictator. Meanwhile, we can reason about the majority competence in the limit of the group size. For the majority rule, the probability of a correct collective judgment converges to certainty whenever common causes have a neutral or beneficial effect. However, whenever they have a competence-decreasing impact, this probability converges to 0. This means that we can approach the question again with a version of the Condorcet Jury Theorem.
For design (1), the majority competence given by \(\sum _{r}P\left( X_{maj}^{1}\mid W_{1}^{r}\right) P\left( W_{1}^{r}\right) \) converges to \(1-P\left( W_{1}^{-}\right) =0.7\), as \(n\rightarrow \infty \). The probability of a correct dictatorship judgment is 0.78. Hence, majority rule underperforms dictatorship rule in the limit of n. In contrast, for design (2), \(\sum _{r}P\left( X_{maj}^{1}\mid W_{2}^{r}\right) P\left( W_{2}^{r}\right) \rightarrow 1-P\left( W_{2}^{-}\right) =0.8\), as \(n\rightarrow \infty \). However, the probability of a correct dictatorship judgment is only 0.62. Here, the majority rule outperforms the dictatorship rule in the limit.
The optimal choice of aggregation rule can also depend on the choice of deliberation design when the group size is much smaller. In Figs. 2 and 3 below, the majority competence for the deliberation designs is plotted as a function of the group size.Footnote 4 The horizontal line represents individual or dictatorship competence, which is equal to majority competence with \(n=1\). For design (1), we see that the majority rule underperforms the dictatorship rule for all \(n>1\), but for design (2), the majority rule outperforms the dictatorship rule for all positive \({\mathbb {N}}\backslash \{1,2,4,6\}\).
Thus, the epistemic ranking of these aggregation rules differs between (1) and (2) for all group sizes except \(\{1,2,4,6\}\). Furthermore, the epistemic ranking of the two deliberation designs is aggregation-rule-dependent for \(n>14\), where design (2) reaches a higher majority competence than design (1). This illustrates my claim that the epistemic justification for deliberation designs and judgment aggregation rules should not be divorced from each other.
3.4 Discussion
One might suspect that the conclusions from the previous subsection are drawn too hastily. Does the result perhaps depend on the assumption that a deliberation design sometimes reduces individual competence? Surely, if it were guaranteed to improve individual accuracy at all times, its epistemic justification would be insensitive to our choice of judgment aggregation rule? I have three responses to this concern.
First, it is important to emphasize that guaranteeing the improvement of individual accuracy with certainty is a rather tall order. In reality, the effects of a deliberative constraint on the opinion dynamics leading up to the post-deliberative opinion profile can critically depend on the broader context of the deliberation. For example, a deliberative norm that encourages deliberators to seek exclusively arguments that support their own position might often succeed in getting a greater number of relevant arguments on the table, given that the deliberators are heterogeneous in their opinions. However, the same norm could possibly cause a homogeneously opinionated group to run into the problem of groupthink, resulting in its convergence on a wrong judgment (cf. Mercier and Sperber 2017). Whether a deliberation design improves everyone’s individual accuracy can thus depend on characteristics of the deliberating group.Footnote 5
Second, there are judgment aggregation rules that perform worse as individual competence increases. Imagine if the chosen aggregation rule were the minority rule that identifies the collective opinion with the least popular opinion, or the anti-unanimity rule that takes the opinion that none of the group members believe to be correct. Governed by such strange aggregation rules, our deliberative designs should instead aim to impair the individual competence. One could reject such aggregation rules as outlandish, but the general point remains. Relative to a narrow subset of aggregation rules, the best choice of deliberation design might indeed remain invariant. However, such a restriction can simultaneously conceal combinations of deliberation designs and aggregation rules that generate even better collective competences.
Third, recall that Jury Theorems rely on two assumptions: (some form of) individual competence and (some form of) probabilistic independence among jury members (Dietrich and Spiekermann 2021). There is a strong tension between these assumptions, precisely because the pursuit of increasing individual competence typically weakens their independence considerably. Yet as soon as we give up the assumption of (conditional) independence, the interdependence of epistemic effects of social deliberation designs and judgment aggregation rules does not disappear even if a deliberation design always improves individual judgments.
Consequently, a deliberation design can impair the epistemic performance of a collective even though it never impairs individual competence. As I will go on to show for numerical estimation problems, this effect can occur relative to the simple (unweighted) averaging rule, one of the most popular aggregation rules in the crowd wisdom literature.
4 A numerical estimation problem
This section is devoted to a discussion of the relation between deliberative norms and aggregation rules in the context of numerical estimation problems. In the previous section, an estimate for the number of asbestos particles only needed to be on the correct side of the safety threshold to be correct. However, if we wanted to use the wisdom of the crowd to estimate not just whether a building is safe, but exactly how safe it is, we should aggregate the individual numerical estimates themselves.
First I adapt the previous model to accommodate aggregation of numerical estimates. The epistemic ranking of deliberation designs and aggregation rules is here determined by the expected squared error of the collective estimate. After introducing the model, I present an example of ‘tragic accuracy improvement’, where collective accuracy is reduced while individual accuracy is increased. I then show that, in the limit of the number of deliberators, this phenomenon can occur under the simple averaging rule even when neither deliberative nor non-deliberative causes have a detrimental effect on individual competence. This implies that deliberative norms and judgment aggregation rules can also be epistemically interdependent in the context of numerical estimation tasks.
4.1 The model
Let us consider the scenario where deliberators make numerical estimates. During their collective deliberation they share their estimates and discuss their reasons, until their post-deliberative judgments are aggregated towards a group estimate. The error of a judgment is taken to be a function of its numerical distance from a target value. Deliberator competence is still understood in terms of the expected error of their estimates.
I introduce a random variable D, called the decision problem. An instance d of D is to be interpreted as one of finitely many possible realizations of the state of world that determines the quantitative target value t that the deliberators are trying to estimate.Footnote 6 It is important to distinguish between the decision problem from the point of view of the agents, who do not know the target value they are estimating, and the decision problem from the point of view of the modeler, who does know it. We will be concerned only with the latter and therefore we can calculate quantities based on the target value of any arbitrary d in order to evaluate how the agents are expected to fare.
Let \(\left\{ d_{0},...,d_{n}\right\} \) be a partition of the sample space S. I formally define \(D:S\rightarrow {\mathbb {R}}\), such that \(D\left( s\right) =t_{i}\) whenever \(s\in d_{i}\). For the sake of exposition, I will sometimes interchangeably refer to d as an instance or value of D. I assume that D has an unknown probability distribution \(P\left( D\right) \) and each instance of D has positive probability.
Besides the fact that determines the target value, deliberators can be influenced by environmental factors. In order to model this, let the partition \({\dot{Z}}\) capture a finite set of causal contexts. Here, \({\dot{Z}}\) gives us the most fine-grained description of all causes of all individuals’ judgments other than the facts that constitute the decision problem itself. Whereas deliberative and non-deliberative common causes were kept separate in the previous section, they are now both included in \({\dot{Z}}\), together with non-common causes.Footnote 7 Let the partition \(Z=\left\{ Z_{j}\right\} _{j\in n}\) be a coarsening of \({\dot{Z}}\), such that each member \(Z_{j}\in Z\) denotes a different deliberation design. An unknown probability distribution \(P\left( Z_{j}\mid D\right) \) is defined over the partition Z.
In what follows, I analyze individual and collective errors conditional on an arbitrary instantiation of the decision problem. That is, all probabilities, expectations, biases, variances, covariances, and other probabilistic properties are conditional on arbitrary instance d of D.Footnote 8 An individual deliberator working on a specific decision problem realization d under deliberation design \(Z_{j}\) is modeled by random variable \(X_{i}\), with some probability distribution \(P\left( X_{i}\mid d,Z_{j}\right) \).
I use the notational convention \(X_{i,D,Z}\) for the random variable \(X_{i}\) distributed according to \(P\left( X_{i}\mid D,Z\right) \), where D and Z can take on values d and \(Z_{j}\).Footnote 9 Alternatively, I use \(X_{i,d,Z_{j}}\) for the random variable \(X_{i}\) distributed according to \(P\left( X_{i}\mid d,Z_{j}\right) \), where the latter probability distribution is defined over the sub-sample space that corresponds with the realization of the specific decision problem instance d under the specific deliberation design \(Z_{j}\). Further, I model each individual deliberator \(X_{i,D,Z}\) or \(X_{i,d,Z_{j}}\) as an unbiased Gaussian random variable that scatters around the target value t with some variance. Being unbiased, the deliberators are just as likely to underestimate the truth as they are to overestimate it. In contrast to the model from the previous section, deliberators need not be interchangeable and can differ with respect to their variance around the target. Let us now consider how introducing social deliberation might change the accuracy of a single collective judgment.
Assume that the introduction of a deliberation design has two effects. First, the deliberation improves the competence of each deliberator. To be clear, this notion of competence is to be understood in terms of expected accuracy, where the expectation is taken over a set of instances of the estimation problem. Second, by promoting the exchange of evidence, social deliberation introduces positive pairwise correlations between the deliberators. We will assume no such correlations in the absence of deliberation. For the aggregation rules, we will compare the dictatorship rule with the simple averaging rule, which makes the arithmetic mean of the individual estimates the collective estimate.
In Sects. 4.3 and 4.4 I show that social deliberation can impair the accuracy of the collective judgment under the simple averaging aggregation rule. Since this is somewhat counterintuitive, I first present an example of a scenario where the group judgment suffers although all group members submit more accurate judgments to aggregate.
4.2 An instance of tragic accuracy improvement
To adapt an example from (Lyon and Pacuit 2013, sec. 4), suppose that the true number of asbestos fibers per liter of air inside a building is 60. Prior to deliberation, a group of 10 deliberators, labeled a, ..., j, produces the following initial estimates: 85, 82, 80, 78, 70, 55, 50, 45, 40, and 39. After deliberating, the following estimates are submitted for the second round: 84, 75, 79, 77, 69, 59, 59, 60, 59, and 55.
As we can see in Table 1, in round 2 each deliberator is closer to the target value of 60 compared to the first round. Thus, under the dictatorship rule, the best group judgment can be obtained from the second round. After all, no matter who among a, ..., j is the ‘dictator’, their estimate is more accurate in round 2 than it was in round 1. Yet under the simple averaging rule, the estimates from the first round produce the better collective judgment. After all, the simple average of the estimates of round 1 is 62.4, while the simple average of the estimates of round 2 is 67.6. Hence, under the averaging rule “each individual’s estimate improves, but the group’s estimate gets worse” (ibid.).
How to diagnose the cause of this tragedy? As we can see from Table (1), each individual’s ex-post accuracy is higher than their ex-ante accuracy and the deliberators who underestimate the true value improve far more than those who overestimate it. They are more inclined to err on the side of overestimating the true number of asbestos particles than on the side of underestimating it. However understandable, the distribution of their estimates around the truth has consequently changed in such a way that their average estimate’s ex-post accuracy is lower than it’s ex-ante accuracy.
For one thing, this phenomenon should caution us about basing our decisions about whether to implement deliberative norms solely on their beneficial effects on individual accuracy. Beneficial individual-level epistemic effects are compatible with adverse effects on the collective accuracy. Yet there is a more general lesson to take away from this result. Once we recognize that the relation between individual accuracy and collective accuracy is mediated by the choice of aggregation rule, we can start looking for more suitable candidates. In this case, we observe the reluctance of deliberators to underestimate the true value, which, after deliberation, leads the underestimators to change their estimates more than the overestimators. As a result, the average of their estimates shifts away from the true value. To compensate for this bias, we could instead adopt an aggregation rule that gives underestimators more weight in the aggregation, that is, a weighted average.
The phenomenon of tragic accuracy improvement can easily arise as an unfortunate chance event: individual estimators might have high variance and yet happen to take a value close to the mean, while estimators with lower variance might happen to take a value further from the mean. Hence, this example does not show how a deliberation design could improve individual competence, that is, expected accuracy, while impairing collective competence at the same time.
We could, however, imagine how ‘tragic competence-raising’ might occur, that is, an improvement of expected individual accuracy at the cost of expected collective accuracy. For example, the deliberators’ fear of underestimating asbestos levels might make them more susceptible to social influence from overestimators. Consequently, even as individual errors become smaller after social deliberation, they become more positively correlated. In the sections below, I give a general characterization of such detrimental group dynamics.
4.3 An improvement of collective competence under dictatorship rule
I use the following notion of competence: a deliberator i is considered to have a higher competence than \(i'\), if and only if the expected error of i’s estimates is smaller than the expected error of \(i'\)’s estimates. This error will be measured according to the squared error loss function, that is, the error loss is considered to grow quadratically as estimates deviate further from the truth, in either direction.Footnote 10
The error loss incurred from a single estimate is \(\left( X_{i,d,z}-t\right) ^{2}\) for some given decision problem instance d with true value t, and further causal influences z. Accordingly, we characterize an individual’s problem specific competence in terms of the expected individual error, where the expectation is taken over all \(z\in Z\):
Since the mean of the deliberators’ distributions is centered on the true value t for all instances d and all instances z of possible causes Z, the competence of any deliberator \(X_{i,d,Z}\) is only determined by \(Var\left( X_{i,d,Z}\mid d\right) \). This can be demonstrated by decomposing the average individual error into a bias and a variance term (Geman et al. 1992).Footnote 11 For any decision problem instance d:
Here, the conditional expectation \(E_{Z}\left[ X_{i,d,Z}\mid d\right] \) is taken with respect to the problem instance specific conditional probability distribution \(P\left( Z\mid d\right) \), and \(Bias\left( X_{i,d,Z}\mid d\right) \) and \(Var\left( X_{i,d,Z}\mid d\right) \) are also both conditionalized on the specific problem realization d. Since we consider the deliberators to be unbiased, the first term on the right hand side is 0. Thus, for any instance of a decision problem, their individual competence equals \(Var\left( X_{i,d,Z}\mid d\right) \).
Assume the deliberation design (1) systematically improves individual competence, compared to the design (0) where deliberation is absent. That is, when we compare the two corresponding members of the partition Z, \(Z_{0}\) and \(Z_{1}\),
In other words, by reducing each individual deliberator’s variance, social deliberation design (1) tends to improve individual accuracy and thus increases the group competence under dictatorship rule, compared to the non-deliberation design. This result survives if we give up the assumption that deliberators are unbiased, as long as the introduction of social deliberation raises the bias by less than it lowers the variance.
4.4 Deteriorating collective competence under the averaging rule
Non-deliberation design
In the design where social deliberation is absent, let us first assume that the estimates of different deliberators are independent and uncorrelated. The assumption of uncorrelatedness is difficult to satisfy in realistic scenarios, unless the deliberators are making truly random guesses. As soon as they are influenced by a common cause, for example, the actual truth that they aim to approach, they will be correlated to some degree. Nevertheless, it is instructive to examine this simplified scenario before discussing more realistic conditions.
Given the assumptions above, it can be shown that the collective estimate produced by the simple averaging rule tends to (i) outperform the dictatorship rule and (ii) approach the truth as the number of individuals increases. The first result will be preserved when the uncorrelatedness assumption is relaxed, the second is not.
As mentioned, all n individuals are modeled by identically distributed real-valued Gaussian random variables. Let \(X_{1:n,d,Z}\) denote the set of random variables \(X_{1,d,Z},...,X_{n,d,Z}\) and let \(X_{\mu ,d,Z}\) denote the collective estimate under the simple averaging rule, where \(X_{\mu ,d,Z}=\frac{1}{n}\sum _{i=1}^{n}X_{i,d,Z}\).
By substituting \(X_{\mu ,d,Z_{j}}\) for \(X_{i,d,Z}\) in Equation (7), we get a problem instance specific ‘ambiguity decomposition’ (Krogh and Vedelsby 1994) for the average collective error, restricted to some deliberation design j:
Since \(X_{\mu ,d,Z_{j}}\) depends on \(X_{1,d,Z_{j}},...,X_{n,d,Z_{j}}\), there is an equivalent expression, known as the ‘bias-variance-covariance decomposition’, that gives us the average collective error in terms of the statistical properties of the individual deliberators. The decomposition is proved by Ueda and Nakano (1996), but their contribution concerns a regression context and their proof omits all but one intermediate step. To show that their result applies to our present discussion, I provide a detailed proof in Appendix (A.2) for the following bias-variance-covariance decomposition:
where
Since the individuals are identically distributed unbiased random variables in the non-deliberation design (0), \({\overline{Var}}\left( X_{1:n,d,Z_{0}}\mid d\right) =Var\left( X_{i,d,Z_{0}}\mid d\right) \) and \({\overline{Bias}}\left( X_{1:n,d,Z_{0}}\mid d\right) =Bias\left( X_{i,d,Z_{0}}\mid d\right) =0\).
Further, in the non-deliberation design, the individuals are uncorrelated, so for any two group members \(i,i'\) such that \(i\ne i'\), \(Cov\left( X_{i,d,Z_{0}},X_{i',d,Z_{0}}\mid d\right) =0\). Equation (9) can thus be reduced to the following equation:
Since \(\frac{1}{n}\rightarrow 0\) as \(n\rightarrow \infty \), \(E_{Z_{0}}\left[ (X_{\mu ,d,Z_{0}}-t)^{2}\mid d\right] \rightarrow 0\) in the number of individuals. In other words, the average of a set of unbiased and independent individuals converges towards the target value in the limit. This is unsurprising, as each of their judgments is sampled from the same conditional distribution, the expected value of which is centered on the target.
Deliberation design
Consider some deliberative design (1) that improves individual competence, without rendering individuals infallible. That is, \(Var\left( X_{i,d,Z_{0}}\mid d\right)>\) \(Var\left( X_{i,d,Z_{1}}\mid d\right) >0\). We might imagine group members exchanging more and better arguments, studying each other’s reasons in more depth, and so on. Yet, as a result, the deliberators become more similar, causing their estimates to be positively correlated. That is, we assume \({\overline{Cov}}\left( X_{1:n,d,Z_{1}}\mid d\right) >0\). In other words, whenever one deliberator overestimates or underestimates the truth, others are more likely to do the same.Footnote 12
Is it worthwhile to trade independence for individual competence? This question can be addressed by appealing again to the bias-variance-covariance decomposition in Equation (9). Since the deliberators are no longer considered to be independent, the covariance term does not fall out. Assuming, as before, that all group members are unbiased, we get the following expression for the error of the post-deliberative group average:
As n increases, \(\frac{1}{n}\) tends to zero and therefore \(\frac{1}{n}{\overline{Var}}\left( X_{1:n,d,Z_{1}}\mid d\right) \) tends to zero. Meanwhile, \(\left( 1-\frac{1}{n}\right) {\overline{Cov}}\left( X_{1:n,d,Z_{1}}\mid d\right) \) converges to \({\overline{Cov}}\left( X_{1:n,d,Z_{1}}\mid d\right) \).
This means that \(E_{Z_{1}}\left[ \left( X_{\mu ,d,Z_{1}}-t\right) {}^{2}\mid d\right] \) approaches \({\overline{Cov}}\left( X_{1:n,d,Z_{1}}\mid d\right) \) as the number of deliberators grows. Hence, beyond some threshold number of deliberators, deliberation design (1) increases the expected collective error compared to the non-deliberation design (0), even though it reduces the expected individual error of each deliberator. After all, the error of the average group judgment converges to zero for (0), while for design (1) it converges to the average covariance, which was assumed to have a positive value.
To conclude, our binary classification problem model’s result that the epistemic ranking of different deliberation designs is aggregation-rule-dependent extends to the real-valued quantity case. First, we have seen that the desirability of the presence of social deliberation is aggregation-rule-dependent. Moreover, it turned out that the model could express mathematically the general trade-off known as the ‘fundamental tension’ between competence and independence. If the improvement of the individuals’ competence comes with a higher positive correlation among their errors, the collective competence can suffer, depending on what aggregation rule is chosen. Second, when social deliberation is present it follows from the bias-variance-covariance trade-off in Eq. (9) that the ranking of social deliberation designs can also be aggregation-rule-dependent. In the limit of the number of deliberators, this happens as soon as one deliberation design yields greater individual competence at the price of introducing stronger positive correlations among the deliberators.
4.5 Discussion
We can make intuitive sense of the result that a large number of unbiased and uncorrelated individuals tend to generate the best collective judgment under the simple averaging rule. After all, because the deliberators are unbiased their errors are always symmetrically distributed around the truth. With a growing number of estimates these individual errors become more likely to cancel each other out in the aggregation, as long as the errors are not correlated. Consequently, the size of the individual errors matters less than the shape of the collective distribution. While an effective deliberation design can increase individual competence, a side-effect may be that individual judgments become more strongly correlated. Along the way, such a deliberation design could simultaneously impair the collective competence under the simple averaging rule.
In the non-deliberation design, I simply assumed an absence of correlation in order to facilitate the result that the expected error converges to zero in the number of group members. Yet this cannot be assumed for realistic tasks: individuals are overwhelmingly likely to be affected by common causes, ranging from exposure to a common physical environment and common evidence, to a common understanding of what the task amounts to.
Note, however, that this zero-correlation assumption can be straightforwardly weakened. Again, we compare non-deliberation design (0) and deliberation design (1). Assume now that \(0<{\overline{Cov}}\left( X_{1:n,d,Z_{0}}\mid d\right) <{\overline{Cov}}\left( X_{1:n,d,Z_{1}}\mid d\right) \) and \(0<{\overline{Var}}\left( X_{1:n,d,Z_{1}}\mid d\right) <{\overline{Var}}\left( X_{1:n,d,Z_{0}}\mid d\right) \). From Eq. (11) it follows that design (1) will underperform (0) under the simple averaging rule, beyond a certain number of deliberators. However, since we assumed \({\overline{Var}}\left( X_{1:n,d,Z_{j}}\mid d\right) =Var\left( X_{i,d,Z_{j}}\mid d\right) \) for any individual i, design (1) will outperform (0) under the dictatorship rule.
What does this mean for a smaller group of deliberators, who pool their estimates using the simple averaging rule? Trivially, for one deliberator the individual competence is all that matters. For two deliberators, i and \(i'\), the deliberation design can still improve the collective opinion as long as they become less than perfectly correlated, or their competence is greatly improved:
After all, \({\overline{Cov}}\left( X_{1:n,d,Z_{j}}\mid d\right) \le {\overline{Var}}\left( X_{1:n,d,Z_{j}}\mid d\right) \),Footnote 13 Accordingly, even if two deliberators are perfectly correlated, a reduction in \({\overline{Var}}\left( X_{1:n,d,Z_{j}}\mid d\right) \) decreases the upper bound on the error component \({\overline{Cov}}\left( X_{1:n,d,Z_{j}}\mid d\right) \). However, for any positive value for the individual variance and positive value for average pair-wise covariance, there will be a threshold number of deliberators n above which \(\frac{1}{n}{\overline{Var}}\left( X_{1:n,d,Z_{j}}\mid d\right) <\left( 1-\frac{1}{n}\right) {\overline{Cov}}\left( X_{1:n,d,Z_{j}}\mid d\right) \). If that occurs, the deliberation design reduces the collective competence under the simple averaging rule.
This result suggests that even smaller, finite groups of deliberators should reflect carefully on how they conduct their social deliberations, depending on how their individual judgments are aggregated. The more information group members learn from each other during social deliberation, the more competent they may become as individuals, but this also introduces dependencies and correlations among the deliberators’ judgments. Whether the interplay of these effects overall increases or reduces their group competence depends on the aggregation rule.
So far, only one direction of the interdependence claim has been demonstrated: the aggregation-rule-dependence of the epistemic ranking of deliberation designs. Meanwhile, it is easy to see that the expected error of the simple averaging rule can never exceed the expected error of the dictatorship rule, regardless of the chosen deliberation design.Footnote 14 However, this does not mean that simple averaging could not be outperformed by a different aggregation rule.
Consider again the scenario from Sect. 4.2 where deliberators were afraid to underestimate the level of asbestos fibers and consequently became too strongly influenced by overestimators. This caused a reduction in the accuracy of the unweighted average of their judgments even as each individual judgment improved. With the bias-variance-covariance trade-off from Eq. (9), we have a general characterization of such detrimental effects of social deliberation under the simple averaging rule. Moreover, this trade-off makes the fundamental tension between preserving independence and boosting competence mathematically precise for the squared error loss function.
This result enables, first, an explanation of how introducing positive correlations among the errors of individual deliberators can give rise to tragic competence-raising. Second, it suggests how we might compensate for these social dynamics by choosing a different judgment aggregation rule. For a final example, imagine that we could simply distinguish two sub-groups: (a) those who are susceptible to influence from overestimators and, (b) those who are not. Accordingly, the average covariance of sub-group (a) exceeds that of subgroup (b). All else being equal, the expected error of sub-group (a) would thus exceed the expected error of sub-group (b) under the simple averaging rule.
We can infer from the bias-variance-covariance trade-off that excluding the judgments from members of subgroup (b) in the simple average would reduce the covariance component of the collective error, albeit at the cost of increasing the variance component, since the latter gets smaller in the number of deliberators whose judgments are included. Nevertheless, the overall effect of adopting this new aggregation rule can be an increase in collective competence, depending on the numbers of individuals in each sub-group and the average covariance introduced by including subgroup (b).
In contrast, a deliberation design that caused an identical reduction in individual error without introducing any positive correlations among the deliberators should not be matched with this new aggregation rule, because the cost of increasing the variance component due to the exclusion of deliberators could be avoided by using the simple averaging rule. Accordingly, the epistemic ranking of judgment aggregation rules is also deliberation-design-dependent.
In the context of the binary classification problem we discussed the tension between the two pillars of Jury Theorems that use the majority rule for aggregation: the assumptions of individual competence and (some form of) probabilistic independence among judgments. The same tension shows up in the context of numerical estimation problems, relative to the unweighted averaging rule. Social deliberation may improve individual competence, but this comes at a price: the introduction of (stronger) correlations among judgments, which can impair the collective competence – depending on the aggregation rule.
5 Discussion and conclusion
I have assumed a strict conceptual distinction between social deliberation (a social process that operates on individual judgments) and judgment aggregation (the mapping of a judgment profile onto a collective judgment). Social deliberation must then necessarily be combined with some form of judgment aggregation in order to yield a collective judgment. This raises the question how we can design deliberative and aggregative practices that work in tandem to produce epistemically good outcomes. Recent work in judgment aggregation acknowledges explicitly that we need to match aggregation procedures to properties of social deliberation. For instance, Pivato (2019) concludes that “[f]uture investigations must use more sophisticated mathematical methods to develop and analyse more realistic models of voter opinion formation, which explicitly describe information flows, cognitive biases, and social influences, in order to design epistemically optimal voting rules” (p. 109).
In this paper I have argued that an analogous conclusion applies to our choice of deliberation design. Interventions on social deliberation and procedures for aggregating post-deliberative opinions have unavoidably interdependent epistemic effects. Normative reflection on the design of collective deliberation would benefit from a greater understanding of this interdependence. For instance, deliberative theorists have traditionally held in high esteem those deliberative norms that encourage an atmosphere of inclusiveness, or a mutual willingness to reconsider one’s position in light of mutual reason-giving (e.g., Bohman 1996; Cohen 1989; Habermas 1991). Such norms are typically assumed to have epistemically beneficial effects on the post-deliberative opinions that stand to emerge from social deliberation. However, even if this is accomplished on the individual level, the effect on resulting collective opinions might be epistemically detrimental. Therefore, to the extent that we are concerned with the accuracy of our collective judgments, we should ensure that our deliberative designs are matched with suitable aggregation rules.
At face value, this conclusion might seem obvious and unimportant: of course we could come up with some outlandish aggregation rule that nullifies the epistemic benefits of even the most helpful deliberative norm! However, we need invoke neither esoteric aggregation rules, nor inherently pernicious deliberation designs to realize this potential for epistemic tragedy. In this paper, I substantiated this claim by presenting two examples that show how popular democratic aggregation rules could underperform the dictatorship rule even if they were matched with a deliberation design that epistemically benefited each individual.
For a binary classification task, introducing social deliberation raised the collective competence relative to the dictatorship rule, but turned out to impair the collective competence relative to the majority rule. Or equivalently, the average post-deliberative group member judgment became more reliable than the group’s democratic majority judgment. The same aggregation-rule-dependence was illustrated for the epistemic ranking of two different social deliberation designs. Similarly, for a numerical estimation task, the introduction of a deliberation design that made each deliberator more likely to be more accurate tended to produce less accurate collective judgments, relative to the simple averaging rule. These examples caution us against choosing social deliberation designs and judgment aggregation rules in isolation from each other.
The examples in this paper have focused on two popular aggregation rules: majority rule and simple averaging. The performance of each was then compared to the collective judgment under dictatorship rule. Since the epistemic adequacy of the collective judgment under dictatorship rule was equivalent with the epistemic performance of any individual, the results of these comparisons uncovered the problem of ‘tragic competence-raising’. That is, the competence of individual group members could be improved at a loss to their collective competence - individual epistemology and social epistemology coming apart.
This equivalence with our individual competence makes the epistemic performance of the dictatorship rule of special interest. We often care not only about the effect of our social deliberation on our collective competence, but also about the effects on our individual competence. Or, at least, I submit that we care more about effects on our individual competence than about effects on what would have been our collective competence under any arbitrary aggregation rule.
The special problem of ‘tragic competence-raising’ can be distinguished from the more general interdependence thesis that I have defended. The epistemic interdependence of deliberation designs and aggregation rules is unavoidable. Accordingly, one could construct similar examples with different aggregation rules.
The presented examples rely on assumptions that might rarely be satisfied in realistic deliberation scenarios. For instance, actual deliberators are unlikely to be completely unbiased and identical with respect to their competence. Indeed, there are many ways in which the presented models could be made more realistic. However, while the examples incorporate simplifying assumptions, groups of real-world deliberators do not escape the general interdependence thesis that these examples aim to illustrate.
The epistemic interdependence of norms for social deliberation and judgment aggregation relates to an existing concern about social deliberation in the literature on crowd wisdom. Several authors have argued that we might just be better off without social deliberation (e.g., Sunstein 2006). Is the result that the majority rule and the simple averaging rule perform better in the non-deliberation design actually a reason to reject social deliberation wholesale in the pursuit of collective competence? An understanding of the interdependence thesis presents us with a better alternative. Rather than discouraging communication, we could design aggregation rules more suited to the opinions being produced in the course of social deliberation. As such, we can aim for social deliberation designs and aggregation rules that result in better collective judgments, as well as improved individual judgments. A similar response can be given to the objection that social deliberation might introduce positively correlated opinions, which has been a concern in the judgment aggregation literature (Hogarth 1978; Kaniovski 2009, 2010; Ladha 1992; Pivato 2017).
Of course, the recognition that our deliberation designs should be matched with suitable aggregation norms does not by itself provide us with the ability to do this. We do not always have perfect insight into what goes on during social deliberation and our attempts to structure it might have unpredictable effects on the opinion dynamics. In order to choose the best combinations of deliberative norms and aggregation rules, we might need to rely on models of social deliberation that have yet to be developed. If so, the interdependence thesis serves to highlight the importance of further social scientific opinion dynamics research in the pursuit of better practices for designing collective deliberation.
Notes
In this figure, the dictatorship competence is equivalent to the majority competence where \(n=1\). The unconditional probability of a correct majority is then calculated as a function of group size n:
$$\begin{aligned}&P\left( X_{maj}^{1}\right) = P\left( E\right) \sum _{k=\lfloor \frac{n}{2}+1\rfloor }^{n}P\left( X_{i}^{1}\mid E\right) ^{k}\left( 1-P\left( X_{i}^{1}\mid E\right) \right) ^{n-k}+\\&\quad P\left( \lnot E\right) \sum _{k=\lfloor \frac{n}{2}+1\rfloor }^{n}P\left( X_{i}^{1}\mid \lnot E\right) ^{k}\left( 1-P\left( X_{i}^{1}\mid \lnot E\right) \right) ^{n-k}. \end{aligned}$$One might object that it is implausible that the probability of encountering an easy problem could be below \(\frac{1}{2}\), arguing that “if more problems are hard than easy, that is, if the voter is more often wrong than right (and if as usual only two opinions, say, ‘yes’ or ‘no’, are possible), then as soon as a voter realizes this (through observing her frequent failures) the voter can systematically reverse each opinion, thereby making herself more often right than wrong” (Dietrich and Spiekermann 2013). For the purposes of our present discussion, this concern can simply be sidestepped by further conditioning on the event that a history of their past performance on similar problems is not among the non-deliberative common causes of the group members. As long as we assume that their judgments are still conditionally independent and conditionally identically distributed, we retain the result that the majority competence is lower than the dictatorship competence for those scenarios where the conditional probability that a problem is easy falls under \(\frac{1}{2}\) – even as the unconditional probability that a problem is easy is over a half.
In other words, I restrict my attention to collective deliberation with a causal structure that leaves individual judgments uncorrelated when we conditionalize on all deliberative and non-deliberative common causes (cf. Dietrich and Spiekermann 2013).
From Eq. (5), the functions for the majority competence under designs (1) and (2) are, respectively:
$$\begin{aligned} f\left( n\right) =0.6\left( 1\right) +0.3\left( \sum _{k=\lfloor \frac{n}{2}+1\rfloor }^{n}\left( {\begin{array}{c}n\\ k\end{array}}\right) 0.4^{k}\left( 1-0.4\right) ^{n-k}\right) +0.1\left( \sum _{k=\lfloor \frac{n}{2}+1\rfloor }^{n}\left( {\begin{array}{c}n\\ k\end{array}}\right) 0.6^{k}\left( 1-0.6\right) ^{n-k}\right) ,\\ g\left( n\right) =0.6\left( \sum _{k=\lfloor \frac{n}{2}+1\rfloor }^{n}\left( {\begin{array}{c}n\\ k\end{array}}\right) 0.7^{k}\left( 1-0.7\right) ^{n-k}\right) +0.2\left( \sum _{k=\lfloor \frac{n}{2}+1\rfloor }^{n}\left( {\begin{array}{c}n\\ k\end{array}}\right) 0.4^{k}\left( 1-0.4\right) ^{n-k}\right) +0.2\left( \sum _{k=\lfloor \frac{n}{2}+1\rfloor }^{n}\left( {\begin{array}{c}n\\ k\end{array}}\right) 0.6^{k}\left( 1-0.6\right) ^{n-k}\right) . \end{aligned}$$.
Furthermore, there might be negative externalities between different deliberative constraints. It is possible that two epistemic norms improve individual accuracy under a wide variety of circumstances in isolation from each other, yet, when implemented together, impair it. Finally, a deliberation design’s effects on the deliberators’ individual accuracy can be causally influenced by the chosen aggregation rule. It is well-known that a given aggregation rule can provide incentives for deliberators to behave strategically in ways that may ultimately undermine the accuracy of their collective judgment (Feddersen Timothy Pesendorfer 1998). By the same mechanism, an aggregation rule may, in tandem with a deliberation design, incentivize deliberators to share their information strategically in a manner that makes them individually less accurate, for example, by producing an information cascade.
This conceptualization of a decision problem diverges from a Savage-style decision problem that specifies not only states, but acts and consequences as well. In this model, the agents’ predictions constitute the acts while the consequences are measured by the error loss function. Since those are already built into the structure of the model, we can reduce the decision problem to what remains: the state of the world.
Accordingly, an instance \(z\in Z_{j}\) might include evidence from which the target value could be inferred, as well as non-evidential factors (e.g., the room temperature, time of day, or mood), and facts about the implemented deliberation design.
My results hold conditionally, for any value of D, but one could marginalize D out to arrive at analogous conclusions that hold unconditionally. This is not needed for our current purposes, however.
Strictly speaking, \(Z_{j}\) is not a value but a member of a partition.
The cost of errors, or ‘error loss’, can be measured in many different ways. For our present purposes, the squared error function will suffice to argue for the epistemic interdependence of deliberative norms and judgment aggregation rules. However, in the face of a real decision problem, the choice of loss function associated with one’s errors should be sensitive to the practical objectives to be achieved. Since underestimating the true levels of asbestos exposure is a far more costly mistake than overestimating them, an asymmetric error loss function would arguably be a more responsible choice.
The proof for this decomposition is reconstructed in Appendix (A.1).
This effect of correlation is well-known in the crowd wisdom literature: “[w]hen two judges’ errors are uncorrelated ... their estimates are equally likely to fall on the same side or opposite sides of the truth, so the bracketing rate is 50%. When their errors are positively correlated, the bracketing rate will be less than 50%.” (Mannes et al. 2014, 280).
To see why, let i and \(i'\) be two different, arbitrary deliberators. Since \(Cov\left( X_{i}X_{i'}\right) {}^{2}\le Var\left( X_{i}\right) Var\left( X_{i'}\right) \), it follows that \(\left| Cov\left( X_{i},X_{i'}\right) \right| \le \max \left\{ Var\left( X_{i}\right) ,Var\left( X_{i'}\right) \right\} \). If the deliberators are identically distributed, \(Var\left( X_{i}\right) =Var\left( X_{i'}\right) ={\overline{Var}}\left( X_{1:n}\right) \). This means that, for all \(i,i'\), \(\left| Cov\left( X_{i},X_{i'}\right) \right| \le {\overline{Var}}\left( X_{1:n}\right) \). Therefore, \({\overline{Cov}}\left( X_{1:n}\right) \le {\overline{Var}}\left( X_{1:n}\right) \).
After all, for all \(Z_{j}\in \left\{ Z_{0},Z_{1},...,Z_{n}\right\} \), \({\overline{Bias}}\left( X_{1:n,d,Z_{j}}\mid d\right) \le Bias\left( X_{i,d,Z_{j}}\mid d\right) \) and \(\frac{1}{n}{\overline{Var}}\left( X_{1:n,d,Z_{j}}\mid d\right) +\left( 1-\frac{1}{n}\right) {\overline{Cov}}\left( X_{1:n,d,Z_{j}}\mid d\right) \le Var\left( X_{i,d,Z_{j}}\mid d\right) \). Hence, it follows from equations (7) and (9) that \(E_{Z_{j}}\left[ \left( X_{\mu ,d,Z_{j}}-t\right) {}^{2}\mid d\right] \le E_{Z_{j}}\left[ \left( X_{i,d,Z_{j}}-t\right) {}^{2}\mid d\right] \).
References
Becker J, Brackbill D, Centola D (2017) Network dynamics of social influence in the wisdom of crowds. In: Proceedings of the National Academy of Sciences, E5070-E5076. https://doi.org/10.1073/pnas.1615978114
Bohman J (1996) Public deliberation: pluralism, complexity, and democracy. MIT Press, Cambridge
Bright LK, Dang H, Heesen R (2018) A role for judgment aggregation in coauthoring scientific papers. Erkenntnis 83(2):231–252. https://doi.org/10.1007/s10670-017-9887-1
Cohen J (1989) Deliberation and democratic legitimacy. Hamlin AP, Pettit P (eds) The good polity. Blackwell, Oxford
De Langhe R (2014) The division of labour in science: the tradeoff between specialisation and diversity. Philos Sci 81(3):444–459. https://doi.org/10.1086/676670
Dietrich F, Spiekermann K (2013) Independent opinions? On the causal foundations of belief formation and jury theorems. Mind 122(487):655–685. https://doi.org/10.1093/mind/fzt074
Dietrich F, Spiekermann K (2021) Jury theorems. Zalta EN (ed) The stanford encyclopedia of philosophy. https://plato.stanford.edu/archives/win2021/entries/jury-theorems/
Feddersen Timothy Pesendorfer W (1998) Convicting the innocent : the inferiority of unanimous jury verdicts under strategic voting. Am Polit Sci Rev 92(1):23–35
Frey V, van de Rijt A (2020) Social influence undermines the wisdom of the crowd in sequential decision making. Manag Sci (Oct), 4273-4286. https://doi.org/10.1287/mnsc.2020.3713
Geman S, Bienenstock E, Doursat R (1992) Neural networks and the bias/variance dilemma. Neural Comput 4(1):1–58. https://doi.org/10.1162/neco.1992.4.1.1
Goldman AI, Shaked M (1991) An economic model of scientific activity and truth acquisition. Philos Stud 63:31–55
Habermas J (1991) The structural transformation of the public sphere: an inquiry into a category of bourgeois society (T. Burger, Trans.). MIT Press, Cambridge
Hahn U, Hansen JU, Olsson EJ (2018) Truth tracking performance of social networks: how connectivity and clustering can make groups less competent. Synthese. https://doi.org/10.1007/s11229-018-01936-6
Hogarth R (1978) A note on aggregating opinions. Organ Behav Human Perform 21:40–46
Kaniovski S (2009) An invariance result for homogeneous juries with correlated votes. Math Soc Sci 57(2):213–222. https://doi.org/10.1016/j.mathsocsci.2008.09.002
Kaniovski S (2010) Aggregation of correlated votes and Condorcet’s jury theorem. Theory Decis 69(3):453–468. https://doi.org/10.1007/s11238-008-9120-4
Kao AB, Berdahl AM, Hartnett AT, Lutz MJ, Bak-Coleman JB, Ioannou CC, Couzin ID (2018) Counteracting estimation bias and social influence to improve the wisdom of crowds. J R Soc Interface 15(141):20180130. https://doi.org/10.1098/rsif.2018.0130
Kitcher P (1990) The division of cognitive labor. J Philos 87(1):5–22. https://doi.org/10.2307/2026796
Krogh A, Vedelsby J (1994) Neural network ensembles, cross validation, and active learning. Adv Neural Netw Process Syst 7:231–238
Ladha KK (1992) The condorcet jury theorem, free speech, and correlated votes. Am J Polit Sci 36(3):617–634. https://doi.org/10.2307/2111584
List C, Pettit P (2011) Group agency: the possibility, design, and status of corporate agents. Oxford University Press, Oxford
Lorenz J, Rauhut H, Schweitzer F, Helbing D (2011) How social influence can undermine the wisdom of crowd effect. Proc Natl Acad Sci 108(22):9020–9025. https://doi.org/10.1073/pnas.1008636108
Lorenz J, Rauhut H, Kittel B (2015) Majoritarian democracy undermines truth-finding in deliberative committees. Res Polit 2(2):1–10. https://doi.org/10.1177/2053168015582287
Lu L, Yuan YC, McLeod PL (2012) Twenty-five years of hidden profiles in group decision making: a meta-analysis. Person Soc Psychol Rev 16(1):54–75. https://doi.org/10.1177/1088868311417243
Lyon A, Pacuit E (2013) The wisdom of crowds: methods of human judgement aggregation. In: Handbook of human computation. Springer, New York, pp. 599-614
Mannes AE, Soll JB, Larrick RP (2014) The wisdom of select crowds. J Person Soc Psychol 107(2):276–299. https://doi.org/10.1037/a0036677
Mercier H, Sperber D (2017) The Enigma of Reason. Harvard University Press, Cambridge
Muldoon R, Weisberg M (2009) Epistemic landscapes and the division of cognitive labor. Philos Sci 76(2):225–252. https://doi.org/10.1086/644786
Pivato M (2017) Epistemic democracy with correlated voters. J Math Econ 72:51–69. https://doi.org/10.1016/j.jmateco.2017.06.001
Pivato M (2019) Realizing epistemic democracy. In: Laslier J-F, Moulin H, Sanver MR, Zwicker WS (eds) The future of economic design: The continuing development of a field as envisioned by its researchers (pp. 103-112). Springer International Publishing
Solomon M (2006) Groupthink versus the wisdom of crowds: the social epistemology of deliberation and dissent. Southern J Philos 44:28–42. https://doi.org/10.1111/j.2041-6962.2006.tb00028.x
Sunstein CR (2006) Deliberating groups versus prediction markets (or Hayek’s challenge to habermas). Episteme 3(03):192–213. https://doi.org/10.3366/epi.2006.3.3.192
Surowiecki J (2005) The wisdom of crowds. Anchor
Ueda N, Nakano R (1996) Generalization error of ensemble estimators. In: Proceedings of international conference on neural networks (icnn’96) (Vol. 1, pp. 90-95). IEEE. Retrieved from http://ieeexplore.ieee.org/document/548872/
Zollman KJS (2007) The communication structure of epistemic communities. Philos Sci 74(5):574–587. https://doi.org/10.1086/525605
Zollman KJ (2010) The epistemic benefit of transient diversity. Erkenntnis 72(1):17–35. https://doi.org/10.1007/s10670-009-9194-6
Acknowledgments
I am extremely grateful to Jan-Willem Romeijn for his invaluable feedback. Additionally, I would like to express my deep appreciation to the anonymous reviewer for their detailed comments on earlier drafts of this article. Many thanks go also to Daniel Herrmann and Nadezhda Vassilyeva for their helpful advice. This study is part of the research program Sustainable Cooperation – Roadmaps to Resilient Societies (SCOOP). The author is grateful to the Netherlands Organization for Scientific Research (NWO) and the Dutch Ministry of Education, Culture and Science (OCW) for generously funding this research in the context of its 2017 Gravitation Program (grant number 024.003.025)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that all sources of funding for this research have been disclosed and that there are no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
1.1 A.1 Bias-variance decomposition
Adapting a proof from (Geman et al. 1992), we are going to show that for arbitrary decision problem instance d:
Proof:
Starting with the squared error of the estimate for a single problem, add and subtract \(E_{Z}\left[ X_{i,d,Z}\mid d\right] \):
We are interested in the expected squared error loss, where the expectation is taken over all instances z of Z. By linearity of expectation:
The term (1) on the right hand side equals \(Bias\left( X_{i,d,Z}\mid d\right) {}^{2}\):
Meanwhile, term (2) equals drops out of the equation:
Hence, we find the bias-variance decomposition of expected individual error for any instance d of D:
1.2 A.2 Bias-variance-covariance decomposition
Reconstructing a proof from (Ueda and Nakano 1996), we show for arbitrary problem instance d that
where
and
Proof:
Let \(X_{1:n,d,Z_{j}}\) denote the set of random variables \(X_{1,d,Z_{j}},...,X_{n,d,Z_{j}}\) and let \(X_{\mu ,d,Z_{j}}=\frac{1}{n}\sum _{i=1}^{n}X_{i,d,Z_{j}}\). Substituting \(X_{\mu ,d,Z_{j}}\) for \(X_{i,d,Z}\) in the problem instance specific bias-variance decomposition from equation (7) gives us the ambiguity decomposition:
Now we want to express the above in terms of the statistical properties of the elements of \(X_{1:n,d,Z_{j}}\). First, we rewrite the \(Bias(X_{\mu ,d,Z_{j}}\mid d)\) term as
This is equivalent to
By linearity of expectation,this is equivalent to
Decomposing \(Var(X_{\mu ,d,Z_{j}}\mid d)\) is a little more involved. First, we rewrite it as
Expanding the square, we get
Now, by distributivity of summation, this equals
This is equivalent to the (rather unwieldy) expression
Separating the sums that only involve \(X_{i,d,Z_{j}}\) from those that involve both \(X_{i,d,Z_{j}}\) and \(X_{i',d,Z_{j}}\), with \(i\ne i'\), we get the equivalent expression
We can now simplify this expression, starting with (1):
Next, we simplify term (2):
Since
we write the simplified term (2) as
Putting (1) and (2) back together, we find that
After we substitute the decompositions of \(Bias(X_{\mu ,d,Z_{j}}\mid d)\) and \(Var(X_{\mu ,d,Z_{j}}\mid d)\) back into the ambiguity decomposition with which we started, we have the bias-variance-covariance decomposition:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Siebe, H. The interdependence of social deliberation and judgment aggregation. Soc Choice Welf (2024). https://doi.org/10.1007/s00355-023-01501-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00355-023-01501-2