Tailored recommendations on a matching platform

Abstract

Matching platforms not only mediate matches but also work as information gatekeepers. When users with private tastes use such a platform to find a partner, the platform asks them to provide match-relevant information; subsequently, it aggregates and distributes the collected data back to each user to facilitate the effective coordination of matches. This study aims to examine how such a platform can design its information flow to make users form matches in a way that is desirable for the platform. I characterize a form of two-way communication that employs both verifiable and non-verifiable messages; then, I delineate the conditions under which a platform can (cannot) achieve its ex-post optimal matching outcome. On a platform that achieves such an outcome, users would fully reveal their private tastes, but the platform would return personalized and only filtered information back to each user in the form of a “recommendation.” I identify three key factors that enable such communication, namely (1) the distance between the distribution of tastes of each side; (2) the uncertainty measure of each distribution; and (3) the population size. As applications, I first study the markets with costly verifiable information and propose a sufficient condition that achieves the optimal matching outcome. Then, I study a two-way communication protocol with non-verifiable messages and demonstrate that communication strictly improves efficiency under any circumstances.

Appendices

Appendix 1: Proof of statements

1.1 Proof of Remark

I prove it by induction on n. Base step: $n=2$

$$\begin{aligned} \left( \theta _{\left( 1;2\right) }-\omega _{\left( 1;2\right) }\right) ^2+\left( \theta _{\left( 2;2\right) }-\omega _{\left( 2;2\right) }\right) ^2&=\left( \theta _{\left( 1;2\right) }-\omega _{\left( 2;2\right) }+\omega _{\left( 2;2\right) }-\omega _{\left( 1;2\right) }\right) ^2\\&\quad +\left( \theta _{\left( 2;2\right) }-\omega _{\left( 1;2\right) }+\omega _{\left( 1;2\right) }-\omega _{\left( 2;2\right) }\right) ^2\\&=\left( \theta _{\left( 1;2\right) }-\omega _{\left( 2;2\right) }\right) ^2+\left( \theta _{\left( 2;2\right) }-\omega _{\left( 1;2\right) }\right) ^2\\&\quad -2\left( \omega _{\left( 2;2\right) }-\omega _{\left( 1;2\right) }\right) \left( \theta _{\left( 2;2\right) }-\theta _{\left( 1;2\right) }\right) \\&\le \left( \theta _{\left( 1;2\right) }-\omega _{\left( 2;2\right) }\right) ^2+\left( \theta _{\left( 2;2\right) }-\omega _{\left( 1;2\right) }\right) ^2 \end{aligned}$$

Induction step: Suppose that $(\theta _{(1;n)},\ldots ,\theta _{(n;n)})$ and $(\omega _{(1;n)},\ldots ,\omega _{(n;n)})$ are given. Match $\theta _{(1;n)}$ with $\omega _{(k;n)}$ for some $k\in \{1,\ldots ,n\}$. The rest

$$\begin{aligned} \left( \theta _{\left( 2;n\right) },\ldots ,\theta _{\left( n;n\right) }\right) \quad {{\text {and}}}\quad \left( \omega _{\left( 1;n\right) },\ldots ,\omega _{\left( k-1;n\right) },\omega _{\left( k+1;n\right) }\cdots ,\omega _{\left( n;n\right) }\right) \end{aligned}$$

can be matched optimally when $\theta _{(j;n)}$ is matched with $\omega _{(j-1;n)}$ if $j\le k$ and $\theta _{(j;n)}$ is matched with $\omega _{(j;n)}$ if $j> k$ by the induction hypothesis. Now I will show $k=1$ minimizes the distance sum. To show this, it is sufficient to show that $k\ne n$. It is because if $k\ne n$, I can apply the induction hypothesis to $(\theta _{(1;k)},\ldots ,\theta _{(k;k)})$ and $(\omega _{(1;k)},\ldots ,\omega _{(k;k)})$, which yields $k=1$. Suppose $k=n$ and note that

$$\begin{aligned} \left( \theta _{\left( 1;n\right) }-\omega _{\left( n;n\right) }\right) ^2+\left( \theta _{\left( n;n\right) }-\omega _{\left( n-1;n\right) }\right) ^2\ge \left( \theta _{\left( 1;n\right) }-\omega _{\left( n-1;n\right) }+\omega _{\left( n;n\right) }-\omega _{\left( n;n\right) }\right) ^2. \end{aligned}$$

Thus, I have

$$\begin{aligned}&\left( \theta _{\left( 2;n\right) }-\omega _{\left( 1;n\right) }\right) ^2+\cdots +\left( \theta _{\left( n;n\right) }-\omega _{\left( n-1;n\right) }\right) ^2+\left( \theta _{\left( 1;n\right) }-\omega _{\left( n;n\right) }\right) ^2\\&\quad \ge \left( \theta _{\left( 2;n\right) }-\omega _{\left( 1;n\right) }\right) ^2+\cdots +\left( \theta _{\left( n;n\right) }-\omega _{\left( n;n\right) }\right) ^2+\left( \theta _{\left( 1;n\right) }-\omega _{\left( n-1;n\right) }\right) ^2, \end{aligned}$$

which contradicts the induction hypothesis.

1.2 Proof of Theorem 1

Suppose that the sufficient condition is satisfied. To find an unraveling equilibrium, I work backward from the users’ partner choice problems. Consider firm j who is recommended to accept worker i. Firm j’s belief on the location of worker i after communication can be denoted by a random variable, $W^i_n(\theta _j)$, which condition on firm j’s reported location $\theta _j$. Given all users’ full revelation to the platform and platform’s assortative recommendation, the recommendation only reveals that firm j and worker i have the same rank¹⁷ in ${\varvec{\theta }}=(\theta _1,\theta _2,\ldots ,\theta _n)$ and ${\varvec{\omega }}=(\omega _1,\omega _2,\ldots ,\omega _n)$, respectively. Since the probability that $\theta _j$ is rank k is given by $F_{(k-1;n-1)}(\theta _j)-F_{(k;n-1)}(\theta _j)$,¹⁸ the associated pdf of $W_n^i(\theta _j)$ is the following:

$$\begin{aligned} \sum ^n_{k=1}[F_{(k-1;n-1)}(\theta _j)-F_{(k;n-1)}(\theta _j)]g_{(k;n)}(\omega ). \end{aligned}$$

which is equivalent to

$$\begin{aligned} \sum ^n_{k=1}{n-1\atopwithdelims ()k-1}F(\theta _j)^{k-1}(1-F(\theta _j))^{n-k}g_{(k;n)}(\omega ). \end{aligned}$$

On the other hand, the location of worker $l\ne i$ can be denoted by a random variable $W^{-i}_n(\theta _j)$, and its associated pdf is

$$\begin{aligned} \sum ^n_{k=1}{n-1\atopwithdelims ()k-1}F(\theta _j)^{k-1}\left( 1-F(\theta _j)\right) ^{n-k}\frac{1}{n-1}\bigg [ng(\omega )-g_{(k;n)}(\omega )\bigg ]. \end{aligned}$$

It is because (1) the pdf of the location of a worker whose rank is not k is $\frac{1}{n-1}\sum _{l\ne k}g_{(l;n)}(\omega )$. (2) The mean of the order statistic density $g_{(k;n)}$ is g. Therefore, I should have

$$\begin{aligned} ng(\omega )=\sum ^n_{l=1}g_{l;n}(\omega )=(n-1)\left[ \frac{1}{n-1}\sum _{l\ne k}g_{(l;n)}(\omega )\right] +g_{(k;n)}(\omega ), \end{aligned}$$

which enables us to express the location of $l\ne i$ in a closed form. Now, if multiple workers including i applies to firm j, j accept i if and only if

$$\begin{aligned} \gamma _f{\mathbb {E}}\left[ 1-\left( \theta _j-W^i_n(\theta _j)\right) ^2\right] \ge \gamma _f{\mathbb {E}}\left[ 1-\left( \theta _j-W^{-i}_n(\theta _j)\right) ^2\right] . \end{aligned}$$

Using the closed form for the location of worker $l\ne i$, the condition is equivalent to the following inequality:

$$\begin{aligned}{\mathbb {E}}\left[ 1-(\theta _j-W^i_n(\theta _j))^2\right] \ge {\mathbb {E}}_\omega \left[ 1-(\theta _j-\omega ))^2\right] .\end{aligned}$$

Similarly, consider worker i who is recommended to apply to firm j. Denote the location of firm j by $\Theta ^j_n(\omega _i)$. Worker i has an incentive to follow the recommendation if

$$\begin{aligned}{\mathbb {E}}\left[ 1-(\Theta ^j_n(\omega _i)-\omega _i)^2\right] \ge {\mathbb {E}}_\theta \left[ 1-(\theta -\omega _i))^2\right] .\end{aligned}$$

Lemma 1

$W^i_n(\theta )\xrightarrow []{d}G^{-1}(F(\theta )),\forall \theta \in [0,1]\,{{\text {and}}}\,\Theta ^j_n(\omega )\xrightarrow []{d}F^{-1}(G(\omega )),\forall \omega \in [0,1].$

Proof

I shall show that $W^i_n(\theta )\xrightarrow []{d}G^{-1}(F(\theta ))$. The same proof can be applied to the second argument. First, note that if $\sqrt{n}(\frac{k}{n}-q)\rightarrow 0$, then $\omega _{(k;n)}\xrightarrow {d}G^{-1}(q)$ for $q\in (0,1)$.¹⁹ Now, for each $\theta$, define a random variable $Q^n_\theta$ whose value is k/n with probability ${n-1\atopwithdelims ()k-1}F(\theta )^{k-1}(1-F(\theta ))^{n-k}$ for $k=1,\ldots ,n$. I will show that

$$\begin{aligned}Q^n_\theta \xrightarrow {p}F(\theta ).\end{aligned}$$

The mean of $Q^n_\theta$ is

$$\begin{aligned}{\mathbb {E}}[Q^n_\theta ]=\sum ^n_{i=1}\frac{i}{n}{n-1\atopwithdelims ()i-1}F(\theta )^{k-1}(1-F(\theta ))^{n-k}=\frac{n-1}{n}F(\theta )\end{aligned}$$

The second equality derived using a property of the mean of a binomial distribution.²⁰ Using a property of the variance of a binomial distribution, I find

$$\begin{aligned}{\text {Var}}[Q^n_\theta ]=\frac{n-1}{n^2}F(\theta )(1-F(\theta )).\end{aligned}$$

Thus,

$$\begin{aligned} {\mathbb {P}}\left[ |Q^n_\theta -{\mathbb {E}}[Q^n_\theta ]|\right]&={\mathbb {E}}\left[ \textbf{1}_{\frac{(Q^n_\theta -{\mathbb {E}}[Q^n_\theta ])^2}{\epsilon ^2}\le 1}\right] \\ {}&\le \frac{1}{\epsilon ^2}{\mathbb {E}}\left[ (Q^n_\theta -\mathbb E[Q^n_\theta ])^2\right] =\frac{1}{\epsilon ^2}\text {Var}[Q^n_\theta ] \end{aligned}$$

Since the last term tends to zero as $n\rightarrow \infty$, I have $Q^n_\theta \xrightarrow {p}F(\theta )$. Combining the two convergence results, the pdf of $W^i_n(\theta _j)$ converges to a function h, where $h(\theta )=0$ if $\theta \ne \theta _j$, where $\theta _j$ is the only point of discontinuity. Thus, I have $W^i_n(\theta )\xrightarrow []{d}G^{-1}(F(\theta ))$. $\square$

Since the utility function is continuous and bounded, I can appeal to Portmanteu theorem. Therefore, the utility of the firm j from following recommendation converges to $1-(\theta _j-G^{-1}(F(\theta _j)))^2$. Now, I will use Lemma 2 to show that this convergence of expected utilities are uniformly convergent.

Lemma 2

(Test for uniform convergence) Given a $\sum ^n_{k=1} a_k(x)b_k(x)$, if $\{a_k(x)\}$ is uniformly bounded and is monotone for each x, while the series $\sum b_k(x)$ is uniformly convergent, then $\sum a_k(x)b_k(x)$ is also uniformly convergent.

Proof

See Hardy (1918) $\square$

For $\theta \in [0,1]$, define $a_k(\theta _j)=\int ^1_0\omega ^mg_{(k;n)}(\omega )d\omega$, which is independent of $\theta$, and $b_k(\theta )={n-1\atopwithdelims ()k-1}F(\theta )^{k-1}(1-F(\theta ))^{n-k}$. Then, I have $\sum ^n_{k=1}b_k(\theta )=1$, $\forall n$ and $\forall \theta$, by the binomial theorem. On the other hand, $a_k(\theta )$ is monotonically increases in k and bounded below by 0 and above by 1 for any $m\in \{0,1,2,\ldots \}$. Since sum of two uniformly convergent functions also uniformly convergent, I conclude that the firm’s expected utility converges uniformly to $1-(\theta _j-G^{-1}(F(\theta _j)))^2$ if it follows the recommendation. Now, by the sufficient condition, I have

$$\begin{aligned} (F^{-1}(x)-G^{-1}(x))^2<\sigma (F)^2,~\forall x\in [0,1] \end{aligned}$$

Since F has a unit support, the above inequality still holds when $x=F(\theta _j)$, $\forall \theta _j\in [0,1]$. Thus, the above inequality is equivalent to

$$\begin{aligned} (\theta _j-G^{-1}(F(\theta _j)))^2<\sigma (F)^2,~\forall \theta _j\in [0,1]. \end{aligned}$$

(1)

On the other hand, since the variance minimizes the distance, I have

$$\begin{aligned} \sigma (F)^2=Var(F)\le {\mathbb {E}}_\omega \left[ (\theta _j-\omega )^2\right] ,~\forall \theta _j\in [0,1]. \end{aligned}$$

(2)

Combining the two inequalities (1) and (2), and using the other condition on 1 in the sufficient condition, I conclude that

$$\begin{aligned} 1-(\theta _j-G^{-1}(F(\theta _j)))^2>1-{\mathbb {E}}_\omega \left[ (\theta _j-\omega )^2\right] . \end{aligned}$$

Define $\epsilon _F=\sigma (F)-Kolm(F^{-1},G^{-1})$. By the uniform convergence result above, I conclude that for $\epsilon _F$, there exists an $N_F\in {\mathbb {N}}$ such that if the population of users on each side is larger than $N_F$, they do not have an incentive to deviate from accepting the recommended worker. Similarly, for $\epsilon _G=\sigma (G)-Kolm(F^{-1},G^{-1})$, there exists $N_G$ such that all workers follow recommendation if the size of population is large than $N_G$. Since any effective deviation should be bilateral, I can consider the case at least one side of users do not have incentive deviate from following the platform’s recommendation.

Now, consider the platform’s strategy. As noted at Remark, a positive assortative matching maximizes the social surplus and the platform’s utility. Thus, given that all users fully reveal their information and follow the recommendations, providing a rank-matching (i.e., assortative) recommendation is optimal for the platform.

Finally, I need to construct a belief system which support full revelation of information. Suppose that a firm with $\theta$ who successfully pretend to have a location of $\theta '$ while other users fully reveal their locations. It’s expected utility from the successful deception is $v(\theta ,\theta ')=1-\mathbb E[(\theta -W_n(\theta '))^2]$. Denote the derivative of v with respect to the second argument by $v_2$. I start by partitioning the unit interval as follows:

$$\begin{aligned}I_{[0,1]}=\cup _{l=1,2,\ldots }P_l\end{aligned}$$

where 1) each $P_l$ is an interval, 2) if $\theta _1,\theta _2\in P_l$, then $v_2(\theta _1,\theta _1)\cdot v_2(\theta _2,\theta _2)\ge 0$, $\forall l\in \{1,2,\ldots \}$ and 3) if $\theta _1\in P_l$ and $\theta _2\in P_{l+1}$, then $v_2(\theta _1,\theta _1)\cdot v_2(\theta _2,\theta _2)\le 0$.²¹ I partition the type space based on the mimicking incentives. If two types are in the same interval, they locally want to masquerade as types in the the same direction. Now, suppose that a message $m\subset [0,1]$ is received from firm j. I find the locally worst case type from each interval, and then show that it also is the globally worst case type. For each $l\in \{1,2,\ldots \}$, if $m\cap P_l\ne \emptyset$, I pick one type from $m\cap P_l$ by

$$\begin{aligned} {\tilde{\theta }}_i=\left\{ \begin{array}{lll} \min m\cap P_i&{}\quad {\text {if}}\,\,v_2(x,x)\ge 0,\forall x\in P_i\\ \max m\cap P_i&{}\quad {\text {if}}\,\,v_2(x,x)\le 0,\forall x\in P_i. \end{array} \right. \end{aligned}$$

Define ${\tilde{\Theta }}$ be the collection of such ${\tilde{\theta }}_i$. The platform’s belief assigns probability 1 to a type ${\tilde{\theta }}\in {\tilde{\Theta }}$ which satisfies

$$\begin{aligned} \not \exists {\tilde{\theta }}'\in {\tilde{\Theta }}~s.t.~v\left( {\tilde{\theta }}',{\tilde{\theta }}\right) >v\left( {\tilde{\theta }}',{\tilde{\theta }}'\right) . \end{aligned}$$

That is, no other type in ${\tilde{\Theta }}$ wants to masquerade as ${\tilde{\theta }}$ even if it is possible to do so.²² If there are multiple types that satisfies the above condition, I can pick one arbitrarily.

To show that a firm with ${\tilde{\theta }}_l\in P_l$ cannot benefit from pretending to be another type which is available to him, I first consider a local incentive within $P_l$ and then global incentive within ${\tilde{\Theta }}$. Suppose first that $v_2(x,x)\ge 0,~\forall x\in P_l$.²³ Since $(k-1){n-1\atopwithdelims ()k-1}=(n-1){n-2\atopwithdelims ()k-2}$ and $(n-k){n-1\atopwithdelims ()k-1}=(n-1){n-2\atopwithdelims ()k-1}$, I have

$$\begin{aligned}&\frac{\partial }{\partial \theta '}{n-1\atopwithdelims ()k-1}F(\theta ')^{k-1}(1-F(\theta '))^{n-k}\\&\quad ={n-1\atopwithdelims ()k-1}\bigg [(k-1)F(\theta ')^{k-2}(1-F(\theta '))^{n-k}-(n-k)F(\theta ')^{k-1}(1-F(\theta '))^{n-k-1}\bigg ]f(\theta ')\\&\quad =(n-1)\bigg [{n-2\atopwithdelims ()k-2}F(\theta ')^{k-2}(1-F(\theta '))^{n-k}-{n-2\atopwithdelims ()k-1}F(\theta ')^{k-1}(1-F(\theta '))^{n-k-1}\bigg ]f(\theta '). \end{aligned}$$

Thus, $v_2$ can be reformulated as

$$\begin{aligned} v_2(\theta ,\theta ')&=\frac{\partial }{\partial \theta '}\sum ^n_{k=1}{n-1\atopwithdelims ()k-1}F(\theta ')^{k-1}(1-F(\theta '))^{n-k}{\mathbb {E}}\left[ 1-(\theta -\omega _{(k;n)})^2\right] \\&=\sum ^n_{k=2}(n-1)f(\theta '){n-2\atopwithdelims ()k-2}F(\theta ')^{k-2}(1-F(\theta '))^{n-k}{\mathbb {E}}\left[ 1-(\theta -\omega _{(k;n)})^2\right] \\&\quad -\sum ^{n-1}_{k=1}(n-1)f(\theta '){n-2\atopwithdelims ()k-1}F(\theta ')^{k-1}(1-F(\theta '))^{n-k-1}{\mathbb {E}}\left[ 1-(\theta -\omega _{(k;n)})^2\right] \\&=(n-1)f(\theta ')\sum ^{n-1}_{k=1}{n-2\atopwithdelims ()k-1}F(\theta ')^{k-1}(1-F(\theta '))^{n-k-1}{\mathbb {E}}\\ {}&\quad \times \left[ (\theta -\omega _{(k;n)})^2-(\theta -\omega _{(k+1;n)})^2\right] \\&=(n-1)f(\theta ')\sum ^{n-1}_{k=1}{n-2\atopwithdelims ()k-1}F(\theta ')^{k-1}(1-F(\theta '))^{n-k-1}\int ^1_0(\theta -\omega )^2\\&\quad \times [g_{(k;n)}(\omega )-g_{(k+1;n)}(\omega )]d\omega \\&=(n-1)f(\theta ')\sum ^{n-1}_{k=1}{n-2\atopwithdelims ()k-1}F(\theta ')^{k-1}(1-F(\theta '))^{n-k-1}[\alpha _k\theta +\beta _k]. \end{aligned}$$

where $\alpha _k=-2\int ^1_0\omega [g_{(k;n)}(\omega )-g_{(k+1;n)}(\omega )]d\omega$ and $\beta _k=\int ^1_0\omega ^2[g_{(k;n)}(\omega )-g_{(k+1;n)}(\omega )]d\omega$. I have $\alpha _k>0$ and $\beta _k<0$ because $G_{(k+1;n)}$ first order stochastically dominates $G_{(k;n)}$. Thus, if $\theta _1,\theta _2\in P_l$ and $\theta _1<\theta _2$ then

$$\begin{aligned}0\le v_2(\theta _1,\theta _1)\le v_2(\theta _1,\theta ')<v_2(\theta _2,\theta '),~\forall \theta '\in \left[ \theta _1,\theta _2\right] , \end{aligned}$$

and, as a consequence,

$$\begin{aligned} v(\theta _2,\theta _1)=\int ^{\theta _1}_0v_2(\theta _1,\theta )d\theta <\int ^{\theta _2}_0v_2(\theta _1,\theta )d\theta =v(\theta _2,\theta _2)\end{aligned}$$

As ${\tilde{\theta }}_l\in P_l$ and $v_2(x,x)\ge 0,~\forall x\in P_l$, the firm only can pretend to have a location $\theta '$ which is lower than ${\tilde{\theta }}_l$ if it tries to mimic other type within $P_l$. However, the inequality above shows that the deception within $P_l$ cannot be beneficial.

Now, consider the mimicking incentive within ${\tilde{\Theta }}$. The only case when ${\tilde{\theta }}_l$ firm can profitably pretend to have another location is that when there is a cycle of the form:

$$\begin{aligned} v({\tilde{\theta }}_l,{\tilde{\theta }}_l)<v({\tilde{\theta }}_l,{\tilde{\theta }}_{m_1}),~v({\tilde{\theta }}_{m_1},{\tilde{\theta }}_{m_1})<v({\tilde{\theta }}_{m_1},{\tilde{\theta }}_{m_2}),~\cdots ,~~v({\tilde{\theta }}_{m_t},{\tilde{\theta }}_{m_t})<v({\tilde{\theta }}_{m_t},{\tilde{\theta }}_{l}). \end{aligned}$$

I will show that there cannot be a cycle of any length.

Lemma 3

If $\exists (m_1,m_2,\ldots , m_t)$ s.t. $v({\tilde{\theta }}_l,{\tilde{\theta }}_l)<v({\tilde{\theta }}_l,{\tilde{\theta }}_{m_1})$ and $v({\tilde{\theta }}_{m_k},{\tilde{\theta }}_{m_k})<v({\tilde{\theta }}_{m_k},{\tilde{\theta }}_{m_k+1})$, for $k=1,2,\ldots , t-1$, then $v({\tilde{\theta }}_{m_t},{\tilde{\theta }}_{m_t})\ge v({\tilde{\theta }}_{m_t},{\tilde{\theta }}_{l}).$

Proof

I first notice that $v(\theta ,\theta ')$ exhibits an increasing difference.

$$\begin{aligned} \frac{\partial ^2}{\partial \theta \partial \theta '}v(\theta ,\theta ')&=\frac{\partial }{\partial \theta }(n-1)f(\theta ')\sum ^{n-1}_{k=1}{n-2\atopwithdelims ()k-1}F(\theta ')^{k-1}(1-F(\theta '))^{n-k-1}[\alpha _k\theta +\beta _k]\\&=(n-1)f(\theta ')\sum ^{n-1}_{k=1}{n-2\atopwithdelims ()k-1}F(\theta ')^{k-1}(1-F(\theta '))^{n-k-1}\alpha _k, \end{aligned}$$

where $\alpha _k=2\int ^1_0\omega [g_{(k+1;n)}(\omega )-g_{(k;n)}(\omega )]d\omega >0$. Now, I will prove the statement by induction on the length of a cycle.

Base step: No cycle of length 2. Let $\theta _1<\theta _2$. By increasing difference, $v(\theta _2,\theta _1)-v(\theta _1,\theta _1)$ is non-decreasing in the second argument:

$$\begin{aligned}v(\theta _1,\theta _2)-v(\theta _1,\theta _1)\le v(\theta _2,\theta _2)-v(\theta _2,\theta _1).\end{aligned}$$

Thus, if $v(\theta _1,\theta _2)\le v(\theta _1,\theta _1)$, then $v(\theta _2,\theta _2)\le v(\theta _2,\theta _1)$. That is, if $\theta _1$ benefits from mimicking $\theta _2$, then $\theta _2$ cannot benefit from mimicking $\theta _1$.

Induction step: Suppose that there is no cycle of length $l-1$. For a contrary, suppose that there is a cycle of length l with $\theta _1,\theta _2,\ldots ,\theta _l$. Without loss of generality, let $\theta _1=\min \{\theta _1,\ldots ,\theta _l\}$ and cycle connects $\theta _i$ to $\theta _{i+1}$ and $\theta _{l}$ to $\theta _1$, for all $i=1,\ldots , l-1$. By increasing difference,

$$\begin{aligned}v(\theta _1,\theta _2)-v(\theta _1,\theta _1)\le v(\theta _k,\theta _2)-v(\theta _k,\theta _2),~\forall k=1,\ldots ,l.\end{aligned}$$

Thus, I have $v(\theta _k,\theta _2)\ge v(\theta _k,\theta _1)>v(\theta _k,\theta _k)$ which implies there is a cycle of length $l-1$. $\square$

Since there is no cycle, any ${\tilde{\Theta }}$ has an element ${\tilde{\theta }}$ s.t. $\not \exists {\tilde{\theta }}'\in {\tilde{\Theta }}~s.t.~v({\tilde{\theta }}',{\tilde{\theta }})>v({\tilde{\theta }}',{\tilde{\theta }}'),$ which completes the proof.

1.3 Proof of Proposition 1

Suppose that users follow the recommendations in the selection stage. As in the proof of Theorem 1, let $v(\omega ,\omega ')$ denote the expected utility of a location x worker when she successfully makes the platform believes her location is $\omega '$ and successfully matches to the partner recommended accordingly. Formally, it can be defined as follows.

$$\begin{aligned} v(\omega ,\omega ')=\sum ^n_{k=1}{n-1\atopwithdelims ()k-1}G(\omega ')^{k-1}(1-G(\omega '))^{n-k}{\mathbb {E}}[\gamma _w V(\omega ,\theta _{(k:n)})]. \end{aligned}$$

According to the proof in Theorem 1, it suffices to show that the cross derivative of v is positive. For given V and v above,

$$\begin{aligned} v_{12}(\omega ,\omega ')&=\frac{\partial ^2}{\partial \omega \partial \omega '}\sum ^n_{k=1}{n-1\atopwithdelims ()k-1}G(\omega ')^{k-1}(1-G(\omega '))^{n-k}{\mathbb {E}}[\gamma _w V(\omega ,\theta _{(k:n)})]\\&=\frac{\partial }{\partial \omega }\sum ^n_{k=2}(n-1)g(\omega '){n-2\atopwithdelims ()k-2}G(\omega ')^{k-2}(1-G(\omega '))^{n-k}{\mathbb {E}}[V(\omega ,\theta _{(k;n)})]\\&\quad -\frac{\partial }{\partial \omega }\sum ^{n-1}_{k=1}(n-1)g(\omega '){n-2\atopwithdelims ()k-1}G(\omega ')^{k-1}(1-G(\omega '))^{n-k-1}{\mathbb {E}}[V(\omega ,\theta _{(k;n)})]\\&=\frac{\partial }{\partial \omega }(n-1)g(\omega ')\sum ^{n-1}_{k=1}{n-2\atopwithdelims ()k-1}G(\omega ')^{k-1}(1-G(\omega '))^{n-k-1}{\mathbb {E}}[V(\omega ,\theta _{(k+1;n)})\\&\quad -V(\omega ,\theta _{(k;n)})]\\&=(n-1)g(\omega ')\sum ^{n-1}_{k=1}{n-2\atopwithdelims ()k-1}G(\omega ')^{k-1}(1-G(\omega '))^{n-k-1}\mathbb E[V_1(\omega ,\theta _{(k+1;n)})\\&\quad -V_1(\omega ,\theta _{(k;n)})]. \end{aligned}$$

Here, we have

$$\begin{aligned}&E[V_1(\omega ,\theta _{(k+1;n)})-V_1(\omega ,\theta _{(k;n)})]\\&\quad =\int ^1_0v_1(\omega ,\theta )\big (f_{(k+1;n)}(\theta )-f_{(k;n)}(\theta )\big )d\theta \\&\quad =v_1(\omega ,\theta )\big [F_{(k+1;n)}(\theta )-F_{(k;n)}(\theta )\big ]^1_{\theta =0}-\int ^1_0v_{12}(\omega ,\theta )\big (F_{(k+1;n)}(\theta )-F_{(k;n)}(\theta )\big )d\theta \\&\quad =\int ^1_0v_{12}(\omega ,\theta )\big (F_{(k;n)}(\theta )-F_{(k+1;n)}(\theta )\big )d\theta >0. \end{aligned}$$

The last inequality holds because of the first order statistic domination relation between $F_{(k;n)}$ and $F_{(k+1;n)}$. Thus, we conclude that $v_{12}(\omega ,\omega ')>0$, $\forall \omega ,\forall \omega '$.

1.4 Proof of Theorem 2

Suppose for a contrary that $\exists x^*\in [0,1]$ that satisfies the inequality. The expected utility of a worker with $\omega ^*=G^{-1}(x^*)$ from following the recommendation converges to $\gamma _w[1-(F^{-1}(x^*)-G^{-1}(x^*))^2]$. If he apply to a firm which is not recommended to him, his expected utility converges to $\gamma _wp\big [1-{\mathbb {E}}_\theta [(\omega ^*-\theta )^2]\big ]$. Thus, the worker benefits from deviation and applying to another firm.

1.5 Proof of Proposition 2

(Sufficiency) I work backward to verify that an unraveling equilibrium indeed exists under the condition. Consider a worker a who is recommended to apply to firm b. By assortative recommendation and truthful revelation, the worker knows that the location of the firm is $F^{-1}(G(\omega _a))$. His updated belief on the location of the other firms remains the same because the revelation of a location of one firm does not reveal any information about the locations of other firms when there are continuum firms. Since $\gamma _wp[1-{\mathbb {E}}_\theta [(\omega _a-\theta )^2]]\le 1-(\omega _a-F^{-1}(G(\omega _a)))^2$, the worker does not have incentive to deviate. Since all firms receive only one application, they will accept their applicant.

Now, to apply “skepticism”, I need to construct a belief system of the platform which makes users have no incentive to withhold any information. Denote the set of roots of $(F-G)(x)$ by²⁴R and suppose that a message m is received from a firm.²⁵ Given message m from a user, consider a collection of subsets of m, $\{m_{\alpha }\}_{\alpha \in \mathscr {I}_p}$, which is constructed in a way that

$$\begin{aligned} {\text {if}}~\theta <\theta '\quad {{\text {and}}}\quad \theta ,\theta '\in m_{\alpha '}~{\text {for\,some}}~\alpha '\in \mathscr {I}_p, ~{\text {then}}~\not \exists r\in R~s.t.~\theta \le r\le \theta '. \end{aligned}$$

Thus, $\{m_{\alpha }\}_{\alpha \in \mathscr {I}_p}\cup (R\cap m)$ constitutes a partition of m. By construction, if $\theta \in m_{\alpha '}$ for some $\alpha '\in \mathscr {I}_p$, then it is either $F(\theta )> G(\theta )$ or $F(\theta )< G(\theta )$. Define $l_{\alpha '}$ by $\sup m_{\alpha '}$ if $F(\theta )> G(\theta )$ and $\inf m_{\alpha '}$ if $F(\theta )< G(\theta )$. Let $\{l_\alpha \}_{\alpha \in \mathscr {I}_p}\cup (R\cap m)=l(m)$. The platform believes the agent type to be

$$\begin{aligned} \arg \min _{x\in l(m)}\bigg \{-\bigg ({x}-G^{-1}\big (F(x)\big )\bigg )^2\bigg \} \end{aligned}$$

(3)

If there are multiple arguments which solves (3), pick one arbitrarily. I need to show that truthful revelation constitutes an equilibrium. Suppose that user with type $\theta$ tries to mimic $\theta '\ne \theta$. First of all, it should be

$$\begin{aligned} \big |{\theta '}-G^{-1}\big (F(\theta ')\big )\big |>\big |{\theta }-G^{-1}\big (F(\theta )\big )\big | \end{aligned}$$

(4)

Otherwise, $\theta '$ wouldn’t be taken over $\theta$ by the platform. Furthermore, it should be

$$\begin{aligned} \big |\theta -G^{-1}\big (F(\theta ')\big )\big |=\big |\theta -\theta '\big |+\big |\theta '-G^{-1}\big (F(\theta ')\big )\big |> \big |\theta -\theta '\big |+\big |\theta -G^{-1}\big (F(\theta )\big )\big |. \end{aligned}$$

The first equality is from the construction of belief system and the second inequality is by inequality (4). Thus, firms do not have incentive to withhold any information, and this completes the proof.

(Necessity) Suppose for a contrary that $\exists x^*$ s.t. $p{[}1-{\mathbb {E}}_y[(F^{-1}(y)-G^{-1}(x^*))^2{]}{]}>1-(F^{-1}(x^*)-G^{-1}(x^*))^2$. Then, a worker with type $\omega =G^{-1}(x^*)$ benefits from deviating and applying to a firm that is not recommended to him. Thus, an unraveling equilibrium cannot exist.

1.6 Proof of Proposition 3

Proof

Let the platform checks the worker i’s (firm j’s, resp.) true location with probability $q^\omega _i(x)$ ($q^\theta _j(x), resp.$) when the received profile of messages is x. Let $Kolm(F^{-1},G^{-1})\le \sqrt{q^*}$ for $q^*=\inf _{x,i\in [0,1],j\in [0,1]} \{q_i^\omega (x),q_j^\theta (x)\}.$ That is, we have

$$\begin{aligned} (sup_{x\in [0,1]} |F^{-1}(x)-G^{-1}(x)|)^2\le q^*. \end{aligned}$$

Since F and G have full support, we can set $x=F(\omega _i)$. With this transformation, the inequality is equivalent to

$$\begin{aligned} (\omega _i-F^{-1}(G(\omega _i)))^2\le q^*,~\forall \omega _i\in [0,1]. \end{aligned}$$

Thus, for any $\omega _i\in [0,1]$, we have

$$\begin{aligned} 1-(\omega _i-F^{-1}(G(\omega _i)))^2\ge 1-q^*\ge (1-q^\omega _i(\omega '))\big (1-(\omega _i-F^{-1}(G(\omega '))^2\big ),~\forall \omega '\in [0.1]. \end{aligned}$$

That is, $\omega _i$ worker cannot benefit from pretending to have $\omega '$. Similarly, we can work out the firm case and show it also cannot benefit from misreport.

For the full revelation of the true locations of the users, we can appeal to Proposition 1. As the utility function satisfies the condition in the proposition, we can be assured that there exists a skeptical belief that achieves the full revelation of the users’ true locations. $\square$

1.7 Proof of Proposition 4

Proof

Consider an equilibrium with thresholds ${\bar{\omega }}$ and ${\bar{\theta }}$ in which all workers whose type is lower than ${\bar{\omega }}$ send $\underline{m}$ and all workers with higher type than ${\bar{\omega }}$ sends ${\overline{m}}$ to the platform. On the other hand, all firms with location lower than ${\bar{\theta }}$ send $\underline{s}$, while firms with location higher than ${\bar{\theta }}$ sends ${\overline{s}}$ to the platform. The platform, after collecting messages, recommends each user in an assortative manner. Let $\#m$ denote the number of message m collected by the platform: If $\#{\bar{m}}>\#{\bar{s}}$ and $\#\underline{m}\le \#\underline{s}$, a worker who sent a lower message, $\underline{m}$, is recommended with a firm who sent a lower message, $\underline{s}$. If a worker sends a higher message, ${\overline{m}}$, then the platform arbitrarily picks $\#{\overline{s}}$ workers and each of them are recommended with a firm who sent a higher message, ${\overline{s}}$. All other workers are recommended with a firm who sent a lower message. If the other case, $\#{\bar{m}}\le \#{\bar{s}}$ and $\#\underline{m}>\#\underline{s}$ happens, the platform provides recommendations in the opposite way. At the last stage of the game, all workers apply to its recommended firm, and all firms accept its applicant.

To show this indeed constitute an equilibrium, I will work backward from the individual’s match choice problem. Suppose that a worker i sent $\underline{m}$, and recommended to apply to firm j. In equilibrium, the partial assortative recommendation reveals that $\theta _j\ge {\bar{\theta }}$ with probability

$$\begin{aligned}\sum ^n_{k=0}{n\atopwithdelims ()k}F({\bar{\theta }})^k(1-F({\bar{\theta }}))^{n-k}\sum ^{n-1}_{j=k}{n-1\atopwithdelims ()j}G({\bar{\omega }})^j(1-G({\bar{\omega }}))^{n-1-j}\left( 1-\frac{k}{1+j}\right) .\end{aligned}$$

He also updates about the location of other firms, say firm $k\ne j$. By ex-ante homogeneity, the probability that j is recommended to i is $\frac{1}{n}$. Using the total law of expectation, $P[\theta _j\ge {\bar{\theta }}]$ is the same as

$$\begin{aligned} \frac{1}{n}{\mathbb {P}}[\theta _j\ge {\bar{\theta }}|j~\text {is recommended to }\,i ]+\frac{n-1}{n}\mathbb P[\theta _j\ge {\bar{\theta }}|j~\text {is not recommended to }\,i ] \end{aligned}$$

By ex-ante homogeneity again,

$$\begin{aligned}P[\theta _j\ge {\bar{\theta }}|j~\text {is not recommended to }\,i ]=P[\theta _k\ge {\bar{\theta }}|k~\text {is not recommended to}\,i ]\end{aligned}$$

Thus, $P[\theta _k\ge {\bar{\theta }}|k~\text {is not recommended to }\,i ]$ is

$$\begin{aligned} \frac{n}{n-1}(1-F({\bar{\theta }}))-\frac{1}{n-1}\mathbb P[\theta _j\ge {\bar{\theta }}|j~\text {is recommended to }\,i ] \end{aligned}$$

For notational simplicity, I denote $P[\theta _j\ge {\bar{\theta }}|j~{\text {is recommended to}}\,i ]$ by $P[\theta _j\ge {\bar{\theta }}|j]$ and $P[\theta _k\ge {\bar{\theta }}|k~{\text {is not recommended to}}\,i ]$ by $P[\theta _k\ge {\bar{\theta }}|\lnot k]$. Given that $1\ge {\bar{1}}$, applying to firm j is better than applying to other firm if

$$\begin{aligned}&{\mathbb {P}}[\theta _j\ge {\bar{\theta }}|j]\mathbb E[1-(\theta _j-\omega _i)^2|\theta _j\ge {\bar{\theta }}]+\mathbb P[\theta _j\le {\bar{\theta }}|j]\mathbb E[1-(\theta _j-\omega _i)^2|\theta _j\le {\bar{\theta }}]\\&\quad \ge \max \left\{ 0,\frac{1}{2}P[\theta _k\le {\bar{\theta }}|\lnot k]\mathbb E[1-(\theta _k-\omega _i)^2|\theta _k\le {\bar{\theta }}]\right. \\&\quad \quad \left. +P[\theta _k\ge {\bar{\theta }}|\lnot k]{\mathbb {E}}[1-(\theta _k-\omega _i)^2|\theta _k\ge {\bar{\theta }}]\right\} \end{aligned}$$

Since $1\ge {\bar{1}}$, I have

$$\begin{aligned}{\mathbb {P}}[\theta _j\ge {\bar{\theta }}|j]{\mathbb {E}}[1-(\theta _j-\omega _i)^2|\theta _j\ge {\bar{\theta }}]+{\mathbb {P}}[\theta _j\le {\bar{\theta }}|j]{\mathbb {E}}[1-(\theta _j-\omega _i)^2|\theta _j\le {\bar{\theta }}]\ge 0.\end{aligned}$$

Using the closed form expression of $P[\theta _k\le {\bar{\theta }}|\lnot k]$ in terms of j, the remaining inequality can be simplified as follows: $[\mathbb P[\theta_j\leq\bar\theta|j]-F(\bar\theta)]\mathbb E[1-(\theta_j-\omega_i)^2|\theta_j\leq\bar\theta]\geq[\mathbb P[\theta_j\leq\bar\theta|j]-F(\bar\theta)]\mathbb E[1-(\theta_j-\omega_i)^2|\theta_j\geq\bar\theta]$

Lemma 4

${\mathbb {P}}[\theta _j\le {\bar{\theta }}|j]>F({\bar{\theta }}),~\forall {\bar{\theta }}\in (0,1)$.

Proof

By a property of the binomial distribution, B(n, p), it is

$$\begin{aligned}\sum ^n_{k=0}{n\atopwithdelims ()k}p^k(1-p)^{n-k}k=np. \end{aligned}$$

On the other hand, using a binomial theorem, it is

$$\begin{aligned}\sum ^{n-1}_{j=0}{n-1\atopwithdelims ()j}G(\omega _i)^k(1-G(\omega _i))^{n-1-j}=1. \end{aligned}$$

Letting $p=F({\bar{\theta }})$, and using the two equalities above, I can express $F({\bar{\theta }})$ in a form of

$$\begin{aligned}F({\bar{\theta }})=\sum ^n_{k=0}{n\atopwithdelims ()k}F({\bar{\theta }})^k(1-F({\bar{\theta }}))^{n-k}\frac{k}{n}\sum ^{n-1}_{j=0}{n-1\atopwithdelims ()j}G(\omega _i)^k(1-G(\omega _i))^{n-1-j}.\end{aligned}$$

Thus,

$$\begin{aligned}&{\mathbb {P}}[\theta _j\le {\bar{\theta }}|j]-F({\bar{\theta }})\\&\quad =\sum ^n_{k=0}{n\atopwithdelims ()k}F({\bar{\theta }})^k(1-F({\bar{\theta }}))^{n-k}\sum ^{k-1}_{j=0}{n-1\atopwithdelims ()j}G(\omega _i)^k(1-G(\omega _i))^{n-1-j}\bigg (1-\frac{k}{n}\bigg )\\&\quad \quad +\sum ^n_{k=0}{n\atopwithdelims ()k}F({\bar{\theta }})^k(1-F({\bar{\theta }}))^{n-k}\sum ^{n-1}_{j=k}{n-1\atopwithdelims ()j}G(\omega _i)^k(1-G(\omega _i))^{n-1-j}\bigg (\frac{k}{1+j}-\frac{k}{n}\bigg )\bigg ]>0. \end{aligned}$$

$\square$

By Lemma 4 I conclude that $\omega _i$ worker follows the recommendation if

$$\begin{aligned} {\mathbb {E}}[1-(\theta _j-\omega _i)^2|\theta _j\le {\bar{\theta }}]\ge {\mathbb {E}}[1-(\theta _j-\omega _i)^2|\theta _j\ge {\bar{\theta }}]. \end{aligned}$$

Before I study the platform’s incentive, I find that ${\bar{\omega }}$ and ${\bar{\theta }}$ should satisfy the arbitrage condition of Crawford and Sobel (1982). That is, by continuity and concavity, ${\bar{\omega }}$ is decided by the following condition:

$$\begin{aligned} {\mathbb {E}}[1-(\theta -\omega )^2|\theta \le {\bar{\theta }}]&\ge {\mathbb {E}}[1-(\theta -\omega )^2|\theta \ge {\bar{\theta }}]~\forall \omega \le {\bar{\omega }}\\ {\mathbb {E}}[1-(\theta -\omega )^2|\theta \le {\bar{\theta }}]&\le \mathbb E[1-(\theta -\omega )^2|\theta \ge {\bar{\theta }}]~\forall \omega \ge {\bar{\omega }}. \end{aligned}$$

Similarly, ${\bar{\theta }}$ is decided by the following condition:

$$\begin{aligned} {\mathbb {E}}[1-(\theta -\omega )^2|\omega \le {\bar{\omega }}]&\ge {\mathbb {E}}[1-(\theta -\omega )^2|\omega \ge {\bar{\omega }}]~\forall \theta \le {\bar{\theta }}\\ {\mathbb {E}}[1-(\theta -\omega )^2|\omega \le {\bar{\omega }}]&\le \mathbb E[1-(\theta -\omega )^2|\omega \ge {\bar{\omega }}]~\forall \theta \ge {\bar{\theta }}. \end{aligned}$$

Now, I need to check the incentive of the platform to provide partially assortative recommendation. Suppose that all users report their location using the binomial message space, and they all follow recommendations of the platform. Consider the situation where worker 1 sent ${\bar{m}}$, worker 2 sent $\underline{m}$, firm 1 sent ${\bar{s}}$, and firm 2 sent $\underline{s}$. Now, for a contrary, suppose that the platform recommends firm 1 to worker 2 and firm 2 to worker 1. Fixing the recommendations to the other workers, other than worker 1 and worker 2, the same, the platform’s expected utility from this non-assortative matching is greater than an assortative matching by

$$\begin{aligned}&{\mathbb {E}}[1-(\theta -\omega )^2|\omega \ge {\bar{\omega }} \wedge \theta \le {\bar{\theta }}]+{\mathbb {E}}[1-(\theta -\omega )^2|\omega \le {\bar{\omega }} \wedge \theta \ge {\bar{\theta }}]\\&\quad -{\mathbb {E}}[1-(\theta -\omega )^2|\omega \le {\bar{\omega }} \wedge \theta \le {\bar{\theta }}]-{\mathbb {E}}[1-(\theta -\omega )^2|\omega \ge {\bar{\omega }} \wedge \theta \ge {\bar{\theta }}]. \end{aligned}$$

Here, by the arbitrage conditions, I have

$$\begin{aligned}&-{\mathbb {E}}[1-(\theta -\omega )^2|\omega \le {\bar{\omega }} \wedge \theta \le {\bar{\theta }}]+{\mathbb {E}}[1-(\theta -\omega )^2|\omega \le {\bar{\omega }} \wedge \theta \ge {\bar{\theta }}]<0~{\text {and}}\\&\quad {\mathbb {E}}[1-(\theta -\omega )^2|\omega \ge {\bar{\omega }} \wedge \theta \le {\bar{\theta }}]-{\mathbb {E}}[1-(\theta -\omega )^2|\omega \ge {\bar{\omega }} \wedge \theta \ge {\bar{\theta }}]<0. \end{aligned}$$

which makes the overall value negative. Thus, the platform cannot benefit from non-assortative recommendation. This complete the proof since the user’s incentive not to deviate at reporting stage is satisfied by the arbitrage condition. $\square$

Appendix 2

1.1 Disutility from unwanted partners

I generalize the main model’s utility function to accommodate the possible negative utility when matched to an unwanted partner. When worker i with $\omega _i$ and firm j with $\theta _j$ are matched, they respectively receive

$$\begin{aligned} v_w-(\theta _j-\omega _i)^2\quad {\text {and}}\quad v_f-(\theta _j-\omega _i)^2, \end{aligned}$$

where $v_w$ and $v_f$ measure users’ tolerance level. When the values are low, users would rather stay unmatched than be matched with a user with dissimilar tastes. Any case with $v_w\ge 1$ and $v_f\ge 1$ is equivalent to the case of the main model. Thus, I focus on the case of $v_w<1$ or $v_f<1$.

On the other hand, the platform, as in the main model, seeks to maximize both the total number of matches and their overall quality. I assume that the platform receives $1-(\theta _j-\omega _i)^2$ from a match of $\omega _i$ and $\theta _j$. Thus, the misalignment of interest between the platform and a user is twofold: First, the platform wants users to be matched even if the generated values for the users are below their outside options. Second, users want to find a partner who is closest to them, while the platform aims to minimize the sum of distances.

Proposition 5

An unraveling equilibrium exists if

$$\begin{aligned} Kolm\left( F^{-1},G^{-1}\right) <\min \left\{ \sigma (F),\sigma (G),v_f^{\frac{1}{2}},v_w^{\frac{1}{2}}\right\} . \end{aligned}$$

Proof

Suppose that the sufficient condition is satisfied. By the condition,

$$\begin{aligned} \left( F^{-1}(x)-G^{-1}(x)\right) ^2<\min \left\{ \sigma (F)^2,v_f\right\} ,~\forall x\in [0,1]. \end{aligned}$$

Applying the same technique as in the proof of Theorem 1, the above inequality is the same as

$$\begin{aligned} \left( \theta _j-G^{-1}(F(\theta _j))\right) ^2<\min \left\{ {\mathbb {E}}_\omega \left[ (\theta _j-\omega )^2\right] ,v_f\right\} , \end{aligned}$$

That is, we have

$$\begin{aligned} v_f-\left( \theta _j-G^{-1}(F(\theta _j))\right) ^2>\max \left\{ 0,v_f-{\mathbb {E}}_\omega \left[ (\theta _j-\omega )^2\right] \right\} , \end{aligned}$$

which means that the user cannot do better off from not following the recommendation by choosing other partner or the outside option. Again, by Proposition 1, there exists a skeptical belief that fully reveals users’ true locations. $\square$

1.2 Explicit bound on N

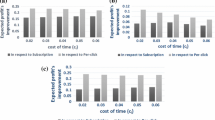
The bound N can be discovered using the following procedure. Let $N^\omega _{\omega _i}\in {\mathbb {N}}$ be the minimum number such that all values of n greater than $N_{\omega _i}\in {\mathbb {N}}$ satisfies (IC-$\omega _i$). For example, let $\omega _i=0.4$, $F(\theta )=\theta ^\alpha$ and $G(\omega )=\omega$, where $\alpha \in (0,1]$. Figure 7 depicts the difference $\mathbb E[1-(\omega _i-\Theta ^i_n(\omega _i))^2]- \mathbb E_\theta [1-(\omega _i-\theta ))^2]$ in terms of the market size n, where $\alpha$ varies from $\alpha =0.1$ to $\alpha =1$. As can be seen, $N^\omega _{0.4}=24$ for $\alpha = 0.4$, while it equals 5 and 3 for $\alpha =0.5$ and $\alpha =0.6$, respectively. For $\alpha \ge 0.7$, we have $N^\omega _{0.4}=1$, while the value of $N^\omega _{0.4}$ is not defined for any $\alpha$ below or equal to 0.3. Theorem 1 guarantees the existence of $N^\omega$ and $N^\theta$ in the following: $N^\omega = sup\{N^\omega _{\omega _i}\}_{\omega _i\in \Omega }$ and $N^\theta = sup\{N^\theta _{\theta _j}\}_{\theta _j\in \Theta }$. We can then take $N=\max \{N^\omega ,N^\theta \}$ (Figs. 5, 6, 7).

Fig. 7

Incentive map for $\omega _i=0.4$