Population ethics under risk

Abstract

Population axiology concerns how to rank populations by the relation “is socially preferred to”. So far, population ethicists have (with important exceptions) focused less on the question of how to rank population prospects, that is, alternatives that contain uncertainty as to which population they will bring about. Most public policy choices, however, are decisions under uncertainty, including policy choices that affect the size of a population (such as climate policy choices). Here, we shall address the question of how to rank population prospects by the relation “is socially preferred to”. We start by illustrating how well-known population axiologies can be extended to population prospect axiologies. And we show that new problems arise when extending population axiologies to prospects. In particular, traditional population axiologies lead to prospect-versions of the problems that they are praised for avoiding in the risk-free settings. Moreover, we show how the axiom of State-Wise Dominance allow us to extend any impossibility theorem in population axiology to impossibility theorems for non-trivial population prospects, that is, prospects that confer probabilities strictly between zero and one on different populations. Finally, we formulate impossibility results that only involve probabilistic axioms.

1 Introduction

Population axiology concerns how to evaluate populations in terms of their “moral goodness” as philosophers call it, that is, how to rank populations by the relation “is socially preferred to”, to use terminology more familiar in social choice theory and welfare economics. So far, discussions of population axiology has focused less on the question of how to rank alternatives that contain uncertainty as to which population they will bring about.¹ The adequacy conditions (i.e., “axioms”) that have been discussed mostly pertain to the ranking of risk-free outcomes and are silent in regard to how to rank (non-trivial) risky prospects. In other words, questions about what we call population prospect axiology—that is, questions about how to rank what we call population prospects—have, in our view, been underexplored.

This exclusion of uncertainty is unfortunate since most public policies that could affect the number and identities of future people contain a great deal of uncertainty as to which population they will bring about.² For instance, as the Intergovernmental Panel on Climate Change acknowledged in their Fifth Assessment Report,³ we should expect that the climate policies we choose will affect the size of the world population. But obviously, climate policies contain a great deal of uncertainty, for instance, uncertainty about what type of population they will bring about.⁴

Since the birth of modern population axiology, starting with Parfit’s informal paradoxes summarised in Parfit (1984), researchers in this area have uncovered a number of impossibility results that establish that no population axiology can consistently satisfy a small number of conditions that many find compelling as adequacy conditions on any such axiology.⁵ Unfortunately, it turns out that the situation is even worse when it comes to population prospect axiology. As we show below, new problems appear when one tries to turn a population axiology into a population prospect axiology. Perhaps most interestingly, we shall see that natural extensions of traditional (risk-free) population axiologies lead to prospect-versions of the problems that they are praised for avoiding in the risk-free setting.

Moreover, we show that an instance of the familiar axiom of State-Wise Dominance opens the door to impossibility results for population prospect axiology that are analogous to the traditional impossibility results for (risk-free) population axiology. Importantly, these results cannot be derived just from the (risk-free) adequacy conditions involved in the traditional impossibility theorems, and they hold for non-trivial prospects (as well as for trivial ones), that is, for prospects that confer probabilities strictly between zero and one on different populations. So, with this adequacy condition on prospects, all the well-known problems from risk-free population axiology are reproduced in the risky setting; and, in addition, new problems appear when risk is introduced.

Now, we know that there are some multi-person decision problems where a solution can be found only if we introduce probabilities. In particular, there are some well-known problems in game theory where a Nash equilibrium exists only if the “players” are allowed to randomise between their available “pure” (i.e., non-probabilistic) strategies (von Neumann and Morgenstern 1944). In a similar vein, one might have hoped that a solution could be found to the problems of population ethics by introducing probabilities. This hope might seem further supported by the fact that the traditional adequacy conditions for population axiology say nothing about how to rank what we above called “non-trivial” prospects, that is, prospects that confer probabilities strictly between zero and one on different populations (as we further explain below).

An axiology for non-trivial population prospects that avoids the traditional risk-free impossibility results would indeed be a great victory from a practical point of view. Policies that could affect the size of a population typically contain considerable uncertainty, as previously mentioned. In fact, it is hard to think of any policy (population-affecting or not) that is certain to deliver a particular outcome. Therefore, one might conjecture that if we have an adequate population prospect axiology, then we will be able to make consistent population policy choices, notwithstanding the traditional impossibility results for risk-free populations. But as we shall soon see, the traditional impossibility results more-or-less reappear when risk is introduced, which, as previously mentioned, moreover brings with it some additional problems.

2 Framework and Background Assumptions

A natural starting point in the search for a population prospect axiology is to consider some extensions of standard population axiologies to situations of uncertainty. But first, we need to introduce a few terms and distinctions used in traditional, risk-free, population axiology, which we will use when formulating the aforementioned extensions.

In traditional population axiology, one often distinguishes between the welfare of a person and the contributive value of a person’s welfare (or well-being; we shall use these two terms interchangeably). By the contributive value of a person’s welfare we shall mean the value that a person’s welfare contributes to the value of a population of which it is a member. More exactly, the contributive value of a person i’s welfare relative to a population x, of which i is a member, is the difference in value between x and the population consisting of all the x-people except i. This distinction is useful for population prospect axiology too, for we can now reformulate one of our main questions as “What is the contributive value of a possible person’s welfare to a prospect?”

Now to our formal framework, which follows closely that of Asheim and Zuber (2014), although suitably extended to prospects based on the framework of Savage (1954). Let ${\mathbb {N}}$ denote the set of natural numbers and ${\mathbb {R}}$ the set of real numbers. ${\mathbb {R}}^-\subset {\mathbb {R}}$ and ${\mathbb {R}}^+\subset {\mathbb {R}}$ are the sets of negative and positive real numbers. Let ${{\textbf {X}}}=\bigcup _{n\in {\mathbb {N}}}{\mathbb {R}}^n$ denote the set of possible finite distributions of lifetime well-being. More formally, ${{\textbf {X}}}$ is a set of vectors of real numbers, where each number (“utility”) represents the lifetime well-being of some person. A generic such vector for a population of m people is denoted ${{\textbf {x}}}=(x_1,\ldots , x_m)$ or ${{\textbf {y}}}=(y_1,\ldots , y_n)$, where, say, $x_i$ denotes the lifetime well-being of individual i. Informally, we shall talk of a vector like this as a population. ${{\textbf {X}}}^-\subset {{\textbf {X}}}$ and ${{\textbf {X}}}^+\subset {{\textbf {X}}}$ are the subsets of such vectors where every number in the vector is negative respectively positive. The size of population x is denoted by $n({{\textbf {x}}})$ (and will, as mentioned, always be finite). For any vector x, we write the average value of its elements as ${\bar{x}}$. So, ${\bar{x}}$ should be interpreted as the average lifetime welfare of people in population x.

Let $(z)_n\in {\mathbb {R}}^n$ denote the perfectly equal population where all n individuals have lifetime well-being z. We let $({{\textbf {x}}}, {{\textbf {y}}})$ denote the population that results when population ${{\textbf {x}}}\in {{\textbf {X}}}$ is conjoined with population ${{\textbf {y}}}\in {{\textbf {X}}}$. And let $({{\textbf {x}}}, (z)_n)$ denote population ${{\textbf {x}}}\in {{\textbf {X}}}$ with n added individuals that all have lifetime well-being z.

The well-being measure is normalised around the “neutral” life. More formally, if i’s life in x is neutral, then $x_i=0$, while if i’s life in x is better for i than a neutral life, then i has positive welfare in x, i.e., $x_i>0$, but if i’s life in x is worse for i than a neutral life, then i has negative welfare in x, i.e., $x_i<0$. We shall remain agnostic about what constitutes well-being and what determines whether a life is neutral (but for different suggestions for the latter, see e.g. Arrhenius, forthcoming, ch. 2 and 9, Arrhenius 2000a, Broome, 2004, and Parfit, 1984, pp. 357-358, and appendix G).

To simplify the formal presentation of views and conditions, we shall assume the standard anonymity assumption, which holds that the “social welfare relations” that we study are invariant under permutations of the vectors in X. So, for instance, let ${{\textbf {x}}}^\prime$ be the vector that results when the lifetime well-being of i and j in x are switched. Then the social welfare relations that we shall consider are all indifferent between x and ${{\textbf {x}}}^\prime$, that is, they deem these two populations to be equally good. Intuitively, this means that it does not matter who receives what welfare; all that matters is how welfare quantities are distributed. This assumption rules out some views in the literature that are called “person affecting” (cf. Glover, 1977, Arrhenius, 2009, Roberts, 2010) as well as desert-based views (Arrhenius 2003a; Feldman 1997). But we should emphasise that anonymity is just a simplifying assumption. Just like the original results in the risk-free setting, the results of this paper can be established without an anonymity assumption, but the argument would then involve more complicated formulations.

We let $\precsim$ on X denote a “social welfare relation” on X, such that for any ${{\textbf {x}}}, {{\textbf {y}}}\in {{\textbf {X}}}$, ${{\textbf {x}}}\precsim {{\textbf {y}}}$ means that y is at least as socially preferable as x, or, as we shall often put it, y is at least as good as x. (So, $\precsim$ is what some philosophers would call a “moral goodness” relation, but we shall from now on refer to it as a social welfare relation.) To simplify the discussion we shall typically assume that the social welfare relation is transitive, reflexive, and complete, which means that the relation generates a social welfare order. It is worth noting, however, that for the impossibility results that we present in section 4 a quasi-order suffices, that is, completeness need not be assumed. In other words, these results are consistent with some populations being incommensurable in value.⁶ The strict relation, $\prec$, and indifference, $\sim$, are respectively the asymmetric and symmetric counterparts of $\precsim$. When we speak of a “social planner”, we mean the (possibly group) agent whose preference is represented by $\precsim$.

Although we shall typically assume that the relevant probabilities are “objective”, or given to the social planner, as in the von Neumann and Morgenstern (1944) framework, we use a more general Savage (1954)-inspired framework—which does not assume the probabilities to be given to the decision-maker—to turn the traditional population axiologies into population prospect axiologies. To that end, let S be a set of (non-overlapping) states of the world, that is, resolutions of uncertainty, with generic elements $s_i, s_j$. For simplicity, we assume S to be finite. Let P be a set of functions from S into X. Generic elements of P will be denoted P, Q, or $P_1$, $P_2$, etc. We interpret the elements in P as population prospects. $P(s_i)\in {{\textbf {X}}}$ is the well-being vector, that is, the population, that results from prospect P if $s_i$ is the actual state of the world. Finally, we assume that the social planner has a probability measure over S, that is, there is a function p from S into [0,1] such that $\sum _{i=1}p(s_i)=1$, which quantifies the social planner’s uncertainty (which may but need not correspond to some objective probability distribution). We use ${\varvec{\precsim }}$ for weak social welfare relation over P, with the corresponding strict relation, ${\varvec{\prec }}$, and indifference, ${\varvec{\sim }}$.

It will be useful to work with events, that is, unions of states, when stating some conditions. To that end, let ${{\textbf {E}}}$ be a Boolean algebra of events generated from S, that is, the set of all possible sets of states in S, closed under the Boolean operators. Generic elements of ${{\textbf {E}}}$ will be denoted E, $\lnot E$, F, etc. Since we assume the social planner to be probabilistically coherent, her probability function extends straightforwardly from S to ${{\textbf {E}}}$. Moreover, probabilistic coherence ensures that if $E\subset {{\textbf {E}}}$ then $p(E)<1$ and $p(\lnot E)>0$, which will be convenient when stating some of the below conditions. Finally, to further simplify notation, when we for instance write $P(E)={{\textbf {x}}}$, this means that every state in E results in x given P, that is, for any $s_i\in E$, $P(s_i)={{\textbf {x}}}$.

Later we shall focus much of our attention on what we call non-trivial prospects. Informally, a prospect is non-trivial if it confers a positive probability on at least two distinct populations; otherwise it is said to be trivial. More formally:

Definition

(Non-trivial prospect) A prospect, $P\in {{\textbf {P}}}$ is called non-trivial just in case there are $P(s_i), P(s_j)\in {{\textbf {X}}}$ where $P(s_i)\not =P(s_j)$ and $p(s_i)>0$, $p(s_j)>0$.

We let ${{\textbf {P}}}_{nt}\subset {{\textbf {P}}}$ denote the set of non-trivial population prospects.

3 Population Prospect Axiologies

Let us now consider how the traditional population axiologies could be extended to situations of uncertainty, using the framework and terminology from the last section.⁷ We start with Total Utilitarianism, according to which the contributive value of a person’s welfare equals her welfare,⁸ and the value of a population is calculated by summing the welfare of all people in the population.

Total Utilitarianism

(TU) For any ${{\textbf {x}}}, {{\textbf {y}}}\in {{\textbf {X}}}$:

$$\begin{aligned} {{\textbf {x}}}\precsim {{\textbf {y}}}\Leftrightarrow TU({{\textbf {x}}})=\sum _{i}x_i \le TU({{\textbf {y}}})=\sum _{i}y_i \end{aligned}$$

A natural way to turn Total Utilitarianism into a population prospect axiology is to sum up weighted Total Utilitarian values of all the possible populations that a prospect might result in, where the weight on the value of each population is determined by the probability that the prospect will result in that population.⁹ Let us call the resulting axiology Prospect Total Utilitarianism.

Prospect Total Utilitarianism

(PTU) For any $P, Q\in {{\textbf {P}}}$:

$$\begin{aligned} P{\varvec{\precsim }} Q\Leftrightarrow \sum _i p(s_i)TU(P(s_i))\le \sum _i p(s_i)TU(Q(s_i)) \end{aligned}$$

One of the great challenges that examinations of different size populations have raised for Total Utilitarianism, is how to respond to the fact that the latter gives rise to what Parfit (1984) called the Repugnant Conclusion. Informally, this conclusion is that for any perfectly equal population (no matter how well off are its members), there is a better population consisting of people with very low positive welfare. More formally¹⁰:

Repugnant Conclusion

For all $y, z\in {\mathbb {R}}$, where $y>z>0$, and for any $k\in {\mathbb {N}}$, there is an $n\in {\mathbb {N}}$, where $n>k$, and such that $(y)_k \prec (z)_n$.

It should be evident that the prospect version of Total Utilitarianism also leads to the Repugnant Conclusion not only in non-risky situations but also in risky ones. For instance, for any prospect P, all of whose possible outcomes are populations where people enjoy very high welfare, there exists some prospect Q, all of whose possible outcomes are larger populations where people have very low positive welfare, such that Prospect Total Utilitarianism will recommend choosing the latter. The result, if we follow the recommendation of Prospect Total Utilitarianism, is that we end up with a large population where people have very low positive welfare when we had the option of some smaller population where people enjoy very high welfare—an instance of the Repugnant Conclusion. Likewise for other potentially counterintuitive implications of Total Utilitarianism in non-risky settings, such as the Very Repugnant Conclusion.¹¹

Moreover, Prospect Total Utilitarianism violates probabilistic analogues of the traditional (risk-free) Quality condition which essentially rules out the Repugnant Conclusion (and which we state in section 4). Let ${\mathbb {H}}\subset {\mathbb {R}}^+$ be welfare levels that are very high—such that a life at a level in ${\mathbb {H}}$ would be deemed excellent—while ${\mathbb {L}}\subset {\mathbb {R}}^+$ are welfare levels that are very low but positive—such that a life at a level in ${\mathbb {L}}$ would be deemed barely worth living. Consider the following probabilistic analogue of the traditional Quality condition, which can be derived from the non-risky condition with help of the traditional State-Wise Dominance principle from decision theory that we discuss in section 4.¹² Informally, what we shall call Probabilistic Quality says that there is some very high welfare level z and some number n of people at that level, such that for any very low but positive welfare level y and any number m of people at that level, if prospects P and Q result in the same population in some state(s), but in states where they result in different populations, P results in a population where n people are at the very high level z whereas Q results in a population where m people are at the very low level y, then P is at least as good as Q. More formally:

Probabilistic Quality

There is a $z\in {\mathbb {H}}$ and an $n\in {\mathbb {N}}$, such that for any ${{\textbf {x}}}\in {{\textbf {X}}}$, any $E\subseteq {{\textbf {E}}}$, any $y\in {\mathbb {L}}$ and any $m\in {\mathbb {N}}$, if $Q(E)={{\textbf {x}}}$ and $Q(\lnot E)=(z)_n$, while $P(E)={{\textbf {x}}}$ and $P(\lnot E)=(y)_m$, then $P{\varvec{\precsim }} Q$.

Prospect Total Utilitarianism of course violates Probabilistic Quality. The expected utility framework we have assumed when extending Total Utilitarianism to Prospect Total Utilitarianism implies that the probability and utility of ${{\textbf {x}}}$ can be ignored when comparing P with Q (this follows from the aforementioned dominance condition). Hence, since m can be very large, compared with n, Prospect Total Utilitarianism violates Probabilistic Quality, for the same reason that Total Utilitarianism leads to the Repugnant Conclusion.¹³

In comparison with other axiologies, Total Utilitarianism arguably handles (non-risky) cases involving negative welfare better than most alternative axiologies, such as Average and Critical-Level Utilitarianism (more on which below). For example, Total Utilitarianism clearly avoids the Very Sadistic Conclusion which is implied by Critical-Level Utilitarianism.¹⁴ Informally, the Very Sadistic Conclusion is that for any population with negative welfare, there is a worse population with positive welfare. More formally:

Very Sadistic Conclusion

For any ${{\textbf {x}}}\in {{\textbf {X}}}^-$ there is a ${{\textbf {y}}}\in {{\textbf {X}}}^+$ such that ${{\textbf {y}}}\prec {{\textbf {x}}}$.

While Total Utilitarianism avoids the Very Sadistic Conclusion, Prospect Total Utilitarianism leads to what we call the Risky Very Sadistic Conclusion.

Risky Very Sadistic Conclusion

For any $E\subset {{\textbf {E}}}$, for any ${{\textbf {x}}}\in {{\textbf {X}}}^-$, for any ${{\textbf {y}}}\in {{\textbf {X}}}^+$, and for any $\gamma \in {\mathbb {R}}^+$, there is a $z\in {\mathbb {R}}$ such that $z<\gamma$ and an $m\in {\mathbb {N}}$ such that if $P(E)={{\textbf {x}}}$ and $P(\lnot E)=(z)_m$, while the trivial prospect Q for sure results in y, then $Q{\varvec{\prec }} P$.

Here is why Prospect Total Utilitarianism implies the Risky Very Sadistic Conclusion. For any probability $p(E)<1$, however high, if m is sufficiently great, then the expected total welfare of prospect P, which has probability p of resulting in x and probability $1-p$ of resulting in $(z)_m$, will be higher than the expected total welfare of prospect Q, which results in y for sure. Thus, Prospect Total Utilitarianism deems P better than Q. This holds irrespective of how much the x-people suffer and of how many they are. In other words, while Total Utilitarianism avoids the Very Sadistic Conclusion, Prospect Total Utilitarianism recommends prospects that will almost certainly result in a population with negative welfare even though a population with positive welfare was available (hence the name of the conclusion). Below we prove a general theorem of which this result is a special case.¹⁵

Now, there is of course a sense in which the above conclusion (as well as the aforementioned general result) is just an instance of a general implication of Expected Utility Theory (EUT)—and, in particular, its probabilistic continuity axiom—that has nothing specifically to do with population ethics.¹⁶ We however make two points about this observation. First, we think that while one might see the Risky Very Sadistic Conclusion as a special case of a more general implication of EUT, that does not change the fact that the special case in question is illuminating for debates in population ethics. In particular, it teaches us something important about Total Utilitarianism, namely, that while the theory is praised for avoiding the Very Sadistic Conclusion, the most natural prospect-extension of the theory comes arbitrarily close to the very same conclusion, in the sense of recommending, for any population with negative welfare, a choice that has an arbitrarily high probability of resulting in that population, even though a population with positive welfare was available. So, the theory comes arbitrarily close to recommending the Very Sadistic Conclusion.¹⁷

Second, it is worth noting that two of the most influential arguments in favour of Utilitarianism assume continuity of the kind that leads total utilitarians to the Risky Very Sadistic Conclusion; this is true both of arguments for Average Utilitarianism (Harsanyi 1953), and Total Utilitarianism (Harsanyi 1955; Hammond 1987, 1988).¹⁸ So, although continuity in probabilities, as assumed by Expected Utility Theory, is largely to blame for the Risky Very Sadistic Conclusion—as well as the Risky Repugnant Conclusion, which we discuss below—utilitarians (in particular Prospect Utilitarians) presumably will be wary of responding by denying such continuity.¹⁹

Faced with the Repugnant Conclusion and other similar problems, a Utilitarian might be tempted to opt for a non-total version of the theory, such as Average Utilitarianism or Critical-Level Utilitarianism, which can respectively be extended to Prospect Average Utilitarianism and Prospect Critical Level Utilitarianism. It is easy to see that these theories avoid the Repugnant Conclusion. However, as is well known, these alternatives to Total Utilitarianism have, in the risk-free setting, their own counterintuitive conclusions to deal with; conclusions that are arguably at least as counterintuitive as the Repugnant Conclusion.²⁰ It should be evident that since Prospect Average Utilitarianism and Prospect Critical Level Utilitarianism are extensions of Average Utilitarianism and Critical Level Utilitarianism to risky situations, they inherit the problems of their ancestors for trivial prospects.²¹ Moreover, it turns out that Prospect Average Utilitarianism and Prospect Critical Level Utilitarianism—and, in fact, any population prospect axiology that satisfies transitivity and State-Wise Dominance—faces additional problems due to the introduction of uncertainty, even when the scope is limited to non-trivial prospects, as we shall soon see.

But first, to appreciate some of the problems that non-total Utilitarian theories are faced with in the risk-free setting, let’s look more closely at Average Utilitarianism, according to which the value of a population is found by summing up the welfare of the people in the population and dividing this sum with the number of people in the population.²² (After examining Average Utilitarianism and its prospect extension, we shall briefly discuss Critical Level Utilitarianism and its prospect extension.) Hence, the contributive value of a person’s welfare depends on the average welfare of the population of which it is a member: The contributive value of a person’s welfare is positive (negative, neutral) if the person has a higher (lower, same) welfare than the average welfare in the population.

Average Utilitarianism

(AU) For any ${{\textbf {x}}}, {{\textbf {y}}}\in {{\textbf {X}}}$:

$$\begin{aligned} {{\textbf {x}}}\precsim {{\textbf {y}}}\Leftrightarrow AU({{\textbf {x}}})={\bar{x}} \le AU({{\textbf {y}}})={\bar{y}} \end{aligned}$$

Now, we can extend this theory to situations of risk—thus creating Prospect Average Utilitarianism—in an analogous way to how Total Utilitarianism was extended to Prospect Total Utilitarianism:

Prospect Average Utilitarianism

(PAU) For any $P, Q\in {{\textbf {P}}}$:

$$\begin{aligned} P{\varvec{\precsim }} Q\Leftrightarrow \sum _i p(s_i)AU(P(s_i))\le \sum _i p(s_i)AU(Q(s_i)) \end{aligned}$$

Average Utilitarianism gives rise to the Sadistic Conclusion, which informally says that it is better to add to a population people with negative rather than positive welfare.²³ More formally:

Sadistic Conclusion

There is an ${{\textbf {x}}}\in {{\textbf {X}}}$, a ${{\textbf {y}}}\in {{\textbf {X}}}^+$, and a ${{\textbf {z}}}\in {{\textbf {X}}}^-$ such that $({{\textbf {x}}},{{\textbf {y}}})\prec ({{\textbf {x}}}, {{\textbf {z}}})$.

Even worse, Average Utilitarianism violates the seemingly unassailable Weak Non-Sadism, which is even logically weaker than what is required to avoid the Sadistic Conclusion. Informally, Weak Non-Sadism implies that there is a negative welfare level and a number of people at this level such that an addition of any number of people with positive welfare is at least as good as an addition of the negative welfare people. More formally:

Weak Non-Sadism

There is a $z\in {\mathbb {R}}^-$ and an $n\in {\mathbb {N}}$, such that for any ${{\textbf {x}}}\in {{\textbf {X}}}$, for any $y\in {\mathbb {R}}^+$, and for any $m\in {\mathbb {N}}$, $({{\textbf {x}}},(z)_n)\precsim ({{\textbf {x}}},(y)_m)$.

Prospect Average Utilitarianism of course violates Weak Non-Sadism too, that is, for trivial prospects. Moreover, it is straightforward to verify that Prospect Average Utilitarianism also violates, for non-trivial prospects, a probabilistic analog of Weak Non-Sadism that is implied by Weak Non-Sadism together with the aforementioned dominance condition:

Probabilistic Weak Non-Sadism

There is a $z\in {\mathbb {R}}^-$ and an $n\in {\mathbb {N}}$, such that for any ${{\textbf {x}}},{\textbf {x'}}\in {{\textbf {X}}}$, any $y\in {\mathbb {R}}^+$, any $m\in {\mathbb {N}}$, any $P,Q\in {{\textbf {P}}}$, and any $E\subseteq {{\textbf {E}}}$, if $P(E)=({{\textbf {x}}},(z)_n)$ and $P(\lnot E)=({{\textbf {x}}},{{\textbf {x}}}')$, while $Q(E)=({{\textbf {x}}},(y)_m)$ and $Q(\lnot E)=({{\textbf {x}}},{{\textbf {x}}}')$, then $P{\varvec{\precsim }} Q$.

Perhaps more interestingly, while Average Utilitarianism (and Critical Level Utilitarianism) of course avoids the risk-free Repugnant Conclusion, Prospect Average Utilitarianism (and Prospect Critical Level Utilitarianism as well as of course Prospect Total Utilitarianism) leads to what we might call the Risky Repugnant Conclusion²⁴:

Risky Repugnant Conclusion

For any $E\subset {{\textbf {E}}}$, for any ${\textbf{y}}, {\textbf{z}} \in {{\textbf {X}}}$, there is an ${{\textbf{x}}}\in {{\textbf{X}}}$, such that if $P(\lnot E)={{\textbf {x}}}$ and $P(E)={{\textbf{z}}}$ while trivial prospect Q results in y for sure, then $Q{\varvec{\prec }} P$.

The above observation means that while Average Utilitarianism (and Critical Level Utilitarianism) avoids the Repugnant Conclusion, Prospect Average Utilitarianism (and Prospect Critical Level Utilitarianism) recommends prospects that will almost certainly result in a Repugnant Conclusion, that is, in the special case where z is a huge population consisting of people who have very low positive welfare while $\mathbf{y}$ is a smaller population where everyone is very well-off. So, again we see that a prospect axiology leads to the probabilistic analogue of the conclusion that the corresponding risk-free axiology is celebrated for avoiding.

For the sake of completeness, and to convince the reader that Prospect Critical Level Utilitarianism really does lead to the Risky Repugnant Conclusion, it is worth formally stating the theory. The general intuition behind Critical Level Utilitarianism is that only people with welfare that is above some “critical level”, which is typically assumed to be higher than the neutral level, can increase the value of a population. More precisely, the risk-free version of the theory states that for some critical level $c\ge 0$:²⁵

Critical-Level Utilitarianism

(CLU) For any ${{\textbf {x}}}, {{\textbf {y}}}\in {{\textbf {X}}}$:

$$\begin{aligned} {{\textbf {x}}}\precsim {{\textbf {y}}}\Leftrightarrow CLU({{\textbf {x}}})=\sum _{i}[x_i-c] \le CLU({{\textbf {y}}})=\sum _{i}[y_i-c] \end{aligned}$$

Blackorby et al. (2005) have extended Critical Level Utilitarianism²⁶ to a prospect theory by essentially applying Expected Utility Theory to population prospects where each population is evaluated by the above formula. That is, they extend Critical Level Utilitarianism in the same way as we have extended Average and Total Utilitarianism (albeit using a somewhat different notation and formal framework than we do). The resulting theory states that:

Prospect Critical-Level Utilitarianism

For any $P, Q\in {{\textbf {P}}}$:

$$\begin{aligned} P{\varvec{\precsim }} Q\Leftrightarrow \sum _i p(s_i)CLU(P(s_i))\le \sum _i p(s_i)CLU(Q(s_i)) \end{aligned}$$

It should be evident that while Critical Level Utilitarianism was partly designed to avoid the Repugnant Conclusion, Prospect Critical Level Utilitarianism leads to the Risky Repugnant Conclusion. For as long as the people in the x population are sufficiently high above the critical level, then Prospect Critical Level Utilitarianism will instruct us to gamble on x rather than getting y for sure, irrespective of how much more likely the gamble is to result in z than in x and irrespective of how much worse off people are in z compared to in y.

Now, average and critical level utilitarians could avoid the Risky Repugnant Conclusion by postulating that there is a limit to how high a person’s welfare can be. But what we take this and the previous result to illustrate—and the point we want to emphasise—is that new problems appear when we try to turn a population axiology into a population prospect axiology. For, as we have seen, natural formulations of each of the three standard versions of Utilitarianism lead to prospect-versions of the conclusions that they avoid in the risk-free settings, as long as they do not put an upper bound on the moral value of a population, for instance, by setting an upper limit on possible individual welfare and population size (in the case of Average Utilitarianism, the former limit suffices).²⁷

Here is a more general way of putting the last observation. The population axiologies we have considered all tell us that the best population maximises some value; e.g., total welfare, average welfare, total welfare above critical level. The focus on this value helps the axiology in question avoid some problem in the risk-free setting; for instance, by focusing on maximising average welfare, Average Utilitarianism avoids the Repugnant Conclusion, while by focusing on total welfare, Total Utilitarianism avoids the Sadistic Conclusion. However, if for each of these theories, the value it wants us to focus on is unbounded from above, then any prospect axiology that is based on expected utility theory will recommend that we choose some prospect that has an arbitrarily high chance of resulting in a terrible population (as judged by that axiology), over a risk-free “prospect” that can only result in a wonderful population (as judged by that axiology). So, formulated as an (informal) impossibility result, the point is that there is no expectational population prospect axiology, whose value is unbounded from above, that avoids recommending a prospect that has an arbitrarily high chance of resulting in a terrible population even when a wonderful population is on offer.²⁸

We can in fact put the last observation as a (very simple) formal and general theorem.²⁹ Recall that the above results hold for axiologies such as Total Utilitarianism and Average Utilitarianism according to which moral value is unbounded (from above). So, now let $V: {{\textbf {X}}}\rightarrow {\mathbb {R}}$ be a generic (i.e., could be totalist, could be averagist, etc.) moral value function that is unbounded from above, that is, for any $k\in {\mathbb {R}}$, there is an ${{\textbf {x}}}\in {{\textbf {X}}}$ such that $V({{\textbf {x}}})>k$.

Expected Value Theorem

For any ${{\textbf {x}}},{{\textbf {y}}}\in {{\textbf {X}}}$ and for any $p\in (0,1)$, there is a ${{\textbf {z}}}\in {{\textbf {X}}}$ such that

$$\begin{aligned} pV({{\textbf {y}}})+(1-p)V({{\textbf {z}}})>V({{\textbf {x}}}) \end{aligned}$$

Proof

Since V is unbounded from above, we can always find some ${{\textbf {z}}}$ such that

$$\begin{aligned} V({{\textbf {z}}})>\frac{V({{\textbf {x}}})-pV({{\textbf {y}}})}{(1-p)} \end{aligned}$$

$\square$

To see why the result that Prospect Average Utilitarianism implies the Risky Repugnant Conclusion is an instance of the Expected Value Theorem, note that the average utilitarian moral value function is an instance of V, and let ${{\textbf {x}}}$ be any population where all members have very high welfare, let ${{\textbf {y}}}$ be some population where all members have very low but still positive welfare, and choose some ${{\textbf {z}}}$ with a sufficiently high average welfare. Similar reasoning shows that the result that Prospect Total Utilitarianism implies the Risky Very Sadistic Conclusion is an instance of the Expected Value Theorem, and so on.

Now, the Expected Value Theorem could be seen as a motivation for seeking population axiologies that put on upper bound on moral value.³⁰ We are personally sceptical of such theories, for reasons that we we do not have the space to discuss here. Still, we acknowledge that the results of this paper might be provide some reason to rethink that scepticism.³¹

For the remainder of this paper, the question we will focus on is whether the impossibility results that have been proven for risk-free population axiology—that is, results showing that no population axiology can satisfy different sets of adequacy conditions (i.e., axioms) that many find to be intuitively compelling—also hold for non-trivial prospects. We know from the study of risk-free population axiology that there is a great advantage to focusing on exploring the logical consistency of different adequacy conditions, rather than formulating new theories in response to the impossibility results that have been found for the old theories. After all, that search has, so far, only resulted in new impossibility results (as reviewed in Arrhenius, forthcoming).

In the spirit of the axiomatic approach, we shall, in the next section, formulate a weak and very plausible state-dominance condition that some would see as ensuring that the ranking of population prospects coheres with the ranking of populations. As we show in section 4, this condition suffices to generate impossibility results for population prospect axiology that are similar to the traditional impossibility results for (risk-free) population axiology. Moreover, as we shall explain in section 4, some condition such as that introduced in the next section is needed to generate impossibility results for non-trivial population prospects, since the traditional adequacy conditions for risk-free population axiology say nothing whatsoever about how to rank non-trivial prospects.

Nevertheless, one might have already suspected that since any prospect axiology should satisfy some condition of continuity in probabilities, the impossibility results for population axiology would reappear in population prospect axiology. For instance, one might think that if a risk-free adequacy condition for population axiology implies that x is better than y, then such a continuity condition for population prospect axiology would ensure that a non-trivial prospect that results in x with a probability that is arbitrarily close to 1 is better than a prospect that results in y with a probability that is arbitrarily close to 1, irrespective of what other populations the two prospects could result in.

The above application of continuity is one simple way of generating population prospects impossibility results on the back of the traditional impossibility results for risk-free prospects. For the remainder of this paper, we will however explore different approaches, that do not assume continuity in probabilities. Instead, we assume (except for in the final result) a dominance condition which some will find  less questionable than continuity, and which the next section formally introduces.

4 Population Prospect Impossibility Theorems

As an illustration of a straightforward comparison of population prospects, consider prospects $P_1$ and $P_2$ in Table 1. We assume, in the below example (and indeed throughout this paper), that the only axiologically relevant features at stake are, first, the welfare of the people in the populations that the prospects might result in, and, second, the probabilities that the prospects result in these populations. Moreover, in the example below, we assume that the only person whose welfare $P_1$ and $P_2$ affect is Ann, who will lead a horrible and suffering life (denoted by “Ann: -100”) if we choose $P_2$. The same is true if we choose $P_1$ and state of the world $s_1$ obtains. However, in state $s_2$ the choice of $P_1$ means that Ann will lead an excellent life (which we denote by “Ann: 100”).

Table 1 Illustration of dominance relationship

It seems evident that $P_1$ is better than $P_2$. After all, Ann is sure to lead a suffering life given the choice of $P_2$, but she could be spared these sufferings and lead an excellent life given the choice of $P_1$.

The above reasoning is an instance of the well-known State-Wise Dominance principle from decision theory. The role of this principle could be seen as ensuring  that the ranking of prospects coheres with the ranking of the outcomes (in our case, the populations) that the prospects could result in.³² We see no reason why one would reject this as an adequacy condition for population prospect axiologies, assuming, as we have done, that the only axiologically relevant feature at stake is the welfare of the people involved and the probabilities of the possible populations (Fleurbaey 2010, 654 makes a similar point).³³ Nevertheless, one of the results we present in the next section does not assume State-Wise Dominance in full generality; and one result does not assume the principle at all.³⁴

Let us call the fully general implication that State-Wise Dominance has for population prospects Population State Dominance, and formulate it thus:

Population State Dominance

If for all $s_i\in {{\textbf {S}}}$, $P_2(s_i)\precsim P_1(s_i)$, then $P_2{\varvec{\precsim }} P_1$; and if, in addition, for at least one non-null³⁵$s_j$, $P_2(s_j)\prec P_1(s_j)$, then $P_2{\varvec{\prec }} P_1$.

We now turn to the question: is it possible to formulate a population prospect axiology that is unburdened by (something like) the traditional impossibility results for population axiology? Although the traditional (risk-free) adequacy conditions are known to be mutually inconsistent as conditions on how to rank populations, they are not mutually inconsistent as conditions on how to rank non-trivial prospects, since none of them says anything about how to rank such prospects. Hence, a condition like Population State Dominance is needed to connect the ranking of outcomes to the ranking of non-trivial prospects.

We shall focus on three adequacy conditions for (risk-free) population axiology that generate a very simple and easy to demonstrate impossibility theorem, which we will extend to population prospect axiology. Some of these conditions can be and have been questioned. For instance, one might want to replace Quality by weaker a weaker condition that does not directly rule out the Repugnant Conclusion. However, as will become evident, the various other impossibility theorems that have been proven with logically weaker and intuitively more compelling adequacy conditions for population axiology, for instance by weakening Quality (see, e.g., Arrhenius 2011, forthcoming), can be extended to population prospect axiology in a way analogous to how we extend the simple theorem. So, the aim here is not to prove an impossibility theorem involving only intuitively compelling adequacy conditions. The aim is instead to describe a recipe for translating any theorem for (risk-free) population axiology into a theorem for prospect population axiology on a domain that contains only non-trivial prospects. (Later we prove a general theorem that establishes that this recipy can indeed be used to extend any axiology-result to a prospect-result.)

Below we make use of one more piece of notation. We stipulate that there is a $\gamma \in {\mathbb {R}}^+$—which can be arbitrarily close to 0—such that for any $x,y\in {\mathbb {R}}^+$ if $y<x$ but $x-y\le \gamma$, then y is “slightly lower” than x. The three adequacy conditions for risk-free population axiology that we focus on are:

Egalitarian Dominance

For any ${{\textbf {x}}}, {{\textbf {y}}}\in {{\textbf {X}}}$, if $n({{\textbf {x}}})=n({{\textbf {y}}})$ and for all $i,j\in {\mathbb {N}}$, $y_i<x_j$ and $x_i=x_j$, then ${{\textbf {y}}}\prec {{\textbf {x}}}$.

Quantity

For any $x,y\in {\mathbb {R}}^+$ such that y is slightly lower than x, and for any $n\in {\mathbb {N}}$, there is an $m\in {\mathbb {N}}$, such that $m>n$, and such that $(x)_n\precsim (y)_m$.

Quality

There is an $x\in {\mathbb {H}}$ and an $n\in {\mathbb {N}}$, such that for any $y\in {\mathbb {L}}$ and any $m\in {\mathbb {N}}$, $(y)_m\precsim (x)_n$.

Egalitarian Dominance is as uncontroversial as a principle of population ethics gets. Quality is a condition that rules out theories that imply the Repugnant Conclusion. Quantity should appeal to those who find some truth “the more of the good, the better”.

It turns out that the above seemingly weak conditions are not mutually compatible, as illustrated by the following simple and well-known impossibility theorem (for risk-free population axiology):

Simple Impossibility Theorem

(SIT) No social welfare relation $\precsim$ on X satisfies Egalitarian Dominance, Quality, and Quantity.³⁶

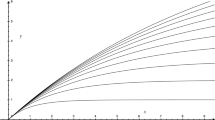
To see why the above theorem is true, consider the sequence in Fig. 1. We assume that well-being is perfectly equally distributed in each population. Moreover, assume that ${{\textbf {x}}}_1$ in the diagram above is a population with very high welfare and that ${{\textbf {y}}}$ is a population with very low positive welfare (the width of a block represents the number of people in the population, the height represents their welfare; dashes indicate that the block in question should really be much wider than shown). According to Quantity, there is a population ${{\textbf {x}}}_2$ with slightly lower welfare than ${{\textbf {x}}}_1$ but which is at least as good as ${{\textbf {x}}}_1$; a population ${{\textbf {x}}}_3$ with slightly lower welfare than ${{\textbf {x}}}_2$ but which at least as good as ${{\textbf {x}}}_2$; and so forth. Hence, we will finally reach population ${{\textbf {x}}}_r$ with very low positive welfare.³⁷ Now, recall that we assume the social welfare relation to be transitive. Hence, ${{\textbf {x}}}_r$ is at least as good as ${{\textbf {x}}}_1$. But y is better than ${{\textbf {x}}}_r$ according to Egalitarian Dominance. Hence, by transitivity, ${{\textbf {y}}}$ is better than ${{\textbf {x}}}_1$. However, by Quality, ${{\textbf {x}}}_1$ is at least as good as ${{\textbf {y}}}$ (for some ${{\textbf {x}}}_1$ and ${{\textbf {y}}}$ that can be used in an argument with the above structure). So, we get a contradiction: ${{\textbf {y}}}$ is better than ${{\textbf {x}}}_1$ which is at least as good as ${{\textbf {y}}}$. Hence, the Simple Impossibility Theorem: there is no social welfare relation—in other words, no population axiology—which satisfies Egalitarian Dominance, Quality, and Quantity.

Fig. 1

Illustration of SIT

The Simple Impossibility Theorem can easily be extended to the following impossibility result for population prospect axiologies, even if we limit the domain of the social welfare relation to prospects that are non-trivial (in the sense described above):

Simple Prospect Impossibility Theorem

(SPIT) No social welfare relation ${\varvec{\precsim }}$ on the set of non-trivial prospects, ${{\textbf {P}}}_{nt}$,³⁸ satisfies Egalitarian Dominance, Quality, Quantity, and Population State Dominance.

Table 2 Prospects that prove SPIT

The prospects in Table 2 establish SPIT. $P_1$ to $P_{r+1}$ are different population prospects, whereas $s_1$ and $s_2$ are different states of the world that determine which population results from the choice of each prospect. We assume that $P_1$ to $P_{r+1}$ are non-trivial, meaning that the probabilities of states $s_1$ and $s_2$ are strictly between zero and one. Now, assume that ${{\textbf {x}}}_1$, ${{\textbf {x}}}_2$, etc., and ${{\textbf {y}}}$ in Table 2 are the populations depicted in Fig. 1. So, for each ${{\textbf {x}}}_i$, ${{\textbf {x}}}_{i+1}$ is at least as good as ${{\textbf {x}}}_i$ according to Quantity, ${{\textbf {y}}}$ is better than ${{\textbf {x}}}_r$ according to Egalitarian Dominance, and thus ${{\textbf {y}}}$ is better than ${{\textbf {x}}}_1$ by transitivity. However, ${{\textbf {x}}}_1$ is at least as good as ${{\textbf {y}}}$ according to Quality. But that means that according to Population State Dominance, $P_{r+1}$ is better than $P_1$ and $P_1$ is at least as good as $P_{r+1}$, irrespective of what population ${{\textbf {z}}}$ represents. So, again we reach a contradiction. Hence, the Simple Prospect Impossibility Theorem: there is no social welfare relation—and thus no population prospect axiology—on a domain of non-trivial prospects which satisfies Egalitarian Dominance, Quality, Quantity, and Population State Dominance. (It is straightforward to see how the result can be extended to multiple non-null states.)

Note that since both Quality and Quantity are stated with the weak preference relation—that is, they are claims about the “at least as good as” relation, to use axiological terms—we need a version of Population State Dominance that applies dominance reasoning even when there is only “weak” state-wise dominance (i.e., where there is only weak preference for one prospect over another given some state). However, by strengthening Quality, we can make do with a weaker dominance condition that only applies dominance reasoning when there is strict state-wise dominance.³⁹

We could of course also replace Population State Dominance with Stochastic Dominance, which, in a state-space framework like ours, entails Population State Dominance. Finally, it might also be worth pointing out that the assumption that the different prospects result in the same population if one of the two states obtains is not essential to the above result (nor the next theorems we introduce). In fact, we can prove the following general theorem, which implies SPIT as a special case.⁴⁰

Dominance Theorem

Let ${\mathcal {A}}$ be a set of adequacy conditions that no social welfare relation on the set of trivial prospects, ${\varvec{\precsim }}$ on ${{\textbf {P}}}\setminus {{\textbf {P}}}_{nt}$, satisfies. Then no social welfare relation ${\varvec{\precsim }}$ on ${{\textbf {P}}}_{nt}$ satisfies ${\mathcal {A}}$ and Population State Dominance.

Proof

For any non-null state $s_i\in {{\textbf {S}}}$, let ${\mathcal {P}}$ denote the set of all prospects that map ${{\textbf {S}}}{\setminus } \{s_i\}$ to some particular population vector ${\mathcal {V}}=({{\textbf {x}}},\ldots , {{\textbf {y}}})$. Now let ${\mathcal {P}}_{{{\textbf {x}}}}$ be the prospect in ${\mathcal {P}}$ that results in population ${{\textbf {x}}}$ in state $s_i$ and similarly for prospect ${\mathcal {P}}_{{{\textbf {y}}}}$ and population ${{\textbf {y}}}$. Now let $P_{{{\textbf {x}}}}$ be the trivial prospect that results in population ${{\textbf {x}}}$ for sure, and similarly for $P_{{{\textbf {y}}}}$ and population ${{\textbf {y}}}$. From Population State Dominance it follows that ${\mathcal {P}}_{{{\textbf {x}}}}{\varvec{\precsim }}{\mathcal {P}}_{{{\textbf {y}}}}$ just in case $P_{{{\textbf {x}}}}{\varvec{\precsim }}P_{{{\textbf {y}}}}$. Now, note that $P_{{{\textbf {x}}}},P_{{{\textbf {y}}}}\in {{\textbf {P}}}{\setminus }{{\textbf {P}}}_{nt}$. Hence, since by assumption, the relation ${\varvec{\precsim }}$ on ${{\textbf {P}}}\setminus {{\textbf {P}}}_{nt}$ fails to satisfy the conditions in ${\mathcal {A}}$, some pair of trivial prospects $P_{{{\textbf {x}}}}, P_{{{\textbf {y}}}}$ establishes that ${\varvec{\precsim }}$ on ${{\textbf {P}}}_{nt}$ cannot satisfy both ${\mathcal {A}}$ and Population State Dominance. $\square$

Before introducing the next theorem, it might be worth reminding the reader of a point that we previously made, namely, that prospect impossibility results such as those proven above cannot be achieved by only using risk-free adequacy conditions, such as Egalitarian Dominance, Quantity, and Quality. For while these risk-free conditions tell us how to rank populations (and hence how to rank trivial population prospects), they tell us nothing about how to rank non-trivial prospects that could result in different populations. For instance, recall that Egalitarian Dominance, Quality, and Quantity together entail that y is better than ${{\textbf {x}}}_1$ and that ${{\textbf {x}}}_1$ is at least as good as y, that is, the conditions entail an inconsistent ranking of populations (or risk-free outcomes). But, in and of itself, that does not suffice to get an impossibility result for non-trivial prospects, since this non-transitive outcome-ranking by itself does not preclude that there exists a consistent (in particular, transitive) ranking of non-trivial prospect. To take a simple (but of course implausible) example, suppose that the only adequacy condition on non-trivial prospects says that all non-trivial prospects are equally preferable. That would not, of course, remove the impossibility result for populations (i.e., risk-free outcomes). But it would mean that the “set” of adequacy conditions on non-trivial prospects is consistent.

So, if a person were to maintain that a decision-maker is never faced with choices between populations, only with choices between population prospects, then they could argue that from a practical (decision-making) point of view, the inconsistency generated by Egalitarian Dominance, Quantity, and Quality is not so worrying. However, if this person accepts Population-State Dominance for prospects, and moreover accept Egalitarian Dominance, Quantity, and Quality for populations, then they would have to admit that it is worrying (even from a practical point of view) that Population-State Dominance results in an inconsistent ranking of prospects when the ranking of the possible outcomes (i.e., populations) satisfies Egalitarian Dominance, Quantity, and Quality.

Another way to derive an impossibility result for non-trivial prospects, without using a condition like Population State Dominance to connect the ranking of outcomes to the ranking of prospects, is to reformulate the standard conditions as prospect conditions, a strategy we next explore. Consider first the following, where state-dominance is essentially built into each condition:

Egalitarian Prospect Dominance

For any ${{\textbf {x}}}, {{\textbf {y}}}, {{\textbf {z}}} \in {{\textbf {X}}}$ such that $n({{\textbf {x}}})=n({{\textbf {y}}})$ and $y_i<x_j=x_i$ for all $i,j\in {\mathbb {N}}$, for any $E\subset {{\textbf {E}}}$, and for any $P,Q\in {{\textbf {P}}}$, if $P(\lnot E)={{\textbf {x}}}$ and $P(E)={{\textbf {z}}}$ while $Q(\lnot E)={{\textbf {y}}}$ and $Q(E)={{\textbf {z}}}$, then $Q{\varvec{\prec }} P$.

Quantity Prospect Dominance

For any ${{\textbf {z}}}\in {{\textbf {X}}}$ and for any $x,y\in {\mathbb {R}}^+$ such that y is slightly lower than x, and for any $n\in {\mathbb {N}}$, there is an $m\in {\mathbb {N}}$, such that $m>n$, and such that for any $E\subseteq {{\textbf {E}}}$ and for any $P,Q\in {{\textbf {P}}}$, if $P(E)=(x)_n$ and $P(\lnot E)={{\textbf {z}}}$, while $Q(E)=(y)_m$ and $Q(\lnot E)={{\textbf {z}}}$, then $P{\varvec{\precsim }} Q$.

Quality Prospect Dominance

There is an $x\in {\mathbb {H}}$ and an $n\in {\mathbb {N}}$, such that for any $y\in {\mathbb {L}}$, any $m\in {\mathbb {N}}$, any ${{\textbf {z}}}\in {{\textbf {X}}}$, any $E\subseteq {{\textbf {E}}}$, and any $P,Q\in {{\textbf {P}}}$, if $P(E)=(x)_n$ and $P(\lnot E)={{\textbf {z}}}$, while $Q(E)=(y)_m$ and $Q(\lnot E)={{\textbf {z}}}$, then $Q{\varvec{\precsim }} P$.

Now, it should be straightforward to see that even if the domain is restricted to non-trivial prospects, that is, prospects that confer a probability strictly between zero and one on different populations, the above three conditions form an inconsistent set. That is, we can prove:

Pure Prospect Impossibility Theorem

(PIT) No social welfare relation ${\varvec{\precsim }}$ on ${{\textbf {P}}}_{nt}$ satisfies Egalitarian Prospect Dominance, Quality Prospect Dominance, and Quantity Prospect Dominance.

The prospects in Table 2, for instance, establish the Pure Prospect Impossibility Theorem. For notice that by transitivity, Egalitarian Prospect Dominance, Quality Prospect Dominance, and Quantity Prospect Dominance result in an inconsistent ranking of the prospects in Table 2, in exactly the same way as the original Egalitarian Dominance, Quality, Quantity and Population State Dominance resulted in an inconsistent ordering of the prospects in Table 2.

One advantage of PIT, as compared to SPIT, is that PIT does not assume Population State Dominance to always hold. So, in particular, those who want to resist Population State Dominance due concern for fairness in the distribution of chances (e.g., Diamond 1967, Stefánsson 2015), might be more troubled by the impossibility identified by PIT, which only assumes that Population State Dominance holds with respect to the populations involved in the conditions.

However, in case someone objects to any appeal to Population State Dominance, even a restricted one as used in the Pure Prospect Impossibility Theorem, it might be worth noting that impossibility results can be generated without any such appeal, albeit with more complex conditions.⁴¹

Consider first Probability-Quantity Tradeoff, the thought behind which is that we can reduce the probability that a prospect results in the population $(x)_m$, where people have very high welfare, without making the resulting prospect worse, as long as we sufficiently increase the number of people in the alternative population that the prospect results in if it does not result in $(x)_m$:

Probability-Quantity Tradeoff

For any $m,n\in {\mathbb {N}}$, any $x\in {\mathbb {H}}$ and $y\in {\mathbb {L}}$, for any $E\in {{\textbf {E}}}$ such that $p(E)=q>0$ and for any $P\in {{\textbf {P}}}$ such that $P(E)=(x)_m$ and $P(\lnot E)=(y)_n$, there is some $F\in {{\textbf {E}}}$, which possibly partly overlaps with E, such that $p(F)=q'<q$, and some $o\in {\mathbb {N}}$, such that if $Q(F)=(x)_m$ and $Q(\lnot F)=((y)_n,(y)_o)$, then $P{\varvec{\precsim }} Q$.

Less formally: For any high welfare population and any low welfare population, and any prospect that with probability q results in the high welfare population and with probability $1-q$ results in the low welfare population, there is another at least as good prospect that with probability $q'<q$ results in the high welfare population and with probability $1-q'$ results in the union of the low welfare population with some additional lives at that same low level of welfare.

Next consider Probability-Quality Tradeoff, the thought behind which is that there is a limit to how much average welfare we are willing to risk foregoing for the sake of a chance at higher total welfare:

Probability-Quality Tradeoff

There is an $x\in {\mathbb {H}}$ and an $n\in {\mathbb {N}}$, such that for any $k,l\in {\mathbb {N}}$, and for any $y\in {\mathbb {L}}$, there are some (possibly overlapping) events, $G,H\in {{\textbf {E}}}$, such that $p(H)<p(G)$, such that if $P(G)=(x)_n$ and $P(\lnot G)=(y)_k$, while $Q(H)=(x)_n$ and $Q(\lnot H)=((y)_k, (y)_l)$, then $Q{\varvec{\prec }} P$.

In plain English: There is some high welfare population, such that for any two disjoint low welfare populations, there are probabilities p and q, where $p>q$, such that a prospect that with probability p results in the high welfare population and with probability $1-p$ results in one of the low welfare populations is better than any prospect that with probability q results in the high welfare population and with probability $1-q$ results in the union of the two low welfare populations.

As can easily be verified, Prospect Average Utilitarianism violates Probability-Quantity Tradeoff whereas Prospect Total Utilitarianism violates Probability-Quality Tradeoff.

To see how Probability-Quantity Tradeoff and Probability-Quality Tradeoff jointly lead to inconsistency, given transitivity, suppose we start with a probability p that is close to 1. (To make the argument as simple as possible, we replace the events/states by their probabilities.) By Probability-Quantity Tradeoff, there is some quantity $\delta$ that we could subtract from p such that the following holds. Suppose that prospect $P_0$ has probability p of resulting in a population $(x)_m\in {\mathbb {H}}^m$ and probability $1-p$ of resulting in some population $(y)_n\in {\mathbb {L}}^n$. Moreover, suppose that prospect $P_1$ has probability $p-\delta$ of resulting in population $(x)_m$ and probability $1-(p-\delta )$ of resulting in $((y)_n, (y)_o)$. Then $P_1$ is no worse than $P_0$. But continuing this reasoning, we can generate a sequence of prospects, by incrementally increasing the quantity that is subtracted from p, until we reach a quantity $\gamma$ for which the following holds. Suppose that $P_n$ has probability $p-\gamma$ of resulting in $(x)_m$ and probability $1-(p-\gamma )$ of resulting in some population $((y)_n, (y)_o,... (y)_p)$, which is much bigger than $(y)_n$. Then $P_n$ is no worse than the immediately preceding prospect in the sequence, and the same is true of any other prospect in the sequence. Hence, by transitivity, $P_n$ is no worse than $P_0$. Since we get this result irrespective of the welfare (and size) of the $(x)_m$ population, and irrespective of p and $\gamma$, we have a violation of Probability-Quality Tradeoff.

5 Concluding Remarks

We have found that the search for a population axiology free from contraintuitive implications is not made easier by the introduction of risk. For instance, we have shown how any impossibility theorem that has been proven for risk-free population axiology can be extended to population prospect axiology with the use of an instance of the traditional State-Wise Dominance axiom from decision theory. Moreover, we have seen that the introduction of risk into population ethics brings with it some new problems. Perhaps most interestingly, we have seen that natural extensions of traditional population axiologies lead to prospect-versions of the problems that they are praised for avoiding in the risk-free setting. In addition, we have seen that impossibility results can be derived from probabilistic axioms only (i.e., without any risk-free axioms). All of this illustrates that contrary to what one might have hoped, the task of finding an attractive axiology for non-trivial population prospects is even harder than the task of finding an attractive population axiology.