Abstract
This paper studies single-peaked domains where the designer is uncertain about the underlying alignment according to which the domain is single-peaked. The underlying alignment is common knowledge amongst agents, but preferences are private knowledge. Thus, the state of the world has both a public and private element, with the designer uninformed of both. I first posit a relevant solution concept called implementation in mixed information equilibria, which requires Nash implementation in the public information and dominant strategy implementation in the private information given the public information. I then identify necessary and sufficient conditions for social choice rules (SCRs) to be implementable. The characterization is used to identify unanimous and anonymous implementable SCRs for different forms of designer uncertainty, which basically boils down to picking the right SCRs from the large class identified by Moulin (Public Choice 35(4):437–455, 1980), and hence this result can be seen as identifying which of Moulin’s SCRs are robust to designer uncertainty.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Consider the following situation: a committee is to be set up each year to select a suitable candidate to fill an official post, say that of a manager. It is reasonable to assume that the committee members, probably after much discussion amongst themselves, have a common concern, such as the age of the applicants—some may prefer a younger, dynamic manager while some may prefer an older, more experienced manager. They would each have some ideal age in mind, which would correspond to their “peak”, and they would find any age further away from this peak less attractive than those that are closer to it. This captures their preference over the alternatives. In evaluating the applicants based on their age, the members thus find themselves having “single-peaked preferences” over them.Footnote 1 The authority creating the committee would like to know what selection rules would be attractive in such situations.
First introduced by Black (1948), single-peaked domains were studied extensively by Moulin (1980). Since then, the literature has studied them in the context of some properties that seem quite natural: first, everybody should find it optimal to report their true preference regardless of what the others say they prefer, second, if everyone agrees on an alternative, then that should be chosen, and third, every agent should be ex-ante equal. These are the properties of strategy-proofness, unanimity, and anonymity, respectively. A nice class of social choice rules (SCRs)—the “fixed ballots" rules—satisfy these conditions, and in fact are the only ones that do so. Essentially these pick the median of the n reported peaks and \(n-1\) “fixed ballots”, using an exogenous underlying alignment according to which the preferences of the agents are known to be single-peaked. Each fixed ballots rule can be uniquely identified by these \(n-1\) “fixed ballots”. Moulin (1980) also showed that an even more general characterization of SCRs—which (Sprumont 1995) terms min–max rules—can be obtained if one drops anonymity.
However, in this analysis it was important to assume that the underlying alignment according to which everyone evaluates the alternatives is known to the authority. In many situations, this may not be reasonable since the authority may not be privy to such information. In the committee example discussed earlier, ex ante the committee members could have many attributes according to which they may view the candidates, and age is only one such attribute. Thus they start out with many possible concerns and arrive at a common concern after discussions, making their preferences single-peaked ex post, and then update their preferred candidate based on that concern. But it is unlikely that the authority setting up the committee would know beforehand the specific concern that they settle on. It would then be prudent to set up a rule that accounts for this uncertainty. It may even be the case that priorities that produce such alignments amongst voters changes drastically over time. Witness the remarkable realignment in the United States Democratic Party’s position on race, from being anti-abolitionist in the 19th century to passing the Voting Rights Act in the 20th century. It is reasonable to expect that long-lasting rules be designed keeping such shifting alignments in mind. Applications also extend to similar settings in auctions, regulation and a variety of other domains.
The objective of this paper is to identify SCRs that will be robust to the designer’s uncertainty about the underlying ordering. In particular, the focus will be on Moulin’s class of SCRs. Given m alternatives and n players, his class contains \({m+n-2}\atopwithdelims (){n-1}\) SCRs for each possible underlying alignment. Clearly a designer then faces a problem of plenty, and our results will help her in identifying which of these will have this additional property i.e. the property of being robust to uncertainty about the underlying ordering.
In order to achieve this objective, it is imperative to first formalize what this robustness notion should be. Note that the information of each agent can be split into two - a public state, which is the underlying alignment, and a private state, which is his own preference. The state of the world then is composed of an alignment that is in the set of alignments that the designer thinks the domain could be single-peaked according to, and a profile of preferences that is single-peaked according to this alignment. Any SCR picks an alternative for each state. Given the mixed information nature of our setting, I posit a suitable solution concept for implementation of SCRs. With respect to the underlying alignment, which is common knowledge amongst the agents, I require Nash implementation. Then, given that the underlying alignment is being truthfully revealed, we require implementation in dominant strategies with respect to the private information i.e. their preferences.
Of course, applying this solution concept directly to SCRs is cumbersome, and hence first there needs to be a characterization of this concept in terms of easy-to-check conditions on SCRs. By the first requirement, implementable SCRs will be strategy proof for states that share the same alignment. By the second, they will have to satisfy a condition that we called shared-monotonicity, which requires that across two states that share a preference profile, the SCR must choose the same outcome at that profile. This is due to the lower contour sets of agents matching exactly for agents with such preferences across the two states, which leads to Nash equilibria in one state being Nash equilibria in the other. These conditions, with no veto power, also turn out to be sufficient.
This characterization makes it possible to carry out the original objective—identify robust unanimous and anonymous SCRs. In fact, this objective had a greater role in inspiring the kind of solution concept that I use than may be apparent from the deductive narrative has been laid out so far. Fix an alignment from the set of all alignments that the designer believes plausible. The axioms characterizing the solution are such that implementable SCRs satisfying unanimity and anonymity must be Moulin’s SCRs. We can then check which of these SCRs satisfy the additional conditions imposed by implementability for different sets of underlying alignments. This then enables us to cleanly answer some of the question of robustness within Moulin’s class that inspired us. In fact, this will form the bulk of this study. The most important of these is the case when the designer believes that the preferences may have been generated by any possible alignment - in this case, only the median SCR, i.e. the SCR that picks the median of the reported peaks of the agents according to the reported underlying alignment, survives the demanding notion of implementability. I also derive results for other interesting forms of designer uncertainty.
Related literature: The setting of this paper is novel since it studies settings in which the state of the world has both public and private elements. There are papers that look at domains which feature multiple single-peaked domains devoid of any asymmetry in information between the designer and the agents about the alignments, such as Reffgen (2015), which derives partial dictatorship results under strategy-proofness. Another closely related paper is Penn et al. (2011), which shows that requiring group strategy-proofness in the domain of all single-peaked preferences (i.e. preferences are single-peaked with respect to some unknown alignment) leads to dictatorships. Thus these papers derive impossibility results in similar domains as ours with stronger solution concepts, while this paper derives a possibility result. Also related is Nicolò and Barberà (2021), in which some agents may have private information relevant for social choice, and the authors characterize social choice rules that implement the same outcome in equilibrium as the full information case. The literature on secure implementation, started by Saijo et al. (2007), also looks at the combination of dominant strategy implementation and Nash implementation, but unlike that literature, here I use these two in parallel for different aspects of the unknown state, while secure implementation requires implementation in both dominant strategies and Nash for the entire state.
2 Model
The environment is the tuple \((N, X, {\mathcal {P}}, A)\) where \(N := \{1, . . . , n\}\) is a set of n agents, X is a finiteFootnote 2 set of alternatives, \({\mathcal {P}}\) is the set of all strict, complete and transitive alignments over X, and \(A \subseteq {\mathcal {P}}\) is non-empty. I assume \(n \ge 3\).
Let \(P = (P_1,...,P_n) = (P_i, P_{-i})\) denote a preference profile, with preference \(P_i \in {\mathcal {P}}\) for all i. Denote by \(P_i(k)\) the kth most preferred alternative according to \(P_i\). \(P_i(1)\) will also be called the “peak" of \(P_i\). I will use \(R_i\) to refer to the weak relation induced by \(P_i\), i.e. \(x R_i y\) if and only if either \(x P_i y\) or \(x = y\). Given an ordering \(\succ \in A\), I write \(a_1 \succ ... \succ a_{|X|}\) to denote which alternative occupies which position according to the ordering. Alternative \(a_1\) will be called the leftmost alternative according to \(\succ \) and \(a_{|X|}\) the rightmost alternative according to \(\succ \), and sometimes these two shall be referred to as the two ends of \(\succ \).
A preference \(Q \in {\mathcal {P}}\) is single-peaked if there exists a way of ordering the collection of alternatives along a left-right scale so that the ranking of the alternatives decreases as one moves away from her peak. Given an alignment \(\succ \), Q is single-peaked according to \(\succ \) if the previous sentence holds given that \(\succ \) is the ordering. A preference profile P is single-peaked according to an alignment \(\succ \) if \(P_i\) is single-peaked according to \(\succ \) for all i. There exists an alignment in A such that each preference profile in my setting is single-peaked according to it, and this alignment is common knowledge amongst the agents.Footnote 3 The preferences of agents are private knowledge, i.e. unknown to both other agents and the designer.
Let \({\mathcal {P}}_{\succ } \subset {\mathcal {P}}\) be the set of all preferences that are single-peaked according to \(\succ \). I assume wlog that the message space of each agent i in any mechanism must be of the form \(M_i = L_i \times {\mathcal {K}}\) where \(L_i\) is allowed to be any arbitrary space, and \({\mathcal {K}} \subseteq {\mathcal {P}} \times {\mathcal {P}}\) contains elements of the form \((\succ , P_i)\) where \(\succ \in A\) and \(P_i \in {\mathcal {P}}_{\succ }\).
Definition 1
A mechanism is the tuple (M, g) where \(M = (M_i)_{i \in N}\) is the message space and \(g:M \rightarrow X\) assigns an outcome to each message profile.
Let \(\Theta \) denote the set of all states. Then, for any state \(\theta \in \Theta \), we can represent it as \(\theta = (\succ ^{\theta }, (P^{\theta }_{i})_{i \in N})\), where \(\succ ^{\theta } \in A\) and represents the public state while \(P^{\theta }_{i}\) represents the private state of agent i. The tuple \((P^{\theta }_{i})_{i \in N}\) identifies a profile of preferences that is single-peaked according to the public state.
Definition 2
A social choice rule (SCR) \(f:\Theta \rightarrow X\) assigns an alternative to each state \(\theta \).
Finally, I formally define the solution concept that we set forth in the introduction. The idea is simple and intuitive - I require Nash implementation in the public component and dominant strategy implementation in the private component of the state given truthful reporting of the public component. Essentially, Nash implementation in the public component ensures nobody has an incentive to unilaterally misreport the common ordering. Then, given the common alignment is being reported truthfully, dominant strategy implementation ensures that the private preferences are also reported truthfully.
Definition 3
A mechanism (M, g) implements a social choice rule f in mixed information equilibria if for every state \(\theta = (\succ ^{\theta }, (P^{\theta }_{i})_{i \in N})\) there exists a message \(m^* = (m^*_i)_{i \in N}\), where \(m^*_i = (l^{*}_i, \succ ^{\theta }, P^{\theta }_{i})\), such that \(g(m^*) = f(\theta )\) and we have:
-
1.
Nash implementation in public information:
-
for all i,
$$g(m^{*}) \ R^{\theta }_i \ g((l_{i}, \succ ^{'}, P^{'}_{i}), m_{-i}^{*})$$for all \(l_i\) for all \((\succ ^{'},P^{'}_{i}) \in {\mathcal {K}}\)
-
if \(\bar{m}\) is a Nash equilibrium and \(\bar{m}_i = (\bar{l_{i}}, \bar{\succ }_i, P^{\theta }_{i})\) for some \( (\bar{l_{i}}, \bar{\succ }_i)\), then \(g(\bar{m}) = g(m^*)\)
-
-
2.
Dominant strategy implementation in private information given truthful public state reporting: for all i,
$$g(m^{*}_{i}, (l_{-i}, \succ ^{\theta }, P_{-i}^{'})) \ R^{\theta }_i \ g((l_{i}, \succ ^{\theta }, P_{i}^{'}), (l_{-i}, \succ ^{\theta }, P_{-i}^{'}))$$for all \((l_i)_{i \in N}\), for all \(P_{i}^{'}\), for all \(P_{-i}^{'}\), with strict preference for some \((l_{-i}, \succ ^{\theta }, P_{-i}^{'})\)
A social choice rule f is said to be implementable in mixed information equilibria if there exists a mechanism that implements it.
It is important here to note some subtleties about the solution concept. Firstly, the second condition requires dominant strategy implementation given the public state rather than the full state. Suppose that the solution concept required that there be dominant strategy implementation when each agent could report any alignment in the set A and any preference single-peaked according to it. This is actually the exact setting of Reffgen (2015), and leads to partial dictatorial results. In contrast to Reffgen (2015), in this paper the underlying alignment is common knowledge amongst the agents, so a weakening of the solution concept with respect to this public information is feasible. Thus, I weaken the solution concept to require dominant strategy implementation only in that part of the state which is private knowledge, given that the true alignment is being reported due to Nash implementation in the public state. Second, Nash implementation is only partial in the full state, since I have only required in the second part of the first condition that equilibrium outcomes coincide whenever the public state is reported differently, rather than the full state. If instead full implementation were required, an immediate necessary condition would be monotonicity of the social choice rule (refer (Maskin 1977)), which in single-peaked domains is almost as strong as requiring strategy-proofness, again leading to us close to the partial dictatorial results of Reffgen (2015).
3 Implementable social choice rules
The primary motive of this study is to understand the nature of social choice rules which can be implemented by the designer in this context. Clearly the definition above of implementability is onerous to check in practice. The obvious first step then would be to arrive at a characterization in terms of some properties that can be directly verified for social choice rules, and this is indeed the step we take. Then, we can apply these properties directly to the SCRs to identify which of them satisfy these properties.
The first result will be to identify necessary and sufficient conditions for SCRs to be implementable in mixed information equilibria. In order to state the result, a few notions will be required.
Given \(\succ \in A\), denote by \(f_{\succ }\) the SCR f restricted to \(\{\theta = (\succ , P)\}\) where P is allowed to be any profile of preferences that is single-peaked according to \(\succ \).
Definition 4
The SCR \(f_{\succ }\) is strategy-proof if for every preference \(P_i\) that is single-peaked according to \(\succ \), either \(f_{\succ }(P_i,P_{-i})\) \(P_i\) \(f_{\succ }(P_i^{'}, P_{-i})\) or \(f_{\succ }(P_i,P_{-i}) = f_{\succ }(P_i^{'}, P_{-i})\) for all deviating preference reports \(P_i^{'}\) and for all preferences of the other agents \((P_{-i})\).
Definition 5
The SCR f is shared-monotonic if for all pairs of alignments \(\succ , \succ ^{'}\) such that there exists a profile of preferences P that is single-peaked according to both \(\succ \) and \(\succ ^{'}\), \(f(\succ , P) = f(\succ ^{'}, P)\).
Definition 6
The SCR f satisfies no veto power (NVP) if for all \(\theta = (\succ , P)\) such that \(P_i(1) = a\) for all but one agent, we have \(f(\theta ) = a\).
Before going through the theorem, let us try to intuitively understand why these conditions are relevant to the notion of implementability. Consider any implementable SCR. By the dominant strategy implementation in the private state, we must have strategy-proofness of \(f_\succ \) for all \(\succ \in A\). Hence the necessity of strategy-proofness of each \(f_\succ \) is obvious. Moreover, if a message is a Nash equilibrium at a state \(\theta \), it will continue to be a Nash equilibrium for states which share the profile of preferences in \(\theta \), since the lower contour sets coincide exactly for each player across the states. So if two different alignments generate some common set of single-peaked preferences, whenever these preferences are held by agents, the outcomes must also be exactly the same. By the requirement of Nash implementation in the public information, we must then have shared-monotonicity.
It turns out that these two conditions, along with NVP, are also sufficient for any SCR to be implementable. I use a fairly standard mechanism to show this. Agents are asked to report the state i.e. an alignment and a preference single-peaked according to that alignment, and also their preferred alternative and an integer. If at least n-1 agents agree on the alignment, then that alignment is fixed as the public state. If not, the agent reporting the highest integer gets his preferred alternative.
Theorem 1
If a social choice rule f is implementable in mixed information equilibria, then \(f_{\succ }\) is strategy-proof for all \(\succ \in A\), and f is shared-monotonic.
Conversely, if a social choice rule f is such that \(f_{\succ }\) is strategy-proof for all \(\succ \in A\), f is shared-monotonic, and f satisfies no veto power, then it is implementable in mixed information equilibria.
4 Implementability of unanimous and anonymous SCRs
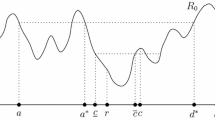
Now, after identifying the right solution concept and the right set of tools to check for it, let us turn towards identifying what implementable SCRs actually look like. Recall that the motivation was to apply robustness requirements on Moulin (1980), looking at unanimous and anonymous SCRs. This classic paper led to the characterization that given the underlying alignment, an SCR is strategy-proof, unanimous and, anonymous if and only if it is a fixed ballots rule. These SCRs have an intuitive and appealing visual representation. First, place the alternatives on a line left to right according to the underlying alignment. Then, place \(n-1\) “fixed ballots" on the alternatives on the line - each fixed ballots rule is associated with a unique placement of these fixed ballots. Given any profile of preferences of the agents, identify each agent’s most preferred alternative, or “peak", and mark them on the line. The outcome of the fixed ballots rule is the median of these n agent peaks and the \(n-1\) fixed ballots.
Part of the appeal of these properties lies in their normative nicety. If all the agents like the same alternative, it would be quite reasonable for an SCR to assign them that alternative. Equality amongst the agents as well is a fairly standard requirement. The intuitive nature of the fixed ballots rules also adds to the appeal of these properties, since in essence they are tied to these SCRs by the characterization. However, importantly, the class of fixed ballots rules is vast. In fact, if we have m alternatives and n agents, Moulin’s result gives us \({m+n-2}\atopwithdelims (){n-1}\) SCRs to choose from. The results in this paper will be able to identify which of these will be robust to designer uncertainty in the underlying alignment.
It will be useful to state Moulin’s result here, after providing some definitions, since we will draw on it later. Note that Moulin’s setting is a special case of ours, with \(A = \{\succ \}\), for some \(\succ \in {\mathcal {P}}\).
Definition 7
Given \(\succ \in {\mathcal {P}}\), the single-peaked domain according to it is given by \({\mathcal {D}}_{\succ } = \{P = (P_1,...,P_n) | P_i \in {\mathcal {P}}_{\succ } \text { for all } i \in N\}\). The SCR \(f:{\mathcal {D}}_{\succ } \rightarrow X\) is a fixed ballots rule if there exists \(F = (F_1, ..., F_{n-1})\) with \(F_i \in X\) for all i, such that for any preference profile \(P \in {\mathcal {D}}_{\succ }\), we have that \(f(P) = Med_{\succ }(P_1(1),...,P_n(1),F)\) where \(Med_{\succ }\) takes the median according to \(\succ \).
Definition 8
The SCR f is unanimous if for all \(\succ \in A\), for all preference profiles \(P \in {\mathcal {D}}_{\succ }\) such that \(P_i(1) = a\) for some \(a \in X\), and for all \(i \in N\), we have \(f_{\succ }(P) = a\).
Definition 9
The SCR f is anonymous if for all \(\succ \in A\), for all preference profiles \(P \in {\mathcal {D}}_{\succ }\), and for all bijective functions \(\sigma :N \rightarrow N\), we have \(f_{\succ }((P_i)_{i \in N}) = f_{\succ }((P_{\sigma (i)})_{i \in N})\).
Theorem 2
(Moulin 1980) In a single-peaked domain, a social choice rule is strategy-proof, anonymous and unanimous if and only if it is a fixed ballots rule.
An example of a fixed ballots rule is shown in Fig. 1—note that \(P_1(1)\) and \(P_2(1)\) are the peak preferences of the agents and \(F_1\) is the fixed ballot that identifies the SCR (Figs. 2, 3, 4, 5).
Definition 10
We call an SCR a no veto fixed ballots SCR (NVFBS) if for all alignments \(\succ \in A\)
-
\(f_{\succ }\) is a fixed ballots rule
-
\(f_{\succ }\) places at least one fixed ballot on both the leftmost and rightmost alternative of \(\succ \)
Since implementable SCRs must be strategy-proof for each \(\succ \), it is clear that adding unanimity and anonymity implies that implementable SCRs must have some fixed ballots rule for each \(f_{\succ }\). A slightly more subtle point relates to the property of no veto power. Consider what happens when there are no fixed ballots of a fixed ballots rule at one of the two extreme ends. Then, one can always construct a profile where a single agent would indeed have a veto—for example with all but one agent having their peak preference at the end without a fixed ballot. At the same time, having at least one fixed ballot on both ends ensures that there is no veto at any profile.
Note that the set A contains the possible alignments according to which the domain of agents’ preferences is single-peaked. A larger set of alignments corresponds to the designer being more uncertain about the underlying alignment. The result in the previous section identifies general conditions on implementable SCRs. The strength of these conditions, in particular shared-monotonicity, is dependent on the set A. I present five results here, progressing in a natural way over the size of the set A.
First, suppose A contains exactly two alignments, each of which is the reverse of the other. We may think of this as a good starting point, since the single-peaked domains produced by each alignment is exactly the same. Let \(\succ ^{-1}\) denote the alignment where the ordering of alternatives of \(\succ \) is exactly reversed.
Observation 1
If \(A = \{\succ , \succ ^{-1} \}\) for some \(\succ \in {\mathcal {P}}\), then any NVFBR with \(f_{\succ } = f_{\succ ^{-1}}\) is implementable.
In this case, any report of preference profiles could have been produced by either of the alignments. Shared-monotonicity then kicks in with full force - it must be the case that the fixed ballot rules chosen for each alignment must then be exactly the same.
This leads us to ask whether there might be cases where shared-monotonicity might have no bite at all. Indeed, whenever the two sets of single-peaked preferences for two alignments are disjoint, shared-monotonicity is satisfied vacuously, and we have the following result.
Proposition 1
If for all \(\succ , \succ ^{'} \in A\), \({\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}} = \emptyset \), then any NVFBR is implementable.
This is a very permissive result, since it gives a free hand to the designer to choose any fixed ballots rule for each alignment, as long as it places at least one fixed ballot on both ends of each alignment.
We would quite naturally be interested to know the circumstances under which the designer would be much more constrained than this in her choices. Consider then the case where the designer is uncertain entirely about the underlying alignment, that is, she places a positive probability over every possible alignment in \({\mathcal {P}}\). This would be the case when the designer wants her mechanism to robust to any possible underlying alignment, for example when designing a voting system where the voters may end up having any common concern, or even any change in the alignment over time.
The next result will require a few notations, which I present before the theorem.
Definition 11
Given \(|X| = 3\), we call an SCR a symmetric order-statistic SCR if for any alignment \(\succ \ \in \{abc, bca, cab\}\) where \(a,b,c \in X\), \(f_{\succ }\) is a fixed ballots rule that places k fixed ballots on the leftmost alternative and \((n-1)-k\) on the rightmost alternative, with \(0 \le k \le (n-1)\). Note that in alignment abc, a is the leftmost alternative and c is the rightmost alternative.
Definition 12
Given n is odd, we call an SCR a median SCR if \(\forall \succ \ \in A\), \(f_{\succ }\) chooses the median of the reported peaks of the agents.
Theorem 3
Suppose \(A = {\mathcal {P}}\). Then
-
1.
If n is odd and \(|X| > 3\), then an anonymous and unanimous SCR is implementable if and only if it is the median SCR.
-
2.
If n is even and \(|X| > 3\), then there are no implementable anonymous and unanimous SCRs.
-
3.
If \(|X| = 3\), then an anonymous and unanimous SCR is implementable only if it is a symmetric order-statistic SCR. Symmetric order-statistic SCRs with at least one fixed ballot each on the leftmost and rightmost alternative are implementable.
The surprising thing about this result is how it picks a handful of SCRs from the vast class identified by Moulin. Denoting \(m = |X|\), from \({m+n-2}\atopwithdelims (){n-1}\) possible SCRs, these have been whittled down to just 1 when we have \(m>3\) and n is odd. What this means is that if the designer thinks that any underlying alignment is possible, she should choose the median so that she can have this additional bulwark of implementability in mixed information equilibria. In the case of \(m=3\), which covers many voting scenarios such as those with agents voting for one of two candidates or abstaining, the designer has more choices but must be consistent across the possible alignments. This result (and others in this study) can thus also be seen as identifying special SCRs within the large class of fixed ballots rules, so that designers can be assisted in choosing from within it.
Let us now try to address what happens when we do not have the full support, but there are still alignments with common preferences in their single-peaked domains. Because a general characterization is bound to be messy, I present an important special case.
Definition 13
Let \(T_{\succ , \succ ^{'}} = \) \(\{x \in X \ | \ x = Q(1) \) for some \( Q \in {\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}} \}\). We say that A has constant shared peaks if \(T_{\succ , \succ ^{'}} = T\) for all \(\succ , \succ ^{'} \in A\), where \(T \subseteq X\) is a fixed subset of the set of alternatives.
In this case, as I show in the appendix, the shared peaks must be a contiguous subordering of each alignment, so one can imagine these peaks as being lumped together in the same order, and then the other alternatives moving around to the left and right of this lump to generate the set A. For such cases, there is a fairly large possibility result.
Proposition 2
Suppose A has constant shared peaks. Then T is a contiguous subordering of each alignment in A. Denote this subordering by R. An anonymous and unanimous SCR is implementable if it is an NVFBR that, given any \(\succ , \succ ^{'} \ \in A\), places
-
1.
the same number of fixed ballots before and after R for both \(\succ \) and \(\succ ^{'}\)
-
2.
the same pattern of fixed ballots on R for both \(\succ \) and \(\succ ^{'}\)
Proposition 2 admits an interesting corollary. Suppose \(|A| = 2\). In this case, regardless of which alignments are part of A, either the two alignments share a given set of preferences or they do not. Thus, the premise of the proposition is met, and we can identify implementable SCRs. \(|A| = 2\) includes practically important situations such as when the designer is uncertain just about the relative alignment of two adjacent alternatives.
5 Discussion
The primary innovation of this paper is the study of a setting in which the state of the world has public and private components, with the designer being uninformed about both components and agents informed of the public state and their own private state. Settings like this merit practical interest, since not all information available to an agent can be neatly bucketed into either something only privately observed or only publicly observed. The solution concept that I use is relevant for this specific case, but there may be others or generalizations of the same which could lead to interesting results.
I focus on the single-peaked domain since my interest is in answering questions related to robustness when the designer is not certain about the underlying alignment of the domain. The general result on implementation in mixed information equilibria, which involves Nash implementation in the public component and dominant strategy implementation in the private component, identifies necessary and sufficient conditions on SCRs for them to be implementable. This is in and of itself useful in practice, since these conditions can be directly checked and it can be verified whether the SCR can be implemented.
It is for anonymous and unanimous SCRs that I go further and identify implementable SCRs. Fixing the public part of the state i.e. the underlying alignment, implementability necessitates that the SCR behave as a Moulin fixed ballots rule. Implementability could also impose further constraints on which SCRs these can be, depending on which alignments are possible. For some sets of alignments, there are no additional constraints imposed, while if the set of alignments is the set of all possible alignments, then only the median SCR is admissible for each alignment. This is how I answer the robustness questions—depending on which alignments the designer thinks are possible, she can identify which SCR she should choose from all of Moulin’s SCRs.
Since I assume that \(n \ge 3\), it is natural to ask what happens if \(n=2\). For \(n=2\), our characterization will go through using the “restricted veto power” property of Moore and Repullo (1990) instead of NVP, which is much too strong in the two agent case.
A more general question to tackle in this setting would be to identify the structure of unanimous implementable SCRs. As alluded to earlier, it is known that unanimous strategy-proof SCRs must be “min–max" rules, and the same questions of robustness to designer uncertainty can be asked about these SCRs. Here my choice was to investigate the fixed ballots rules since they have an intuitive visualization and also because anonymity is a fairly standard normative requirement. The literature post Moulin (1980) has also focused a great deal on fixed ballots rules for their wealth of desirable properties. Other than being the only strategy proof SCRs, they are also uniquely Nash implementable, and as shown recently in Núñez et al. (2021), they are also Bayes–Nash implementable by “detail-free” mechanisms. An interesting point relates to requiring group strategy-proofness for the implementation in the private state, given the public alignment \(\succ \). The results actually carry through as is, since fixed ballots rules are also group strategy-proof given \(\succ \).
Notes
In this example the agents have multi-dimensional single-peaked preferences ex-ante and end up with single-peaked preferences along the agreed dimension, but one could also imagine examples where the agents form preferences after agreeing on a common dimension. This too would fit in within the formal contours of my model, and I’d like to thank a referee for pointing this out.
Much of the analysis would go through with minor tweaks for an infinite set, but I focus on the finite case for the purpose of exposition.
Note that any alignment and its exact reverse, for example \(a \succ b \succ c\) and \(c \succ b \succ a\), produce the same single-peaked domain, and hence are equivalent for our purposes. All claims pertain to this equivalence class.
We reiterate that an alignment and its exact reverse are equivalent for our purposes, so this statement and the rest in this paper should be considered up to these equivalence classes.
References
Black D (1948) On the rationale of group decision-making. J Political Econ 56(1):23–34. ISSN 00223808, 1537534X. http://www.jstor.org/stable/1825026
Maskin E (1977) Nash equilibrium and welfare optimality. Mimeo, New York
Moore J, Repullo R (1990) Nash implementation: a full characterization. Econometrica 58(5):1083–1099. ISSN 00129682, 14680262. http://www.jstor.org/stable/2938301
Moulin H (1980) On strategy-proofness and single peakedness. Public Choice 35(4):437–455. ISSN 1573-7101. https://doi.org/10.1007/BF00128122
Nicolò A, Barberà S (2021) Information disclosure with many alternatives. Soc Choice Welf. ISSN 0176-1714. https://doi.org/10.1007/s00355-021-01341-y
Núñez M, Pimienta C, Xefteris D (2021) On the implementation of the median. J Math Econ 102595. ISSN 0304-4068. https://doi.org/10.1016/j.jmateco.2021.102595
Penn EM, Patty JW, Gailmard S (2011) Manipulation and single-peakedness: a general result. Am J Political Sci 55(2):436–449. https://doi.org/10.1111/j.1540-5907.2010.00502.x
Reffgen A (2015) Strategy-proof social choice on multiple and multi-dimensional single-peaked domains. J Econ Theory 157:349 – 383. ISSN 0022-0531. https://doi.org/10.1016/j.jet.2014.12.010
Saijo T, Sjostrom T, Yamato T (2007) Secure implementation. Theor Econ 2(3):203–229
Sprumont Y (1995) Strategyproof collective choice in economic and political environments. Can J Econ 28(1):68–107. https://EconPapers.repec.org/RePEc:cje:issued:v:28:y:1995:i:1:p:68-107
Funding
Open Access funding provided by the MIT Libraries.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Guidance by Arunava Sen and Debasis Mishra is gratefully acknowledged. I am thankful to Stephen Morris and Alex Wolitzky for insightful comments. This paper has also greatly benefited from the thoughtful comments of the Editor, AE, and two referees.
A Proofs
A Proofs
Proof of Theorem 1
Let f be an implementable SCR, and let (M, g) be the mechanism that implements it.
Let \(\succ \in A\). Fix an agent i and a preference \(P_i\) single-peaked according to \(\succ \). Let \(P{'}\) be an arbitrary preference profile single-peaked according to \(\succ \). Then, there exists an \(m^*\) such that \(m^{*}_{i} = (l^{*}_i, \succ , P_{i})\), \(m^{*}_{-i} = (l^{*}_{-i}, \succ , P^{'}_{-i})\), and \(g(m^*) = f(\succ , P_i, P_{-i}^{'})\). Also, there exists an \(m^{**}\) such that \(m^{**}_{i} = (l^{**}_i, \succ , P_{i}^{'})\), \(m^{**}_{-i} = (l^{*}_{-i}, \succ , P^{'}_{-i})\), and \(g(m^{**}) = f(\succ , P_{i}^{'}, P_{-i}^{'})\). By dominant strategy implementation in private information, \(g(m^{*}_{i}, (l^{*}_{-i}, \succ , P_{-i}^{'})) \ R_i \ g((l^{**}_{i}, \succ , P_{i}^{'}), (l^{*}_{-i}, \succ , P_{-i}^{'}))\), which implies \(g(m^*) R_i g(m^{**})\), and hence we have \(f(\succ , P_i, P_{-i}^{'}) R_i f(\succ , P_{i}^{'}, P_{-i}^{'})\). Since \(P_{i}^{'}\) and \(P_{-i}^{'}\) were arbitrary, this means that \(f_{\succ }\) is strategy-proof.
Let \(\theta = (\succ , P)\) and \(\theta ^{''} = (\succ ^{''}, P)\) be two states. Let \(m^* = (m_{1}^{*}, m_{2}^{*}, ..., m_{n}^{*})\) with \(m_{i}^{*} = (l^{*}_i, \succ , P_{i})\) be the implementing message in state \((\succ , P)\) and \(m^{**} = (m_{1}^{**}, m_{2}^{**}, ..., m_{n}^{**})\) with \(m_{i}^{**} = (l^{**}_i, \succ ^{''}, P_{i})\) in state \((\succ ^{''}, P)\). By the first condition of Nash implementation in public information, for all i for all \(l_i\) for all \((\succ ^{'},P^{'}_{i}) \in {\mathcal {K}}\),
Since \(\theta \) can be replaced by \(\theta ^{''}\) in this equation without changing the preference profile,
This means that \(m^*\) is a Nash equilibrium in state \(\theta ^{''}\) as well and hence by the second condition of Nash implementation in public information, \(f(\succ , P) = g(m^*) = g(m^{**}) = f(\succ ^{''}, P)\). Thus shared-monotonicity is satisfied.
For the other direction, let f be such that \(f_{\succ }\) is strategy-proof for all \(\succ \in A\), f is shared-monotonic, and f satisfies no veto power. Consider the following mechanism:
-
\(M_i = {\mathbb {N}} \times X \times {\mathcal {K}}\) for all i, where \({\mathbb {N}}\) is the set of natural numbers.
-
if messages are of the form \(m_i = (l_i, x_i, \succ , P_i)\) for all except at most one agent j i.e. at least \(n-1\) agents agree on the alignment, \(g(m) = f(\succ , (Q,P_{-j}))\) where \(Q \in {\mathcal {P}}_{\succ }\) is some preference such that \(Q(1) = P_j(1)\).
-
if not, select the agent with the lowest index amongst those sending the highest natural number, say j. Set \(g(m) = x_j\).
To verify dominant strategy implementation in private information, note that given \(\succ \), truth-telling is a dominant strategy since \(f_{\succ }\) is strategy proof and unilateral deviations along \({\mathbb {N}} \times X\) do not change the outcome. To verify Nash implementation in public information, note first that unilateral deviations for the alignment do not change the outcome. Second, if all but one agent i report the same alignment but i reports a different alignment, we can have a Nash equilibrium in the public information only if the outcome chosen is the best alternative for all agents but i, since otherwise one of them can announce a higher natural number and be strictly better off. But then, by NVP, this outcome coincides with \(f(\succ , P)\). Finally, if all agents report a different alignment, by shared-monotonicity the outcome is the same as \(f(\succ , P)\). \(\square \)
Proof of Theorem 3
Before proving this theorem, we prove a lemma that will be useful for this result and later results.
Let \(T_{\succ , \succ ^{'}} = \) \(\{x \in X \ | \ x = Q(1) \) for some \( Q \in {\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}} \}\).
Lemma 1
[Symmetry] Suppose \(\succ \) and \(\succ ^{'}\) are such that \({\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}} \ne \emptyset \). Let \(x,y \in T_{\succ , \succ ^{'}}\) be such that x and y are adjacent to each other with x before y, in both \(\succ \) and \(\succ ^{'}\). If an implementable f is such that \(f_{\succ }\) and \(f_{\succ ^{'}}\) are fixed ballots rules, then \(f_{\succ }\) and \(f_{\succ ^{'}}\) must have the same number of fixed ballots with peaks on or before x.
Proof of Lemma 1
Let \(Q_x \in {\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}}\) denote the preference with x at peak and \(Q_y \in {\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}}\) denote the preference with y at peak. For any \(k,l \in \{0,1,...,n\}\) such that \(k+l=n\), we must have that reports of k number of \(Q_x\) and l number of \(Q_y\) preferences must lead to the same outcome across \(\succ \) and \(\succ ^{'}\). If the number of fixed ballots before x were not the same across the two alignments, this would not be possible. \(\square \)
Since Lemma 1 establishes that Symmetry is necessary, we first show that for \(|X| = 3\), everything but the symmetric order-statistic SCRs will violate Symmetry and, for \(|X| > 3\), we show that all except the median with odd agents will violate it. For \(|X| > 3\), it is then sufficient to show that the median satisfies NVP and shared-monotonicity in order to establish the theorem. For \(|X| = 3\), it is sufficient to show that the symmetric order-statistic SCRs satisfy shared-monotonicity.
Our first claim is that for \(|X|\ge 3\), fixed ballots cannot be placed on the interior for any alignment, where interior of an alignment is anything not at the two ends. Suppose the SCR chosen for some alignment, say \(\succ \), contains fixed ballots in the interior. Select one alternative in the interior which has a fixed ballot on it, and call it y. Let the alternative to the left of it be x and the one to its right be z. Suppose there are k fixed ballots on or before x, and l fixed ballots on or before y. By assumption, \(k < l\). Consider the alignment, say \(\succ ^{'}\), with z pulled to the left of x, but everything else in the same position. Since we have full support, this alignment is in A. Clearly, \(\succ \) and \(\succ ^{'}\) share preferences with peaks at x and y. Thus, there must continue to be k fixed ballots before x in \(\succ ^{'}\). Consider the alignment, say \(\succ ^{''}\), with y and z interchanged in \(\succ \), with all other alternatives at the same position. \(\succ \) and \(\succ ^{''}\) share preferences with peaks at y and z, so after y in \(\succ ^{''}\), we must have l fixed ballots. Now, note that \(\succ ^{'}\) and \(\succ ^{''}\) share preferences with peaks at x and z. Before x in \(\succ ^{'}\), we have k fixed ballots but after x in \(\succ ^{''}\) we have at least l (since y is to the right of x), which is a contradiction. Note that for \(|X|=3\), this claim by itself establishes that everything except the symmetric order-statistic SCRs are ruled out for \(|X|=3\). By this claim, the ballots are placed on a and c in abc, and on c and b in cab. By Symmetry, fixed ballots on or before a must be the same in number across both (since they have at least one preference that is single-peaked according to both; in particular, Q such that aQbQc), so both a in abc and c in cab have the same number of ballots. Extending this argument on all three alignments in the domain gives us a symmetric order-statistic SCR.
Second, we claim that the number of fixed ballots must be the same on both ends for all alignments when \(|X| > 3\). Suppose the SCR chosen for some alignment, say \(\succ \), contains k fixed ballots at the left end. Let a, b, c, d be the first four alternatives in \(\succ \), in that order. Consider the alignment, say \(\succ ^{'}\), with a, d, b, c as the first four alternatives, in that order, and the rest the same as \(\succ \). Clearly, \(\succ \) and \(\succ ^{'}\) share preferences with peaks at b and c, so \(\succ ^{'}\) must have k fixed ballots on a. Consider the alignment, say \(\succ ^{''}\), with c, b, a, d as the first four alternatives, in that order, and the rest the same as \(\succ \). Clearly, \(\succ ^{'}\) and \(\succ ^{''}\) share preferences with peaks at a and d, so \(\succ ^{''}\) must have k fixed ballots on c. Now, note that \(\succ ^{'}\) and \(\succ ^{''}\) share preferences with peaks at a and b, so in \(\succ \), there must be k fixed ballots on the right end. Thus, when \(|X| > 3\), combining these two claims, we get that all ballots must be equally divided on the two extreme ends. It is straightforward to see that this is exactly the median SCR when n is odd—the median of the set of the fixed ballots and the agent preference tops, and the median of the set of the agent preference tops, coincide when the fixed ballots are distributed equally on both ends. So all but the median SCR are ruled out for odd n. When n is even, \(n-1\) is odd and hence there is no way to place equal number of fixed ballots (recall that the number of fixed ballots is \(n-1\)) on both ends—and hence there is no SCR that survives.
We close by noting that the median satisfies both NVP and shared-monotonicity and the symmetric order-statistic SCRs satisfy shared-monotonicity. Consider the median SCR. NVP is satisfied by definition since the number of fixed ballots is the same on both ends of every alignment. To see shared-monotonicity, consider any two \(\succ \), \(\succ '\) such that \({\mathcal {D}}_{\succ } \cap {\mathcal {D}}_{\succ '} \ne \emptyset \). Suppose P is such that \(P \in {\mathcal {D}}_{\succ } \cap {\mathcal {D}}_{\succ '}\) and \(a = Med_{\succ }(P) \ne Med_{\succ '}(P) = b\). Wlog let b be to the left of a according to \(\succ \). If a is to the left of b in \(\succ '\), then consider all alternatives \(x \in T_{\succ , \succ ^{'}}\) such that x are to the right of b in \(\succ '\), denoted \(X_r\). If they are all to the left of a in \(\succ \), then a cannot be the median in \(\succ \) since the alternatives \(x \in X_r\) have \((n-1)/2\) of tops, and both these tops and the tops on b would be to the left of a. So at least one top, say c, is to the right of a in \(\succ \) and b in \(\succ '\). But then, such a preference cannot be shared across the two alignments since a and b are both to the left of c in both alignments, and in different orders in both. This is a contradiction. Now instead if a is to the right of b in \(\succ '\), consider all elements \(x \in T_{\succ , \succ ^{'}}\) such that x are to the right of a in \(\succ \). At least one of them, say c, must be to the left of b in \(\succ '\) since otherwise b cannot be the median in \(\succ '\). But again, such a preference cannot be shared across the two alignments since a and b are in different relative orders to c in the two alignments. For the symmetric order-statistic SCRs, shared-monotonicity is easier to establish since for any two orderings in \(\{abc,bca,cab\}\), preferences are shared across the two orderings if and only if the tops of the preferences are in the same order in both orderings (for example, ab in abc and cab). Since the ballots are symmetrically distributed at the two ends, this means that the outcome must be the same across the two orderings. \(\square \)
Proof of Proposition 2
For this result, we will use the following lemma:
Lemma 2
[Consistency] Suppose A has constant shared peaks and \(\succ \), \(\succ ^{'} \in A\). Then the following hold
-
1.
\(|T_{\succ , \succ ^{'}}| \ge 2\).
-
2.
Let \(T_{\succ , \succ ^{'}} = \{x_1, x_2,...,x_{|T|}\}\). Then \(x_1, x_2,...,x_{|T_{\succ , \succ ^{'}}|}\) are adjacent in both \(\succ \) and \(\succ ^{'}\), and they are in the same order in both \(\succ \) and \(\succ ^{'}\).Footnote 4
Proof of Lemma 2
-
1.
Note that \(T_{\succ , \succ ^{'}} \ne \emptyset \). Let \(x \in T_{\succ , \succ ^{'}}\). Then, there exists a preference \(Q \in {\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}}\) such that \(x = Q(1)\). Let \(y = P(2)\). Consider a preference \(Q^{'}\) such that \(Q^{'}(1) = y\) and \(Q^{'}(2) = x\) and \(Q^{'}(i) = P(i) \ \forall \ i > 2\). Since this change continues to make the new ordering single-peaked with respect to whatever Q was single-peaked according to, we must have \(Q^{'} \in {\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}}\). Since this implies \(y \in T_{\succ , \succ ^{'}}\), we are done.
-
2.
Let \(x, y \in T_{\succ , \succ ^{'}}\) such that in \(\succ \), t lies between x and y for all \(t \in T_{\succ , \succ ^{'}}\). Now, let \(z \in X\) be in between x and y in \(\succ \). Let us check where z will be in \(\succ ^{'}\). Suppose it is not in between the two. Without loss of generality, let it be to the left of both x and y in \(\succ ^{'}\). Since \(y \in T_{\succ , \succ ^{'}}\), \(\exists \ Q \in {\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}}\) such that \(y = Q(1)\). By single-peakedness, zQx in \(\succ \) but xQz in \(\succ ^{'}\), which is a contradiction. Thus, z must be in between x and y in \(\succ ^{'}\) as well.
It is straightforward to show by a similar argument that if both \(z_1\) and \(z_2\) are in between x and y in \(\succ \), then the four must be in the same order in \(\succ ^{'}\) as well. Thus, the order between x and y is preserved across \(\succ \) and \(\succ ^{'}\).
Now, let z be next to x in \(\succ \) and between x and y. Since \(x \in T_{\succ , \succ ^{'}}\), \(\exists \ Q^{'} \in {\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}}\) such that \(x = Q^{'}(1)\). Consider a preference \(Q^{''}\) such that \(Q^{''}(1) = z\) and \(Q^{''}(2) = x\) and \(Q^{''}(i) = P^{'}(i) \ \forall \ i > 2\). We must have \(Q^{''} \in {\mathcal {P}}_{\succ } \cap {\mathcal {P}}_{\succ ^{'}}\). In this manner, \(z \in T_{\succ , \succ ^{'}}\) for all z in between x and y, which proves our hypothesis.
\(\square \)
The result now follows directly from Lemmas 2 and 1. Note that Consistency implies that the shared peaks must be a contiguous subordering of each alignment in S, and Symmetry then implies parts 1. and 2. of the proposition. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Narayanan, A. Single-peaked domains with designer uncertainty. Soc Choice Welf 60, 561–578 (2023). https://doi.org/10.1007/s00355-022-01431-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-022-01431-5