Obvious manipulations in cake-cutting

Abstract

In the classical cake-cutting problem, strategy-proofness is a very costly requirement in terms of fairness: for $n=2$ it implies a dictatorial allocation, whereas for $n\ge 3$ it implies that one agent receives no cake. We show that a weaker version of this property recently suggested by Troyan and Morril (J Econ Theory 185:104970, 2019) is compatible with the fairness property of proportionality, which guarantees that each agent receives 1/n of the cake. Both properties are satisfied by the leftmost-leaves mechanism, an adaptation of the Dubins–Spanier moving knife procedure. Most other classical proportional mechanisms in the literature are obviously manipulable, including the original moving knife mechanism and some other variants of it.

1 Introduction

The division of a single good among several agents who value different parts of it distinctly is one of the oldest fair division problems, going as far back as the division of land between Abram and Lot (Genesis 13). Since its formalization as the cake-cutting problem (Steinhaus 1948), this research question has inspired a large interdisciplinary research for finding mechanisms that produce fair allocations without giving agents incentives to misrepresent their preferences over the cake. Unfortunately, besides some restricted preference domains, this research has so far produced mainly negative results, showing a strong tension between fairness and incentive properties (see section 2).

Nevertheless, recent results in applied mechanism design have shown that, even if mechanisms can be manipulated in theory, they are not always manipulated in practice. Some manipulations are more likely to be observed than others, particularly those which are salient or require less computation. Based on this observation, Troyan and Morrill (2019) have proposed a weaker version of strategy-proofness for direct mechanisms, called not obvious manipulability (NOM). They define a manipulation as obvious if it yields a higher utility than truth-telling in either the best- or worst-case scenarios. A mechanism is NOM if it admits no obvious manipulation. Their notion of NOM is a compelling one, since it does not require prior beliefs about other agents’ types, and compares mechanisms only based on two scenarios which are particularly salient and which require less cognitive effort to compute. They show that NOM accurately predicts the level of manipulability that different mechanisms experience in practice in school choice and auctions.

In this paper, we provide a natural extension of NOM to indirect mechanisms, and show that the stark conflict between fairness and truth-telling in cake-cutting disappears if we weaken strategy-proofness to NOM. In particular, NOM is compatible with the strong fairness property of proportionality, which guarantees each agent 1/n of the cake. Both properties are satisfied by an adaptation of the moving knife mechanism (Dubins and Spanier 1961), in which all agents cut the cake simultaneously and the agent with the smallest cut receives all the cake to the left of his cut and leaves. This procedure is also procedurally fair and easy to implement in practice.

NOM is violated by most other classical proportional mechanisms, even by the original Dubins–Spanier procedure, which shows that theoretically equivalent mechanisms may have different incentive properties for agents whose capability to assess the outcomes of manipulations is bounded.

2 Related literature

The cake-cutting problem has been studied for decades, given its numerous applications to the division of land, inheritances, and cloud computing (Brams and Taylor 1996; Moulin 2004; Segal-Halevi et al. 2017; Segal-Halevi and Nitzan 2019). Most of the literature studies indirect revelation mechanisms, in particular, Robertson–Webb mechanisms (Robertson and Webb 1998), in which agents can only use two types of messages to reveal their preferences over the cake: either an agent cuts a piece of the cake having a specific value, or he evaluates an existing piece by revealing his utility for it. Most well-known mechanisms can be expressed as a combination of these two operations.

In cake-cutting with three or more agents, every strategy-proof Robertson–Webb mechanism assigns no cake to at least one agent, whereas with two agents every Robertson–Webb strategy-proof mechanism is a dictatorship (Kurokawa et al. 2013; Brânzei and Miltersen 2015). These results assume that a Robertson–Webb protocol may cut the cake only in cut-points determined by agents’ replies to queries. Without this assumption, there is a trivial strategy-proof mechanism that simply ignores the agents’ actions and gives each agent a fixed non-empty piece of cake. Such a mechanism clearly does not achieve proportionality.

To allow for some degree of fairness and truth-telling, the literature has considered four research avenues. The first one is to use randomized mechanisms (e.g. Mossel and Tamuz 2010). In this paper we consider deterministic mechanisms only.

The second is to restrict the set of possible valuations over the cake. In this line, Chen et al. (2013) provide a deterministic mechanism that is both strategy-proof and proportional for a restricted class of utilities called piecewise linear. Their mechanism may waste unassigned pieces of cake, something that never occurs with our proportional and NOM mechanism.

A third research avenue studies allocation mechanisms in which an agent can only increase his utility by $\epsilon$ by misrepresenting his preferences, compared to the utility he obtains from truth-telling. Menon and Larson (2017) and Kyropoulou et al. (2021) obtain bounds on the amount of extra utility that agents can guarantee by lying in proportional cake-cutting mechanisms.

In this paper, we explore a fourth way to escape the conflict between fairness and truth-telling, which is relaxing the strategy-proofness definition to the one of NOM. NOM is a stronger version of an existing weak truth-telling property in the cake-cutting literature proposed by Brams et al. (2006, 2008), called maximin strategy-proofness.¹ We discuss the relationship between non in detail in the next section.

The concept of not-obvious-manipulability was introduced by Troyan and Morrill (2019) to mechanism design, in particular to analyse matching problems and auctions. Recently, Aziz and Lam (2021) have applied this concept to compare voting rules. They show that some common voting rules (e.g. k-approval voting) are obviously-manipulable, and prove that a large class of rules (the “almost-unanimous” rules) are NOM.

3 Model

3.1 Outcomes, agents and types

In a general mechanism design problem, there is a set of possible outcomes ${\mathcal {X}}$, a set of agents N of cardinality n, and a set of possible agent-types $\Theta = \Pi _{i \in N} \Theta _i$. In the particular case of cake cutting (Nicolò and Yu 2008; Procaccia 2016), there is an interval [0, 1] called the cake. A union of subintervals of [0, 1] is called a piece of the cake. The outcome-set ${\mathcal {X}}$ is the set of allocations—ordered partitions of [0, 1] into n disjoint pieces. $X\in {\mathcal {X}}$ denotes an arbitrary allocation and $X_i$ denotes the piece allocated to agent i.

The type-set $\Theta$ is the set of possible utility functions, where a utility function is a non-atomic measure—an additive set function that maps each piece to a real number.

The cakes we consider in most of the paper are all-good, in the sense that the utility of every piece is weakly-positive for each agent. These cakes are by far the most studied in the literature. Section 7 extends the results to an all-bad cake, in which the utility of every piece is weakly-negative for each agent. Extending the results to a mixed cake, which may have both positive and negative parts remains an open problem, given that this set-up is substantially more difficult as we show in subsection 7.2.

The utility of agent i with type $\theta _i$ is denoted by $u_i$. That $u_i$ is non-atomic allows us to ignore the boundaries of intervals. Another implication of nonatomicity is that $u_i$ is divisible, i.e. for every subinterval [x, y] and $0\le \lambda \le 1$, there exists a point $z \in [x, y]$ such that $u_i([x, z];\theta _{i}) = \lambda \, u_i([x, y];\theta _{i})$.² The utility functions are normalized so that $u_i([0,1];\theta _i)=1$ for all $\theta _i \in \Theta _i$ and all $i \in N$.

3.2 Extensive forms and mechanisms

An extensive form is an arborescence A that consists of a set of labelled nodes H and a set of directed edges E.³ The root node is $h_0$. Each terminal node is labelled with an allocation of the cake. Each non-terminal node h is labelled with a non-empty subset of agents N(h) who have to answer a query about their type. N(h) is said to be the set of players active at h.

In a general extensive form, the query may be arbitrary, for example asking agents to fully reveal their type. In a Robertson–Webb extensive form, only two types of queries are allowed (answers to these queries correspond to players’ strategies in the corresponding game):

• 1. Eval query: the query $\textsc {Eval}\left( i; x, y\right)$ asks agent i for its value for the interval [x, y], that is, eval$(i; x, y) = u_i([x, y];\theta _i)$ where $x,y \in [0,1]$.

• 2. Cut query: the query $\textsc {Cut}\left( i;x,\alpha \right)$ asks agent i for the smallest $y \in [0,1]$ such that $u_i([x,y];\theta _i)=\alpha$; where $\alpha \in {\mathbb {R}}$ and $x \in [0,1]$.

All the mechanisms that we consider in this paper can be expressed as a Robertson–Webb extensive form. All agents must reply to the queries and their answers must be dynamically consistent, meaning that there must be a possible type for which such a sequence of answers is truthful.⁴ However, agents’ answers may be untruthful.

For every possible combination of agents’ answers to the queries at node h, there is an edge from h to another node $h'$. Thus, answers to queries and edges have a one-to-one relationship. Note that, since the valuations are real numbers, there are uncountably many edges emanating from each node. Figure 1 illustrates a small subset of an extensive form.

Fig. 1

An example of an extensive form representing cut and choose

We make the following two standard informational assumptions (Moore and Repullo 1988). First, at each node h all agents know the entire history of the play. Second, if more than one agent is active at node h, they answer their corresponding queries simultaneously.

The indirect mechanism M corresponding to extensive form A takes as input the answers to each query in A and returns the allocation obtained at the corresponding terminal node. That is, the input to the mechanism consists of a path from the root node to a terminal node labelled with an allocation.

At node h, the edge corresponding to a truthful answer by all agents in N(h) with a type profile $\theta$ is denoted by $e^h(\theta )$, and $E(\theta )=\{e^h(\theta ) | h \in H\}$. This is, $E(\theta )$ is the set of all edges corresponding to truthful reports. An alternative set of edges in which all agents except i answer all queries truthfully, and agent i answers the queries as if he were of type $\theta _i'$, is denoted by $E(\theta _i',\theta _{-i})$. By our assumption of dynamically-consistent answers, each possible set of untruthful answers by each agent is associated to a possible type in $\Theta _i$.

$\Theta (h)$ denotes the set of possible agents’ types consistent with the history of play from the root node $h_0$ until node h. If a player i has not been active in any node until h, then $\Theta _i(h)=\Theta _i$, i.e, the set of possible types for agent i is unrestricted.

$M_i(E(\theta _i',\theta _{-i}''))$ denotes agent i’s individual allocation in mechanism M when agents’ answers correspond to the set of edges $E(\theta _i',\theta _{-i}'')$.

A special case of our definition is a direct revelation mechanism. In such a mechanism, there is a unique non-terminal node, which is the root $h_0$. The set of active agents there is $N(h_0)=N$, and the query for each of the agents is to fully reveal their type.

A mechanism M is called proportional if it guarantees to a truthful agent a utility of at least 1/n, regardless of what every other agent reports at any node of the corresponding extensive form. Formally, for all $i \in N$, all $\theta _i \in \Theta _i$ and all $\theta '_{-i} \in \Theta _{-i}$:

$$\begin{aligned} u_i(M_i(E(\theta _i,\theta '_{-i}));\theta _i)\ge 1/n. \end{aligned}$$

3.3 Manipulations

A manipulation by agent i with type $\theta _i$ at a node h in which he is active, corresponds to an untruthful answer to a query corresponding to pretending to be of type $\theta _i' \in \Theta _{i}(h)$, that is, corresponding to be of a different type $\theta _i'$ that is consistent with the history of play until node h.

A manipulation $\theta _i'$ is called profitable (for mechanism M and type $\theta _i$) if $u_i(M_i(E(\theta '_i,\theta _{-i}));\theta _i) > u_i(M_i(E(\theta _i,\theta _{-i}));\theta _i)$ for at least one $\theta _{-i}$. If, for some type $\theta _i$ of some agent i, there exists a profitable manipulation $\theta _i'\ne \theta _i$, then mechanism M is called manipulable.

A mechanism is called strategy-proof (SP) if it is not manipulable, that is, $u_i(M_i(E(\theta '_i,\theta _{-i}));\theta _i) \le u_i(M_i(E(\theta _i,\theta _{-i}));\theta _i)$ for all $i \in N$, for all $\theta _i, \theta '_i \in \Theta _i$, and all $\theta _{-i} \in \Theta _{-i}$. This definition of SP is very demanding: it requires a truthful report from every agent, every time he is asked to answer a query. Even if just one type of an agent has an incentive to give a non-truthful answer to a single query, the mechanism is no longer strategy-proof.

Troyan and Morrill (2019) suggest a weaker version of SP for direct-revelation mechanisms, which only compares the best and worst case scenarios from both truthful and untruthful behavior. We extend their definition to indirect mechanisms as follows.

Definition 1

(Obvious manipulation) Let h be a non-terminal node. Let i be an agent active at h, with true type $\theta _i$. A manipulation $\theta _i' \in \Theta _i(h)$ is called obvious at h for type $\theta _i$ if at least one of the following conditions holds:⁵

$$\begin{aligned} \inf _{\theta _{-i} \in \Theta _{-i}(h)} u_i(M_i(E(\theta '_i,\theta _{-i}));\theta _i)> \inf _{\theta _{-i} \in \Theta _{-i}(h)} u_i(M_i(E(\theta _i,\theta _{-i}));\theta _i) \\ \sup _{\theta _{-i} \in \Theta _{-i}(h) } u_i(M_i(E(\theta '_i,\theta _{-i}));\theta _i) > \sup _{\theta _{-i} \in \Theta _{-i}(h)} u_i(M_i(E(\theta _i,\theta _{-i}));\theta _i) \end{aligned}$$

Recall that $\Theta _{-i}(h)$ is the set of all types of the other agents that are consistent with the history of play from the root until node h. So, if the worst case for agent i, over all possible dynamically-consistent actions of the other agents at h, is better when i manipulates than when i is truthful, then this manipulation is obvious at h; similarly, if the best case for i, over all possible dynamically-consistent actions of the other agents at h, is better when i manipulates, then this manipulation is obvious at h.

Definition 2

(Not obviously manipulable mechanism) A mechanism M is not obviously manipulable (NOM) if for any node h in the arborescence of M, for every agent i active at h, and for every consistent true type $\theta _i\in \Theta (H)$, no manipulation is obvious at h for type $\theta _i$. In other words: for any type $\theta _i' \in \Theta _{i}(h)$, the following two conditions hold:

$$\begin{aligned}&\inf _{\theta _{-i} \in \Theta _{-i}(h)} u_i(M_i(E(\theta '_i,\theta _{-i}));\theta _i) \le \inf _{\theta _{-i} \in \Theta _{-i}(h)} u_i(M_i(E(\theta _i,\theta _{-i}));\theta _i) \end{aligned}$$

(1)

$$\begin{aligned}&\sup _{\theta _{-i} \in \Theta _{-i}(h) } u_i(M_i(E(\theta '_i,\theta _{-i}));\theta _i) \le \sup _{\theta _{-i} \in \Theta _{-i}(h)} u_i(M_i(E(\theta _i,\theta _{-i}));\theta _i) \end{aligned}$$

(2)

NOM is a strictly stronger condition than maximin strategy-proofness (Brams et al. 2006, 2008), which only requires the intuitive condition (1). That is, a maximin-strategyproof mechanism cannot be manipulated by a risk-averse agent who would only misrepresent her preferences if she knows that the utility that she can guarantee from lying is higher than the utility she can guarantee from telling the truth. However, condition (1) by itself does not have much bite on its own and a large class of cake-cutting mechanisms satisfy it.⁶ Condition (2) rules out many well-known cake-cutting mechanisms that could be manipulated by a risk-loving agent, who would misrepresent her preferences if by doing so she could obtain a best-case scenario payoff higher than that obtained with truth-telling. Not obvious manipulability is a desirable truthfulness criterion since it rules out many, but not all, cake-cutting mechanisms (section 4).

4 Results

4.1 Obviously manipulable mechanisms

We first show, using an example, that many classic cake-cutting procedures are obviously manipulable.

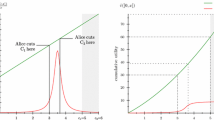
The example considers a cake-cutting problem with positive piecewise uniform valuations, i.e. agents either like or dislike certain intervals, each desirable interval of the same length has the same positive value, and each undesirable interval has a value of 0. One agent, called Blue, has valuations as in Fig. 2.

Fig. 2

Agent Blue only values the pieces shown in blue

Fig. 3

Obvious manipulations for agent blue (black arrow), supporting preferences for the other agent (red), final allocation received by blue agent (green)

We now consider several classic mechanisms in turn.

Cut and choose In this well-known mechanism, one agent cuts the cake into two pieces and lets the other agent choose her most preferred one. Blue (the cutter) is asked $\textsc {Cut}\left( \text {Blue}; 0 , 1/2 \right)$. Truthful behavior requires him to cut at 0.5, guaranteeing a utility of 0.5 in all cases. If Blue chooses a profitable manipulation instead, say to cut at 0.4, the best case is that the other agent chooses the left piece of the cake, leaving to Blue a utility of 0.75. Thus, in inequality (2), the supremum at the left-hand side is at least 0.75 while the supremum at the right-hand side is 0.5. Cut-and-choose is therefore obviously manipulable, which implies that its generalization by Kuhn (1967) to n players is obviously manipulable too.⁷

Cut middle In this mechanism, both agents are asked $\textsc {Cut}\left( i;0,1/2\right) = x_i$ simultaneously, and the cake is divided at $\frac{x_1+x_2}{2}$, with each agent obtaining the part of the cake which contains his cut. If Blue is truthful and cuts at 0.5, the best case is that the other agent cuts at $\epsilon$ (or $1-\epsilon$) and thus the cut point becomes $\frac{0.5+\epsilon }{2}\approx 0.25$, so Blue receives 0.75 utility. Nevertheless, if Blue chooses a profitable manipulation such as cutting at $\epsilon$, the best that could happen is that the other agent cuts at $\eta < \epsilon$, and thus Blue receives a utility almost equal to 1. In inequality (2), the supremum at the left-hand side is 1 and the supremum at the right-hand side is 0.75.

We conclude that cut-middle, too, is obviously manipulable.

Cut-and-choose and cut-middle are mechanisms for dividing a cake among two agents. We now turn to mechanisms that can be used to divide cake among two or more agents.

Banach-Knaster (Last Diminisher) In this mechanism (Steinhaus 1948), agents are assigned a fixed order. The first agent is asked the point $x_1=\textsc {Cut}\left( 1;0,1/n\right)$, and is tentatively assigned the piece $[0, x_1]$. Then, the second agent, after observing the first agent’s cut, has an option to “diminish” this piece: he is asked the point $x_2=\textsc {Cut}\left( 2;0,1/n\right)$, and if $x_2<x_1$, then the previous tentative assignment is revoked, and agent 2 is now tentatively assigned the piece $[0, x_2]$. This goes on up to agent n. Then, the tentative assignment becomes final: some agent k receives the piece $[0,x_k]$ and the other agents recursively divide the remaining cake $[x_k,1]$.

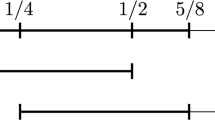
This procedure is obviously manipulable even with two agents. For example, consider the valuations depicted in Fig. 3a. Suppose agent 1 (blue) answers truthfully $x_1 = 0.5$. If agent 2 (red) answers truthfully $x_2 = 0.2$, then agent 2 receives the interval [0, 0.2), which gives her a utility of 0.5. A profitable manipulation for agent 2 is to answer $x_2' = 0.4$, so that she receives the interval [0, 0.4) which gives her a utility of 1 (see Fig. 4). This is true in both the best- and worst-case scenarios, which are the same in this case.

Fig. 4

Banach-Knaster is obviously manipulable (The manipulation by agent 2 at node h corresponds to the thick edge)

Dubins-Spanier In this procedure (Dubins and Spanier 1961), a knife moves continuously over the cake from left to right, the first agent who shouts “stop!” stops the knife and receives the piece to its left, and the process repeats with the remaining agents. Since this procedure is continuous, it does not fit our discrete model of a mechanism. Below we describe two common adaptations of this procedure to a discrete mechanism, both of which are obviously manipulable.

First, consider the following adaptation. In period 1, all agents i are simultaneously asked $\textsc {Cut}\left( i ; 0, 1/n\right)$, and the agent who replied with the smallest number (say $x^1$) receives the piece $[0,x^1]$. Then, in each period $t=2,\ldots ,n-1$, all agents i are simultaneously asked $\textsc {Cut}\left( i ; x^{t-1}, 1 / n\right)$, the agent who replied with the smallest number ($x^t$) receives the piece $[x^{t-1},x^t]$. Finally, agent n receives the piece $[x^{n-1},1]$.

To see that this variant is obviously manipulable, consider the case of a truthful agent i, who has uniform preferences over the whole [0, 1] interval and has to cut the cake against 2 other agents. Her first cut is $x^1_i=1/3$, which guarantees her a utility of at least 1/3. Suppose the lowest cut (submitted by someone else) was $x^1=0.1$. So in period $t=2$, the remaining cake is [0.1, 1], and agent i is asked $\textsc {Cut}\left( i; 0.1,1/3\right)$ to which the truthful answer is $\approx 0.43$, leading to a worst-case utility of 1/3. However, there is a manipulation that is guaranteed to yield i a higher utility in the worst-case scenario. If she cuts the cake instead at ${\hat{x}}_i^2=0.55$ (i.e. the point at which $u_i([0.1,{\hat{x}}_i^2];\theta _i)=0.45$), in the worst-case scenario, in which her cut is the lowest, she would guarantee herself a utility of $0.45 > 1/3$. If her cut was not the lowest, by continuing to cut the cake at the point ${\hat{x}}_i^t$ such that $x^t_i=\frac{([x^{t-1},1])}{n-t+1}$ for all subsequent t, she could make sure to receive a utility of at least 0.45 (see Lemma 1 below), which is larger than the worst-case utility 1/3 received by being truthful.

Second, consider the adaptation in which a knife moves from 0 to 1 in discrete increments of size $\delta$, which can be an arbitrarily small positive number. After each increment, every agent is asked whether $u_i([0,x];\theta _i) \ge 1/n$, where x is the current knife location. Whenever one or more agents answer “yes”, the knife is stopped, and one of these agents (with the smallest index) receives the interval [0, x]. The remaining agents then divide the rest of the cake in the same fashion.

This variant is obviously manipulable even with two agents. For example, consider Fig. 3a and suppose $\delta = 10^{-k}$, for some integer $k\ge 1$. When the knife arrives at $x=0.2$, the truthful action of agent Red is to say “yes” and stop the knife. A profitable manipulation for agent Red is to say “no” until $x > 0.4$ (since in the best-case scenario agent Blue does not answer yes before agent Red). This manipulation yields a payoff of 1 for Red.

4.2 A non obviously manipulable mechanism

We now present a third adaptation of the Dubins–Spanier mechanism, in which, in each period, all agents are asked the cut query simultaneously. We call this variant leftmost-leaves. It is presented as Algorithm 1.⁸

Despite leftmost-leaves being outcome-equivalent to the Dubins–Spanier moving knife mechanism, they differ in terms of obvious manipulability.

Theorem 1

The leftmost-leaves mechanism is proportional and not obviously manipulable.

Before presenting the proof, let us present a few remarks. First, the leftmost-leaves mechanism differs subtly from the first adaptation of Dubins-Spanier presented in subsection 4.1. The difference is that in the former adaptation, the agents in period t are asked $\textsc {Cut}\left( i ; x^{t-1}, 1/n\right)$, while in leftmost-leaves, they are asked $\textsc {Cut}\left( i ; x^{t-1}, {u_i([x^{t-1},1];\theta _i)\over n-t+1}\right)$. In the previous example of an agents with uniform preferences over the cake, leftmost-leaves asks the agent to cut the cake, at each period t, at a point such that she receives a utility of $[x^{t-1},1]/(n-t)$. The former adaptation always asks agents to cut the cake at a point in which their utility is 1/n, which is suboptimal in later division rounds as the cake available in period 2 ($[x^{1},1]$) is worth more than $(n-1)/n$ to all remaining agents, the cake available at period 3 ([$x^{2},1]$) is worth more than $(n-2)/n$ to all remaining agents, and so on; yet cutting at a point that gives a utility for the left piece of 1/n leads to a worst-case utility of exactly 1/n, whereas the worst-case utility in leftmost-leaves is $[x^{t-1},1]/(n-1)\ge 1/n$. This apparently small change makes a big difference in terms of strategic properties: the former adaptation is obviously manipulable while the latter is not.

Second, leftmost-leaves is theoretically equivalent to Dubins–Spanier moving knife mechanism, in the sense that when applied to the same vector of truthful types, both mechanisms always yield the same allocation (up to the arbitrarily small increment $\delta$, (Procaccia 2016)). How can mechanisms that are theoretically equivalent, such as the two we just presented, rank differently in terms of incentives? The intuition is as follows: in leftmost-leaves, agents have no restriction in the prior about their opponents’ types when they reveal their type through their cuts; whereas in the moving-knife procedure, the fact that the knife has reached some point tells agents something about their opponents’ types, and thus modifies what to expect in the best- and worst-case scenarios.

5 Proof of Theorem 1

We denote the leftmost-leaves mechanism by $M^{ll}$. We show that $M^{ll}$ is not obviously manipulable.

We first show that no manipulation yields a higher utility in the worst-case scenario. We use the following lemma, where for convenience we define $x^0 = 0$.

Lemma 1

For every agent i and all $t\ge 1$, at period t, the smallest possible utility of agent i when playing truthfully is

$$\begin{aligned} \inf _{\theta _{-i}} u_i(M^{ll}_i(E(\theta _i,\theta _{-i}));\theta _i) = \frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}. \end{aligned}$$

Proof

If $x_i^t$ is chosen as the smallest cut at period t, then i receives the piece $[x^{t-1},x^t] = [x^{t-1},x_i^t]$ and the result is immediate.

Otherwise, $x^t\le x_i^t$. Since we assume that the cake is all-good, this implies that

$$\begin{aligned} u_i([x^{t-1},x^t];\theta _i) \le u_i([x^{t-1},x_i^t];\theta _i) = \frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}, \end{aligned}$$

so the piece given away $[x^{t-1},x^t]$ is worth for i at most $\frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}$.

Therefore, the remainder of the cake $[x^t,1]$ must be worth at least $\frac{n-t}{n-t+1}$ of $u_i((x^{t-1},1);\theta _i)$, i.e.

$$\begin{aligned} u_i([x^t,1];\theta _i) \ge \frac{n-t}{n-t+1} u_i([x^{t-1},1];\theta _i) \end{aligned}$$

Dividing both sides by $n-t$,

$$\begin{aligned} \frac{u_i([x^t,1];\theta _i)}{n-t} \ge \frac{ u_i([x^{t-1},1];\theta _i)}{n-t+1} \end{aligned}$$

Note that the left-hand side of the previous expression is the utility that the truthful agent i would receive if his cut was chosen as the smallest cut in period $t+1$. If his cut was not the smallest at period $t+1$, an inductive argument shows that he would receive a share of the cake that he values even more in period $t+2$. Thus, the worst that can happen to a truthful agent in period t is to obtain a utility of $\frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}$. $\square$

We make two observations here. First, note that setting $t=1$ in Lemma 1 shows that leftmost-leaves is proportional. Second, the intuition behind the proof of Lemma 1 is simple: leftmost leaves is proportional at every step of its execution. When $n^*$ players are available, if a truthful player is chosen she guarantees $1/n^*$ of the cake, or else she guarantees at least $\frac{1}{n^*-1}$ of the remaining cake available, which is always more than $\frac{n^*-1}{n^*}$.

Now we show that any manipulation at period t, ${\hat{x}}_i^t \ne x_i^t$, yields for agent i a utility weakly smaller than $\frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}$ in the worst-case scenario.

Suppose that, from period t onwards, agent i manipulates in some way, while all other $n-t$ agents behave exactly as a truthful agent i would behave (i.e., they answer all queries as if their utility function is $u_i$). By Lemma 1, each such agent j must receive some piece $X_j$ such that $u_i(X_j ;\theta _i) \ge \frac{1}{n-t+1}u_i([x^{t-1},1];\theta _i)$. The total value of the pieces given to these $n-t$ agents is at least $\frac{n-t}{n-t+1}u_i([x^{t-1},1];\theta _i)$. Hence, the value remaining for agent i is at most $\frac{1}{n-t+1}u_i([x^{t-1},1];\theta _i)$. This upper bound holds in a specific case; hence the same upper bound holds in the worst case.

This concludes the proof that no manipulation yields a higher utility than truth-telling in the worst-case scenario, so inequality (1) is satisfied.

Next, we show that no manipulation yields a higher utility in the best-case scenario. We use the following lemma.

Lemma 2

For every agent i and all $t\ge 1$, at period t, the largest possible utility of agent i when playing truthfully is

$$\begin{aligned} \sup _{\theta _{-i}} \, u_i(M^{ll}_i(E(\theta _i,\theta _{-i}));\theta _i) = u_i([x^{t-1},1];\theta _i) \end{aligned}$$

This is, agent i, by being truthful in period t, can expect (in the best-case scenario) to obtain the whole cake available in period t.

Proof

The supremum is obviously at most $u_i([x^{t-1},1];\theta _i)$, since the agent cannot get more than the whole remaining cake. To prove that the supremum is at least $u_i([x^{t-1},1];\theta _i)$, it is sufficient to prove that, for every $\epsilon >0$, there exists some $\theta _{-i}$ such that $u_i(M^{ll}_i(E(\theta _i,\theta _{-i}));\theta _i) \ge u_i([x^{t-1},1];\theta _i) - \epsilon$.

Let us remember that a truthful agent i cuts the cake at a point $x_i^t > x^{t-1}$ such that

$$\begin{aligned} u_i([x^{t-1},x_i^t];\theta _i)=\frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}. \end{aligned}$$

Given some $\epsilon >0$, let $\theta _{-i}$ be such that the smallest cut at each period $t' \ge t$, denoted $x^{t'}$, is to the left of the cut of agent i, but only slightly to the right of the previous cut. Formally:

$$\begin{aligned} x^{t'-1}< x^{t'}&< x_i^{t'} \\ u_i([x^{t'-1},x^{t'}];\theta _i)&\le \epsilon /n \end{aligned}$$

Such $x^{t'}$ values exist due to the standard assumption that the utilities are divisible ($u_i$ is a continuous function).

With such a sequence of cuts, agent i remains the last agent, and receives the piece $X_i=[x^{n-1},1]$. Since the pieces given to each of the other agents are worth for i at most $\epsilon /n$, the remaining piece is worth for him at least $u_i([x^{t-1},1];\theta _i)-\epsilon$. $\square$

Since this is the maximum utility attainable, inequality (2) in the NOM definition is satisfied. This concludes the proof that no manipulation gives a higher utility to a truthful agent in the best-case scenario.

We conclude that no manipulation is better than truth-telling in either the best or the worst-case scenario, thus no manipulation is obvious and leftmost-leaves is NOM.

6 Alternative mechanisms

A natural follow-up question to Theorem 1 is whether leftmost-leaves is the only proportional and NOM mechanism in cake-cutting. The answer is no, as shown below.

6.1 Query-based mechanisms

Leftmost-leaves can be slightly modified in several ways retaining both NOM and proportionality. One such modification is to start cutting the cake from the right instead of from the left. Another less trivial one is an adaptation of the protocol of Even and Paz (1984), which works the same as leftmost-leaves for $n=2$, but requires fewer queries for larger values of n. The adaptation works as follows (for simplicity we present it for n that is a power of 2). Given a cake [y, z], all agents choose cuts $x_i$ such that $u_i([y,x_i];\theta _i)=u_i([y, z];\theta _i)/2$. Order the cuts in increasing order, and let $x^*$ be the cut number n/2 from the left. Then the procedure breaks the cake-cutting problem into two: all agents who choose cuts $x_i \le x^*$ are to divide the cake $[y,x^*)$, whereas all agents who chose cuts above $x^*$ are to divide the cake $[x^*,z]$. Each half is divided recursively among the n/2 partners assigned to it. Finally, when the procedure is called with two agents, they divide the remaining cake among them using leftmost-leaves. For example, if $n=4$, agents cut the cake in two equivalent pieces and the cake is cut at the second smallest cut. Then the two agents with the smallest (largest) cuts play leftmost-leaves on the left (right) side of the cake.

The proof that this variant of Even–Paz is NOM is similar to the proof of Theorem 1: at each period an agent can still obtain the remaining cake entirely in the best case, and deviating from telling the truth may lead to a worse than proportional outcome.

Obtaining a characterization of all NOM and proportional mechanisms remains an interesting, albeit challenging, open question.

6.2 Direct-revelation mechanisms

While leftmost-leaves is proportional and connected, it does not satisfy other desirable properties such as envy-freeness (no agent prefers the piece of cake received by someone else over his own piece) and Pareto-optimality (no other allocation is better for one agent and not worse for the others).

In the Robertson–Webb model, we could not yet find NOM mechanisms satisfying these properties. For example, the classic mechanism of Selfridge–Conway for three agents (see Brams and Taylor 1996 for a detailed description) is envy-free, but it is obviously manipulable. In this mechanism, the first agent cuts the cake into three pieces of equal worth. A truthful agent knows that one of those pieces will never belong to him, and thus he can achieve a maximum utility of at most 0.67. However, a lying agent can cut the cake in one piece of value $1-\epsilon$, and two pieces of almost no value at all. In the best case scenario, he will keep the most valued piece entirely, showing that the Selfridge–Conway procedure is obviously manipulable.

Interestingly, NOM is easier to achieve in the direct-revelation model.⁹

Lemma 3

Every direct-revelation mechanism that always returns proportional allocations satisfies inequality (1).

Proof

By proportionality, a truthful agent always receives a utility of at least 1/n. Consider now an untruthful agent i who reports a type $\theta _i'\ne \theta _i$ (equivalently, reports a utility function $u_i'\ne u_i$). Consider the case when all other $n-1$ agents have type $\theta _i$ (the true type of agent i). A proportional mechanism must give each of these $n-1$ agents a piece with a value, by the function $u_i$, of at least 1/n. Hence, the piece remaining for agent i has a value, by the function $u_i$, of at most 1/n. Hence, in inequality (1), the infimum is at most 1/n at the left and at least 1/n at the right, and the inequality holds. $\square$

Lemma 4

Every direct-revelation mechanism that always returns Pareto-optimal allocations satisfies inequality (2).

Proof

Fix some $\epsilon \in (0,1)$. Consider the case when agent i is truthful, all other $n-1$ agents assign a positive value only to $[0,\epsilon ]$, and assign a value of 0 to the rest of the cake. A Pareto-optimal mechanism must give agent i all parts of $[\epsilon ,1]$ that are valued positively by agent i. When $\epsilon \rightarrow 0$, the value allocated to agent i approaches 1. Hence, in inequality (2), the supremum in the right-hand side equals 1 and the inequality holds. $\square$

Theorem 2

There exists a NOM direct-revelation mechanism that finds envy-free and Pareto-optimal allocations.

Proof

The Nash-optimal mechanism is a direct-revelation mechanism that, given n utility functions, selects an allocation that maximizes the product of utilities. Such an allocation is known to be Pareto-optimal and envy-free (Segal-Halevi and Sziklai 2019), hence it is also proportional. Hence, by Lemmas 3 and 4, the mechanism is NOM. $\square$

When the utility functions are piecewise-constant, the Nash optimal mechanism can be computed by an efficient algorithm (Aziz and Ye 2014). In contrast to the leftmost-leaves rule, the Nash-optimal rule may return disconnected pieces, which is undesirable for division of resources like land. However, it is known that any Pareto-optimal envy-free rule may have to return disconnected pieces (see Example 5.1 in Segal-Halevi and Sziklai (2018)). Since Pareto-optimality is crucial in the proof of Theorem 2, it remains an open question whether there exists a NOM mechanism that is both connected and envy-free for three or more agents.

A related open question is whether there exists an algorithm that finds connected, proportional and Pareto-optimal allocations. If such an algorithm exists, then by Lemmas 3 and 4, it is NOM.

7 Dividing a cake with negative parts

7.1 All-bad cakes

When all utilities are weakly-negative, the rightmost-leaves mechanism (Algorithm 2) is proportional and NOM. The main difference from the leftmost-leaves mechanism is that, at each step, the largest cut-point is selected instead of the smallest. This adaptation is well-known for moving-knives procedures. We now show that it can be done in a NOM way.

Lemma 1 is true as-is for the rightmost-leaves mechanism when the cake is all-bad: for all $t\ge 1$, at period t, the smallest possible utility of a truthful agent i is $\frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}$ (note that this utility is now a negative number). The proof is very similar. The piece given away at each step t is at least as large as the piece that agent i values at $\frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}$, and the cake is all-bad, so the value of the piece given away is still at most $\frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}$. Thus, rightmost-leaves is proportional, and inequality (1) is satisfied.

Instead of Lemma 2, we have

Lemma 5

For all $t\ge 1$, at period t,

$$\begin{aligned} \sup _{\theta _{-i}} \, u_i(M^{rl}_i(E(\theta _i,\theta _{-i}));\theta _i) = 0 \end{aligned}$$

This is, agent i, by being truthful in period t, can expect (in the best-case scenario) to obtain no bad cake at all.

Proof

The supremum is obviously at most 0 since the cake is all-bad. To prove that the supremum is at least 0, it is sufficient to prove that, for every $\epsilon >0$, there exists some $\theta _{-i}$ such that $u_i(M^{rl}(E(\theta _i,\theta _{-i}));\theta _i) \ge - \epsilon$.

Let us remember that a truthful agent i cuts the cake at a point $x_i^t > x^{t-1}$ such that

$$\begin{aligned} u_i([x^{t-1},x_i^t];\theta _i)=\frac{u_i([x^{t-1},1];\theta _i)}{n-t+1}. \end{aligned}$$

Given some $\epsilon >0$, let $\theta _{-i}$ be such that the largest cut at period t, denoted $x^{t}$, is to the right of the cut of agent i, and only slightly to the left of 1, such that:

$$\begin{aligned} x_i^{t} <&x^{t} \\ u_i([x^{t},1];\theta _i)&\ge -\epsilon \end{aligned}$$

With such a cut, the rightmost cutter at period t takes almost all of the remaining cake, and the piece that remains is so small that its value for agent i at least $-\epsilon$. Regardless of what happens in the following rounds, the utility of agent i is at least $-\epsilon$. $\square$

Since 0 is the largest possible utility, inequality (2) is satisfied too, so rightmost-leaves is NOM.

7.2 Mixed cakes

In the most general cake model, the utility of each agent to every piece of cake may be either positive or negative. So far, we could not adapt the leftmost-leaves mechanism to handle this general setting while keeping its NOM property. We provide an Example in Fig. 5 to show that adapting the leftmost-leaves mechanism to this setup is not trivial. In this example, the agent whose preferences we depict (Alice) gets a utility of 1 if she gets the whole cake, a utility of 1 for each blue piece of length 0.1, and a utility of -1 for each red piece of length 0.1.

Fig. 5

A mixed cake in which leftmost-leaves is OM. Good parts of the cake appear in blue, bad parts in red

In a mixed cake, unlike in an all-good or all-bad cake, a $\textsc {Cut}\left( i; x,\alpha \right)$ query can be answered by several disconnected values, since the function $u_i([x,y])$ is not a monotonic function of y. For example, in Fig. 5a, the $\textsc {Cut}\left( i; 0,0.5\right)$ query has three disconnected truthful answers, marked by x, y, z. Each of these answers guarantees Alice a value of 0.5 if she wins in the first round. Otherwise, the other agent wins some piece adjacent to the left end of the cake, and Alice gets the remaining piece, which is adjacent to the right end of the cake. The largest possible value that Alice can get from a piece adjacent to the right end of the cake is 2 (for the piece [0.8, 1]). Therefore the best-case utility of a truthful agent is 2.

However, if Alice answers 0.4 (denoted by m in Fig. 5b), then in the best case she wins the piece [0, 0.4] in the first round and her utility is 3.

We conjecture that, in the Robertson–Webb model, there is no NOM mechanism that produces a connected and proportional allocation of a mixed cake. We leave further investigation of this interesting question for future research.

8 Concluding remarks

8.1 Experimental evidence

Troyan and Morril’s concept of non-obvious manipulability is theoretically appealing. Furthermore, its predictions are testable using real-life data. In this section, we examine whether NOM cake-cutting mechanisms are manipulated more often than obviously manipulable ones using the data from two lab experiments reported in Kyropoulou et al. (2021).¹⁰

In the first experiment (EXP1), subjects divide a cake against truthful automata. In the second one (EXP2), subjects divide a cake versus other real-life subjects who may manipulate as well. Agents are incentivized to obtain as much of their desired cake as possible. We refer the reader to their paper for details regarding the experiment, as here we are only concerned by the percentage of truthful cake cuts observed in NOM and OM mechanisms, which are presented in Table 1.¹¹

Table 1 Percentage of truthful cuts in lab experiments

In EXP1, NOM mechanisms are less manipulated than their OM counterparts. Leftmost-leaves was significantly less manipulated than Banach–Knaster last diminisher when subjects played against 2 automata (difference of 24 percentage points, p-value smaller than 0.0001) and 3 automata (difference of 16 percentage points, p-value smaller than 0.0001). The Even–Paz modification of leftmost-leaves, which is NOM too, was also significantly less manipulated than Banach–Knaster (difference of 35 percentage points, p-value smaller than 0.0001).

In EXP2, however, NOM mechanisms are manipulated just as or more than OM ones. Leftmost-leaves was manipulated just as much as cut and choose and cut-middle (difference of 1 and 4 percentage points respectively, p-values of 0.62 and 0.19). However, leftmost-leaves was significantly more manipulated than Banach–Knaster last diminisher when 3 subjects divided the cake (difference of 11 percentage points, p-value smaller than 0.0001).

It is unclear why we observe different levels of truth-telling in EXP1 and EXP2, and more experimental research (with potentially different experimental designs) would help to answer this question. So far, the data is inconclusive and we do not consistently observe that NOM mechanisms are less often manipulated than obviously manipulable ones.

8.2 Conclusion

Although it is impossible to cut a cake in a strategy-proof manner that is not completely unfair to some agent, we can divide a cake in a fair, proportional way that cannot be obviously manipulated using an easily implementable mechanism called leftmost-leaves. The majority of other commonly studied proportional mechanisms are obviously manipulable.

NOM, however, is a property satisfied by several cake-cutting mechanisms besides leftmost-leaves. An interesting open question is to find a non manipulability concept that is weaker than strategy-proofness but more strict than NOM that has a sensible interpretation and is satisfied by a unique proportional mechanism. We leave this question for future research.