Abstract
We study a game with two candidates and two interest groups. The groups offer two kinds of costly contributions to achieve political influence: (a) pre-election campaign contributions to their favourite candidates that increase their probability of winning the election and (b) post-election lobbying contributions to the winning candidate to affect the implemented policy. The candidates are the first to act by strategically choosing the lobbying prices they will charge the groups if they are elected. We characterise the equilibrium values of the lobbying prices set by the candidates as well as the equilibrium levels of the campaign and lobbying contributions chosen by the groups. We show, endogenously, that in the case with symmetric groups and symmetric politicians, a candidate announces to charge the group that supports her in the election a lower lobbying price, justifying this way the preferential treatment to certain groups from the politicians in office. We also consider two extensions (asymmetric groups and politicians who do not commit to the announced prices) and show that the results of the benchmark model hold under specific conditions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is generally admitted that interest groups play an important role in the political process. A significant part of the lobbying literature (Austen-Smith 1987; Baron 1994) considers interest groups with electoral motives. These groups take the candidates’ positions as given and offer them campaign contributions. These contributions are typically spent by candidates on campaign activities that aim at persuading the constituency to vote for them and, thus, affecting their probability of winning. Another strand of the literature assumes that lobbying occurs after the election. Lobbying takes the form of either monetary contributions offered to the incumbent politician (Krueger 1974; Becker 1983; Lohmann 1995; Bennedsen and Feldmann 2006; Martimort and Semenov 2008) or informational lobbying with exogenous lobbying costs (Potters and van Winden 1992). That is, the relative literature typically considers political influence either before or after the election as separate cases.Footnote 1
Nevertheless, political influence is a continuous activity that does not end once the election is concluded. After the election, and regardless of the winner, the interest groups need to influence the implemented policies. Tripathi et al. (2002) use data from the 1995 Lobby Disclosure Act and find a strong connection between campaign expenditures and lobbying. More specifically, “groups that have both a lobbyist and a PAC [...] account for fully 70% of all interest group expenditures and 86% of all PAC contributions”.
In this paper, we jointly consider pre- and post-election political influence and, endogenously, determine the optimal level of the “access” price the politicians charge the interest groups. We model the above situation as a three-stage game with two interest groups and two candidates. At stage zero (pricing stage), the two candidates announce the level of lobbying prices they plan to charge the two groups if they are elected. At the first stage (election stage), each group offers a monetary contribution to its favourite candidate that is used by her in order to grow her electoral support and, then, the election takes place. At the second stage (lobbying stage), the two groups compete exerting lobbying efforts towards the elected candidate to increase their probability of winning the final “prize”. This prize might be the assignment of a project, trade protection or the implementation of the group’s favourite policy. The lobbying prices announced at stage zero can be understood as access prices or the weights a politician is going to put on the lobbying efforts made by the two lobbies when deciding the winner of the final prize (i.e., the lower the price for a group, the greater the weight politicians put on this group’s effort).
The first and second stage have the characteristics of a two-stage Tullock contest. The groups compete against each other twice, once before and once after the election takes place. At the lobbying stage (the second stage of the “contest”), the two groups engage in a contest for a given “prize” by exerting costly lobbying efforts.Footnote 2 A unit of lobbying effort by a group can be viewed as an hour spent in the incumbent’s office trying to persuade her about the group’s eligibility for a project assignment or informing her about a relevant policy issue.Footnote 3 At the election stage (the first stage of the “contest”), the two groups compete by offering campaign contributions to their favourite candidate so that they affect the electoral outcome.Footnote 4 This is, like Austen-Smith (1987) and Baron (1994), the groups have an electoral motive, meaning that each group takes as given the candidates’ positions and offers a contribution to its favourite candidate in order to increase her probability of winning the election. The “award” the two groups fight for at the election stage is an endogenously determined (lower) lobbying price at the lobbying stage and, hence, preferential treatment by the candidate in office.
The lobbying prices asked by the winning candidate are chosen strategically by the two candidates at the pricing stage (the stage before the contest) and maximise the candidates’ expected utility from lobbying. By announcing the offered lobbying prices, the candidates simultaneously affect both their probability of being elected and their utilities from lobbying if they are elected.
Starting from the benchmark case with symmetric candidates, our main result shows that a candidate announces a lower lobbying price for the group that is going to support her at the election. This is, our results support the idea that contributions may buy “access” for lobbying activities such as “preferential treatment” by the incumbent or amplification of the group’s message (Wright 1990). As put by Wright (1990), our results demonstrate that “representatives may ‘hear you better’ [...] when a contribution precedes lobbying”. Thus, we show endogenously that the group supporting the eventual winner of the election is treated favourably compared to the opposite group.
In an extension of the benchmark model, we consider the case where the groups have a different valuation of the final prize depending on which politician has won the election. Specifically, we permit a group to value the final prize higher if the elected politician is the one it supported in the election than if she is the one supported by the other group. This way, we provide an exogenous link between a group and its favourite politician. This link can be, for instance, aligned policy preferences between a group and a politician. The analysis of this case shows that, for specific levels of difference in prize valuations, the results of the benchmark case are robust in this case, as well. Specifically, they indicate that if the difference between the groups’ prize valuations is sufficiently small, the politicians announce greater lobbying prices for their supporting groups. The opposite holds when the difference in prize valuations is relatively large. In this case, the politicians may announce a lobbying price for the opposing group lower than the price for the favourite group.
Finally, we analyse the case where the winner politician does not commit to the announced prices with certainty. Again, we show that the two politicians announce a lower price for the group supporting them but, now, the results depend on how credible the announced access prices are. In particular, the lower the probability that a winner politician commits to the announced prices, the lower the contributions made by the two groups.
1.1 Link to the literature
The paper contributes to two strands of the literature: lobbying literature and contest theory literature.
1.1.1 Lobbying literature
The concept of price-setter candidates is similar to Austen-Smith (1998) where an incumbent politician commits to the contribution level she requires from groups in order to consider them as potential information providers. After the contributions have been offered, the politician grants access to one of the groups that have contributed and gathers relevant information from it. The main difference between the above study and ours is that in the latter, we consider two politicians who set prices before the election takes place. Therefore, these prices also affect contributions by the groups and, consequently, the election outcome. Moreover, in our model, we allow for different prices for each group as well as for more than one group able to be granted access to the legislator.
The paper is also relative to the study of Cotton and Déllis (2016) which analyses how much information a politician should collect from interest groups and of Cotton and Li (2018) which considers a model with a politician who acquires information before interest groups offer money to her in exchange for policy favours. Both models assume informational or monetary lobbying to an incumbent politician. Our model, instead, also incorporates an election game before the lobbying game so that there is uncertainty on who the eventual incumbent is and her election depends on the groups’ contributions. Last, Ellis and Groll (2019) study a model with a policymaker and one lobby focusing on how the politician and lobby’s resource constraints affect lobbying activities. In our study, the engagement of the groups in a two-stage contest, combined with the introduction of a stage before the contest, allows us to consider an environment where political influence begins before an election and continues after it.Footnote 5
There are, also, other studies that model lobbying as a contest. For instance, Epstein and Nitzan (2006) provide micro-foundations for the public-policy contest and illustrate the possible rationalisation of random government behaviour in both all-pay auctions and Tullock contests. Two relevant and more recent studies are Duggan and Gao (2020) and Sasso and Alexander (2020). In the former, lobbying is modelled as a “tug of war” where lobbies make effort to pull a policy outcome in their preferred locations. The latter study considers a two-stage game where at the first stage, politicians commit to a level of concession they are going to give to their favourite group if elected and at the second stage, groups offer campaign contributions and the election takes place. In contrast to the above-mentioned studies, ours involves political influence through both campaign contributions and post-election lobbying.Footnote 6
1.1.2 Contest theory
The endogenous choice of lobbying prices constitutes our main contribution also to the existing literature in contest theoryFootnote 7 and, more particularly, works on multi-stage contests (Gradstein and Konrad 1999; Moldovanu and Sela 2006; Konrad and Kovenock 2009; Fu et al. 2015).
For instance, Clark et al. (2018) consider a two-stage contest in which the winner of the first stage faces by assumption a lower cost of effort at the second stage. Not only does our study provide support to this assumption, but also our results differ significantly due to the different assumed objective functions. In contrast to this study, Clark et al. (2018) are concerned about the maximisation of the total effort exerted at the two stages of the contest and they find that the optimal level of the second-stage cost offered by an effort-maximising contest designer should be zero. As a result, the two-stage contest reduces to a one-shot contest since the loser of the first stage does not make any effort at the second stage. The fact that we are concerned about the candidates’ expected utility, rather than the groups’ total effort, makes the two-stage contest meaningful and allows us to determine the optimal utility-maximising level of the second-stage effort cost. Clark et al. (2018), instead, assume that this cost is out of the designer’s control and study the optimal prize distribution between the two stages.
In previous work, Clark and Nilssen (2013) also consider a two-stage contest in which they exogenously assume that the greater the effort exerted by a player at the first stage, the lower her effort cost at the second stage. In our model, instead, the levels of lobbying prices (effort cost) are set by the candidates endogenously before the contributions (first-stage effort) are made.
Another study close to ours is Beviá and Corchón (2013). It considers a two-period contest in which the second-stage asymmetry between the players depends on the outcome of the first stage. Specifically, each player’s second-stage ability depends on the share of the prize earned in the first period. In our study, first, there is no award for the interest groups at the election stage and, second, only the group that supported the winner of the election benefits at the lobbying stage, regardless of the level of expenditures it made before the election.
The rest of the paper goes as follows. In Sect. 2, we formalise the game. In Sect. 3, we analyse the benchmark symmetric game and present the results of the analysis. In Sect. 4, we present some extensions of the model and Sect. 5 concludes the study. All proofs are included in Appendix A.
2 Benchmark model
Consider two symmetric candidates, \(\{A,B\}\), and two symmetric interest groups, \(\{a,b\}\), where groups a and b support candidates A and B, respectively. The game consists of three stages: the pricing stage, the election stage and the lobbying stage.
At stage zero (pricing stage), the two candidates, having as an objective the maximisation of their expected utility from lobbying, announce the lobbying prices they are going to charge each group if they win the election. Denote by \(c_{I,i}>0\) the lobbying price announced by candidate I for the group that is going to support her at the election, group i, and \(c_{I,j}>0\) for the opposite group, group j, where for \(I=A\), \(i=a\) and \(j=b\) and for \(I=B\), \(i=b\) and \(j=a.\)Footnote 8
At the first stage (election stage), the two groups choose their levels of contribution to their favourite candidate. The contributions received by the two candidates are spent at this specific stage for campaign purposes and determine their probability of winning the election.Footnote 9 Particularly, the probability that a specific candidate wins is increasing in the contribution received by her and decreasing in the contribution received by her opponent. Let \(x_i\ge 0\) denote the contribution made by group i to candidate I and the marginal cost of contribution be the same for both groups and normalised to 1. Since each candidate I is supported by group i, we express the probability that candidate I wins at the election stage as a lottery contest success function first introduced by Tullock (1980), namely
while the probability that she loses, or, equivalently, candidate J, supported by group j, wins is \(q_J=1-q_I.\)Footnote 10
At the final stage (lobbying stage), the two groups lobby the winner of the election. Assume that the winner is candidate I who was supported by group i. Denote the lobbying effort of group i by \(y_i\ge 0.\) The lobbying price group i is charged is \(c_{I,i},\) while the price group j is charged is \(c_{I,j}.\) Considering linear cost functions for the two groups, the cost function of group i is \(C_i\left( y_i\right) =c_{I,i} y_i,\) while the cost function of group j is \(C_j\left( y_j\right) =c_{I,j}y_j.\) The probability that group i wins at the lobbying stage is
while the probability that group j wins is \(p_j=1-p_i.\) The winning group of the lobbying stage enjoys the implementation of its favourite policy, the valuation of which is equal for both groups and normalised to 1. The expected payoff of each group is the probability of winning minus its lobbying expenditure. Hence, at the lobbying stage, the expected payoffs of groups i and j are, respectively,
Going backwards, at the election stage, the expected payoff of group \(i,\, \Pi _i,\) is the following: the probability that its favourite candidate wins times its lobbying-stage payoff if she wins, plus the probability that her favourite candidate loses times its lobbying-stage payoff is she loses (slightly abusing notation we refer to this as \(\pi _{-i}\)), minus its contribution. Making use of eq. (1), we have that at the election stage, the expected payoff of group i is
At the first stage of the game, the two candidates set the lobbying prices they are going to charge if they win the election. They do so having as objective to maximise their utility from lobbying, where losing the election implies zero payoffs. Therefore, at the beginning of the game, candidate I’s expected utility, \(r_I,\) is equal to the probability that she wins the election times her utility if she wins, namely,
We proceed with the analysis of the game.
3 Results
We make use of backward induction to determine the sub-game perfect Nash equilibrium of the game in pure strategies.
3.1 Lobbying stage
This stage of the game is an asymmetric Tullock contest previously analysed, among others, by Nti (1999). Assume that the winner of the election is candidate I. Maximising eq. (2) with respect to \(y_i\) and \(y_j,\) respectively, we find that in equilibrium, the lobbying efforts of groups i and j are, respectively,
yielding payoffs
We observe that if \(c_{I,i}\le c_{I,j},\) then \(y_i^*\ge y_j^*\) and \(\pi _i^*\ge \pi _j^*.\) If a politician charges one group a lower lobbying price, then this group exerts a greater lobbying effort and earns a higher payoff than the other one.
3.2 Election stage
Group i chooses the level of contribution, \(x_i,\) to offer to her favourite candidate, I, in order to maximise its expected payoff. Using eq. (3) and eq. (6), the maximisation problem of group i is
The equilibrium contributions offered by the two groups are given by the following proposition.
Proposition 1
In the equilibrium of the symmetric election stage game, group i offers contribution
The first thing we notice in Proposition 1 is that, at the election stage, either both groups choose not to make any contributions or both groups make a positive contribution. Particularly, if \(\frac{c_{I,i}}{c_{I,j}}\ge \frac{c_{J,i}}{c_{J,j}}\) the two groups do not make any contributions whatsoever. This indicates that if an interest group is not treated by the candidates sufficiently well compared to how the other group is treated and the announced lobbying prices are not favourable to it, then, it prefers to remain inactive at the election stage.
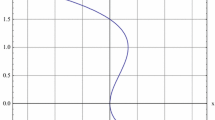
The equilibrium characterisation also offers several interesting comparative statics (for details, see Appendix B). First, the equilibrium effort of group \(i,\, x_i^*,\) is decreasing in the price its favourite candidate has announced to charge it, \(c_{I,i},\) i.e., \(\partial x_i^*/\partial c_{I,i}<0.\) This indicates that as a candidate decreases the price she is going to charge the group that supports her if she wins the election, the group supporting her contributes more in order to increase this candidate’s probability of winning and, therefore, the probability that the group will pay this lower price (blue curve in Fig. 1). Second, \(x_i^*\) is increasing in the price its favourite candidate has announced to charge the opposite group j, \(c_{I,j},\) i.e., \(\partial x_i^*/\partial c_{I,j}>0.\) This shows that a group increases the contribution to its favourite candidate as she increases the lobbying price she chooses to charge the opposite group if she wins. By increasing its contribution, a group increases the probability that its favourite candidate wins the election and, in consequence, it will win the prize at the lobbying stage since the opposite group will make a low lobbying effort having to pay a high lobbying price.
However, differentiating \(x_i^*\) with respect to \(c_{J,j},\) we find that the effect of a change in the lobbying price candidate J announces to charge her favourite group on the contribution received by candidate I is non-monotonic (green curve in Fig. 1). More specifically, if a candidate announces for the group supporting her a relatively low lobbying price, in case she wins, the payoff of the opposite group at the lobbying stage will be low. As this price goes up, the latter group may increase its contribution in order to increase the probability that its favourite candidate wins and, consequently, decrease the probability that it will get a low payoff. If now the lobbying price a candidate announces for her favourite group is relatively high, in case she wins, the payoff of the opposite group is going to be high as well. Thus, as this price increases even more, the latter group has an incentive to decrease its contribution to its favourite candidate in order to increase the probability that the opposite candidate wins and, therefore, the probability that it gets a high payoff.Footnote 11
3.3 Pricing stage
Candidate I, having as an objective to maximise eq. (4) taking into consideration eq. (5) and eq. (8), sets the level of prices, \(c_{I,i}\) and \(c_{I,j},\) to announce to groups i and j, respectively. Candidate I’s maximisation problem is, then,
Let us explore how a candidate’s expected utility varies for different levels of lobbying prices (for a complete analysis, see Appendix B). First, candidate I’s expected utility is strictly increasing in the lobbying price candidate J announces for group j, i.e., \(\partial r_i^*/\partial c_{J,j}>0.\) This is because group j decreases its contribution to her favourite candidate J and, therefore, the probability that candidate I wins goes up increasing I’s expected utility. Moreover, candidate I’s expected utility is strictly decreasing in the lobbying price candidate J announces for group i, i.e., \(\partial r_i^*/\partial c_{J,i}<0.\) This occurs because I’s expected utility decreases through her probability of winning the election which is decreasing in the lobbying price J announces for group i.
However, while a candidate’s expected utility is monotonic in the lobbying prices announced by the opposite candidate, this is not the case for the lobbying prices announced by her. Candidate I’s expected utility is decreasing in \(c_{I,i},\) i.e., \(\partial r_i^*/\partial c_{I,i}<0,\) if \(c_{I,j}\) and \(c_{J,j}\) are sufficiently low. This happens because as \(c_{I,i}\) goes up, group i decreases its contribution to candidate I and, also, because \(c_{I,j}\) is low, group j increases its contribution to its own favourite candidate, candidate J. These two effects lead to a decrease in candidate I’s probability of winning and, thus, to a reduction in her expected utility. On the other hand, candidate I’s expected utility is increasing in \(c_{I,i},\) i.e., \(\partial r_i^*/\partial c_{I,i}>0,\) if \(c_{I,j}\) is sufficiently high and \(c_{J,j}\) sufficiently low, or if just \(c_{J,j}\) is sufficiently high. Now, while along with group i also group j decreases its contribution making the effect in candidate I’s probability of winning ambiguous, it is the positive effect of an increase in \(c_{I,i}\) and a high \(c_{I,j}\) on her utility if she wins that makes her expected utility increasing in \(c_{I,i}.\)Footnote 12
The candidates’ maximisation problem highlights the main trade-off they face when optimally setting the “access” prices interest groups will have to pay to them if they win the office. On the one hand, as a candidate opts for higher lobbying prices, the higher her utility from lobbying if she wins the election. On the other hand, higher lobbying prices decrease the contribution received at the election stage and, therefore, the probability of winning the election. Balancing these two opposing effects appropriately determines the optimal lobbying prices as characterised in the following proposition.
Proposition 2
There are multiple equilibria in the symmetric pricing stage game in all of which the lobbying prices candidate \(I\in \{A,B\}\) charges the two groups satisfy the ratio \(c_I^*\equiv \tfrac{c_{I,i}^*}{c_{I,j}^*}=\tfrac{1}{2}\left( \sqrt{5}-1\right) \equiv \varphi -1.\)Footnote 13 Each candidate receives contribution \(x^*=\frac{1}{4}\left( \sqrt{5}-2\right)\) and her utility is \(r^*=\sqrt{5}-2.\) The expected payoff of each group is \(\Pi ^*=\tfrac{3-\sqrt{5}}{4}.\)
Since \(c_I^*<1\), Proposition 2 states that each candidate’s optimal strategy is to announce a lower price for her favourite group than for the opposite group. This is an interesting result since we obtain endogenously—and not assume a priori like the majority of the studies in the literature—that the interest group that supports a candidate will be in an advantageous position after the election if this specific candidate wins.
Proposition 2 highlights that a candidate’s expected contributions received and utility from lobbying do not depend on the absolute values of the lobbying prices she sets but only on the ratio of these prices. A candidate can announce any lobbying prices she wants as long as they satisfy the ratio of Proposition 2.
4 Extensions
In this section, we extend our benchmark model in three meaningful and realistic directions.
4.1 Groups with asymmetric valuations
In this variation of the model, we assume that the interest groups differ in their valuation of the final prize depending on which politician has won the election. Specifically, we assume that if candidate I wins the election, group i’s valuation of the prize is V whereas group j’s valuation is \(v<V.\) This way, we provide grounds for groups’ preferences for specific politicians, namely, a group supports a politician because, in case of winning, it values the contested prize more than in the case that the other politician wins.
We can interpret the difference of the prize valuations as a component that adds to a group’s valuation for one politician being elected as opposed to the other. Note that although politicians are motivated by winning the election, additional utility could capture an alignment between the group and politicians’ preferences. For instance, consider the case where a progressive politician wins the election. The politician is likely to bring bills that affect social issues, e.g., drug legalisation, abortion rights, etc. The lobby that supported this politician is possibly more concerned about these issues than the opposite one and, therefore, overall may have a greater total valuation of the final prize.
Following the analysis in Sect. 3, in this case, we have that at the lobbying stage, if politician I has won the election at the previous stage, the expected payoffs of groups i and j are
respectively.Footnote 14 The equilibrium lobbying efforts by the two groups are
and their corresponding payoffs
It goes without saying that once different valuations of the prize are introduced, the analysis of the rest of the game quickly becomes highly complicated (see Appendix B). Nevertheless, we can provide a numerical presentation of the results as well as some graphical examples.
Table 1 provides the equilibrium lobbying prices announced by the two politicians for different levels of groups’ prize valuations. We observe that, for a given level of price for the opposite groups,Footnote 15 the politicians announce a greater lobbying price for their supporting groups as the difference between V and v increases. In fact, for some levels of valuation, specifically for lower levels of v and greater levels of V, the politicians find it optimal even to announce a lobbying price greater for the group supporting them than for the opposing group. This occurs because the groups value the final prize, if their favourite candidate wins, sufficiently high that they are even willing to incur greater prices during the lobbying process.
However, the results from our benchmark model are preserved as the value of v goes up and the range of valuations becomes more narrow. In particular, we observe that for levels of v greater than 0.8, the politicians always choose to announce lower prices for their supporting groups than for the opposite ones regardless of the level of V. Finally, for equal levels of v and V, the table verifies the results from Sect. 3, i.e., \({\tilde{c}}_I\equiv c^{*}_I =\tfrac{1}{2}\left( \sqrt{5}-1\right) \approx 0.62.\)
Figure 2 provides a graphical representation of the two groups’ reaction functions for two different levels of range between v and V. In the first graph, we consider the case where \(v=0.3\) and \(V=0.4\) while in the second graph, we keep V at the same level as before but we assume that \(v=0.1.\) We can observe that when the difference between v and V is relatively small (first graph), in equilibrium, the politicians announce a lower price for their supporting group (\(c_I<c_{I,j}=1\)). This result indicates that if a group has not much to lose if the opposite politician wins—its value for the contested prize will be v which is not much lower than V—a politician has an incentive to announce a lower price for her favourite group in order to increase its expected payoff in case of winning and, therefore, incentivise her to contribute more in the election.
On the other hand, when the difference between the prize valuations is relatively big (second graph), the equilibrium prices announced by the politicians may be greater for their supporting groups than for the opposing groups (\(c_I>c_{I,j}=1\)). In this case, a group has definitely more to lose if the opposite politician wins since it will value the final prize quite low. Hence, the politicians, knowing this, afford to announce a greater price for their favourite group as it will still have the incentive to contribute to her in the election and, therefore, increase the probability to win the highly valued contested prize at the final stage.
4.2 Price setting with no commitment
Thus far, we have assumed that if the politicians win the election, they commit to the lobbying price announced at the pricing stage. In the following, we consider politicians who, once they win the election, might deviate and set the optimal price for the last stage of the game, i.e., equal prices for both groups.Footnote 16 For instance, term-limited politicians have higher chances to deviate from the announced prices compared to politicians who are going to participate in future elections and, probably, get punished by groups in case of no commitment to the announced price. In that case, maximising the expected payoff of the two groups, we can find that it is optimal for them to exert lobbying effort equal to \(\tfrac{1}{4}\) each and earn payoff equal to \(\tfrac{1}{4}\) each, as well. We assume, then, that with probability \(s\in [0,1]\) the two groups make lobbying efforts and earn payoffs given by (5) and (6), respectively, whereas with probability \(1-s,\) their efforts and payoffs are equal to \(\tfrac{1}{4}.\) We have, then, that at the election stage, the maximisation problem of group i is
The equilibrium contribution made by group i is, then,
where \(\frac{c_{I,i}}{c_{I,j}}\le \frac{c_{J,i}}{c_{J,j}}\) and \(x_i^*\) is given by (8). We observe that the lower the probability of commitment, the lower the contributions made by the two groups. For instance, if s is low, meaning that the politicians deviate from the announced prices and charge the two groups prices equal to each other with high probability, the groups find it optimal to decrease their contributions as, now, the expected potential advantage at stake is lower. The case \(s=1\) is the case of Sect. 3.
If the politician who has won the election deviates from the price she has announced, her utility from lobbying is equal to \(\frac{1}{2}.\) Politician I’s expected utility at stage zero is, then,
We observe that introducing the possibility that the politicians deviate from the announced price does not affect their probability of winning. Maximising the above quantity for both politicians with respect to the prices, we obtain the following result.
Proposition 3
Assume that politician I commits to the announced prices with probability \(s\in \left( \frac{1}{5},1\right] .\) In equilibrium, she announces the price ratio
and earns payoff \({\hat{R}}=\sqrt{s \left( 4s+1\right) }-2s.\)
It is not difficult to check that \({\hat{c}}_I<c_I^*\equiv \tfrac{1}{2}\left( \sqrt{5}-1\right) ,\) meaning that also, in this case, the politicians announce a lower lobbying price for the groups supporting them and, actually, a lower ratio than the one of the benchmark case. Since now there is some probability that the politicians, in case of winning the election, will deviate at the final stage and get a greater payoff, they have an incentive to announce a lower price ratio. By doing so, the politicians make the two groups more asymmetric at the final stage in case of commitment, and therefore, moderate the decrease in the received election contributions due to the possibility of deviation. Indeed, differentiating the price ratio with respect to s, we obtain that
which shows that the probability of commitment and the group asymmetry the politicians want to achieve go the opposite way. The greater the probability of commitment, the greater the price ratio and, hence, the lower the symmetry between the groups.
5 Conclusion
We have analysed lobbying access “pricing” in a game with two candidates and two interest groups. First, the candidates announce the lobbying prices they will charge if they win the election. Then, each group contributes to its favourite candidate to help her win the election. After the election, the two groups make lobbying efforts in order to affect the incumbent politician’s implemented policy.
We have obtained, endogenously, that an elected politician chooses to announce a lower lobbying price to the group that supported her during the election than to the group that supported the other candidate. We also illustrate how aligned candidates and groups, for instance due to similar preferences, interact. Broadly speaking, our results shed light on the strategic interaction between politicians and lobbies and are in line with the common view that some specific groups may be treated favourably by the politicians in power.
Notes
See, for instance, Baron (1994); Grossman and Helpman (1994, 1996). Two papers that study both combine campaign contributions and lobbying are Austen-Smith (1995) and Felli and Merlo (2012). However, Austen-Smith (1995) “abstracts from details of the electoral process” assuming that the probability that a candidate wins is exogenous and, thus, not affected by the campaign contributions she receives. Moreover, Felli and Merlo (2012) focus on groups lobbying elected politicians without considering campaign contributions by interest groups to favourite politicians.
We implicitly assume that a group only reveals information that is not potentially harmful to it. For instance, as mentioned in Austen-Smith (1998), Philip Morris would never report experiment results showing that smoking causes cancer.
We assume that contributions cannot be carried over to the next stage and, thus, the whole amount is spent at the election stage.
For a review of the literature on competition for access and lobbying with various tools, see Gregor (2017).
For the sake of tractability, in this study, we follow the literature that considers interest groups contributing only to one candidate and politicians who commit to the announced lobbying prices. In Sect. 4, we relax the latter assumption considering politicians who do not commit with certainty to the prices they have announced.
We require strictly positive prices so that the contest in the last stage is meaningful as well as to avoid additional assumptions and notation for the case of zero prices (see, for instance, Clark and Nilssen (2013) and Clark et al. (2018)). Note that in our setup, this assumption should not be a concern, as the politicians, given their payoff functions, would never choose to announce prices equal to zero at the pricing stage.
At the election stage, we assume that the probability that a party wins is given by a Tullock contest success function depending only on the efforts of the two groups. Jia (2008) and Jia et al. (2013) show that this CSF is microfounded when voters are impressionable with utility \(t^i\left( x_i,x_j,\theta ^i\right) =x_i\theta ^i,\) where \(\theta ^i\) is a random variable, independently drawn from an Inverse Exponential Distribution, that measures how much voter i is affected by campaign spending. See also Balart et al. (2018).
A similar intuition applies for the effect of a change in \(c_{I,j}\) on \(x_j^*.\)
A similar intuition applies for the effect of a change in \(c_{I,j}\) on \(r_I.\)
\(\varphi \approx 1.618\) is the golden ratio.
To keep the model neat, we do not introduce new notation. However,the variables in this section are different to the ones in the previous section.
Without loss of generality, we assume that \(c_{I,j}=1.\)
Recall that at the last stage of the game, the winner politician’s utility from lobbying is equal to
$$\begin{aligned} c_{I,i}y_i^*+c_{I,j}y_j^*=\frac{2 c_{i,i} c_{i,j}}{\left( c_{i,i}+c_{i,j}\right) {}^2}. \end{aligned}$$The above expression is maximised when the politician sets \(c_{I,i}=c_{I,j}\) yielding a payoff equal to \(\frac{1}{2}.\)
References
Austen-Smith D (1987) Interest groups, campaign contributions, and probablistic voting. Public Choice 54:123–139
Austen-Smith D (1995) Campaign Contributions and Access. Am Polit Sci Rev 89(03):566–581
Austen-Smith D (1998) Allocating Access for Information and Contributions. J Law Econ Organ 14(2):277–303
Balart P, Casas A, Troumpounis O (2018) Technological change, campaign spending and Polarization
Balart P, Flamand S, Troumpounis O (2016) Strategic choice of sharing rules in collective contests. Soc Choice Welf 46(2):239–262
Baron DP (1994) Electoral Competition with Informed and Uninformed Voters. Am Polit Sci Rev 88(01):33–47
Becker GS (1983) A Theory of Competition Among Pressure Groups for Political Influence. Q J Econ 98(3):371
Bennedsen M, Feldmann SE (2006) Informational lobbying and political contributions. J Public Econ 90(4–5):631–656
Besley T, Coate S (2001) Lobbying and Welfare in a Representative Democracy. Rev Econ Stud 68(1):67–82
Beviá C, Corchón LC (2013) Endogenous strength in conflicts. Int J Ind Organ 31(3):297–306
Clark DJ, Nilssen T (2013) Learning by doing in contests. Public Choice 156(1–2):329–343
Clark DJ, Nilssen T, Yngve J (2018) Dynamic Win Effects in Sequential Contests
Corchón LC, Serena M (2017) Contest theory. In: Corchón LC, Marini MA (eds) Handbook of game theory and industrial organization. Edward Elgar, Cheltenham, UK
Cotton CS, Déllis A (2016) Informational Lobbying and Agenda Distortion. J Law Econ Organ 32(4):762–793
Cotton CS, Li C (2018) Clueless Politicians: On Policymaker Incentives for Information Acquisition in a Model of Lobbying. J Law Econ Organ 34(3):425–456
Duggan J, Gao J (2020) Lobbying as a multidimensional tug of war. Soc Choice Welf 54(1):141–166
Ellis CJ, Groll T (2019) Strategic Legislative Subsidies: Informational Lobbying and the Cost of Policy. Am Polit Sci Rev 114(1):179–205
Epstein GS, Nitzan S (2006) The politics of randomness. Soc Choice Welf 27(2):423–433
Felli L, Merlo A (2012) Endogenous Lobbying. J Eur Econ Assoc 4(1):180–215
Fu Q, Lu J, Pan Y (2015) Team contests with multiple pairwise battles. Am Econ Rev 105(7):2120–2140
Gradstein M, Konrad KA (1999) Orchestrating Rent Seeking Contests. Econ J 109(458):536–545
Gregor M (2017) Lobbying Mechanisms. State, Institutions and Democracy: Contributions of Political Economy. Springer, Cham, pp 17–52
Grossman GM, Helpman E (1994) Protection for Sale. Am Econ Rev 84(4):833–850
Grossman GM, Helpman E (1996) Electoral Competition and Special Interest Politics. Rev Econ Stud 63(2):265
Jia H (2008) A stochastic derivation of the ratio form of contest success functions. Public Choice 135(3–4):125–130
Jia H, Skaperdas S, Vaidya S (2013) Contest functions: Theoretical foundations and issues in estimation. Int J Ind Organ 31(3):211–222
Konrad KA (2009) Strategy and Dynamics in Contests. Oxford University Press, Oxford
Konrad KA, Kovenock D (2009) Multi-battle contests. Games Econom Behav 66(1):256–274
Krueger AO (1974) The Political Economy Seeking of the Society. Am Econ Rev 64(3):291–303
Lohmann S (1995) Information, access, and contributions: A signaling model of lobbying. Public Choice 85(3–4):267–284
Martimort D, Semenov A (2008) Ideological uncertainty and lobbying competition. J Public Econ 92(3–4):456–481
Moldovanu B, Sela A (2006) Contest architecture. J Econ Theory 126(1):70–96
Nitzan S (1994) Modelling rent-seeking contests. Eur J Polit Econ 10(1):41–60
Nti KO (1999) Rent-seeking with asymmetric valuations. Public Choice 98:415–430
Potters J, van Winden F (1992) Lobbying and asymmetric information. Public Choice 74(3):269–292
Sasso G, Alexander D (2020) Campaign Spending and Lobbying
Tripathi M, Ansolabehere S, Snyder JM (2002) Are PAC Contributions and Lobbying Linked? New Evidence from the 1995 Lobby Disclosure Act. Bus Polit 4(02):131–155
Tullock G (1980) Efficient Rent Seeking. In Buchannan J, Tollison R, Tullock G (eds) Toward a Theory of Rent-Seeking Society, pages 97–112. College Station: Texas A&M University Presss
Wright JR (1990) Contributions, Lobbying, and Committee Voting in the U.S. House or Representatives. American Political Science Review, 84(2)
Acknowledgements
This article is based on the third chapter of my PhD thesis at Lancaster University. I am grateful to Orestis Troumpounis for his excellent supervision. Comments from Maggie Penn (editor) and four anonymous referees have significantly improved the quality of the paper and are much appreciated. I would also like to thank Carmen Beviá, Alexander Matros, Florian Morath, David Rietzke, Stergios Skaperdas, Eyal Winter and Dimitrios Xefteris for their useful comments. The paper has also benefited from comments by participants at the 8th RES-York Symposium and Mini-Courses on Game Theory, the 2017 Contests: Theory and Evidence (Norwich), the 3rd Lancaster Game Theory Conference, the 2018 NWSSDTP Economics Conference 2018 (Liverpool), the 1st Lancaster PhD Summer School on Applied Microeconomics and the seminar audience in Lancaster. Any errors are my own.
Funding
Open access funding provided by University of Innsbruck and Medical University of Innsbruck.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Appendix
Proof of Proposition 1
Differentiating eq. (7) with respect to \(x_i,\) yields
which is negative for \(\frac{c_{I,i}}{c_{I,j}}> \frac{c_{J,i}}{c_{J,j}}.\) Thus, under this condition, the payoff function of group i is decreasing in its contribution and, therefore, it chooses to contribute the least possible, i.e., \(x_i^*=0.\)
Now, setting (12) equal to zero, we get
Solving the above equation for \(x_i,\) we obtain group i’s best response function, namely
where we require \(\frac{c_{I,i}}{c_{I,j}}\le \frac{c_{J,i}}{c_{J,j}}\) for the quantity in the square root to be non-negative. Notice that for \(\frac{c_{I,i}}{c_{I,j}}= \frac{c_{J,i}}{c_{J,j}},\) since the efforts cannot be negative, we have \(x_i^*=0.\)
Setting, without loss of generality, \(I=A,\,J=B,\,i=a\) and \(j=b,\) we obtain the system of equations
Let us set \(\left( c_{A,a}+c_{A,b}\right) \left( c_{B,a}+c_{B,b}\right) =Q,\,c_{A,b} c_{B,a}-c_{A,a} c_{B,b}=R,\, c_{A,a} c_{B,b}+c_{A,b} \left( c_{B,a}+2 c_{B,b}\right) =S\) and \(c_{B,b} c_{A,a}+c_{B,a} \left( c_{A,b}+2 c_{A,a}\right) =T.\)
Substituting \(x_b\) given by the second equation of (13) to the first one and after some algebra, we obtain
Substituting \(x_a\) given by the above equation to the second equation of (13), we obtain
Replacing \(Q,\,R,\,S,\,T\) with their values in terms of prices and after conducting simple algebra, we obtain the results in Proposition 1.
The second-order sufficient condition for a maximum is
which is true, fact that completes the proof. \(\square\)
Proof of Proposition 2
To solve the candidates’ maximisation problem, we find the first-order conditions of eq. (9) which are
The above first-order conditions for \(c_{I,i}\) and \(c_{I,j}\) yields the following reaction functions.
Solving the above system of equations simultaneously for the two candidates yields infinite solutions which satisfy the equation in the proposition. Substituting this result to eq. (8), eq. (7) and eq. (9), we find the expected contributions candidates receive, the expected payoffs of the two groups and the two candidates’ expected utility from lobbying, respectively.
To guarantee that these solutions constitute a Nash equilibrium, we proceed as follows. Assume that candidate J sets \(c_J^*=\tfrac{1}{2}\left( \sqrt{5}-1\right) .\) We will check whether candidate I has an incentive to set a lobbying price ratio different from \(c_I^*=\tfrac{1}{2}\left( \sqrt{5}-1\right) ,\) say \(c'_I=k>0,\) and gain utility greater than \(\sqrt{5}-2.\) Substituting \(c_{J,j}=\tfrac{1}{2}\left( \sqrt{5}-1\right) c_{J,i}\) and \(c_{I,i}=kc_{I,j}\) to candidate I’s objective function, eq. (9), and after some algebra, we obtain
Consider the function \(f\left( k\right) =k\left[ \left( \sqrt{5}-1\right) k+2 \sqrt{5}\right] -\left( \sqrt{5}-2\right) \left( 1+\sqrt{5}\right) \left( k+1\right) ^3,\) where \(k\in \left( 0,\infty \right) .\) Differentiating f, we have \(f'\left( k\right) =k \left[ 3\left( \sqrt{5}-3\right) k+8 \sqrt{5}-20\right] +5\sqrt{5}-9\) which is equal to zero when \(k=\tfrac{1}{2}\left( \sqrt{5}-1\right) .\) The second derivative is \(f''\left( k\right) =-6\left( 3-\sqrt{5}\right) k-\left( 20-8\sqrt{5}\right) <0,\) so f is concave, meaning that at \(k=\tfrac{1}{2}\left( \sqrt{5}-1\right) ,\,f\) is maximised. At this point, we also have that \(f\left( \tfrac{\sqrt{5}-1}{2}\right) =0\) which indicates that the function cannot be greater than zero. Thus, candidate I does not have an incentive to deviate. \(\square\)
Proof of Proposition 3
The FOC of group i’s maximisation problem at the election stage is
Following a similar process as in the proof of Proposition 1, we obtain the solution \({\hat{x}}_i=sx_i^*.\)
The SOC of group i’s maximisation problem at the election stage is
which is satisfied given the condition \(\frac{c_{I,i}}{c_{I,j}}<\frac{c_{J,i}}{c_{J,j}}.\)
Regarding the two candidates, the FOC of candidate I’s maximisation problem is
Following a similar process as in the proof of Proposition 1 and after some algebra, we find that, in equilibrium,
Assuming positive prices, we require that
By substituting (14) into (11), we also find that the two candidates’ expected utility is equal to \(\sqrt{s \left( 4s+1\right) }-2s.\)
The SOC of candidate I’s maximisation problem is
Plugging (14) into the above inequality, we get
which is true, indicating that at the equilibrium level of prices, candidate I’s utility function has a local maximum. Since \(R_I\left( c_{I,i}\right)\) is a continuous function with one critical point and that critical point is a local maximum, then, it is also a global maximum. \(\square\)
B Appendix
1.1 Comparative statics of \(x_i^*\)
Differentiating \(x_i^*\) with respect to \(c_{I,i},\) we obtain
since \(c_{I,j}c_{J,i}>c_{I,i}c_{J,j}\) and, therefore, \(2c_{I,j}c_{J,i}>c_{I,i}c_{J,j}.\)
Differentiating \(x_i^*\) with respect to \(c_{I,j},\) we have
since \(c_{I,i}c_{J,j}<c_{I,j}c_{J,i}\) and, therefore, \(c_{I,i}c_{J,j}<2c_{I,j}c_{J,i}.\)
Differentiating \(x_i^*\) with respect to \(c_{J,j},\) we have
Some manipulation of the above expression yields that
Differentiating \(x_i^*\) with respect to \(c_{J,i},\) we have
which yields that
1.2 Behaviour of \(r_I\)
Differentiating eq. (9) with respect to \(c_{J,j},\) we have
while differentiating with respect to \(c_{J,i},\) we get
Now, if we differentiate eq. (9) with respect to \(c_{I,i},\) we obtain
Manipulation of the above equation yields
Similarly, differentiating eq. (9) with respect to \(c_{I,j},\) we have
and
1.3 Maximisation problem of groups with asymmetric valuations
The election game is similar to the one of the basic model including the payoffs from (10) instead. The FOC for group i is
which yields the equilibrium contribution by group i
Let us assume that \(c_{I,j}=c_{J,i}=1.\) Substituting the above expression in the candidate’s maximisation problem and differentiating w.r.t. \(c_{I,i}\), we obtain candidate I’s FOC, i.e.,
The above FOC, together with the assumption that \(c_{A,a}=c_{B,b}\) since the game is symmetric, gives us the numerical and graphical results of Sect. 4.1. Also, the SOC are satisfied at the levels of the prices in Table 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Protopappas, K. Optimal lobbying pricing. Soc Choice Welf 59, 37–61 (2022). https://doi.org/10.1007/s00355-021-01383-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-021-01383-2