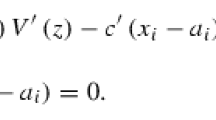Competitive balance when winning breeds winners

Abstract

In contest settings, heterogeneity between contestants generally leads to low effort provision, and many instruments have been suggested to restore competitive balance. We suggest that heterogeneity may evolve depending upon the outcome of previous contests. Restoring competitive balance in this setting is challenging, and we consider the choice faced by a principal who can distribute a prize fund over two consecutive all-pay auction contests. Contestants are heterogeneous in the sense that one of them has a head start in the first contest. The winner of contest one gains the stage prize and a net head start in contest two; the size of this net head start also varies between players. The head start of the early leader can be increased, neutralized or overturned. The principal aims to maximize total effort. We show how the potential head start that the initial underdog can gain is critical in determining expected efforts. When this parameter is small, the principal can do no better than running a single contest. When the initial underdog can catch up and surpass the first-contest favourite, there is scope to do better. Indeed, it is possible to completely neutralize the initial heterogeneity and capture all of the surplus from the players, inciting a level of expected effort equal to the prize value. Competitive balance is achieved by a judicious division of the prize budget.

1 Introduction

Competitive situations are often characterized by the fact that winning breeds winners, making success self-fulfilling. When competition is modelled as a contest, it has long been established that heterogeneity in the participants may lead to outcomes involving low effort provision.¹ Adding to this the fact that winners may evolve and gain further advantage in subsequent contests can exacerbate this problem. How then should an incentive scheme be organized to ensure that laggards do not simply give up, leaving the spoils to a superior competitor? In this paper, we discuss this question in a contest setting where a principal has a prize fund available and must choose whether to put all of it in a single contest or to spread it out over several contests. We assume a synergy between the contests which reflects the fact that success in a previous contest affects the likelihood of success in the current one. We find that the optimal prize division depends upon contestants’ heterogeneity, in particular on the interplay of their ex-ante heterogeneity and the difference in how they respond to an early win to affect that ex-ante heterogeneity. In a case with two participants, when one contestant’s ex-ante head start is small relative to the other contestant’s ability to use an early win to catch up with and even overtake the rival, the principal should spread the prize fund over more than one contest in order to maximize participants’ total expected efforts. Indeed, our most striking result is that the principal can, in some cases, use the prize division to even out the ex-ante heterogeneity between the contestants, capturing all of their surplus.

Contest theorists have been interested in how competitive balance can be improved in situations where contestants do not meet on a level playing field. Several instruments have been considered, such as the form of the contest success function with different types of biases and/or differential taxation of rewards (Mealem and Nitzan 2016), adjusting the prize structure (Sisak 2009), and introducing limits on efforts (Che and Gale 1998). This levelling is needed in order to avoid the discouragement effect where those lagging behind simply give up since this is detrimental to the interests of an effort-maximizing principal (Konrad 2012; Konrad and Kovenock 2009). The stage game that we consider is a complete-information all-pay auction with a head start, which can lead to a laggard giving up if the opponent’s head start is sufficiently large. This head start may reflect for example an incumbency advantage in political competition, a prior investment made by a player, or some technological superiority. When one player has a head-start advantage, he can expend effort at a lower level than the opponent and still win the prize.

In their model of a patent race, Fudenberg et al. (1983) show that an arbitrarily small lead will preclude competition as long as the favorite has an advantage at each stage. In order to achieve competition, it is necessary for a laggard to be able to leapfrog the initial leader at some stage in the race.² We utilize this in our two-contest competition, by assuming that the winner of the first contest receives a boost or momentum before the second one. If the player with the ex-ante head start wins the first contest, then he augments this head start before the second one; if the initial laggard wins contest one, then he reduces the head start of the leader, and may even get a head start himself. The momentum created by a win in contest one may be due to the physiological or psychological effects of winning, or due to increased access to material resources. Our model also captures the possibility that a win by the initially favored player may give him a lower head start in the second contest than the first; the win still ensures a head start to the player, but of lower magnitude. This could be caused by fatigue, for example, which has been investigated theoretically by Ryvkin (2011) and experimentally by Angelova et al. (2020).

The “ winner effect” has been well documented in biology, with the male of a species experiencing an increase in the testosterone level following a win in a (territorial or survival) contest, while the loser has a reduced level of testosterone (Chase et al. 1994). Hence, the winner is in better physiological shape to compete in the next contest, as documented in male judo competitions by Cohen-Zada et al. (2017) and in male tennis competitions by Page and Coates (2017) and Gauriot and Page (2019). Rather than affecting the physiology of competitors, a successful contestant may gain a psychological boost (Krumer 2013). Batters in baseball perceive the ball as bigger when they have had recent success in hitting, for instance (Witt and Proffitt 2005). The case for the existence of psychological momentum is persuasively made by Iso-Ahola and Dotson (2014), who evaluate previous attempts to identify this phenomenon in sports and other contexts. On the other hand, successful players in some competitions may gain access to material goods that make competing easier. In sales-force management, more successful agents may be given less administrative duties, better access to back-office resources, more training than the less successful, and better territories; see, e.g., Skiera and Albers (1998), Farrell and Hakstian (2001), and Krishnamoorthy et al. (2005).

The phenomenon that winning creates winners may be recognized by scientists who compete for research grants. As noted by Gallini and Scotchmer (2002; p. 54): “ [F]uture grants are contingent upon previous success. The linkage between previous success and future funding seems even more specific in the case of the National Science Council” . Those who succeed in obtaining research grants may experience an increase in status, winning a grant to fund current work and build up a competent research team, which again improves their chance of winning further grants. Losing teams must use time and resources in seeking presumably inferior forms of funding; in sum, this gives an advantage in future rounds of competition for scarce research funding. Strumpf (2002) suggests that in political competitions, the winner of a first election round may gain additional media attention and funding from campaign contributors, which helps to build future momentum. Mehlum and Moene (2016) note that incumbency can be a source of advantage in the current situation, and in the future. These can be seen as examples of the Matthew effect, coined by Merton (1968) to describe situations in which the rich get richer or where success breeds success. An initial advantage can be self-amplifying, and such mechanisms are prevalent whether we consider “ economic wealth, political power, prestige, knowledge, or in fact any other scarce or valued resource” (Perc 2014; p. 1). Faced with a contestant with initial advantage, it may seem likely that the laggard will give up. How might the principal divide his prize fund to mitigate this effect? We show that the answer depends on the size of the initial advantage, and how this advantage evolves; there is no guarantee that the initial leader will maintain the advantage in the future. In his extensive review of the Matthew effect, Rigney (Rigney 2010; p. 1) states that “[i]nitial advantage does not always lead to further advantage, and initial disadvantage does not always lead to further disadvantage”. By allowing for the possibility that an initially disadvantaged player can catch up and surpass the initial leader, we show that the principal can incite the contestants to exert so much effort that they dissipate the whole value of the prize.

Our modeling choices and analysis are based on two premises which feature prominently in the contest literature: a stage game consisting of a complete-information two-player all-pay auction with a head start, and the principal wishing to maximize the total expected level of effort. Head starts in a single contest have been analyzed by several authors, notably by Konrad (2002), Meirowitz (2008), Kirkegaard (2012), Li and Yu (2012), Hirata (2014), Segev and Sela (2014), Siegel (2014), and Franke et al. (2018). Among these papers, Konrad (2002) and Hirata (2014) discuss two-stage situations where players can take actions in the first stage that create head starts in the second stage, while Li and Yu (2012) and Franke et al. (2018) discuss the principal’s optimal choice of head start in a single contest in order to maximize expected effort. Our framework differs from these approaches: it is not the actions in the first round that determine the head start in the second, rather it is the act of winning, and the boost that this provides. Also, the principal in our model controls the budget division, and not the head start advantage held by a player. While there exist cases where the principal may legitimately give a head start to a contestant, affirmative action being one, there are other cases where granting a head start may not be deemed feasible. One such case is the running of a research contest in which favoritism is difficult. Here, the principal must use the budget division in lieu of a more direct instrument to balance the competition.

With two players and a single contest, Li and Yu (2012) show that the optimal head start is given to the player with the lower valuation at an amount equal to the difference between the valuations of the two players. This shifts the stronger player’s equilibrium effort distribution upwards by the amount of the head start, whilst that of the weaker player is unchanged. Hence, the stronger player has an increase in effort that offsets the head start, and this increase accrues to the contest organizer.³ The logic behind the result of Li and Yu (2012) points to one of the mechanisms at work in our story: while the principal cannot manipulate the head start directly, he can affect the (continuation) valuations of the players of winning by a judicious division of the prize mass across contests. The principal must seek to balance out the valuations and the head start over the course of the two contests, and the design problem is not trivial. In setting the stage prizes, the principal must be mindful of the fact that the relationship between the head start and the prize in a stage contest will determine whether the players will exert effort, or if one player gives up, as well as the magnitude of efforts. The fact that the principal can directly take actions that lead a player to give up completely is an interesting knife-edge problem that has not previously been examined. The principal must also take account of how the head start will evolve for various outcomes of the first contest.

Critical for our results is the relative ability of the initial laggard to turn a win into a head start. The main case that we consider involves each player getting a positive boost from winning the first contest. We find that, when the laggard gains a small head start following a win, the principal’s optimal choice is to spend all the money in the first contest, which in practice means running only that contest. Gaining a small head start does not incentivize the laggard to exert much effort in the first contest, and also the leader can then slack off. If the laggard can gain a sufficiently large head start before contest two, the principal prefers to run two contests. How much surplus he can extract from the players depends on the extent that the initial laggard can turn a win into a head start; we show when expected effort is increasing in this parameter, and when the whole prize fund is dissipated.

A further case that we consider is when the initial leader, because of decay, ends up with a head start following a first contest win that is positive, but still smaller than his initial head start. Now it is the case that the principal will always prefer to run two contests, and for a large potential head start for the initial laggard, the previous results go through. When the head starts in the second contest are small, however, the heterogeneity between the players is reduced; since heterogeneity leads to lower expected effort, the principal puts the whole prize fund into the second contest since it is more even. The first contest is fought purely for position.

Clark and Nilssen (2018) have looked at win-loss dynamics in a long series of contests with a common stage prize and ex-ante symmetric contestants. Ex-ante symmetry implies that the whole of the rent is dissipated, so that the design problem considered in the current paper does not exist there; rather, they consider situations in which the lagging player will give up, and those in which he will fight intensely to reduce the size of the disadvantage. Clark and Nilssen (2020) consider a similar design problem to this paper, but with a productivity bias instead of a head start.⁴ Some results for full rent dissipation are achieved for competitions longer than two rounds in that paper, since one does not meet the possibility of zero efforts in any stage game; the knife-edge problem is hence not a complicating issue in that paper.⁵

This paper is organized as follows. The model framework is presented in Sect. 2, and the solution and main result in Sect. 3 . We then consider in Sect. 4 how the results are affected when the head start for the initial leader can be reduced after he wins the first contest. Section 5 concludes. All proofs are contained in the “Appendix”.

2 The model

A risk-neutral principal has a prize fund of size 1 to distribute among two risk-neutral contestants. He does this by setting up two consecutive all-pay auctions with a prize of $1-v$ available in the first and a prize of v in the second, where $0\le v\le 1$.⁶ In the first contest, we assume that one of the players—player 1 without loss of generality—has a head start $h\in \left( 0,1\right)$, which means that this player can win the contest with less effort than the rival. Specifically, we assume the following contest success function for player $i=1,2,$ in contest 1, given efforts $x_{i,1}$:

$$\begin{aligned} p_{1,1}\left( x_{1,1},x_{2,1}\right)= & {} \left\{ \begin{array}{ll} 1&{}\quad \text { if }h+x_{1,1}>x_{2,1} \\ \frac{1}{2}&{}\quad \text { if }h+x_{1,1}=x_{2,1} \\ 0&{}\quad \text { if }h+x_{1,1}<x_{2,1} \end{array} \right. \\ p_{2,1}\left( x_{1,1},x_{2,1}\right)= & {} 1-p_{1,1}\left( x_{1,1},x_{2,1}\right) \end{aligned}$$

The winner of the first contest gets not only the stage prize $1-v$, but also a net head start in the second. This net head start captures different situations that can arise after the first contest. A win by the initially favoured player 1 that leads to a larger head start in contest two indicates that he has received a positive momentum from winning; if the net head start is lower than in contest one but still positive, then he remains the favorite, but the initial lead has decayed or been reduced due to fatigue. If player 2 wins the first contest, two possibilities arise: a positive net head start for this player means that winning has allowed him to overtake the head start of the initial winner; a negative net head start for player 2 indicates that winning has made him catch up some, but not all, of the initial lead.

Denote by $z_{i}$ the net head start in contest two of player i who has won the first contest. Should player 1 win the first contest, he gets the head start $z_{1}>0$ in contest two; by assuming that the head start of player 1 is positive following a win, we ensure that he maintains some momentum from contest one to two. If $z_{1}>h$ then he has augmented the initial lead, becoming more of a favorite in contest two.⁷ On the other hand, if $h>z_{1}>0$, he still has an advantage at the beginning of the second contest, but the head start has decayed compared with contest one.⁸ In the second contest with effort $x_{1,2}$, player 1 has a contest score of $z_{1}+x_{1,2}$; the score of player 2 will simply be his effort in contest two, $x_{2,2}$.

Should player 2 win the first contest, his head start in the second one modifies his effort $x_{2,2}$ by $z_{2}$, giving him a contest score of $z_{2}+x_{2,2}$; player 1 in this case has a second-contest score of $x_{1,2}$. If $z_{2}>0$, then player 2 becomes favorite in contest two. If $z_{2}<0$, then player 1 has lost the first contest, but retains a lead going in to the second; it is natural, however to assume that some of the lead has been eroded by player 2 winning the first contest, so that $\left| z_{2}\right| \le h$ in this case. The second-contest score of player 1 will then be $x_{1,2}$, while player 2 has a score of $x_{2,2}+z_{2}<x_{2,2}$, with $0>z_{2}\ge -h$.⁹

No efforts are carried over from the first contest to the second. The player with the largest score in contest two is designated the winner of that contest, gaining the stage prize v. The game then ends.

Formally, let $p_{i,2}\left( x_{1,2},x_{2,2};j\right)$ indicate the win probability for player i in the second contest, given that player j has won the first, $i,j\in \left\{ 1,2\right\}$.

$$\begin{aligned} p_{1,2}\left( x_{1,2},x_{2,2};1\right)= & {} \left\{ \begin{array}{ll} 1&{}\quad \text { if }z_{1}+x_{1,2}>x_{2,2} \\ \frac{1}{2}&{}\quad \text { if }z_{1}+x_{1,2}=x_{2,2} \\ 0&{}\quad \text { if }z_{1}+x_{1,2}<x_{2,2} \end{array} \right. \\ p_{2,2}\left( x_{1,2},x_{2,2};1\right)= & {} 1-p_{1,2}\left( x_{1,2},x_{2,2};1\right) , \end{aligned}$$

and

$$\begin{aligned} p_{1,2}\left( x_{1,2},x_{2,2};2\right)= & {} \left\{ \begin{array}{ll} 1&{}\quad \text { if }x_{1,2}>z_{2}+x_{2,2} \\ \frac{1}{2}&{}\quad \text { if }x_{1,2}=z_{2}+x_{2,1} \\ 0&{}\quad \text { if }x_{1,2}<z_{2}+x_{2,1} \end{array} \right. \\ p_{2,2}\left( x_{1,2},x_{2,2};2\right)= & {} 1-p_{1,2}\left( x_{1,2},x_{2,2};2\right) . \end{aligned}$$

In what follows, we shall suppress the effort arguments in the probability functions, writing simply $p_{i,2}(j)$.

Similarly, denote by $\pi _{i,2}\left( j\right)$ the expected payoff function of player i in the second contest, given that j has won the first, $i,j\in \left\{ 1,2\right\}$. Then

$$\begin{aligned} \pi _{i,2}\left( j\right) =p_{i,2}\left( j\right) v-x_{i,2}, \end{aligned}$$

since the loser gains 0 in this final contest. Hence, contest two is an all-pay auction with common valuations, and with a head start to one of the players (determined by the outcome of the first contest). Contest one, on the other hand, is an all-pay auction with a common stage prize, continuation values that depend on the course of play, and a head start of size h to player 1. Denoting the expected equilibrium payoff in contest two with an asterisk, we can write the expected payoff function of player i in contest one as

$$\begin{aligned} \pi _{i,1}= & {} p_{i,1}\left[ 1-v+\pi _{i,2}^{*}\left( i\right) \right] +\left( 1-p_{i,1}\right) \pi _{i,2}^{*}\left( j\right) -x_{i,1} \nonumber \\= & {} \pi _{i,2}^{*}\left( j\right) +p_{i,1}W_{i,1}-x_{i,1},\ i\ne j, \end{aligned}$$

(1)

where

$$\begin{aligned} W_{i,1}:=1-v+\pi _{i,2}^{*}\left( i\right) -\pi _{i,2}^{*}\left( j\right) . \end{aligned}$$

Should player i win the first contest, he gains the stage prize $1-v$ and the payoff that the contest-one winner expects in the second contest, $\pi _{i,2}^{*}\left( i\right)$. If player i loses the first contest, then he gains no stage prize and expects $\pi _{i,2}^{*}\left( j\right)$ in contest two. $W_{i,1}$ is thus a measure of what player i has to fight for in the first contest.

Lemma 1 in Section A1 in the “Appendix” gives the general solution of an all-pay auction with asymmetric valuations and a head start. Effort in such a contest is driven by the relative size and direction of the difference in the contestants’ valuations and the head start to the advantaged player. Consider contest two in which there is no difference in the players’ valuations of winning. If the head start of the favored player in contest two is at least as large as the value of the second-contest prize, then the laggard will never find it profitable to exert effort enough to catch up the head start. Hence each player has zero effort, and the player with the head start wins the second contest. If the second-contest prize is larger than the head start, then the players will exert effort chosen from mixed strategies, and each will have a positive probability of winning. However, only the leader will have a positive expected payoff (in the magnitude of the head start), whilst the laggard expects zero.

In contest one, player 1 has a head start of h. If $h\ge W_{2,1}$, then player 2 cannot profitably catch up the head start and both players have zero effort with player 1 winning the first contest without effort. Hence, the principal must ensure that the prize structure is set so that $W_{2,1}>h$ in order to get positive effort in the first contest. One particularly useful result from the “Appendix” is that, for $W_{2,1}-W_{1,1}\le h<W_{2,1}$ , total efforts in contest one are

$$\begin{aligned} Ex_{1,1}^{*}+Ex_{2,1}^{*}=W_{2,1}-h+\frac{\left( W_{2,1}^{2}-h^{2}\right) \left( W_{2,1}-W_{1,1}\right) }{2W_{1,1}W_{2,1}}. \end{aligned}$$

(2)

3 Optimal prize division

Given the structure of the game, the principal wishes to distribute the fixed budget between the two contests in order to obtain the most expected effort in aggregate. Effort in the first contest is affected by the amount of the asymmetry (h), the stage prize, and the value of the continuation payoff which is in turn dependent on the potential head starts that each player can achieve. Intuitively, saving more of the prize fund for the second contest will increase the efforts in that contest. However, the efforts in that contest will also be affected by the direction and magnitude of the head start that evolves after the first contest.

The two-contest model is solved by backwards induction. A key ingredient is Lemma 1 in Section A1 in the “Appendix”; this considers a static all-pay auction where player 1 has a head start of $\Delta >0$, and the players value the prize at $V_{1}$ and $V_{2}$, respectively. It is shown that, if $V_{1}-V_{2}+\Delta >0$, then player 1 expects a payoff in equilibrium of exactly this size, and player 2 expects zero; if, on the other hand, $V_{2}-V_{1}-\Delta >0$, then this is the payoff of player 2, and player 1 expects zero. This is used to calculate the equilibrium efforts and payoffs in contest two, and then insert these into (1). The same method is then used for computing the solution to the first contest. In equilibrium, only one of the players expects a positive payoff whilst the rival expects zero. Since the size of the prize fund is fixed at 1, the total amount of effort in equilibrium can be recovered by subtracting the payoff from the total prize.

Denote $Ex^{*}$ as the sum of expected effort by both players in both contests. We first consider the case in which a win by the initial leader gives him a greater net head start in the second contest than he had in the first. The following Proposition solves for the optimal division of the principal’s budget between the two contests.

Proposition 1

Consider a sequence of two all-pay auctions with two players and a total prize budget equal to 1, so that the prize in the second contest is $v\in \left[ 0,1\right]$ and the prize in the first contest is $1-v$. Let player 1 have a head start in contest one of $h\in (0,1)$, and let player i’s net head start in contest two be $z_{i}$ if he won contest one, for $i\in \left\{ 1,2\right\}$, where $z_{1}\in \left( h,1\right)$, and $z_{2}\in \left[ -h,1\right)$. A principal who wants to maximize total expected effort over the two contests should set v as follows:

• (i) If $-h\le z_{2}\le 0$, then $v=0$ is optimal, and $Ex^{*}=1-h$.

• (ii) If $0<z_{2}\le z_{1}$, then any $v\in [0,z_{2}]$ is optimal, and $Ex^{*}=1-h$.

• (iii) If $z_{1}<z_{2}<h+z_{1}$, then any $v\in [z_{2},1]$ is optimal, and $Ex^{*}=1-\left( h+z_{1}\right) +z_{2}$.

• (iv) If $h+z_{1}\le z_{2}<1$, then $v=h+z_{1}$ is optimal, and $Ex^{*}=1$.

Note that we, in Proposition 1, put upper limits on the head starts in contest two that ensure that the prizes in parts (ii), (iii), and (iv) are less than the budget limit of 1 and that the total expected effort in part (iii) is positive.¹⁰

In case (i), even if player 1 loses the first contest, he still has a head start in contest two, albeit reduced compared to the initial situation. In the other cases, it is the winner of contest one that has the head start in contest two.

Proposition 1 delineates cases when the principal can influence the players by the budget division, and when this is not possible. Key for the result is the extent to which the contest-one laggard can use a win to build a head start over the initial leader. If player 2, following a win in contest one, achieves less of a head start in contest two than player 1 , then case (i) or case (ii) occurs and the principal gets the level of expected effort that can be achieved in a single all-pay auction with a prize of 1 and a head start of h. When the initial leader retains some advantage even if he loses the first contest (case i), the principal does not want to incite effort in both contests, preferring to run a single contest ($v=0$) and getting the amount of effort $1-h$.¹¹ Case (ii) illustrates that this effort level can also be achieved by running two contests where the amount saved for the second contest lies in the interval $\left[ 0,z_{2} \right]$; if it is costly to run several contests, then a single contest is preferred.

Achieving more effort in expectation than this is dependent on player 2 developing a sufficiently large head start following a win, as shown in cases (iii) and (iv), with the latter providing the most striking result. Not only can the principal use the budget division to even out differences between the competitors, it can be done in such a way as to dissipate the whole value of the prize. In case (iv), the initially disadvantaged player has a potential head start in the second contest that is larger than the sum of the head starts achievable by player 1: $z_{2}\ge h+z_{1}$. A judicious setting of the prize division, saving $v=h+z_{1}$ for the second contest, allows the principal to balance the first contest in spite of the initial asymmetry due to the head start. The disadvantaged player has more to fight for—as outlined in detail below—which makes him exert a high level of effort in spite of lagging behind at the start; this incites the advantaged player to exert effort also, and in sum the expected efforts equal the total value of the prize budget. When this is not possible, the principal can still achieve more effort in expectation than a single contest as long as the potential head start to player 2 in contest two is larger than that of the rival: $z_{2}>z_{1}$ (case iii).

Fig. 1

Total expected effort

Figure 1 illustrates the connection between the potential head start of player 2 and the total expected effort over the two contests. Whilst we have set up the possibility that the principal may use two contests in order to solicit the most effort, it is fully possible to award the whole prize in the first one. As noted above, total expected effort here is $1-h$, which forms a minimum effort that the principal seeks to increase by manipulating the prize instrument. This is only possible when a win for player 2 gives a sufficient leap past player 1 in terms of head start, should player 2 win the first contest. From Fig. 1, it is clear that if player 2 can at least catch up the rival’s head start ($z_{2}>z_{1}$) then the principal can achieve more expected effort than $1-h$, and the whole surplus is captured for $z_{2}>h+z_{1}$. If the head starts of player 1 are too large in sum ($h+z_{1}>1$), then the full dissipation result cannot be achieved, and case (iii) gives the best possible solution for the principal.

Figure 2 depicts the optimal prize $v^{*}$ in the second contest, as well as the types of contest behavior that one may see there. The proof of Proposition 1 relies in part on looking at the patterns of behavior that can arise in each contest. If there is no effort in contest one, then player 1 wins $1-v$ and gets a head start in contest two of $z_{1}$. In contest two, each player has the same valuation of the prize, and efforts are $1-z_{1}$. Since $z_{1}\ge h$, this is not greater than what can be achieved by running a single contest with $v=0$.¹² This means that we can limit the search for optimal budget divisions to cases in which there is effort in the first contest. We delineate four cases depending on the second contest:

• (A) Effort in contest two whoever wins the first;

• (B) No effort in contest two;

• (C) Effort in contest two only if player 2 has won the first;

• (D) Effort in contest two only if player 1 has won the first.

The areas A, B, C, and D are marked in Fig. 2. If player 1 wins the first contest, then there will be effort in contest two as long as $v>z_{1}$ ; effort in contest two is ensured following a win by player 2 if $v>z_{2}$ . In the areas marked by A in Fig. 2, both of these inequalities hold, and there is effort in contest two whoever wins the first. In area D, $z_{2}>v>z_{1}$, and effort will only be made in contest two following a win by player 1. Cases B and C can occur also when $z_{2}<0$, so that the lead of player 1 is reduced but not overturned following a win by 2. When $v<z_{1}$, no effort is made following a win by player 1; if v is below the line marked $v=-z_{2}$ for $z_{2}<0$, or below $v=z_{2}>0$, there is no effort in contest two following a win by player 2. Hence, area B gives parameter combinations that give no effort in the second contest whoever wins the first. The remaining area C is such that there will be effort in contest two only after a win for player 2.

Fig. 2

Optimal second contest prize

In Fig. 2, the optimal second-contest prize $v^{*}$ can be seen for each of the cases of Proposition 1, depending on the propensity of player 2 to turn a win into a head start as measured by $z_{2}$. When player 2 is the underdog in contest two even if he wins the first ($-h<z_{2}\le 0$), then $v^{*}=0$, which is case (i). The principal’s optimal choice in cases (ii) and (iii) is a range of contest-two prizes, represented by the checkered areas in Fig. 2; if player 1 stands to gain a larger head start from a first contest win than player 2, then the second contest prize is limited. If player 2 has the larger potential head start in contest two, then higher prizes are used in contest two, and these give incentives to effort above the single contest case. Finally, when player 2 can potentially build a big lead, $z_{2}\in [h+z_{1},1)$, the optimal second round prize follows a specific rule given by $v^{*}=h+z_{1}$; this is case (iv) of the Proposition.

For low values of the potential head start for the disadvantaged player 2, $z_{2}\in [-h,z_{1})$, the principal can do no better than run a single contest. In the other cases, it is interesting to consider how much of the prize fund is saved for contest two. In case (iii), a range of possibilities occurs since the principal can choose the second-contest prize from an interval. In the extreme, he can distribute the whole prize mass in the second contest, so that the first is simply a contest for position. In case (iv), the prize must be set at a certain level in order to gain the maximum level of total expected efforts; the rule is simple, since the value of the second contest prize is just the sum of the head starts that the advantaged player 1 can achieve. The larger the sum of head starts for this player, the more of the prize is saved for the second contest.

The most striking result is contained in case (iv), since this represents full prize dissipation despite the initial heterogeneity between the contestants and the different ways in which this heterogeneity can evolve over the two contests. The optimal prize structure here induces effort in contest two only if player 1 wins the first. In the proof of Proposition 1 in the “Appendix”, we show, for this case, that the initial head start of player 1 is completely cancelled out by the induced difference in the players’ valuations in the first contest: $h=W_{2,1}-W_{1,1}$, and hence neither player expects a positive surplus.¹³ With a prize of $z_{1}\le v\le z_{2}$ in contest two, the players exert effort in that contest only if player 1 wins the first, in which case the players compete for the same prize (v) in contest two; player 1 expects a second-contest payoff of $z_{1}$, and player 2 expects zero. Hence, total expected effort in the second contest, by part (ii) of Lemma 1 in the “Appendix”, equals $v-z_{1}$. Seen from the first contest, player 1 has a value of winning of $1-v$ (the stage prize in the first contest) plus $z_{1}$ from contest two: $W_{1,1}=1-v+z_{1}$. Player 2 wins the second contest with certainty if he wins contest one, gaining prize v, and winning contest one gives a stage prize of $1-v$, so that: $W_{2,1}=1-v+v=1$. Hence $W_{2,1}-W_{1,1}=v-z_{1}$. Putting these values into (2) reveals that total effort in contest one is increasing in v. Hence, v should be set as high as possible in case (iv): $v=h+z_{1}$. Then the induced prize spread is equal to the initial head start, $W_{2,1}-W_{1,1}=h$, and total expected effort in the first contest is given, by (2), as $1- \frac{h(1-h)}{2}$. The probability of positive effort in the second contest is the probability that player 1 wins the first, which from part (ii) of Lemma 1 is $\frac{1-h}{2}$; and with $v=h+z_{1}$, we have an expected effort in the second contest of h. Hence, total expected effort is $1- \frac{h(1-h)}{2}+\frac{h(1-h)}{2}=1$. The principal captures all of the surplus in this case.¹⁴

In case (iii) of Proposition 1, it is still beneficial to run two contests, although this does not lead to full dissipation of the prize. The second-contest prize is optimally set sufficiently high that there will be effort in contest two, irrespective of who wins the first, $v\in [z_{2},1]$. The winner of the first contest will thus have a positive expected payoff in contest two. The value of winning the first contest is hence, for each player, the stage prize $1-v$ plus the expected payoff in contest two: $W_{1,1}=1-v+z_{1}$, and $W_{2,1}=1-v+z_{2}$. Player 2 has more to gain, since $W_{2,1}-W_{1,1}=z_{2}-z_{1}>0$; however, it is not possible to set the induced first-contest prize to completely even out the initial heterogeneity since $h>W_{2,1}-W_{1,1}$ when we are in case (iii). Total expected effort is $1-\left( h+z_{1}\right) +z_{2}>$ $1-h$ from a single contest; the inequality holds when $z_{1}>z_{2}$, which is true in case (iii).

In cases (i) and (ii) of Proposition 1, it is not possible to improve on a single contest. In case (i), player 1 has a head start in the second contest even if the rival wins the first. In contest two, player 1 will have a head start of $z_{1}$ or $-z_{2}$. With a second-contest prize $v<-z_{2}<z_{1}$, player 2 will not find it worthwhile to fight, and player 1 wins v with no effort in contest two. Hence, the total effort would come simply from the first contest. In contest one, the players fight over the same prize $1-v$, since the payoff in contest two is not affected by who wins the first. Given that player 1 has a head start of h, total efforts are $1-v-h$, which is maximized for $v=0$, so that the principal runs a single contest.

The intuition for case (ii) is broadly similar, although now it is the winner of contest one that will have the head start in contest two. Player 2 has the lower positive head start in contest two if he wins contest one, since $z_{2}<z_{1}$ in this case. By the same reasoning as above, setting a prize of $v<z_{2}$ in contest two will induce no effort in that contest, and the winner of the first contest wins also the second-contest prize v. Seen from the first contest, the value of winning is $(1-v)+v=1$ for each player, and hence total efforts are $1-h$ given the initial head start. Any second-contest prize up to $z_{2}$ will achieve this result, since no prize in this range induces effort in contest two.

Note that Fig. 2 is also valid if $h=z_{1}$, so that player 1 retains the same head start following a win. Proposition 1 is unchanged in this case, except for the fact that, at $z_{2}=z_{1}=h$, any $v\in \left[ 0,1\right]$ gives the amount of effort $1-h=1-z_{1}$.

4 Advantage decay

Proposition 1 considers the case in which a win by the advantaged player 1 leads to him building upon his initial head start which then increases in contest two. There are situations in which one can think of the second contest advantage as being reduced in relation to that of contest one. One instance may be fatigue, so that player 1 retains an advantage at the beginning of the second contest which is positive, but diminished in size compared to the initial situation. Another possibility is that the two contests are different in nature, and that player 1 is in some way better than the rival in the task of contest one, but 2 is better in contest two. A research contest may be divided in two parts, for example, where the first is a draft proposal (or a prototype), and the second is a full application (a tested product). Player 1 may be a creative team that is expert in idea creation, and 2 is better at producing a well-argued application, or finished product. Hence, the initial advantage of 1 may be eroded in relation to the original lead. In terms of the model, $h>z_{1}>0$. This modifies the results as indicated in the following proposition which is proved in the “Appendix”:

Proposition 2

In the two-contest series, suppose that $z_{1}\in \left( 0,h\right)$ and $z_{2}\in \left( -h,1\right)$. A principal who wants to maximize total expected effort over the two contests should set v as follows:

• (I) If $-h<z_{2}\le h$, then $v=1$ is optimal, and $Ex^{*}=1-z_{1}$.

• (II) If $h+z_{1}>z_{2}>h$, then any $v\in [z_{2},1]$ is optimal, and $Ex^{*}=1-\left( h+z_{1}\right) +z_{2}$.

• (III) If $1>z_{2}\ge h+z_{1}$, then $v=h+z_{1}$ is optimal, and $Ex^{*}=1$.

The striking result here is that it is now always optimal to run two contests. In case (I), the first contest is purely for position, with the whole prize mass saved until contest two. Heterogeneity is bad for effort, and under the conditions of part (I), the head start in the second contest will be lower in magnitude than in the first. Hence, the principal rationally saves the prize for contest two, so that player 1 wins the first with no effort and gets a lower head start in contest two. Note that this is valid under the condition that $h>z_{1}>0$. As $z_{1}$ approaches h from below, it is optimal to exploit the fact that there is less heterogeneity in contest two under the conditions in part (I) of Proposition 2, setting $v=1$. At $z_{2}=z_{1}=h$ this is no longer possible since the level of heterogeneity is constant across contests. In this case, any $v\in \left[ 0,1\right]$ is optimal, as indicated in the discussion of Fig. 2.

In parts (II) and (III), the winner of the first contest gets the positive net head start in the second, and this is larger in magnitude than the initial head start if player 2 wins the first. If it is sufficiently large, then full prize dissipation ensues as before. Indeed, part (III) of Proposition 2 and part (iv) of Proposition 1 are identical. The intermediate cases (II) and (iii) give the same effort, defined over $z_{2}\in (h,h+z_{1})$ in Proposition 2 and $z_{2}\in \left( z_{1},h+z_{1}\right)$ in Proposition 1.

5 Conclusion

A head start in a contest may reflect a previous investment made by a competitor, some technological superiority, or an incumbency advantage. In some situations, the initial advantage can be self-amplifying, leading to the Matthew effect where “success breeds success”. In a contest setting, this may lead to discouragement of the laggard, and a fall in contest efforts. With the same set of contestants and a series of contests, we suggest that the head start can adjust over time to reflect previous contest outcomes. A win by the initial leader can augment his head start, whereas a win for the underdog will reduce the advantage of the leader, or even turn it in favor of the initially disadvantaged player.

In this setting, we have considered a design question in which a principal may divide up the prize mass in order to maximize the expected effort of the players. When the initial underdog has limited ability to turn a win into a future head start, the principal can do no better than to run a single contest with the whole prize mass on offer. If this ability is sufficiently large, then the principal prefers to run two contests, dividing the prize mass between the two. The design problem would seem to be quite complex since the synergy between contests makes the principal mindful of the fact that the prize division can lead to contests in which the contestants prefer not to compete, and he also needs to take into account the development of the head start from one contest to the next. We have shown that a quite simple design can increase the amount of expected effort over and above that of a single contest—that it can even lead to full dissipation of the prize. This result is also robust to cases in which the initial head start of the leading player erodes even if he wins the first contest.

Extending the analysis to more than two contests is an obvious, but challenging, extension of our analysis. One may also like to consider a combination of a win advantage and an effort advantage where some part of previous efforts may affect the evolution of the head start; we have simply assumed exogenous win advantages here. Nevertheless, we believe that our analysis opens up an interesting design issue in a setting with synergy in the head start between contests in a series. Rather than balancing the contest by allowing the principal to choose head starts as in the extant literature, we have shown what might be achieved simply by a judicious division of the prize mass.

A Appendix

In order to prove Proposition 1, we first discuss the stage game.

1.1 A1 An asymmetric all-pay auction with a head start

Consider a single all-pay auction in which two risk-neutral players, $i=1,2$ , have asymmetric initial scores ($S_{i}$), and different valuations ($V_{i}$ ) of winning the prize. In the all-pay auction, a player is given a score which is comprised of his initial head start and his effort to win the prize: $S_{i}+X_{i}$. Without loss of generality, assume that $S_{1}\ge S_{2}$. Define player 1’s head start $\Delta :=S_{1}-S_{2}\ge 0$. The probability that player 1 wins the prize, $\rho _{1}\left( X_{1},X_{2}\right)$, is given by the following contest success function:

$$\begin{aligned} \rho _{1}\left( X_{1},X_{2}\right) =\left\{ \begin{array}{ll} 1&{}\quad \text { if }S_{1}+X_{1}>S_{2}+X_{2} \\ \frac{1}{2}&{}\quad \text { if }S_{1}+X_{1}=S_{2}+X_{2} \\ 0&{}\quad \text { if }S_{1}+X_{1}<S_{2}+X_{2} \end{array} \right. \end{aligned}$$

The probability that player 2 wins is $\rho _{2}\left( X_{1},X_{2}\right) =1-\rho _{1}\left( X_{1},X_{2}\right)$. The expected utilities of the two players can be written as

$$\begin{aligned} EU_{i}=\rho _{i}\left( X_{1},X_{2}\right) V_{i}-X_{i},\quad i=1,2 \end{aligned}$$

Let $F_{i}(X_{i})$ represent the cumulative distribution function of player i’s mixed strategy. Clark and Riis (1995) prove the following result:¹⁵

Lemma 1

(Clark and Riis 1995).

• (i) If $\Delta \ge V_{2}$, then $X_{1}=X_{2}=0$, $EU_{1}=V_{1}$, and $EU_{2}=0$.

• (ii) If $V_{2}-V_{1}\le \Delta <V_{2}$, then the unique mixed-strategy Nash equilibrium is

  $$\begin{aligned} F_{1}\left( X_{1}\right)= & {} \frac{\Delta +X_{1}}{V_{2}},X_{1}\in \left[ 0,V_{2}-\Delta \right] ; \\ F_{2}\left( X_{2}\right)= & {} 1-\frac{V_{2}-\Delta }{V_{1}},X_{2}\in [0,\Delta ];\quad F_{2}\left( X_{2}\right) =1-\frac{V_{2}-X_{2}}{V_{1}} ,X_{2}\in \left( \Delta ,V_{2}\right] . \end{aligned}$$

Expected efforts and win probabilities are

$$\begin{aligned} EX_{1}= & {} \frac{\left( V_{2}-\Delta \right) ^{2}}{2V_{2}};EX_{2}=\frac{ V_{2}^{2}-\Delta ^{2}}{2V_{1}}; \\ \rho _{1}= & {} 1-\frac{V_{2}^{2}-\Delta ^{2}}{2V_{1}V_{2}};\rho _{2}=\frac{ V_{2}^{2}-\Delta ^{2}}{2V_{1}V_{2}}; \end{aligned}$$

with expected net payoffs

$$\begin{aligned} EU_{1}=V_{1}-V_{2}+\Delta ;EU_{2}=0. \end{aligned}$$

• (iii) If $0\le \Delta \le V_{2}-V_{1}$, then the unique mixed-strategy Nash equilibrium is

  $$\begin{aligned} F_{1}\left( X_{1}\right)= & {} 1-\frac{V_{1}-X_{1}}{V_{2}},X_{1}\in \left[ 0,V_{1}\right] ; \\ F_{2}\left( X_{2}\right)= & {} 0,X_{2}\in [0,\Delta ];\quad F_{2}\left( X_{2}\right) =\frac{X_{2}-\Delta }{V_{1}},X_{2}\in \left( \Delta ,V_{1}+\Delta \right] . \end{aligned}$$

  Expected efforts and win probabilities are

  $$\begin{aligned} EX_{1}= & {} \frac{V_{1}^{2}}{2V_{2}};EX_{2}=\frac{V_{1}}{2}+\Delta ; \\ \rho _{1}= & {} \frac{V_{1}}{2V_{2}};\rho _{2}=1-\frac{V_{1}}{2V_{2}}; \end{aligned}$$

  with expected net payoffs

  $$\begin{aligned} EU_{1}=0;EU_{2}=V_{2}-V_{1}-\Delta . \end{aligned}$$

In terms of our model, the first contest is such that $\Delta =h$, and $V_{i}=W_{i,1},i=1,2$. The second contest sets $V_{i}=v$ and $\Delta \in \{z_{1},z_{2}\}$.

1.2 A2 Proof of Proposition 1

For the purpose of this proof, for $i,t\in \left\{ 1,2\right\}$, let player i’s expected equilibrium effort in contest t be $x_{it}^{*}$, total expected equilibrium effort across the two players in contest t be $x_{t}^{*}:=x_{1t}^{*}+x_{2t}^{*}$, and total expected equilibrium efforts across contests be $x^{*}$. We use the notation in Lemma 1 in determining expected efforts in each stage game in the proof below.

Part (i)  By using a single contest with a prize of size 1, the principal expects $1-h$ in total effort.

Since player 1 has a head start in contest two whoever wins the first, $V_{2}=1-v$ in contest one. If $h\ge 1-v$, i.e., $\Delta \ge V_{2}$ , then player 1 wins contest one without effort, by part (i) of Lemma . Total expected efforts are therefore the ones in contest two following a contest-one win by player 1, which are $v-z_{1}$, and this is maximized at $v=1$, with total expected efforts at $1-z_{1}$. This is inferior to a single contest since the proposition assumes $z_{1}>h$.

If $h<1-v$, then efforts will be expended in contest one. In terms of Lemma 1, the expected payoff function of player i in contest one can be written as

$$\begin{aligned} \pi _{i,1}=\pi _{i,2}^{*}\left( j\right) +p_{i,1}V_{i}-x_{i,1},\ i\ne j. \end{aligned}$$

(A1)

In part (i), $-h\le z_{2}\le 0$ so that player 1 has an advantage in the second contest, irrespective of the first-round outcome (or the second contest is unbiased if $z_{2}=0$). This implies that $V_{1}\ge V_{2}=1-v$, and $\pi _{1,2}^{*}\left( 2\right) =\left| z_{2}\right| >0$. Using Lemma 1 and (A1), the payoff to each player in equilibrium is

$$\begin{aligned} \pi _{1,1}^{*}= & {} \left| z_{2}\right| +\left( V_{1}-V_{2}+h\right) ; \\ \pi _{2,1}^{*}= & {} 0. \end{aligned}$$

With risk-neutrality and linear costs, the total amount of effort expected is equal to the prize pot (size 1) minus the expected payoff of player 1:

$$\begin{aligned} x^{*}=1-\pi _{1,1}^{*}. \end{aligned}$$

The two-contest setup gives more effort in expectation than a single contest if

$$\begin{aligned} 1-\left| z_{2}\right| -\left( V_{1}-V_{2}+h\right)> 1-h \, \Leftrightarrow -\left| z_{2}\right|> & {} V_{1}-V_{2}, \end{aligned}$$

which is not possible, since $V_{1}-V_{2}\ge 0$. Hence, it is not optimal to incite efforts in the first contest of a two-contest series, and a single contest is preferred ($v=0$).

Parts (ii)-(iv). For parts (ii) through (iv) of the Proposition, we have $z_{2}>0$, implying that the winner of contest one has a head start in contest two. This means that $\pi _{1,2}^{*}\left( 1\right) =\min \left\{ v,z_{1}\right\}$, $\pi _{2,2}^{*}\left( 2\right) =\min \left\{ v,z_{2}\right\}$, and $\pi _{i,2}^{*}\left( j\right) =0$. (If player 1 wins contest one, and $v\le z_{1}$, then he wins the contest-two prize of v with no effort; if $z_{1}>v$, he must fight and has an expected payoff of $z_{1}$ by Lemma 1).

The choice of v will influence in which contest the players exert effort. We consider the different possibilities below, where we denote Effort by E and No Effort by NE. [E, NE], for example, denotes effort in contest one and none in contest two. Effort in the second contest can be conditional upon who has won the first contest. If the second-contest prize is above the highest head start in contest two, then there will be efforts in contest two whoever wins contest one; if the prizes in contest two lies between the highest and lowest head start, then there will be effort in the second contest only if the player with the low second-contest head start wins the first. We denote this possibility by $E^{C}\left( i\right)$ below, where $i=1,2$ is the identity of the player with the lowest head start in contest two. (Note that it is not possible to achieve effort in the second contest if the player with the high second-contest head start won the first).

(a)  [E, NE]. If $\min \left\{ z_{1},z_{2}\right\} >v\ge 0$, then there will be no effort in contest two. The player who wins contest one gets the prize $1-v$ and the head start in contest two, thus gaining v with no effort. Hence, $V_{1}=V_{2}=1-v+v=1$, and total effort is $x^{*}\left[ E,NE \right] =1-h$, which can be achieved by setting $v\in [0,\min \left\{ z_{1},z_{2}\right\} )$.

(b)  [NE, E]. With effort in the second contest, we have $V_{2}=1-v+z_{2}$ in contest one. If $h>V_{2}$, i.e., $v>1-h+z_{2}$, then there is no effort in contest one, which is then won by player 1. In the second contest, we have effort of at most $x^{*}\left[ NE,E\right] =1-z_{1}$ which is less than $x^{*}\left[ E,NE\right]$ under the conditions in the proposition.

(c)  [E, E]. If $1\ge v>\max \left\{ z_{1},z_{2}\right\}$, then there is effort in contest two whoever wins the first; effort in contest one is secured if $V_{2}>h$. Then $V_{1}=1-v+z_{1},V_{2}=1-v+z_{2}$. If $V_{2}>h\ge V_{2}-V_{1}$, then Lemma 1, part (ii), determines the expected payoffs in equilibrium as $\pi _{1,1}^{*}=V_{1}-V_{2}+h,\pi _{2,1}^{*}=0$. If $V_{2}-V_{1}\ge h\ge V_{2}$, then Lemma 1, part (iii), gives $\pi _{1,1}^{*}=0,\pi _{2,1}^{*}=V_{2}-V_{1}-h$. The amount of effort in this case is $x^{*}\left[ E,E\right] =1-\max \left\{ V_{1}-V_{2}+h,V_{2}-V_{1}-h\right\}$, which by insertion gives

$$\begin{aligned} x^{*}\left[ E,E\right] =\min \left\{ 1-\left( h+z_{1}\right) +z_{2},1+\left( h+z_{1}\right) -z_{2}\right\} . \end{aligned}$$

(d)  $\left[ E,E^{C}\left( 1\right) \right]$. If $z_{2}\ge v\ge z_{1}$, then effort is exerted in the second contest if and only if player 1 wins the first. Thus, if player 2 wins the first contest, he wins the second one without effort, getting $1-v$ from winning the first and v from the second: $V_{1}=1-v+z_{1},V_{2}=1$. As in case (c), either player 1 or 2 can expect a positive payoff, so that $x^{*}\left[ E,E^{C}\left( 1\right) \right] =1-\max \left\{ V_{1}-V_{2}+h,V_{2}-V_{1}-h\right\}$ which gives

$$\begin{aligned} x^{*}\left[ E,E^{C}\left( 1\right) \right] =\min \left\{ 1+v-\left( h+z_{1}\right) ,1-v+\left( h+z_{1}\right) \right\} . \end{aligned}$$

Note that setting $v=h+z_{1}$ yields the maximum level of effort in this case, with $x^{*}\left[ E,E^{C}\left( 1\right) \right] =1$. If $h+z_{1}>z_{2}$, then this level of effort cannot be obtained, and the minimum condition gives $x^{*}\left[ E,E^{C}\left( 1\right) \right] =1+v-\left( h+z_{1}\right)$, which is maximized by setting $v=z_{2}$, giving $x^{*}\left[ E,E^{C}\left( 1\right) \right] =1-\left( h+z_{1}\right) +z_{2}$.

(e)  $\left[ E,E^{C}\left( 2\right) \right]$ occurs for $z_{1}\ge v\ge z_{2}$, giving $V_{1}=1$ and $V_{2}=1-v+z_{2}$ in contest one. Since $V_{1}-V_{2}\ge 0$, Lemma 1 determines that player 1 gets a positive expected payoff, and efforts are

$$\begin{aligned} x^{*}\left[ E,E^{C}\left( 2\right) \right] =1-v-h+z_{2}. \end{aligned}$$

In the interval for v, this expression is maximized by choosing the second contest prize as low as possible ($v=z_{2}$), which yields

$$\begin{aligned} x^{*}\left[ E,E^{C}\left( 2\right) \right] =1-h. \end{aligned}$$

Finding the optimal v involves comparing conditions under which the efforts in (a) through (e) are largest for $z_{2}>0$. Note that, since $z_{1}>h$, case (b) cannot be optimal and can be discounted. Expected effort is equal to the prize mass in case (d), and this solution is permitted for $z_{2}\ge v=h+z_{1}\ge z_{1}$, which implies $z_{2}\ge h+z_{1}$. This is part (iv) of the proposition. When $h+z_{1}>z_{2}$, the minimum condition in case (c) gives $x^{*}\left[ E,E\right] =1-\left( h+z_{1}\right) +z_{2}$ (which is the same as case (d) for this parameter restriction). This is at least as good as the $1-h$ obtained from cases (a) and (e) if $1-\left( h+z_{1}\right) +z_{2}\ge 1-h$, i.e., if $z_{2}\ge z_{1}$. Hence, for $h+z_{1}>z_{2}\ge z_{1}$, the maximal amount of effort is $x^{*}=1-\left( h+z_{1}\right) +z_{2}$, which is invoked by setting $v\in \left[ z_{2},1\right]$, where the closed lower bound comes from case (d). This is part (iii) of the proposition. When $h+z_{1}>z_{1}\ge z_{2}>0$, it follows that the maximum amount of effort that can be obtained is $1-h$. From cases (a) and (e), this can be achieved by setting any $v\in [0,z_{2}]$. This is part (ii) of the proposition.

1.3 Proof of Proposition 2

Part (I)  Suppose first that $-h<z_{2}\le 0$, which implies that player 2 expects zero in contest two whoever wins the first one, and hence $V_{2}=1-v$. If $h\ge 1-v$, i.e., $\Delta \ge V_{2}$, then player 1 wins contest one without effort, by part (i) of Lemma 1. Total expected efforts are therefore the ones in contest two following a contest-one win by player 1, which are $v-z_{1}$, and this is maximized at $v=1$, with total expected efforts at $1-z_{1}$. This is better than using a single contest, since the proposition assumes $h>z_{1}$.

If $h<1-v$, then there are efforts in contest one. As in the proof of Proposition 1, part (i), expected effort in this case is $1-\left| z_{2}\right| -\left( V_{1}-V_{2}+h\right) =1-\left| z_{2}\right| -z_{1}-h$. For this to give more effort than saving the whole prize for the second contest, we need $1-\left| z_{2}\right| -z_{1}-h>1-z_{1}$, which cannot occur. Hence, it is optimal to set $v=1$ and get effort $1-z_{1}$ in this case.

Optimal prize division in part (I), for $h\ge z_{2}>0$, and parts (II) and (III) involves comparing the efforts that can be achieved from the combinations $\left[ E,NE\right]$, $\left[ NE,E\right]$, $\left[ E,E\right]$, $\left[ E,E^{C}\left( 1\right) \right]$, and $\left[ E,E^{C}\left( 2\right) \right]$ outlined in the proof of Proposition 1. As in that proposition, we have $x^{*}\left[ E,NE\right] =\left[ E,E^{C}\left( 2\right) \right] =1-h$ for $v\in \left[ 0,z_{2}\right]$, and $x^{*} \left[ NE,E\right] =1-z_{1}$, where the latter holds for $v=1$. Under the conditions of this proposition we now have $x^{*}\left[ NE,E\right] >x^{*}\left[ E,NE\right] =\left[ E,E^{C}\left( 2\right) \right]$.

Again, it is possible to achieve $\left[ E,E^{C}\left( 1\right) \right] =1$ by setting $v=h+z_{1}$ for $z_{2}\ge h+z_{1}$. This is part (III) of the proposition.

When $h+z_{1}>z_{2}$, we have $x^{*}\left[ E,E\right] =1-\left( h+z_{1}\right) +z_{2}$, and hence $x^{*}\left[ E,E\right] >x^{*} \left[ NE,E\right]$ for $z_{2}>h$. As before $x^{*}\left[ E,E\right]$ can be achieved by setting $v\in \left[ z_{2},1\right]$, and this is part (II) of the proposition.

It follows that $x^{*}\left[ NE,E\right] =1-z_{1}$ is the most effort that can be achieved when $h\ge z_{2}>0$, and here $v=1$, proving the remainder of part (I).