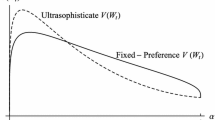
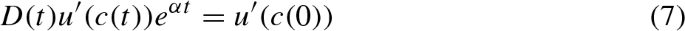Abstract
Agents with declining discount rates who are unable to commit to their future decisions can either be sophisticated—meaning that they anticipate their future behavior and take it into account in their consumption choices—or naive. Previous studies have shown that sophistication may lead to higher or lower consumption rates, but have not resolved the implications for welfare, arguably the most important question from an economic point of view. Since neither the sophisticated nor the naive solutions are Pareto-efficient, their own welfare ranking is not obvious. This paper shows that the ‘better saver’ amongst the two (lower consumption rate) is always better-off, from all temporal perspectives.
Similar content being viewed by others
Notes
O’Donoghue and Rabin (1999) compare sophisticated and naive behavior in a model in which an agent has to undertake a certain action exactly once in a given period of time, and that action can either carry immediate rewards or immediate costs. When commitment is unfeasible, the naive agent acts too late if actions involve immediate costs and acts too soon if actions involve immediate rewards. Sophistication mitigates the tendency to delay but exacerbates the tendency to act too soon, and strikingly, this can make the agent worse off than if she were naive. As the authors note, it is not entirely clear how these findings might carry over to the saving problem, since it lies outside the domain of their model.
In the ‘beta–delta’ model, an agent’s present discounted utility is given as \(u(c_0) + \beta \delta u(c_1) + \beta \delta ^2 u(c_2) + \beta \delta ^3 u(c_3) +\cdots \), so that the discount factor of the first period, relative to period 0, is \(\beta \delta \), whereas the discount factor of every other period relative to the preceding one is \(\delta \). When \(\beta \) is assumed to be lower than unity, discount rates are declining.
Most existing comparisons of the naive and sophisticated saving rates are carried out in discrete time. In their seminal analysis,Phelps and Pollak (1968) use the ‘beta–delta’ model. Salanié and Treich (2006) compare the naive and sophisticated saving rates in a three period model, but with a completely general discount factor. Grout (1981), like the present analysis, compares not only the saving rate, but also the welfare of naive and sophisticated saving plans in a discrete time model in which utility of consumption is iso-elastic but an agent cares about the utility of consumption in only the present and one following period.
Barro (1999) discusses the sophisticated consumption plan with general production functions under various assumptions on commitment ‘technologies’ and iso-elastic utility of consumption. Karp (2007), Barro (1999), and Ekeland and Lazrak (2006) carefully discuss the definition, existence and characterization of sophisticated equilibria in such continuous time models.
To derive Eq. 10, integrate the Euler equation,
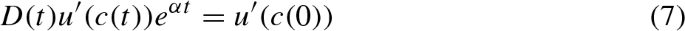
which equates marginal instantaneous utility at all future times, and use the transversality condition

which states no amount of capital stock of significant present value should be left unused in the far future.
Note that in the knife-edge case when \(\gamma _S=\alpha \) the dynamics have a steady state. In that case, we find
$$\begin{aligned} \frac{1}{\gamma _S}={\displaystyle \int \nolimits _{0}^{\infty }} D(\tau ) d\tau \end{aligned}$$which is in agreement with the results of Barro (1999) and Karp (2007), who consider a general equilibrium model and interest-rate taking agent, respectively. When the rate of return to capital is constant, their results agree.
References
Barro RJ (1999) Ramsey meets laibson in the neoclassical growth model. Q J Econ 114(4):1125–1152
Bernheim BD, Antonio R (2005) Behavioral public economics: welfare and policy analysis with non-standard decision-makers. No. w11518. National Bureau of Economic Research
Ekeland I, Lazrak A (2006) Being serious about non-commitment: subgame perfect equilibrium in continuous time. arXiv:math/0604264
Goldman SM (1979) Intertemporally inconsistent preferences and the rate of consumption. Econ J Econ Soc 47(3):621–626
Grout PA (1981) Welfare aspects of naive and sophisticated decision making. In: Social choice and welfare. North-Holland, Amsterdam
Grout P (1983) Efficiency of sophisticated choice. Econ Lett 12(3–4):229–234
Hickman B (2009) Introduction to probability theory for graduate economics. http://www.homeuchicagoedu/hickmanbr/. Accessed 4 Nov 2016
Karp L (2007) Non-constant discounting in continuous time. J Econ Theory 132(1):557–568
Laibson DI (1996) Hyperbolic discount functions, undersaving, and savings policy. No. w5635. National bureau of economic research
Laibson D (1997) Golden eggs and hyperbolic discounting. Q J Econ 112(2):443–478
Laibson D (1998) Life-cycle consumption and hyperbolic discount functions. Eur Econ Rev 42(3):861–871
O’Donoghue T, Matthew R (1999) Doing it now or later. Am Econ Rev 89(1):103–124
O’Donoghue T, Rabin M (2000) The economics of immediate gratification. J Behav Decis Making 13(2):233–250
O’Donoghue T, Rabin M (2001) Choice and procrastination. Q J Econ 116(1):121–160
Peleg B, Yaari ME (1973) On the existence of a consistent course of action when tastes are changing. Rev Econ Stud 40(3):391–401
Phelps ES, Pollak RA (1968) On second-best national saving and game-equilibrium growth. Rev Econ Stud 35(2):185–199
Pollak RA (1968) Consistent planning. Rev Econ Stud 35(2):201–208
Salanié F, Treich N (2006) Over-savings and hyperbolic discounting. Eur Econ Rev 50(6):1557–1570
Strotz RH (1955) Myopia and inconsistency in dynamic utility maximization. Rev Econ Stud 23(3):165–180
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
I thank Geoffrey Heal, Larry Karp, Stergios Athanassoglou, Prajit Dutta, Christian Gollier, Bernard Salanie, Francoise Salanie, Jeffrey Sachs, and Nicolas Treich for their suggestions and comments. All errors in the analysis are entirely my own.
Proofs
Proofs
Derivation of equation (14)
Let \(c_{\gamma }(K_0,t)\) be the consumption plan resulting from applying the CRC \(\gamma \) and starting with a stock \(K_0\). Let \(\epsilon \) be a small time interval, and separate the contribution to present discounted utility into
where \(O(\epsilon )\) is independent of \(c_0\). Expanding gives
which upon re-arrangement results in
Differentiating w.r.t. \(c_0\) and noting that \(u'(c)=c^{-\theta }\) and that \(c_0=\gamma K\) gives
Taking the limit as \(\epsilon \rightarrow 0\) derives Eq. (14).
The following Lemma will be useful in the proofs that follow. It does not appear in the main text.
Lemma 2
Let f(t) be a non-negative function integrable on \([0,\infty )\) and g(t) be a non-negative strictly decreasing function on \([0,\infty )\). Then
Proof
Define the following probability densities on \([0,\infty )\):
Since g(t) is decreasing, the density \(\psi _f\) strictly Likelihood Ratio Dominates\(\psi _{fg}\):
A well known result (Hickman 2009) implies that \(\psi _f\) also strictly First Order Stochastic Dominates\(\psi _{fg}\). In particular, it follows that \({\mathbb {E}}_{\psi _{fg}}(t) < {\mathbb {E}}_{\psi _{f}}(t)\), which is the desired result. \(\square \)
Proof of Proposition 1
Noting that \(c(t)=\gamma K(t)\) and that \(\frac{dK}{dt}=\alpha K-c(t) = (\alpha -\gamma )K(t)\) and integrating w.r.t to time gives \(K(t)=K(0)e^{(\alpha -\gamma )t}\). Substituting into the definition of \(W(K,\gamma )\), it is straightforward to calculate that
Differentiating w.r.t. to K gives
Proposition 1 therefore states that there is a unique solution \(\gamma \ge \alpha \) to the equation
or
Existence: Note that \(F(\gamma ) \) is continuous. Suppose \(\theta >1\). When \(\gamma \rightarrow 0\), \(F(\gamma ) \rightarrow 0\) (recall that \(\alpha \le \delta _0\), so the integral converges when \(\gamma =0\)). When \(\gamma \rightarrow \alpha - \delta _0/(1-\theta )\) the integral diverges. Thus, because of the continuity of \(F(\gamma )\) there is an intermediate value of \(\gamma \) for which \(F(\gamma )=1\). Suppose now that \(\theta <1\). Again, when \(\gamma \rightarrow 0\), \(F(\gamma ) \rightarrow 0\). When \(\gamma \rightarrow \infty \), note that \(F(\gamma ) \ge \gamma \int _0^\infty e^{-d(0)t} e^{(\alpha -\gamma )(1-\theta )t} dt = \frac{\gamma }{d(0)+(\gamma -\alpha )(1-\theta )} \rightarrow \frac{1}{1-\theta } > 1\). Again, there is an intermediary value of \(\gamma \) for which \(F(\gamma )=1\).
Uniqueness: Consider now the derivative of \(F(\gamma )\):
Uniqueness will follow from showing that \(F'(\gamma ) \ge 0\). When \(\theta \ge 1\) this is obvious. When \(\theta <1\), we need to show that
Decomposing the discount factor as \(D(t) = v(t) e^{-\delta _0 t}\) where v(t) is decreasing, we can rewrite the LHS of (26) as \(\frac{ \int _{0}^{\infty } v(\tau ) e^{-x \tau } \tau d\tau }{\int _{0}^{\infty } v(\tau ) e^{-x \tau } d\tau }\) where \(x=\delta _0+(\gamma -\alpha )(1-\theta )\). Applying Lemma 2 with \(f(t)=e^{-xt}\), \(g(t)=v(t)\), we get
where the last inequality follows from the assumption that \(\alpha \le \delta _0\). \(\square \)
Proof of Proposition 2
The proof uses
Holder’s Inequality: Let \(0 \le \nu ,\mu \le 1\), \(\nu +\mu =1\). Let f(x) and g(x) be two non-negative integrable on \([0,\infty )\). Then:
with equality occurring only if f(x) and g(x) are proportional.
To begin the proof, suppose first that \(\theta <1\). Rewrite (24) as
and apply Holder’s inequality to obtain (note that the inequality is strict since the two integrands cannot be proportional to each other if the discount factor is strictly hyperbolic, as we assume throughout)
or
which completes the proof.
Now suppose that \(\theta >1\). Rewrite (10) as (the \(\gamma \) exponentials cancel out)
Apply Holder’s inequality to to obtain
from which it follows that \(\gamma _N \ge \gamma _S\). Note that when \(\theta =1\), it can be directly seen in (10) and (24) that \(\gamma _N = \gamma _S = \frac{1}{{\displaystyle \int \nolimits _{0}^{\infty }}D(\tau )d\tau }.\)\(\square \)
The following two Lemmas will be useful in the proofs that follow. It does not appear in the main text.
Lemma 3
Let H(t) be a (strictly) Hyperbolic discount factor (as defined in (3)). Then
Proof
Changing the integration variables to \(x=t+s, y=t-s\), for which the Jacobian is \(-1/2\), we see that the (RHS) equals \(\frac{1}{2} \int _0^{\infty }dx H(x) \int _{-x}^{x} dy = \int _0^{\infty }H(x)xdx\). \(\square \)
Lemma 4
Let H(t) be a hyperbolic discount factor (as defined in (3)) and \(x > 0\).
Proof
Again, note that if H(t) is a Hyperbolic discount factor, then so is \(H(t)e^{-xt}\) for any \(x\ge 0\). It follows from Lemma 3 that
which ensures the derivate of the RHS is always larger than that of the LHS. The result follows from the equality of the LHS and RHS at \(x=0\). \(\square \)
Proof of Proposition 3
(a) Suppose first that \(\theta <1\). As \(\gamma \rightarrow 0\), \(G(\gamma ) \rightarrow 0\). When \(\gamma \rightarrow \infty \) the only contribution to the integral in (17) comes from near \(t=0\), so we can take \(D(t) \approx 1\), and
Thus, \(G(0)=G(\infty )=0\), and since G is non-negative, we deduce the existence of an interior maximum in \((0,\infty )\). Suppose now that \(\theta >1\). In this case, \(G(\gamma ) \rightarrow -\infty \) when either \(\gamma \rightarrow 0\) or \(\gamma \rightarrow \infty \) so there is again an interior maximum.
(b) Differentiating (17), we see that every interior maximum \(\gamma _M\) satisfies the F.O.C.
Recall that \(\gamma _S\) satisfies (24)
Note that if H(t) is a Hyperbolic discount factor, then so is \(H(t)e^{-xt}\) for any \(x\ge -\delta _0\). Thus, Lemma 3 can be applied to \(\phi (\tau )=D(\tau ) \gamma e^{(\alpha -\gamma )(1-\theta )\tau }\), and it follows that \(F_1(\gamma ) > F_2(\gamma )\) for all \(\gamma \). Since \(\frac{1}{\gamma }\) intersects \(F_1 (\gamma )\) at \(\gamma _{M}\) and \(F_2 (\gamma )\) at \(\gamma ^{S}\) it follows that \(\gamma _{M} < \gamma _S\).
(c) Again, let \(\gamma _M\) be an interior maximum. When \(\theta >1\), the claim follows immediately from Proposition 2 and part (b) of this proposition, proved above: \(\gamma _N>\gamma _S>\gamma _{M}\). Assume then that \(\theta <1\). Using (39) and Lemmas 3 and 4, applied to \(x=(\alpha -\gamma _{M}) (1-\theta )\), we have:
Also, from ‘hyperbolicity’, \(D(t)>D(\theta t)^{\frac{1}{\theta }}\) so that
It follows that \(\gamma _{M}<\gamma _N\). This concludes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Fishman, R. Welfare implications of naive and sophisticated saving. Soc Choice Welf 54, 623–638 (2020). https://doi.org/10.1007/s00355-019-01222-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-019-01222-5