Equilibrium competition, social welfare and corruption in procurement auctions

Abstract

We study the effects of corruption on equilibrium competition and social welfare in a public procurement auction. A government pays costs to invite firms to the auction, and a bureaucrat who runs the auction may request a bribe from the winning firm. We first show that, with no corruption, the bureaucrat will invite more than the socially optimal number of firms to the auction. Second, the effects of corruption on equilibrium outcomes vary across different forms of bribery. For a fixed bribe, corruption does not affect equilibrium competition, yet it does induce social welfare loss. For a proportional bribe, the bureaucrat may invite either fewer or more firms, depending on how much he weights his private interest relative to the government payoff. Finally, we show that information disclosure may consistently induce more firms to be invited, regardless of whether there is corruption.

1 Introduction

Public procurements account for a substantial part of economies worldwide. In the European Union (EU), more than 250,000 public authorities spend approximately 14% of GDP on the purchase of services and supplies each year.¹ Naturally, corruption is a common concern in public procurements. To prevent corruption, most countries implement laws and regulations to guarantee the necessary competition and transparency in public procurements. For instance, the EU requires a minimum of 35 days for a public contract notice in an open procedure, for which any business can submit a bid; and in a restricted procedure, for which only those who are pre-screened are invited to submit a bid, a public authority must invite at least 5 bidders to the competition process.² The belief underlying these rules is that competition may help improve efficiency and reduce corruption.

The literature has mainly focused on the effects of competition on corruption, yet has paid relatively less attention to the reverse causality between them. In this paper, we provide a theoretical investigation of the effects of corruption on equilibrium competition and social welfare in a public procurement auction. Specifically, in our model, there is a government agent, such as the Department of Defense, a bureaucrat who runs the auction on behalf of the government, and a number of potential firms who can submit bids for the government contract if invited. The government needs to pay costs to screen and invite firms to participate, and the corrupt bureaucrat may request a bribe from the winning firm.³

We consider a standard first-price procurement auction, which is common in practice.⁴ In the auction, the firm with the lowest production cost wins, and the price received by the firm is equal to its bid. Given the value of the contract, the government’s objective is to minimize the government spending, e.g., the sum of the invitation costs and the price paid to the winning firm. The bureaucrat, if corrupt, cares about a weighted average of the bribe received by him and the government payoff; if honest, his objective is in line with that of the government.

In the absence of corruption, we first show that the bureaucrat will invite more than the socially optimal number of firms to the auction, under the standard assumptions that firms’ cost distribution is of decreasing reversed hazard rate (DRHR) and that there is a positive invitation cost.⁵ In other words, the optimal number of firms that maximizes the government’s payoff is larger than the efficient number of firms that maximizes social welfare. This over-invitation result is not surprising as the government is not modeled as a social planner in our model. The intuition behind the result is that inviting an extra firm reduces the expected total surplus of the firms, due to increased competition, which is ignored by the payoff-maximizing government but is taken into account in the total social welfare.

We then introduce corruption into the model, in which the bureaucrat requests a bribe from the winning firm of the auction. We consider two common forms of bribery. The first is a fixed bribe in which the bureaucrat requests the winning firm to pay a fixed amount as a bribe. For instance, the fixed bribe can be in the form of a commission fee or a kickback that is common in the real world (Inderst and Ottaviani 2012). The second is a proportional bribe, whereby the winning firm must share a proportion of its revenue with the corrupt bureaucrat (Acemoglu and Verdier 2000; Amir and Burr 2015). For example, in Indonesia, the former president Suharto was publicly known as “Mr. Twenty-Five Percent” because he required that all major contracts throughout the nation give him 25% of the income.⁶

Our main result is that the effects of corruption on equilibrium competition and social welfare vary across different forms of bribery. When the bribe is a fixed amount, the corrupt bureaucrat invites the same number of firms as in the absence of corruption, as his marginal incentive of inviting firms remains the same as before. Therefore, corruption in this form does not affect equilibrium competition. However, it does change social welfare and resource allocation in equilibrium. We show that, under the expectation of paying a fixed bribe upon winning, all firms will mark up their bids by the same amount, which in turn increases the expected payment of the government to the winning firm. As a result, the fixed bribe is paid by the government, and it does not hurt the firms at all. The increased public expenditure by the government then implies welfare loss due to the marginal cost of distortion of public funds.

By contrast, under a proportional bribe, the corrupt bureaucrat may invite either fewer or more firms to the auction, depending on how much the bureaucrat weights his personal interest relative to the government payoff. We first show that, in this case, firms will adjust their bids proportionally in equilibrium. Second, there are two opposite effects on the equilibrium competition. On the one hand, as firms’ bids increase proportionally, the distribution of the bids becomes more dispersed, which decreases competition in the auction. In response to it, the bureaucrat needs to encourage competition by inviting more firms. On the other hand, the bureaucrat also has an incentive to discourage competition, as the winning firm’s revenue is decreasing in the number of firms in the auction. The relative magnitude between these two opposite effects determines the equilibrium level of competition.

We further investigate the effects of government information disclosure on auction outcomes. When firms’ areas of specialization are differentiated, revealing more project information by the government may induce a more dispersed distribution of firms’ cost estimates. For example, information disclosure may drive up the cost estimates of some firms that find it is a mismatch to their areas of specialization, while driving down those of others that find it to be a good match. As a result, firms’ cost estimates become more dispersed. We show that information disclosure increases both the efficient and the optimal number of firms in procurement auctions. The intuition is that under information disclosure, firms’ cost estimates become more dispersed, and the auction becomes less competitive than before. It is then better to invite more firms to participate in the auction.

Finally, we also explore the policy implications of our results. For the regulation of public procurements, we show that imposing a requirement on the minimum number of bidders may be effective only when it lies in a reasonable range. For instance, if it is too low, it will not impose real restrictions on a corrupt bureaucrat’s choice; if it is too high, it may instead cause a welfare loss.

Motivated by Rose-Ackerman (1978)’s argument that increasing in competition helps reduce corruption, there is a strand of literature studying the effects of competition on corruption in a large variety of economic contexts, and the results suggest that the relationship is complicated. For example, Shleifer and Vishny (1993) and Bliss and Di Tella (1997) show that the effect of competition on corruption depends on the nature of corruption. In the empirical studies, Ades and Di Tella (1999) and Emerson (2006) find that market competition and corruption are negatively related, while Alexeev and Song (2013) find a positive relationship between the strength of competition and the extent of corruption. The existing literature has paid relatively less attention to the effects of corruption on competition, though its empirical importance has been emphasized. One exception is Amir and Burr (2015), who examine theoretically the effects of corruption in the entry-certifying process on market structure and social welfare for a Cournot industry.

Our paper joins a small but growing literature that restricts attention to corruption in public procurements.⁷ Specifically, two papers examine the relationship between competition and corruption in procurement. Celentani and Ganuza (2002) study the impact of the number of potential suppliers on equilibrium corruption in the agency model and find that corruption may be higher in a more competitive environment. Compte et al. (2005) analyze the effect of corruption on price competition in which the corrupt bureaucrat may offer a firm an opportunity to readjust its bid and firms compete for this favor by making bribe offers. In this paper, we investigate the effects of various forms of bribery on the number of invited firms and social welfare in procurement auctions.

In the context of auctions, corruption is commonly described as an act in which a bureaucrat manipulates the auction rules in exchange for bribes. For example, Compte et al. (2005) and Menezes and Monteiro (2006) consider a corruption model in which the bureaucrat may offer a favored firm an opportunity to readjust its initial bid in exchange for a bribe. Other related papers include Burguet and Perry (2009) and Arozamena and Weinschelbaum (2009). Another strand of literature studies corruption in multidimensional procurement auctions, whereby the government may care about both the price and quality of the project. Celentani and Ganuza (1999, 2002) and Burguet and Che (2004) examine corruption in which the bureaucrat manipulates the quality assessment to favor the firms offering higher bribes. In our paper, the auction rule is taken as given, yet the bureaucrat may endogenously determine the competition level in the auction. Specifically, the bribery studied in our paper is a form of “harassment bribe” (Basu 2011), in which the bribe is exchanged for delivering entitled services rather than undue favors.

Our paper is also related to the literature on auctions with participation costs. The participation costs can be either paid by the bidders (McAfee and McMillan 1987; Levin and Smith 1994), or by the auctioneer (Szech 2011; Li 2017; Lee and Li 2018). The benchmark setting of our model is closely related to Szech (2011). Though different from her model of ascending second-price auction, we study a first-price procurement auction, yet the extension is straightforward according to standard auction theory. The key differences in our model are twofold: first, we consider a public procurement auction with a broader definition of social welfare, which takes Szech (2011) as a special case; second, the focus of our paper is on the effects of corruption on equilibrium bidding strategy, competition and social welfare in a public procurement auction.

The remainder of this paper is organized as follows. Section 2 introduces the benchmark model of procurement auction with no corruption. Section 3 studies the equilibrium outcomes under corruption, and there are two cases, the fixed bribe and proportional bribe. Section 4 provides some further discussions, and Sect. 5 presents our concluding remarks.

2 Benchmark: no corruption

Consider a public procurement auction in which a government plans to allocate an indivisible contract among a number of firms. A bureaucrat runs the auction on behalf of the government. We assume there are a large number of potential firms qualified for this contract, and n firms are invited to the auction at a cost of C(n), which is paid by the government. The value of the contract to the government is V. The cost function C(n) is increasing and weakly convex, that is, $C'(n)>0$ and $C''(n)\ge 0$. The firms are ex ante homogenous whose production cost X conforms to the distribution of $F(\cdot )$ on [0, V], with strictly positive density $f(\cdot )$. Assume all players are risk-neutral.

For those invited firms, let $\{X_{i}\}^{n}_{i=1}$ be n independent draws from the same distribution $F(\cdot )$, where $X_{i}$ is the production cost for firm i. The distribution of $F\left( \cdot \right)$ is common knowledge, yet the realization of $X_{i}$ is only observed by firm i. Let $X^{(k)}_n$ denote the kth lowest cost of the n invited firms and

$$\begin{aligned} X^{(1)}_n\le X^{(2)}_n\le \cdots \le X^{(n)}_n. \end{aligned}$$

Let $F^{(k)}_n\left( \cdot \right)$ and $f^{(k)}_n\left( \cdot \right)$ be the cumulative distribution function and probability density function of $X^{(k)}_n$.

We consider a sealed-bid first-price procurement auction, which is common in practice. It is well known that the symmetric equilibrium bidding strategy in a first-price procurement auction is given by (e.g., Krishna 2002, p.17),

$$\begin{aligned} b(x)=E\left[ X^{(1)}_{n-1}|X^{(1)}_{n-1}>x\right] =x+\int _{x}^{V} \frac{\bar{F}^{(1)}_{n-1}(y)}{\bar{F}^{(1)}_{n-1}(x)}dy, \end{aligned}$$

where $\bar{F}^{(1)}_{n-1}(x)=1-F^{(1)}_{n-1}(x)$ is the survival function. The firm with the lowest cost $X^{(1)}_n$ wins, and its revenue is equal to its bid $b(X^{(1)}_n)$. The rent for the winning firm is thus

$$\begin{aligned} R(n)=b(X^{(1)}_n)-X^{(1)}_n. \end{aligned}$$

(1)

The government’s payoff is equal to the net project benefit minus the invitation cost, which is

$$\begin{aligned} \Pi (n)=V-b(X^{(1)}_n)-C(n). \end{aligned}$$

(2)

It is worth noting that we do not model the government as a social planner. Instead, we model it as a government agency that cares about its own payoff rather than the overall social welfare. For example, the Department of Defense in the U.S. procures weapons systems, and its primary concerns are the budget spending and the performance of the weapons system procured.

We next consider the social welfare. Government spending is financed through taxation, which includes the payment to the winning firm, $b(X^{(1)}_n)$, and the invitation cost C(n). We assume there is a marginal cost of public funds, $\lambda \in \left[ 0,1\right)$, due to the allocative distortion caused by taxation (Laffont and Tirole 1987). The social welfare W(n) is then measured by the sum of the firms’ winning rent in (1) and the government payoff in (2), minus the distortion cost of public funds, that is

$$\begin{aligned} W(n)=V-X^{(1)}_n-\lambda b(X^{(1)}_n)-(1+\lambda )C(n). \end{aligned}$$

(3)

By introducing $\lambda$, the marginal cost of public funds, into our model of public procurements, we provide a broader definition of social welfare than that in standard auction literature, e.g., Szech (2011), which corresponds to the special case of $\lambda =0$ in our model.

The Revenue Equivalence Theorem shows that the expected payment to the winning firm is equal to the expected second-lowest production cost, that is, $E[b(X^{(1)}_n)]=E[X^{(2)}_n]$. To further characterize the properties of $E[X^{(1)}_n]$ and $E[X^{(2)}_n]$, we make the following standard assumption in procurement auctions, that the distribution of X satisfies the property of decreasing reversed hazard rate.

Definition 1

The distribution of X is of decreasing reversed hazard rate (DRHR) if its reversed hazard rate of f(x) / F(x) is decreasing in x.

The DRHR assumption in the procurement auction is analogous to the regularity condition of increasing failure rate in the standard ascending price auction (Myerson 1981). The difference is that in a procurement auction, the bidder offering the lowest bid wins the auction, whereas in a standard ascending price auction the bidder offering the highest bid wins. There are many examples of DRHR distributions, such as uniform, truncated normal and exponential distributions. Lemma 1 below provides some properties of $E[X^{(1)}_n]$ and $E[X^{(2)}_n]$.

Lemma 1

• (i) $E[X^{(1)}_n]$ is strictly decreasing and strictly convex in n, and $\lim _{n\rightarrow \infty } E[X^{(1)}_n]=0$.

• (ii) If the distribution of X is of DRHR, then $E[X^{(2)}_n]$ is strictly decreasing and strictly convex in n, and $\lim _{n\rightarrow \infty }E[X^{(2)}_n-X^{(2)}_{n+1}]=0$.

• (iii) If the distribution of X is of DRHR, then $E[R(n)]=E[X^{(2)}_n-X^{(1)}_n]$ is strictly decreasing and strictly convex in n, and $\lim _{n\rightarrow \infty }E[R(n)]=0.$

Proof

Please refer to the Appendix for all the omitted proofs in this paper. $\square$

Lemma 1 is analogous to Lemma 1–4 in Szech (2011).⁸ The monotonicity property of $E[X^{(1)}_n]$ is straightforward as $X^{(1)}_n$ is the smallest order statistic. As n increases, $E[X^{(1)}_n]$ will naturally decrease and converge to zero. The similar property holds for $E[X^{(2)}_n]$ under the assumption of DRHR. If the distribution of X is of DRHR, we have the result that the expected rent of the winning firm will gradually squeeze out as the number of firms increases. A direct implication of Lemma 1 is that

$$\begin{aligned} E\left[ X^{(2)}_n-X^{(2)}_{n+1}\right] >E\left[ X^{(1)}_n-X^{(1)}_{n+1}\right] , \end{aligned}$$

(4)

that is, if one more firm joins the auction, the expected value of $E[X^{(2)}_n]$ drops faster than $E[X^{(1)}_n]$.

The bureaucrat runs the auction on behalf of the government, and he decides how many firms to invite. In the absence of corruption, the bureaucrat just chooses the optimal number of firms, denoted by $n^*$, that maximizes the expected payoff of the government. We are also interested in social welfare and denote $n^{**}$ as the efficient number of firms that maximizes the expected social welfare. By definition,

$$\begin{aligned} n^{*}=\arg \max _{n}E[\Pi (n)]\text { and } n^{**}=\arg \max _{n}E[W(n)]. \end{aligned}$$

The results in Lemma 1 imply that both $E[\Pi (n)]$ and E[W(n)] are concave in n under the DRHR assumption, and therefore, both $n^*$ and $n^{**}$ are well-defined and finite. Our first result is that, when there is no corruption, the bureaucrat will invite more than the socially optimal number of firms to the auction.

Proposition 1

If the distribution of X is of DRHR, then

$$\begin{aligned} n^{*}\ge n^{**}. \end{aligned}$$

(5)

The over-invitation result is not surprising, and a similar result is also reported in Szech (2011, Proposition 1) in a model of ascending second-price auction. Here, we instead study a descending first-price auction, and more importantly, we explicitly consider the distortion cost of public funds and provide a more general definition of social welfare, which takes Szech’s model as a special case of $\lambda =0$. Therefore, Proposition 1 provides a non-trivial extension of the results in the literature.

We would like expatiate a little more on the insights of the over-invitation result. For increasing n, the marginal change in the expected government payoff is

$$\begin{aligned} \Delta E[\Pi (n)]=E\left[ X^{(2)}_n-X^{(2)}_{n+1}\right] -(C(n+1)-C(n)), \end{aligned}$$

and we can normalize the marginal change of the expected social welfare as

$$\begin{aligned} \frac{1}{1+\lambda }\Delta E[W(n)]=\frac{1}{1+\lambda }E\left[ X^{(1)}_n-X^{(1)}_{n+1}\right] + \frac{\lambda }{1+\lambda }E\left[ X^{(2)}_n-X^{(2)}_{n+1}\right] -(C(n+1)-C(n)). \end{aligned}$$

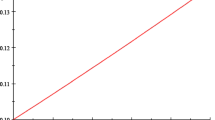
Inequality (4) then implies that $\Delta E[\Pi (n)]$ is greater than $\frac{1}{1+\lambda }\Delta E[W(n)]$. That is, for any given n, the marginal government payoff is greater than the normalized marginal social welfare, and therefore, the expected government payoff approaches its maximum more slowly than the expected social welfare. The economic intuition is that, when n increases, the expected winning rent of the firms decreases, which is ignored by the government but is taken into account in the total social welfare. Figure 1 below illustrates the result of over-invitation.

Fig. 1

Over-invitation Result: When there is no corruption and a positive invitation cost, the bureaucrat will invite more than the socially optimal number of firms to the auction

We next provide a simple example where X conforms to a uniform distribution, that may help illustrate the over-invitation result.

Example 1

Let $X\sim U[0,V]$, and $C(n)=nc$, where c is constant. The distribution functions of $X^{(1)}_n$ and $X^{(2)}_n$ are given in (12) in the Appendix, and it follows that $E[X^{(1)}_n]=\frac{V}{n+1}$ and $E[X^{(2)}_n]=\frac{2V}{n+1}$.

With no corruption, the bureaucrat chooses n to maximize the government’s expected payoff,

$$\begin{aligned} \max _{n}E[\Pi (n)]=V-E[X^{(2)}_n]-nc=V-\frac{2}{n+1}V-nc. \end{aligned}$$

The marginal government payoff is $\Delta E[\Pi (n)]=\frac{2V}{(n+1)(n+2)}-c$, and the optimal condition for $n^{*}$ is

$$\begin{aligned} n^{*}(n^{*}+1)\le \frac{2V}{c}<(n^{*}+1)(n^{*}+2). \end{aligned}$$

We next solve the problem of maximizing the expected social welfare:

$$\begin{aligned} \max _{n}E[W(n)]=V-E[X^{(1)}_n]-\lambda E[X^{(2)}_n]-(1+\lambda )nc. \end{aligned}$$

The normalized marginal change in social welfare is

$$\begin{aligned} \frac{1}{1+\lambda }\Delta E[W(n)]{=}\frac{1}{1+\lambda }\cdot \frac{V}{(n+1)(n+2)}+ \frac{\lambda }{1+\lambda }\cdot \frac{2V}{(n+1)(n+2)}-c{<}\Delta E[\Pi (n)]. \end{aligned}$$

The optimal condition for $n^{**}$ is thus

$$\begin{aligned} n^{**}(n^{**}+1)\le \frac{(1+2\lambda )V}{(1+\lambda )c} <(n^{**}+1)(n^{**}+2). \end{aligned}$$

It follows that, $n^{*}\ge n^{**}$, as $\frac{1+2\lambda }{1+\lambda }\le 2$. For example, if $\lambda =0.2$, $c=2$ and $V=36$, then we have $n^{*}=5$ and $n^{**}=4$. This result confirms the over-invitation result of (5) in Proposition 1.

3 Corruption in procurement auctions

We next introduce corruption into the public procurement auction. As Jain (2001) states, corruption is an act in which the power of public office is used for personal gain in a manner that contravenes the rules of the game. In this paper, we consider the case whereby a corrupt bureaucrat has discretion to determine the number of firms to invite and can request a bribe of B(n) from the winning firm. We assume that the invited firms are fully aware of the request and that they accept this tacit rule prior to the auction. As only the winner pays the bribe, our setting rules out sunk investments for the firms as lobbying activities, as in all-pay auctions or other standard rent-seeking models.

In particular, we consider two forms of bribery: a fixed bribe amount, $B(n)=B$, and a proportional bribe, $B(n)=\eta b(X^{(1)}_n)$, $\eta \in [0,1]$. In the first case, the fixed bribe amount is specified by the bureaucrat, and all the firms know this condition before offering their bids. In the second case, the fraction $\eta$ is exogenously given, and the bribe is just a proportion of the winning revenue. These two forms of bribery are relatively pervasive in the real practice of public procurements.⁹

We assume that the bureaucrat cares about not only his private bribe B(n) but also the government payoff, $\Pi (n)$. Specifically, the bureaucrat’s payoff is a weighted average of these two terms, as follows:

$$\begin{aligned} U(n)=\alpha \Pi (n)+(1-\alpha )B(n), \end{aligned}$$

where $\alpha \in [0,1]$ is the weight for government payoff. We may think of the simple utility function U(n) as a reduced form description of a situation in which the bureaucrat is more (high $\alpha$) or less (low $\alpha$) inclined to serve the government’s interest. For example, $\alpha$ is higher if he is a benevolent officer or is more concerned about being found out and punished.

We do not consider a penalty for corruption if detected, although it could be introduced in a straightforward way, for example, a detecting probability that is decreasing in $\alpha$ and a penalty that is proportional to B(n). Our main focus here is on the effects of corruption on equilibrium competition and social welfare in the procurement auction. The introduction of a penalty will at most temper but will not change the direction of the results; therefore, we avoid that complication in our model.

3.1 Fixed bribe

In the case of fixed bribe, the bureaucrat requests the winning firm to pay a fixed bribe of B after the auction. As mentioned above, the firms are fully aware of the request prior to the auction, and accept it as a tacit rule. The fixed amount of bribe B therefore appears to be a part of the cost, conditional on winning the auction. The virtual cost for firm i is now $X_{i}^{\prime }=X_{i}+B$, conditional on winning. To avoid confusion, let subscript ‘I’ denote the case of fixed bribe. The symmetric equilibrium bidding strategy is then $b_{I}(X_i)=b(X'_i)$, which satisfies the following property:

Lemma 2

The symmetric equilibrium bidding strategy in a first-price procurement auction, with a fixed bribe of B, is given by

$$\begin{aligned} b_{I}(x)=E[X^{(1)}_{n-1}|X^{(1)}_{n-1}>x]+B=b(x)+B. \end{aligned}$$

That is, all firms will increase the bid by the amount of the bribe.

As a result, the lowest cost firm wins with a bid of $b(X^{(1)}_n)+B$, and the payment it receives is the same as the bid. Thus, the rent for the winning firm remains the same as in Eq. (1), which is

$$\begin{aligned} R_{I}(n)=b(X^{(1)}_n)-X^{(1)}_n. \end{aligned}$$

(6)

However, under the fixed bribe, the government needs to pay the amount of B more than before in Eq. (2), and its payoff is now

$$\begin{aligned} \Pi _{I}(n)=V-B-b(X^{(1)}_n)-C(n). \end{aligned}$$

(7)

The social welfare is equal to the sum of the rent of the winning firm (6), the government’s payoff (7), and the fixed bribe for the bureaucrat B, and then minus the distortion cost of public funds $\lambda (B+b(X^{(1)}_n)+C(n))$. Thus, the total social welfare is

$$\begin{aligned} W_{I}(n)=V-X^{(1)}_n-\lambda (B+b(X^{(1)}_n))-(1+\lambda )C(n). \end{aligned}$$

(8)

Compared with Eq. (3), the social welfare in the case of no corruption, we find that $W_{I}(n)$ is smaller than W(n) by the extra cost of $\lambda B$.

The corrupt bureaucrat’s optimization problem is

$$\begin{aligned} \max E[U_{I}(n)]=\alpha E[\Pi _{I}(n)]+(1-\alpha )B. \end{aligned}$$

(9)

When the distribution of X is of DRHR, $E[\Pi _{I}(n)]$ is strictly increasing and concave in n. The optimization conditions for Eq. (9) are thus

$$\begin{aligned} E[X^{(2)}_{n-1}-X^{(2)}_n]\ge C(n)-C(n-1) \end{aligned}$$

and

$$\begin{aligned} E[X^{(2)}_n-X^{(2)}_{n+1}]< C(n+1)-C(n), \end{aligned}$$

which are equivalent to the optimization conditions in the case of no corruption. If we denote the optimal number of firms in this case of fixed bribe as $n_{I}^{*}$, then the following result is obvious.

Proposition 2

If the distribution of X is of DRHR, then under a fixed bribe, a corrupt bureaucrat will invite the same number of firms into the procurement auction, as in the case of no corruption. That is,

$$\begin{aligned} n_{I}^{*}=n^{*}. \end{aligned}$$

(10)

However, the fixed bribe causes a welfare loss of $\lambda B$.

The result indicates that bribery in the form of a fixed bribe has no effect on equilibrium competition. The intuition underlying this result is straightforward. As the bribe is fixed at a given level, the bureaucrat’s objective remains the same as in the benchmark case of no corruption, which is to maximize the expected government payoff. Therefore, the fixed bribe will not change the incentive for the corrupt bureaucrat to invite the firms. However, it changes resource allocation and the social welfare in equilibrium. As all the firms mark up their bid by the fixed amount of bribe B, the bribe is actually paid by the government and will not hurt the firms. Furthermore, as the government expenditure increases by B in this case, the distortion cost of public funds implies that the amount of social welfare loss is $\lambda B$. In other words, we then have $W_{I}(n_{I}^{*})-W(n^{*})=-\lambda B$ from Eqs. (3), (8) and (10).

3.2 Proportional bribe

We next consider the case of proportional bribe, and assume that the winning firm needs to pay a proportion of $\eta \in [0,1]$ of its winning bid to the corrupt bureaucrat. We first derive the new equilibrium bidding strategy of the firms, which shows that if the bureaucrat requests a bribe of the proportion $\eta$ of the winning bid, the firms will also exaggerate their bids proportionally by $1/(1-\eta )$.

Lemma 3

The symmetric equilibrium bidding strategy in a first-price procurement auction, with a proportion bribe, is given by

$$\begin{aligned} b_{P}(x)=\frac{1}{1-\eta }E\left[ X^{(1)}_{n-1}|X^{(1)}_{n-1}>x\right] =\frac{b(x)}{1-\eta }. \end{aligned}$$

That is, all firms will increase the bid by the ratio of $\frac{1}{1-\eta }$.

Under the proportional bribe, the rent for the winning firm is

$$\begin{aligned} R_{P}(n)=(1-\eta )b_{P}(X^{(1)}_n)-X^{(1)}_n=b(X^{(1)}_n)-X^{(1)}_n, \end{aligned}$$

where the subscript ‘P’ denotes the case of proportional bribe. It is obvious that the government’s payoff function is no longer the same as in Eq. (2), and it is now

$$\begin{aligned} \Pi _{P}(n)=V-b_{P}(X^{(1)}_n)-C(n)=V-\frac{b(X^{(1)}_n)}{1-\eta }-C(n). \end{aligned}$$

The corrupt bureaucrat receives the bribe $B(n)=\eta b_{P}(X^{(1)}_n)$. As before, the total social welfare is the sum of the payoffs of the three parties, minus the distortion cost of public funds, which is

$$\begin{aligned} W_{P}(n)=V-X^{(1)}_n-\frac{\lambda }{1-\eta }b(X^{(1)}_n)-(1+\lambda )C(n). \end{aligned}$$

The corrupt bureaucrat’s payoff function is a weighted average of his bribe and the government’s payoff, and his problem is thus

$$\begin{aligned} \max E[U_{P}(n)]=\alpha E[\Pi _{P} (n)]+(1-\alpha )\eta E[b_{P}(X^{(1)}_n)]. \end{aligned}$$

(11)

Under the DRHR assumption, we know that $E[\Pi _{P} (n)]$ is concave, and $\eta E[b_{P}(X^{(1)}_n)]$ is convex in n, and this does not imply that a convex combination of them is necessarily concave. However, $E[U_{P}(n)]$ can be rewritten as

$$\begin{aligned} E[U_{P}(n)]=\alpha (V-C(n))-\frac{\alpha -(1-\alpha )\eta }{1-\eta }E[X^{(2)}_n]. \end{aligned}$$

We know $E[X^{(2)}_n]$ is strictly decreasing and convex in n, and thus $E[U_{P}(n)]$ is strictly concave if $\alpha -(1-\alpha )\eta > 0$.

Lemma 4

If the distribution of X is of DRHR and $\eta <\frac{\alpha }{1-\alpha }$, then $E[U_{P}(n)]$ is strictly concave in n.

The condition of $\eta <\frac{\alpha }{1-\alpha }$ means that the bribe proportion is small relative to the weight of government payoff in the corrupt bureaucrat’s utility function. Considering that the sizes of public procurements usually are quite large, we could reasonably think that $\eta$ is normally small and this condition would be satisfied in most cases. If it does not hold and $\eta \ge \frac{\alpha }{1-\alpha }$, we would be in the environments of extreme corruption, in which either the weight $\alpha$ is quite small or the bribe proportion $\eta$ is quite large, then the bureaucrat’s objective function, $E[U_{P}(n)]$, is strictly decreasing in n, and thus, the optimal number of firms is equal to 1, i.e., the single bid scenario. The problem then becomes trivial in this case. Here, we consider the non-trivial scenario under the condition of $\eta <\frac{\alpha }{1-\alpha }$. Denote $n^{*}_{P}$ as the optimal number of firms in the case of proportional bribe, and then we have the following result.

Proposition 3

If the distribution of X is of DRHR and $0<\eta <\frac{\alpha }{1-\alpha }$, then under a proportional bribe, a corrupt bureaucrat invites either fewer or more firms into the procurement auction than in the benchmark case of no corruption. Specifically,

• (i) if $\alpha \in [0,1/2]$, then $n_{P}^{*}\le n^{*}$;

• (ii) if $\alpha \in [1/2,1]$, then $n_{P}^{*}\ge n^{*}$.

The optimal number of firms under a proportional bribe can be either greater or smaller than the competition without corruption, which depends on the relative magnitude of two opposite effects: (i) the first term of Eq. (11), $E[\Pi _{P}(n)]$, implies that he may encourage competition, as firms raise their bids and therefore the distribution of bids turns out to be more dispersed than before, which decreases the level of competition in the auction; (ii) the second term of Eq. (11) implies that the bureaucrat may discourage competition, as $E[b_{P}(X^{(1)}_n)]$ is decreasing in n. Thus, the effect of the proportional bribe on the competition depends on how much the bureaucrat weights his individual interest relative to the government payoff. As a result, when the corrupt bureaucrat cares more about his personal interest, $\alpha <1/2$, he will dampen competition in the auction, and when he cares more about the government payoff, $\alpha >1/2$, he will encourage competition.

Finally, let us turn to the socially efficient number of firms in different cases. If we denote the socially optimal number of firms in the cases of fixed and proportional bribe by $n_{I}^{**}$ and $n_{P}^{**}$ respectively, then we have the following result.

Proposition 4

The order of socially efficient numbers of firms is

$$\begin{aligned} n^{**}=n^{**}_{I}<n^{**}_{P}. \end{aligned}$$

This result suggests that the effects of bribery on efficient competition vary on the formats of bribery. Although the fixed bribe does not change the socially efficient competition, the bribery incurs some social cost. Specifically, we have

$$\begin{aligned} W_{I}(n_{I}^{**})+\lambda B=W(n^{**}), \end{aligned}$$

from Eqs. (3) and (8). Under proportional bribery, firms exaggerate their bids and the distribution of the winning bids becomes more dispersed, which implies a larger number of firms for social efficiency.

Let us extend the previous numerical example to the case of corruption, which helps us to understand the various effects of corruption.

Example 2

We introduce corruption into our previous Example 1 of uniform distribution. We have already known that $E[X^{(1)}_n]=\frac{V}{n+1}$ and $E[X^{(2)}_n]=\frac{2V}{n+1}$. In the case of a fixed bribe B, we have

$$\begin{aligned} E[U_{I}(n)]=\alpha E[\Pi _{I}(n)]+(1-\alpha )B. \end{aligned}$$

The optimal number of firms is $n_{I}^{*}=n^{*}$ as shown in Proposition 2.

In the case of proportional bribe, we have

$$\begin{aligned} E[U_{P}(n)]= & {} \alpha (V-C(n))-\frac{\alpha -(1-\alpha )\eta }{1-\eta }E[X^{(2)}_n]=\left[ \alpha -\frac{\alpha -(1-\alpha )\eta }{1-\eta }\frac{2}{n+1}\right] \\&\times V-\alpha nc. \end{aligned}$$

If $\eta \ge \frac{\alpha }{1-\alpha }$, then $E[U_{P}(n)]$ is strictly decreasing in n, so $n_{P}^{*}=1$, that is the minimum possible number of firms. The problem then becomes trivial in this case.

Let us consider $0<\eta <\frac{\alpha }{1-\alpha }$, then $E[U_{P}(n)]$ is concave in n. The optimal condition for $n_{P}^{*}$ is

$$\begin{aligned} n(n+1)\le \frac{\alpha -(1-\alpha )\eta }{(1-\eta )\alpha }\cdot \frac{2V}{c}<(n+1)(n+2). \end{aligned}$$

• If $\alpha \le 1/2$, we have $\frac{\alpha -(1-\alpha )\eta }{(1-\eta )\alpha }\le 1$, and then $n_{P}^{*}\le n^{*}$. For example, if $c=2$ and $V=36$, we have already known $n^*=5$. Let us now select $\alpha =1/3$ and $\eta =1/4$ such that $\frac{\alpha -(1-\alpha )\eta }{(1-\eta )\alpha }=2/3$, we have the optimal number of firms under the proportional bribe, $n^{*}_{P}=4$, which is less than $n^{*}=5$.

• If $\alpha \ge 1/2$, we have $\frac{\alpha -(1-\alpha )\eta }{(1-\eta )\alpha }\ge 1$, and then $n_{P}^{*}\ge n^{*}$. For example, if $c=2$ and $V=36$, and then $n^{*}=5$. Now we select $\alpha =2/3$ and $\eta =2/5$ such that $\frac{\alpha -(1-\alpha )\eta }{(1-\eta )\alpha }=4/3$, we have the optimal number of firms under the proportional bribe, $n^*_{P}=6$, which is greater than 5.

4 Further discussion

4.1 Second-price procurement auctions

It is a natural question whether corruption has different effects on competition in the second-price procurement auction. As we know, bidding the true production cost $X_{i}$ is a weakly dominant strategy in the second-price auction. In the benchmark case of no corruption, it is easy to show that the result of Proposition 1 holds in the second-price scenario. We now consider the results with corruption.

In the case of fixed bribe, the bureaucrat requests the winning firm to pay a fixed bribe of B after the auction, and then the fixed bribe amount appears to be a part of firms’ cost condinional on winning the auction. As the virtual cost for firm i is now $X'_{i}=X_{i}+B$, bidding $X'_i$ is thus a weakly dominant strategy for firm i, and all firms will mark up their bids by the fixed amount of B. Therefore, the fixed bribe has the same effect on the bidding function from Lemma 2, and we can derive the same result of Proposition 2 in the second-price setting.

Considering the case of a proportional bribe, we assume that the winning firm needs to pay a proportion of $\eta$ of its revenue to the corrupt bureaucrat. We have the following result:

Lemma 5

If the winning firm needs to pay a proportion of $\eta$ of its revenue to the corrupt bureaucrat in the second-price procurement auction, bidding $\frac{1}{1-\eta }$ times the production cost is a weakly dominant strategy.

Recalling Lemma 3, it is obvious that the results of a proportional bribe all remain the same in the second-price auction setting. In sum, the Revenue Equivalence result between the first- and second-price auctions still holds with corruption. Therefore, the effects of corruption on equilibrium competition and social welfare are the same in both first- and second-price procurement auctions.

4.2 Information disclosure

As shown in the recent literature (Johnson and Myatt 2006; Ganuza and Penalva 2010; Jewitt and Li 2015), information disclosure may induce more dispersed distribution of consumers’ valuations. The intuition is that when consumers’ preferences are horizontally differentiated, revealing product information may drive up the valuations of some consumers, while driving down those of others; therefore, the distribution of posterior consumer valuations becomes more dispersed.

A similar argument can be applied in our context of public procurements. For example, the firms may have different expertise or areas of specialization, and revealing information on the details of the public contract may have differentiated impacts on their cost estimates. That information may be good news for some firms when they find it is a good match for their areas of specialization, whereas it may be bad news for others. Consequently, the distribution of firms’ cost estimates becomes more dispersed under information disclosure. Though similar arguments and results have been provided in Ganuza and Penalva (2010, Theorem 6) and Szech (2011, Proposition 2), we think it would still be desirable to provide some further discussions here, where we explicitly consider the distortion cost of public funds and the possibility of corruption in public procurement auctions.

Let us denote Y as the new cost for the firms after information disclosure, and the corresponding distribution is $G(\cdot )$. Compared with the initial cost of X with distribution $F(\cdot )$, we know the distribution of Y is more dispersed, or formally, $X\preceq _{disp}Y$, defined as follows:

Definition 2

The random variable X is smaller than Y in the dispersive order, denoted by $X\preceq _{disp}Y$, if

$$\begin{aligned} F^{-1}(q)-F^{-1}(p)\le G^{-1}(q)-G^{-1}(p) \end{aligned}$$

for all $0<p<q<1$.

It is intuitive that when the distribution of firms’ cost estimates becomes more dispersed, the procurement auction becomes less competitive than before, and the winning rent of the firms will increase. It is then natural that, in general, more firms need to be invited in this case. The similar results hold in our procurement settings with or without corruption. Specifically, let $n^{*}$ ($n^{**}$) denote the optimal (socially efficient) number of firms under the distribution $F(\cdot )$; let $\hat{n}^{*}$ ($\hat{n}^{**}$) denote the optimal (socially efficient) number of firms under the distribution $G(\cdot )$; and the subscripts ‘I’ and ‘P’ denote the cases of fixed bribe and proportional bribe, respectively. Proposition 5 below then shows that, for government payoff and social welfare maximization, with or without corruption, and with a fixed bribe or a proportional bribe, when the distribution of firms’ costs become more dispersed under information disclosure, more firms need to be invited for the competition in the public procurement.

Proposition 5

If $X\preceq _{disp}Y$, and the distribution of $F(\cdot )$ and $G(\cdot )$ are DRHR, then we have

$$\begin{aligned}&n^{*}\le \hat{n}^{*},\; n^{**}\le \hat{n}^{**};\\&n^{*}_{I}\le \hat{n}^{*}_{I},\; n^{**}_{I}\le \hat{n}^{**}_{I};\\&n^{*}_{P}\le \hat{n}^{*}_{P},\; n^{**}_{P}\le \hat{n}^{**}_{P}. \end{aligned}$$

The results may raise the concern that, with the possibility of information manipulation, the bureaucrat can make it impossible to infer the existence of corruption from the observation of the number of firms invited into the procurement auction. For example, suppose that the ex ante cost distribution is $F(\cdot )$, the optimal number of firms without corruption is $n^{*}$, and that number under a proportional bribe is $n^{*}_{P}$ which is smaller than $n^{*}$. If the bureaucrat has the discretion of manipulating information, then he can induce a more dispersed cost distribution of $G(\cdot )$ through information disclosure, and invite $\hat{n}^{*}_{P}$ firms into the auction, which is larger than $n^{*}_{P}$ and possibly closer to $n^{*}$. If the government is not aware of the change of underlying cost distribution, it may believe that the bureaucrat is honest as he chooses a number of firms that is close to $n^{*}$.

4.3 Government regulations

The above results show that the effects of corruption on equilibrium competition and social welfare vary across different forms of bribery. They also raise the question of optimal and effective regulations by a central government to ensure sound public services and improve social welfare. In the case of fixed bribe, although it will not affect the equilibrium competition, it does incur more public spending by the government, which induces social welfare loss. To prevent corruption in that form, the government needs to conduct a strict audit of the project budget, guarantee sufficient transparency over the entire competition process, and carefully evaluate the cost estimates reported by firms.

In the case of proportional bribe, the corrupt bureaucrat may favor either less or more competition in the auction, depending on how much he weights his private interest relative to the government payoff. In the case of extreme corruption, e.g., $\eta \ge \frac{\alpha }{1-\alpha }$, the bureaucrat prefers as less competition as possible and will invite only a single firm to the auction. In the case of moderate corruption, e.g., $\eta <\frac{\alpha }{1-\alpha }$, if the corrupt bureaucrat weights his private interest much higher (i.e., $\alpha <1/2$ in Proposition 3), he would also have incentives to dampen competition in the auction. In this case, it would be helpful for the government or regulators to impose requirements on the minimum number of firms in public procurements. For example, in the regulations for public procurements in the European Union, a public authority must invite at least five candidates possessing the capabilities required to submit tenders in the restricted procedure.¹⁰

5 Concluding remarks

It is important to study the mutual interaction between corruption and competition in public procurements. In this paper, we examine the specific effects of corruption on equilibrium competition and social welfare in a public procurement auction. In our model, it is costly for a government to invite the firms to the auction, and a bureaucrat who runs the auction on behalf of the government may request a bribe from the winning firm. The bribery can be in the form of either a fixed bribe or a proportional bribe.

We show that the effects of corruption on equilibrium competition and social welfare vary across different forms of bribery. First, under a fixed bribe, corruption does not affect equilibrium competition, but it does induce social welfare loss in equilibrium. This is because, in expectation of the fixed bribe, all firms will mark-up their bids by the same amount of bribe, which will not change the bureaucrat’s incentive to invite firms, and the level of equilibrium competition remains the same as before. In this case, it is the government that pays the fixed bribe in the end, and the increased government spending implies social welfare loss due to the distortion cost of public funds.

Second, under a proportion bribe, we show that all firms increase their equilibrium bids proportionally, and corruption may induce either less or more competition in equilibrium, depending on how the bureaucrat weights his private interest relative to the government payoff. The intuition is straightforward. On the one hand, as firms’ equilibrium bids become more dispersed, the auction becomes less competitive than before, which negatively affects the government’s payoff. On the other hand, less competition is beneficial for the bureaucrat’s private interest, as it implies more bribery from the winning firm. As a result, the relative magnitude between these two opposite effects determines the level of equilibrium competition. For instance, if the bureaucrat cares more about his private interest, he will invite fewer firms; otherwise, he will invite more firms.

We further discuss some policy implications of our model. First, our results suggest that the optimal regulation rules are necessarily contingent on the specific forms of corruptions. Therefore, it is essential to investigate the exact and dominant forms of bribery before proposing relevant regulation rules (Sect. 4.3). Second, given that information disclosure may dampen equilibrium competition in public procurements, a corrupt bureaucrat may intentionally manipulate information for his benefits. It is then crucial for regulators to carefully design the rules of information disclosure in public procurements (Sect. 4.2). Third, we also show that the main results of our model still hold in other auction formats (Sect. 4.1).

There are many possible directions for further extending the framework developed in this paper. For example, we may consider a model where a corrupt bureaucrat may have more discretion in manipulating the auction rules, besides just controlling the number of invited firms. Another interesting example would be scoring auctions with costly participation, which are common in public procurements. In a scoring auction, the quality information is commonly non-verifiable, and therefore a corrupt bureaucrat may also manipulate the scoring rules in exchange for a bribe.

Appendix: Omitted Proofs

Proof of Lemma 1

For result (i), it holds that $E[X^{(1)}_n] = \int _{0}^{V}xdF^{(1)}_{n}\left( x\right) =\int _{0}^{V} \left( 1-F\left( x\right) \right) ^{n}dx$, which implies

$$\begin{aligned} E[X^{(1)}_{n+1}-X^{(1)}_n] = -\int _{0}^{V}F\left( x\right) \left( 1-F\left( x\right) \right) ^{n}dx<0. \end{aligned}$$

As $f\left( x\right) >0$, then $E[X^{(1)}_{n+1}-X^{(1)}_n]$ is strictly increasing in n. We then show that $E[X^{(1)}_n]$ is strictly increasing and strictly convex in n. Furthermore, as $f\left( x\right) >0$, it is clear that $\lim _{n\rightarrow \infty }E[X^{(1)}_n]=\lim _{n\rightarrow \infty }\left[ \int _{0}^{V}\left( 1-F\left( x\right) \right) ^{n}\mathrm {d}x \right] =0$.

For result (ii), we first have

$$\begin{aligned} F^{(1)}_{n}(x)=1-\bar{F}(x)^n \text { and}\quad F^{(2)}_n(x)=1-\bar{F}(x)^{n-1}[1+(n-1)F(x)], \end{aligned}$$

(12)

where $\bar{F}(x)=1-F(x)$ is the survival function. It then follows that

$$\begin{aligned} E[X^{(2)}_n-X^{(2)}_{n+1}]=\int _{0}^{V}[F^{(2)}_{n+1}(x)-F^{(2)}_n(x)]dx=\int _{0}^{V} \frac{F^2(x)}{f(x)}dF^{(1)}_{n}(x)>0. \end{aligned}$$

When $F(\cdot )$ is of DRHR, the function $h(x)=\frac{F^2(x)}{f(x)}$ is increasing. Thus, $E[X^{(2)}_n]$ is strictly decreasing and convex in n. Furthermore, as $\lim _{x\rightarrow 0}h(x)=0$, we have $\lim _{n\rightarrow \infty }E[X^{(2)}_n-X^{(2)}_{n+1}]=0$.

For result (iii), we have $E[X^{(2)}_n-X^{(1)}_n]=\int _{0}^{V}[F^{(1)}_{n}(x)-F^{(2)}_n(x)]dx= \int _{0}^{V}\frac{F(x)}{f(x)}dF^{(1)}_{n}(x).$ Let $h(x)=\frac{F(x)}{f(x)}$, it is increasing under the DRHR assumption, and $\lim _{x\rightarrow 0}h(x)=0$. Following the same proof as in (i), we obtain the results. $\square$

Proof of Proposition 1

If $F(\cdot )$ is DRHR, $E[R(n)]=E[X^{(2)}_{n}-X^{(1)}_{n}]$ is strictly decreasing in n, then

$$\begin{aligned} E\left[ X^{(2)}_{n}-X^{(1)}_{n}\right]>E\left[ X^{(2)}_{n+1}-X^{(1)}_{n+1}\right] \Leftrightarrow E\left[ X^{(2)}_{n}-X^{(2)}_{n+1}\right] >E\left[ X^{(1)}_{n}-X^{(1)}_{n+1}\right] . \end{aligned}$$

From $n^{*}=\arg \max E[\Pi (n)]$, the optimization condition implies

$$\begin{aligned} E\left[ \Pi (n^{*})-\Pi (n^{*}-1)\right] \ge 0 >E[\Pi (n^{*}+1)-\Pi (n^{*})], \end{aligned}$$

which is equivalent to

$$\begin{aligned} E\left[ X^{(2)}_{n^{*}-1}-X^{(2)}_{n^{*}}\right] \ge C(n^*)-C(n^*-1) \end{aligned}$$

and

$$\begin{aligned} E\left[ X^{(2)}_{n^{*}}-X^{(2)}_{n^{*}+1}\right] <C(n^*+1)-C(n^*). \end{aligned}$$

Similarly, for $n^{**}=\arg \max E[W(n)]$, we have

$$\begin{aligned} \frac{1}{1+\lambda }E[X^{(1)}_{n^{**}-1}-X^{(1)}_{n^{**}}] +\frac{\lambda }{1+\lambda } E[X^{(2)}_{n^{**}-1}-X^{(2)}_{n^{**}}]\ge C(n^{**})-C(n^{**}-1) \end{aligned}$$

and

$$\begin{aligned} \frac{1}{1+\lambda }E\left[ X^{(1)}_{n^{**}}-X^{(1)}_{n^{**}+1}\right] +\frac{\lambda }{1+\lambda }E\left[ X^{(2)}_{n^{**}}-X^{(2)}_{n^{**}+1}\right] <C(n^{**}+1)-C(n^{**}). \end{aligned}$$

As for all n,

$$\begin{aligned} E\left[ X^{(2)}_{n-1}-X^{(2)}_{n}\right] >\frac{1}{1+\lambda }E\left[ X^{(1)}_{n-1} -X^{(1)}_{n}\right] +\frac{\lambda }{1+\lambda }E\left[ X^{(2)}_{n-1}-X^{(2)}_{n}\right] ; \end{aligned}$$

thus, the result of $n^{*}\ge n^{**}$ is obvious. $\square$

Proof of Lemma 2

Denote the new increasing bidding strategy in a symmetric equilibrium by $b_{I}\left( x\right)$, and bidders $i=2,\ldots ,n$ stick to this strategy. Denote $Y=\min \left\{ X_{2},\ldots ,X_{n}\right\} =X^{(1)}_{n-1}$, and then $b_{I}\left( Y\right)$ is the lowest bid of those bidders. Bidder 1 wins the auction whenever his bid $\beta <b_{I}\left( Y\right)$ bidder, and he chooses the bid to maximize his expected payoff

$$\begin{aligned} \mathrm {E}\left[ \left( \beta -x\right) \cdot \mathbf {1}_{\beta <b_{I}\left( Y\right) }\right] =\left( \beta -x-B\right) \left[ 1-F^{(1)}_{n-1}\left( b_{I}^{-1}\left( \beta \right) \right) \right] . \end{aligned}$$

Taking the first-order condition with respect to $\beta$, it follows that

$$\begin{aligned} \left[ 1-F^{(1)}_{n-1}\left( b_{I}^{-1}\left( \beta \right) \right) \right] -\left( \beta -x-B\right) \frac{f^{(1)}_{n-1}\left( b_{I}^{-1}\left( \beta \right) \right) }{b_{I}^{\prime }\left( b_{I}^{-1}\left( \beta \right) \right) }=0. \end{aligned}$$

In symmetric equilibrium, $\beta =b_{I}\left( x\right)$, and thus

$$\begin{aligned} b_{I}^{\prime }\left( x\right) \left[ 1-F^{(1)}_{n-1}\left( x\right) \right] -b\left( x\right) f^{(1)}_{n-1}\left( x\right) =-\left( x+B\right) f^{(1)}_{n-1}\left( x\right) , \end{aligned}$$

or equivalently,

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}x}\left[ b_{I}\left( x\right) \left[ 1-F^{(1)}_{n-1}\left( x\right) \right] \right] =-\left( x+B\right) f^{(1)}_{n-1}\left( x\right) . \end{aligned}$$

Since $b\left( V\right) =V+B$, then

$$\begin{aligned} b_{I}\left( x\right) =\int _{x}^{V}\left( y+B\right) \mathrm {d}\frac{ F^{(1)}_{n-1}\left( y\right) }{\bar{F}^{(1)}_{n-1}\left( x\right) }=\left( x+B\right) +\int _{x}^{V}\frac{\bar{F}^{(1)}_{n-1}\left( y\right) }{\bar{F}^{(1)} _{n-1}\left( x\right) }\mathrm {d}y. \end{aligned}$$

$\square$

Proof of Lemma 3

Denote the new increasing bidding strategy in a symmetric equilibrium by $b_{P}\left( x\right)$, and bidders $i=2,\ldots ,n$ stick to this strategy. Denote $Y=\min \left\{ X_{2},\ldots ,X_{n}\right\} =X^{(1)}_{n-1}$, and then $b_{P}\left( Y\right)$ is the lowest bid of those bidders. Bidder 1 wins the auction whenever his bid $\beta <b_{P}\left( Y\right)$ bidder, and he chooses bid to maximize his expected payoff

$$\begin{aligned} \mathrm {E}\left[ \left( \left( 1-\eta \right) \beta -x\right) \cdot \mathbf {1 }_{\beta <b_{P}\left( Y\right) }\right] =\left[ \left( 1-\eta \right) \beta -x\right] \left[ 1-F^{(1)}_{n-1}\left( b_{P}^{-1}\left( \beta \right) \right) \right] . \end{aligned}$$

Taking the first-order condition with respect to $\beta$, it follows that

$$\begin{aligned} \left( 1-\eta \right) \left[ 1-F^{(1)}_{n-1}\left( b_{P}^{-1}\left( \beta \right) \right) \right] -\left[ \left( 1-\eta \right) \beta -x\right] \frac{ f^{(1)}_{n-1}\left( b_{P}^{-1}\left( \beta \right) \right) }{b_{P}^{\prime }\left( b_{P}^{-1}\left( \beta \right) \right) }=0. \end{aligned}$$

In symmetric equilibrium, $\beta =b_{P}\left( x\right)$, and thus

$$\begin{aligned} b_{P}^{\prime }\left( x\right) \left[ 1-F^{(1)}_{n-1}\left( x\right) \right] -b_{P}\left( x\right) f^{(1)}_{n-1}\left( x\right) =-\frac{xf^{(1)}_{n-1}\left( x\right) }{1-\eta }, \end{aligned}$$

or equivalently,

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}x}\left[ b_{P}\left( x\right) \left[ 1-F^{(1)}_{n-1}\left( x\right) \right] \right] =-\frac{xf^{(1)}_{n-1}\left( x\right) }{1-\eta }. \end{aligned}$$

Since $b\left( V\right) =V/\left( 1-\eta \right)$, then

$$\begin{aligned} b_{P}\left( x\right) =\int _{x}^{V}\frac{y}{1-\eta }\mathrm {d}\frac{ F^{(1)}_{n-1}\left( y\right) }{\bar{F}^{(1)}_{n-1}\left( x\right) }=\frac{1}{1-\eta } b\left( x\right) . \end{aligned}$$

$\square$

Proof of Proposition 3

If $0<\eta <\frac{\alpha }{1-\alpha }$, Lemma 4 implies $E[U_{P}(n)]$ is strictly concave in n. Then, the optimization conditions for $n^{*}_{P}$ are

$$\begin{aligned} \frac{\alpha -(1-\alpha )\eta }{1-\eta }E\left[ X^{(2)}_{n-1}-X^{(2)}_n\right] \ge \alpha (C(n)-C(n-1)) \end{aligned}$$

and

$$\begin{aligned} \frac{\alpha -(1-\alpha )\eta }{1-\eta }E\left[ X^{(2)}_n-X^{(2)}_{n+1}\right] < \alpha (C(n+1)-C(n)). \end{aligned}$$

Compared with the optimization conditions for $n^{*}$, we imply that,

If $\frac{\alpha -(1-\alpha )\eta }{1-\eta }\le \alpha$, i.e., $\alpha \le 1/2$, then we have $n^{*}_{P}\le n^{*}$.

If $\frac{\alpha -(1-\alpha )\eta }{1-\eta }> \alpha$, i.e., $\alpha >1/2$, we have $n^{*}_{P}>n^{*}$. $\square$

Proof of Proposition 4

Apparently, $n^{**}_{I}=n^{**}$, in which both follow the same optimization conditions

$$\begin{aligned} \phi (n)\ge C(n)-C(n-1) \end{aligned}$$

and

$$\begin{aligned} \phi (n+1)< C(n+1)-C(n), \end{aligned}$$

where $\phi (n)=\frac{1}{1+\lambda }E\left[ X^{(1)}_{n-1}-X^{(1)}_n\right] +\frac{\lambda }{1+\lambda } E[X^{(2)}_{n-1}-X^{(2)}_n]$. Under proportional bribe, the optimization conditions are

$$\begin{aligned} \phi (n)+\frac{\alpha \eta }{(1+\alpha )(1-\eta )}E\left[ X^{(2)}_{n-1}-X^{(2)}_n\right] \ge C(n)-C(n-1) \end{aligned}$$

and

$$\begin{aligned} \phi (n+1)+\frac{\alpha \eta }{(1+\alpha )(1-\eta )}E\left[ X^{(2)}_n-X^{(2)}_{n+1}\right] < C(n+1)-C(n). \end{aligned}$$

Thus, we have $n^{**}_{P}>n^{**}$. $\square$

Proof of Lemma 5

Let us denote the increasing bidding function by $b_{P}(x)$ for a firm with cost x. Given other firms that follow this strategy, we derive the equilibrium for firm 1. Denote $Y=\min \{X_2,\ldots ,X_n\}$, and then $b_{P}(Y)$ is the lowest bid of those $n-1$ rival bidders. Bidder 1 wins the auction whenever his bid $\beta <b_{P}(Y)$. The objective function is

$$\begin{aligned} E\left[ ((1-\eta )b_{P}(Y)-x)\cdot 1_{\beta<b_{P}(Y)}\right] =E\left[ \left( b_{P}(Y)-\frac{x}{1-\eta }\right) \cdot 1_{\beta <b_{P}(Y)}\right] . \end{aligned}$$

It is clear that $\beta =\frac{x}{1-\eta }$ is a weakly dominant strategy. $\square$

Proof of Proposition 5

From Theorem 5.3.1 of Arnold et al. (2008), we have the following recurrence relationship

$$\begin{aligned} iE\left[ X^{(i+1)}_{n}\right] +(n-i)E\left[ X^{(i)}_{n}\right] =nE\left[ X^{(i)}_{n-1}\right] . \end{aligned}$$

Therefore,

$$\begin{aligned} E\left[ X^{(2)}_{n-1}-X^{(2)}_n\right] =\frac{2}{n} E\left[ X^{(3)}_{n}-X^{(2)}_n\right] \le \frac{2}{n} E\left[ Y^{(3)}_{n}-Y^{(2)}_{n}\right] =E\left[ Y^{(2)}_{n-1}-Y^{(2)}_{n}\right] , \end{aligned}$$

where the inequality is implied by the result that $E[X^{(j)}_{n}-X^{(j-1)}_{n}]\le E[Y^{(j)}_{n}-Y^{(j-1)}_{n}]$. Thus, we can conclude that $n^{*}\le \hat{n}^{*}$. Similarly, we can also prove the result that $n^{**}\le \hat{n}^{**}$. From Proposition 2, it is clear that $n^{*}_{I}=n^{*}$ and $\hat{n}^{*}_{I}=\hat{n}^{*}$, and then $n^{*}_{I}\le \hat{n}^{*}_{I}$. From Proposition 4, we have $n^{**}_{I}\le \hat{n}^{**}_{I}$.

Now let us prove that $n_{P}^{*}\le \hat{n}_{P}^{*}$. First, if $n_{P}^{*}$ is the corner solution that $n_{P}^{*}=1$, then $n_{P}^{**}\le \hat{n}_{P}^{**}$ is clearly true as $\hat{n}_{P}^{**}\ge 1$. Second, if $n_{P}^{*}$ is an interior solution such that the optimization conditions for $n^{*}_{P}$ are

$$\begin{aligned} \frac{\alpha -(1-\alpha )\eta }{1-\eta }E\left[ X^{(2)}_{n-1}-X^{(2)}_n\right] \ge \alpha (C(n)-C(n-1)) \end{aligned}$$

and

$$\begin{aligned} \frac{\alpha -(1-\alpha )\eta }{1-\eta }E\left[ X^{(2)}_n-X^{(2)}_{n+1}\right] < \alpha (C(n+1)-C(n)). \end{aligned}$$

Thus, we can conclude that $n^{*}_{P}\le \hat{n}^{*}_{P}$. The similar result $n^{**}_{P}\le \hat{n}^{**}_{P}$ can be implied from the optimization conditions as in the Proof of Proposition 4. $\square$