Dividing bads under additive utilities

Abstract

We compare the Egalitarian rule (aka Egalitarian Equivalent) and the Competitive rule (aka Comeptitive Equilibrium with Equal Incomes) to divide bads (chores). They are both welfarist: the competitive disutility profile(s) are the critical points of their Nash product on the set of efficient feasible profiles. The C rule is Envy Free, Maskin Monotonic, and has better incentives properties than the E rule. But, unlike the E rule, it can be wildly multivalued, admits no selection continuous in the utility and endowment parameters, and is harder to compute. Thus in the division of bads, unlike that of goods, no rule normatively dominates the other.

1 Introduction

User-friendly platforms like SPLIDDIT, Adjusted Winner, or The Fair Division Calculator¹ implement theoretical solutions to a variety of fair division problems, among them the classic distribution of a bundle of divisible private commodities (the “manna”). The key simplification is that these platforms ask visitors to report linear preferences (additive utilities), instead of potentially complex Arrow–Debreu preferences. Say we divide the family heirlooms: each participant on SPLIDDIT must distribute 1000 points over the different objects, and these “bids” are interpreted as her fixed marginal rates of substitution. Eliciting complementarities between these objects is already a complex task with six objects and is virtually impossible with ten or more. Hence the design choice of deliberately ignoring them. For the same reason combinatorial auction mechanisms never ask buyers to report a ranking of all subsets of objects (Bouveret and Lang 2008; de Vries and Vohra 2003; Cramton et al. 2006). The proof of the pudding is in the eating: visitors use these sites in the tens of thousands, fully aware of the interpretation of their bids (Goldman and Procaccia 2014).

Unsurprisingly, the two sites above implement the two division rules at the heart of the theoretical discussions in the last four decades: the Competitive Equilibrium with Equal Incomes, for short Competitive rule, or simply C rule, and the Egalitarian Equivalent, for short Egalitarian rule, or E rule (Varian 1974; Pazner and Schmeidler 1978). The latter finds an efficient allocation where everyone is indifferent between his share and a common fraction of the entire manna. The former identifies prices and a common budget constraint at which the competitive demands are feasible, and implements these demands.

Here we critically compare the performance of these two rules in the additive domain and for fair division problems involving bads (non disposable items generating disutility). Think of distributing job shifts among substitutable workers (house chores, teaching loads, babysitting), cities sharing noxious facilities, managers allocating cuts in the company’s workforce between their respective units, and so on.

In the much better understood problem of dividing goods (disposable, desirable commodities) both rules, Competitive and Egalitarian, are single-valued (utilitywise), easy to compute, and vary continuously in the marginal utility and endowment parameters. This is easy to check for the E rule, and for the C rule it follows from the celebrated Eisenberg–Gale theorem (Eisenberg and Gale 1959; Shafer and Sonnenschein 1993): the competitive allocations also maximize the Nash product of utilities over all feasible allocations. In particular both rules are welfarist: the feasible set of utility profiles is all we need to identify the profiles that each rule selects. And the C rule is the more appealing of the two because it alone picks an Envy Free allocation, and meets Maskin Monotonicity (MM), which in the additive domain has a very intuitive formulation, see below.

When we divide bads the normative comparison of the two rules yields much more nuanced conclusions. Both rules are still welfarist but the C rule selects, among efficient and feasible disutility profiles, all critical points of their Nash product: in turn a problem may have many different competitive utility profiles, even exponentially many in the smallest of the number of bads and of agents (Sect. 5.4). There is no easy way to deal with this embarrassing multiplicity, in particular any selection of the Competitive correspondence is discontinuous in the parameters, marginal utilities and endowments, of the economy; in fact any selection of the much larger correspondence of efficient and envy-free allocations is discontinuous as well (Sect. 6).

Thus classic monotonicity properties like Resource Monotonicity (when there is more of a bad to share, everyone is weakly worse off) and Population Monotonicity (when one more agent shares the bundle of bads, everyone is weakly better off) cannot be satisfied for any selection of the C rule, except in a local sense.

Finally, computing the competitive allocations of bads is not a convex optimization problem as in the case of goods, and with more than two agents we do not know of any efficient algorithms to discover them all, or just a reasonable single-valued selection.

By contrast the E rule to divide bads is the mirror image of the rule for goods, and shares the same properties: it is single-valued and remains continuous in the utility and endowment parameters, and population monotonic.

If the paramount concerns are simplicity of the definition and computation of the rule, and continuity in the parameters of the problem, the Egalitarian rule is called for. But the competitive rule retains its appeal because it is envy-free and meets the property we call Independence of Lost Bids (ILB). If at (one of) the chosen allocation(s) z agent i does not consume bad a, it (z) remains chosen when we increase the (marginal) disutility of i for a by an arbitrary amount: the division rule does not take into account how strongly i dislikes a if she does not eat any. This property is precisely Maskin monotonicity in our model.

Contents After the literature review in Sect. 2, the model is defined in Sect. 3, and our two division rules in Sect. 4. Section 5 discusses the multiplicity issue of the C rule, and gives precise bounds for simple problems with two agents or two bads. Section 6 is devoted to our main impossibility result: there is no continuous selection of the envy free and efficient correspondence. We also note that resource monotonicity is out of reach when we divide bads. Section 7 reformulates the MM axiom as ILB, and explains its role in characterizing the C rule.

2 Related literature

1. In the companion paper Bogomolnaia et al. (2017) we consider the more general problem of dividing a “mixed manna” containing both goods and bads, as when we dissolve a partnership with both valuable assets and liabilities. Our first observation is that the E rule is no longer well defined, because there may be no efficient allocation where everybody is indifferent to consuming a common fraction of the entire manna (or of any common benchmark bundle). So the C rule wins our contest by default.

Our main message is that mixed manna problems are of two types. If goods overwhelm bads² the C rule behaves just like in an all goods problem: it maximizes the product of utilities, yields a unique utility profile, is resource monotonic and continuous. But if instead bads overwhelm goods, we are back to the potentially messy situation of an all bads problems with a host of different competitive divisions corresponding to the critical points of the product of disutilities on the Pareto frontier.

Here we give precise bounds for the maximal number of competitive allocations (Theorem 1, Sect. 5), and for the number of connected components of the set of efficient and envy Free allocations (Proposition 2). This is the key to the non existence of a continuous selection of the C rule (Theorem 2, Sect. 6).

2. Our work complements recent research in algorithmic mechanism design on the fair division of goods, recognizing the practical convenience of additive utilities and the conceptual advantages of the C rule. For instance Megiddo and Vazirani (2007) show that the competitive utility profile depends continuously upon the rates of substitution and the total endowment; Jain and Vazirani (2010) and Lee (2015) find that it can be computed in time polynomial in the dimension $n+m$ of the problem (m is the number of goods). The C rule can be extended to cake-cutting problems, which allow for continuum of goods, and is still resource monotonic in this more general setup, see Segal-Halevi and Sziklai (2015).

Papers (Babaioff et al. 2017 and Budish 2011) propose extensions of the Competitive rule to indivisible goods; Budish and Cantillon (2010) applies such an extension to allocate seats in over-demanded courses.

3. Four decades earlier, the microeconomic literature on the fair division of private goods insisted on working in the much larger domain of Arrow–Debreu preferences, where the relation between the Nash product of utilities and the Competitive rule is lost, and provided several axiomatic characterizations of the latter. The most popular result appears first in Hurwicz (1979) and Gevers (1986), and is refined by Thomson (1987) and Nagahisa (1991): any efficient and Pareto indifferent rule meeting Maskin Monotonicity must contain the Competitive rule. A closer look at these seminal results, in particular the most recent one (Nagahisa 1991), reveals that they do not apply to the additive domain (Sect. 7). We fill this gap by, first, rewriting MM as the Independence of Lost Bids axiom then characterizing the C rule on the additive domain (Proposition 4).

3 Division problems and division rules

The finite set of agents is N with generic element i, and $|N|=n\ge 2$. The finite set of divisible bads is A with generic element a and $|A|=m\ge 2$. Without loss of generality, we assume there is one unit of each bad.

Agent i’s allocation (or share) is $z_{i}\in [0,1]^{A}$; the profile $z=(z_{i})_{i\in N}$ is a feasible allocation if $\sum _{N}z_{i}=e^{A}$, where $e^{A}$ is the vector in $\mathbb {R} _{+}^{A}$ with all coordinates equal to 1. The set of feasible allocations is $\Phi (N,A)$.

Each agent is endowed with linear preferences over $[0,1]^{A}$, represented by a disutility function $u_{i}\in \mathbb {R} _{+}^{A}$. Only the underlying preferences matter: for any $\lambda >0$, $u_{i}$ and $\lambda u_{i}$ carry the same information. This restriction is formally included in Definition 1 below.

Given an allocation z we write agent i’s corresponding disutility as $U_{i}=u_{i}\cdot z_{i}=\sum _{A}u_{ia}z_{ia}$.

The problem is trivial if the utility profile $U=0$ is feasible, as it is then the uniquely efficient profile. This happens if and only if each bad is harmless to at least one agent ($\forall a\exists i:u_{ia}=0$): we rule such problems out in the definitions below. Similarly if a bad a gives $u_{ia}=0$ for all i, it is harmless and can be ignored.

Definition 1

A division problem is a triple $\mathcal {Q}=(N,A,u)$ where $u\in \mathbb {R} _{+}^{N\times A}$ is such that the $N\times A$ matrix $[u_{ia}]$ has no null row, no null column, and there is at least one column with no null entry.

We write $\Psi (\mathcal {Q})$ for the set of feasible disutility profiles, and $\Psi ^{eff}(\mathcal {Q})$ for its subset of efficient disutility profiles. i. e., the South West frontier of $\Psi (\mathcal {Q})$.

The structure of efficient allocations in the linear domain, which is described by the following two lemmas, is key to several of our results. Given $z\in \Phi (N,A)$ we define the $N\times A$-bipartite consumption graph$\Gamma (z)=\{(i,a)|z_{ia}>0\}$.

Lemma 1

Fix a problem $\mathcal {Q} =(N,A,u)$. If $U\in \Psi ^{eff}(\mathcal {Q})$ there is some $z\in \Phi (N,A)$ achieving U such that $\Gamma (z)$ is a forest (an acyclic graph).

This implies that any efficient disutility profile can be represented by an allocation, where almost all $z_{ia}$ are zeros. Indeed, a forest with $n+m$ vertices contains at most $n+m-1$ edges and thus the allocation z with acyclic graph $\Gamma (z)$ has at least $(n-1)(m-1)$ zero entries. This observation has important consequences for the manipulability of division rules, which we discuss in Sect. 7.

Proof

Pick some z representing $U\in \Psi ^{eff}(\mathcal {Q})$ and assume there is a K-cycle $\mathcal {C}$ in $\Gamma (z)$: $z_{ka_{k}},z_{ka_{k-1}}>0$ for $k=1,\ldots ,K$, where $a_{0}=a_{K}$. It is enough to check that there is another allocation $z'$ representing U with $\Gamma (z')$ having fewer edges: then we repeatedly eliminate edges until the consumption graph has no cycles.

If $u_{ka_k}=0$ for some k, then we define $z'$ by giving $a_k$ to agent k in full. This does not change the vector of disutilities (indeed, by efficiency no agent with $u_{ia_k}>0$ consumed $a_k$ at z).

Assume that $u_{ka_k}>0$ for all k. Consider a product $\pi (\mathcal {C})=\prod _{k=1}^K \frac{u_{k a_{k-1}}}{u_{{k}a_{k}}}$. If $\pi (\mathcal {C})>1$ we can pick arbitrarily small positive numbers $\varepsilon _{k}$ such that $u_{k a_{k-1}}\varepsilon _{k-1}> u_{k a_{k}}\varepsilon _{k}$ for $k=1,\ldots , K$. Then the corresponding transfer to each agent k of $\varepsilon _{k}$ units of a bad $a_k$ against $\varepsilon _{k-1}$ units of a bad $a_{k-1}$ is a Pareto improvement, contradiction. Therefore, $\pi (\mathcal {C})\le 1$ but the opposite strict inequality is similarly ruled out so we conclude $\pi (\mathcal {C})= 1$.

Now if we perform a transfer as above with $u_{k a_{k-1}}\varepsilon _{k-1}= u_{k a_{k}}\varepsilon _{k}$ the utility profile U is unchanged. Define $z'$ by choosing the numbers $\varepsilon _{k}$ as large as possible for feasibility, this will bring at least one entry $z'_{k a_k}$ or $z'_{k a_{k-1}}$ along the cycle $\mathcal {C}$ to zero, so $\Gamma (z')$ has fewer edges.

The last statement follows at once from the fact that a forest with $n+m$ vertices contains at most $n+m-1$ edges. $\square$

Lemma 2

Fixing N, A, on an open dense subset $\mathcal {U}^{*}(N,A)$ of matrices $u\in \mathbb {R} _{+}^{N\times A}$, every efficient disutility profile $U\in \Psi ^{eff}(N,A,u)$ is achieved by a single allocation z.

Proof

Define $\mathcal {U}^{*}(N,A)$ to be a subset of $\mathbb {R}_{++}^{N\times A}$ such that for any cycle $\mathcal {C}$ in the complete bipartite graph $N\times A$ we have $\pi (\mathcal {C)}\ne 1$ (the condition from the proof of Lemma 1 fails). It is clearly an open dense subset of $\mathbb {R} _{+}^{N\times A}$.

We pick a problem $\mathcal {Q}\$with $u\in \mathbb {R} _{+}^{N\times A}$, fix $U\in \Psi ^{eff}(\mathcal {Q)}$ and assume there are two different $z,z^{\prime }\in \Phi (N,A)$ such that $u\cdot z=u\cdot z^{\prime }=U$. Pick a pair $1,a_{1}$ such that $z_{1a_{1}}>z_{1a_{1}}^{ \prime }$. Because $a_{1}$ is eaten in full there is some agent 2 such that $z_{2a_{1}}<z_{2a_{1}}^{\prime }$ and because $u_{2}\cdot z_{2}=u_{2}\cdot z_{2}^{\prime }$ there is some bad $a_{2}$ such that $z_{2a_{2}}>z_{2a_{2}}^{\prime }$. Continuing in this fashion we build a sequence $1,a_{1},2,a_{2},3,a_{3},\ldots$, such that $\{z_{ka_{k-1}}<z_{ka_{k-1}}^{\prime }$ and $z_{ka_{k}}>z_{ka_{k}}^{\prime }\}$ for all $k\ge 2$. The number of vertices is finite and so we must reach the same vertex twice. Denote the corresponding cycle by $\mathcal {C}$.

Note that the allocation $z^{\prime \prime }=\frac{ (z+z\prime )}{2}$ also represents U. By the construction $\Gamma (z^{\prime \prime })$ contains the cycle $\mathcal {C}$ and hence the argument from the proof of Lemma 1 implies $\pi _\mathcal {C}=1$. Thus u is not in $\mathcal {U}^{*}(N,A)$, as was to be proved. $\square$

We use two equivalent definitions of a division rule, one in terms of disutility profiles, the other, of feasible allocations. As this will cause no confusion, we use the “division rule” terminology in both cases. Notation: when we rescale each $u_{i}$ as $\lambda _{i}u_{i}$ the new profile is written $\lambda *u$.

Definition 2

(i) A division rule F associates to every problem $\mathcal {Q}=(N,A,u)$ a set of disutility profiles $F(\mathcal {Q})\subset \Psi (\mathcal {Q})$. Moreover $F(N,A,\lambda *u)=\lambda *F(N,A, u)$ for any rescaling $\lambda$ with $\lambda _{i}>0$ for all i.

(ii) A division rule f associates to every problem $\mathcal {Q}=(N,A,u)$ a subset $f(\mathcal {Q})$ of $\Phi (N,A)$ such that for any $z,z^{\prime }\in \Phi (N,A)$ :

$$\begin{aligned} \{z\in f(\mathcal {Q}){\text { and }}u_{i}\cdot z_{i}=u_{i}\cdot z_{i}^{\prime } {\text { for all }}i\in N\}\Longrightarrow z^{\prime }\in f(\mathcal {Q}) \end{aligned}$$

(1)

Moreover $f(N,A,\lambda *u)=f(\mathcal {Q})$ for any rescaling $\lambda$ where $\lambda _{i}>0$ for all i .

The one-to-one mapping from F to f is clear. Definition 2 makes no distinction between two allocations with identical welfare consequences, a property often called Pareto-Indifference.

We speak of a single-valued division rule if $F(\mathcal {Q})$ is a singleton for all $\mathcal {Q}$, otherwise the rule is multi-valued . Single-valued rules are much more appealing, as they eschew the further negotiation required to converge on a single division.

4 Two division rules

The definition of the Egalitarian rule goes back to Pazner and Schmeidler (1978), who introduced it as a welfarist alternative to the competitive approach. In our context we first normalize disutilities so that eating the entire pile of items gives a disutility of 1 to each participant, then find an efficient disutility profile where normalized disutilities are equal.

We call a problem $\mathcal {Q}$ in Definition 1normalized if $u_{i}\cdot e^{A}=1$ for all i. Because division rules are invariant to rescaling, it is enough to define such a rule F on the subdomain of normalized division problems: if $\mathcal {Q}=(N,A,u)$ is not normalized we simply set $F(\mathcal {Q})=\lambda *F(N,A,\widetilde{u})$ where $\widetilde{u}_{i}=\frac{1}{\lambda _{i}}u_{i}$ and $\lambda _{i}=u_{i}\cdot e^{A}$ for all i.

Definition 3

Fix a normalized problem $\mathcal {Q }=(N,A,u)$. The Egalitarian division rule for bads $F^{eg}$ picks the efficient disutility profile $U^{eg}$ such that $U_{i}^{eg}=U_{j}^{eg}$ for all i, j.

Interestingly the definition of the Egalitarian rule is simpler when we divide bads rather than goods. When we divide goods and utilities are additive, if the matrix $u_{ia}$ has zero entries an efficient normalized utility profile such that $U_{i}^{eg}=U_{j}^{eg}$ for all i, j may fail to exist, so that egalitarian allocations of goods are more complicated to describe: they maximize the leximin ordering of utility profiles over feasible allocations.

We check that Definition 3 makes sense. Set $\theta =\min _{\Psi (\mathcal {Q} )}\max _{i}U_{i}$ and pick $\overline{U}$ in $\Psi (\mathcal {Q})$ achieving $\theta$. Note that $\theta$ is positive. Suppose $\overline{U}_{1}<\theta$ : then for any $i\ge 2$ such that $u_{i}\cdot z_{i}=\theta$ we take a small amount of some a such that $u_{ia}>0$ and $z_{ia}>0$, and give it to agent 1. If these amounts are small enough, we get an allocation $z^{\prime }$ where $u_{i}\cdot z_{i}^{\prime }<\theta$ for all i, including 1, contradicting the definition of $\theta$. Thus $\overline{U} _{i}=\theta$ for all i. Now check that $\overline{U}$ is efficient by a similar argument: if there is some $z\in \Phi (N,A)$ such that $u_{i}\cdot z_{i}\le \theta$ for all i and $u_{1}\cdot z_{1}<\theta$, we can transfer some bads from any agent i such that $u_{i}\cdot z_{i}=\theta$ to agent 1, and contradict again the definition of $\theta$.

Definition 4

Fix a problem $\mathcal {Q}=(N,A,u)$ . We call the allocation $z\in \Phi (N,A)$ a competitive allocation of bads if there is a price $p\in \mathbb {R} _{+}^{A}$ such that $\sum _{A}p_{a}=n$ and

$$\begin{aligned} z_{i}\in \arg \min _{y_{i}\in \mathbb {R} _{+}^{A}}\{u_{i}\cdot y_{i}|p\cdot y_{i}\ge 1\}\quad \text { for all } \ i \end{aligned}$$

(2)

and for all $a\in A$

$$\begin{aligned} p_{a}=0\text { if }u_{ia}=0\quad \text { for some } \ i\in N \end{aligned}$$

(3)

We write the competitive rule as $f^{c},F^{c}$: it selects all competitive allocations or disutility profiles. Existence of such allocations both for goods and for bads is well known, as explained in the companion paper (Bogomolnaia et al. 2017).

Definition 4 is standard (see e.g. Mas-Colell 1992; Bogomolnaia et al. 2017): instead of utility-maximization agents minimize their disutilities and the sign in the budget constraint is reversed. The additional property (3) rules out inefficient solutions of system (2). For example assume two bads, two agents and the following matrix of marginal disutilities:

$$\begin{aligned} \begin{array}{ccc} &{} a &{} b \\ u_{1} &{} 2 &{} 1 \\ u_{2} &{} 0 &{} 1 \end{array} \end{aligned}$$

There are three solutions of (2)

$$\begin{aligned} \begin{array}{ccc} &{} a &{} b \\ z_{1} &{} 1/4 &{} 1 \\ z_{2} &{} 3/4 &{} 0 \\ p &{} 4/3 &{} 2/3 \end{array} ; \quad \begin{array}{ccc} &{} a &{} b \\ z_{1} &{} 0 &{} 1/2 \\ z_{2} &{} 1 &{} 1/2 \\ p &{} 0 &{} 2 \end{array} ; \quad \begin{array}{ccc} &{} a &{} b \\ z_{1} &{} 0 &{} 1 \\ z_{2} &{} 1 &{} 0 \\ p &{} 1 &{} 1 \end{array} \end{aligned}$$

The left one is inefficient, and (3) additionally rules out the right one (though it is efficient).³

Critical to most of our results are two additional characterizations of competitive allocations, to which we now turn. The first one is a simple and intuitive system of inequalities.

Lemma 3

Fix a problem $\mathcal {Q}=(N,A,u)$. Then $U\in F^{c}(\mathcal {Q})$ if and only if $U\gg 0$ and $U=(u_{i}\cdot z_{i})_{i\in N}$ for some $z\in \Phi (N,A)$ such that for all $i\in N$

$$\begin{aligned} \text {for all }a\in A\text {: }z_{ia}>0\Longrightarrow \left\{ \frac{u_{ia} }{U_{i}}\le \frac{u_{ja}}{U_{j}}\text { for all }j\in N\right\} \end{aligned}$$

(4)

Proof

Fix $\mathcal {Q},U,z$ meeting (4) and $U\gg 0$ and check that z is a competitive allocation. Define $A^{0}=\{a\in A|u_{ia}=0$ for some $i\in N\}$ and set $p_{a}=0$ for those bads. By (4) the bads in $A^{0}$ can only be eaten by agents who don’t mind them: $z_{ia}>0\Longrightarrow u_{ia}=0$. We set $p_{a}=\frac{u_{ia}}{U_{i}}$ for all i who eat some a. This implies $p\cdot z_{i}=1$ for all i. For all a such that $z_{ia}=0$ we have $\frac{u_{ia}}{U_{i}}\ge p_{a}$: therefore $z_{i}$ is agent i’s Walrasian demand at price p, and z is a competitive allocation.

Conversely we fix a competitive allocation z with competitive price p. Inequality $U\gg 0$ holds because agent i must buy some bad a with $p_a>0$, and by (3) $u_{ia}>0$. For a bad a with zero price (4) holds because by (2) such a bad can be consumed only by agents i with $u_{ia}=0$. Denote by $A^*$ the set of bads a with $p_a>0$. Since $z_{i}$ is i’s demand at price p, bads from $A^*$ consumed by i minimize the ratio $\frac{u_{ia}}{p_{a}}$ over $A^*$; denote this minimal value by $\pi _i$. We have: $\sum _{a\in A^*}u_{ia}z_{ia}=\pi _{i}(\sum _{a\in A^*}p_{a}z_{ia})\Longrightarrow \pi _{i}=U_{i}$. So $\frac{ u_{ia}}{U_{i}}=p_{a}$ whenever i consumes a and $\frac{u_{ib}}{U_{i}} \ge p_{b}$ if i does not eat any b; this yields (4) for bads from $A^*$. Note that this argument also implies that for a given competitive allocation z the competitive price p is unique. $\square$

The next result is a geometric representation of competitive allocations. Recall the well known result by Eisenberg and Gale (1959) about the division of goods. The Competitive utility profile is the unique maximizer of the Nash product $\mathcal {N}(U)={\Pi }_{i\in N}U_{i}$ in $\Psi ( \mathcal {Q})$. This geometric characterization extends for bads in a non-trivial way. Given $\mathcal {Q}$ we call U a critical point of the Nash productin$\Psi (\mathcal {Q})$ if $U\in \Psi ( \mathcal {Q}),U\gg 0$, and the hyperplane supporting the upper contour of $\mathcal {N}$ at U supports $\Psi (\mathcal {Q})$ as well. Such critical points include the strictly positive local maxima, local minima, and saddle-points of $\mathcal {N}$ in $\Psi (\mathcal {Q})$.

Proposition 1

Fix a problem $\mathcal {Q} =(N,A,u)$. The Competitive disutility profiles are exactly all the critical points of the Nash product $\mathcal {N}$ in $\Psi ^{eff}(\mathcal {Q})$.

A more general version of this result is proven in Bogomolnaia et al. (2017), to which we refer the reader. Proposition 1 can also be proved directly by observing that the first-order conditions of criticality are equivalent to inequalities (4).

A consequence of Definition 3 and Proposition 1 is that both rules $F^{eg},F^{c}$ are “welfarist”, in the sense that the utility profiles they choose are entirely determined by the set of feasible utilities.

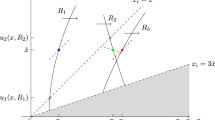
The geometry behind the competitive and Egalitarian rules is illustrated by Fig. 1, which depicts the Competitive and Egalitarian disutility profiles for a division problem $\mathcal {Q}$ with two agents and two bads and the following marginal disutility matrix.

$$\begin{aligned} \begin{array}{ccc} &{} a &{} b \\ u_{1} &{} 10 &{} 6 \\ u_{2} &{} 5 &{} 1 \end{array} \end{aligned}$$

Fig. 1

The grey polytope is the set of $\Psi (\mathcal {Q})$. The blue circle and the blue square depict $F^{c}(\mathcal {Q})$ and $F^{eg} (\mathcal {Q})$, respectively; the gray point corresponds to the equal split. The hyperbolas are the level curves of $\mathcal {N}$ (color figure online)

The egalitarian and competitive divisions (both unique in this example) are:

$$\begin{aligned} z^{eg}= \begin{array}{ccc} &{} a &{} b \\ z_{1} &{} 24/35 &{} 0 \\ z_{2} &{} 11/35 &{} 1 \end{array} ; \quad z^{c}= \begin{array}{ccc} &{} a &{} b \\ z_{1} &{} 3/5 &{} 0 \\ z_{2} &{} 2/5 &{} 1 \\ p &{} 5/3 &{} 1/3 \end{array} \end{aligned}$$

At $F^{c}(\mathcal {Q})$ the level curve of $\mathcal {N}(U)$ touches $\Psi ^{eff}(\mathcal {Q})$ (the South-West boundary of $\Psi (\mathcal {Q})$) from inside, see Fig. 1. This means that $U^{c}$ is a critical point of $\mathcal {N}$ but not a global extremum.

5 Multiple competitive divisions

In the above example in Sect. 4 the competitive rule is single valued. The simplest illustration of the unpalatable multiplicity issue has two agents and two bads:

$$\begin{aligned} \begin{array}{ccc} &{} a &{} b \\ u_{1} &{} 1 &{} 2 \\ u_{2} &{} 3 &{} 1 \end{array} { \ \ }z^{c_{1}}= \begin{array}{ccc} &{} a &{} b \\ z_{1} &{} 1 &{} 1/4 \\ z_{2} &{} 0 &{} 3/4 \\ p &{} 2/3 &{} 4/3 \end{array} \text { }z^{c_{2}}= \begin{array}{ccc} &{} a &{} b \\ z_{1} &{} 1 &{} 0 \\ z_{2} &{} 0 &{} 1 \\ p &{} 1 &{} 1 \end{array} \text { }z^{c_{3}}= \begin{array}{ccc} &{} a &{} b \\ z_{1} &{} 2/3 &{} 0 \\ z_{2} &{} 1/3 &{} 1 \\ p &{} 3/2 &{} 1/2 \end{array} \end{aligned}$$

See Fig. 2. Note that at $z^{c_{1}}$ agent 1 gets only his Fair Share utility level, while agent 2 grabs all the surplus above equal split; at $z^{c_{3}}$ agents 1 and 2 exchange roles.

Fig. 2

Multiple competitive disutility profiles for bads (blue dots) (color figure online)

Our first main result evaluates the extent of the multiplicity issue.

Theorem 1

For any problem $\mathcal {Q}$ with bads:

• (i) The set $F^{c}(\mathcal {Q})$ of competitive utility profiles is finite.

• (ii) For general $n=|N|,m=|A|$, $|F^{c}( \mathcal {Q})|$ can be as high as $2^{\min \{n,m\}}-1$.

• (iii) For $n=2$ t he upper bound on $|F^{c}(\mathcal {Q})|$ is $2m-1$.

• (iv) For $m=2$ the upper bound on $|F^{c}(\mathcal {Q})|$ is $2n-1$.

Theorem 1 has important consequences for practical implementation of the Competitive rule. If we divide goods, the outcome of $f^{c}$ can be computed in a reasonable time: there is an algorithm Vazirani (2007) polynomial in the size of the problem $n+m$. Item (ii) leaves no hope for existence of such an algorithm for computing all competitive allocations of bads since the number of such allocations itself can be exponential.

Can we compute all the outcomes of $F^{c}$ in polynomial time if one of the parameters n or m is fixed? For n or m equal to 2 the answer is positive: items (iii) and (iv) show that for $2\times m$ or $n\times 2$ problems $|F^{c}(\mathcal {Q})|$ is bounded by a linear function of the size, and the proof provides a polynomial algorithm. For general n and m we leave this important question open. Another open question is the existence of an algorithm for computing some particular single-valued selection of $F^{c}$ in polynomial time, when both n and m are large.

A by-product of our proofs is that $|F^{c}(\mathcal {Q})|$ is odd on an open dense subset of the problems where $n=2$ and/or $m=2$: see the last paragraph of Sects. 5.3.1 and 5.4 respectively. A very plausible conjecture is that this is true as well for any n, m.

Another widely open problem is to find restrictions on the marginal disutility matrix ensuring that $F^{c}$ is single-valued. And if disutilities are generated by a simple random process, how likely is it that $F^{c}$ is multi-valued?

5.1 Proof of Theorem 1

Overview Item (i) is an easy corollary of Lemma 1 and the characterization of $F^{c}(\mathcal {Q})$ in Lemma 3. The proof also implies a simple exponential upper bound on $|F^{c}(\mathcal {Q})|$. Item (ii) is proved by an example. The longer proofs of statements (iii) and (iv) rely on the fact that for $n=2$ a problem is entirely described by the sequence of ratios $\frac{u_{1a}}{u_{2a}}$, and for $m=2$ by the sequence of ratios $\frac{u_{ia}}{u_{ib}}$. This allows a closed form description of all competitive allocations.

5.1.1 Statement (i)

Fix $\mathcal {Q}$ and recall from Lemmas 1 and 3 that each $U\in F^{c}( \mathcal {Q})$ is strictly positive and achieved by some $z\in f^{c}(\mathcal { Q})$ such that $\Gamma (z)$ is a forest. There are finitely many (bipartite) forests in $N\times A$ therefore it is enough to check that to each forest $\Gamma$ corresponds at most one U in $F^{c}(\mathcal {Q})$. The number of bipartite forests on $n+m$ vertices is bounded by $2^{(n+m)\log _{2}(nm)}$⁴ and we get a simple exponential upper bound on the number of distinct Competitive allocations.

Consider a tree T in $\Gamma$ with vertices $N_{0},A_{0}$. If agents $i,j\in N_{0}$ are both linked to $a\in A_{0}$, system (4) implies that $U_{i},U_{j}$ are proportional to $u_{ia},u_{ja}$ . Repeating this observation along the paths of T we see that the profile $(U_{i})_{i\in N_{0}}$ is determined up to a multiplicative constant. Now in total the agents in $N_{0}$ consume exactly $A_{0}$ so by efficiency we cannot have two distinct $(U_{i})_{i\in N_{0}}$ meeting (4).⁵

5.2 Statement (ii)

Consider the following example with n agents and $n-1$ bads. The first $(n-1)$ agents are single-minded, each over a different bad. The last agent n is flexible, he dislikes all bads equally

$$\begin{aligned} \begin{array}{ccccc} \text {bad} &{} a_{1} &{} a_{2} &{} \cdots &{} a_{n-1} \\ u_{1} &{} 1 &{} 3 &{} 3 &{} 3 \\ u_{2} &{} 3 &{} 1 &{} 3 &{} 3 \\ \cdots &{} 3 &{} 3 &{} 1 &{} 3 \\ u_{n-1} &{} 3 &{} 3 &{} 3 &{} 1 \\ u_{n} &{} 1 &{} 1 &{} 1 &{} 1 \end{array} \end{aligned}$$

(5)

The symmetric allocation, where each single-minded agent receives $\frac{n-1 }{n}$ units of his bad while the flexible agent n eats $\frac{1}{n}$-th of each bad is competitive at the uniform price $\frac{n}{n-1}$ for each bad: the flexible agent n gets no benefit above his equal split share. However there are many more competitive divisions, all with different utility profiles, and breaking at least partially the above symmetry.

Recall that for any $S\subseteq A$ the vector ${e}^{S}\in \mathbb {R} ^{A}$ has $e_{a}^{S}=1$ if $a\in S$ and zero otherwise. Fix a non-empty subset T of $\{1,2,\ldots ,n-1\}$ and check that the allocation

$$\begin{aligned} z_{i}=\frac{|T|}{|T|+1}e^{a_{i}}\text { for }i\in T; \quad z_{j}=e^{a_{j}} \text { for }j\in \{1,2\ldots n-1\}\setminus T;\quad z_{n}=\frac{1}{|T|+1} e^{\{a_{i},\ i\in T\}} \end{aligned}$$

(6)

is competitive for the prices $p_{a_{i}}=\frac{|T|+1}{|T|}$ for $i\in T$ and $p_{a_{j}}=1$ for $j\in \{1,2,\ldots ,n-1\}\setminus T$. In particular agent n’s disutility varies from $\frac{1}{2}$ to $\frac{n-1}{n}$. We could have chosen any other subset T. Thus there are at least $2^{n-1}-1$ different competitive allocations and ii) is proven for $m=n-1$.

To adapt the construction above for $n-1>m$ we add enough $n-1-m$ copies of agent n. For the case $n-1<m$ we split the bad $a_{n-1}$ into $m-n+2$ identical pieces (the vector disutilities for each piece is $1/(m-n+2)$ of the initial vector). We omit the details.

5.3 Statement (iii) and the structure of competitive allocations for $n=2$

We fix $\mathcal {Q=}(\{1,2\},A,u)$. We label the bads by $k\in \{1,\ldots ,m\}$ so that the ratios $\frac{u_{1k}}{u_{2k}}$ increase weakly in k, with the convention $\frac{1}{0}=\infty$.

5.3.1 The sequence of ratios increases strictly

We first prove (iii) under this assumption. Efficiency implies that if agent 1 eats some k and 2 some $k^{\prime }$, then $k\le k^{\prime }$ . Hence all the efficient allocations z are of the following form

$$\begin{aligned} \begin{array}{ccccccccc} \text {bad} &{} 1 &{} 2 &{} \cdots &{} k-1 &{} k &{} k+1 &{} \cdots &{} m \\ z_{1} &{} 1 &{} 1 &{} 1 &{} 1 &{} x &{} 0 &{} 0 &{} 0 \\ z_{2} &{} 0 &{} 0 &{} 0 &{} 0 &{} 1-x &{} 1 &{} 1 &{} 1 \end{array} \end{aligned}$$

We call such an allocation a k-split. For $x\in (0,1)$ the k- split is strict; if $x=1$ we call this allocation the $k/k+1$-cut. Disutility profiles of $k/k+1$-cuts are peak points of $\Psi ^{eff}(\mathcal { Q})$; k-splits correspond to 1-dimensional faces of $\Psi ^{eff}( \mathcal {Q})$.

Lemma 4

Denote $\sum _{1}^{k}u_{1\ell }$ by $U_{1}(k)$ and $\sum _{k}^{m}u_{2\ell }$ by $U_{2}(k)$.

• (i) Then the $k/k+1$ cut is in $f^{c}(Q)$ if and only if

  $$\begin{aligned} \frac{u_{1k}}{u_{2k}}\le \frac{U_{1}(k)}{U_{2}(k+1)}\le \frac{u_{1(k+1)}}{ u_{2(k+1)}} \end{aligned}$$

  (7)

• (ii) A strict k-split is competitive for some $x\in (0,1)$ iff

  $$\begin{aligned} \left| \frac{U_{1}(k-1)}{u_{1k}}-\frac{U_{2}(k+1)}{u_{2k}}\right| <1 \end{aligned}$$

  (8)

  For a fixed k there is at most one such x.

Statement (iii) of Theorem 1 follows from Lemma 4: $|f^{c}(\mathcal {Q)}|$ is at most $2m-1$, because the maximal number of $k/k+1$-cuts and k-split allocations is respectively $m-1$ and m.

Lemma 4 can be deduced from the geometric characterization of competitive allocations in Proposition 1. We will prove it directly.

Proof

By Lemma 3, the $k/k+1$-cut is competitive iff the system (4) holds. Since the sequence $\frac{u_{1k}}{u_{2k}}$ is increasing, (4) reduces to two inequalities: $\frac{u_{1k}}{U_1(k)}\le \frac{u_{2k}}{U_2(k+1)}$ for the demand of agent 1 and $\frac{u_{2(k+1)}}{U_2(k+1)}\le \frac{u_{1(k+1)}}{U_1(k)}$ for agent 2. Combining them we get (7).

Consider a strict k-split allocation, where agent 1 gets a fraction $x\in (0,1)$ of a bad k. Again, by the increasing property, the system (4) reduces to just one equality, which comes from the fact that k belongs to the demand of both agents: $\frac{u_{1k}}{U_1}=\frac{u_{2k}}{U_2}$, i. e,

$$\begin{aligned} \frac{u_{1k}}{U_1(k-1)+xu_{1k}}=\frac{u_{2k}}{U_2(k+1)+(1-x)u_{2k}}. \end{aligned}$$

Thus there is a competitive k-split iff this equation has the solution $x\in (0,1)$. This condition is equivalent to (8). $\square$

Finally we give an example where this bound is achieved. With the notation $(x)_{+}=\max \{x,0\}$ we set:

$$\begin{aligned}&u_{1k}=2^{(k-2)_{+}}\text { for }1\le k\le m-1 ; \quad u_{1m}=2^{m-2}+1\\&u_{21}=2^{m-2}+1; \quad u_{2k}=2^{(m-1-k)_{+}}\quad \text { for } \ 2\le k\le m \end{aligned}$$

Check first $U_{1}(k-1)=u_{1k}$ and $U_{2}(k+1)=u_{2k}$ for $2\le k\le m-1$ ; also $U_{2}(2)=U_{1}(m-1)=2^{m-2}<u_{21}=u_{1m}$ so (8) holds for all k. Next $\frac{U_{1}(k)}{U_{2}(k+1)}=\frac{u_{1(k+1)}}{u_{2k}}$ for $2\le k\le m-2$, so that (7) is clear for such k. And (7) holds as well for $k=1,m-1$. This example is clearly robust: small perturbations of the disutility matrix preserve $|F^{c}(\mathcal {Q)}|$ .

We check now that $|F^{c}(\mathcal {Q})|$ is odd for almost all u. Recall that $F^{c}(\mathcal {Q})$ is the set of critical points of the Nash product in $\Psi ^{eff}(\mathcal {Q})$. Excluding the set of disutility profiles u such that $\frac{U_{1}(k-1)}{u_{1k}}-\frac{U_{2}(k+1)}{u_{2k}}|=1$ (see (8)), it follows that the $k/k+1$ cut is competitive if and only if it is a local minimum of $\mathcal {N}$. On the other hand the disutility profile of a k-split allocation is a one-dimensional face of $\Psi ^{eff}( \mathcal {Q})$, and is competitive if and only if it is a local maximum of $\mathcal {N}$. Then the statement follows from the fact that if a continuous non-negative function on the interval is zero at the end-points, the number of its local maxima exceeds the number of its local minima (different than the end-points) by one: the extrema alternate and the closest to the end-points are the maxima.

Note that the above argument implies that in a typical problem with two agents, if $|F^{c}(\mathcal {Q})|=1$ then the competitive allocation is a $k/k+1$-split, and if $|F^{c}(\mathcal {Q})|\ge 2$, at least one k-cut allocation is competitive.

5.3.2 The sequence of ratios is not strictly increasing

If $\frac{u_{1k}}{u_{2k}}=\frac{u_{1(k+1)}}{u_{2(k+1)}}$ for some k, then we can clearly merge bads k and $k+1$ into a bad $k^{*}$ with disutilities $u_{ik^{*}}=u_{ik}+u_{i(k+1)}$ without changing the feasible set $\Psi (\mathcal {Q})$. Since $F^{c}$ is completely determined by $\Psi (\mathcal {Q})$ (see Proposition 1), the set of competitive disutility profile is invariant with respect to such merging. Thus when we successively merge all the bads sharing the same ratio $\frac{u_{1k}}{u_{2k}}$, the number $|F^{c}(\mathcal {Q)}|$ does not change, and we reach a problem with fewer bads where the ratios $\frac{u_{1k}}{u_{2k}}$ increase strictly in k , for which statement (iii) is already proved.

5.4 Statement (iv) and the structure of competitive allocations for $m=2$

Though the set of efficient allocations for two bads does not have such a simple one-dimensional structure as in the case of $n=2$ just discussed, the set of efficient envy-free allocations can be easily described. This allows to characterize competitive allocations for $m=2$ in a closed form.

We fix $\mathcal {Q=}(N,\{a,b\},u)$ and label the agents $i\in \{1,\ldots ,n\}$ in such a way that the ratios $\frac{u_{ia}}{u_{ib}}$ increase weakly in i.

For $2\le i\le n-1$ we call an allocation z an i-split if there are two numbers x, y such that

$$\begin{aligned}&z_{j}=\left( \frac{1-x}{i-1},0\right) \quad \text { for } \ j\le i-1\text { ; }z_{j}=\left( 0,\frac{1-y}{ n-i}\right) \quad \text { for } \ j\ge i+1 \end{aligned}$$

(9)

$$\begin{aligned}&z_{i}=(x,y)\quad \text { with } \ 0\le x\le \frac{1}{i}, \quad 0\le y\le \frac{1}{ n-i+1}. \end{aligned}$$

(10)

Also, z is a 1-split if $z_{1}=(1,y)$ and $z_{j}=\big (0,\frac{1-y}{n-1}\big )$ for $j\ge 2$; and z is a n-split if $z_{n}=(x,1)$ and $z_{j}=(\frac{1-x }{n-1},0)$ for $j\le n-1$.

Lemma 5

If the sequence $\frac{u_{ia}}{u_{ib}}$ increases strictly, then any efficient envy-free allocations z is an i-split for some i. For a weakly-increasing sequence $\frac{u_{ia}}{u_{ib}}$ the set of all i-split allocations contains, utility-wise, all efficient and envy-free allocations.

Proof

For a strictly-increasing sequence of ratios, we have, by efficiency: for all j, k$\{z_{ja}>0$ and $z_{kb}>0\}$ implies $j\le k$. In particular at most one agent i is eating both bads. Let $z_i=(x,y)$. If agents $j,k< i$ do not envy each-other, they are consuming the same amount of a; the symmetric statement holds for $j,k>i$ and their share of b; since there is a unit amount of both bads we get (9). Inequalities (10) follow from the fact that nobody envies i.

Consider an efficient and envy free allocation z when the sequence $\frac{u_{ia}}{u_{ib}}$ increases only weakly, for instance $\frac{u_{ia}}{u_{ib}}=\frac{u_{(i+1)a}}{ u_{(i+1)b}}$. We may have $z_{(i+1)a}>0$ and $z_{ib}>0$, however we can find $z^{\prime }$ delivering the same disutility profile and such that one of $z_{(i+1)a}^{\prime }$ and $z_{ib}^{\prime }$ is zero. Indeed no envy and the fact that $u_{i}$ and $u_{i+1}$ are parallel gives $u_{i}\cdot z_{i}=u_{i}\cdot z_{i+1}$ and $u_{i+1}\cdot z_{i+1}=u_{i+1}\cdot z_{i}$, from which the claim follows easily. $\square$

Define now the $i/i+1$-cut$z^{i/i+1}$ for $1\le i\le n-1$ by: $z_{j}^{i/i+1}=\big (\frac{1}{i},0\big )$ for $j\le i$, and $z_{j}^{i/i+1}=(0,\frac{1}{ n-i})$ for $j\ge i+1$. Note that the cut $z^{i/i+1}$ is both an i-split and an $i+1$-split. We call an i-split strict if it is not a cut, which happens if and only if both x, y in (9) are strictly positive.

Lemma 6

The cut $z^{i/i+1}$ is in $f^{c}(\mathcal {Q})$ iff

$$\begin{aligned} \frac{u_{ia}}{u_{ib}}\le \frac{i}{n-i}\le \frac{u_{(i+1)a}}{u_{(i+1)b}} \quad \text { for } \ 1\le i\le n-1 \end{aligned}$$

(11)

A strict i-split is competitive for some x and y iff

$$\begin{aligned} \frac{i-1}{n-i+1}<\frac{u_{ia}}{u_{ib}}<\frac{i}{n-i} \end{aligned}$$

(12)

(with the convention $\frac{1}{0}=\infty$). For any i at most one strict i-split allocation is competitive.

Proof

If $z^{i/i+1}$ is competitive, the corresponding price is $p=(i,n-i)$, and the system (4) reads $\frac{u_{ja}}{i}\le \frac{u_{jb}}{n-i}$ for $j\le i$, $\frac{u_{jb}}{n-i} \le \frac{u_{ja}}{i}$ for $j\ge i+1$, which boils down to (11).

If a strict i-split allocation z is in $f^{c}(\mathcal {Q})$, the price must be $p=n\left( \frac{u_{ia}}{ u_{ia}+u_{ib}},\frac{u_{ib}}{u_{ia}+u_{ib}}\right)$ and each agent must be spending exactly 1:

$$\begin{aligned} p_{a}\frac{1-x}{i-1}=p_{b}\frac{1-y}{n-i}=p_{a}x+p_{b}y=1 \end{aligned}$$

which gives

$$\begin{aligned} x=\frac{1}{nu_{ia}}{\large ((n-i+1)u}_{ia}-(i-1)u_{ib}{\large )}\text { ; }y= \frac{1}{nu_{ib}}{\large (iu}_{ib}-(n-i)u_{ia}{\large )} \end{aligned}$$

(13)

By (13), we can find x and y if and only if (12) holds. $\square$

Statement iv) of Theorem 1 immediately follows from this result since the total number of cuts $z^{i/i+1}$ is $n-1$ and there are at most n competitive (strict) i-split allocations.

An example where the bound is achieved uses any sequence $\frac{u_{ia}}{ u_{ib}}$ meeting (12) for all $i\in \{1,\ldots ,n\}$, as these inequalities imply (11) for all $i\in \{1,\ldots ,n-1\}$.

We check finally that $|F^{c}(\mathcal {Q})|$ is typically odd. For the utility profiles such that all the inequalities (11) and (12) are strict, we draw the two sequences $\frac{u_{ia}}{u_{ib}}$ and $\frac{i}{n-i}$ on the real line. Clearly the left-most and the right-most competitive allocations must be splits: if there is no competitive i-split allocation for $1\le i\le i^{*}$ then (12) gives successively $\frac{u_{1a} }{u_{1b}}>\frac{1}{n-1}$, then $\frac{u_{2a}}{u_{2b}}>\frac{2}{n-2},\ldots , \frac{u_{i^{*}a}}{u_{i^{*}b}}>\frac{i^{*}}{n-i^{*}}$, hence the $i^{*}/i^{*}+1$-cut is not competitive. Similarly one checks that between two adjacent competitive split allocations there is exactly one competitive cut allocation.

6 Impossibility results for single-valued rules

In order to bypass the unpalatable multiplicity issue we would like to identify a normatively appealing single-valued selection from the set of competitive divisions of bads. For instance if the problem involves only two agents and/or two bads, the set of efficient and envy-free allocations has a simple line structure (as explained in the proof of Theorem 1) with, generically, an odd number of competitive allocations, so we can choose the median allocation.

Alternatively, in problems of any size we can pick among efficient allocations the one maximizing the product of disutilities: it is competitive and generically unique (Lemmas 3, 4 in Bogomolnaia et al. 2017).

But any selection of the C rule single-valued everywhere must fail some familiar normative requirements of regularity or solidarity. Our next two results uncover logical incompatibilities specific to the efficient and single-valued division of bads.

6.1 Continuity versus envy-freeness

Small inaccuracies in reported preferences should not dramatically affect the outcome of the rule:

Continuity (CONT) of the single-valued division rule F: For all N, A, the function $u\rightarrow F(N,A,u)$ is continuous in $\mathbb {R} _{++}^{N\times A}$.⁶

Envy-freeness (EF) of the allocation $z\in \Phi (N,A)$ at problem $\mathcal {Q}$:

$$\begin{aligned} u_{i}\cdot z_{i}\le u_{i}\cdot z_{j}\quad \text { for all } \ i,j\in N \end{aligned}$$

As usual the set of efficient and envy-free allocations contains much more than the competitive ones. It is therefore surprising, and disappointing, that this fairly permissive test is incompatible with continuity.

Theorem 2

Say we divide at least two bads between at least four agents and fix a division rule f, F. If F is single-valued and continuous, then f cannot be also efficient and envy-free.

Any two of the three axioms CONT, EF and efficiency are compatible. A single-valued selection of $f^{c}$ is efficient and envy-free; by this result it cannot be continuous. The rule $F^{eg}$ is efficient and continuous, and clearly not envy-free. Finally the rule dividing equally all bads, irrespective of disutilities,⁷ is envy-free and continuous.

We prove Theorem 2 as a corollary of Proposition 2 describing the topological structure of the set $\mathcal {A}$ of efficient and envy-free allocations.

Proposition 2

If we divide at least two bads between at least three agents, there are problems $\mathcal {Q}$ where the set $\mathcal {A}$ of efficient and envy-free allocations, and the corresponding set of disutility profiles, have $\lfloor \frac{2n+1}{ 3}\rfloor$ connected components.

6.1.1 Proof of Proposition 2

The case of two bads$\{a,b\}$ Consider a problem, where the ratios $r_{i}=\frac{u_{ia}}{u_{ib}}$ increase strictly in $i\in \{1,\ldots ,n\}$. We write $S^{i}$ for the closed rectangle of i-split allocations (see Sect. 5.4). The sets $S^{i}\cap S^{i+1}$ intersect by the $i/i+1$-cut allocation $z^{i/i+1}$ for $i=1,\ldots ,n-1$, and $S^{i}\cap S^{j}=\varnothing$ if $|i-j|>1$. We saw that envy-free and efficient allocations must be in the connected union of rectangles $\mathcal { B}={\cup }_{i=1}^{n}S^{i}$, see Fig. 3.

Fig. 3

The structure of $i/i+1$-cuts and i-splits for a general problem with four agents

Writing $\mathcal {EF}$ for the set of envy-free allocations, we describe now the connected components of $\mathcal {A}=\mathcal {B\cap EF}$. Clearly the set of corresponding disutility profiles has the same number of connected components.

We let the reader check that the cut $z^{i/i+1}\in \mathcal {EF}$ iff it is competitive, i. e. inequalities (11) hold, that we rewrite as:

$$\begin{aligned} r_{i}\le \frac{i}{n-i}\le r_{i+1} \end{aligned}$$

(14)

If $z^{i/i+1}\in \mathcal {EF}$ then both $S^{i}\cap \mathcal {EF}$ and $S^{i+1}\cap \mathcal {EF}$ are in the same component of $\mathcal {A}$ as $z^{i/i+1}$, because they are convex sets containing $z^{i/i+1}$. If both $z^{i-1/i}$ and $z^{i/i+1}$ are in $\mathcal {EF}$, so is the linear segment $[z^{i-1/i},z^{i/i+1}]$ between them; then these two cuts as well as $S^{i}\cap \mathcal {EF}$ are in the same component of $\mathcal {A}$. And if $z^{i/i+1}\in \mathcal {EF}$ but $z^{i-1/i}\not \in \mathcal {EF}$, then the component of $\mathcal {A}$ containing $z^{i/i+1}$ is disjoint from any component of $\mathcal {A}$ in ${\cup }_{1}^{i-1}S^{j}$ (if any), because $S^{i}\cap {\cup }_{1}^{i-1}S^{j}=\{z^{i-1/i}\}$; a symmetrical statement holds if $z^{i-1/i}\in \mathcal {EF}$ but $z^{i/i+1}\not \in \mathcal {EF}$.

Finally if $S^{i}\cap \mathcal {EF}\ne \varnothing$ while neither $z^{i-1/i}$ nor $z^{i/i+1}$ is in $\mathcal {EF}$, the convex set $S^{i}\cap \mathcal {EF}$ is a connected component of $\mathcal {A}$. In this case we speak of an interior component of $\mathcal {A}$.

Lemma 7

$S^{i}$ contains an interior component if and only if

$$\begin{aligned} \frac{i-1}{n-i+1}<r_{i-1}<r_{i}<r_{i+1}<\frac{i}{n-i} \end{aligned}$$

(15)

where for $i=1$ this reduces to the two right-hand inequalities, and for $i=n$ to the two left-hand ones.

Before proving Lemma 7 at the end of this subsection, we describe a problem where $\mathcal {A}$ has the desired number of connected components. We choose the ratios $r_{i}$ such that:

$$\begin{aligned} \frac{3q}{n-3q}<r_{3q}<r_{3q+1}<r_{3q+2}<\frac{3q+1}{n-(3q+1)},\quad q=0,1,\ldots ,\left\lfloor \frac{n}{3}\right\rfloor \end{aligned}$$

(inequalities involving $r_{i}$ for $i=0$ or $i>n$ must be ignored). By (14) we have $z^{i/i+1}\in \mathcal {EF}$ for $i=3q-1,$ and $1\le q\le \lfloor \frac{n}{3}\rfloor$, and no two of those cuts are adjacent so they belong to distinct components. Moreover by Lemma 7, $S^{i}$ contains an interior component of $\mathcal {A}$ for $i=3q-2,$ and $1\le q\le \lfloor \frac{n+2}{3}\rfloor$, and only those. So the total number of components of $\mathcal {A}$ is $\lfloor \frac{n}{3}\rfloor +\lfloor \frac{n+2}{3}\rfloor =\lfloor \frac{2n+1}{3}\rfloor$ as desired. We let the reader check that we cannot reach a larger number of components.

More than two bads Start from a problem $\mathcal {Q}$ with two bads constructed at the previous step and use the same trick as in the proof of statement (iii) of Theorem 1 (Sect. 5.3.2): cut a bad b into $m-1$ equal pieces and call them bads $b_{1},\ldots ,b_{m-1}$. We get a new division problem $\mathcal { Q^{\prime }}$ with m bads, which is equivalent to $\mathcal {Q}$. In particular, the number of connected components of the set $\mathcal {A}$ is the same for both problems.

Proof of Lemma 7

Pick $z\in S^{i}$ and note first that for $2\le i\le n-1$, the envy-freeness inequalities reduce to just four inequalities: agents $i-1$ and i do not envy each other, and neither do agents i and $i+1$ (we omit the straightforward argument). Formally

$$\begin{aligned}&\frac{1}{r_{i+1}}\left( \frac{1}{n-i}-\frac{n-i+1}{n-i}y\right) \le x\le \frac{1}{r_{i}}\left( \frac{1}{n-i}-\frac{n-i+1}{n-i}y\right) \end{aligned}$$

(16)

$$\begin{aligned}&r_{i-1}\left( \frac{1}{i-1}-\frac{i}{i-1}x\right) \le y\le r_{i}\left( \frac{1}{i-1}-\frac{i}{i-1}x\right) \end{aligned}$$

(17)

In the (non negative) space (x, y) define the lines $\Delta (\lambda )$: $y=\lambda (\frac{1}{i-1}-\frac{i}{i-1}x)$ and $\Gamma (\mu )$: $x=\mu (\frac{ 1}{n-i}-\frac{n-i+1}{n-i}y)$. When $\lambda$ varies $\Delta (\lambda )$ pivots around $\delta =(\frac{1}{i},0)$, corresponding to $z^{i/i+1}$, and similarly $\Gamma (\mu )$ pivots around $\gamma =(0,\frac{1}{n-i+1})$, corresponding to $z^{i-1/i}$. The inequalities (16, 17) say that (x, y) belong to the intersection of two cones: the cone $\Delta ^{*}$ of points between $\Delta (r_{i})$ and $\Delta (r_{i-1})$, and the cone $\Gamma ^{*}$ between $\Gamma (\frac{1}{r_{i}})$ and $\Gamma (\frac{ 1}{r_{i}+1})$ (see Fig. 4). $\square$

Fig. 4

The intersection of the cones corresponds to $S^i\cap \mathcal {EF}$. The leftmost figure a represents the only scenario, when $S_i$ contains the interior component: on b the cone $\Gamma ^*$ contains $\delta$, which means that the cut $z^{i/i+1}$ is in $\mathcal {EF}$; on c the cones do not intersect and hence $S^i\cap \mathcal {EF}=\emptyset$

Thus $S^{i}$ has an interior component iff the two cones have non-empty intersection (this rules out the situation depicted on Fig. 4c), but this intersection does not contain $\delta$ and $\gamma$ (rules out Fig. 4b). Note that the situation when $\gamma$ is above $\Delta ^{*}$ and $\delta$ is to the right from $\Gamma ^{*}$ is impossible as it would imply$\frac{1}{n-i+1}>\frac{r_{i}}{i-1}$ and $\frac{1}{i}>\frac{1}{r_{i}(n-i) }$, a contradiction.

We conclude that $S^{i}$ contains an interior component iff $\gamma$ is below $\Delta ^{*}$ and $\delta$ is to the left of $\Gamma ^{*}$ (see Fig. 4a), which is exactly the system (15).

We leave to the reader proving (15) in the easier case of $i=1$ and $i=n$.

6.1.2 Proof of Theorem 2

Assume first $n=4$, $m=2$. Fix a single-valued, efficient rule f meeting NE. Consider $\mathcal {Q}^{1}$ where, with the notation in the proof of Proposition 2, we have

$$\begin{aligned} r_{1}<r_{2}<\frac{1}{3}<1<3<r_{3}<r_{4} \end{aligned}$$

By Lemma 7 combined with (14)  $\mathcal {A}$ has three components: one interior to $S^{1}$ (excluding the cut $z^{1/2}$), one around $z^{2/3}$ intersecting $S^{2}$ and $S^{3}$, and one interior to $S^{4}$ excluding $z^{3/4}$, see Fig. 5a.

Fig. 5

a, b The set $\mathcal {A}$ for problems $\mathcal {Q}^1$ and $\mathcal {Q}^2$ is marked by red. For $\mathcal {Q}^1$ the rule f selects an allocation point in the connected component around $z^{2/3}$. For $\mathcal {Q}^2$ the set $\mathcal {A}$ has only one connected component which is inside $S^1$, so is the outcome of f (color figure online)

Assume without loss that f selects an allocation in the second or third component just listed, and consider $\mathcal {Q}^{2}$ where $r_{1},r_{2}$ are unchanged but the new ratios $r_{3}^{\prime },r_{4}^{\prime }$ are

$$\begin{aligned} r_{1}<r_{2}<\frac{1}{3}<r_{3}^{\prime }<1<r_{4}^{\prime }<3 \end{aligned}$$

Here, again by (14) and (15), $\mathcal {A}$ has a single component interior to $S^{1}$, the same as in $\mathcal {Q}^{1}$: none of the cuts $z^{i/i+1}$ is in $\mathcal {A}$ anymore, and there is no component interior to another $S^{i}$. When we decrease continuously $r_{3},r_{4}$ to $r_{3}^{\prime },r_{4}^{\prime }$, the allocation $z^{1/2}$ remains outside $\mathcal {A}$ and the component interior to $S^{1}$ does not move. Therefore the allocation selected by f cannot vary continuously in the ratios $r_{i}$ , or in the underlying disutility matrix u.

We can clearly construct a similar pair of problems to prove the statement when $n\ge 5$ and $m=2$. And for the case $m\ge 3$ we cut one of the bads into $m-1$ pieces as in the proof of Proposition 2.

6.2 Resouce monotonicity

This solidarity property has played a major role in the modern fair division literature: (Moulin and Thomson 1988; Thomson 2010). To introduce it we must extend the definition of a rule to include problems where we must share $\omega _{a}$ units of bad a, and $\omega \in \mathbb {R} _{++}^{A}$. A rule F in Definition 2 has a canonical extension $\widetilde{ F}$ to such problems:

$$\begin{aligned} {\widetilde{F}(N,A,\omega ,u)=F(N,A,\omega \cdot {u})}\quad \text { where } \ {(\omega \cdot u)_{ia}={\omega _{a}u_{ia}}} \end{aligned}$$

It is easy to check that $\widetilde{F}$ is invariant to a change of units for measuring any bad a, and is the only extension of F with this property.

We now define, for a single-valued rule F:

Resource monotonicity (RM): for any $\mathcal {Q=} (N,A,\omega ,u)$, $\mathcal {Q}^{\prime }\mathcal {=}(N,A,\omega ^{\prime },u)$

$$\begin{aligned} \omega \le \omega ^{\prime }\Longrightarrow \widetilde{F}(\mathcal {Q)}\le \widetilde{F}(\mathcal {Q}^{\prime }) \end{aligned}$$

Recall also the familiar lower bound on individual welfare corresponding to the consumption of a $\frac{1}{n}th$ share of each bad:

Fair share guarantee (FSG): for any $\mathcal {Q=}(N,A,\omega ,u)$, any $U\in F(\mathcal {Q})$ and any i, we have $U_{i}\le \frac{1}{n} u_{i}\cdot \omega$.

Both rules, Egalitarian and Competitive, meet FSG. However

Proposition 3

With three or more agents and two or more bads, no efficient single-valued rule can be resource monotonic and meet Fair Share Guarantee.

Proof

The essence of the argument is captured by a two-person, two-bad example in Subsection 7.2 of Bogomolnaia et al. (2017), that we reproduce for completion. Suppose the efficient rule F meets RM and FSG and consider the two-agent two-bad problem

$$\begin{aligned} u= \begin{array}{ccc} \text {bads} &{} a &{} b \\ u_{1} &{} 1 &{} 4 \\ u_{2} &{} 4 &{} 1 \end{array} \quad \text {and}\quad \omega =(1,1) \end{aligned}$$

(18)

Set $U=F(\mathcal {Q})$. Because (1, 1) is an efficient disutility profile and F is efficient, one $U_{i}$ is bounded above by 1, say $U_{1}\le 1$ . Then consider the problem $\mathcal {Q}^{\prime }$, where we decrease $\omega$ to $\omega ^{\prime }=(1/9,1)$. Pick $z^{\prime }\in \widetilde{f}( \mathcal {Q}^{\prime })$. By FSG, the definition of $\widetilde{F}$, and feasibility, we have

$$\begin{aligned} z_{2b}^{\prime }\le u_{2}\cdot z_{2}^{\prime }\le \frac{1}{2}u_{2}\cdot \omega ^{\prime }=\frac{13}{18}\Longrightarrow z_{1b}^{\prime }\ge \frac{5}{ 18}\Longrightarrow u_{1}\cdot z_{1}^{\prime }=U_{1}^{\prime }\ge \frac{10}{9 }>U_{1} \end{aligned}$$

contradicting RM. We omit the straightforward generalization of this argument to any $n\ge 3,m\ge 2$. $\square$

For goods an impossibility result similar to Proposition 3 is known for the general Arrow–Debreu domain of preferences (Moulin and Thomson 1988). But in the additive sub-domain the C rule satisfies RM while the E rule does not. This is a strong argument in support of the former rule, which disappears when we divide bads.

We note finally that the E rule is Population Monotonic (if one new agent shows up to share the bundle of bads, every old agent is weakly better off), whether we divide goods or bads (this is clear from Definition 3), whereas the axiom does not apply to the multivalued C rule (and we conjecture that no single-valued selection of this rule satisfies it).

7 A remark about Maskin monotonicity

In the additive domain, the familiar Maskin Monotonicity axiom (Maskin 1999) has an equivalent, simple formulation. This new property, dubbed Independence of Lost Bids (ILB) is predicated on the observation that, when disutilities are additive, at an efficient allocation most of the entries in the consumption matrix z are zero. We call agent i’s marginal utility $u_{ia}$ her “bid” for item a; and we say that i’s bid is “lost” at problem $\mathcal {Q}=(N,A,u)$ if $z_{ia}=0$. ILB states that changing i’s lost bid $u_{ia}$ should have no effect on the outcome, as long this bid remains lost.

Definition 5

The division rule f is Independent of Lost Bids (ILB) if for any two problems $\mathcal {Q}, \mathcal {Q}^{\prime }$ on N, A where $u,u^{\prime }$ differ only in the entry ia, and such that $u_{ia}<u_{ia}^{ \prime }$, we have

$$\begin{aligned} \forall z\in f(\mathcal {Q}):z_{ia}=0\Longrightarrow z\in f(\mathcal {Q} ^{\prime }) \end{aligned}$$

(19)

Lemma 8

Independent of Lost Bids is equivalent to Maskin monotonicity.

Proof

Recall that a rule f satisfies MM if for any two problems $\mathcal {Q}=(N,A,u),\mathcal {Q}^{\prime }=(N,A,u^{\prime })$ and $z\in f(\mathcal {Q})$ we have

$$\begin{aligned} \{\forall i\in N,\forall w\in \mathbb {R} _{+}^{A}:u_{i}\cdot z_{i}\ge u_{i}\cdot w\Longrightarrow u_{i}^{\prime }\cdot z_{i}\ge u_{i}^{\prime }\cdot w\}\Longrightarrow z\in f(\mathcal {Q} ^{\prime }) \end{aligned}$$

(20)

We fix $\mathcal {Q},i\in N$ and $z\in f(\mathcal {Q})$ and define $A^{0}=\{a|z_{ia}=0\}$ and $A^{+}=A\diagdown A^{0}$. The implication in the premise of (20) reads

$$\begin{aligned} \forall w\in \mathbb {R} _{+}^{A}\text { }u_{i}\cdot (w-z_{i})\le 0\Longrightarrow u_{i}^{\prime }\cdot (w-z_{i})\le 0 \end{aligned}$$

The cone with vertex 0 generated by the vectors $w-z_{i}$ when w covers $\mathbb {R} _{+}^{A}$ is $C=\{\delta \in \mathbb {R} ^{A}|\delta _{a}\ge 0$ for $a\in A^{0}\}$. By Farkas Lemma the implication $\{\forall \delta \in C:$$u_{i}\cdot \delta \le 0\Longrightarrow u_{i}^{\prime }\cdot \delta \le 0\}$ means that, up to rescaling $u_{i}^{\prime }$, we have

$$\begin{aligned} u_{ia}^{\prime }=u_{ia}\text { on }A^{+}; \quad u_{ia}\le u_{ia}^{\prime } \quad \text { on } \ A^{0} \end{aligned}$$

Now (20) is precisely (19) if $u_{i}^{\prime }$ differs from $u_{i}$ in only one coordinate, and other $u_{j}$-s are unchanged, and the converse implication is clear as well. $\square$

Of course the competitive rule meets ILB because it meets MM, the latter under much more general preferences. One can also check ILB directly from the characterization of the C rule in Lemma 3. It is also clear that the Egalitarian rule fails ILB.

Consider the classic result by Nagahisa (1991) using MM to characterize the C rule: any efficient, individually rational, and Pareto indifferent rule meeting Maskin monotonicity⁸ must contain the competitive rule. However this result applies to a domain of preferences incompatible with additive utilities because indifference curves cannot touch the axis (Assumption A.3, p. 109).⁹ So it is useful to notice that on the additive domain, the same characterization result applies.

Equal treatment of equals (ETE) is the familiar requirement that the rule F should not discriminate between two agents with identical characteristics. For all $\mathcal {Q}$ and $i,j\in N$

$$\begin{aligned} u_{i}=u_{j}\Longrightarrow U_{i}=U_{j}\quad \text { for all } \ U\in F(\mathcal {Q}) \end{aligned}$$

Proposition 4

If bads under additive utilities are divided and a rule f meets efficiency, independence of lost bids, and at least one of equal treatment of equals and fair share guaranteed, it contains the competitive rule.

An analog of Proposition 4 with the same proof holds in case of goods.

Proof

We already checked that the rule $f^{c}$ meets ILB; also ETE and FSG are clear. Conversely we fix f meeting EFF, ETE or FSG, and ILB and an arbitrary problem $\mathcal {Q}=(N,A,u)$. In the proof we consider several problems (N, A, v) where v varies in $\mathbb {R} _{+}^{N\times A}$, and for simplicity we write f(v) in lieu of f(N, A, v).

We pick $z\in f^{c}(u\mathcal {)}$ and check that $z\in f(u\mathcal {)}$ as well. Set $U_{i}=u_{i}\cdot z_{i}$ and let p be the competitive price at z. In the proof of Lemma 3 we saw that $p_{a}=\frac{u_{ia}}{U_{i}}$ for all i such that $z_{ia}>0$, and for all j we have $p_{a}\le \frac{u_{ja}}{U_{j}}$. Moreover $p\cdot z_{i}=1$ for all i, and $p\cdot e^{A}=n$.

Consider the problem $\mathcal {Q}^{*}=(N,A,w)$ where $w_{i}=p$ for all i. The equal split allocation is efficient in $\mathcal {Q}^{*}$ therefore ETE implies $F(w)=e^{N}$ and so does FSG, because $p\cdot (\frac{1 }{n}e^{A})=1$. Now if we set $\widetilde{w}_{i}=U_{i}p$ the scale invariance property of F (Definition 2) gives $F(\widetilde{w})=U$; moreover $z\in f( \widetilde{w})$ because $\widetilde{w}_{i}\cdot z=U_{i}$ for all i. If $z_{ia}>0$ we have $u_{ia}=U_{i}p_{a}=\widetilde{w}_{ia}$; if $z_{ia}=0$ we have similarly $u_{ia}\ge \widetilde{w}_{ia}$. Apply finally ILB: after raising every lost bid $\widetilde{w}_{ia}$ to $u_{ia}$, the allocation z is still in f(u), as desired. $\square$