On existence of ex post Nash consistent representation for effectivity functions

Abstract

We consider effectivity functions for finitely many players and alternatives. We assume that players have incomplete information—with private values—about the preferences of the other players. Our main result is the characterization of effectivity functions which have an ex post Nash consistent representation, i.e., there is a game form such that (i) the distribution of power among coalitions of players is the same as in the effectivity function and (ii) there is an ex post Nash equilibrium (in pure strategies) for any preference profile.

1 Introduction

An effectivity function (Moulin and Peleg 1982) describes the allocation of power among coalitions of individuals. More precisely, given a set of individuals and a set of alternatives, an effectivity function assigns to each coalition of individuals a collection of subsets of alternatives. Effectivity functions derive from many concepts in game theory and social choice theory: for example game forms, social choice correspondences, simple games. More generally, effectivity functions can be used to describe the distribution of power or rights. For instance, a constitution can be modelled as an effectivity function (Gärdenfors 1981; Peleg 1998): alternatives are social states, and to say that a coalition is effective for a set of alternatives means that this group of individuals is legally entitled to the social state being in the designated set.

According to this last interpretation an effectivity function is a centralized concept describing the rights of individuals. This leads directly to the question whether we can find a set of decentralized rules (practical laws) such that individuals and coalitions, by acting according to these rules, obtain the same rights as described by the effectivity function. In more formal terms: can we find a game form which provides all coalitions with the same power as the effectivity function? This question was already answered in Moulin (1983), who showed that any monotonic and superadditive effectivity function can be represented by a game form. An important further question is whether we can find rules (in accordance with the constitution) such that there is a situation in which the society is stable, that is, in some state of equilibrium. Peleg et al. (2002) answered this question by characterizing effectivity functions that have a Nash consistent representation, i.e., a game form representing the effectivity function and having a Nash equilibrium for any profile of preferences of the individuals. See Peleg and Peters (2010) for an extensive treatment of this topic and related issues.

An important open question in this area is the following. If we take into account that information may be incomplete—individuals are not sure about the preferences, i.e., types, of other individuals—when is it possible to have a representation of an effectivity function that is Bayesian Nash consistent? d’Aspremont and Peleg (1988) consider ordinal Bayesian incentive compatible representations of committees: they study effectivity functions derived from simple games and their representation by so-called decision schemes, which assign probability distributions over the alternatives, such that there exists a Bayesian incentive compatible Nash equilibrium under incomplete information with private values. Recently, Peleg and Zamir (2014) show that, without additional restrictions except for the standard ones, effectivity functions can be Bayesian Nash consistently represented by generalized decision schemes; their proof of this result uses the uniform core (Abdou and Keiding 1991). The question under which conditions such a representation by a deterministic game form exists, remains open.

In the present paper we consider the case of incomplete information with private values: the preference of a type of a player does not depend on the types of the other players. Compared to d’Aspremont and Peleg (1988) and Peleg and Zamir (2014) we impose a considerably stronger requirement: given an effectivity function, when does there exist a representing game form such that, for any information structure (i.e., vector of type sets of the players), there exists an ex post Nash equilibrium for any preference profile, that is, a strategy combination which results in a Nash equilibrium for every realization of the types?

On the one hand, this is a very desirable situation, since players do not have to rely on their beliefs about the types of the others, and they do not have to spend time and effort on finding out the types of the other players. Moreover, every ex post equilibrium has the no regret property which means that no player has an incentive to change his action even if he were to be informed of the true types of the other players. These considerations are similar to the ones justifying implementation in ex post Nash equilibrium (e.g., Bergemann and Morris 2008). It is also a first step towards characterizing Bayesian Nash consistent representations, as every ex post Nash equilibrium is a Bayesian Nash equilibrium for any vector of beliefs.

On the other hand, as can be expected, this requirement turns out to be rather restrictive. Our main result is as follows. An effectivity function (for $n$ individuals or players) has an ex post Nash consistent representation exactly if there exists an $(n-1)$-player coalition and a subset $C$ of alternatives for which this coalition is effective, such that all other $(n-1)$-player coalitions are effective for all singletons in this set $C$. The intuition behind this condition is that in equilibrium there is one player restricted to choose his most preferred alternative from $C$, while all other players are restricted in such a way that they are not able to influence the outcome by unilateral deviation. In the case $n=2$ this condition is equivalent to at least one of the two players being a so-called singleton player: a singleton player is a player for whom all minimal sets for which this player is effective, are singletons. We also show that, if only one of the players has more than one type, then ex post Nash consistency imposes no additional restrictions compared to Nash consistency (as in Peleg et al. 2002). In the final part of the paper we provide a short discussion on effectivity functions that have no ex post Nash consistent representation, but for which a representation exists if we restrict the number of types—a special case being the mentioned one where only one player has more than one type. Throughout the paper we concentrate on existence of ex post Nash equilibria and leave other possible properties (e.g., Pareto optimality of such equilibria) from consideration.

The approach of looking for equilibrium consistent representations of effectivity functions should be distinguished from the approach followed by implementation theory. Suppose we are given a social choice correspondence. In implementation theory one looks for a game form of which, for each profile of preferences, the set of equilibrium outcomes coincides with the set of outcomes assigned by the social choice correspondence. No condition is put on off equilibrium outcomes. In contrast, in an equilibrium consistent representation the outcomes attainable in the game form by individuals and coalitions should coincide with the outcomes attainable via the social choice correspondence or, equivalently, its associated effectivity function. In this sense, requiring equilibrium consistent representation is a strengthening compared to implementation; the weakening is that only existence of an equilibrium outcome is required. Nevertheless, for a given equilibrium consistent representing game form, one can construct a social choice correspondence by assigning all equilibrium outcomes to a given preference profile; then, obviously, this social choice correspondence is implemented by the game form.

The literature on implementation theory also deals with implementation in ex post equilibrium. This solution concept is mainly used in situations with interdependent valuations, because of tractability and robustness against informational assumptions. Several authors show that for one-dimensional signals, ex post implementation is possible if the single crossing property is satisfied (Cremer and McLean 1985; Dasgupta and Maskin 2000; Bergemann and Välimäki 2002; Perry and Reny 2002). More recent work deals with ex post equilibria in multidimensional signal settings. Jehiel et al. (2006) show that the only ex post implementable social choice functions in a generic class of environments are constant functions, whereas Bergemann and Morris (2008) provide conditions for full implementation in ex post equilibrium if the genericity requirement fails.

The organization of the paper is as follows. Section 2 introduces definitions and notations. In Sect. 3, we present our basic representing game form. This game form is extended and modified in several ways in the rest of the paper. Section 4 analyzes the case of two players, and Sect. 5 generalizes to more than two players.

Notation For a finite set $D$, $\vert D \vert$ denotes the number of elements of $D$; $P(D)$ denotes the set of all subsets of $D$; $P_0(D)$ denotes the set of all non-empty subsets of $D$.

2 The model

Let $N=\{1,\ldots ,n\}$ (where $n\ge 2$) be the set of players, and let $A$ be a finite set of alternatives, $\vert A \vert \ge 2$. A binary relation $R$ over $A$ is a subset $R\subseteq A\times A$, where $(a,b)\in R$ is written as $aRb$ (read $aRb$ as $a$ is weakly preferred over $b$). A binary relation is complete if for all $a,b\in A$, we have $aRb$ or $bRa$. A binary relation is transitive if $aRb$ and $bRc$ jointly imply $aRc$, for all $a,b,c\in A$. A preference ordering $R$ on $A$ is a complete and transitive binary relation. The set of all preference orderings on $A$ is denoted by $W$. If $R\in W$ and $a,b\in A$, then $a P b$ means $aRb$ and not $bRa$. If $a\in A$ and $R\in W$, then $L(a,R)=\{b\in A\mid aRb\}$ is the lower contour set of $a$, i.e. the set of alternatives not strictly preferred to $a$. For a set $S$, $W^S=\{f\mid f:S\rightarrow W\}$ is the set of mappings from $S$ to $W.$

An effectivity function (EF) is a function $E{:} P(N)\rightarrow P(P_0(A))$ that satisfies the following conditions: (i) $E(N)=P_0(A)$; (ii) $E(\emptyset )=\emptyset$; and (iii) $A\in E(S)$ for all $S\in P_0(N)$. As a general interpretation, $B\in E(S)$ means that coalition $S$ can force the final alternative to be an element of $B$. The interpretation of the three conditions is fairly obvious: (i) the grand coalition has complete power in terms of $E$, (ii) the empty set has no power, and (iii) an alternative from $A$ must prevail.

An effectivity function $E$ is monotonic (with respect to players as well as alternatives) if

$$\begin{aligned}{}[B\in E(S),B'\in P_0(A), B\subseteq B', \hbox { and } S\subseteq S']\Rightarrow B'\in E(S'). \end{aligned}$$

For $B\in P_0(A)$ and $S\in P_0(N)$, $B$ is minimal for coalition $S$ if $B\in E(S)$ and there is no $B'\in E(S)$ such that $B'\varsubsetneq B$. A monotonic effectivity function $E$ is completely determined by these minimal sets.

The effectivity function $E$ is superadditive if

$$\begin{aligned}{}[B_i\in E(S_i),i=1,2, \text{ and } S_1\cap S_2=\emptyset ] \Rightarrow B_1\cap B_2\in E(S_1\cup S_2). \end{aligned}$$

Note that a superadditive effectivity function is also monotonic with respect to players: for $S\subseteq S'$ and $B\in E(S)$, superadditivity implies that $B=B\cap A\in E(S\cup (S'{\setminus } S))=E(S')$. Monotonicity and superadditivity are natural properties in view of the interpretation given above. Moreover, effectivity functions derived from game forms have these properties.

The polar of $E$ is the effectivity function $E^*$ defined by: $E^*(\emptyset )=\emptyset$, and for $S\in P_0(N)$

$$\begin{aligned} E^*(S)=\{B\in P_0(A) \mid B\cap B'\ne \emptyset \text{ for } \text{ all } B'\in E(N{\setminus } S)\}. \end{aligned}$$

Thus, if $B\in E^*(S)$, then the complementary coalition $N{\setminus } S$ cannot prevent $S$ from obtaining an alternative from $B$; in particular, $A{\setminus } B\notin E(N{\setminus } S)$. The function $E^*$ reflects a weaker effectivity condition than $E$: whereas $E$ tells us what each coalition can guarantee on its own, $E^*$ tells us what each coalition cannot be kept from.

$E$ is maximal if $E$ is superadditive and $E=E^*$. Observe that if $E$ is superadditive, then $E(S)\subseteq E^*(S)$ for all $S$: if $B \in E(S)$ then superadditivity implies $B \cap B' \ne \emptyset$ for all $B' \in E(N {\setminus } S)$, so that $B \in E^*(S)$. Also notice that a maximal effectivity function is monotonic. Indeed, a superadditive effectivity function is monotonic with respect to players; and if $B\in E^*(S)$ and $B\subseteq C$, then obviously $C\cap B'\ne \emptyset$ for all $B'\in E(N{\setminus } S)$ and thus $C\in E^*(S)$. Hence, if $E$ is maximal then $E$ is monotonic with respect to alternatives since $E^*$ is.

The following results are well-known (e.g., Peleg and Peters 2010; Boros et al. 2010; or Crama and Hammer 2011). For completeness, we provide the proofs.

Proposition 2.1

Let $E$ be a monotonic effectivity function. The following statements are equivalent:

• (i) $E=E^*$.

• (ii) For all $B\in P_0(A)$ and for all $S\in P_0(N)$, $B\in E(S)$ if and only if $B\cap B'\ne \emptyset$ for all $B'\in E(N{\setminus } S)$.

• (iii) For all $B\in P_0(A)$ and for all $S\in P_0(N)$, $B\in E(S)$ if and only if $A{\setminus } B\notin E(N{\setminus } S)$.

Proof

The implication $(i)\Rightarrow (ii)$ is obvious. To prove implication $(ii)\Rightarrow (iii)$, assume $(ii)$. If $B\in E(S)$ for some $B \in P_0(A)$ and $S \in P_0(N)$, then, by $(ii)$, $A {\setminus } B \notin E(N{\setminus } S)$. Conversely, if $A{\setminus } B\notin E(N{\setminus } S)$ for some $B \in P_0(A)$ and $S \in P_0(N)$, then by $(ii)$ there must be some $B'\in E(S)$ such that $(A{\setminus } B) \cap B'=\emptyset$. Clearly, $B'\subseteq B$, so that $B\in E(S)$, again by $(ii)$.

Finally, to prove the implication $(iii) \Rightarrow (i)$, assume $(iii)$. If $B \in E^*(S)$ for some $B \in P_0(A)$ and $S \in P_0(N)$, then $A {\setminus } B \notin E(N {\setminus } S)$, hence $B \in E(S)$ by $(iii)$. Conversely, if $B \in E(S)$ for some $B \in P_0(A)$ and $S \in P_0(N)$, then $A {\setminus } B \notin E(N {\setminus } S)$ by $(iii)$. Let $B' \in E(N {\setminus } S)$, then $B' \not \subseteq A {\setminus } B$ by monotonicity, so that $B \cap B' \ne \emptyset$. So $B \in E^*(S)$. $\square$

Remark 2.2

Note that, in the proof of Proposition 2.1, monotonicity of $E$ is only used to prove that $E(S) \subseteq E^*(S)$ for all $S \in P(N)$ in the last part of the proof. This would also follow directly from superadditivity of $E$. Hence, Proposition 2.1 also holds with superadditivity instead of monotonicity.

The following result will be useful in the sequel.

Proposition 2.3

Let $E$ be a maximal effectivity function. Then for each minimal $B\in E(S)$ and alternative $a\in B$, there is a minimal $B'\in E(N{\setminus } S)$ such that $B\cap B'=\{a\}$.

Proof

Let $S\in P_0(N)$, $B \in E(S)$, and $a \in B$. By superadditivity, $B \cap B' \ne \emptyset$ for all $B' \in E(N {\setminus } S)$. Suppose that for each minimal $B' \in E(N{\setminus } S)$ there is some $b \ne a$ such that $b \in B \cap B'$. Then $(B {\setminus } \{a\}) \cap B' \ne \emptyset$ for all minimal $B'\in E(N {\setminus } S)$, hence for all $B'\in E(N {\setminus } S)$. Thus, $B {\setminus } \{a\} \in E^*(S) = E(S)$. So $B$ is not minimal in $E(S)$.

$\square$

A game form is an $(n+2)$-tuple $\Gamma =(\Sigma ^1,\ldots ,\Sigma ^n;\pi ;A)$, where (i) $\Sigma ^i$ is the (non-empty, finite) set of possible actions¹ of player $i\in N$; and (ii) $\pi :\Sigma ^1\times \dots \times \Sigma ^n\rightarrow A$ is the outcome function. Throughout the paper we assume that $\pi$ is surjective. For $S\in P_0(N)$ we denote $\Sigma ^S=\prod _{i\in S} \Sigma ^i$.

Let $\Gamma =(\Sigma ^1,\ldots ,\Sigma ^n;\pi ;A)$ be a game form. For $S\in P_0(N)$ and $\sigma ^S\in \Sigma ^S$, we define $B (\sigma ^S)=\{\pi (\sigma ^S,\sigma ^{N{\setminus } S})\mid \sigma ^{N{\setminus } S}\in \Sigma ^{N{\setminus } S}\}$. The effectivity function $E^{\Gamma }$, associated with $\Gamma$, is defined in the following way: $E^{\Gamma }(\emptyset )=\emptyset$ and for $S\in P_0(N)$,

$$\begin{aligned} E^{\Gamma }(S)=\{B \in P_0(A) \mid B(\sigma ^S) \subseteq B \quad \text{ for } \text{ some } \sigma ^S\in \Sigma ^S\}. \end{aligned}$$

Note that $E^{\Gamma }$ is monotonic and superadditive. Let $E:P(N)\rightarrow P(P_0(A))$ be an effectivity function. A game form $\Gamma$ is a representation of $E$ if $E(S)=E^{\Gamma }(S)$ for every $S\in P_0(N)$. Basically, this means that the game form distributes the same power among the players as the effectivity function does.

Remark 2.4

If $B\in P_0(A)$ is a minimal set of coalition $S\in P_0(N)$ in $E^{\Gamma }(S)$, then there exists an action profile $\sigma ^S\in \Sigma ^S$ such that $B(\sigma ^S)=B$.

An information structure is an $n$-tuple $T=(T^1,\ldots ,T^n)$, where $T^i$ is the finite set of types of player $i=1,\ldots ,n$. We denote by $T^N = \prod _{i\in N} T^i$ the set of type profiles. With some abuse of notation we denote by $W^{T}$ the set of all preference ordering profiles: a profile $R^{T} \in W^{T}$ has dimension $\sum _{i\in N} |T^i|$ and assigns a preference ordering to each type of each player. We assume that preferences are private valued, i.e., they do not depend on types of the other players. If $\Gamma =(\Sigma ^1,\ldots ,\Sigma ^n;\pi ;A)$ is a game form, then $(\Gamma ,T,R^{T})$ is a game of incomplete information in the sense of Harsanyi (1967). The set of strategies of player $i$ in this game is the set $S^i=\{s^i\mid s^i: T^i\rightarrow \Sigma ^i\}$. We denote $S^N=\prod _{i\in N} S^i$. We do not introduce type probabilities since we will only consider ex post Nash equilibrium. A strategy profile $s=(s^1,\ldots ,s^n)\in S^N$ is an ex post $(Nash)$ equilibrium (EPE) of $(\Gamma ,T,R^{T})$ if for all $i\in N$, all $t=(t^1,\ldots ,t^n)\in T^N$ and all $\sigma ^i\in \Sigma ^i$,

$$\begin{aligned} \pi (s(t))R^{t^i} \pi (s^{-i}(t^{-i}),\sigma ^i), \end{aligned}$$

where $s^{-i}(t^{-i})$ is the vector $(s^j(t^j))_{j\ne i}$. Let $s\in S^N$ be an EPE, then we call $\pi (s(t))$ the Nash outcome for $t\in T^N$. Game form $\Gamma$ is ex post $(\textit{Nash})$ consistent for $T$ if $(\Gamma ,T,R^{T})$ has an EPE for every $R^{T} \in W^{T}$. If $\mathcal {T}$ is an arbitrary collection of information structures – that is, with possibly different type set cardinalities – then we say that game form $\Gamma$ is ex post $(Nash)$ consistent for $\mathcal {T}$ if $(\Gamma ,T,R^{T})$ has an EPE for every $T \in \mathcal {T}$ and every $R^{T} \in W^{T}$. Specifically, if $\mathcal {T}= \{T\}$ with $\vert T^i\vert =1$ for every $i\in N$, then an ex post consistent game form $\Gamma$ is Nash consistent (cf. Peleg et al. 2002). We say that effectivity function $E$ has an ex post consistent representation for a collection $\mathcal {T}$ of information structures if there exists a game form $\Gamma$ such that $\Gamma$ is a representation of $E$ and $\Gamma$ is ex post consistent for $\mathcal {T}$. We say that $E$ has an ex post consistent representation if there exists a game form $\Gamma$ such that $\Gamma$ represents $E$ and $\Gamma$ is ex post consistent for every information structure $T$.

Lemma 2.5

Suppose $s\,{=}\,(s^1,\ldots ,s^n)\in S^N$ is an EPE of $(\Gamma ,T,R^T)$. Then $B(s^{-i}(t^{-i}))\subseteq L(\pi (s(t)),R^{t^i})$ for all $t\in T^N$.

Proof

Let $t\in T^N$. Let $a\in B(s^{-i}(t^{-i}))$. Then there is $\sigma ^i\in \Sigma ^i$ such that $\pi (s^{-i}(t^{-i}),\sigma ^i)=a$. Hence $\pi (s(t))R^{t^i}a$, since $s$ is an EPE. Therefore $a\in L(\pi (s(t)),R^{t^i})$.

Remark 2.6

If $s\in S^N$ is an EPE of $(\Gamma ,T,R^T)$, then Lemma 2.5 and monotonicity imply $L(\pi (s(t)),R^{t^i})\in E^{\Gamma }(N{\setminus }\{i\})$ for every $i \in N$ and every $t^i\in T^i$.

Notation In the sequel, instead of $E(\{i\})$, we usually write $E(i)$.

3 A representing game form

In this section we present the basic game form which is used throughout the paper. We focus on this particular game form as it is one of the simplest game forms that yields the desired results. Later, we will extend and modify this game form to obtain our main results. Alternative representing game forms can be found in many places, notably Peleg (1998), Peleg et al. (2002), Peleg and Peters (2010), and Boros et al. (2010).

Let $E$ be a monotonic and superadditive effectivity function. We fix a numbering of the alternatives in $A$, say $A=\{a_1,\ldots ,a_{|A|}\}$. For $i\in N$ let $F^i=\{(S,B)\mid i\in S\subseteq N \text{ and } B\in E(S)\}$. We define the game form $G_0=(\Sigma ^1,\ldots ,\Sigma ^n;\pi ;A)$ as follows. The set of actions of $i\in N$ is the set $\Sigma ^i=\{(f,k)\mid f\in F^i \text{ and } k\in \{1,\ldots ,\vert A\vert \}\}$. The idea is that if $B\in E(S)$ and $f^i=(S,B)$ for all $i\in S$, then the outcome is guaranteed to be within $B$. The integer $k$ is to make sure that every $i\in S$ can cause every $a\in B$ to be the outcome.

Let $\sigma =(\sigma ^1,\ldots ,\sigma ^n)\in \Sigma ^N = \prod _{i\in N}\Sigma ^i$, where $\sigma ^i=(f^i,k^i)\in \Sigma ^i$ for $i\in N$. We say that coalition $S\in P_0(N)$ is formed if there is $B\in E(S)$ such that $f^i=(S,B)$ for all $i\in S$. Define $D\in P_0(A)$ as follows. If no coalition is formed, then $D=A$. Otherwise, let $\{S_1,\ldots ,S_r\}$ be the collection of formed coalitions. For each $j\in \{1,\ldots ,r\}$, there is $B_j \in E(S_j)$ such that $f^i=(S_j,B_j)$ for all $i\in S_j$. Then let $D=\bigcap _{j=1}^r B_j$. Note that $D\ne \emptyset$ because $E$ is superadditive and formed coalitions are pairwise disjoint. Suppose $D=\{a_{j_1},\ldots ,a_{j_{|D|}}\}$ with $j_1 < \ldots < j_{|D|}$. We define $\pi (\sigma )=a_{j_p}$, where $p=\sum \limits _{i\in N} k^i \text{(mod } |D|\text{) }+1$. Thus, given $D$, every player can cause any $a\in D$ to be the outcome by choosing $k^i$ accordingly.

Proposition 3.1

$G_0$ is a representation of $E$.

Proof

We first show that $E(S)\subseteq E^{G_0}(S)$ for all $S\in P_0(N)$. Let $S\in P_0(N)$ and $B\in E(S)$. Choose $\sigma ^i=((S,B),1)$ for all $i\in S$. Then the coalition $S$ is formed and hence by definition of $\pi$, $\pi (\sigma ^{S},\tau ^{N{\setminus } S})\in B$ for all $\tau ^{N{\setminus } S}\in \Sigma ^{N{\setminus } S}$. So, $B(\sigma ^S)\subseteq B$.

In order to prove the converse inclusion, let $S\in P_0(N)$ and $B\in E^{G_0}(S)$. Since $E(N)=P_0(A)$ and $A\in E(S)$ for all $S\in P_0(N)$, we can assume that $S\ne N$ and $B\ne A$. We show that $B\in E(S)$. Let $\sigma ^S\in \Sigma ^S$ be such that $B(\sigma ^S)\subseteq B$ and for each $i \in N {\setminus } S$ choose $\tau ^i$ such that $f^i=(N{\setminus } S,A)$. Consider the action profile $(\sigma ^S,\tau ^{N{\setminus } S})$. In this profile, since $B \ne A$, $S$ contains at least one formed coalition. Let $\{S_1,\ldots ,S_r\}$ denote the set of all formed coalitions within $S$; hence, for each $j=1,\ldots ,r$ and $i\in S_j$, $\sigma ^i=(f^i,k^i)$ with $f^i=(S_j,B_j)$ for some $B_j \in E(S_j)$. Thus, for $(\sigma ^S,\tau ^{N{\setminus } S})$, the set of formed coalitions is $\{S_1,\ldots ,S_r,N{\setminus } \bigcup _{j=1}^r S_j\}$. Since $B_j\in E(S_j)$ for all $j\in \{1,\ldots ,r\}$, and $\bigcup _{j=1}^r S_j\subseteq S$, superadditivity and monotonicity imply $\bigcap _{j\in J} B_j\in E(S)$. It remains to show that $\bigcap _{j\in J} B_j\subseteq B(\sigma ^S)$, since then monotonicity implies that $B\in E(S)$.

Take $a\in \bigcap _{j\in J} B_j$. Since $S\ne N$, given $\sum _{i\in S}k^i$, $N{\setminus } S$ is able to choose $\sum _{i\in N{\setminus } S}k^i$ such that $\pi (\sigma ^S,\tau ^{N{\setminus } S})=a$. Hence $a\in B(\sigma ^S)$ for every $a\in \bigcap _{j\in J} B_j$, which completes the proof. $\square$

4 Two-person effectivity functions

Throughout this section we assume that $N=\{1,2\}$. The following result is from Peleg et al. (2002), see Remark 3.13 in the paper.

Lemma 4.1

Let $E$ be a superadditive and monotonic effectivity function. The following statements are equivalent:

• (i) $E$ has a Nash consistent representation.

• (ii) $E$ is maximal.

The original condition for the existence of a Nash consistent representation is condition (ii) in Lemma 5.1 below. However, for two players, it follows as a corollary from superadditivity and condition (ii) in Lemma 5.1 that $E$ must be maximal.

4.1 One-sided incomplete information

In this subsection, we consider the case of one-sided incomplete information. Without loss of generality, we assume that $\vert T^1\vert \ge 1$ and $\vert T^2\vert =1$. This means that the preference ordering of one player is commonly known, while the other player possibly has multiple types.

The main theorem of this subsection shows that in case of one-sided incomplete information, ex post consistent representation imposes no further conditions on the effectivity function compared to Nash consistent representation.

Theorem 4.2

Let $E$ be a superadditive and monotonic effectivity function. Let $\mathcal {T}= \{(T^1,T^2) \mid \vert T^1\vert \ge 1 \text{ and } \vert T^2\vert =1\}$. The following statements are equivalent:

• (i) $E$ has a Nash consistent representation.

• (ii) $E$ has an ex post consistent representation for $\mathcal {T}$.

Proof

To prove the implication $(i)\Rightarrow (ii)$, suppose $E$ has a Nash consistent representation, and let $T \in \mathcal {T}$. Then by Lemma 4.1 $E$ is maximal. We consider the representing game form $G_0$ from Sect. 3 and show that this game form always contains an EPE. Let $R^2\in W$ be the preference ordering of player 2, and write $a_1 R^2 \ldots R^2 a_m$, where $m = |A|$. Let $j\in \{1,\ldots ,m\}$ such that $L(a_j,R^2)\in E^{\Gamma }(1)$ and $L(a_{j+1},R^2)\notin E^{\Gamma }(1)$ (where we define $L(a_{m+1},R^2)=\emptyset$). Define $B_2=\{a_1,\ldots ,a_j\}$. By Proposition 2.1 (iii), $B_2\in E^{\Gamma }(2)$. Consider the strategy profile where player 2 plays $\sigma ^2=((\{2\},B_2),1)$, and every type $t^1\in T^1$ plays $\sigma ^1=$ $((\{1\},L(a,R^2)),k)$, with $a\in B_2$ such that $a R^{t^1} b$ for all $b\in B_2$ and with $k$ such that $\pi (\sigma ^1,\sigma ^2)=a$. It is straightforward to check that this strategy profile is an EPE.

To prove the implication $(ii)\Rightarrow (i)$, suppose $E$ has an ex post consistent representation $\Gamma$ for $\mathcal {T}$. In particular, the game form $\Gamma$ has an ex post equilibrium if all types of player 1 have the same preference ordering. This is equivalent to saying that $E$ has a Nash consistent representation. $\square$

4.2 Two-sided incomplete information

In this subsection, still for two players, we consider the case of two-sided incomplete information.

A player $i\in N$ is a singleton player if all minimal sets of player $i$ in $E(i)$ are singletons.

Example 4.3

Let $A=\{a,b\}$ with $a \ne b$. There are two possible maximal effectivity functions (if we omit effectivity functions obtainable from these two by permutations of players or alternatives):

• (i) $E(1)=E(\{1,2\})=\{\{a\},\{b\},A\}$ and $E(2)=\{A\}$

• (ii) $E(1)=E(2)=\{\{a\},A\}$ and $E(\{1,2\})=\{\{a\},\{b\},A\}$

Note that in (i) player 1 is a ‘dictator’. Also, both effectivity functions contain a singleton player.

The following theorem characterizes all two-player effectivity functions with an ex post consistent representation for all information structures in which both players have at least two types. In fact, its proof shows that if there exists an ex post consistent representation of $E$, then any representation is ex post consistent.

Theorem 4.4

Let $E$ be a maximal effectivity function. Let $\mathcal {T}= \{ (T^1,T^2) \mid |T^1|,|T^2| \ge 2 \}$. The following statements are equivalent:

• (i) $E$ has an ex post consistent representation for $\mathcal {T}$.

• (ii) $E$ contains a singleton player.

Proof

To prove the implication $(i)\Rightarrow (ii)$, suppose $E$ does not contain a singleton player. We will present a preference profile for $T \in \mathcal {T}$ with $|T^1|=|T^2|=2$ such that no EPE exists in any representing game form.

Let $B_1$ be minimal for player 1 with $\vert B_1\vert \ge 2$ and let $B_2$ be minimal for player 2 with $\vert B_2\vert \ge 2$ (these sets exist, since there is no singleton player). Take $a\in B_1\cap B_2\ne \emptyset$ (this is possible by superadditivity), and $b\in B_1$ with $b\ne a$ (this is possible since $|B_1| \ge 2$). We can assume that $\vert A\vert \ge 3$, because if $\vert A\vert = 2$ then every maximal effectivity function contains a singleton player (see Example 4.3). Consider the following preference profile:

Now let $\Gamma$ be a representing game form and suppose that $(s^1,s^2)$ is an EPE in the game with this preference profile. We derive a contradiction.

• (a) Claim $b\in B(s^2(t^{2,1}))$.

  Proof of claim: Since $B_1{\setminus }\{b\}\notin E^{\Gamma }(1)$ ($B_1$ is minimal for player 1), Remark 2.6 implies $\pi (s^1(t^{1,1}),s^2(t^{2,1}))\notin B_1{\setminus }\{b\}$. Since $A{\setminus } B_1\notin E^{\Gamma }(2)$ (by superadditivity), Remark 2.6 implies $\pi (s^1(t^{1,1}),s^2(t^{2,1}))\notin A{\setminus } B_1$. Hence $\pi (s^1(t^{1,1}),s^2(t^{2,1}))=b$, which implies that $b\in B(s^2(t^{2,1}))$.

• (b) Claim $B(s^1(t^{1,2}))=B_1$.

  Proof of claim: Since $b\in B(s^2(t^{2,1}))$ by the previous claim, and $b$ is $t^{1,2}$’s most preferred element, $\pi (s^1(t^{1,2}),s^2(t^{2,1}))=b$. This implies, by Lemma 2.5 and minimality of $B_1$, that $B(s^1(t^{1,2}))=B_1$.

Now, since $B(s^1(t^{1,2}))=B_1$ and $a$ is $t^{2,2}$ ’s most preferred alternative from $B_1$, $\pi (s^1(t^{1,2}),$ $s^2(t^{2,2}))=a$. Hence, by Remark 2.6, $\{a\} = L(\pi (s^1(t^{1,2}), s^2(t^{2,2})),R^{t^{1,2}}) \in E^{\Gamma }(2)$. Since $a \in B_2$, this contradicts minimality of $B_2$.

In order to prove the implication $(ii)\Rightarrow (i)$, assume that $E$ contains a singleton player, and let $T \in \mathcal {T}$. We show that for any representing game form $\Gamma$ and any $R^T \in W^T$, the game $(\Gamma ,T,R^T)$ has an EPE. Without loss of generality assume that player 1 is a singleton player. Let $B_2=\{a\in A\mid \{a\} \hbox { is a minimal set for player 1}\}$. By Proposition 2.1 (ii), we have $B_2 \in E(2)$. Consider the strategy profile in which every type $t^1\in T^1$ plays an action $\sigma ^1\in \Sigma ^1$ such that $B(\sigma ^1)=\{a\}$ for $a\in B_2$ such that $a R^{t^1} b$ for all $b\in B_2$; and in which every type $t^2\in T^2$ plays an action $\sigma ^2\in \Sigma ^2$ such that $B(\sigma ^2)=B_2$. It is easy to see that this strategy profile is an EPE. $\square$

5 More than two players

Throughout this section, unless stated otherwise, we assume that $\vert N\vert \ge 3$. The following result is from Peleg et al. (2002), in particular Remark 3.11 there.

Lemma 5.1

Let $E$ be a superadditive and monotonic effectivity function. The following statements are equivalent:

• (i) $E$ has a Nash consistent representation.

• (i) $B_i\notin E(N{\setminus }\{i\})$ for all $i\in N \Rightarrow A{\setminus } \bigcup _{i=1}^n B_i\ne \emptyset$.

In order to see that condition (ii) is a necessary condition, suppose that the condition does not hold true, i.e., there are $B_i\notin E(N{\setminus }\{i\})$ for all $i\in N$ such that $\bigcup _{i=1}^n B_i=A$. If each player $i\in N$ prefers the alternatives in the complement of $B_i$ to the alternatives in $B_i$, then there is no Nash alternative (observe that each alternative is in some $B_i$ and since $B_i\notin E(N{\setminus }\{i\})$, player $i$ has a profitable deviation).

5.1 Incomplete information

In this subsection, we consider the case of incomplete information. Our main result is the characterization of effectivity functions that have an ex post consistent representation for any number of types. The next theorem extends Theorem 4.4 to $n>2$. The game form that we introduce consists of two parts: actions that assure representation (as in $G_0$), and equilibrium actions.

The idea behind condition (ii) is that in an ex post Nash equilibrium, player $i$ is restricted to choose his most preferred alternative from $C$ and no other player is able to change the outcome by unilateral deviation. So each such $C$ is a set of possible equilibrium outcomes. For an illustration, see Example 5.6.

Theorem 5.2

Let $E$ be a superadditive and monotonic effectivity function. The following statements are equivalent:

• (i) $E$ has an ex post consistent representation.

• (ii) There exists an $i\in N$ and $C\in E(N{\setminus }\{i\})$ such that $\{a\}\in E(N{\setminus }\{j\})$ for all $a\in C$ and for every $j\ne i$.

Proof

We first prove the implication $(i)\Rightarrow (ii)$. We assume that for every $i\in N$ and every $B_i\in E(N{\setminus }\{i\})$, there is $a\in B_i$ such that $\{a\}\notin E(N{\setminus }\{j\})$ for some $j\ne i$. First, we define a specific preference profile. Second, we show that for this particular preference profile no EPE exists in any representing game form.

We define the sets $A_{1,i}=\{a\in A\mid \{a\}\notin E(N{\setminus }\{i\}) \text{ and } \{a\}\in E(N{\setminus }\{j\}) \text{ for } \text{ all }j\ne i\}$ for all $i\in N$, and $A_2=\{a\in A\mid \text{ there } \text{ are } i,j\in N, \text{ with } i\ne j\text{, } \text{ such } \text{ that } \{a\}\notin E(N{\setminus }\{i\}) \text{ and } \{a\}\notin E(N{\setminus }\{j\})\}$. By our assumption, $\bigcup _{i=1}^n A_{1,i}\cup A_2=A$. Moreover, $A_{1,i}\cap A_2=\emptyset$ for all $i\in N$ and $A_{1,i}\cap A_{1,j}=\emptyset$ for all $i\ne j$.

The definition of the announced preference profile will be given by an algorithm, as follows. We start with an information structure $(T^1,\ldots ,T^n)$ such that $\vert T^i \vert =1$ for all $i\in N$. Let $t=(t^1,\ldots ,t^n)\in T^1\times \cdots \times T^n$ denote the corresponding type vector. In the algorithm, for every $i\in N$, two sets $H_i \subseteq A$ and $L_i \subseteq A$ are defined, and a preference ordering $R^{t^i}$ over $H_i\cup L_i$ such that for all $a\in H_i$ and all $b\in L_i$, $aP^{t^i}b$ (alternatives in $H_i$ are strictly preferred to alternatives in $L_i$). We iteratively extend this preference ordering by adding an $a\in A$ to either $H_i$ or $L_i$ for every $i\in N$, until $H_i\cup L_i=A$. Under a specific condition, extra types may be added. See Algorithm 1.²

Consider the constructed preference profile $R^T$ with associated information structure $T$ and let $\Gamma$ be a representing game form. Suppose that $(s^1,\ldots ,s^n)$ is an EPE in $(\Gamma , T, R^T)$. We derive a contradiction.

Let $i\in N$. Since for all $a\in A_{1,i}$, $\{a\}\in E^{\Gamma }(N{\setminus }\{j\})$ for all $j\ne i$, our initial assumption implies $A_{1,i}\notin E^{\Gamma }(N{\setminus }\{i\})$. Thus, for all $i\in N$ and for all $a\in A_{1,i}$, we have $L(a,R^{t^i})\notin E^{\Gamma }(N{\setminus }\{i\})$. Hence, by Remark 2.6, we have $\pi (s(t))\notin \bigcup _{i=1}^n A_{1,i}$ and thus $\pi (s(t))\in A_2$ with $L(\pi (s(t)),R^{t^i})\in E^{\Gamma }(N{\setminus }\{i\})$ for all $i\in N$.

Let $a=\pi (s(t))$. If no new types were added in the algorithm, then there was a player $k \in N$ such that $L(a,R^{t^k}) = L(\pi (s(t)),R^{t^k}) \notin E(N {\setminus } \{k\})$, but this contradicts Remark 2.6. So we may assume that there are $i,j\in N$, with $i\ne j$, be such that $t'^i$ and $t'^j$ are added for $a$. In the step of the algorithm where $t'^i$ and $t'^j$ are added, $a$ becomes the most preferred element of $L_i$ for $t^i$ and the least preferred element of $H_j$ for $t^j$. Since each remaining alternative $b\in A_2{\setminus }\{a\}$ becomes either the new best alternative of $L_i$ or $L_j$ or the new worst alternative of $H_i$ or $H_j$, we have at the end of the algorithm $b P^{t^i} a$ and $a P^{t^j} b$ for all remaining $b\in A_2{\setminus }\{a\}$. So in fact, the preference orderings of $t'^i$ and $t'^j$ are as follows:

Observe the following:

• (a) Lemma 2.5 implies that $B(s^{-i}(t^{-i}))\subseteq L(a,R^{t^i})$. Since $L(a,R^{t^i}) \in E(N {\setminus } \{i\})$ by the condition for adding types $t'^i$ and $t'^j$ in the algorithm, and $\{a\} \notin E(N{\setminus }\{i\})$ since $a \in A_2$, we have $L(a,R^{t^i}) {\setminus } \{a\} \ne \emptyset$. Since $a$ is $t'^i$’s least preferred element, we have $\pi (s^{-i}(t^{-i}),s^ i(t'^i))\in L(a,R^{t^i}){\setminus }\{a\}$. But this implies that $\pi (s^{-i,j}(t^{-i,j}),s^i(t'^i),s^j(t'^j))\ne a$ and $\pi (s^{-i,j}(t^{-i,j}),s^i(t'^i),s^j(t'^j))\notin A{\setminus } L(a,R^{t^i})$.³

• (b) Lemma 2.5 implies that $B(s^{-j}(t^{-j}))\subseteq L(a,R^{t^j})$. Similarly as in (a), we have $L(a,R^{t^j}) {\setminus } \{a\} \ne \emptyset$. Since $a$ is $t'^j$’s least preferred element, we have $\pi (s^{-j}(t^{-j}),s^j(t'^j))\in L(a,R^{t^j}){\setminus }\{a\}$. But this implies that $\pi (s^{-i,j}(t^{-i,j}),s^i(t'^i),s^j(t'^j))\notin A{\setminus } L(a,R^{t^j})$.

If we show that $\{a\}\cup A{\setminus } L(a,R^{t^i})\cup A{\setminus } L(a,R^{t^j})=A$, then we have proved that there is no Nash outcome for $(t^{-i,j},t'^i,t'^j)$, which is in contradiction with the assumption that $(s^1,\ldots ,s^n)$ is an EPE. Note that it is sufficient to show that $L(a,R^{t^i}){\setminus }\{a\}\subseteq A{\setminus } L(a,R^{t^j})$.

Take $b\in L(a,R^{t^i})$, with $b\ne a$. Since $aP^{t^i}b$, in the algorithm $b$ became the new best element of $L_i$ for $t^i$ before $a$ became the new best element of $L_i$ for $t^i$. So also, $b$ became the new worst element of $H_j$ for $t^j$ before $a$ became the new worst element of $H_j$ for $t^j$. Hence $bP^{t^j}a$ and thus $b\in A{\setminus } L(a,R^{t^j})$. This concludes the proof of the implication $(i)\Rightarrow (ii)$.

We now prove the implication $(ii)\Rightarrow (i)$. We assume that there exists an $i\in N$ and $C\in E(N{\setminus }\{i\})$ such that $\{a\}\in E(N{\setminus }\{j\})$ for all $a\in C$ and for every $j\ne i$. W.l.o.g. assume $i=1$. We write $C=\{a_1,\ldots ,a_{|C|}\}$.

We extend $G_0=(\Sigma ^1,\ldots ,\Sigma ^n;\pi ;A)$ from Sect. 3 to a game form $G_1=(\Sigma _1^1,\ldots ,\Sigma _1^n;\pi _1;A)$ as follows. The set of actions of $i\in N$ is the set $\Sigma _1^i=\{(f,k){\mid } f\in F^i\cup \{v\} \text{ and } k\in \{1,\ldots ,\vert A\vert \}\}$.

Let $\sigma =(\sigma ^1,\ldots ,\sigma ^n)\in \Sigma _1^N$, where $\sigma ^i=(f^i,k^i)\in \Sigma _1^i$ for every $i\in N$. Define $K=\{i\in N{\mid } f^i\in F^i\}$ and $L=\{i\in N{\mid } f^i=v\}$. Then $N=K\cup L$ and $K\cap L=\emptyset$. To define $\pi _1(\sigma )$, we distinguish two cases:

• (i) $\vert L\vert <n-1$. Then $\pi _1(\sigma )=\pi (\sigma )$, with $\pi$ the outcome function of $G_0$ (see Sect. 3).

• (ii) $\vert L\vert \ge n-1$. Then $\pi _1(\sigma )=a_p\in C$, where $p=k^{1} \text{(mod } |C|\text{) }+1$.

Claim $G_1$ is a representation of $E$.

To prove this claim we first show that $E(S)\subseteq E^{G_1}(S)$ for all $S\in P_0(N)$. Let $S\in P_0(N)$ and $B\in E(S)$. We distinguish three cases

• $\vert S\vert \ge 2$. Choose $\sigma ^i=((S,B),1)$ for all $i\in S$. Then coalition $S$ is formed and hence by definition of $\pi _1$, $\pi _1(\sigma ^{S},\tau ^{N{\setminus } S})\in B$ for all $\tau ^{N{\setminus } S}\in \Sigma _1^{N{\setminus } S}$. So, $B(\sigma ^S)\subseteq B$.

• $S=\{1\}$. Choose $\sigma ^{1}=((\{1\},B), k^{1})$, where $k^{1}$ is defined as follows. Since $C\in E(N{\setminus }\{1\})$, superadditivity implies that $A{\setminus } C\notin E(1)$ and thus $B\cap C\ne \emptyset$. This implies that we can choose $k^{1}$ such that $\pi _1(\sigma ^{1},\tau ^{N{\setminus }\{1\}})\in B$ if $\tau ^{N{\setminus }\{1\}}$ is such that $f^j=v$ for all $j\in N{\setminus }\{1\}$. For all other $\tau ^{N{\setminus }\{1\}}\in \Sigma _1^{N{\setminus }\{1\}}$, it is sufficient to note that coalition $\{1\}$ forms.

• $S=\{i\}$, with $i\ne 1$. Choose $\sigma ^i=((\{i\},B), 1)$. Since $\{a\}\in E(N{\setminus }\{i\})$ for all $a\in C$, superadditivity implies that $B\supseteq C$. Thus, by definition of $\pi _1$, $\pi _1(\sigma ^i,\tau ^{N{\setminus }\{i\}})\in B$ for all $\tau ^{N{\setminus }\{i\}}\in \Sigma _1^{N{\setminus }\{i\}}$.

  In order to prove the converse inclusion, let $S\in P_0(N)$ and $B\in E^{G_1}(S)$. We show that $B\in E(S)$. Let $\sigma ^S\in \Sigma ^S$ such that $B(\sigma ^S)\subseteq B$. We only treat the case where $\vert S\vert =n-1$ and $\sigma ^S$ is such that $f^i=v$ for all $i\in S$. For all other cases, it is sufficient to note that $G_1$ is an extension of $G_0$. We distinguish two cases.

• $1\notin S$. Then, by construction of the game form, $B(\sigma ^S)= C$. By assumption, $C\in E(N{\setminus }\{1\})=E(S)$ and thus by monotonicity $B\in E(S)$.

• $1\in S$ and $j\notin S$. Then by construction $B(\sigma ^S)=\{a\}$ for some $a\in C$. By assumption, $\{a\}\in E(N{\setminus }\{j\})=E(S)$, and thus by monotonicity $B\in E(S)$.

This concludes the proof of the claim.

Now let $T$ be an arbitrary information structure. It remains to prove that $G_1$ is ex post consistent for $T$. Let $R^T\in W^T$. Consider the following strategy profile $s\in S^N$. For every $t^{i}\in T^{i}$, with $i\ne 1$, $s(t^i)=(v, 1)$. For every $t^{1}\in T^{1}$, $s(t^{1})=(v, k^{1})$ such that $k^{1}$ selects alternative $a\in C$, where $aR^{t^{1}}b$ for all $b\in C$.

If $t^1\in T^1$ deviates, $t^1$ is able to choose an alternative from $C$. Since $aR^{t^{1}}b$ for all $b\in C$, $t^1$ is not able to improve. If $t^i\in T^i$, with $i\ne 1$, deviates, the outcome does not change. Hence this profile is an EPE. $\square$

Remark 5.3

It is not difficult to verify that condition (ii) of Theorem 5.2 implies condition (ii) of Lemma 5.1.

Corollary 5.4

Let $E$ be a superadditive and monotonic effectivity function with a Nash consistent representation. If $E(N{\setminus }\{i\})=\{A\}$ for some $i\in N$, then $E$ has an ex post consistent representation.

Proof

If $E(N{\setminus }\{i\})=\{A\}$ for some $i\in N$, then Lemma 5.1 (ii) implies that $E(N{\setminus }\{j\})=P_0(A)$ for all $j\ne i$. By Theorem 5.2, $E$ has an ex post consistent representation. $\square$

The next example illustrates the construction of a preference profile without an ex post Nash consistent representation in the proof of Theorem 5.2.

Example 5.5

Let $N=\{1,2,3\}$ and $A=\{a,b,c,d,e\}$. Let $E$ be a superadditive and monotonic effectivity function with

$$\begin{aligned} E(\{1,2\})= & {} \{\{c\},\{d\},\{e\},\{a,b\}\}^+ \\ E(\{1,3\})= & {} \{\{a\},\{b\},\{e\},\{c,d\}\}^+ \\ E(\{2,3\})= & {} \{\{a\},\{c\},\{b,d\},\{b,e\},\{d,e\}\}^+\;. \end{aligned}$$

(The superscript $+$ indicates that all supersets are included as well.) We illustrate the procedure of Algorithm 1. We have $A_{1,1}=\{e\}$, $A_{1,2}=\{c\}$, $A_{1,3}=\{a\}$ and $A_2=\{b,d\}$. After the first while loop, we have the following preference profile:

After the second while loop, we have the following preference profile:

This is the profile, used in the proof of Theorem 5.2, for which there is no ex post Nash equilibrium. However, in this example there is another preference profile with less types for which also no representing game form with an EPE exists. This can be shown by using similar arguments (omitted here) as in the proof of Theorem 4.4.

Thus, the algorithm used in the proof of Theorem 5.2 is not always the most efficient one in terms of the number of types needed in order to obtain nonexistence of an ex post Nash equilibrium.

The following example displays an effectivity function with an ex post Nash consistent representation.

Example 5.6

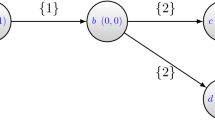
Let $N=\{1,2,3\}$ and $A=\{a,b,c\}$. Consider the following effectivity function: $E(1)=E(2)=\{\{a,b\},A\}$, $E(3)=\{A\}$, $E(\{1,2\})=\{\{a,b\},\{a,c\},\{b,c\}\}^+$ and $E(\{1,3\})=E(\{2,3\})=\{\{a\},\{b\}\}^+$. By Theorem 5.2, this effectivity function has an ex post consistent representation. Consider the following representation:

$$\begin{aligned} \begin{array}{c|ccc} M_1 &{} L &{} M &{} R \\ \hline T&{} a &{} a &{} a\\ C&{} a &{} b &{} c\\ B&{} a &{} c &{} b \end{array}\quad \begin{array}{c|ccc} M_2 &{} L &{} M &{} R \\ \hline T&{} b &{} b &{} b\\ C&{} b &{} c &{} a\\ B&{} b &{} a &{} c \end{array} \end{aligned}$$

in which $\Sigma ^1=\{T,C,B\}$, $\Sigma ^2=\{L,M,R\}$ and $\Sigma ^3=\{M_1,M_2\}$. This representation is ex post consistent for any $T$. Namely, the following strategy profile always constitutes an EPE: all $t^1\in T^1$ play $T$, all $t^2\in T^2$ play $L$ and all $t^3\in T^3$ with $aR^{t^3}b$ play $M_1$ and all $t^3\in T^3$ with $bP^{t^3}a$ play $M_2$. Observe that $E$ has no ‘dictator’ (i.e., a player who is effective for every singleton. In the given equilibrium, however, player 3 can act as if he is the dictator over $\{a,b\}$.

5.2 Discussion

Theorem 5.2 characterizes all effectivity functions for which no ex post consistent representation exists, i.e., there is no game form that represents the effectivity function and that has an ex post Nash equilibrium for any information structure $T=(T^1,\ldots ,T^n)$ and any profile of preferences for all types. Although it is not difficult to derive an upper bound on the number of types needed such that no ex post consistent representation exists (e.g., by considering Algorithm 1), it is less obvious how to derive a sharp upper bound (depending on the effectivity function at hand).

As a first partial answer, Proposition 5.7 extends Theorem 4.2 to $n>2$. Its (more involved) proof is delegated to the Appendix.

Proposition 5.7

Let $E$ be a superadditive and monotonic effectivity function. Let $\mathcal {T}= \{(T^1,\ldots ,T^n) \mid \vert T^1 \vert \ge 2 \text{ and } \vert T^i \vert = 1 \text{ for } \text{ all } i\ne 1\}$. The following statements are equivalent:

• (i) $E$ has a Nash consistent representation.

• (i) $E$ has an ex post consistent representation for $\mathcal {T}$.

As a second partial answer, we present an example of an effectivity function that has no ex post consistent representation for any number of types, but has one if we restrict to two types per player.

Example 5.8

Let $N=\{1,2,3\}$ and $A=\{a,b,c,d,e\}$. Let $E$ be a superadditive and monotonic effectivity function with $E(\{1,2\})=P_0(A)$ and $E(\{1,3\})=E(\{2,3\})=\{\{x,y\}\mid x,y\in A, x\ne y\}$. By Theorem 5.2, $E$ has no ex post consistent representation. Let $T$ be an information structure with $|T_i|=2$ for $i=1,2,3$. Then $E$ has an ex post consistent representation for $T$. Such a representation is constructed in the Appendix.

Appendix

Proof of Proposition 5.7

To prove the implication $(i)\Rightarrow (ii)$, assume that $E$ has a Nash consistent representation, and let $T \in \mathcal {T}$. By Lemma 5.1, if $B_i\notin E(N{\setminus }\{i\})$ for all $i\in N$ then $A{\setminus } \bigcup _{i=1}^n B_i\ne \emptyset$.

We extend $G_0=(\Sigma ^1,\ldots ,\Sigma ^n;\pi ;A)$ from Sect. 3 to a game form $G_2=(\Sigma _2^1,\ldots ,\Sigma _2^n;\pi _2;A)$, as follows. A selection is a function $\phi {:}P_0(A)\rightarrow A$ such that $\phi (B)\in B$ for every $B\in P_0(A)$. Denote by $\Phi$ the set of all selections. The set of actions of $i\in N$ is the set $\Sigma _2^i=\{(f,k,\phi )\mid f\in F^i\cup W^{N{\setminus }\{1\}} \text{, } k\in \{1,\ldots ,\vert A\vert \} \text{ and } \phi \in \Phi \}$.

Let $\sigma =(\sigma ^1,\ldots ,\sigma ^n)\in \Sigma _2^N$, where $\sigma ^i=(f^i,k^i,\phi ^i)\in \Sigma _2^i$ for every $i\in N$. Define $K=\{i\in N\mid f^i\in F^i\}$ and $L^{R^{N{\setminus }\{1\}}}{=}\{i\in N\mid f^i=R^{N{\setminus }\{1\}}\}$ for all $R^{N{\setminus }\{1\}}\in W^{N{\setminus }\{1\}}$. Note that every $i\in N$ is either in $K$ or in $L^{R^{N{\setminus }\{1\}}}$ for some $R^{N{\setminus }\{1\}}\in W^{N{\setminus }\{1\}}$. In order to define $\pi _2(\sigma )$, we consider two cases.

• (i) If $\vert L^{R^{N{\setminus }\{1\}}}\vert <n-1$ for all $R^{N{\setminus }\{1\}}\in W^{N{\setminus }\{1\}}$, then we define $\pi _2(\sigma )=\pi (\sigma )$, with $\pi$ as in $G_0$ (Sect. 3).

• (ii) Suppose $\vert L^{R^{N{\setminus }\{1\}}}\vert \ge n-1$ for some $R^{N{\setminus }\{1\}}\in W^{N{\setminus } \{1\}}$. For every $i\ne 1$, we define $B_i\notin E(N{\setminus }\{i\})$ as follows. Let $R^i$ be the preference ordering of player $i$ in the profile $R^{N{\setminus }\{1\}}$, say $a_1 R^i \ldots R^i a_m$, where $m = |A|$. Choose $j\in \{1,\ldots ,m\}$ such that $L(a_j,R^i)\in E(N{\setminus }\{i\})$ and $L(a_{j+1},R^i)\notin E(N{\setminus }\{i\})$ (where we define $L(a_{m+1},R^i)=\emptyset$). Then we define $B_i=L(a_{j+1},R^i)$. Since $B_i\notin E(N{\setminus }\{i\})$ for all $i\ne 1$, we have $A{\setminus }\bigcup _{i\ne 1}B_i\ne \emptyset$. This implies that $C^{R^{N{\setminus }\{1\}}} \in E(N {\setminus } \{1\})$, where $C^{R^{N{\setminus }\{1\}}}=A{\setminus }\bigcup _{i\ne 1}B_i$. To define $\pi _2(\sigma )$, we distinguish two further subcases:

  • (ii.a) If $L^{R^{N{\setminus }\{1\}}}=N{\setminus }\{i\}$ with $i\ne 1$, then we define $a=\phi ^1(C^{R^{N{\setminus }\{1\}}})$, and $\pi _2(\sigma )=\phi ^i(L(a,R^i))$.

  • (ii.b) If $L^{R^{N{\setminus }\{1\}}}=N{\setminus }\{1\}$ or $L^{R^{N{\setminus }\{1\}}}=N$, then we define $\pi _2(\sigma )=\phi ^1(C^{R^{N{\setminus }\{1\}}})$.

Claim $G_2$ is a representation of $E$.

To prove this claim, we first show that $E(S)\subseteq E^{G_2}(S)$ for all $S\in P_0(N)$. Let $S\in P_0(N)$ and $B\in E(S)$. We distinguish three cases.

• $\vert S\vert \ge 2$. Choose $\sigma ^i=((S,B),1,\phi ^i)$, with $\phi ^i$ chosen arbitrarily, for all $i\in S$. Then the coalition $S$ is formed and hence by definition of $\pi _2$, $\pi _2(\sigma ^{S},\tau ^{N{\setminus } S}) = \pi (\sigma ^{S},\tau ^{N{\setminus } S}) \in B$ for all $\tau ^{N{\setminus } S}\in \Sigma _2^{N{\setminus } S}$. So, $B(\sigma ^S)\subseteq B$.

• $S=\{1\}$. Choose $\sigma ^{1}=((\{1\},B), 1,\phi ^1)$, where $\phi ^1$ is such that $\phi ^1(B')\in B$ for all $B'$ with $B'\cap B\ne \emptyset$.

  If $\tau ^{N{\setminus }\{1\}}$ is such that $f^j=R^{N{\setminus }\{1\}}$ for all $j\in N{\setminus }\{1\}$, we have $C^{R^{N{\setminus }\{1\}}}\in E(N{\setminus }\{1\})$ and thus by superadditivity $A{\setminus } C^{R^{N{\setminus }\{1\}}}\notin E(1)$. Hence, by monotonicity, $B\cap C^{R^{N{\setminus }\{1\}}} \ne \emptyset$, which means that $\phi ^1$ selects an alternative from $B$.

  For all other $\tau ^{N{\setminus }\{1\}}\in \Sigma _1^{N{\setminus }\{1\}}$, coalition $\{1\}$ forms. Thus, by definition of $\pi _2$, $\pi _2(\sigma ^{1},\tau ^{N{\setminus }\{1\}}) = \pi (\sigma ^{1},\tau ^{N{\setminus }\{1\}}) \in B$ for all $\tau ^{N{\setminus }\{1\}}\in \Sigma _2^{N{\setminus }\{1\}}$.

• $S=\{i\}$, with $i\ne 1$. Choose $\sigma ^i=((\{i\},B), 1,\phi ^i)$, where $\phi ^i$ is such that $\phi ^i(B')\in B$ for all $B'$ with $B'\cap B\ne \emptyset$.

If $\tau ^{N{\setminus }\{i\}}$ is such that $f^j=R^{N{\setminus }\{1\}}$ for all $j\in N{\setminus }\{i\}$, the definition of $C^{R^{N{\setminus }\{1\}}}$ implies $L(a,R^i)\in E(N{\setminus }\{i\})$ for all $a\in C^{R^{N{\setminus }\{1\}}}$. Then superadditivity implies that $A{\setminus } L(a,R^i)\notin E(i)$. Hence $B\cap L(a,R^i)\ne \emptyset$ for all $a\in C^{R^{N{\setminus }\{1\}}}$, which means that $\phi ^i$ selects an alternative from $B$.

For all other $\tau ^{N{\setminus }\{i\}}\in \Sigma _2^{N{\setminus }\{i\}}$, coalition $\{i\}$ forms. Thus, by definition of $\pi _2$, $\pi _2(\sigma ^i,\tau ^{N{\setminus }\{i\}}) = \pi (\sigma ^i,\tau ^{N{\setminus }\{i\}}) \in B$ for all $\tau ^{N{\setminus }\{i\}}\in \Sigma _2^{N{\setminus }\{i\}}$.

In order to prove the converse inclusion, let $S\in P_0(N)$ and $B\in E^{G_2}(S)$. Since $E(N)=P_0(A)$ and $A\in E(S)$ for all $S\in P_0(N)$, we can assume that $S\ne N$ and $B\ne A$. We show that $B\in E(S)$. Let $\sigma ^S\in \Sigma ^S$ be such that $B(\sigma ^S)\subseteq B$. We only treat the case where $\vert S\vert = n-1$ and $\sigma ^S$ is such that $f^i=R^{N{\setminus }\{1\}}$ for some $R^{N{\setminus }\{1\}}\in W^{N{\setminus }\{1\}}$ and for all $i\in S$. For all other cases, it is sufficient to note that $G_2$ is an extension of $G_0$. We distinguish two subcases.

• $1\notin S$. Then, by construction of the game form, $B(\sigma ^S)= C^{R^{N{\setminus }\{1\}}}$. By definition of $C^{R^{N{\setminus }\{1\}}}$, we have $C^{R^{N{\setminus }\{1\}}}\in E(N{\setminus }\{1\})=E(S)$ and thus by monotonicity $B\in E(S)$.

• $1\in S$ and $j\notin S$. Then by construction $B(\sigma ^S)=L(a,R^j)$ for some $a\in C^{R^{N{\setminus }\{1\}}}$. By definition of $C^{R^{N{\setminus }\{1\}}}$ and since $j\ne 1$, we have $L(a,R^j)\in E(N{\setminus }\{j\})=E(S)$ for all $a\in C^{R^{N{\setminus }\{1\}}}$ and thus, by monotonicity, $B\in E(S)$.

This concludes the proof of the Claim.

We now prove that $G_2$ is ex post consistent for $T$. Let $R^T\in W^T$. Consider the following strategy profile $s\in S^N$. For every $t^i\in T^i$ with $i\ne 1$, $s(t^i)=(R^{T^{-1}}, 1,\phi ^i)$, with $\phi ^i$ chosen arbitrarily. For every $t^1\in T^1$, $s(t^{1})=(R^{T^{-1}}, 1,\phi ^1)$ is such that $\phi ^1$ selects alternative $a\in C^{R^{N{\setminus }\{1\}}}$, where $aR^{t^{1}}b$ for all $b\in C^{R^{N{\setminus }\{1\}}}$.

If $t^1\in T^1$ deviates, $t^1$ is able to choose an alternative from $C^{R^{N{\setminus }\{1\}}}$. Since for $a\in C^{R^{N{\setminus }\{1\}}}$ we have $aR^{t^{1}}b$ for all $b\in C^{R^{N{\setminus }\{1\}}}$, $t^1$ is not able to improve. If $t^i\in T^i$, with $i\ne 1$, deviates, $t^i$ is able to choose from $L(a,R^{t^i})$. Since $aR^{t^{i}}b$ for all $b\in L(a,R^{t^i})$, $t^i$ is not able to improve. Hence this profile is an EPE.

For the implication $(ii)\Rightarrow (i)$, assume that $E$ has an ex post consistent representation $\Gamma$ for $\mathcal {T}$. In particular, the game form $\Gamma$ should contain an ex post equilibrium if all types of player 1 have the same preference ordering. This is equivalent to saying that $E$ has a Nash consistent representation. $\square$

Construction of the representation in Example 5.8

The construction proceeds in several steps.

Step 1 We modify $G_0=(\Sigma ^1,\Sigma ^2,\Sigma ^3;\pi ;A)$ from Sect. 3 to a game form $G_3=(\Sigma _3^1,\Sigma _3^2,\Sigma _3^3;\pi _3;A)$, as follows. Let $\tilde{T}=(T^1,T^2)$. The set of actions of $i\in N$ is the set $\Sigma _3^i=\{(f,r,k,\phi )\mid f\in F^i\cup W^{\tilde{T}} \text{, } r\in T^i \text{, } k\in \{1,\ldots ,\vert A\vert \} \text{ and } \phi \in \Phi \}$. Here, $\Phi$ is the set of all selections, as in the game form $G_2$ in the proof of Proposition 5.7.

Let $\sigma =(\sigma ^1,\sigma ^2,\sigma ^3)\in \Sigma _3^N$, where $\sigma ^i=(f^i,r^i,k^i,\phi ^i)\in \Sigma _3^i$ for $i\in N$. Define $K=\{i\in N\mid f^i\in F^i\}$ and $L^{R^{\tilde{T}}}=\{i\in N\mid f^i=R^{\tilde{T}}\}$ for all $R^{\tilde{T}}\in W^{\tilde{T}}$. Note that every $i\in N$ is either in $K$ or in $L^{R^{\tilde{T}}}$ for some $R^{\tilde{T}}\in W^{\tilde{T}}$. We define $\pi _3(\sigma )$ as follows.

• If $\vert L^{R^{\tilde{T}}} \vert <2$ for all $R^{\tilde{T}} \in W^{\tilde{T}}$, then $\pi _3(\sigma )=\pi (\sigma )$ with $\pi$ as in $G_0$ (see Sect. 3).

• If $\vert L^{R^{\tilde{T}}} \vert \ge 2$ for some $R^{\tilde{T}}\in W^{\tilde{T}}$, then we distinguish two cases. Assume without loss of generality that $R^{t^{1,1}}$ orders the elements of $A$ as $abcde$.

  • (i) There are $x,y,z\in A$, with $x\ne y$, $x\ne z$ and $y\ne z$, such that $xR^{t^{1,1}}z$ and $yR^{t^{1,1}}z$, and $xR^{t^{1,2}}z$ and $yR^{t^{1,2}}z$. Then we define

    $$\begin{aligned} \pi _3(\sigma )={\left\{ \begin{array}{ll} x &{}\quad \text{ if } [L^{R^{\tilde{T}}}=\{1,2\} \text{ or } L^{R^{\tilde{T}}}=N] \text{ and } xR^{r^2}y.\\ y &{}\quad \text{ if } [L^{R^{\tilde{T}}}=\{1,2\} \text{ or } L^{R^{\tilde{T}}}=N] \text{ and } yP^{r^2}x.\\ \phi ^2(\{x,y\})&{}\quad \text{ if } L^{R^{\tilde{T}}}=\{1,3\}.\\ \phi ^1(\{x,z\})&{}\quad \text{ if } L^{R^{\tilde{T}}}=\{2,3\} \text{ and } xR^{r^2}y.\\ \phi ^1(\{y,z\})&{}\quad \text{ if } L^{R^{\tilde{T}}}=\{2,3\} \text{ and } yP^{r^2}z. \end{array}\right. } \end{aligned}$$

  • (ii) There are $x,y\in \{a,b,c\}$, with $x\ne y$, such that $dR^{t^{1,2}}x$ and $dR^{t^{1,2}}y$, and $eR^{t^{1,2}}x$ and $eR^{t^{1,2}}y$. Then we define

    $$\begin{aligned} \pi _3(\sigma )={\left\{ \begin{array}{ll} x &{}\quad \text{ if } L^{R^{\tilde{T}}} \in \{\{1,2\}, N\},\ r^1=t^{1,1}, \text{ and } xR^{r^2}y.\\ y &{}\quad \text{ if } L^{R^{\tilde{T}}} \in \{\{1,2\}, N\},\ r^1=t^{1,1}, \text{ and } yP^{r^2}x.\\ d &{}\quad \text{ if } L^{R^{\tilde{T}}} \in \{\{1,2\}, N\},\ r^1=t^{1,2}, \text{ and } dR^{r^2}e.\\ e &{}\quad \text{ if } L^{R^{\tilde{T}}} \in \{\{1,2\}, N\},\ r^1=t^{1,2}, \text{ and } eP^{r^2}d.\\ \phi ^2(\{x,y\})&{}\quad \text{ if } L^{R^{\tilde{T}}}=\{1,3\} \text{ and } r^1=t^{1,1}.\\ \phi ^2(\{d,e\})&{}\quad \text{ if } L^{R^{\tilde{T}}}=\{1,3\} \text{ and } r^1=t^{1,2}.\\ \phi ^1(\{x,d\})&{}\quad \text{ if } L^{R^{\tilde{T}}}=\{2,3\},\ xR^{r^2}y, \text{ and } dR^{r^2}e.\\ \phi ^1(\{x,e\})&{}\quad \text{ if } L^{R^{\tilde{T}}}=\{2,3\},\ xR^{r^2}y, \text{ and } eP^{r^2}d.\\ \phi ^1(\{y,d\})&{}\quad \text{ if } L^{R^{\tilde{T}}}=\{2,3\},\ yP^{r^2}x, \text{ and } dR^{r^2}e.\\ \phi ^1(\{y,e\})&{}\quad \text{ if } L^{R^{\tilde{T}}}=\{2,3\},\ yP^{r^2}x, \text{ and } eP^{r^2}d. \end{array}\right. } \end{aligned}$$

We now show that the game form $G_3$ is properly defined, in particular, that the cases (i) and (ii) cover all preference orderings. Suppose we are not in case (i). Then there are no $x,y,z\in A$, with $x\ne y$, $x\ne z$ and $y\ne z$, such that $xR^{t^{1,1}}z$ and $yR^{t^{1,1}}z$, and $xR^{t^{1,2}}z$ and $yR^{t^{1,2}}z$. For $z=e$, this implies that there is at most one alternative preferred to $e$ for $t^{1,2}$.

If $dR^{t^{1,2}}e$, then this means $eP^{t^{1,2}}a$, $eP^{t^{1,2}}b$ and $eP^{t^{1,2}}c$ and by transitivity, $dP^{t^{1,2}}a$, $dP^{t^{1,2}}b$ and $dP^{t^{1,2}}c$. Hence we are in case (ii).

If $eP^{t^{1,2}}d$, then for $z=d$, the supposition that we are not in case (i) implies that there is at most one alternative from $\{a,b,c\}$ preferred to $d$ for $t^{1,2}$. This means there are at least two alternatives from $\{a,b,c\}$ to which $d$ is strictly preferred. By transitivity, $e$ is also strictly preferred to these two alternatives and hence we are in case (ii).

Step 2 We show that $G_3$ is a representation of $E$. First, we show that $E(S)\subseteq E^{G_3}(S)$ for all $S\in P_0(N)$. Let $S\in P_0(N)$ and $B\in E(S)$. We distinguish three cases:

• (a) $\vert S\vert \ge 2$. Choose $\sigma ^S$ such that $f^i=(S,B)$ for all $i\in S$. Then the coalition $S$ is formed and hence by definition of $\pi _3$, $\pi _3(\sigma ^{S},\tau ^{N{\setminus } S})\in B$ for all $\tau ^{N{\setminus } S}\in \Sigma _3^{N{\setminus } S}$. So, $B(\sigma ^S)\subseteq B$.

• (b) $S=\{i\}$, with $i=1,2$. Choose $\sigma ^i$ such that $f^i=(\{i\},B)$ and $\phi ^i$ is such that $\phi ^i(B')\in B$ for all $B'$ with $B'\cap B\ne \emptyset$.

If $\tau ^{N{\setminus }\{i\}}$ is such that $f^j=R^{\tilde{T}}$ for all $j\in N{\setminus }\{i\}$, then player $i$ is able to choose from $\{x,y\}$ for some $x,y\in A$ and $x\ne y$. Since $\{x,y\}\in E(N{\setminus }\{i\})$, superadditivity implies $A{\setminus } \{x,y\}\notin E(1)$. Hence $B\cap \{x,y\}\ne \emptyset$, which means that $\phi ^i$ will select an alternative from $B$.

For all other $\tau ^{N{\setminus }\{i\}}\in \Sigma _3^{N{\setminus }\{i\}}$, it is sufficient to note that coalition $\{i\}$ forms. Thus, by definition of $\pi _3$, $\pi _3(\sigma ^{i}, \tau ^{N{\setminus }\{i\}})\in B$ for all $\tau ^{N{\setminus }\{i\}}\in \Sigma _3^{N{\setminus }\{i\}}$.

• (c) $S=\{3\}$. It is sufficient to note that since $E(\{1,2\})=P_0(A)$, superadditivity implies that $E(3)=\{A\}$.

In order to prove the converse inclusion, let $S\in P_0(N)$ and $B\in E^{G_3}(S)$. Since $E(N)=P_0(A)$ and $A\in E(S)$ for all $S\in P_0(N)$, we can assume that $S\ne N$ and $B\ne A$. We show that $B\in E(S)$. Let $\sigma ^S\in \Sigma ^S$ be such that $B(\sigma ^S)\subseteq B$. We only treat the case $\vert S\vert = 2$ and $\sigma ^S$ is such that $f^i=R^{\tilde{T}}$ for some $R^{\tilde{T}} \in W^{\tilde{T}}$ and for all $i\in S$. For all other cases, it is sufficient to note that $G_3$ is an extension of $G_0$.

If $3\notin S$, then it is sufficient to note that $E(S)=E(\{1,2\})=P_0(A)$.

If $3\in S$, then by construction $B(\sigma ^S)=\{x,y\}$ for some $x,y\in A$ and $x\ne y$. Since $\{x,y\}\in E(S)$, monotonicity implies that $B\in E(S)$.

Step 3 It remains to prove that $G_3$ is ex post consistent. Let $R^T\in W^T$. Consider the following strategy profile $s\in S^N$. For every $t^i\in T^i$ and for all $i\in N$, $s(t^i)=(R^{\tilde{T}},t^i,1,\phi ^i)$, with $\phi ^i$ chosen arbitrarily.

For case (i) in Step 1, all $t^1\in T^1$ prefer $x$ to $z$ and $y$ to $z$ and all $t^2\in T^2$ obtain their preferred element from $\{x,y\}$. Hence these types have no incentive to deviate.

For case (ii) in Step 1, $t^{1,1}\in T^1$ prefers $x$ and $y$ to $d$ and $e$, whereas $t^{1,2}\in T^1$ prefers $d$ and $e$ to $x$ and $y$. Moreover, if $r^1=t^{1,1}$, all $t^2\in T^2$ obtain their preferred element from $\{x,y\}$, and if $r^1=t^{1,2}$, all $t^2\in T^2$ obtain their preferred element from $\{d,e\}$. Thus, none of these types is able to improve.

Since no $t^3\in T^3$ is able to affect the outcome under this strategy profile, we have an EPE. $\square$