Abstract
In this paper, we theoretically characterize robust empirically implementable normative criteria for evaluating socially risky situations. Socially risky situations are modeled as distributions, among individuals, of lotteries on a finite set of state-contingent pecuniary consequences. Individuals are assumed to have selfish Von Neumann–Morgenstern preferences for these socially risky situations. We provide empirically implementable criteria that coincide with the unanimity, over a reasonably large class of such individual preferences, of anonymous and Pareto-inclusive Von Neuman Morgenstern social rankings of risks. The implementable criteria can be interpreted as sequential expected poverty dominance. An illustration of the usefulness of the criteria for comparing the exposure to unemployment risk of different segments of the French and US workforce is also provided.




Similar content being viewed by others
Notes
The generalization to societies involving different numbers of individuals is immediate.
In Fleurbaey (2010) socially risky situations are described as probability distributions over profiles of VNM utility levels. The restriction of the analysis to a finite set \(\mathbb {X}\) is a pedagogical simplification that enables us to use the version of Harsanyi social aggregation theorem provided by Weymark (1991) as a theoretical justification to our criteria.
An ordering is a reflexive, complete and transitive binary relation.
A VNM preference is strictly risk averse if the function \(U\) whose expectation numerically represents it satisfies, for every \(j\in \Omega \) and \(y\in \{1,\ldots ,m-2\}\), \(U(j,y+2)-2U(j,y+1)+U(j,y)<0\).
For the individual state \(j\) and the income level \(y\), the discrete Arrow–Pratt coefficient is the number \(a(j,y)\) defined by:
$$\begin{aligned} a(j,y)=\frac{-[U(j,y+2)-2U(j,y+1)+U(j,y)]}{U(j,y+1)-U(j,y)} \end{aligned}$$We are cheating a bit here with respect to the discrete setting in which the rest of the analysis is conducted by considering a differentiable framework.
However, the need literature typically assumes that incomes are available in any (real) quantity whatsoever. This difference with the current setting is not essential.
See Howes (1994) for a critical appraisal of this inference methodology, that can be contrasted with another, more conservative, Intersection–Union (IU) one.
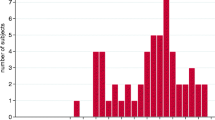
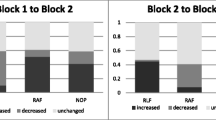
Another empirical use of the criteria developed in this paper to understand the evolution of the exposures of Indian citizens to risks of death is provided in Gravel et al. (2008).
References
Atkinson AB, Bourguignon F (1982) The comparison of multi-dimensioned distribution of economic status. Rev Econ Stud 49:183–201
Atkinson AB, Bourguignon F (1987) Income distributions and differences in needs. In: Feiwel GR (ed) Arrow and the foundation of the theory of economic policy. Macmillan, London
Bazen S, Moyes P (2003) Comparisons of income distributions accross heterogenous populations. Res Econ Inequal 9:85–115
Berge C (1959) Espaces topologiques et fonctions multivoques. Dunod, Paris
Bishop CM, Formby JP, Thistle PD (1989) Statistical inference, income distributions and social welfare. In: Slotje DJ (ed) Research on economic inequality. JAI Press, Greenwich
Clark AE, Oswald AJ (1994) Happiness and unemployment. Econ J 104:648–659
Dutta I, Foster J, Mishra A (2011) On measuring vulnerability to poverty. Soc Choice Welf 37:743–761
Farber HS (2004) Job loss in the United States, 1981–2001. Res Labor Econ 23:69–117
Fishburn PC, Vickson RG (1978) Theoretical foundations of stochastic dominance. In: Withmore GA, Findlay MC (eds) Stochastic dominance. Lexington Books, Lanham
Fleurbaey M (2010) Assessing risky social situations. J Polit Econ 118:649–680
Givord P, Maurin E (2004) Changes in job security and their cause: an empirical analysis for France, 1982–2002. Eur Econ Rev 48:595–615
Gottschalk P, Moffit R (1999) Changes in job instability and insecurity using monthly survey data. J Labor Econ 17:S91–S126
Gravel N, Moyes P, Tarroux B (2009) Robust international comparisons of distributions of disposable income and access to regional public goods. Economica 76:432–461
Gravel N, Mukhopadhyay A (2010) Is India better off now than fifteen years ago ? A robust multidimensional answer. J Econ Inequal 8:173–195
Gravel N, Mukhopadhyay A, Tarroux B (2008) A robust normative evaluation of India’s performance in allocating risks of death. Indian Growth Dev Rev 1:95–111
Harsanyi J (1955) Cardinal welfare, individualistic ethics, and interpersonal comparisons of utility. J Polit Econ 63:309–321
Heckman JJ (1979) Sample selection bias as a specification error. Econometrica 47:153–161
Howes, S (1994) Testing for dominance: inferring population rankings from sample data. Unpublished paper, Policy Research Department, World Bank
Jakobsson U (1976) On the measurement of the degree of progression. J Public Econ 8:161–168
Jenkins SP, Lambert PJ (1993) Ranking income distributions when needs differ. Rev Income Wealth 39:337–356
Kolm SC (1977) Multidimensional egalitarianisms. Q J Econ 91:1–13
Postel-Vinay F (2003) Evolution du Risque de Perte d’Emploi: Changements Structurels ou Changements Institutionnels ? Econ Stat 366:24–29
Viscusi WK (2007) Regulation of health, safety and environmental risks. In: Shavell AMPS (ed) Handbook of law and economics. Elsevier, Amsterdam
Viscusi WK, Evans WM (1990) Utility functions that depend on health status: estimates and economic implications. Am Econ Rev 80:353–374
Weymark JA (1991) A reconsideration of the Harsanyi–Sen debate on utilitarianism. In: Elster J, Roemer J (eds) Interpersonal comparisons of well-being. Cambridge University Press, Cambridge, pp 255–320
Author information
Authors and Affiliations
Corresponding author
Additional information
This work has immensely benefited from the comments made by Conchita d’Ambrosio, Marc Fleurbaey, Patrick Moyes, Alain Trannoy and two anonymous referees. The usual disclaimer applies.
Appendix: Proofs of theorems 1–2
Appendix: Proofs of theorems 1–2
1.1 Proof of theorem 1
For the first implication, assume that \(p\succsim _{\mathbb {U}_{1}}q\). Then, the inequality:
holds for every function \(U:\Omega \times \mathbb {I}\rightarrow \mathbb {R}\) in \(\mathbb {U}_{1}\). Consider, for any \(k\in \{1,\ldots ,l\}\) and \(t\in \mathbb {I}\), the function \(V^{kt}:\Omega \times \mathbb {I}\rightarrow \mathbb {R}\) defined, for any \(j\in \Omega \) and \(y\in \mathbb {I}\) by:
It can be checked that the function \(V^{kt}\) so defined belongs to \(\mathbb {U}_{1}\) for any \(k\in \{1,\ldots ,l\}\) and \(t\in \mathbb {I}\). Hence, inequality (16) holds for the functions \(V^{kt}\) so that we have:
as required by (6).
For the other implication, consider a subdivision of the interval \([0,1]\) into \(r\) sub-intervals \([\rho _{h},\rho _{h+1}]\) for \(h=0,\ldots ,r-1\) such that:
and, for all \(i\in N\), \(j\in \Omega \) and \(y\in \mathbb {I}\), there are \(h\) and \(h^{\prime }\in \{0,1,\ldots ,r\}\) such that \(p(i,j,y)=\rho _{h}\) and \(q(i,j,y)=\rho _{h^{\prime }}\). We this notation, we can write (16) as:
where, for \(h=1,\ldots ,r\), \(j=1,\ldots ,l\) and \( y=1,\ldots ,m \),
(we of course allow for the possibility that the cardinality of either of the two sets that enters in (18) be zero). We now proceed by decomposing the left hand side of (17) using Abel identity (see for instance Fishburn and Vickson 1978; eq 2.49). Doing first the decomposition with respect to the \(y\)-indexed summation operator yields:
Decomposing (19) using Abel identity applied this time to the \(j\)-indexed sum operator yields:
Now, using (18), one can see that that, for every \(t\in \mathbb {I}\) and \(k\in \Omega :\)
Combining this with the fact that:
we can write (20) as:
As can be seen, having:
for all \(j\in \Omega \) and all \(k\in \mathbb {I}\) is sufficient for inequality (22) to hold for all state-dependent utility functions \(U_{j}\) in \(\mathbb {U}_{1}\).
1.2 Proof of theorem 2
Assume first that \(p\succsim _{\mathbb {U}_{2}}q\) and, accordingly, that inequality (16) holds for all utility functions \(U:\Omega \times \mathbb {I}\ \rightarrow \mathbb {R}\) in \(\mathbb {U}_{2}\). Consider, for any \(k\in \Omega \) and \(t\in \mathbb {I}\), the function \(\widetilde{V} ^{kt}:\Omega \times \mathbb {I}\ \rightarrow \mathbb {R}\) defined, for \(j\in \Omega \) and \(y\in \mathbb {I}\), by:
For a given \(j\in \Omega \), the function \(\widetilde{V} ^{kt}\) is the “angle” function used in the classical proof of the Hardy-Littlewood-Polya theorem made by Berge (1959). The reader can verify that the functions \(\widetilde{V}^{kt}\) belong to \(\mathbb {U}_{2}\). For this reason the inequality:
holds for every \(k\) and \(t\). Using the definition of the functions \(\widetilde{V}^{kt}\), inequality (23) writes:
as required by condition (8) of SEPG dominance. To obtain condition (9) of SEPG dominance, we consider, for every \(k\in \Omega \), the functions \(V^{k}\): \(\Omega \times \mathbb {I} \rightarrow \mathbb {R}\) defined, for \(j\in \Omega \) and \(y\in \mathbb {I}\), by:
These \(k\)-indexed functions clearly satisfy \( V^{k}(j+1,y)\ge V^{k}(j,y)\) for every \(y\in \mathbb {I}\) and \(j=1,\ldots ,l-1\) and are all (trivially) increasing with respect to income for every \(j\). It can be checked that these functions satisfy (very often trivially) the conditions imposed on the functions in \(\mathbb {U}_{2}\). Hence, inequality (16) holds for any such functions \(V^{k}\) so that we have, for all \(k\in \Omega \):
or
as required by condition (9). For the other implication, it proceeds just as in the Proof of theorem 1 by writing inequality (16) in the form of (17) and by doing the Abel decomposition of (17) until one reaches condition (20). If one then goes one step further and Abel decomposes each term of (20) with respect to the inner (\(y\)-indexed) term, one obtains:
where:
Noticing that:
and remembering Eq. (21) in the proof of theorem 1, one can write (24) as:
For any combination of functions \(U_{j}\) (for \(j\in \Omega \)) belonging to \(\mathbb {U}_{2}\), it is sufficient for (25) to hold to have, for all \(k\in \Omega \):
and:
for all \(t\in \mathbb {I}\), which is the definition of SEPG dominance.
Rights and permissions
About this article
Cite this article
Gravel, N., Tarroux, B. Robust normative comparisons of socially risky situations. Soc Choice Welf 44, 257–282 (2015). https://doi.org/10.1007/s00355-014-0833-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-014-0833-8