Abstract
We study one-to-one matching problems and analyze conditions on preference domains that admit the existence of stable and strategy-proof rules. In this context, when a preference domain is unrestricted, it is known that no stable rule is strategy-proof. We introduce the notion of the no-detour condition, and show that under this condition, there is a stable and group strategy-proof rule. In addition, we show that when the men’s preference domain is unrestricted, the no-detour condition is also a necessary condition for the existence of stable and strategy-proof rules. As a result, under the assumption that the men’s preference domain is unrestricted, the following three statements are equivalent: (i) a preference domain satisfies the no-detour condition, (ii) there is a stable and group strategy-proof rule, (iii) there is a stable and strategy-proof rule.



Similar content being viewed by others
Notes
Though we will consider the DA’s properties henceforth, in the symmetric setup, we can define the women-proposing DA rule and show it has the same properties.
Dubins and Freedman (1981) show that the DA rule is not manipulable by any group of men. Demange et al. (1987) show that no group of men and women can manipulate the DA rule so successfully that every member of the group strictly prefers the new outcome to every stable matching under the true preferences.
In this figure, \(m \ P_w \ m'\) is represented by
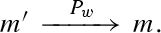
That is, the head of the arrow is preferred to the tail of the arrow at the preference described on the arrow. A similar notation is used throughout this paper.
Several types of acyclicity conditions for preference profiles are used to study matching problems or school choice problems e.g., Ergin (2002); Kesten (2006); Haeringer and Klijn (2009); Klaus and Klijn (2013); Romero-Medina and Triossi (2013). Our acyclicity is the same as the acyclicity condition in Romero-Medina and Triossi (2013), but different from the others in our setting. For the relation with the other acyclicity conditions, see Haeringer and Klijn (2009) and Romero-Medina and Triossi (2013).
See Example 1 in Romero-Medina and Triossi (2013).
Correctly speaking, Alcalde and Barberà (1994) assume that the sets of preferences for women is anonymous. This corresponds with our assumption when every woman has strict preferences.
By definition, if there is a cycle, then there are two women and their preferences such that (i) there are at least two acceptable men under each of their preferences; (ii) their preferences over the two men are different. Now that this is not satisfied, \(\fancyscript{D} \) is acyclic.
In fact, Sönmez (1996) shows that in college admissions if each college has a capacity of at least as many as students, then there is a stable and strategy-proof rule on each preference domain.
\(\mu ' (M^{\mu '}(P))\) is the image of \(M^{\mu '}(P)\) through \(\mu '\), that is,
$$\begin{aligned} \mu '\left( M^{\mu '}(P)\right) =\{w \in W: \mu '(m)=w \ \text {for some} \ m \in M^{\mu '}(P) \}. \end{aligned}$$\(m_{\ell +1}\) is defined before \(w_{\ell +1}\) by following the algorithm.
We represent a preference of each agent as a list as in Table 1. Since only rankings of acceptable mates matters for analysis, we write only acceptable mates in a list. For example, under \(P_{m_1}\) in Table 1, \(w_1\) is most preferred, \(w_{\ell }\) is secondly most preferred, and only \(w_1\) and \(w_{\ell }\) are acceptable.
References
Akahoshi T (2012) Acyclicity and the uniqueness of stable matchings in many-to-one matching problems. RIBA working paper series, 2012–001. Waseda University, Tokyo (2012)
Alcalde J, Barberà S (1994) Top dominance and the possibility of strategy-proof stable solutions to matching problems. Econ Theory 4(3):417–435
Demange G, Gale D, Sotomayor MAO (1987) A further note on the stable matching problem. Discrete Appl Math 16(3):217–222
Dubins LE, Freedman DA (1981) Machiavelli and the Gale–Shapley algorithm. Am Math Month 88(7): 485–494
Ergin H (2002) Efficient resource allocation on the basis of priorities. Econometrica 70(6):2489–2497
Gale D, Shapley LS (1962) College admissions and the stability of marriage. Am Math Month 69(1):9–15
Gusfield D, Irving RW (1989) The stable marriage problem: structure and algorithms. MIT Press, Cambridge
Haeringer G, Klijn F (2009) Constrained school choice. J Econ Theory 144(5):1921–1947
Kesten O (2006) On two competing mechanisms for priority-based allocation problems. J Econ Theory 127(1):155–171
Klaus B, Klijn F (2013) Local and global consistency properties for student placement. J Math Econ 49:222–229
Moulin H (1980) On strategy-proofness and single peakedness. Public Choice 35(4):437–455
Romero-Medina A, Triossi M (2013) Acyclicity and singleton cores in matching markets. Econ Lett 118:237–239
Roth AE (1982) The economics of matching: stability and incentives. Math Oper Res 7(4):617–628
Roth AE, Sotomayor MAO (1990) Two-sided matching: a study in game–theoretic modeling and analysis. Cambridge University Press, Cambridge
Sönmez T (1996) Strategy-proofness in many-to-one matching problems. Econ Des 1(1):365–380
Sönmez T (1999) Strategy-proofness and essentially single-valued cores. Econometrica 67(3):677–689
Acknowledgments
I am very grateful to my advisor, Hiroo Sasaki, for his warm guidance and helpful suggestions. I appreciate helpful discussions with Hidekazu Anno, Kazuhiro Hara and Yoichi Kasajima. I am also grateful to the editors, two anonymous referees, Kohei Kawamura, Toyotaka Sakai, Ken Sawada, William Thomson, and the seminar participants at Hitotsubashi University and Waseda University for their suggestions and comments. This work was supported by JSPS KAKENHI Grant-in-Aid for Young Scientists (B) Number 24730177.
Author information
Authors and Affiliations
Corresponding author
Appendix: Proof of theorem
Appendix: Proof of theorem
To prove the Theorem, we use three lemmata. The first one is know as the blocking Lemma.
Lemma 1
(Hwang, c.f., Lemma 3.5 in Roth and Sotomayor 1990) Given \(P \in \fancyscript{D} \), let \(\mu =DA(P)\) and \(\mu ' \in \fancyscript{M}^{\textit{IR}}(P)\). Let \(M^{\mu '}(P) \equiv \{m \in M: \mu '(m) \ P_m \ \mu (m)\}\). Then, if \(M^{\mu '}(P) \ne \emptyset \), there is a pair \((m, w) \in M\setminus M^{\mu '}(P) \times \mu '\left( M^{\mu '}(P)\right) \) who blocks \(\mu \) under \(P\).Footnote 9
The second lemma shows that the NDC is sufficient for the DA to be group strategy-proof. Note that, again, to prove this lemma, we do not need the assumption that the set of preferences for each man is unrestricted.
Lemma 2
If \(\fancyscript{D} \) satisfies the NDC, then the DA rule is group strategy-proof on \(\fancyscript{D} \).
Proof
Suppose that \(\fancyscript{D} \) satisfies the NDC. We prove that \(DA \in GSP(\fancyscript{D} )\) by contradiction. Suppose that \(DA\) is manipulated by a group \(C \subseteq M \cup W\) by misstating \(P'_C\) instead of \(P_C\). To simplify the notations, let \(P' \equiv (P'_C, P_{-C}), \mu \equiv DA(P)\) and \(\mu ' \equiv DA(P')\). Then \(\mu '(x) \ P_x \ \mu (x)\) for all \(x \in C\).
Claim 1
\(\mu ' \in \fancyscript{M}^{\textit{IR}}(P)\).
Proof of Claim 1
Suppose not. Then there exists an agent \(z \in M \cup W\) such that \(z\) prefers being unmatched to \(\mu '(z)\) under \(P_z\). If \(z \not \in C\), then \(P_z=P'_z\), which immediately violates \(\mu ' \in \fancyscript{M}^{\textit{IR}}(P')\). Therefore, \(z \in C\). Then \(z\) prefers being unmatched to \(\mu (z)\), which violates \(\mu \in \fancyscript{M}^{\textit{IR}}(P)\). (Claim 1 ends.)
Claim 2
\(C \subseteq W\).
Proof of Claim 2
Suppose that \(M^{\mu '}(P) = \{m \in M: \mu '(m) \ P_m \ \mu (m)\} \ne \emptyset \). By Lemma 1, there is \((m, w) \in M \setminus M^{\mu '}(P) \times \mu '\left( M^{\mu '}(P)\right) \) such that \(w \ P_m \ \mu '(m)\) and \(m \ P_w \ \mu '(w)\). Since \(m \in M \setminus M^{\mu '}(P), \mu (m) \ R_m \ \mu '(m)\). Therefore, \(m \not \in C\). If \(w \not \in C\), then \(P_m=P'_m\) and \(P_w=P'_w\). This implies that \((m, w)\) also blocks \(\mu '\) under \(P'\), which contradicts \(\mu ' \in \fancyscript{M}^{S}(P')\). Therefore, \(w \in C\).
Let \(\tilde{m} \equiv \mu '(w)\). Since \(w \in \mu '\left( M^{\mu '}(P)\right) \),
Since \(w \in C\),
Then \((\tilde{m}, w)\) blocks \(\mu \) under \(P\), which violates \(\mu \in \fancyscript{M}^{S}(P)\). Therefore, \(M^{\mu '}(P)=\emptyset \), and \(C \subseteq W\) (Claim 2 ends).
Step 1: Construction of a cycle. By Claim 2, there is \(w\in W\cap C\) such that \(\mu '(w) \ P_w \ \mu (w)\). Suppose that \(w_1\) is such a woman; namely
We construct a sequence of women and men \(\{m_2, w_2, m_3, w_3, \ldots \}\) by means of the following algorithm:
Algorithm (Fig. 4)
-
(A)
Initialize \(k\), i.e., let \(k=0\).
-
(B)
Increase \(k\) by one. Define \(m_{k+1} \equiv \mu '(w_k)\) and \(w_{k+1} \equiv \mu (m_{k+1})\). If \(w_{k+1} \ne w_1\), then go back to the beginning of (B). If not, then the algorithm terminates.
We show that the algorithm is well-defined. We first check if \(m_2 \in M\) is well-defined. If \(\mu '(w_1) =m_0\), then by (1), \(\mu \not \in \fancyscript{M}^{\textit{IR}}(P)\), which violates \(\mu \in \fancyscript{M}^{S}(P)\). Therefore \(\mu '(w_1) \in M\) and we can define \(m_2 \in M\) by \(m_2 \equiv \mu '(w_1)\).
To check if \(w_2\) is well-defined, we show that \(\mu (m_2) \ P_{m_2} \ \mu '(m_2)\). Suppose not, then \(\mu '(m_2) \ R_{m_2} \ \mu (m_2)\). Since \(w_1=\mu '(m_2)\) and \(\mu '(w_1) \ne \mu (w_1)\) by (1), \(\mu '(m_2) \ne \mu (m_2)\). Therefore, \(w_1 \ P_{m_2} \ \mu (m_2)\). Since we have \(m_2 \ P_{w_1} \ \mu (w_1)\) by (1), it must be that \((m_2, w_1)\) blocks \(\mu \) under \(P\). This is a contradiction. Therefore, \(\mu (m_2) \ P_{m_2} \ \mu '(m_2)\). Since \(P_{m_2}=P'_{m_2}, \mu '(m_2) \ne w_0\) and \(\mu ' \in \fancyscript{M}^{IR}(P')\),
Therefore \(\mu (m_2) \in W\) and we can define \(w_2 \equiv \mu (m_2) \in W\). Note that \(w_2 \ne w_1\) by (2).
To check if \(m_3\) is well-defined, we show that \(\mu '(w_2) \ P_{w_2} \ \mu (w_2)\). Since \(\mu '(m_2)=w_1 \ne w_2=\mu (m_2), \mu '(w_2) \ne \mu (w_2)\). In the case that \(w_2 \in C\), we have \(\mu '(w_2) \ P_{w_2} \ \mu (w_2)\). In the other case, we have
Since \(w_2, m_2 \not \in C\), we have \(P_{w_2}=P'_{w_2}\) and \(P_{m_2}=P'_{m_2}\). Therefore, \((m_2, w_2)\) blocks \(\mu '\) under \(P'\), which contradicts \(\mu ' \in \fancyscript{M}^{S}(P')\). Therefore, since \(\mu \in \fancyscript{M}^{\textit{IR}}(P)\) and \(\mu (w_2)\ne m_0\),
By repeating the argument above, we can show that if \(m_k\) is defined for some \(k \ge 2\), then
-
1.
\(w_k\) is defined by \(w_k \equiv \mu (m_k)\), and if \(w_k \ne w_1\) then
$$\begin{aligned} \mu '(w_k) \ P_{w_k} \ \mu (w_k) \ P_{w_k} \ m_0. \end{aligned}$$
Moreover, if \(w_k \ne w_1\), then
-
2.
\(m_{k+1}\) is defined by \(m_{k+1} \equiv \mu '(w_k)\), and
$$\begin{aligned} \mu (m_{k+1}) \ P_{m_{k+1}} \ \mu '(m_{k+1}) \ P_{m_{k+1}} \ w_0. \end{aligned}$$
We next check if all the men defined by following the algorithm are distinct and so are all the women. To this end, suppose that \(m_i\) and \(m_k (i<k)\) are defined and \(m_i= m_k\). Then, \(w_{i-1}=\mu '(m_i)=\mu '(m_k)=w_{k-1}\) and \(m_{i-1}= \mu (w_{i-1})= \mu (w_{k-1})=m_{k-1}\). By repeating this procedure, \(w_{1}=w_{k-(i-1)}\) and \(k-(i-1) \ne 1\). The algorithm should terminate at the step where \(w_{1}=w_{k-(i-1)}\). Therefore it terminates before defining \(w_k\), which is a contradiction. Therefore, the men defined by following the algorithm are all distinct, which immediately implies that so are the women.
By the finiteness of \(M\) and \(W\), this algorithm terminates in finitely many steps. Hence, there is \(\ell +1 \ge 2\) such that \(w_{\ell +1}=w_1\). Define \(m_1\) by \(m_1 \equiv m_{\ell +1}\).Footnote 10 Since \(\mu \in \fancyscript{M}^{\textit{IR}}(P)\) and \(\mu (w_1)=\mu (w_{\ell +1})=m_{\ell +1}=m_1 \ne m_0\), together with (1),
Then \((P_{w_1}, P_{w_2}, \ldots , P_{w_{\ell }}; m_1, m_2, m_3, \ldots , m_{\ell })\) is a cycle. (Step 1 ends.)
Figure 5 illustrates the connection of agents and the structure of preferences with respect to the cycle. Note that \(w_1\) is chosen arbitrarily from the women who are members of \(C\).
The connection of the agents and the structure of their preferences in Step 1 in the proof of Lemma 2 (any man–woman pair conned by a line means that the man is matched to the woman at \(\mu \). Similarly, any man–woman pair connected by a double line means that the man is matched to the woman at \(\mu '\)).
Step 2: Checking if there is a cycle with a detour. We consider two cases:
Case 1 \(\mu \not \in \fancyscript{M}^{\textit{IR}}(P')\). There exists an agent \(z\) whose assignment at \(\mu \) is not acceptable under \(P'_z\). Since \(\mu \in \fancyscript{M}^{\textit{IR}}(P)\), it must be that \(P_z \ne P'_z\), that is, \(z \in C\). Since \(z \in W\) by Claim 2, we rename \(z\) as \(w_1 \in W\). By Step 1, we can construct a cycle, \((P_{w_1}, P_{w_2}, \ldots , P_{w_{\ell }}; m_1, m_2, m_3, \ldots , m_{\ell })\), where \(m_1 \equiv \mu (w_1)\).
We show that the cycle has a detour from \(m_1\) with \(x=m_0\). Since \(\mu '(w_1) \ne m_0\) by (4) and \(\mu ' \in \fancyscript{M}^{\textit{IR}}(P')\),
Since \(\mu \in \fancyscript{M}^{\textit{IR}}(P)\),
Therefore, the cycle has a detour from \(m_1\).
Case 2 \(\mu \in \fancyscript{M}^{\textit{IR}}(P')\). Let \(M^{\mu }(P') \equiv \{m \in M: \mu (m) \ P'_m \ \mu '(m)\}\). Note that again, since \(C \subseteq W\) by Claim 2, for each \(m \in M\), we have \(P'_m=P_m\). Therefore, \(M^{\mu }(P')=M^{\mu }(P)\). By Step 1, it is obvious that \(M^{\mu }(P) \ne \emptyset \). By Lemma 1, there is \((\widehat{m}, \widehat{w}) \in M \setminus M^{\mu }(P) \times \mu \left( M^{\mu }(P)\right) \) such that \((\widehat{m}, \widehat{w})\) blocks \(\mu \) under \(P'\).
If \(\widehat{w} \not \in C\), then \(P_{\widehat{w}}=P'_{\widehat{w}}\). Then, since \(\widehat{m} \not \in C\), the pair also blocks \(\mu \) under \(P\), which violates \(\mu \in \fancyscript{M}^{S}(P)\). Therefore,
By Claim 2, \(M^{\mu '}(P)=\emptyset \). Therefore, \(\widehat{m} \in M \setminus M^{\mu }(P)\) implies \(\mu (\widehat{m})=\mu '(\widehat{m})\). Since \((\widehat{m}, \widehat{w})\) blocks \(\mu \) under \(P'\) and \(P_{\widehat{m}}=P'_{\widehat{m}}\),
and
Since \(\mu \in \fancyscript{M}^{S}(P)\) and \(\mu ' \in \fancyscript{M}^{S}(P')\), it must be that
Since \(\mu (\widehat{m})\ne \widehat{w}\) by (6), \(\mu (\widehat{w})\ne \widehat{m}\). Since \(\mu (\widehat{m})=\mu '(\widehat{m})\), we have \(\mu '(\widehat{w}) \ne \widehat{m}\). Therefore, by (8),
and
Here, rename \(\widehat{w}\) as \(w_1\). Since \(w_1 \in C\), by applying Step 1, we can construct a cycle \((P_{w_1}, P_{w_2}, \ldots , P_{w_{\ell }}; m_1, m_2, \ldots , m_{\ell })\), where \(m_1 \equiv \mu (w_1)\).
We show that the cycle has a detour from \(m_1\) with \(x=\widehat{m}\). Note that since \(\widehat{m} \in M \setminus M^{\mu }(P)\) and \(m_1, m_2, \ldots , m_\ell \in M^{\mu }(P)\), we have \(\widehat{m} \in \left( M \cup \{m_0\} \right) \setminus \{m_1, m_2, \ldots , m_\ell \}\).
Since \(\mu \in \fancyscript{M}^{IR}(P')\) in this case, \(\mu (w_1) \ R'_{w_1} \ m_0\). By (11),
By (9),
Hence, by (11), (12) and (13), the cycle has a detour from \(m_1\).
In both cases, there exists a cycle with a detour. This contradicts the assumption that \(\fancyscript{D} \) satisfies the NDC. Therefore, \(DA \in GSP(\fancyscript{D} )\). \(\square \)
The third lemma shows that the NDC is a necessary condition for the DA to be strategy-proof under an additional assumption.
Lemma 3
Suppose that the set of preferences for each man is unrestricted. If the DA rule is strategy-proof, then \(\fancyscript{D} \) satisfies the NDC.
Proof
Suppose that \(\fancyscript{D} _{m}=\fancyscript{P}_M\) for all \(m \in M\). We prove that \(\fancyscript{D} \) satisfies the NDC by contradiction. Let \((P_{w_1}, P_{w_2}, \ldots , P_{w_{\ell }}; m_1, m_2, m_3, \ldots , m_{\ell })\) be a cycle on \(\fancyscript{D} \), that is, for each \(k \in \{1, 2, \ldots , \ell \}\),
where \(m_{\ell +1} \equiv m_1\). Suppose that this cycle has a detour, say from \(m_1\). Then there is \(x \in \left( M \cup \{m_0\} \right) \setminus \{m_1, m_2, \ldots , m_{\ell }\}\), and \(P'_{w_1} \in \fancyscript{D} _{w_1}\) such that
-
1.
\(m_2 \ P'_{w_1} \ x \ P'_{w_1} \ m_1\),
-
2.
\(x \ R'_{w_1} \ m_0\), and
-
3.
\(m_1 \ P_{w_1} \ x\).
Case 1 \(x \ne m_0\). Rename \(x\) as \(x \equiv \widehat{m} \in M\). Then \(\widehat{m} \ne m_1, m_2, \ldots , m_{\ell }\). Let \(P_{m_1}, P_{m_2}, \ldots , P_{m_{\ell }}, P_{\widehat{m}}\) be defined as in Table 1.Footnote 11 Let the preferences of the remaining men, if any, be such that the option of being unmatched is most preferred. For each woman \(w \in W \setminus \{w_1, w_2, \ldots , w_{\ell }\}\), let \(P_{w}\) be an arbitrary preference in \(\fancyscript{D} _w\).
It is easy to see that
On the other hand, if \(w_1\) misrepresents her preference as \(P'_{w_1}\) instead of \(P_{w_1}\), then
Therefore, since
\(w_1\) can manipulate \({\textit{DA}}\) by misrepresenting her preference as \(P'_{w_1}\) when her true preference is \(P_{w_1}\).This contradicts \({\textit{DA}} \in {\textit{SP}}(\fancyscript{D} )\).
Case 2 \(x=m_0\). Define \(P_{m_1}, P_{m_2}, \ldots , P_{m_{\ell }}\) as in Table 2 and let the preferences of the remaining men be such that being unmatched is most preferred.
In this case,
On the other hand, if \(w_1\) represents her preference as \(P'_{w_1}\) instead of \(P_{w_1}\), then
Therefore, since
\(w_1\) can manipulate \({\textit{DA}}\) by misrepresenting her preference as \(P'_{w_1}\) when her true preference is \(P_{w_1}\). This contradicts \({\textit{DA}} \in {\textit{SP}}(\fancyscript{D} )\). \(\square \)
By using Lemmas 2 and 3, we provide a Proof of Theorem.
Proof of Theorem
Suppose that \(\fancyscript{D} \) satisfies the NDC. By Lemma 2, the DA is group strategy-proof. Therefore, there is a stable and strategy-proof rule. To prove the converse, suppose that there exists a stable and strategy-proof rule. By Fact, it is the DA rule. Since the DA is now strategy-proof, by Lemma 3, the NDC is satisfied. \(\square \)
Rights and permissions
About this article
Cite this article
Akahoshi, T. A necessary and sufficient condition for stable matching rules to be strategy-proof . Soc Choice Welf 43, 683–702 (2014). https://doi.org/10.1007/s00355-014-0803-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-014-0803-1