A Deep Learning Method to Forecast COVID-19 Outbreak

Abstract

A new pandemic attack happened over the world in the last month of the year 2019 which disrupt the lifestyle of everyone around the globe. All the related research communities are trying to identify the behaviour of pandemic so that they can know when it ends but every time it makes them surprise by giving new values of different parameters. In this paper, support vector regression (SVR) and deep neural network method have been used to develop the prediction models. SVR employs the principle of a support vector machine that uses a function to estimate mapping from an input domain to real numbers on the basis of a training model and leads to a more accurate solution. The long short-term memory networks usually called LSTM, are a special kind of RNN, capable of learning long-term dependencies. And also is quite useful when the neural network needs to switch between remembering recent things, and things from a long time ago and it provides an accurate prediction to COVID-19. Therefore, in this study, SVR and LSTM techniques have been used to simulate the behaviour of this pandemic. Simulation results show that LSTM provides more realistic results in the Indian Scenario.

Introduction

The novel coronavirus emerges from the city of Wuhan, China on 31st December 2019 [1, 2]. It shows its first presence in India on 30th January, 2020 in the Thrissur district of Kerala and after that, it continues and now on 15th September, 2020 a total number of 4.6 million cases were reported [3]. Out of these total cases, 1.76 million are active, 2.88 million are recovered and 0.56 million are deceased which shows that the recovery rate on 15th September, 2020 is reported 62.06% [4,5,6]. These statistics show how scary the pandemic is in India. Pathogens are not certainly responsible for a disease. When bacteria, viruses, or any other microbes get inserted into the human body and start replicating themselves then infection occurs. This infection starts damaging body cells and symptoms of the illness appear in the body of an individual. The intensity of the infection depends on the type of the pathogen and the degree of immunity of an individual. Ministry of Health and Family Welfare, Govt. of India is responsible to manage and control the infection in the country. National Institute of Virology, Pune and National Centre of Disease Control, New Delhi are the two important laboratories for the study of infection and suggesting the controlling measures. Public health laws of the country will be important to control the infection. Under these public laws Govt. can put certain measures including isolation in containment zones, restricting the opening of crowd places, and deploying regional public curfews. Besides, Govt. can make aware the public of taking self measures like sensitization, frequent hand wash, and maintaining social distancing. Infectious diseases can have major four phases include susceptible, exposed, infectious, and recovered or deceased. In all different phases, a delay will play differently to increase or decrease the infection. In the case of the susceptible phase, an individual needs more prolonged measures to avoid exposure and it leads more cost, more exposure time increases the chance of infection, delay in control of infection leads more hosts to spread infection, and delay in recovery or deceased leads more cost to the system. The infection has multiple phases and it leads to multiple rates of transmission from one phase to another phase. Besides, external factors like recovery with countermeasure increases the population of the previous phase. As it is continuously spreading in India along with other countries of the world and threaten the human community so, we have to find the behaviour of it. Once, the behaviour is identified it helps us to manage the health measures to overcome the pandemic. These characteristics will only be simulated with a proper prediction model. Memory models like long short-term memory (LSTM) and support vector regression (SVR) methods are better fit for the purpose. Therefore, we used the SVR and LSTM to simulate and analyse its behaviour.

The further text of this paper includes “Review of literature”, which represents the related work, “Methodology” and “Simulations” is devoted to methodology and simulation, “Results and discussion” articulates about the analysis of results and finally, “Conclusion” concludes the paper.

Review of Literature

As there are less number of papers on the prediction of COVID-19 cases so in the literature, we have referred few of them and are presented. Wang et al. [7] have reported a patient information-based algorithm (PIBA) for estimating the number of deaths due to this COVID-19 in China. The overall death rate in Hubei and Wuhan was predicted 13% and 0.75–3% in the rest of China. They also reported that the mortality rate would vary according to different climates and temperatures. In [8], a case was presented, which showed that there is a direct relationship between temperature and COVID-19 cases based on the United States spread analysis. It showed that there would be a drastic reduction in the number of cases in India in the summer months which actually didn’t happen. Ahmar and Val [9] have used ARIMA and Sutte ARIMA for short-term forecasting of COVID-19 cases and Spanish stock market. They have reported their predictions with MAPE of 3.6% till April 16, 2020. Ceylan [10] have used ARIMA models for predicting the number of positive cases in Italy, Spain, and France. He has reported MAPE in the range of 4–6%. Fanelli and Piazza [11], have done forecasting and analysis of COVID-19 in Italy, France, and China. Based on their analysis, they have forecasted the number of ventilation units required in Italy. They have divided the population into susceptible, recovered, infected and dead, and based on that they have predicted the number of cases. Reddy and Zhang [12] have used a deep learning model (LSTM) for predicting the end date of this epidemic in Canada. Their model accuracy is 93.4% for short-term whereas 92.67% for long-term. The important challenge is to analysing the output patterns in the trend of values and then utilising this pattern to predict and analyse the future. As predicting the future is a very difficult task by using the normal program so the use of deep learning has proven significantly to give better patterns analysis in the case of structured data and unstructured data also. So as to identify the patterns in a long trend of data, we need networks to analyse patterns across time. Recurrent networks are commonly used for learning and forecasting such data. It is also important to understanding the long and short-term memory relational dependencies or temporal differences. In our implementations, we have try to propose two forecasting models implementing LSTM networks and SVR using Keras application development environment.

Methodology

Long Short Term Memory (LSTM)

The long short term memory (LSTM) network is kind of recurring neural network used in the field of deep learning and is quite helpful when the neural network desires to switch among remembering current things, and things from a long time ago [13]. It maintains two memories one is long-term memory and the other is short-term memory, these memories help to retain patterns. In RNN, the output from the last step is given as an input to the current step [14, 15]. LSTM handles the issue associated with long-term dependencies of RNN where it cannot predict the word accumulated in the long term memory except can provide more precise predictions from the current information. Now, as the length of gap augments RNN does not give a proficient performance. The LSTM can by default preserve the data for a long period of time that can be used for predicting, processing, and classifying on the basis of series data time. LSTM deals with the disadvantage of RNNs i.e. Vanishing Gradient Descent [7, 16, 17].

Structure of LSTM

Theory of LSTM

To explain LSTM let's take an example—let consider that we have a television show on nature and science. We have seen a lot of forest animals. We recently have seen Squirrels and trees. Our job is to predict whether the given animal is a dog or wolf. So what LSTM does? LSTM maintains three memories, short-term, long-term memory and event as represented by Fig. 1. In long-term memory, we have the idea that the show is about science and nature, forest animals. In short-term memory, we have recently seen squirrels and trees [18]. We also maintain event which is to find whether the animal is a dog or wolf.

Fig. 1

An example for long short term memory

Now, we will use all three memories to update the long-term memory as depicted in Fig. 2a and short-term memory will be updated as depicted in Fig. 2b.

Fig. 2

Updating of long-term memory

We forget about science and since we recently saw a tree so we remember a tree and our long-term memory is updated. Again we use those three memories to update Short term memory. Short Term memory is updated as we forget about trees and update short-term memory with event [19]. LSTM has a chain formation that restrains four neural structures and several memory blocks known as cells as depicted in Fig. 3.

Fig. 3

LSTM chain structure

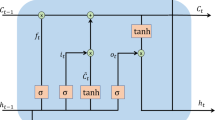
The memory is manipulated by the gates and the data is retained cells manipulations. It has four gates which help in updating the memories. These gates are forget gate, input/learn gate, output/remember gate, and use gate.

Forget Gate: the forget gate is used to erase the information that is no longer useful. The two inputs such as x_t that is input at the particular time and h_t−1 which is the input of previous cell output are supplied to the gate and then multiplied with the weight matrix trailed by the bias addition. Further, the resultant is conceded using an activation function that provides the binary output [18, 19]. In case, the output is 0 for a particular cell state, then the piece of data is beyond where the data is retained when the output is 1 for future use. This phenomenon is depicted in Fig. 4.

Fig. 4

LSTM cell structure with forget gate

Input gate/learn gate: the learn and input gate is used to provide some additional information where the data are initially regulated through sigmoid function and then filters the values to be memorized similar to the previous gate (forget gate) using h_t−1 and x_t. Further, a vector is generated through tanh function that provides output from − 1 to + 1 that contains all the possible information from h_t−1 and x_t. Finally, the regulated data and the information of the vector are multiplied to get the useful record as depicted by Fig. 5.

Fig. 5

LSTM structure with input gate

Output gate/remember gate: the task of remember gate is to extort the useful record from the current cell that is stated to be presented as an output. Initially, a vector is created by pertaining tanh function on the cell, after that the record is regulated through a sigmoid function that again filters out the data to be remembered through two inputs h_t−1 and x_t [20]. Finally, the regulated information and values of the vector are multiplied that are sent as an input and output to the next cell as shown in Fig. 6.

Fig. 6

LSTM structure output gate

Figure 7 depicts the arrangement of the four gates to updating both the memories in LSTM.

Fig. 7

Gates involved in LSTM

Let’s see how these gates help with a given task. The long-term memory goes to the forget gate where it forgets the things which are not needed. The short-term memory and event are joined together in the learn gate where it collects the information we have recently learnt and removes unnecessary information. The long-term memory that we have not forgotten yet and the new information we have recently learnt are joined together in the remember gate. This information becomes the new updated long-term memory. Finally, the use gate is the one that decides which information will be used from previously known and recently learnt data to make the prediction. The output from this gate becomes the prediction and the new short-term memory [18, 21].

Mathematically, an LSTM structure evaluates a mapping using an input sequence defined as x = (x₁, …, x_T) to an output sequence represented as y = (y₁, …, y_T) by computing the I run it activations iteratively through the following equations from t = 1 to T:

$$i_{t} = \sigma (W_{{ix}} x_{t} + W_{{im}} m_{{t - 1}} + W_{{ic}} c_{{t - 1}} + b_{i} )$$

(1)

$$f_{t} = \sigma (W_{{fx}} x_{t} + W_{{fm}} m_{{t - 1}} + W_{{fc}} c_{{t - 1}} + b_{f} )$$

(2)

$$ct = f_{t} \odot c_{{t - 1}} + i_{t} \odot g(W_{{cx}} x_{t} + W_{{cm}} m_{{t - 1}} + b_{c} )$$

(3)

$$o_{t} = \sigma (W_{{ox}} x_{t} + W_{{om}} m_{{t - 1}} + W_{{oc}} ct + b_{o} )$$

(4)

$$m_{t} = {\text{ }}o_{t} \odot h(c_{t} )$$

(5)

$$y_{t} = {\text{ }}\varphi (W_{{ym}} m_{t} + b_{y} )$$

(6)

where the W requisites determine weight matrices such as Wix is the weights matrix from the input gate to the input function and, W_ic, W_fc, W_oc are diagonal matrices of weights for a peephole associations, further, the b provisos represents bias vectors where b_i is the input gate bias vector, σ is the logistic sigmoid function, and I, f, o and c are respectively the input gate, f or get gate, output gate, and cell activation vectors all of which are of the same size as the cell output activation vector m, is the element-wise $\odot$ product of the vectors, g and h are the cell input and cell output activation functions [19, 22, 23].

Support Vector Regression

The support vector regression (SVR) depicts the principle as support vector machine (SVM) which is to compute a function that analysis mapping from an input domain to real numbers on the foundation of a training record as shown in Fig. 8.

Fig. 8

Analysis of the mapping from an input sphere to real numbers

Let us consider a collected set of data values $\left\{ {(x_{1} ,y_{1} ),\ldots,(x_{l} ,y_{l} )} \right\}$, where for each value of $x_{i} \in X \subset R^{n}$, and let $X$ is select to be in the input sample space, and respective output/target values, $y_{i} \in R$ for $i = 1,\ldots,l$ (where l is the size of values offers for training), generally most of the regression problems used to compute a function $f:R^{n} \to R$ which can approximately find the required value of y as and when the value of x is not present in the trained dataset [24, 25].

So the evaluating function $f$ can be written as:

$$f\left( x \right) = \left( {w^{{\text{T}}} \Phi \left( x \right)} \right) + b,$$

(7)

where value $w \in R^{m}$ is the regression coefficient and is a vector. The value $b \in R$ is the bias, which is the threshold values, and $\Phi$ denotes as a nonlinear function from the set of $R^{n}$ to a maximize dimensional sample space $R^{m}$ and ($m > n$).

In $\epsilon$ based support vector regression, the main objective is to compute an estimation function $f\left( x \right)$ that has a maximum $\epsilon$ value deviation with respect to the normal targeted value $y_{i}$ for all trained dataset and it is considered to be as sequential as possible in the same instant of time [25]. The flatness value is a very small value for $w$. To find out this, the Euclidean norm is to be minimized i.e. $\left| {\left| w \right|} \right|^{2}$ as shown in Fig. 9. This value is represented as a convex optimal problem by considering,

$${\text{Minimize}}\;{\text{value}}\quad \frac{1}{2}\left| {\left| w \right|} \right|^{2}$$

(8)

$${\text{Subject to}}\left\{ {\begin{array}{*{20}c} {y_{i} - (w \cdot x_{i} ) - b \le \varepsilon } \\ {(w \cdot x_{i} ) + b - y_{i} \le \varepsilon } \\ \end{array} } \right..$$

Fig. 9

Convex optimization problem by requiring minimization

The objective is to calculate the value of $w$ and $b$, where the estimated functional value $f\left( x \right)$ can be minimised otherwise the factor is considered to be at risk as shown in Fig. 10.

$$R_{{{\text{reg}}}} \left( f \right) = C \mathop \sum \limits_{{i = 1}}^{n} L_{\epsilon } \left( {y_{i} ,f ( {x_{i} } )} \right) + \frac{1}{2}\left| {\left| w \right|} \right|^{2}$$

(9)

Fig. 10

The aim is to find the value of w and b by minimizing the risk

The first term $C\sum\nolimits_{{i = 1}}^{n} {L_{\epsilon } \left( {y_{i} ,f\left( {x_{i} } \right)} \right)}$ is also called the empirical error which is considered to be at risk and estimated by the value $\epsilon$-insensitive loss function. In the same way, the second term of the said Eq. (9) i.e. $\frac{1}{2}\left| {\left| w \right|} \right|^{{2}}$ is taken as the regularisation term and that will save the highest over learning and also used to control the functional threshold [25]. Hence the value of $L_{\epsilon }$ is the extension value of the $\epsilon$-insensitive loss as function outlined and is represented as:

$$L_{\epsilon } = \left\{ {\begin{array}{*{20}c} {|y - z| - \varepsilon ,} & {|y - z| \ge \varepsilon } \\ {0,} & {{\text{otherwise}}} \\ \end{array} } \right..$$

(10)

The loss-function offers the advantages of utilizing a set of data values to add with the generated function (7). $\epsilon$-value is the size of the tube of SVM and the C value is a fixed value of regularization which can be represented as the swapping among the normal-term value and an empirical-error factor.

Outlining the slack-variables, $\zeta _{i}$ and $\zeta _{i}^{*}$, the issues in Eq. (5) can be also be represented as,

$${\text{Minimize}}\quad R_{{{\text{SVMs}}}} \left( {w,\zeta _{i}^{{\left( * \right)}} } \right) = C\left[ {\mathop \sum \limits_{{i = 1}}^{l} \left( {\zeta _{i} + \zeta _{i}^{*} } \right)} \right] + \frac{1}{2}\left| {\left| w \right|} \right|^{2} .$$

(11)

Subject to condition,

$$y_{i} - w^{{{\text{T}}}} \Phi \left( {x_{i} } \right) {-}b \le \epsilon + \zeta _{i}$$

$$w^{{\text{T}}} \Phi \left( {x_{i} } \right) + b - y_{i} \le \epsilon + \zeta _{i}^{*}$$

$$\zeta _{i} \ge 0,\quad \zeta _{i}^{*} \ge 0.$$

The Eq. (6) can be resolve using the primal-dual scheme to find the equivalent dual problems. To obtain the Lagrange multipliers ($\{ \alpha _{i} \} _{{i = 1}}^{l}$ and $\{ \alpha _{i}^{*} \} _{{i = 1}}^{l}$) that exploit the objective function.

$$Q\left( {\alpha _{i} ,\alpha _{i}^{*} } \right) = \mathop \sum \limits_{{i = 1}}^{l} y_{i} \left( {\alpha _{i} - \alpha _{i}^{*} } \right) - \epsilon \mathop \sum \limits_{{i = 1}}^{l} \left( {\alpha _{i} - \alpha _{i}^{*} } \right) - \frac{1}{2}\mathop \sum \limits_{{i = 1}}^{l} \mathop \sum \limits_{{j = 1}}^{l} \left( {\alpha _{i} - \alpha _{i}^{*} } \right)\left( {\alpha _{j} - \alpha _{j}^{*} } \right)K\left( {x_{i} - x_{j} } \right),$$

(12)

where

$$\mathop \sum \limits_{{i = 1}}^{l} \left( {\alpha _{i} - \alpha _{i}^{*} } \right) = 0$$

(13)

$$0 \le \alpha _{i} \le C,\quad 0 \le \alpha _{i}^{*} \le C.$$

(14)

Here $i = 1, \ldots ,l$ and $K:X \times X \to R$ is the Mercer Kernel interpreted by:

$$K\left( {x,z} \right) = \Phi \left( x \right)^{{\text{T}}} \Phi \left( z \right)$$

(15)

$K\left( {x_{i} ,x_{j} } \right)$ is the Kernel utility. The obtained value is equivalent to the inner product of 2 vectors $x_{i}$ and $x_{j} {\text{}}$ in the feature space $\Phi \left( {x_{i} } \right)$ and $\Phi \left( {x_{j} } \right)$ i.e. $K\left( {x_{i} ,x_{j} } \right) = \Phi \left( {x_{i} } \right) \cdot \Phi \left( {x_{j} } \right)$.

The benefit of using kernel is that it can efforts with the characteristic spaces of arbitrary dimensionality lacking calculating the map $\Phi \left( x \right)$.

The solution to the primal-dual formula yields:

$$w = \mathop \sum \limits_{{i = 1}}^{l} \left( {\alpha _{i} - \alpha _{i}^{*} } \right) \Phi \left( {x_{i} } \right),$$

(16)

where b is computed through the Karush–Kuhn–Tucker situations such as:

$$\alpha _{i} \left( {\epsilon + \zeta _{i} - y_{i} + w^{{\text{T}}} \Phi \left( {x_{i} } \right) + b} \right) = 0$$

$$\begin{aligned} \alpha _{i} \left( {\epsilon + \zeta _{i} - y_{i} + w^{{\text{T}}} \Phi \left( {x_{i} } \right) + b} \right) &= 0 \hfill \\ \alpha _{i}^{*} \left( {\epsilon + \zeta _{i}^{*} + y_{i} - w^{{\text{T}}} \Phi \left( {x_{i} } \right) - b} \right) &= 0 \hfill \\ \end{aligned}$$

(17)

$$\left( {C - \alpha _{i} } \right)\zeta _{i} = 0\quad {\text{and}}\quad \left( {C - \alpha _{i}^{*} } \right)\zeta _{i}^{*} = 0\quad {\text{where}}\quad i = 1, \ldots ,l.$$

(18)

Though $\alpha _{i} \cdot \alpha _{i}^{*} = 0$ both $\alpha _{i}$ and $\alpha _{i}^{*}$ cannot be considered as non-zero. So there is some value of $i$ for which either $\alpha _{i} \in \left( {0,C} \right)$ or $\alpha _{i}^{*} \in \left( {0,C} \right)$ and Hence $b$ can be obtained using the formula

$$\begin{gathered} b = y_{i} - \mathop \sum \limits_{{j = 1}}^{l} \left( {\alpha _{j} - \alpha _{j}^{*} } \right)K\left( {x_{j} ,x_{i} } \right) - \epsilon \quad {\text{for}}\quad 0 < \alpha _{i} < C \hfill \\ b = y_{i} - \mathop \sum \limits_{{j = 1}}^{l} \left( {\alpha _{j} - \alpha _{j}^{*} } \right)K\left( {x_{j} ,x_{i} } \right) + \epsilon \quad {\text{for}}\quad 0 < \alpha _{i}^{*} < C \hfill \\ \end{gathered}$$

(19)

The value of x_i equivalent to the parameters ($0 < \alpha _{i} < C$) and $(0 < \alpha _{i}^{*} < C)$ are known as Support vectors. Using the equations to find the values of w and b in the Eqs. (10) and (13), the value of common Support Vector Regression Function can be calculated as [20, 26, 27],

$$\begin{gathered} f\left( x \right) = \mathop \sum \limits_{{i = 1}}^{l} \left( {\alpha _{i} - \alpha _{i}^{*} } \right)\left( {\Phi \left( {x_{i} } \right)^{{\text{T}}} \Phi \left( x \right)} \right) + b\quad {\text{or}} \hfill \\ f\left( x \right) = \mathop \sum \limits_{{i = 1}}^{l} \left( {\alpha _{i} - \alpha _{i}^{*} } \right)K\left( {x_{i} ,x} \right) + b. \hfill \\ \end{gathered}$$

(20)

COVID-19 Data Set and Parameters

In India, only those underlying Cases that are susceptible to COVID-19 infection have been tested, who have travelled from affected countries or come in contact with a confirmed positive cases and shown symptoms after 2 weeks of quarantine. So the number of affected positive cases or vulnerable cases depends upon the underlying cases that susceptible to infection transmission Rate and the total number of infection cases. This section outlines and analyse the formulated parameters. Here we have used a detailed COVID-19 dataset of Orissa state. It is a day’s wise information related to Date, Total test cases, Total positive cases, Cumulative positive cases, Recovered cases, cases, Rate of Positive, Rate of recovered, Rate of negative, Cumulative death cases, etc. [25, 28]. From 30th January 2020 to 11th June 2020. The detailed steps and different properties of the dataset are shown in Tables 1 and 2.

Table 1 Detail steps

Table 2 Dataset properties

Parameters

Test Cases or Total Number of Sample Tested

It is defined as one of the significant tools/process in the fight with COVID-19 and to slow and lessen the impact and spread of the virus. Tests permit us to identify non-vulnerable cases, susceptible cases, positive cases or vulnerable cases after clinical identification.

Non-vulnerable Cases

The test-negative cases or after clinical treatment the recovered cases from the vulnerable category and having no symptom of COVID-19 infections are called non-vulnerable cases.

Susceptible Cases

The susceptible cases are the cases that are exposed to COVID-19 and help in the transmission of infection. Some susceptible cases which are exposed to COVID-19 and affected and carried out the transmission are called vulnerable cases and some are exposed but still, they cannot help in the transmission of infection. Some cases are the Recovered and Discharged after successful clinical treatment.

Positive Cases or Vulnerable Cases

These are the cases that can be exploited by COVID-19 i.e. the reported whole cumulative count of laboratory and detected that may sometimes depend on the country exposure them and the criterion approved at the time confirmed positive and sometimes may depend on the country exposure principles that is suspect, presumptive, or show probable belongings of detected illness. So, the total active cases = Total cases − total recovered cases − total deaths cases.

Transmission Rate

The transmissibility and attack rate to know how rapidly the disease is spreading from a virus is designated by its reproductive number that is Ro, which is pronounced as r-zero or R-nought that presents the average count of people where a single infected person may spread the virus to others.

Recovered Cases

These are the Recovered and Discharged case after successful clinical treatment. This statistic is highly important for COVID-19 treatment. The total recovered cases = total cases − active cases − total deaths. The recover cases are the subset of vulnerable cases. After successful recovery from the COVID-19 infection it is recommended to check the symptoms resolve successfully and two negative tests conform within 24 h or symptoms determine and additional 14 days isolations as directed. But after the recovery if again the recovered case is exposed to COVID-19 then the case can be a susceptible case and may help in the transmission of infection.

Infection Outbreak

An outbreak is when an illness happens in unexpectedly high numbers. It is the occurrence of belongings in excess of standard expectancy. The case count varies depending on the disease-causing mediators, and the type and size existing and previous experience to the agent. Infection outbreaks are generally caused by transmitted or infection throughout the contact of animal-to-person, person-to-person, or from the environment or other media. The outbreaks may also happen subsequent exposure to radioactive and chemicals materials. An outbreak can last for days or years.

Rate of Positive Cases

Rate of positive cases R₀ is the ratio between the total number of affected positive cases or vulnerable cases to the underlying Cases that susceptible to infection that can be made per cases with transmission rate R₀. This is the rate which gives the case of a newly infected person from a single case. The average positive rate is the difference of total susceptible cases to total negative cases in a day. A number of groups have estimated the positive rate for COVID-19 to be somewhere approximately between 1.5 and 5.5.

Rate of Negative Cases

The test negative cases rate is the ratio between total cases of negative cases to the total cases of test conducted. Test negative cases must be approaching the total number of test conducted.

Rate of Recover Cases

The total recovered cases = total cases − active cases − total deaths. So, the rate of Recovery is the ratio between the total recovery cases to the total number of affected positive cases.

Rate of Death Cases

Total deaths cases are the cumulative number of deaths among detected positive cases.

Simulations

According to the data set the susceptible underlying cases (total test cases day-wise and cumulative test cases) are exposed to COVID-19 infection and have been tested clinically. Out of the total test cases, some cases that are exposed to COVID-19 and help in the transmission of infection are considered as test positive cases which are exposed to COVID-19 are affected and carried out transmission.

Some susceptible cases are exposed but still they cannot help in the transmission of infection are called Test negative cases. The test cases are increases in an exponential manner and it’s very clear from the graph that if the number of test cases is increasing more than it is easier to identify the total positive cases in due time so that necessary actions can be taken. The test positive cases or vulnerable cases are the cases that can be exploited by COVID-19 i.e. the reported entirety cumulative count of laboratory and detected that sometimes depend on the country treatment and the criteria accepted at the time confirmed the positive cases and sometimes it may depend on the country treatment standards that suspect, presumptive or probable number of detected infections. Figures 11 and 12 represent the growth of Cumulative Positive test cases and Positive test cases day-wise. The positive cases are also increasing in an exponential manner throughout the world as there are no clinically confirm treatments available till now for the new pandemic.

Fig. 11

Growth of cumulative positive cases during 30th January 2020 to 11th June 2020

Fig. 12

Growth of day-wise positive cases during 30th January 2020 to 11th June 2020

The total active cases = total cases − total recovered cases − total deaths cases. And the total recovered cases = total cases − active cases − total deaths. The recovered cases are the sub-set of vulnerable cases. After successful recovery from the COVID-19 infection, it is recommended to check the symptoms resolve successfully and two negative tests conform within 24 h or symptoms resolve and additional 14 days isolations as directed. But after the recovery, if again the recover case is exposed to COVID-19 then the case can be susceptible case and may help in the transmission of infection. The cumulative growths of total recover case and daily recovered cases is as depicted in Figs. 13 and 14.

Fig. 13

Growth of cumulative recover cases during 30th January 2020 to 11th June 2020

Fig. 14

Growth of daily recover cases during 30th January 2020 to 11th June 2020

Total deaths cases are the cumulative number of deaths among detected positive cases as shown in Fig. 15 and the growth of daily death cases are depicted in Fig. 16.

Fig. 15

Growth of total death cases during 30th January 2020 to 11th June 2020

Fig. 16

Growth of daily death cases during 30th January 2020 to 11th June 2020

Prediction Using LSTM

The future forecasting is the process of predicting future trends using the most recent and past data values. The important challenge is to analysing the output patterns in the trend of values and then utilising this pattern to predict and analyse the future. As predicting the future is a very difficult task by using the normal program so the use of deep learning has proven significantly to give better patterns analysis in the case of structured data and unstructured data also. So as to identify the patterns in a long trend of data, we need networks to analyse patterns across time. Recurrent networks are commonly used for learning and forecasting such data. It is also important to understand the long and short-term memory relational dependencies or temporal differences. In our implementations, we have try to propose two forecasting models implementing LSTM networks and SVR using Keras application development environment.

Here, we have used a detailed COVID-19 dataset from an India scenario. It is a day’s wise information related to days, date, total test cases, total positive cases, cumulative positive cases, recovered cases, cases, rate of positive, rate of recovered, rate of negative, cumulative death cases etc. during 30th January 2020 to 11th June 2020. For trend with respect to our data set we analyse, and train our model for the first 70% of the record and test it for the remaining 30% data. The pictorial representations in Fig. 17a–f clearly depict that the predicted values and the actual value for all the parameters have somewhat overlap trends in both LSTM and SVR. However, if you see fitting is not so perfect as expected in SVR but it is acceptable in the case of LSTM. The predicting the future, it is always recommended that a good possibility of getting the output is acceptable to some extent. So the predicted model’s output is given as input back into it.

Fig. 17

Prediction using LSTM

Prediction Using SVR

The SVR approach for time series forecasting has considered being an efficient tool in real value function estimation. It is used to predict a continuous variable which value is predefined. Other regression models often try to minimize the errors that occurred while SVR tries to fit best in any threshold value. We have also used a detailed COVID-19 dataset from an India scenario as used for LSTM. For trend with respect to our data set here also we analyse, and train our model for the first 70% of record and test it for the remaining 30% data. But the fitting function is less perfect as expected in SVR. The detail is represented in Fig. 18a–f.

Fig. 18

Prediction using SVR

Results and Discussion

Performance Criteria

We have chosen different significant performance metrics for the comparison of the performance criteria like normalized mean squared error (NMSE), mean absolute error (MAE), directional symmetry (DS) and root mean squared error (RMSE) for SVR and LSTM as shown in Table 3. The detailed values of the metrics are illustrated in Table 3. RMSE, MAE and NMSE, present the divergence among actual and predicted values for the total death cases, total recover cases and total conformed positive cases. Hence, smaller values indicate better prediction accuracy. Directional symmetry (DS) indicated the predictive direction. So greater directional symmetry (DS) value points to higher accuracy which is shown in Table 4 and further this information is well depicted in Fig. 19. Table 5 depicts that both SVR and LSTM have the same directional symmetry, while LSTM has a much better accuracy score as compared to SVR over the COVID-19 Data set.

Table 3 Formula for performance criteria

Table 4 RMSE, MSE, MAE, and TVS of SVR & LSTM

Table 5 Directional symmetry and accuracy score of SVRVSLSTM

Fig. 19

Comparison of RMSE, MSE, MAE, and TVS of SVR vs LSTM

Conclusion 

Finally, we have concluded that the LSTM approach is a better forecasting approach for the prediction of the behaviour of COVID-19. The total cumulative positive cases, total recovered cases, total death case as a whole and daily wise represented in figures. There will be an incremental trend that remains existed for a long time like more than 200 days until a vaccine or other effective measures are not identified and applied. Therefore, a prediction for COVID-19 spread behaviour is simulated for the next 80 days. This study will be helpful in the jurisdictions and mitigation strategies for dealing with the pandemic. Our illustrative study reveals require for policymakers to obtain immediate and hostile actions, and if they do so, considerable mortality may be prevented. The performance of LSTM is 95.46% which is a significant figure and hence we proceed with the forecasting of pandemic behaviour.