Abstract
In the frame of the European funded H2020 project RETALT (retro propulsion-assisted landing technologies), the unsteady aerodynamics of vertically descending and landing launchers have been investigated. In this paper, experimental data of the landing burn tested in the Vertical Free-Jet Facility Cologne at DLR in Cologne are presented. The landing burn was simulated with a cold gas jet of pressurized air opposing the wind tunnel free stream. Tests with several jet conditions were compared to results without active jet. Proper orthogonal decomposition of schlieren recordings and spectral analyses of their time histories are performed and are compared to frequencies in pressure measurements. Dominant frequencies were found, which are strongest at Mach 0.8. Especially, a Strouhal number of 0.2 was found to be most dominant. The intensity of the dominant frequencies can be lowered if the engine is active. The normalized root mean square pressure fluctuations are between 0.1 and 0.3 during the landing maneuver. Additionally, the steady flow features scale well with the ambient pressure ratio and the momentum flux ratio. The unsteady flow field dynamics of the subsonic retro propulsion flow field can likely be linked to large-scale turbulent structures in the supersonic jet, triggering large-scale pressure fluctuations and altering the overall flow field.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The successful retro propulsive landing of the first stage of the SpaceX Falcon 9, heavy lift launcher in 2015 and the successive application of this method in its operations, resulted in establishing that landing vehicles vertically with the aid of retro propulsion can be considered to be state of the art in the USA. This created large interest in Europe, which resulted in the RETALT (retro propulsion-assisted landing technologies) project which was funded by the European Union in the frame of the Horizon 2020 framework program under the grant agreement No 821890, to study key technologies identified for retro propulsive descent and landing (Marwege et al. 2019, 2022a, 2022e). One of the main goals of the project was to create a foundation for the understanding of the complex unsteady aerodynamics for such vehicles during the descent and landing approach. Unsteady aerodynamics or unsteady aerodynamic excitation mechanism with inherent pressure fluctuations can impose high loads on the structures of space transportation systems (Daub et al. 2022; Saile and Gülhan 2021) which can even lead to the failure of a system or a launcher (Arianespace Flight 157—Inquiry Board 2003, David and Radulovic 2005). Therefore, the focus of this paper is the description of the dynamics of the flow field during the landing burn of a descending and landing first stage and its comparison to phases without active engine to understand the underlying physics and identify critical flight phases and load cases.
The mission concept of the RETALT1 reference launcher, which was investigated in the project, is shown in Fig. 1. It is similar to the mission concept applied by SpaceX for the Falcon 9. After the ascent, the main engine cutoff (MECO) and the stage separation, either a down range landing (DRL) on a seagoing platform or a return to launch site (RTLS) can be performed. The two mission concepts mainly differ in the boost-back burn which needs to be performed in the RTLS scenario to bring the first stage back to the launch site. During the descent, a re-entry burn is performed at high altitudes to slow the vehicle down in order to decrease heat loads and dynamic pressure in the following aerodynamic phase (De Zaiacomo et al. 2022). After the purely aerodynamic phase, the landing burn is performed to decelerate the vehicle down to nearly zero velocity for touch down (Botelho et al. 2022). The characteristics of the RETALT1 vehicle are described in Marwege et al. (2019, 2022a, 2022e) and are summarized in Table 1, and the outline is shown in Fig. 2. The aerodynamics of RETALT1 have been studied with the aid of exhaustive wind tunnel test series at the Department of Supersonic and Hypersonic Technologies of the German Aerospace Center (DLR) in Cologne. The re-entry burn was modeled in the Hypersonic Wind Tunnel Cologne (H2K) (Marwege et al. 2022c, d), the aerodynamic phase was studied in the Trisonic Wind Tunnel Cologne (TMK) (Marwege et al. 2022b, c) and the landing burn was tested in the Vertical Free-Jet Facility Cologne (VMK) (Marwege et al. 2022c).
RETALT1 mission concept (De Zaiacomo et al. 2022)
Outline of the RETALT1 configuration as presented in Marwege et al. (2019)
This paper is focused on cold gas tests of the landing burn. While some insights on the flow field in this flight phase were presented in Marwege et al. (2022c), a dedicated modal and frequency analysis was not performed, which is the aim of the work at hand. Furthermore, an averaged modal solution is proposed for a comprehensive description of the flow field phenomena. The paper is laid out as follows. First, an overview of the state of the art in the subsonic retro propulsion is given. Then, the experimental setup and test conditions are described. Subsequently, the landing burn is analyzed in detail regarding its general flow field and its dynamics with the aid of proper orthogonal decomposition (POD) and spectral analyses. Finally, conclusions and an outlook close the paper. A complementary analysis of the unsteady aerodynamics of the hypersonic re-entry burn can be found in Marwege and Gülhan (2023).
2 Subsonic retro propulsion
Subsonic retro propulsion refers to a supersonic jet being directed against a subsonic free stream. The flow phenomena are similar to the long penetration mode in supersonic retro propulsion (SRP) flow fields where the jet is directed against a supersonic free stream [see, e.g., (Venkatachari et al. 2015)]. However, due to the absence of a bow shock upstream of the jet, the exhaust plume extends farther into the free stream, exhibiting a multi-cell structure (Korzun et al. 2020). This is shown in a snapshot of a schlieren video in Fig. 3, where the free stream is coming from the left and a supersonic jet from the right in the image. In Fig. 4, the variance for each pixel was evaluated over 200 images (Marwege et al. 2022c). In the resulting image, the multi-cell structure of the retro propulsion jet is visible. Furthermore, high fluctuations can be observed in the stagnation region between the jet and the free stream, as the variance is especially high in this region. In subsonic retro propulsion flows, the characteristic flow feature, the plume length, depends on the square root of the momentum flux ratio (MFR) as shown in Jarvinen and Hill (1973), and in Marwege et al. (2022c) using recent experimental data. The MFR is defined as (Jarvinen and Hill 1973):
where \({\rho }_{e}\) and \({u}_{e}\) are the density and the velocity at the nozzle exit and \({\rho }_{\infty }\) and \({u}_{\infty }\) are the density and velocity in the free stream. The pressure coefficient on the forward facing base area decreases with increasing aerodynamic thrust coefficients (Jarvinen and Adams 1970).
Snapshot of a subsonic retro propulsion flow field at Mach 0.7 (Marwege et al. 2022c)
Variance of the subsonic retro propulsion video (over 200 images) at Mach 0.7 (Marwege et al. 2022c)
Some efforts have been made with computational fluid dynamics (CFD) with Reynolds averaged Navier–Stokes (RANS) methods in Bykerk and Karl (2023); Ecker et al. (2022); Ertl et al. (2022) to study such flow fields, and it was found that the plume shape and length strongly depend on the turbulence modeling. The dynamics of subsonic retro propulsion flows has been studied with detached eddy simulations (DES) in Korzun et al. (2020, 2022) and time series of aerodynamic force and moment coefficients have been reported. However, no modal analysis was performed.
3 Experimental setup
3.1 Vertical Free-Jet Facility Cologne (VMK)
As mentioned in Introduction, the landing burn of the RETALT1 configuration was simulated in the Vertical Free-Jet Facility Cologne (VMK) at the Department of Supersonic and Hypersonic Technologies of the German Aerospace Center. The exhaust plume was simulated with a cold gas jet.
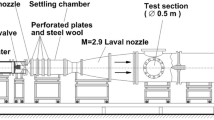
The VMK is a blow-down facility from pressurized air of up to 60 bar down to ambient pressure, with an open test section. This enables testing sea level conditions in the facility for Mach numbers up to 2.8. The maximum Mach number that can be tested in the facility is 3.2. The subsonic nozzle used in the experiments presented in this paper has an exit diameter of 340 mm. A sketch of the wind tunnel is shown in Fig. 5a, the performance map is shown in Fig. 5b.
3.2 Wind tunnel model and instrumentation
The test setup for the cold gas tests in the VMK with counterflow environment (retro propulsion) is shown in Fig. 6. The wind tunnel model concept is shown in Fig. 7. The model was also prepared for hot gas testing with hydrogen and oxygen. For cold gas testing, high-pressure air was supplied through the manifold assembly and blown out through the wind tunnel model nozzle. The wind tunnel model for the RETALT1 configuration has a scale of 7/600 with respect to the flight configuration. Hence, it has a base diameter of 70 mm. The reference area is the base area, \({A}_{B}\), of 28.27 m2 for the flight configuration. The scaling follows a trade-off of best meeting the similarity parameters of the flight conditions, while keeping design restrictions. The model nozzle was designed as parabolic approximation of a bell nozzle with a fixed expansion area ratio and a fixed nozzle exit angle. It has an expansion area ratio of 5.5, resulting in an exit Mach number of 3.275 (for air), with a throat diameter of 5.45 mm, an exit diameter of 12.77 mm and an exit angle of 5.57°. The exit angle was chosen to be 5.57° to match the nozzle exit angle of the RETALT1 first stage engine which has a thrust optimized contour with an area expansion ratio of 15 (Marwege and Gülhan 2023).
Test setup in VMK for cold gas tests (Marwege et al. 2022c)
The choice of an expansion area ratio of 5.5 is shortly reasoned in the following. In the study of Marwege and Gülhan (2023), the scaling approach for the expansion area ratio for the wind tunnel model nozzle for the hypersonic retro propulsion experiments of the RETALT1 vehicle in the H2K were explained in detail. It was designed to achieve the best possible similarity in the thrust coefficient and the ambient pressure ratio. As the thrust coefficient and the momentum flux ratio can be used interchangeably as similarity parameters for retro propulsion configurations (Mejia and Schmidt 2022), the same approach as used in Marwege and Gülhan (2023) can be applied for the subsonic retro propulsion configuration presented in this paper. Marwege and Gülhan (2023) showed that the thrust coefficient similarity is proportional to the inverse of the engine scaling parameter, and the ambient pressure ratio similarity is directly proportional to the engine scaling parameter. The engine scaling parameter, in turn, is a parameter only dependent on the nozzle exit conditions (and the free stream heat capacity ratio). It was shown that both similarities are met at an expansion area ratio of 5.5. As the same configuration as in Marwege and Gülhan (2023) was tested in the experiments presented in this paper, the engine scaling parameter is the same, and, hence, the expansion area ratio of 5.5 is also the optimum for the VMK model to meet both similarities and was therefore selected for the wind tunnel model nozzle.
The positioning of the model in the wind tunnel facility can be adjusted with the movable support drive. For the cold gas tests, the model was positioned at a distance of 183 mm from the wind tunnel nozzle.
The distribution of pressure sensor locations in the base area of the model is shown in Fig. 8. The first index shows the radial distance of the sensor, the second the angular position. The sensors on the right-hand side have positive signs, the ones on the left have negative signs. In the rings 0 and 1 steady pressure measurements were performed with pressure tubes. In rings 2 and 3, high-frequency pressure measurements were performed with XCQ-080-3.5BARA and XCE-080-3.5BARA Kulite pressure sensors. The uncertainties of the pressure coefficients were computed with Gaussian error propagation. The uncertainties of the pressure measurements are listed in Table 2. The uncertainty in the heat capacity ratio, \({\gamma }_{\infty }\), was derived from data in Böge and Böge (2014). The tests were recorded with schlieren imaging at 25 kHz with a continuous light source and an exposure time of 1.429 \(\mu s\). The schlieren knife edge was positioned perpendicular to the flow. The high-frequency pressure measurements were performed at 50 kHz.
4 Test conditions
In Fig. 9, the Mach numbers tested in the wind tunnel facilities at DLR in Cologne are mapped on the reference trajectory presented in Marwege et al. (2019). In addition to the tests performed in the VMK, which are part of this paper, also the Mach numbers tested in the Trisonic Wind Tunnel Cologne (TMK) (Marwege et al. 2022b, c) and in the Hypersonic Wind Tunnel Cologne (H2K) (Marwege and Gülhan 2023; Marwege et al. 2022d) are included. One can see that the wind tunnel facilities are well suited to rebuild the descent and landing trajectory of the vehicle as they cover all flight phases.
Mapping of Mach numbers tested in the wind tunnel facilities at DLR in Cologne over the reference trajectory presented in Marwege et al. (2019)
The free stream and jet conditions for the tests in the VMK discussed in this paper are summarized in more detail in Table 3. The measured pressures and the normalized pressure fluctuations can be found in Tables 4 and 5 in appendix.
5 Averaged modal solution
As will be shown in Sect. 6.1, in subsonic retro propulsion flow fields, the average image over time does not reveal the relevant flow features (see for example Fig. 16). Due to their strongly unsteady behavior the flow features are averaged out. As a solution to this problem, it is proposed here to perform a proper orthogonal decomposition (POD), then to exclude the zeroth mode, which corresponds mainly to the steady flow field, and just average over the remaining modes. This approach can be interpreted as a cutoff filter excluding the highest energetic mode and revealing lower energetic structures contributing to the mean flow field. This approach reveals the flow features of the flow field better without the need to plot all of the first modes. This averaged solution will be called the “averaged modal solution”. The time history of this reconstructed mode can even capture the most important frequency information as shown in this section. The procedure is described in the following.
The Proper Orthogonal Decomposition (POD) was first applied in fluid dynamics by Lumley (1987), who introduced this method to extract coherent structures from turbulent flow fields (Taira et al. 2017). There are three main methods to perform POD, which are the classical or direct method, the snapshot POD, introduced by Sirovich (1987), and the singular value decomposition (SVD) approach (Taira et al. 2017, Weiss 2019).
Here, the SVD approach [similar to the description in Brunton and Kutz (2019)] will be followed for its simplicity and good interpretability. The images of the schlieren video are reshaped to one dimensional column vectors \({{\varvec{x}}}_{0}, {{\varvec{x}}}_{1}, \dots , {{\varvec{x}}}_{n-1}\) with a length \(m\), where \(n\) is the number of images and \(m\) is the number of pixels in the image. The image vectors are then stacked together to build a two-dimensional matrix \({\varvec{X}}\in {\mathbb{R}}^{m\times n}\):
A singular value decomposition (SVD) of the matrix \({\varvec{X}}\) is then performed:
To save storage, the economy SVD is performed. Therefore, \({\varvec{U}}\in {\mathbb{R}}^{m\times n}\) are the left singular vectors \({{\varvec{u}}}_{0}, {{\varvec{u}}}_{1}, \dots , {{\varvec{u}}}_{n-1}\), which correspond to the spatial modes, \({\varvec{\Sigma}}\in {\mathbb{R}}^{n\times n}\) is the diagonal matrix with the singular values, \({\sigma }_{0}, {\sigma }_{1},\dots ,{\sigma }_{n-1}\), and \({\varvec{V}}\in {\mathbb{R}}^{n\times n}\) are the right singular vectors representing the time history of the modes, \({{\varvec{v}}}_{0}, {{\varvec{v}}}_{1},\dots ,{{\varvec{v}}}_{n-1}\):
The idea in this section is to select a certain number of modes, starting with mode \(s\) and ending with \(r\), and merge them in one averaged mode. The matrices of the selected modes are \(\widetilde{{\varvec{U}}}\), \(\widetilde{{\varvec{\Sigma}}}\) and \(\widetilde{{\varvec{V}}}\):
To obtain the averaged solution the time histories of the POD modes are averaged over the time steps:
Then the averaged mode \({{\varvec{u}}}_{st}\) is constructed by:
The term \(\widetilde{{\varvec{U}}}\widetilde{{\varvec{\Sigma}}}{\overline{\widetilde{{\varvec{v}}}} }^{T}\) is divided by its length such that \({{\varvec{u}}}_{st}\) is a unitary vector. The time series \({{\varvec{v}}}_{st}\) and the singular value \({\sigma }_{st}\) of this new POD mode can be reconstructed as follows. The averaged modal solution shall reconstruct the original image snapshots \({\varvec{X}}\):
Bringing \({{\varvec{u}}}_{st}\) on the left side of the equation follows in:
where \({{\varvec{u}}}_{st}^{+}\) is the pseudoinverse of \({{\varvec{u}}}_{st}\). As \({{\varvec{v}}}_{st}\) needs to be unitary it follows:
and hence:
Averaging the time series and constructing a spatial mode \({{\varvec{u}}}_{st}\) from that is equivalent to averaging the spatial flow field snapshots reconstructed from the selected modes. In other words, averaging the time series and then solving the matrix equation is equivalent to first solving the matrix equation and averaging afterward:
This shows that the averaged modal solution can be interpreted as the mean flow field of a low order model which captures the selected modes. If the mean flow field is not subtracted from the flow field images before the POD is performed, a small content of the mean flow field is being spread over the remaining modes, apart from the zeroth mode, which makes it visible in the averaged modal solution. If only higher modes with less energy are included in the averaged modal solution, one could think of the average modal solution as a cutoff filter omitting the highest energetic mode in the mean flow field and revealing lower energetic structures contributing to it. To further illustrate this statement, a simple example case of the applied averaged modal solution was constructed in appendix.
The averaged modal solution flow field for a subsonic retro propulsion flow field, resulting from the procedure described above is shown in Fig. 10 starting with mode 1 (s = 1) (the wind tunnel nozzle, the schlieren window and the wind tunnel model were masked in black). One can see that, due to the exclusion of the zeroth mode, the structures of the unsteady flow features become visible (see Fig. 10c). The higher the number of included modes (larger \(r\)), the clearer the smaller structures are visible. Also the pressure waves in the flow field can be observed.
As stated in Eq. (10) the time history of the averaged modal solution is computed from the pseudo inverse \({{\varvec{u}}}_{st}^{+}\). The pseudo inverse minimizes the solution of a system of linear equations in the Euclidian norm (Dahmen and Reusken 2006). In this case the solution of the system of linear equations is \({{\sigma }_{st}{\varvec{v}}}_{st}^{T}\). Hence \({{\varvec{v}}}_{st}^{T}\) is the time history best reconstructing the original data \({\varvec{X}}\) with the averaged modal solution \({{\varvec{u}}}_{st}\). In other words, if \({\varvec{x}}\) are all possible solutions to the system of linear equations it follows that:
Therefore, \({{\varvec{v}}}_{st}^{T}\) can capture some of the frequency content present in that data as it is constructed to rebuild its variation in time.
In Fig. 11, the average values of the time series of the original modes, \(\overline{v },\) are depicted. For larger modes, their values decay, which indicates that the smaller modes contribute more to the overall averaged modal solution, as also the singular values decay for larger modes. Figure 12 shows the power spectral density (PSD) of the time series of the averaged modal solution. For the computation of the PSD, a short time Fourier transform was computed over 8000 time steps. It was performed with a Hann window with a length of 500, shifting the window by 16 time steps between single spectra. The spectra were then averaged over the time steps [method by Welch (1967)]. The frequency was resolved with 2048 bins, resulting in a frequency resolution of 12.21 Hz. The PSD is plotted for various included numbers of modes. Apparently, the PSD is quite independent of the number of included modes. It is compared here to the average of the PSDs of the first 12 original modes. The PSD of the averaged modal solution captures the low frequency peaks well, while the peaks of the higher frequencies are not resolved. The lower frequency peaks are slightly shifted to lower values.
This analysis shows that it is possible to reconstruct an averaged modal solution from the POD modes that can even capture the low frequency content in the flow field.
6 Results
In this section, the subsonic retro propulsion flow field will be analyzed regarding its steady and unsteady flow field features.
6.1 General subsonic retro propulsion flow field features
Figure 13 shows a snapshot of a subsonic retro propulsion flow field at Mach 0.8 with an Ambient Pressure Ratio (APR) of 0.389. The APR is defined as the ratio of the nozzle exit pressure \({p}_{e}\) and the free stream static pressure \({p}_{\infty }\):
The flow field shows a strongly unsteady behavior. The large-scale flow features that can be observed are: The unsteady jet which meets the free stream at the contact surface, pressure waves emerging from the contact surface, and large-scale fluctuations downstream of the contact surface. The unsteadiness of the flow field is evident by comparing Fig. 13 with Figs. 14 and 15, which are images from the same schlieren video at different points in time. The plume length varies strongly and the jet structure can become asymmetric as shown in Fig. 14.
Snapshot of the same schlieren recording as in Fig. 14 at a different point in time
Figure 16 shows the mean image of the flow field over 200 images, and Fig. 17 shows the standard deviation over these 200 images. It is apparent that unsteady flow features cannot be seen in the mean image (as expected) but the plume structure close to the model nozzle exit is well captured. In the standard deviation image the flow structures are somewhat clearer than in the mean image. Figure 18 shows the mean image over 200 images of the jet without couterflow (\({M}_{\infty }=0\)) for approximately the same APR. The multi-cell structure of the jet can be well observed, in contrast to the jet with active counterflow.
In Fig. 19, a detail of the flow field near the nozzle exit of the jet without counterflow is shown. The flow features which are characteristic for such over-expanded jets are sketched in the image. As the plume is strongly over-expanded, it exhibits a Mach reflection at the centerline [see for example (Frey 2001; Saile 2019)] passing through an oblique lip shock and a Mach disc, where the lip shock is reflected at the Mach disk. After the following expansion, the flow is recompressed by a new incident shock, again exhibiting a Mach reflection. Downstream of the second Mach disk also the slip line between the flow passing through the incident shock and its reflection at the Mach disc, and the flow passing through the Mach disk is visible.
Detail of mean flow at \({M}_{\infty }=0\) and \(APR=0.387\) (Fig. 18) with sketched flow features
In Fig. 20, the flow features as sketched in Fig. 19 are overlaid over the flow field with active counterflow at \({M}_{\infty }=0.8\), with the same APR. Here, instead of the mean image, the standard deviation image was used as it shows the flow structures more clearly. The flow features without counterflow match the exit flow with active counterflow very well. This shows that the APR is the correct scaling parameter for the description of the plume structure at the nozzle exit.
Detail of standard deviation at \({M}_{\infty }=0.8\) and \(APR=0.389\) overlaid with flow features at \({M}_{\infty }=0\) sketched in Fig. 19
This is an interesting finding, as in supersonic retro propulsion flow fields it was found that the APR is not representative for the exhaust plume structure, but rather the exit pressure ratio (EPR) (Gutsche et al. 2021), which is the ratio of the exit pressure, to the dead air pressure in the recirculation zone at the nozzle exit. In the subsonic retro propulsion case, the EPR seems to be close or equal to the APR, which is why the APR can be used directly as similarity parameter.
This is reasonable as the strong bow shock that is present in the supersonic retro propulsion flow field is absent. Hence, the alteration of the free stream induced by the jet is weaker and the flow conditions in the recirculation region close to the nozzle exit are more strongly dictated by the free stream rather than by the jet. Furthermore, with the large plume length, the jet pushes the stagnation point, where the free stream and the jet plume meet, far into the free stream, leaving the nozzle exit area in the wake of the jet, such that the flow field has enough running length to adapt to the free stream parameters. Hence, it is reasonable to assume the static pressure in the free stream, \({p}_{\infty }\), to be acting in this region.
In summary, there are two dominant similarity parameters that describe the steady flow field of the subsonic retro propulsion flows: While the momentum flux ratio (MFR) describes the interaction of the jet with the counterflow and the jet plume length (Jarvinen and Hill 1973), the APR describes the flow structure at the nozzle exit.
In Fig. 21 the pressure coefficients (\({C}_{p}=(p-{p}_{\infty })/{q}_{\infty }\)) for different APRs are shown. Due to the increase of the plume length with the MFR (see Sect. 6.2), it increases with increasing APR and with decreasing Mach numbers. That is why in Fig. 21 for higher APRs the lower Mach numbers were not evaluated, as the plume is reaching the wind tunnel nozzle exit. One can observe that the pressure coefficients are clustered by the radial position. The pressures in ring 1 and 2 lie on top of each other. The pressure coefficients in ring 3 are negative as they are positioned around the shoulder of the base area where the flow is expanded. The various APRs show that while a relatively large difference of the jet-off case to the cases with active jet can be observed, the difference between the different jet cases is small. For the active jet, the absolute values of the pressure coefficients decrease and they become quite independent of the Mach number.
The lower pressures in the active jet cases, come from the fact that the jet pushes the stagnation point further upstream in the free stream, as explained above, leaving the base area in the wake of the jet. This also explains why the APR and the Mach number have little influence on the pressure values, since the wake area is less dependent on the free stream conditions than the stagnation region.
6.2 Unsteady flow field dynamics
Figure 22 shows snapshots of the schlieren video of the test case at \({M}_{\infty }=0.8\) and \(APR=0.389\) in timesteps of 80 μs (at a frequency of 12.5 kHz). The main effect dominating the unsteady behavior of the flow field is the overall unsteady jet and the large-scale pressure fluctuations. One can observe, that pressure waves radiate away from the stagnation region in the upstream direction. In contrast, pressure disturbances in the wake region of the jet move downstream toward the nozzle exit.
Following the snapshots in time, from left to right and from top to bottom, the larger pressure fluctuations move downstream in the direction of the free stream, toward the base area of the launcher configuration while the pressure waves of the stagnation area move in the opposite direction. It seems that, as soon as the strong pressure waves and the strong pressure fluctuations are not dominating the flow field anymore, features common for supersonic jets, such as Mach waves radiating from large turbulent structures (Tam 2009; Tam et al. 2008), can be observed. In the stagnation region, only weaker pressure waves can be observed. However, when larger pressure fluctuations are generated, likely triggered by large turbulent structures of the jet, these lead to stronger pressure waves radiating again upstream. This generates larger pressure fluctuations in their wake which move downstream. The strong pressure waves and the pressure fluctuations alter the flow field and therefore change the pressure around the nozzle exit and hence temporally the EPR (exit pressure ratio) leading to an overall fluctuating jet.
In turbulent jets, three main effects are contributing to the flow dynamics, the turbulent mixing noise, the broadband shock-associated noise and the screech (or screeching) tones (Tam 1995) where the turbulent mixing noise is created by the fine-scale turbulent structures and Mach waves that are radiated from large turbulent structures (Tam 2009; Tam et al. 2008). The large coherent structures that occur in the form of wave packets (Jordan and Colonius 2013) have been studied with spectral proper orthogonal decomposition in Schmidt et al. (2018) and were found to contribute substantially to the jet dynamics. As mentioned above, the jet dynamics are likely coupled closely with the dynamics of the supersonic retro propulsion flow field, as especially larger turbulent structures, when interacting with the freestream, can generate large flow field alterations. However, the large-scale pressure fluctuations and the overall strongly fluctuating jet seem to dominate the flow field.
To further understand the unsteady behavior of the subsonic retro propulsion flow field, a proper orthogonal decomposition (POD) was performed over 8000 images as described in Sect. 5. Figure 23 shows the first 12 modes and four higher modes of the same retro propulsion flow field at \({M}_{\infty }=0.8\), \(\text{APR}=0.387\), \(\text{MFR}=6.52\), and at a Reynolds number of \({\text{Re}}_{\infty }=1.68\times 1{0}^{6}\) (\({\text{Re}}_{\infty }=({u}_{\infty }{\rho }_{\infty }{D}_{\text{ref}})/{\mu }_{\infty }\), were \({D}_{\text{ref}}\) is the base diameter). The values in the images were scaled to the maximum values being white and the minimum values in the mode being black. The upper schlieren window, the wind tunnel model and the wind tunnel nozzle exit were masked in black.
The pixel intensity in schlieren images is proportional to the density gradient along the line of sight (Prasad and Gaitonde 2022). As the knife edge was positioned perpendicular to the flow, only the density gradient in the free stream direction is accounted for. As the POD was performed applying an SVD approach, the modes are ordered by the singular values which are proportional to the density gradient. Note that, if the POD is computed with the direct method or the snapshot POD the resulting eigenvalues are the squares of the singular values (Weiss 2019) which results in the square of the density gradient as, e.g., applied in Berry et al. (2017).
As the mean image was not subtracted from the single schlieren images before the POD was performed, the zeroth mode mainly shows the steady flow features. The lower modes then show the larger fluctuations, while the larger modes show the smaller structures. The first modes of the subsonic retro propulsion flow field are symmetric. The symmetric modes are followed by antisymmetric modes, which are then followed by symmetric ones again and so forth. However, with higher modes the symmetry is slowly lost.
The flow field is dominated by the large, downstream moving, pressure fluctuations shown in Fig. 22, which can clearly be seen in the first three modes. Also the stagnation region is captured in the modes 1, 3, 4 and higher modes, which accounts for the change in the plume length. The modes 9 and 10 show the smaller scale pressure fluctuations. Higher modes capture smaller structures of the flow field, such as small-scale pressure fluctuations and turbulent structures in and around the jet.
In Fig. 24 and in Fig. 25, the singular values and the cumulative energy of the singular values (sum of singular values up to the current one, divided by the sum of all singular values) are plotted. One can see, especially in the cumulative energy, that a large number of modes is necessary to capture the energy of the flow field, e.g., approximately 5000 modes are necessary to capture about 80% of the energy. The reason for this is probably that the pressure waves moving through the flow field need a large number of modes to be captured correctly. However, it was shown in Fig. 23 that the larger modes rebuild the smaller structures. Hence, if the macroscopic motion shall be represented, less modes are required.
In Fig. 26, the first twelve singular values of the POD modes of the retro propulsion flow field are shown. The POD modes of the retro propulsion flow field can be clustered into groups of three modes (1, 2, 3; 4, 5, 6; 7, 8, 9 etc.), where the energy decays from group to group. This is reasonable as, e.g., the first three modes capture the large-scale pressure fluctuations, which is why they have the same order of magnitude.
As can be seen in Fig. 16, the average image does not reveal the flow structure in the retro propulsion flow field as the flow features are disappearing due to the averaging. However, as detailed in Section 5 averaging the time series of the Modes, without including the zeroth mode, and reconstructing a mean solution from that, the flow features can be nicely merged in one image.
Fig. 27 shows the averaged modal solution for several APRs and Mach numbers. The schlieren window, the wind tunnel nozzle exit and the wind tunnel model were masked in black in these images again. The square root of the MFR is also reported. The similarity with the MFR can be clearly seen as the flow fields on the diagonals of the image matrix (bottom left to top right) have similar MFRs. It is clearly observable that these flow fields have a similar appearance.
In Jarvinen and Hill (1973), it was shown that the plume length in retro propulsion jets can be estimated with:
where\({\rho }_{e}\), \({T}_{e}\) and \({u}_{e}\) are the density, the temperature and the velocity at the nozzle exit, \({T}_{cc}\) is the total temperature in the combustion chamber, and \({\rho }_{\infty }\) and \({u}_{\infty }\) are the density and velocity in the free stream. In Marwege et al. (2022c), this dependence could be confirmed with the same experimental data as presented in this paper. However, the plume length was measured in schlieren snapshots, where the plume length can vary strongly. In this paper, the visualizations with the averaged modal solution were used to measure the plume length as indicated in the images in Fig. 27 with the white arrows. The stagnation point is assumed to be at the point where the smaller structures in the plume are still visible. With those measurements, the plot of the plume length in dependence of Eq. (15) as presented in Marwege et al. (2022c) was revised and is shown in Fig. 28. The factor found for the linear dependence only varies slightly; here 2.48 was found while in Marwege et al. (2022c) a factor of 2.57 was reported. In supersonic retro propulsion flow fields, the coefficient of variation image was used for the determination of the distances of the flow field features in Bathel et al. (2020), and in Marwege et al. (2022d), the flow field features could be tracked in the schlieren video directly. These procedures could not be applied for the subsonic flow field features, as the standard deviation does reveal the jet structure well (see Fig. 17), and as the flow field features strongly vary over time which makes it hard to track them automatically. Hence, the jet structures were measured in the averaged modal solution images here. As the measurements are conducted in the images, they possess a certain level of subjectivity. Nevertheless, they provide valuable insights into the relationships between plume length and MFR.
Plume length versus the square root of the MFR. The numbers on the data points indicate the Mach number (revised graphic from (Marwege et al. 2022c))
In Fig. 29, the power spectral density (PSD) of the first 12 Modes of the retro propulsion flow field at \({M}_{\infty }=0.8\), \(APR=0.387\) and \(\text{MFR}=6.52\) is shown. For the computation of the PSD, the method proposed by Welch (1967) was applied. A short time Fourier transform was computed over 8000 time steps. It was performed with a Hann window with a length of 500, shifting the window by 16 time steps between single spectra. The spectra were then averaged over the time steps. The frequency was resolved with 2048 bins, which results in a frequency resolution of 12.21 Hz. In the top row of Fig. 29 the PSD is plotted over the frequency, in the bottom row it is plotted over the Strouhal number, were the Strouhal number \({\text{Sr}}_{D}\) is defined as:
With the frequency \(f\), the reference length \({D}_{\text{ref}}\) and the free stream velocity \({u}_{\infty }\). The reference length was chosen to be the base diameter, which is 70 mm, as this makes the Strouhal numbers comparable to studies on near-wake flows of (ascending) space transportation systems where this definition was used, as, e.g., in Saile (2019).
One can observe that the PSD is dominated by a broadband peak at low frequencies around a Strouhal number of 0.05. In turbulent jets such broadband peaks can be associated to the large-scale turbulent structures in form of wave packets (Jordan and Colonius 2013) and the broadband shock-associated noise (Prasad and Morris 2020; Tam 1995, 2009). Hence, as mentioned above, the noise generating mechanisms in the jet could be connected to the unsteady subsonic retro propulsion flow field, as they create the pressure fluctuations that trigger the large-scale fluctuations of the flow field.
Frequency peaks can be seen especially for the first 4 modes at low frequencies of 637 Hz, 1261 Hz and 1812 Hz. For the higher modes, the lowest frequency shifts somewhat to a higher frequency of 733 Hz and also the frequency of about 1800 Hz can be observed again. Furthermore, also for the higher modes (mode 9 and mode 12) the frequency of about 1300 Hz can be observed which was also present in the lower modes (mode 1 and mode 2). For the higher modes a further frequency peak at around 5300 Hz can be observed. Referring to the Strouhal numbers corresponding to the frequencies, the PSD peaks can be observed at 0.180, 0.357 and 0.512 in the lowest modes and at 0.207, 0.376, 0.533, 1.506 and 1.513 in the higher modes. Interestingly, the lower Strouhal numbers are close to frequencies expected for near-wake flows. The so-called cross-pumping in near-wake flows commonly occurs at \({\text{Sr}}_{D}\approx 0.1\), the vortex shedding and cross-flapping motion at \({\text{Sr}}_{D}\approx 0.2\), and the shear layer swinging at \({\text{Sr}}_{D}\approx 0.35\) (Saile and Gülhan 2021; Statnikov et al. 2017). Hence, the \({\text{Sr}}_{D}\) at 0.180 and 0.2 observed in the retro propulsion flow field are close to the vortex shedding and cross-flapping frequency (\({\text{Sr}}_{D}=0.2\)), and the \({\text{Sr}}_{D}\) of 0.357 is close to the shear layer swinging (\({\text{Sr}}_{D}=0.35\)). This should be considered in the design of a vertical landing vehicle, especially as Saile and Gülhan (2021) theorized that these mechanisms, if in resonance with the acoustics of the jet (screeching), can generate high unsteady loads on the engine. This was found to be one likely reason for the failure of the maiden flight of the Ariane 5 Evolution Cryotechnique type A (ECA) (Saile 2019; Saile and Gülhan 2021). Hence, even though the underlying phenomena leading to these frequencies in the retro propulsion flow field differ from the mechanisms in the near-wake flows, the frequencies can be critical. It should be noted that the frequencies presented in this paper are based on cold gas jet experiments. Kirchheck et al. (2021) found that the coupling mechanism in near-wake flows and the resulting prominent frequencies differs for cold gas and hot gas experiments. Hence, a detailed frequency analysis of hot plume retro propulsion experiments should be performed in the future to confirm these findings.
In Fig. 30a the PSD over the frequency is plotted for the first 2000 modes. One can observe that the most dominant frequencies can be found in the lower modes, whereas the higher modes do not show dominant frequencies. Figure 30b shows the same contour plot but only for the first 200 modes. There is a trend of the dominant frequencies to increase with higher modes. Furthermore, the frequencies associated to Strouhal numbers of 0.512 and to 0.207 are persisting in the frequency content up to higher modes.
To see if the frequencies found in the modes of the retro propulsion flow field can be directly related to frequencies in the jet, a PSD of the first 12 modes present in the jet, without counterflow, was performed. The result is shown in Fig. 31. It can be seen that there is only one dominant frequency at 7092 Hz. This frequency was not found in the PSD analysis of the retro propulsion jet (Fig. 29). Hence, the frequencies in the retro propulsion flow field do not seem to come from frequencies in the jet alone. Figure 32 shows the PSD of the first 12 modes of a run at Mach 0.8 without active jet, where several peaks can be observed. Also the Strouhal numbers of 0.194, 0.387 and 0.581 are close to the observed 0.207, 0.357 and 0.533 with active retro propulsion. Hence, these frequencies can be associated to an interaction of the vehicle with the free stream. To verify this a POD was performed for a selected area around the base of the vehicle. The first four spatial modes are shown in Fig. 35 and the PSD of the first 12 modes of this selected area is shown in Fig. 33. The spatial modes reveal that the frequencies observed in the base area can be attributed to unsteady regions near the engines (white circles) which are presumably generated by vortices in these regions. Furthermore, strong unsteady modes can be observed upstream of the engines (black circle) resulting from pressure waves upstream of the base area, which can be seen in the snapshot of the schlieren video in Fig. 34. Comparing the PSD of the flow field without active engine (no jet) in Fig. 32, with the PSD of the flow field with active jet in Fig. 29, it is apparent that the frequency peaks are much more pronounced in the case without active jet. Hence, if buffeting loads on the engines shall be reduced, it can be advisable to fly through the transonic regime with the engine active. In Fig. 36, the PSD is shown for several Mach number and APR combinations. The dominant frequencies of \({\text{Sr}}_{D}\) of 0.2, 0.35, 0.5 and 1.5 are highlighted with lines. The bottom row shows the PSD for the condition without counterflow. One can see that frequency peaks are observable close to a Strouhal number of 0.2, 1.5 and 3 (harmonic of 1.5) for Mach 0.8. For Mach 0.6 and 0.7, only the Strouhal numbers close to 0.35 and 1.5 can be seen. The strongest frequency peaks for several Strouhal numbers can be observed for Mach 0.8. Interestingly, this is the Mach number at which also the strongest unsteady loads for near-wake flow configurations were observed (Saile and Gülhan 2021). For Mach 0.8 with active jet, these frequencies are still visible, however, as mentioned earlier, to a much smaller extent. It seems that the magnitude of the thrust level plays a subordinate role as the frequency content is comparable for all shown APRs. For the higher Mach number of 0.9, the characteristic Strouhal numbers of 0.2, 0.35 and 1.5 cannot be observed and the Strouhal number of 0.5 is not as strongly pronounced as for the lower Mach numbers. However, for this Mach number, in the active jet cases frequencies at Strouhal numbers around 0.15 and 0.25 are visible. In general, in the cases with active jet, the frequency content has a very similar appearance regardless of the Mach number or APR. Hence as for the pressure coefficients (see Sect. 6.1), the activation of the jet seems to have a larger influence than the specific jet conditions. For all Mach numbers, the presence of the jet seems to dampen the dominant frequencies which appear in the jet-off case (Figs. 35 and 36).
Fig. 37 shows the PSD of the high-frequency pressure measurements on the base of the wind tunnel model, where the mean value was subtracted before the PSD was performed. The PSD was performed with the method by Welch (1967) over 20000 time steps with a Hann window of a width of 500 with a step size of 39 time steps between the spectra. The frequencies were again resolved with 2048 bins, which results in a frequency resolution of 24.41 Hz. The results are shown for the outer two circles of the pressure sensors.
For the cases with no jet, mainly two normalized frequencies of 0.2 and 1.5 can be observed. However, the Strouhal number of 0.2 can only be observed for Mach 0.8. For all cases with active jet, the dominant normalized frequency of 0.2 is found. The reason could be that this frequency comes from the interaction of the jet with the free stream and is therefore absent in the cases with no active jet. For Mach 0.8 the frequency is a combination of the interaction of the free stream with the jet and the strong dominant frequency present in the jet-off case. For Mach 0.9 the additional dominant frequency of 0.1 already found in the schlieren videos can be observed. Neither the normalized frequency of 1.5, nor the other dominant frequencies which were found in the schlieren videos (0.35 and 0.5) are observed in the jet-on cases. It seems that the observed frequencies are independent of the thrust level (APR), as for all Mach number and APR combinations the frequency content is very similar. This confirms the statement made above that activating the jet (igniting the engine), regardless of the thrust level, mitigates most frequencies. The peak at 0.2 persists, but it is less prominent.
Figure 38 shows the root mean square values of the pressure fluctuation normalized with the dynamic pressure (\({p}_{\text{rms}}^{\prime}/{q}_{\infty }\)). As for the pressure coefficients (see Sect. 6.1), the pressure fluctuations are clustered by the radial position of the sensors. The pressure fluctuations on the base area (ring 2) are higher than the ones around the shoulder (ring 3). For the case without active jet, the fluctuations generally decrease with increasing Mach number. For Mach 0.8 a slight peak in this decreasing trend can be observed, due to the strong dominant frequencies for this Mach number. For the cases with active jet, the fluctuations are relatively independent of the Mach number and keep at a level of 0.2 around the shoulder and 0.3 on the base area. Hence, while the activation of the jet mitigates the dominant frequencies, it does not lower the level of pressure fluctuations, but slightly increases it. The level of pressure fluctuations is one order of magnitude higher than in near-wake flows, which were measured to be between 0.06 for Mach 0.5 and 0.01 for Mach 0.9 (Saile 2019). This observation emphasizes the importance of the investigation of unsteady pressure loads during the landing burn.
The results discussed in this section can be summarized as follows. In the subsonic and transonic landing phase, dominant frequencies can be observed. The Strouhal numbers are around 0.1, 0.2, 0.35, 0.5 and 1.5. In the pressure measurements only 0.1, 0.2 and 1.5 were measured. In particular 0.2 is a critical Strouhal number as it was found to be a critical frequency in near-wake flow mechanisms which were found to be one likely reason for the failure of the Ariane 5 ECA maiden flight. However, to judge if this frequency could lead to a coupling with the structures of the launcher which could lead to critical loads on the structures or actuators, the flow phenomena need to be understood in more detail. Active retro propulsion mitigates most of the strongly prominent frequencies. However, the normalized frequency of 0.2 persists. The pressure fluctuations are one order of magnitude higher than in the near-wake flows, independently of the activation of the jet.
7 Conclusions
Subsonic retro propulsion flow fields have been analyzed in detail in this paper. To characterize the unsteady flow fields, proper orthogonal decomposition (POD) was performed of high-speed schlieren videos and power spectral density (PSD) analyses were performed of the time series of the POD modes and of high-frequency pressure measurements.
The analysis of the subsonic retro propulsion flow fields showed that the ambient pressure ratio (APR) is a good scaling parameter for the flow structure close to the engine, while the momentum flux ratio (MFR) is a good scaling parameter for the larger scale flow features. This could be visualized with the aid of an average modal solution.
The subsonic retro propulsion flow field showed strongly unsteady behavior. It was reasoned that the unsteady effects are likely to be linked to the flow dynamics in turbulent supersonic jets, as the large-scale fluctuations in the retro propulsion flow field could be triggered by large coherent turbulent structures in the shear layer of the jet.
Strouhal numbers of 0.2 and 1.5 could be observed in the transonic and subsonic phase of the landing approach, if the jet is not active. They are close to frequencies occurring in near-wake flows which were found in literature to have caused high unsteady loads on the Ariane 5 ECA during its maiden flight. The strongest frequency peaks were observed at Mach 0.8 which is the Mach number where also the strongest frequency peaks were observed for the near-wake flows in earlier studies. The dominant frequencies are mostly mitigated if the jet is activated. The normalized frequency of 0.2 persists, but is less prominent. Therefore, it could be advisable to start the landing burn at Mach numbers larger than 0.8 to mitigate buffeting loads on the engines in the last phase of the descent and landing.
The normalized pressure fluctuations are between 0.1 and 0.3. They are slightly larger if the jet is active and are relatively independent of the thrust level of the jet.
It became evident in this work that critical frequencies can occur during retro propulsive landing phases. This is especially the case for the landing approach with subsonic retro propulsion, in comparison with near-wake flows. For a better understanding of the underlying flow phenomena, the generalization of the results and the development of more detailed underlying feedback models is crucial in the future in order to predict the behavior in flight and mitigate unsteady loads during descent and landing. Furthermore, a detailed analysis and understanding of the coupling effects of retro propulsion flow fields with the acoustic phenomena present in supersonic jets is essential.
Data availability
Not applicable.
References
Arianespace Flight 157 - Inquiry Board (2003) Arianespace Flight 157 - Inquiry Board submits findings. https://www.esa.int/Enabling_Support/Space_Transportation/Arianespace_Flight_157_-_Inquiry_Board_submits_findings2. Accessed 2023
Bathel BF, Litzner CR, Jones SB, Berry SA, Smith NT, Garbeff TJ II (2020) High-speed schlieren analysis of retropropulsion jet in mach 10 flow. J Spacecr Rocket 57:33–48. https://doi.org/10.2514/1.A34522
Berry MG, Magstadt AS, Glauser MN (2017) Application of POD on time-resolved schlieren in supersonic multi-stream rectangular jets. Phys Fluids. https://doi.org/10.1063/1.4974518
Böge A, Böge W (2014) Handbuch Maschinenbau. Springer Fachmedien Wiesbaden, Wiesbaden, Germany
Botelho A, Martinez M, Recupero C, Fabrizi A, De Zaiacomo G (2022) Design of the landing guidance for the retro-propulsive vertical landing of a reusable rocket stage. CEAS Space J 14:551–564. https://doi.org/10.1007/s12567-022-00423-6
Brunton SL, Kutz JN (2019) Data-driven science and engineering: machine learning, dynamical systems, and control. Cambridge University Press, Cambridge
Bykerk T, Karl S (2023) Preparatory CFD studies for subsonic analyses of a reusable first stage launcher during landing within the RETPRO project. In: 10th EUCASS–9th CEAS conference 2023, Lausanne, Switzerland, https://elib.dlr.de/194477/
Dahmen W, Reusken A (2006) Numerik für Ingenieure und Naturwissenschaftler. Springer-Verlag
Daub D, Willems S, Gülhan A (2022) Experiments on aerothermoelastic fluid–structure interaction in hypersonic flow. J Sound Vib 531:116714. https://doi.org/10.1016/j.jsv.2021.116714
David C, Radulovic S (2005) Prediction of buffet loads on the ariane 5 Afterbody. In: 6th Symposium on launcher technologies, Noordwijk, The Netherlands,
De Zaiacomo G, Blanco Arnao G, Bunt R, Bonetti D (2022) Mission engineering for the RETALT VTVL launcher. CEAS Space J 14:533–549. https://doi.org/10.1007/s12567-021-00415-y
Ecker T, Ertl M, Klevanski J, Krummen S, Dumont E (2022) Aerothermal characterization of the CALLISTO vehicle during descent. In: 9 th European conference for aeronautics and aerospace sciences (EUCASS), Lille, Frankreich, https://elib.dlr.de/187034/
Ertl M, Ecker T, Klevanski J, Dumont E, Krummen S (2022) Aerothermal analysis of plume interaction with deployed landing legs of the CALLISTO vehicle. In: 9th European conference for aeronautics and aerospace sciences (EUCASS), Lille, France, https://elib.dlr.de/187068/
Frey M (2001) Behandlung von Strömungsproblemen in Raketendüsen bei Überexpansion. Universität Stuttgart, Institut für Aerodynamik und Gasdynamik, p 136
Gutsche K, Marwege A, Gülhan A (2021) Similarity and key parameters of retropropulsion assisted deceleration in hypersonic wind tunnels. J Spacecr Rocket 58:984–996. https://doi.org/10.2514/1.A34910
Jarvinen PO, Adams RH (1970) The aerodynamic characteristics of large angled cones with retrorockets. CR-124720, NASA
Jarvinen PO, Hill JAF (1973) Penetration of retrorocket exhausts into subsonic counterflows. J Spacecr Rocket 10:85–86. https://doi.org/10.2514/3.27737
Jordan P, Colonius T (2013) Wave Packets and Turbulent Jet Noise. Annu Rev Fluid Mech 45:173–195. https://doi.org/10.1146/annurev-fluid-011212-140756
Kirchheck D, Saile D, Gülhan A (2021) Rocket wake flow interaction testing in the hot plume testing facility (HPTF) cologne. In: Adams NA, Schröder W, Radespiel R et al (eds) Future space-transport-system components under high thermal and mechanical loads: results from the DFG collaborative research center TRR40. Springer International Publishing, Cham, pp 145–162
Korzun AM, Nielsen E, Walden A et al (2020) Computational investigation of retropropulsion operating environments with a massively parallel detached eddy simulation approach. ASCEND. https://doi.org/10.2514/6.2020-4228
Korzun AM, Nastac G, Walden A, Nielsen EJ, Jones WT, Moran P (2022) application of a detached eddy simulation approach with finite-rate chemistry to mars-relevant retropropulsion operating environments. AIAA Scitech 2022 Forum, https://doi.org/10.2514/6.2022-2298
Lumley JL (1987) The structure of inhomogeneous turbulent flows. In: Proceedings of the international colloquium on the fine scale structure of the atmosphere and its influence on radio wave propagation, Nauka, Moscow
Marwege A, Gülhan A (2023) Unsteady aerodynamics of the retropropulsion reentry burn of vertically landing launchers. J Spacecr Rockets 0:1–15. https://doi.org/10.2514/1.A35647
Marwege A, Gülhan A, Klevanski J, et al. (2019) Retro propulsion assisted landing technologies (RETALT): current status and outlook of the eu funded project on reusable launch vehicles. Washington D.C., USA, 10.5281/zenodo.5770046
Marwege A, Gülhan A, Klevanski J et al (2022a) RETALT: review of technologies and overview of design changes. CEAS Space J 14:433–445. https://doi.org/10.1007/s12567-022-00458-9
Marwege A, Hantz C, Kirchheck D et al (2022b) Wind tunnel experiments of interstage segments used for aerodynamic control of retro-propulsion assisted landing vehicles. CEAS Space J 14:447–471. https://doi.org/10.1007/s12567-022-00425-4
Marwege A, Kirchheck D, Klevanski J, Gülhan A (2022d) Hypersonic retro propulsion for reusable launch vehicles tested in the H2K wind tunnel. CEAS Space J 14:473–499. https://doi.org/10.1007/s12567-022-00457-w
Marwege A, Hantz C, Kirchheck D, et al. (2022c) Aerodynamic phenomena of retro propulsion descent and landing configurations. IN: 2nd international conference on flight vehicles, aerothermodynamics and re-entry missions and engineering, Heibronn, Germany, 10.5281/zenodo.6783922
Marwege A, Klevanski J, Hantz C, et al. (2022e) Key technologies for retro propulsive vertical descent and landing–RETALT–an overview. IN: 2nd International conference on flight vehicles, aerothermodynamics and re-entry missions and engineering, Heibronn, Germany, 10.5281/zenodo.6783915
Mejia NA, Schmidt BE (2022) Experimental investigation of flow interaction dynamics in supersonic retropropulsion. J Spacecr Rocket 59:1753–1762. https://doi.org/10.2514/1.A35228
Prasad C, Gaitonde DV (2022) A robust physics-based method to filter coherent wavepackets from high-speed schlieren images. J Fluid Mech 940:R1. https://doi.org/10.1017/jfm.2022.230
Prasad C, Morris PJ (2020) A study of noise reduction mechanisms of jets with fluid inserts. J Sound Vib 476:115331. https://doi.org/10.1016/j.jsv.2020.115331
Saile D, Gülhan A (2021) Aeroacoustic coupling effect during the ascent of space transportation systems. AIAA J 59:2346–2356. https://doi.org/10.2514/1.J059747
Saile D (2019) Experimental analysis on near-wake flows of space transportation systems. rheinisch-westfälische technische hochschule aachen (RWTH), Aachen
Schmidt OT, Towne A, Rigas G, Colonius T, Brès GA (2018) Spectral analysis of jet turbulence. J Fluid Mech 855:953–982. https://doi.org/10.1017/jfm.2018.675
Sirovich L (1987) Turbulence and the dynamics of coherent structures. I. Coherent Struct Q Appl Math 45:561–571
Statnikov V, Meinke M, Schröder W (2017) Reduced-order analysis of buffet flow of space launchers. J Fluid Mech 815:1–25. https://doi.org/10.1017/jfm.2017.46
Taira K, Brunton SL, Dawson STM et al (2017) Modal analysis of fluid flows: an overview. AIAA J 55:4013–4041. https://doi.org/10.2514/1.J056060
Tam CKW (1995) Supersonic jet noise. Annu Rev Fluid Mech 27:17–43. https://doi.org/10.1146/annurev.fl.27.010195.000313
Tam CKW (2009) Mach wave radiation from high-speed jets. AIAA J 47:2440–2448. https://doi.org/10.2514/1.42644
Tam CKW, Viswanathan K, Ahuja KK, Panda J (2008) The sources of jet noise: experimental evidence. J Fluid Mech 615:253–292. https://doi.org/10.1017/S0022112008003704
Venkatachari BS, Mullane M, Cheng G, Chang C-L (2015) Numerical study of counterflowing jet effects on supersonic slender-body configurations. In: 33rd AIAA applied aerodynamics conference, https://doi.org/10.2514/6.2015-3010
Weiss J (2019) A Tutorial on the Proper Orthogonal Decomposition. AIAA Aviation 2019 Forum, Dallas, Texas, United States, https://doi.org/10.2514/6.2019-3333
Welch P (1967) The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroacoust 15:70–73. https://doi.org/10.1109/TAU.1967.1161901
Acknowledgements
The authors want to greatly thank Daniel Kirchheck for many discussions on the results presented in this paper, for a lot of input during the test campaigns and for the common development of the design of the wind tunnel model. Furthermore, the authors want to thank the VMK team for their support and expertise. Without them, acquiring the results presented in this paper wouldn’t have been possible. Equally we want to express our special thanks to Markus Miketta, the designer of the wind tunnel model, for his effort and passion put into their detailed elaboration. The RETALT project has received funding from the European Union’s Horizon 2020 research and innovation framework program under grant agreement No 821890.
Funding
Open Access funding enabled and organized by Projekt DEAL. The RETALT project has received funding from the European Union’s Horizon 2020 research and innovation framework program under grant agreement No 821890.
Author information
Authors and Affiliations
Contributions
Ansgar Marwege wrote the manuscript text and prepared the figures. He also generated the data and the results presented. Ali Gülhan reviewed the results and the manuscrip and contributed with discussions and ideas to the content of the paper.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Ethical approval
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Example case for the averaged modal solution
To visualize the concept of the averaged modal solution further, an example case was constructed and analyzed with the averaged modal solution. The modes were constructed with the values as shown in Fig. 39. The first and the second mode were then multiplied with uniform white noise between − 1 and 1, while the steady mode was simply kept steady. The modes were then added up. The constructed modes are marked with an asterisk in the following to differentiate them from the POD modes.
The POD was then performed on 8000 images. Figures 41 and 40 show the resulting modes. The images were scaled to the maximum value in the mode being white and the smallest being black. In Fig. 40 the resulting POD modes are shown, where the mean field was subtracted from each frame. In Fig. 41 the POD modes are shown for the case were the mean field was not subtracted. If the mean field is subtracted, the modes 0, 1 and 2 represent the modes 1* and 2* well. However, the modes 1* and 2* are not separated completely but combined in the resulting POD modes. The center part of the steady field is partly contained in mode 2 and 3. If the mean flow field is not subtracted (see Fig. 41), the zeroth mode is showing the mean flow field. The first mode is rebuilding mode 1* and is completely separated from mode 2*. Mode 2 is a combination of the steady field and the mode 2*. Hence, the steady field is not only contained in mode 0 but also in mode 2.
In Fig. 42 the cumulative energy of both cases is shown. As expected, already the modes 0, 1 and 2 capture nearly all of the energy in the field. If the mean field is not subtracted the zeroth mode captures high amounts of the energy as it resembles most of the steady field.
In Fig. 43 the averaged modal solution of the example case is shown. In Fig. 43a the modes 0 to 3 were used, where the mean field was not subtracted. As the low order model rebuilds nearly 100% of the energy of the system, the mean field of the reconstruction (the averaged modal solution) equals the mean flow field of the original data. Hence, Fig. 43a shows the mean field. In Fig. 43b only the modes 1 to 3 are included. As the mode 0, which captures the main part of the steady field, is omitted, the averaged modal solution (which is the mean field of the modes 1 to 3) shows partly the steady field, as it is contained in mode 2. As the random noise used to generate the time history of the modes is not completely symmetric around 0, also mode 1 is visible, overlaid on the steady field. Figure 43c shows the averaged modal solution of the field if the mean field is subtracted. Modes 0 and 1 seem to cancel out such that only mode 2 is visible. The middle square part of the steady field can be seen in the center of the averaged modal solution.
Hence, it can be concluded that the averaged modal solution can overlay all flow features in one image, making them visible all in one image. While some features, also unsteady ones, are missing if the mean field is subtracted, they are all visible if the mean field is not subtracted. Therefore, it was decided to use this approach in the paper at hand to analyze the unsteady flow fields and the mean field was not subtracted before the POD was performed.
1.2 Tables of surface pressures and normalized surface pressure fluctuations
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marwege, A., Gülhan, A. Aerodynamic characteristics of the retro propulsion landing burn of vertically landing launchers. Exp Fluids 65, 115 (2024). https://doi.org/10.1007/s00348-024-03851-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-024-03851-8