An assessment of effective slope as a parameter for turbulent drag prediction over multi-scaled roughness

Abstract

The streamwise effective slope (${\rm ES}_x$), which is the mean absolute streamwise gradient of the roughness, is considered to be a key parameter in predicting the drag penalty of rough-wall turbulent boundary-layers. However, many real-world rough surfaces are multi-scaled. For such surfaces, ${\rm ES}_x$ can be unbounded and its value can be dominated by scales of the topography that are invisible to the flow. To illustrate this, a campaign of drag balance measurements was conducted with a set of machined surfaces. A baseline surface is prepared with fine machining parameters. By coarsening the machining precision, artefacts called ‘scallops’ are introduced which increases the ‘measured’ ${\rm ES}_x$ without changing other geometrical statistics. The drag of the ‘scalloped’ surfaces is higher than the baseline surface, with the relative drag increase scaling with the viscous scaled scallop height, but only when their height exceeds $2\sim 3$ times the viscous length scale. Further, the drag of one of the ‘scalloped’ cases, even when the scallop height is $\mathcal {O}(10)$ viscous units, is seen to be much lower ($\sim 28$%) than a case with matched ${\rm ES}_x$, but where the ${\rm ES}_x$ results from larger scale features. These findings confirm that for multi-scaled surfaces, ${\rm ES}_x$ may be a misleading topographical metric for drag (or $k_s$) prediction and one must consider which scales contribute to the average slope of a surface.

1 Introduction

The hydrodynamic drag on walls adjacent to turbulent boundary layers (TBL) is further increased in the presence of surface roughness. In many engineering applications with wall-bounded turbulent flows, such as ships, aeroplanes and gas-turbines, the presence of surface roughness is often unavoidable (Schultz 2007; Shin 1996; Bons 2010). For the Reynolds number associated with these applications, the roughness only needs to be of $\mathcal {O}(1)$ $\upmu$m to $\mathcal {O}(10)$ $\upmu$m to affect the flow (Chung et al. 2021). Considering operational wear such as the deterioration of surface finish, or the deposition of foreign materials, very few practical wall-bounded flows can be considered to be aero- or hydro-dynamically smooth. The drag penalty of roughness ultimately results in an increase in energy consumption and operating costs of these applications with deleterious impacts on the environment and the economy. However, present methods for full-scale drag prediction are fraught with large uncertainties which are estimated to cost billions each year (Chung et al. 2021). Therefore, studies that lead to improvements in the accuracy of drag prediction due to roughness continue to remain highly desirable.

Fig. 1

Example of a realistic multi-scale rough surface—the roughness height-map, h(x, y), is a function that maps the surface elevation in terms of the in-plane coordinates, x and y. $L_x$ and $L_y$ are the sampling lengths, and $A_s$ is the sampled area

1.1 Full-scale drag penalty prediction

In order to make a full scale predictions of the drag penalty due to a rough surface it is necessary to ascertain the equivalent sand grain roughness, $k_s$, of that surface. Unfortunately, $k_s$ can not be measured directly from the roughness topography. Rather, it is a quantity obtained from the measured drag of the surface, and the only way that it can be obtained is by exposing the surface to a wall-bounded turbulent flow across a range of Reynolds numbers. Since this process is very expensive for the routine determination of drag penalty, there is a tendency to rely on empirical correlations that relate certain topographical properties of the surface roughness to $k_s$.

An example of a realistic, multi-scale rough surface is shown in Fig. 1. From the height-map of this roughness (i.e. h(x, y), where x and y are the in-plane coordinates), several topographical properties can be obtained. These include, but are not limited to, the root mean square height $S_q$, skewness $S_{sk}$, mean absolute roughness amplitude $S_a$, peak-to-valley height $S_z$, and the streamwise Effective Slope ${\rm ES}_x$. These quantities are defined in Eqs. 1–5.

$$\begin{aligned} S_q \equiv \sqrt{\frac{1}{A_s} \int _{A_s} \left( h-\overline{h}\right) ^2 {\rm d}A_s} \end{aligned}$$

(1)

$$\begin{aligned} S_{sk} \equiv \frac{1}{S_q^3} \frac{1}{A_s} \int _{A_s} \left( h- \overline{h} \right) ^3 {\rm d}A_s \end{aligned}$$

(2)

$$\begin{aligned} S_{a} \equiv \frac{1}{A_s} \int _{A_s} \arrowvert h- \overline{h} \arrowvert {\rm d}A_s \end{aligned}$$

(3)

$$\begin{aligned} S_z \equiv \max {(h)} - \min {(h)} \end{aligned}$$

(4)

$$\begin{aligned} {\rm ES}_x \equiv \frac{1}{A_s}\int \limits _{A_s}\left| \frac{\partial h}{\partial x} \right| {\rm d}A_s \end{aligned}$$

(5)

Here, $\overline{h}$ is the mean elevation of the heights and $A_s = L_x L_y$ is the total sampled area ($50 \times 50$ mm$^2$ in Fig. 1). Thus, the main challenge for the reliable and accurate prediction of full-scale drag is to develop robust empirical correlations for $k_s$ from such topographical properties of the roughness.

Fig. 2

a A roughness profile is synthetically generated following a power law distribution $\Phi _{hh} \sim k_x^\beta$, where $\beta \approx -1.9$. b The profile is presented for various measurement resolutions—(i) $\Delta x \approx 0.01 \upmu$m; (ii) $\Delta x \approx 10 \upmu$m; (iii) $\Delta x \approx 50 \upmu$m; (iv) $\Delta x \approx 100 \upmu$m. c The percentage change in the calculated roughness properties from that obtained at the smallest measurement resolution plotted against the measurement resolution. The inset in (c) shows the percentage change for $10^2 \le \Delta x \le 10^4$ $\upmu$m for clarity. The grey strip in (c) indicates the approximate range of the viscous-length scale, $\nu /U_\tau$, for experiments in air

1.2 Limitations of ${\rm ES}_x$ for drag penalty prediction

It is towards this goal that the streamwise effective slope, ${\rm ES}_x$, has emerged as a popular metric for quantifying roughness effects in turbulent flows (Eq. 5). Although not a new measure of surface roughness (it is related to frontal solidity ${\rm ES}_x = 2\Lambda _F$ (Thakkar et al. 2016), which was proposed by Schlichting 1936), many studies have shown that ${\rm ES}_x$ is an important metric for drag prediction in both the transitionally rough and fully rough regimes for regular as well as irregular roughness (Musker 1980; Van Rij et al. 2002; Napoli et al. 2008; Chan et al. 2015; MacDonald et al. 2016; Forooghi et al. 2017; De Marchis et al. 2020; Abdelaziz et al. 2023). However, when it comes to practical, multi-scale surfaces, the boundedness of ${\rm ES}_x$ can be problematic. To demonstrate this, a synthetic roughness profile is generated, h(x) (limited to one dimension for simplicity). The profile follows a power law formulation—i.e. the energy spectrum of the surface ($\Phi _{hh}$) is related to the wave-number ($k_x$) by a power law relation, $\Phi _{hh} \sim k_x^\beta$, with exponent $\beta \approx -1.9$ as shown in Fig. 2a. This relationship, with $-3 \le \beta \le -1.2$, is typical of naturally occurring rough surfaces (Anderson and Meneveau 2011). Measurement of physical surfaces requires some level of discretisation. This is usually determined by the measurement tools available. The measurement resolution can range from $\sim 0.2\upmu$m for confocal microscopes (Cox and Sheppard 2004) to $\sim$10$\upmu$m for laser triangulation sensors (Li et al. 2021). The area of the measured surface is another factor that limits the accuracy of measurements, particularly for heterogeneous roughness. For the example roughness profile based on the power-law formulation, the resolution is set to $\Delta x \approx 0.01 \upmu$m, which is much finer than most commercially available measurement tools. This profile is shown in Fig. 2b(i) by the () line. The same profile is also shown for coarser measurement resolutions in Fig. 2b(ii–iv). These profiles demonstrate an important attribute of many practical multi-scale rough surfaces: as the measurement resolution is refined, an increasing range of small-scale features are captured revealing the ‘fractal’ like nature of the roughness. Hence, the choice of the measurement resolution used to characterise any rough surface needs to be made thoughtfully.

In Fig. 2c, the variation of the roughness properties of the synthetically generated profile as a function of the measurement resolution, $\Delta x$, is shown. The variation is shown as the percentage change in the quantity against its measurement at the finest measurement resolution ($\Delta x \approx 0.01$ $\upmu$m). Bounded values are obtained for $S_q$ and $S_a$ even at coarse resolutions ($\Delta x \approx 10^3$ $\upmu$m). Although some small ($< 2\%$) variation is seen in $S_{sk}$ at large resolutions, a bounded value is obtained when $\Delta x \lesssim 10^{2}$ $\upmu$m. This suggests that these properties are chiefly determined by the large scale features and are relatively insensitive to the small scales. On the other hand, the value of ${\rm ES}_x$ () exhibits a continual variation as the measurement resolution is refined. This is because the energy spectra of the gradient of the heights scales with an exponent of $\beta + 2$ (Anderson and Meneveau 2011). Therefore, for such power-law surfaces, when $\beta \ge -3$, the gradients are dominated by the smallest scales and the integral contribution of these derivative values towards ${\rm ES}_x$ becomes increasingly dominant as $\Delta x \rightarrow 0$. Therefore, ${\rm ES}_x$ can remain unbounded until all the modes are resolved. This suggests that some cut-off in the measurement resolution is required if we wish to relate the resultant value of ${\rm ES}_x$ to the drag penalty of the surface. It is not obviously apparent what this cut-off for practical surface roughness should be. If a measurement resolution is arbitrarily selected, say based on the convergence of $S_{sk}$, the resulting value of ${\rm ES}_x$ could lead to the incorrect prediction of drag.

Fig. 3

Samples of the machined surfaces with increasing step-over distance (s) of the tool: a $s=0.25$ mm, b $s=0.50$ mm, c $s=0.75$ mm, d $s=0.95$ mm and e $s=1.10$ mm. f Surface elevation profile from each case at a matched location, indicated by the yellow line in (e). The tool diameter and the step-over distance for the S4 case are also illustrated in (f) (ordinate scaled 4:1 to show the scallops clearly). The nominal scallop height is given as $k_{\text {scallop}}$. Flow direction for all cases is indicated by the red arrow

The effect of filtering (or retaining) particular scales of roughness on the flow has been previously studied. Barros et al. (2018) studied the effect of high-pass filtering a set of numerically generated power-law surfaces and reported that properties like $S_q$ are more sensitive to the long wavelength roughness scales (i.e. lower modes) than ${\rm ES}_x$. By removing the contributions to the topography at these wavelengths, the $S_q$ of the filtered surface was seen to match the trend of the measured drag. This suggests that not all roughness scales have a significant contribution to the drag. Consequently, Barros et al. (2018) suggested that ${\rm ES}_x$ can be a robust quantity for drag prediction models due to its relative insensitivity to the lower modes. However, Busse et al. (2015) showed that as the cut-off wavelength for a low-pass spectral filter on the scan of a graphite rough surface is reduced, the mean flow statistics converge. Similar observations were reported by Mejia-Alvarez and Christensen (2010) when applying single-value decomposition to a turbine roughness scan. Thus, as the scales of the topography get finer, their effect on the flow also becomes limited. From these studies, it follows that only the parts of the roughness topography that will be perceived by the flow should be included in its characterisation. The question is then, which parts of the topography? For rough-wall bounded turbulent flows, the length scale of importance is the viscous length scale, $\nu /U_\tau$. Here $\nu$ is the kinematic viscosity and $U_\tau \equiv \sqrt{\tau _w/\rho }$ is the friction velocity, where $\tau _w$ is the wall-shear stress and $\rho$ is the density. When surfaces have features that lie entirely within the viscous sublayer of the smooth-wall TBL, it is widely accepted that their effect on the flow can be ignored (Tennekes and Lumley 1972, p 165). Such surfaces are considered to be hydrodynamically smooth (if $k_s^+ \equiv k_s U_\tau /\nu \lesssim \mathcal {O}(5)$). The present study seeks to determine if such a criterion can be analogously extended to the small scales of the topography of a multi-scaled rough wall. To this end, a series of rough surfaces have been prepared where the small-scales of the topography have been systematically varied such that only ${\rm ES}_x$ is changed. By comparing the drag penalty of these surfaces, the study aims to determine the flow defined length scale at which the small-scale features, which cause an appreciable increase in ${\rm ES}_x$, also cause an increase in drag. Additionally, the study also considers two surfaces with matched $S_q$, $S_{sk}$ and ${\rm ES}_x$, but where the effective slope is comprised from different scales, to see if they exhibit matched drag.

2 Experiment setup

2.1 Baseline roughness generation

A realistic roughness topography (i.e. irregular, three-dimensional) is generated for this study using the multi-scale anisotropic rough surface (MARS) algorithm (Jelly and Busse 2019). The algorithm takes linear combinations of Gaussian random number matrices using a moving average process and user-specified correlation functions. Surfaces with desired properties (in terms of ${\rm ES}_x$ or ${\rm ES}_y$) can be obtained by varying the number of points in the correlation functions. The generated roughness is multi-scaled and broadband with scales ranging from 4 mm $\lesssim \lambda \lesssim 50$ mm, where $\lambda$ is the in-plane wavelength. While the energy-spectra of the surface does not follow a power-law distribution, the energy of the scales do exhibit a decay with wave-number. The insets in Fig. 4 show the surface energy spectra against wave-number without pre-multiplication. See the works of Jelly et al. (2022), Jelly and Busse (2019) and Ramani et al. (2020) for additional examples of rough surfaces generated using this algorithm. The topography for this study is generated on a 300 mm $\times$ 300 mm computational tile. The roughness is isotropic (${\rm ES}_x \approx {\rm ES}_y \approx 0.135$, where ${\rm ES}_y$ is the spanwise effective slope and is defined analogously to Eq. 5) and nearly-Gaussian ($S_{sk}\approx 0$, kurtosis $\approx 3$) with doubly-periodic edges. The value of ${\rm ES}_x \approx {\rm ES}_y \approx 0.135$ of the numerically generated topography is selected in order to have a sparse or wavy roughness that can be accurately reproduced by the manufacturing process, which is discussed next.

2.2 Manufacturing and case generation

The physical surfaces are reproduced from the numerically generated topography using an in-house CNC router (MultiCAM). Each physical tile is 900 mm $\times$ 900 mm in size (i.e. each physical tile is a $3\times 3$ array of a single 300 mm $\times$ 300 mm doubly-periodic surface). The surfaces are machined from acetaldehyde co-polymer sheets (11 mm thick) in two passes. First, a rough-pass is carried out using a ball-nosed cutter of 3 mm diameter, then a finishing pass is a carried out with a 2 mm diameter (d) ball-nosed cutter which finishes the surface in a raster pattern with a fixed step-over distance (s). Surface statistics are acquired by virtually reconstructing the machined surface directly from the CNC toolpath for the given tool geometry. Details of this method are provided in “Appendix A”. The virtually reconstructed surfaces are shown in Fig. 3a–e where the step-over distance is increased from 0.25–1.1mm respectively. The statistics of the most finely machined surface (Fig. 3a, $s=0.25$ mm) agree well with the original numerically generated surface. Therefore, this surface is set to be the ‘baseline’ case for the measurements. Owing to the hemispherical shape of the cutting tool and the step-over distance for the finishing pass, small cusps of the raw material are left behind on the finished surface between adjacent passes of the tool. We refer to these features as ‘scallops’, which are small-scale features that lie over the large-scale features of this roughness topography. For two level passes of the cutting tool, the nominal height of the scallops is related to the step-over distance of the tool and the tool diameter, as shown in Fig. 3f, and is given as:

$$\begin{aligned} k_{\text {scallop}} = \frac{d}{2} - \sqrt{\left( \frac{d}{2}\right) ^2 - \left( \frac{s}{2}\right) ^2}. \end{aligned}$$

(6)

By increasing the step-over distance while keeping the tool size constant, $k_{\text {scallop}}$ can be increased. This is evident, both in the surfaces with increasing step-over displayed in Fig. 3a–e, and also the surface elevation profile at a matched location for all cases shown in Fig. 3f. Using this technique, four more cases of ‘rough scalloped’ surfaces are prepared with $s \in [0.50, 0.75, 0.95, 1.10]$ mm. These cases are referred to as S1–S4 respectively. The pre-multiplied energy spectra of each case are plotted against the in-plane streamwise and spanwise wavelengths respectively in Fig. 4a and b. In the streamwise direction, which is orthogonal to the toolpath direction, we see a secondary bulge in the pre-multiplied energy spectra (Fig. 4a). This additional energy is broadband (owing to the non-sinusoidal shape of the scallops) and is centred at the tool step-over distance (shown by the dashed lines in Fig. 4a). It is absent in the spanwise direction (Fig. 4b) since the tool cutting path is along this direction. The spectra is also identical for all the cases at the larger wavelengths implying that the large-scale features are unaffected by the tool step-over distance. Thus, by increasing s, the relative size of the small-scale features, i.e. scallops, can be increased while preserving the underlying large-scale features from the numerically generated surface. The corresponding roughness properties for the machined cases are summarised in Table 1. Following this method, ${\rm ES}_x$ is increased from 0.136 for the baseline case to ${\rm ES}_x \approx 0.294$ for case S4. Evidently, the increase in ${\rm ES}_x$ is due to the increased contribution of the small-scaled features (scallops). While there is a slight increase in the peak-to-valley height, $S_z$, by $\sim 10\%$ from the baseline case to S4, this is expected due to the increase in the prominence of the scallops as s is increased. Other measures of the roughness, such as $S_a$, $S_q$ and $S_{sk}$ are nearly matched for all the cases ($\pm 1\%$ for $S_a$, $\pm 5\%$ for $S_{sk}$). Finally, all cases lie in the sparse or wavy regimes of roughness where drag is expected to increase with increasing ${\rm ES}_x$ (Napoli et al. 2008).

Fig. 4

Pre-multiplied energy spectra of the surface elevation map in each in-plane direction plotted against the corresponding in-plane wavelengths: a $k_x \Phi _{h(x)h(x)}$ against $\lambda _x$ and b $k_y \Phi _{h(y)h(y)}$ against $\lambda _y$. Here, $k = 2\pi /\lambda$ is the wave-number. In both panels, the inset shows the energy-spectra against the respective wave-numbers without pre-multiplication. The spectra of the roughness generated with the MARS algorithm () is also shown for comparison. In (a) the vertical dashed lines correspond to the tool step-over distance (s) used for the preparation of the corresponding cases. See Table 1 for legend. The abscissa at the top of each figure shows the range of the viscous length scaled in-plane wavelengths, $\lambda ^+ = \lambda U_\tau /\nu$ at the lowest (lower ticks) and highest (upper ticks) ${\rm Re}_\mathrm{{unit}}$ of the measurements

Fig. 5

Setup for the rough-wall drag measurement experiments: a Schematic of the drag balance apparatus used for direct measurements of flow induced drag. The wall shear stress, $\tau _w$, generates a moment about the pivot, which is balanced by the normal force N provided by the restorative balance (load-cell). The gain is set by the ratio of the arms $H/L \approx 2.1$. The uneven static pressure distribution on the surface of the drag plate, shown by the blue arrows, induces a net integrated moment, $M_p$, which is compensated in each measurement. b A close-up of the drag plate showing the edge setup for the rough-wall cases. c Layout of the rough surfaces and the location of the drag plate in the working section of the wind tunnel

Table 1 Details of the rough and smooth test surfaces prepared for the study

In addition to these cases, two more surfaces are also manufactured. The first is a rough case that has matched ${\rm ES}_x$ and ${\rm ES}_y$ to the S3 ‘rough scalloped’ case shown in Fig. 3d. The difference between these two surfaces is that while the ${\rm ES}_x \approx 0.257$ of the S3 case is achieved due to the inclusion of the small scales (i.e. the scallops), the ${\rm ES}_x \approx 0.244$ of the matched case is attained through large scale features only (machining parameters of $d = 1.5$ mm and $s = 0.25$ mm). By comparing these two cases, the importance of the scales of roughness that contribute to ${\rm ES}_x$ can be assessed. It is noted that cases S1—S4 and the matched ${\rm ES}_x$ case are anisotropic (i.e. ${\rm ES}_x \ne {\rm ES}_y$). However, the degree of anisotropy varies due to ${\rm ES}_x$ alone and ${\rm ES}_y$ is nearly matched ($\lesssim 2\%$ variation) across all the cases. Thus, the influence of anisotropy for the comparative assessment of these cases is negligible (Jelly et al. (2022) note a 4% variation in $C_f$ when ${\rm ES}_y$ is varied by 200%). Finally, a flat-wall case with scallops is also manufactured (with a tool of $d = 2$ mm and $s = 0.625$ mm) to assess the impact of the small-scale features in the absence of any large-scale roughness. Details of these additional cases are also presented in Table 1.

2.3 Facility and drag measurement setup

All measurements were carried out in the open-return type boundary-layer wind tunnel at the Walter Bassett Aerodynamics Lab at the University of Melbourne. The wind-tunnel has a working section length of 6.7 m and a cross-section area of $0.94\times 0.38$ $\text {m}^2$. The boundary layer is tripped at the inlet of the tunnel by a spanwise strip of P40 grit sandpaper. The measurements are carried out in nominal zero-pressure gradient (ZPG) conditions. More details about the wind-tunnel facility are given in Nugroho et al. (2013) and Harun et al. (2013).

The focus of this study is the sensitivity of the turbulent flow induced drag to small changes in surface roughness. For this, direct measurements of $C_f$ are obtained with an in-house developed drag balance that follows the schema described by Krogstad and Efros (2010). A diagram of the balance is shown in Fig. 5a. The wall-parallel wall shear-stress, $\tau _w$, acting on the drag plate is converted to a vertical force, N, acting at the load cell via the moment arms of the balance. The mechanical gain of the balance is $H/L \approx 2.1$. The normal force, N, is balanced by a restorative load-cell (Ohaus Pioneer series with $\mathcal {O}(10^{-4})$ N precision), which is directly sampled at approximately 1 Hz. The drag plate has dimensions of 290 mm in the spanwise direction and 420 mm in the streamwise direction (430 mm for the smooth and flat-scalloped cases). The nominal gap with the surrounding walls is $\sim 0.6$ mm (see Fig. 5b).

Fig. 6

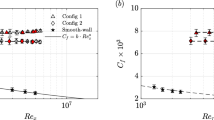
a Measured average skin-friction coefficient, $\overline{C_f}$ obtained from the drag balance for the cases in Table 1. The smooth-wall curve from the drag balance is also shown for comparison. b Relative increase in drag, $\Delta \overline{C_f}$, over the baseline S1 case (${\rm ES}_x \approx 0.136$). The abscissa in both figures is the unit Reynolds number, ${\rm Re}_\mathrm{{unit}} = U_\infty /\nu$ [m$^{-1}$]. The shaded regions are the uncertainty associated with the drag balance measurements for each case based on the scatter in the measurements of $M_p$

For this design of the drag balance, one of the main sources of error is due to an uneven static pressure distribution on the surface of the drag plate (illustrated by the blue arrows in Fig. 5a). The resultant of these forces may introduce an additional moment ($M_p$) that contaminates the measurements. Due to the large streamwise length of the drag plate, this moment can lead to a significant error. This is particularly important for the smooth-wall case where the shear stress is small when compared to the rough-wall cases ($M_p$ is $\sim 10\%$ of the moment due to N for the smooth-wall measurements). To compensate, a smooth-wall drag plate with 45 static pressure taps distributed across the surface is deployed. Measurements from these pressure taps allow $M_p = M_p(U_\infty )$ to be determined. The $C_f$ across the area of the drag plate is then given by:

$$\begin{aligned} C_f = \frac{(NL + M_{p})}{\frac{1}{2} \rho U_\infty ^2 A_p H} . \end{aligned}$$

(7)

Here $\rho$ is air density and $A_p$ is the area of the drag plate. Multiple independent measurements are obtained for each case studied here. The measurement process is validated for the smooth-wall case by comparison against oil film interferometry (OFI) measurements in the same facility. The average of the repeated measurements, denoted as $\overline{C_f}$, is seen to match the OFI curve to within $\pm 1\%$ for tunnel free-stream velocities $U_\infty \gtrsim 9$ ms$^{-1}$. Further details on the drag measurement, validation and uncertainty of the balance are included in “Appendix B”.

The centre of the drag plate is located at a streamwise position of $x\approx 3.9$ m from the trip. For the ‘baseline’ and cases S1—S4, the surface of the wind-tunnel from 1.8 m $\le x \le 4.5$ m is covered with $900 \times 900$ mm$^2$ tiles of the baseline surface, shown by the light grey tiles in Fig. 5c. Only the drag plate is changed between experiments. The surface far upstream of the drag measurement location (i.e. 0 m $\le x \le 1.8$ m, dark grey tiles in Fig. 5a) is covered with a different existing rough surface (irregular, three-dimensional, isotropic roughness with similar $S_q \approx 0.3$ and ${\rm ES}_x \approx {\rm ES}_y \approx 0.24$) to reduce the time spent on manufacturing the baseline surface, which owing to the fine tool size and step-over, required extremely high machining times (nearly 120 h per tile). At the transition between the two surfaces (at $x = 1.8$ m), an internal boundary-layer will develop. This internal boundary-layer grows over a fetch of about $42\delta$, where $\delta$ is the boundary-layer thickness of the oncoming flow at $x \approx 1.8$ m. This is well in excess of the 26$\delta$ limit at which the internal layer is expected to fully develop (Li et al. 2021). For the smooth cases, the entire working section of the wind-tunnel is covered with smooth-wall sections. Due to the surface change at $x=1.8$ m for the rough cases, the drag measurements are reported against the unit Reynolds number, ${\rm Re}_\mathrm{{unit}} \equiv U_\infty /\nu$, to avoid any uncertainty in ${\rm Re}_x$. Finally, for all cases $0.04 \gtrsim S_z/\delta \gtrsim 0.038$.

3 Results and discussion

3.1 Drag measurements

First, we consider the average skin-friction coefficient curves, $\overline{C_f}$, obtained for the baseline and rough scalloped cases (S1–S4, Table 1). This is shown in Fig. 6a against the ${\rm Re}_\mathrm{{unit}}$ of the flow. The smooth-wall curve is also shown for reference. The uncertainty in the measurement of $\overline{C_f}$ for the baseline and the smooth-wall cases are shown by the shaded regions. This uncertainty is based on the scatter expected from the $M_p$ measurements described in §2.3. For a clearer comparison between the rough scalloped surfaces (S1–S4) and the baseline case, the relative increase in drag,

$$\begin{aligned} \Delta {\overline{C_f}}_n = \frac{{\overline{C_f}}_n - {\overline{C_f}}_{\text {baseline}}}{{\overline{C_f}}_{\text {baseline}}}, \end{aligned}$$

(8)

is plotted in Fig. 6b. Here the subscript ($_n$) indicates the different cases. Across the two figures, it is evident that the drag of the larger scalloped surfaces (higher ${\rm ES}_x$ cases) gradually increases over that of the baseline case as ${\rm Re}_\mathrm{{unit}}$ of the flow increases. For ${\rm Re}_\mathrm{{unit}} \lesssim 0.5\times 10^6$, all cases have a measured value of $\overline{C_f}$ that is within the uncertainty of the measurement for the baseline case. Nevertheless, a clear trend of increasing drag with an increase in scallop height is evident at ${\rm Re}_\mathrm{{unit}} \approx 0.5 \times 10^6$. As anticipated, at low ${\rm Re}_\mathrm{{unit}}$ and low scallop height, the effect of the scallops is not felt. This suggests that not all scales that contribute to ${\rm ES}_x$ also contribute to the drag penalty. Further, while the baseline case is nearing the fully rough regime, i.e. where $\partial \overline{C_f}/\partial {\rm Re}_{\text {unit}} \rightarrow 0$, the scalloped cases (S1–S4) appear to be transitionally rough even at the highest ${\rm Re}_{\text {unit}}$ of the measurements.

Fig. 7

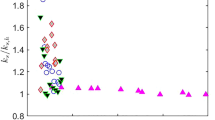
a Viscous scaled nominal scallop height, $k_{\text {scallop}}^+=k_{\text {scallop}}U_\tau /\nu$, obtained from Eq. 6 plotted against ${\rm Re}_\mathrm{{unit}}$. The () line marks $k_\mathrm{{scallop}}^+ =5$. b Relative change in $\overline{C_f}$ over the baseline case for the rough scalloped cases plotted against $k_{\text {scallop}}^+$. Also shown is the relative change in $\overline{C_f}$ between the flat scalloped surface and the smooth-wall case

3.2 Assessing the impact of the scallops

The viscous scaled scallop height, $k_{\text {scallop}}^+ = k_\mathrm{{scallop}}U_\tau /\nu$ (where $k_{\text {scallop}}$ is obtained using Eq. 6), is plotted against ${\rm Re}_\mathrm{{unit}}$ in Fig. 7a. Here $U_\tau = U_\infty \sqrt{\overline{C_f}/2}$ where $\overline{C_f}$ is measured from the drag balance. For the baseline case, $k_{\text {scallop}}^+ < 1$ for all ${\rm Re}_\mathrm{{unit}}$. For the S1 and S2 cases, $k_{\text {scallop}}^+$ does not exceed 5 even at the highest ${\rm Re}_\mathrm{{unit}}$ tested. For cases S3 and S4, the minimum $k_{\text {scallop}}^+$ exceeds the viscous length scale and rises above 5 at high ${\rm Re}_\mathrm{{unit}}$.

In Fig. 7b, it is observed that the relative increase in drag, $\Delta \overline{C_f}$ for cases S1–S4 scales with the viscous scaled scallop height, $k_\mathrm{{scallop}}^+$. This suggests that for multi-scaled roughness, the contribution to drag from the different scales of the roughness topography should be assessed relative to their viscous scaled heights. Firstly, it can be concluded that scales of the roughness topography that are small relative to the viscous length scale (i.e. $\lesssim 2 - 3 \nu /U_\tau$) do not make a significant contribution to drag. However, by including these features in the characterisation of the surface roughness, artificially high values of ${\rm ES}_x$ are obtained, which can lead to incorrect predictions of the drag penalty. Thus, some flow dependent filtering of the roughness topography should be applied prior to characterising the surface roughness for drag prediction. Secondly, as ${\rm Re}_{\text {unit}}$ is increased and $k_{\text {scallop}}^+$ increases beyond the viscous length-scale, $\overline{C_f}$ also increases (Fig. 7b) and the surface becomes transitionally rough. Even the S4 case, where $k_{\text {scallop}}^+ \lesssim 12$ for all ${\rm Re}_{\text {unit}}$ measured, is transitionally rough. This suggests that the fully-rough regime may be attained only when all scales of a multi-scaled topography are much larger than the viscous length scale. For the flat-scalloped case, where the maximum $k_{\text {scallop}}^+\approx 3$, the apparent fully-rough behaviour ($\partial \overline{C_f}/\partial Re_{\textrm{unit}} \rightarrow 0$ for $Re_{\textrm{unit}} \gtrsim 1.5 \times 10^6$, observed in Fig. 6a) is likely to be the inflection point corresponding to the Nikuradse (1933) type transitional behaviour (Allen et al. 2005).

This behaviour of the rough scalloped surfaces, S1–S4, is qualitatively similar to that of the flat scalloped case, which has an ${\rm ES}_x \approx 0.16$ with no underlying large-scale features. The drag of the flat scalloped surface is included in Fig. 6a as the dashed line and is seen to gradually depart from the smooth-wall levels as the ${\rm Re}_\mathrm{{unit}}$ of the flow is increased. Compared to the rough scalloped cases, the drag of the flat scalloped case increases at a higher rate (when measured from the smooth case) with $k_\mathrm{{scallop}}^+$ as shown in Fig. 7b. This may be partly attributed to the fact that the smooth wall $\overline{C_f}$ continues to decrease with ${\rm Re}_{\text {unit}}$ while the baseline case approaches a constant value. However, some sections of the rough-scalloped surface will be sheltered by the surrounding large scale features as well and thus not all scallops on the rough cases will contribute to the drag increase. This apparent non-linear coupling between the small-scale and large-scale features means that the isolated (flat scalloped) small-scale drag cannot be used to predict drag of a multi-scale surface. This is perhaps not surprising, since $\Delta C_f$ is non-linear with $k_s$ (see for example Hutchins et al. 2023).

Fig. 8

Estimate of the roughness function $\Delta U^+$ against $k_s^+$ obtained from the drag balance measurements showing the influence of the scallops. See Table 1 for legend. Also shown are the two types of transitionally rough behaviour i.e. Colebrook (1939) () and Nikuradse (1933) (); and the fully-rough asymptote given by Eq. 10 ()

Fig. 9

Samples of two rough surfaces with nearly matched values of ${\rm ES}_x$ but composed of different scales of the topography: a the S3 surface with ${\rm ES}_x\approx 0.257$ where the high slope results due to the scallops and b a surface with ${\rm ES}_x \approx 0.244$ which is constituted of large scale features only. c Comparison of the pre-multiplied energy spectra, $k_x \Phi _{h(x)h(x)}$ of the two surfaces, plotted against the in-plane wavelengths $\lambda _x$. Here, $k = 2\pi /\lambda$ is the wave-number. The S3 case is shown by () while the matched ${\rm ES}_x$ case is shown by (). In (c) the vertical lines correspond to the tool step-over distance (s) used for the preparation of the corresponding cases. The abscissa at the top of (c) shows the range of the viscous length scaled in-plane wavelengths, $\lambda ^+ = \lambda U_\tau /\nu$ at the lowest (lower ticks) and highest (upper ticks) ${\rm Re}_\mathrm{{unit}}$ of the measurements

3.3 Transitionally rough behaviour

The Hama roughness function, $\Delta U^+$, at matched friction Reynolds numbers can be estimated from:

$$\begin{aligned} \Delta U^+ = U_{\infty , \textrm{S}} ^+ (\delta ^+) - U_{\infty , \textrm{R}} ^+ (\delta ^+), \end{aligned}$$

(9)

where $\delta ^+ = \delta U_\tau /\nu$ is the friction Reynolds number (${\rm Re}_\tau$) and $\delta$ is the boundary-layer thickness. The subscripts indicate smooth (S) and rough (R) respectively. From the drag balance measurement, $U_{\infty ,\textrm{R}}^+$ can be obtained. To obtain $U_{\infty ,\textrm{S}}^+$ at a matched $\delta ^+$, a mean velocity profile with logarithmic and wake components is assumed (with $\Pi = 0.683$ based on fitting to a smooth-wall velocity profile in the wind-tunnel and the wake function, $\mathcal {W}$, given by Jones et al. 2001). To obtain $k_s$, the $\Delta U^+$ obtained for the measurement at the highest ${\rm Re}_\mathrm{{unit}}$ for each case is assumed to lie on Nikuradse’s (1933) fully-rough asymptote given by:

$$\begin{aligned} \Delta U^+ = \kappa ^{-1} \log k_s^+ + A - A_{FR} . \end{aligned}$$

(10)

The von Kármán constant, $\kappa$, and the smooth-wall intercept, A, are assumed to be 0.384 and 4.17 respectively (Nagib et al. 2007), while $A_{FR}=8.5$ is Nikuradse’s intercept of the fully-rough asymptote. The mapping between $\Delta U^+$ and $k_s^+$ obtained using this procedure is shown in Fig. 8. Also shown are the curves for the Colebrook (1939) (cf. Grigson 1992) () and Nikuradse (1933) behaviours (cf. Hutchins et al. 2023) () along with the fully-rough asymptote (). The baseline case shows a Colebrook behaviour in the transitionally rough regime. As ${\rm ES}_x$ and the contribution of the small-scales is increased (i.e. $k_\mathrm{{scallop}}$ is increased) from case S1 to S4, the curves shift towards a Nikuradse behaviour. The case with the largest scallop seems to exhibit the slowest approach to the fully rough asymptote. Thus, the transitional behaviour observed is related to the multi-scale nature of the roughness.

Fig. 10

Drag curves, $\overline{C_f}$, of the two surfaces compared to the baseline and smooth-wall cases against ${\rm Re}_\mathrm{{unit}}$. The shaded regions are the uncertainty associated with the drag balance measurements for each case based on the scatter in the measurements of $M_p$

3.4 Relative importance of scales

In this section we compare two cases with similar ${\rm ES}_x$, but comprised of different scales. The rough scalloped case S3 with ${\rm ES}_x \approx 0.257$, shown again in Fig. 9a is now compared to another surface (shown in Fig. 9b) with similar ${\rm ES}_x \approx 0.244$ but where the effective slope arises from larger scale features. The nominal scallop height for the ‘matched ${\rm ES}_x$’ case remains below the viscous length scale for all ${\rm Re}_\mathrm{{unit}}$ tested. The difference between the two cases is in the relative contribution of the scales of the topography that make up the surface and hence determine ${\rm ES}_{x}$. This is evident in the pre-multiplied energy spectra of the corresponding rough surfaces, which are plotted against the in-plane streamwise wavelength in Fig. 9c. Case S3 is essentially bimodal, comprised of large scale features with low slope (${\rm ES}_x \approx 0.136$ of the underlying baseline surface) but superimposed with high slope scallops, which have smaller amplitudes. Conversely, the matched ${\rm ES}_x$ case only comprises of large scale features at shorter wavelengths than case S3 (and is essentially, a single mode distribution). Despite these differences, the two cases have similar ${\rm ES}_x$ and indeed are similar by most measures of their roughness as presented in Table 1.

Figure 10 shows that the two surfaces yield starkly different drag penalties. The rough scalloped S3 case has a lower drag than the matched ${\rm ES}_x$ case for the entire range of the ${\rm Re}_\mathrm{{unit}}$ of the measurements (nearly 28% lower at the highest ${\rm Re}_\mathrm{{unit}}$ tested). These observations suggest that, regardless of ${\rm ES}_x$, the drag behaviour of a rough surface at a given Reynolds number is dominated by the large-scale features. As the Reynolds number increases, the small scale features become visible to the flow and lead to a further increase in the drag. However, this drag increase is only a small penalty over the levels established by the underlying large scale features of the topography. Consequently, for multi-scale surfaces such as the ones considered in this study, ${\rm ES}_x$ can be a misleading metric for drag prediction without appropriate flow dependant scale weighting of the topography.

Together, these results highlight the challenge in developing predictive correlations based on ${\rm ES}_x$, particularly for multi-scaled roughness. Firstly, only the scales that exceed the viscous length scale of the flow condition should be considered towards the characterisation of the roughness. And secondly, even when this first condition is met, the relative sizes of the features that contribute to the average slope appears to be important. For the second issue, the mean in-plane wavelength of the surface, which may be obtained from the spectral moments (Townsin 2003), might permit a scale-weighted measure of the effective slope, denoted $\hat{{\rm ES}_x}$, to be defined. A rigorous assessment of this method is beyond the present scope, but its application to the rough surfaces studied here is discussed in “Appendix C”. For the first issue (the need to impose a cut-off filter at the viscous length scale), since the viscous length-scale is not known a priori, an iterative approach may be required. As an example, an estimate of $k_s$ may be obtained using some predictive correlation (i.e. Forooghi et al. 2017; Chan et al. 2015). Next, $U_\tau$ may be estimated using a boundary-layer evolution method (Monty et al. 2016) or the Moody (1944) chart. Using this estimate of the viscous length scale, a refined measure of effective slope could be obtained from the filtered spectra of the surface, which in turn would yield a new estimate of $k_s$ and $U_\tau$, permitting reiteration. However, the convergence of this method is unproven and would depend on the chosen correlation.

These findings also provide guidance for future rough-wall experimental and numerical studies. Although machining or manufacturing artefacts can alter the measure of ${\rm ES}_x$, if they are small compared to the viscous length scale, then these artefacts will have a weak effect on the flow measurements. For the present set of rough scalloped cases, the $\overline{C_f}$ of the surfaces with $k_\mathrm{{scallop}}^+ \lesssim 3$ varies from the baseline case by less than $3\%$ (Fig. 7b). Manufacturing options may be selected to produce the rough surfaces accordingly. In a similar manner, computational studies may elect not to resolve the smallest scales of surface roughness, where these features lie below $2\sim 3$ viscous scaled lengths.

4 Conclusions

For multi-scaled roughness, the streamwise effective slope (${\rm ES}_x$) can be an unbounded quantity. The integral effect of the gradients associated with the small-scales can become increasingly dominant as the measurement resolution is refined, raising the measured value of ${\rm ES}_x$. To assess the influence of the small scales, drag balance measurements are conducted with a set of rough surfaces. A numerically generated realistic, multi-scale roughness with ${\rm ES}_x \approx 0.136$ is machined using fine cutting parameters. A set of surfaces with increasing ${\rm ES}_x$ is obtained by coarsening the cutting parameters. This introduces small scale machining artefacts, called ‘scallops’, on the cut surface which result in an increase in ${\rm ES}_x$. The increase in drag of the larger scalloped cases over the baseline case scales with the viscous scaled scallop height. The data suggests that scales of roughness that are smaller than $\sim$3 times the viscous length scale have a weak effect on the drag despite strongly contributing to ${\rm ES}_x$. Further, for the case where the scallops are $\sim$10 times the viscous length scale, the increase in measured $\overline{C_f}$ is much lower ($\sim 28$%) than it is for a case with matched topographical properties, but where ${\rm ES}_x$ is comprised only of large scale features. Therefore, effective slope, when used to predict $k_s$, requires scale weighting, with the drag depending more on the slope of the larger scale features. Based on these findings, when it comes to multi-scaled roughness, ${\rm ES}_x$ should be used with caution as it can be an unreliable measure of the impact of the roughness on the flow.

Appendices

Appendices

Virtual machining method

The statistics of the rough surfaces have been obtained by virtually reconstructing the machined surface and incorporating the tool geometry. Details of this method are provided here. A custom C program extracts the tool-tip coordinates from the GCode file that instructs the CNC machine for the finishing pass. These coordinates are interpolated onto a uniform grid and the tool-geometry is superimposed along the tool-path to obtain the finished surface. The virtual reconstruction of a sample machined surface is compared to a scan obtained from a confocal microscope (HiRox RH-2000) in Fig. 11a. The contours of the sample surface are shown in Fig. 11a–b. In Fig. 11c–d, the surface profiles at a matched location and the pre-multiplied energy spectra in the y-direction obtained from both methods are shown respectively. Together, these figures show that the virtually reconstructed surface and the scanned surface are in good agreement with each other. Importantly, the broadband bulge in the spectra corresponding to the scallops () is also accurately captured. The microscope is limited to scan an area of 50 mm $\times$ 25 mm and has a finite in-plane resolution ($5 \upmu$m). It is also necessary to apply a dark coloured coating to the surface to enhance the contrast on the topography. Further, the raw output from the microscope requires de-trending and spectral filtering in both in-plane directions to remove the scanning artefacts and noise. Thus, the virtual machining method is preferred as an accurate representation of the machined surface.

Fig. 11

Contours of a machined rough surface obtained from a a confocal microscope scan and b the GCode reconstruction. In c the surface profiles from a matched location for the scan () and GCode () methods are shown. In d the pre-multiplied energy spectra along the y-direction obtained from both methods are shown

Fig. 12

Schematic figures illustrating the systematic errors that affect the calculation of the net pressure induced moment on the drag plate: a mounting offset, $\delta _\mathrm{{MTG}}$ and b angular error of drag plate $\alpha _S$. The effective moment arm due to these errors is illustrated in (c). Note that in all cases, the drag plate is co-planar with the tunnel floor, as indicated by the () lines, in both figures

Further details on the drag balance

In Sect.2, the method to improve the accuracy of the drag balance measurements by compensating for the moment induced by the static pressure distribution on the drag plate is discussed. Here, additional details of this method are provided. The static pressure distribution over the area of the drag balance tile is obtained with an identical smooth-wall plate with 45 pressure taps. The net moment due to the static pressure about the pivot is computed as:

$$\begin{aligned} M_{p} = \sum _i p_i A_i r_i . \end{aligned}$$

(11)

Here, p is the measured static pressure, r is the moment arm and $A_i$ is the area associated with the ith pressure tap. When computing this correction for the various cases, two systematic errors require consideration. The first one is the offset in the mounting of the drag plate over the apparatus, $\delta _\mathrm{{MTG}}$, and the second one is the angular error of the 90$^\circ$ bracket and the flow-side plane of the drag plate, $\alpha _\mathrm{{S}}$. These two offsets are illustrated in Fig. 12. The former occurs due to the manual location of the mounting holes on the drag tile, while the latter occurs due to shims being placed under the drag tile to ensure it is flush with the wind tunnel floor (which has a small streamwise tilt of $\approx 0.5^\circ$). Accounting for both these terms, the effective moment arm becomes:

$$\begin{aligned} r_{i,\textrm{eff}} = (r_i+\delta _\mathrm{{MTG}}) \text {cos} (\alpha _{S}) + H \text {tan} (\alpha _{S}). \end{aligned}$$

(12)

Thus for each measurement, both $\delta _\mathrm{{MTG}}$ and $\alpha _S$ are measured and the appropriate moment is computed. In addition to this pressure compensation, further minimisation of noise and error is achieved through the following implementations in the design. First, a 30$^\circ$ chamfer is incorporated on the leading and trailing edges of the drag plate to minimise pressure forces on the forward and backward facing faces (see Fig. 5c). Second, the entire apparatus under the working section of the tunnel is placed inside a perspex box to isolate the setup from any ambient flow outside the wind-tunnel. Third, any drift in the load-cell is accounted for by measuring with no flow before and after the measurement at each $U_\infty$. Individual measurements of $C_f$ for a smooth-wall using the drag balance are shown in Fig. 13 by () lines. The scatter in the individual measurements is $\pm \sim 3\%$ at the highest ${\rm Re}_\mathrm{{unit}}$, which agrees with the scatter expected from the $M_p$ measurements.

Fig. 13

Measured skin-friction coefficient, $C_f$, for a smooth-wall obtained from the drag balance plotted against ${\rm Re}_\mathrm{{unit}}$. The () lines show individual measurements while the () shows their average ($\overline{C_f}$). The grey patch shows the expected uncertainty based on scatter in the measurement of $M_p$. The drag balance result is compared with OFI measurements in the same facility (). The mean of all the OFI measurements () is also shown. (Inset) Percentage error between the $\overline{C_f}$ curves from the two methods

To validate these measurements, $C_f$ was also obtained using oil film interferometry (OFI) in the same facility. This is shown in Fig. 13 by the () marks. The average curve of all the drag balance measurements () is seen to converge to within $\pm 1\%$ of the average curve of the OFI measurements () for ${\rm Re}_\mathrm{{unit}} \gtrsim 0.6\times 10^6$ (shown in the inset in Fig. 13). This corresponds to $U_\infty \gtrsim 9$ ms$^{-1}$ in the wind tunnel.

Scale-weighted measure of slope

In Sect. 3.2 of the manuscript, it was shown that to accurately characterise multi-scaled surfaces for drag prediction, a flow-based filter is required that removes scales of the topography that are smaller than the 2–3 times the viscous length scale. Even with such a filter applied, Sect. 3.4 shows that a scale weighting is also needed in order to determine the relative contribution of the scales to the average slope. Although no general recommendations can be made, a potential flow-based filter with scale-weighting is discussed here.

The first step is to identify the range of the viscous length scale with respect to the amplitudes of the scales of the topography. The threshold of $2 \times \nu /U_\tau$ (available from the drag measurements) is shown against the spectra of the roughness cases in Fig. 14a. Parts of the spectra that are lower than this threshold (at a given ${\rm Re}_{\text {unit}}$) may be disregarded towards characterising the surface. Next, we consider the mean in-plane wavelength of the surface characterised by the remaining spectral contribution, which can be obtained from the ratio of the spectral moments (Townsin 2003) and is given as:

$$\begin{aligned} \overline{\lambda _x} = 2\pi \frac{m_{0x}}{m_{1x}}. \end{aligned}$$

(13)

Here, $m_n = \int _{0}^{\infty }k^n \Phi _{hh} dk$ is the n-th spectral moment. The mean in-plane wavelength, therefore, is weighted by the spectral contribution of each scale - i.e. the scales that contribute the most to $S_q$ also contribute the most to $\overline{\lambda }$. Thus, the multi-scaled surface can be considered to be a wave of wavelength $\overline{\lambda _x}$ with amplitude $S_q$. The average absolute slope of this wave is denoted as $\hat{{\rm ES}_x}$ and is defined as:

$$\begin{aligned} \hat{{\rm ES}_x} = \frac{1}{\overline{\lambda _x}}\int \limits _0^{\overline{\lambda _x}} |S_q \sin \left(2\pi \frac{x}{\overline{\lambda _x}}\right)| dx. \end{aligned}$$

(14)

As ${\rm Re}_{\text {unit}}$ is increased and the cut-off threshold is decreased, a flow dependent measure of $\hat{{\rm ES}_x}$ is obtained. This is shown in Fig. 14b for the baseline, S1–S4 and matched ${\rm ES}_x$ cases. For the S1 and S2 cases, when $k_{\text {scallop}}^+ < 2$ at low ${\rm Re}_{\text {unit}}$ of the measurements, $\hat{{\rm ES}_x}$ is seen to match that of the baseline case. As ${\rm Re}_{\text {unit}}$ is increased, $\hat{{\rm ES}_x}$ is also seen to gradually increase from the baseline case as the energy of the scallops begins to contribute to the measure of $\overline{\lambda _x}$. Cases S3 and S4 also appear to converge towards the baseline case at the lowest ${\rm Re}_{\text {unit}}$ of the measurements. However, importantly for the S3 case, $\hat{{\rm ES}_x}$ is seen to be much lower ($\sim$30%) than that of the matched ${\rm ES}_x$ case, capturing the different drag behaviour observed for these two cases. In Fig. 14c, the relative change in the drag penalty of the S1–S4 cases from the baseline case, $\Delta \overline{C_f}$, is plotted against $\hat{{\rm ES}_x}$. The relative drag increase is seen to approximately scale with the values of the $\hat{{\rm ES}_x}$ computed in this manner.

Therefore, the drag behaviour or $k_s$ of multi-scaled roughness may be more reliably predicted from the gradient of its mean in-plane wavelength after filtering the scales that lie below $\sim 2 \nu /U_\tau$. However, as noted in Sect. 3.4, the applicability of this method to a wider range of roughness topographies remains to be tested. For example, as Fig. 7b suggests, the arrangement of the small scales with respect to the large scales also requires to be considered.

Fig. 14

a Energy spectra of the surfaces in this study compared to the threshold of $2 \nu /U_\tau$. The range shown indicates the variation across the ${\rm Re}_{\text {unit}}$ of the measurements. b A scale-weighted effective slope, $\hat{{\rm ES}_x}$, obtained from the mean in-plane wavelength, $\overline{\lambda _x}$ (Eq. 13) of the filtered spectra against ${\rm Re}_{\text {unit}}$. c The relative change in $\overline{C_f}$ plotted against $\hat{{\rm ES}_x}$