A wavelet-based detector function for characterizing intermittent velocity signals

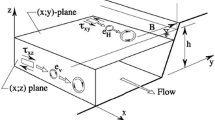
Abstract

In this work, we propose a new detector function based on wavelet transform to discriminate between turbulent and non-turbulent regions in an intermittent velocity signal. The traditional detector functions based on first or second derivative of velocity signal, which are commonly used in intermittency calculation schemes, show large fluctuations within turbulent parts of the signal and require averaging over a certain “smoothing period” to remove the fake dropouts, introducing subjectivity in calculating intermittency. The new detector function proposed here is obtained by averaging the “pre-multiplied wavelet energy” over the entire frequency range, which can be interpreted as wavelet energy contained in the first derivative of the velocity signal. We demonstrate the effectiveness of our detector within the framework of the widely used method by Hedley and Keffer (J Fluid Mech 64:625, 1974), for a range of velocity signals representing the different stages of roughness-induced transition. We show that the wavelet detector is much smoother than the double-derivative-based detector of Hedley and Keffer, and at the same time has a good discriminatory property (due to pre-multiplication by frequency). This makes the choice of the smoothing period unnecessary and removes the subjectivity associated with it. The wavelet detector function works equally well in detecting the edge intermittency of a canonical turbulent boundary layer, thereby highlighting its generality. The performance of the proposed detector to calculate edge intermittency is compared with a recent energy-based method by Chauhan et al. (J Fluid Mech 742:119, 2014), showing a favorable match. Our detector can, in principle, be used with any of the methods used for specifying threshold for obtaining an indicator function.

Appendices

Appendix A

In this appendix, a comparison is made between the detector functions obtained by various mother wavelets. Three wavelets namely, Morse, Morlet and Bump, have been selected for the current study as shown in Fig. 19. The corresponding detector functions are shown in Fig. 20. Further details about the wavelets can be found in the documentation of “cwt" command in MATLAB (The MathWorks 2022). As can be seen from Fig. 20, all three detector functions are smooth in nature and act as an envelope over the HK-detector. The Bump wavelet does not perform very well in the laminar intervals as it shows relatively high values there, limiting the quality of discrimination between laminar/turbulent regions. The detectors for Morse and Morlet wavelets are close to each other with the latter showing lower values within laminar intervals thereby giving a slightly better contrast between laminar and turbulent regions near the leading and trailing edges of the spots. We therefore choose Morlet wavelet for the present analysis. Note that the Morlet wavelet has been used previously by researchers for detecting turbulent spots (Zhang et al. 2018; Anand and Diwan 2020), supporting our choice of this wavelet. A more extensive analysis on the effect of mother wavelet on the detector function is out of the scope of the present study.

Fig. 19

Real parts of the three mother wavelets used for the analysis, namely Morlet, Morse and Bump

Fig. 20

a Mid-Transitional velocity signal (scaled from 0 to 1) vs. time (s). b Detector function by HK-method and by the three mother wavelets, namely Morlet, Morse and Bump (Fig. 19)

Fig. 21

Comparison of real parts of the Morlet wavelet and its first derivative

Fig. 22

Comparison of the scaled (on maximum amplitude) envelope of the Morlet wavelet and its first derivative

Appendix B

The wavelet transform of the velocity derivative at a fixed spatial point, $\frac{du}{dt}$, is given as (Farge 1992).

$$\begin{aligned} C_{w,L2}\bigg [\frac{d u}{d t}\bigg ]=-\int _{-\infty }^\infty \frac{u(t') }{\sqrt{a}}\frac{d}{dt} \bigg [ \psi ^{*}\bigg (\frac{t-t'}{a}\bigg ) \bigg ]dt' \end{aligned}$$

(B1)

$$\begin{aligned} =-\int _{-\infty }^\infty \frac{u(t') }{a\sqrt{a}}\phi ^{*}\bigg (\frac{t-t'}{a}\bigg )dt', \end{aligned}$$

(B2)

where

$$\begin{aligned} \phi ^{*}=\frac{d}{d\big ((t-t')/a \big )} \psi ^{*}\bigg (\frac{t-t'}{a}\bigg ). \end{aligned}$$

(B3)

This gives

$$\begin{aligned} C_{w,L2}\bigg [\frac{d u}{d t}\bigg ]=-\frac{1}{a}\int _{-\infty }^\infty \frac{u(t') }{\sqrt{a}}\phi ^{*}\bigg (\frac{t-t'}{a}\bigg )dt' \end{aligned}$$

(B4)

$$\begin{aligned} =-\frac{f}{\Omega _c}\int _{-\infty }^\infty \frac{u(t') }{\sqrt{a}}\phi ^{*}\bigg (\frac{t-t'}{a}\bigg )dt', \end{aligned}$$

(B5)

where $\Omega _c = (\omega _c^2 + \sqrt{2 + \omega _c^2 })/4 \pi$ from Eq. 5. The integral in Eq. B4 represents wavelet transform of u(t) using the derivative of Morlet wavelet given in Eq. B3. Figure 21 shows a comparison between $\psi$ and $\phi =\frac{d\psi }{dt}$ for $t' =0$ and $a=1$. As can be seen, $\phi$ is shifted in phase w.r.t. $\psi$ and shows higher magnitude than $\psi$. However, the qualitative behavior and the temporal “support” of both the wavelets are similar. This is further seen by a comparison of the scaled envelope between $\phi$ and $\psi$, plotted in Fig. 22, which shows an exact match of the two scaled envelopes. Since in this work we are concerned with the square magnitudes of wavelet coefficients, one can expect that the wavelet transform w.r.t. $\phi$ will cause a proportionate increase in the square magnitudes of wavelet coefficients as compared to the transform w.r.t. $\psi$, i.e.

$$\begin{aligned} {\tilde{C}}^{2}_{w,L2}[u]\propto C^{2}_{w,L2}[u], \end{aligned}$$

(B6)

where

$$\begin{aligned} {\tilde{C}}_{w,L2}[u]=\int _{-\infty }^\infty \frac{u(t')}{\sqrt{a}}\phi ^{*}\bigg (\frac{t-t'}{a}\bigg )dt'. \end{aligned}$$

(B7)

Eq. B5 in conjunction with Eq. B6 gives

$$\begin{aligned} C^{2}_{w,L2}\bigg [\frac{d u}{d t}\bigg ]\propto f^{2}C^{2}_{w,L2}[u]=fC^{2}_{w}[u] \end{aligned}$$

(B8)

where $C_w$ is the wavelet coefficient in L1-norm (see Sect. 4). Thus the pre-multiplied wavelet energy $(\text {PMWE}=fC_w^2[u])$ used here to define detector function has a flavor of the square magnitude of the wavelet coefficients of the velocity derivative. It thus signifies the energy contained in the velocity derivative rather than the velocity itself. In this sense, the present detector function is distinct from that proposed by Chauhan et al. (2014) who use kinetic energy of fluctuations to define their detector function.