Turbulent flow and friction in a pipe with repeated rectangular ribs

Abstract

Measurements were conducted in the fully developed turbulent flow in a pipe with internal diameter $D$ at a Reynolds number of ${\text{Re}}_{{\text{D}}} = 1.6 \times 10^{5}$. The pipe walls were equipped with regularly spaced square ribs of relative height $h/D = 0.154$, while the pitch-to-roughness height was varied between $p/h = 1.67$ and $p/h = 6.67$. The measurements include mean velocity components, Reynolds shear and normal stresses and pressure losses. It is investigated whether the effects of the large roughness on the (time and axially averaged) velocity profile can be described by the classical rough-wall formulation by allowing the value of the von Kármán constant to deviate from its standard value of 0.41.

1 Introduction

In many engineering problems involving fluid flow, the relevant surfaces are rough. This may be the unintentional result of corrosion, wear, fouling (as in case of the formation of deposits on the walls of industrial boilers or the hull of a ship), or the result of a manufacturing process (like the presence of weld lines or riveting). In other cases, the wall roughness is intentionally created to promote turbulence and enhance heat transfer (as in heat exchanger tubes). Pipe flow is of particular practical importance, and the effects of surface roughness on the main parameter of interest, i.e., the friction factor, has been the topic of many experimental and numerical investigations, see e.g. Jiménez (2004), or more recently, Chung et al. (2021) for an overview. Because of its practical relevance, there is a strong need for models that are able to reliably predict the mean flow and turbulence characteristics in pipes with (large) surface roughness and high Reynolds number, not only to determine the friction factor, but also to determine the occurrence of, e.g., cavitation (Schenker et al. 2013) or sound production (Eckeveld et al. 2020). The problem is complicated by the fact that there is a wide variation in shapes, sizes, and spatial distributions of the roughness elements, and multiple length scales may be needed to characterize a rough surface (Langelandsvik et al. 2008; Tao 2009; Tomas et al. 2017).

Initial experimental research on the effects of surface roughness in pipe flow was conducted in the 1930’s by Nikuradse who determined the (Darcy) friction factor ${f}_{\mathrm{D}}$ as a function of Reynolds number for a smooth wall and for walls with uniform sand grains of height ${k}_{\mathrm{s}}$, see e.g. Nikuradse (1950). Here, the friction factor ${f}_{\mathrm{D}}$ is defined as:

$$ f_{{\text{D}}} = \Delta p\frac{D}{L}/\left( {\frac{1}{2}\rho V_{D}^{2} } \right) $$

(1)

where $\Delta p$ is the pressure drop over a pipe segment with length L and inner diameter D, ρ the fluid density, and ${V}_{\mathrm{D}}$ the bulk velocity. For several other types of rough surfaces (e.g. staggered arrays of spheres, cones, etc.), Schlichting proposed to determine the equivalent sand grain size ${k}_{\mathrm{s}}$ that yields the same friction factor as that of the real rough surface in the fully rough regime (Schlichting 1936). The equivalent sand grain size of a particular rough surface cannot be determined from the geometrical characteristics of the roughness elements, but typically follows from an experiment where the friction factor of that rough surface is determined in the fully rough regime. Colebrook (1939) proposed the following equation for the friction factor in the intermediate and fully rough regime:

$$ f_{{\text{D}}} = \left( { - 2{\text{log}}\left( {\frac{{k_{{\text{s}}} }}{3.7D} + \frac{2.51}{{{\text{Re}}_{{\text{D}}} \sqrt {f_{{\text{D}}} } }}} \right)} \right)^{ - 2} , $$

(2)

where ${\text{Re}}_{{\text{D}}}$ is the Reynolds number based on the bulk velocity $V_{{\text{D}}}$ and the pipe inner diameter $D$. The well-known Moody chart displays the values of the friction factor $f_{{\text{D}}}$ as determined from Eq. (2) for rough pipe walls with different values of $k_{{\text{s}}} /D$ up to $k_{{\text{s}}} /D \approx 0.04$. For the (internal or external) flow over a rough wall, the mean velocity profile in the outer region is described by

$$ u^{ + } = \frac{1}{{\upkappa }}\ln \left( {y^{ + } } \right) + {\text{C}} - \Delta u^{ + } + \frac{2\prod }{{\upkappa }}W(y/R), $$

(3)

where ${\upkappa }\left( { = 0.41} \right)$ is the von Kármán constant, $C$ is a constant with a typical value of 5.1 (for smooth walls), $\Delta u^{ + }$ the roughness function, $W$ the wake function, and ${\Pi }$ the wake strength. Furthermore, $u^{ + } = u/u_{\tau }$ and $y^{ + } = yu_{\tau } /\nu$, where ${u}_{\tau }$ is the friction velocity, $y$ the wall normal distance, and $\nu$ the fluid kinematic viscosity. The use of Eq. (3) for the mean velocity profile in the outer region is based on Townsend’s similarity hypothesis (Townsend 1976) for flows over rough surfaces where it is assumed that the primary effect of the surface roughness on the logarithmic part of the outer layer is a shift of the mean velocity profile that is determined by the roughness function $\Delta u^{ + }$.

According to Jimenez (2004), the above classical approach is valid when the ratio of the roughness height $h$ to the boundary layer thickness δ (or pipe radius $R$) is less than approximately 0.025. The requirement $h/\delta < 0.025$ is not sufficient to guarantee the validity of classical theory. This was shown by Morgan and McKeon (2018) who considered boundary layer flow with periodic roughness with $h/\delta < 0.025$ but the roughness was such that the wall parallel length scales were much larger than h. Jimenez (2004) states that when the relative roughness height is sufficiently large $\left( {h/\delta > 0.025} \right)$ the effects of the roughness is no longer limited to the roughness sublayer, but instead extends across the shear layer and there will be little left of the original flow dynamics that characterize the classical theory. According to Jimenez (2004) such flows, i.e. when $h/\delta > 0.025$, can be better described as flows over obstacles, which implies that the effects of the roughness on the shear layer have to be investigated in detail for every roughness (or obstacle) geometry. This has severe consequences for many practical applications with relative roughness heights that are (much) larger than $h/\delta > 0.025$. For example, the ship-to-ship transfer of liquefied natural gas (LNG) relies on the use of flexible corrugated hoses with $h/R \approx 0.2$. An accurate prediction of the pressure loss in this high Reynolds number flow $\left( {{\text{Re}}_{{\text{b}}} > 10^{6} } \right)$ is very important since the LNG is transferred at near-boiling conditions, which makes it prone to local gas formation and cavitation (van Bokhorst and Twerda 2014).

There is, however, substantial evidence that the classical theory has a larger validity range in terms of $h/R$. Flack et al (2007) carried out measurements on smooth and rough flat plate boundary layers using sandpaper and wire mesh as roughness. They reported that there was no influence of the roughness on the mean velocity profile and Reynolds stresses in the outer layer even for the largest roughness elements considered with $h/\delta = 0.053$. Castro (2007) and Amir and Castro (2011) performed experiments in flat plate boundary layers and showed that for several types of rough surfaces both the mean velocity profiles and Reynolds stresses collapse for values of $\delta /R$ up to 0.15. Leonardi et al. (2003) used direct numerical simulations to study turbulent channel flow with transverse square bars mounted on one wall. The ratio of the bar height $h$ and the channel half height $H$ was $h/H = 0.2$. The results indicated that the measured mean velocities exhibited a logarithmic region, and could be fitted to the mean velocity profile in the outer region. Ryu et al. (2007) reported on the results of a numerical study of the flow through ribbed channels with $h/H = 0.1$. Their results indicated that the time- and space averaged velocity profile shows a logarithmic region even for the largest rib height.

In general, one may distinguish rough surfaces with the roughness elements placed at random locations from surfaces with structured roughness elements. Within the latter category, two-dimensional (2D) roughness elements (known as ribs) typically produce larger disturbances in the velocity field than their 3D equivalent (Flack and Schultz 2014). Repeated ribs refer to ribs that are placed at a regular streamwise spacing (or pitch) $p$. Perry et al. (1969) distinguished two types of repeated ribs denoted as d-type (which occurs for relatively small values of the pitch to roughness height ratio $p/h < 4$) and k-type roughness (which occurs for $p/h > 4$). An intermediate regime is defined around $p/h \approx 4$. In d-type roughness, more or less stable vortices are formed in the cavities in between the ribs with little shedding of vortices from these cavities, and the bulk flow is not strongly affected by the roughness height h. In k-type roughness, there is strong interaction between the cavity flow and the bulk flow through vortex shedding, and the characteristics of the flow strongly depend on the roughness height h.

Webb et al. (1971) performed a systematic investigation of flows through ribbed tubes specifically for ribs with a square cross section. They proposed a correlation for the friction factor valid for $p/h>10$. Han et al. (1978) considered the flow through channels that were equipped with repeated ribs (with square cross section) and extended the correlation proposed by Webb et al. (1971) to include the range $5 \le p/h \le 10$. However, both studies were limited to relatively small roughness heights $\left( {0.01 \le k/D \le 0.04} \right)$.

The present investigation focuses on the flow through ribbed pipes with very large relative roughness $(h/D=0.154)$ at relatively large Reynolds numbers $\left( {{\text{Re}}_{{\text{D}}} > 10^{5} } \right)$. The pitch to roughness height ratios considered vary between $p/h = 1.67$ and $p/h = 6.67$, which includes the intermediate regime. The main objective is to determine whether it is possible to describe the flow using a classical rough wall approach, despite the very large relative roughness. A secondary objective is to produce an accurate and extensive database on the turbulent flow through ribbed pipes with (large) repeated ribs that can be used for model development and validation.

2 Experimental setup

2.1 The flow loop

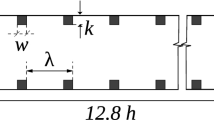
Figure 1 (top) shows a schematic of the flow loop that was used in this study. It includes a centrifugal pump, a flow meter, a 2.5-m long pipe segment (with internal diameter D = 50 mm) that is followed by the measurement section (also with 50 mm internal diameter). The pressure drop ${\Delta }p$ over the measurement section is measured with a differential pressure sensor (Validyne DP15 with 0–140 kPa pressure range and an inaccuracy of 0.25% of the full scale). The flow meter used in the experiment is a KROHNE electromagnetic flow meter (type: IFS 4000F/6) with an inaccuracy of 0.3% of the reading. Downstream of the measurement section is a diffuser that gradually increases the internal pipe diameter to 100 mm. This low-speed part of the flow loop acts as a de-aeration section. A Pt-100 thermometer measures the temperature of the water. This temperature was used to determine the viscosity and the density of the water. The maximum Reynolds number (based on bulk velocity and internal pipe diameter) that can be reached in this facility is ${\text{Re}}_{{\text{D}}} \approx 3.6 \times 10^{5}$. Figure 1 (bottom) shows a photograph of the measurement section when equipped with a number of ribs. The ribs have a rectangular cross section with a width $w/D = 0.19$ and a height $h/D = 0.15$ giving rise to a rib inner diameter of $d/D = 0.70$. The ribs are connected to each other with threaded brass rods, and only one rib is connected to the tube wall with screws as can be seen in the photograph. The number of ribs mounted in the measurement section varied between 5 and 10, while the pitch p (defined as the distance between the upstream edges of two consecutive ribs) varied between $p/h = 2.00$ and $p/h = 6.67$ in steps of $p/h = 0.667$. Some measurements were carried out for a smaller pitch of $p/h = 1.67$.

Fig. 1

Top: schematic of the flow loop with its main components. Bottom: photograph of the measurement section with ribs

2.2 PIV measurements

The PIV system uses a dual-cavity Nd:YLF laser (Litron LDY 304) as the light source. The laser emits a pulsed beam, which is transformed into an approximately 2 mm thick light sheet passing vertically upward through the centerline of the pipe. The laser sheet is somewhat wider than the field of view to reduce the effect of a lower light intensity near the edges of the light sheet. A telecentric lens (Vicotar, T240/0,27a) is mounted on a high speed camera (Photron Fastcam APX-RS) that is equipped with a CMOS sensor with 1024 × 1024 pixels of size 17 μm × 17 μm. The field of view has dimensions 65 × 65 mm² which is sufficient to cover the full pipe diameter and at least two ribs inside the field of view. A so-called “optical box”, consisting of a thin-walled rectangular box filled with the same liquid as the working fluid, i.e. water, is used to minimize optical distortion. It is not possible to obtain velocity data in the region between the top of the ribs $\left( {{\text{at}}\,{{\text{r}}} = D/2 - h} \right)$ and the centreline $\left( {{\text{at}}\,{{\text{r}}} = 0} \right)$, since the ribs are not fully transparent, and the refractive index of the rib material does not match the refractive index of water. Hollow glass spheres (Sphericel 110 P8) with a mean diameter of 10 μm were used as seeding particles.

Before applying the PIV algorithms, the individual images are pre-processed in three steps. Although the Nd:YLF laser used has a low pulse-to-pulse variation in energy, all images were normalized to minimize effects due to global intensity variations. Background subtraction is applied to remove reflections from the ribs and pipe walls. Finally, a 9 × 9 min–max filter (Adrian and Westerweel 2011) is used to normalize the contrast of the particle images; this reduces the occurrence of spurious vectors in the PIV evaluation. A digital mask was used to process only those parts of the images that contain PIV data. Details of the image preprocessing can be found in the thesis of Schenker-van Rossum (2022).

The estimated relative errors in the mean flow velocity and turbulence intensity are determined by using Eq. (9.41) and Eq. (9.47), respectively, presented in the book by Adrian and Westerweel (2011). Images were recorded at frame rates between 1000 and 7000 fps (depending on the flow velocity) with either 7561 or 14,563 frames collected; each data set covered at least 300 integral time scales, see Schenker-van Rossum (2022) for details. The error in the mean velocity relative to the bulk velocity is around 0.8% (r.m.s. value), for all flow conditions (given that the particle-image displacement complies with the 1/4-rule). The error in the turbulence level, i.e. $\left( {\overline{{u^{\prime 2} }} } \right)^{1/2}$, relative to the wall friction velocity is 4% (r.m.s. value).

3 Results

3.1 Pressure drop and friction factor

The pressure drop $\Delta p$ over the measurement section was measured for different bulk velocities and for different number of ribs in the measurement section. The pressure drop is then made dimensionless by introducing a loss factor $K$ as in

$$ K = \Delta p/\left( {\frac{1}{2}\rho V_{{\text{d}}}^{2} } \right), $$

(4)

where ρ is the water density and $V_{{\text{d}}}$ is the bulk velocity based on the rib inner diameter d. Figure 2 shows the loss factor $K$ as a function of the (rib inner diameter based) Reynolds number ${\text{Re}}_{{\text{d}}}$ for different values of the pitch as determined for a measurement section with eight ribs.

Fig. 2

Loss factor $K$ as a function of the Reynolds number ${\text{Re}}_{{\text{d}}}$ for different values of the pitch p and a measurement section with eight ribs

By repeating measurements for different number of ribs in the measurement section, the pressure loss factor per rib $K_{{{\text{rib}}}}$ in fully developed flow can be determined. Figure 3 illustrates the procedure to determine the value of $K_{{{\text{rib}}}}$ for an experiment with a pitch $p/h = 3.33$ and Reynolds number ${\text{Re}}_{{\text{d}}} = 2.8 \times 10^{5}$. The graph indicates that the value of $K$ linearly increases with the number of ribs when eight or more ribs are used. The slope of the linear trend line then gives the value of $K_{{{\text{rib}}}}$. The linear regime to which the trend line is fitted exists for every pitch and Reynolds number considered, indicating that the additional loss for every added rib becomes constant for sufficiently large number of ribs. The flow is considered fully developed in this regime.

Fig. 3

Illustration of the fitting procedure used to determine the dimensionless pressure loss per rib $K_{{{\text{rib}}}}$ for fully developed flow $(p/h = 3.33$, ${\text{Re}}_{{\text{d}}} = 2.8 \times 10^{5} )$. The goodness-of-fit for the dashed line is $R^{2} = 0.983$

The values of $K_{{{\text{rib}}}}$ obtained for every available Reynolds number are transformed into a Darcy-Weissbach friction factor $f_{{\text{D}}}$ to enable a direct comparison between the flow through the ribbed pipe and the more generic flow through pipes with sand grain type roughness. The relation between the friction factor $f_{{\text{D}}}$ and the loss factor per rib $K_{{{\text{rib}}}}$ is given by

$$ f_{{\text{D}}} = K_{{{\text{rib}}}} \frac{D}{p}\left( \frac{D}{d} \right)^{4} . $$

(5)

Figure 4a shows the friction factor $f_{{\text{D}}}$ as a function of Reynolds number ${\text{Re}}_{{\text{D}}}$ for different values of the pitch. The dashed lines in Fig. 4a represent the Colebrook friction correlation (see Eq. (2)) for several values of the relative roughness $k_{{\text{s}}} /D$. The representation of the friction factors determined from the Colebrook relation as in Fig. 4a implies that the geometry is interpreted as a pipe with inner diameter D with the roughness (due to the ribs) extending inward from the surface. As can be seen from the magnitudes of the relative equivalent roughness $k_{{\text{s}}} /D$ indicated on the right-hand side of Fig. 4a, this representation does not lead to a meaningful comparison as relative roughness values above 0.5 are clearly not physical.

Fig. 4

a Friction factor $f_{{\text{D}}}$ as a function of the bulk Reynolds number ${\text{Re}}_{{\text{D}}}$ for repeated ribs with square cross section. The dashed lines mark the friction factor as determined from the Colebrook correlation (Eq. (2)) for different values of the relative equivalent sand grain height $k_{{\text{s}}} /D$. b Friction factor based on the rib inner diameter $f_{{{\text{D}},{\text{rib}}}}$ as a function of ${\text{Re}}_{{\text{d}}}$ for repeated ribs with square cross section

Figure 4b shows the friction factor based on the same data as in Fig. 4a but with a different interpretation, i.e., the cavities between the ribs are considered roughness elements extending outward from a pipe with inner diameter $d$. This change in interpretation results in adjustment factors from ${\text{Re}}_{{\text{D}}} \;{\text{to}}\;{\text{Re}}_{{\text{d}}}$ of $D/d$ and from ${f}_{\mathrm{D}}$ to the friction factor based on the rib inner diameter $f_{{{\text{D}},{\text{rib}}}}$ of $\left( {d/D} \right)^{5}$. The results shown in Fig. 4b now appear shifted relative to the Colebrook friction correlation. The equivalent sand-grain roughness for both approaches can be calculated using Eq. (2), and are seen to be much smaller than in Fig. 4a.

It can be seen in Fig. 4a that the values of the friction factor $f_{{\text{D}}}$ approach an asymptotic value for sufficiently high Reynolds numbers. Figure 5 shows the dependence of the asymptotic value on the pitch. (The asymptotic values were determined as the mean of the friction factor values for ${\text{Re}}_{{\text{D}}} > 8.0 \times 10^{4}$). The graph indicates a linear trend of the friction factor with pitch, with the exception of the data point for $p/h = 1.67$, which indicates a change in regime coinciding with the transition between d-type roughness and intermediate-type roughness described in literature (see e.g. Perry et al. 1969). The linear trend line crosses the line $f_{{\text{D}}} = 0$ at a pitch of approximately 10 mm, which corresponds to the width of the ribs, $w$. This suggests that the physically relevant parameter for the scaling of the friction factor is the cavity width $l = p - w$ rather than the pitch $p$. The linear increase in the friction factor with increasing $p/h$ does not match the friction factor correlation for k-type roughness proposed by Webb et al. (1971) who have reported on a decreasing friction factor with increasing pitch for $p/h > 10$. However, the results for the pressure drag reported by Vijiapurapu and Cui (2007), who used large eddy simulations to study turbulent flow through ribbed pipes, indicated an increase in the friction factor between $p/h = 2$ and $p/h = 5$ which is consistent with the results shown in Fig. 5. The linear trend observed in the present measurements thus matches the characteristics of the intermediate roughness regime, despite the fact that the transition from intermediate-type to k-type roughness is expected to occur at a relative pitch of $p/h = 6$ (Jiménez 2004).

Fig. 5

The asymptotic values of the friction factor $f_{{\text{D}}}$ (extracted from Fig. 4) as a function of dimensionless pitch p/h. Note that this graph includes data for p/h = 1.67 (p = 12.5 mm)

3.2 Mean velocity and Reynolds shear stress distributions

Figure 6 displays the distribution of the axial mean velocity for two values of the pitch $\left( {p/h = 3.33\;{\text{and}}\;p/h = 5.33} \right)$ at ${\text{Re}}_{{\text{d}}} = { 1}.{6} \times {1}0^{{5}}$. When the axial mean velocity distribution is made dimensionless with the bulk velocity it appears that the distributions are virtually independent of Reynolds number. Therefore, in the remainder of this work the main focus will be on results for a single Reynolds number $\left( {{\text{Re}}_{{\text{d}}} = 1.6 \times 10^{5} } \right)$. Figure 6 indicates that the overall structure of the mean axial velocity distribution is that of a core flow with strong velocity gradients just above rib height, and recirculating flow inside the cavities in between the ribs. It can be seen that the mixing layer between the cavity and core flow is much thicker, and penetrates further into the cavity, for the larger pitch. It can also be seen that the streamwise variation of the mean flow increases with increasing pitch.

Fig. 6

Distribution of the mean axial velocity $\overline{u}$ for different values of the pitch at ${\text{Re}}_{{\text{d}}} = 1.6 \times 10^{5}$. Left: $p/h = 3.33$ (p = 25 mm), right: $p/h = 5.33$ (p = 40 mm). All dimensions are in mm. The bulk flow is from left to right. White lines represent streamlines. Vertical dashed lines indicate 25% (blue), 50% (green), and 75% (red) of the cavity width, see also Figs. 8 and 9

Figure 7 shows the distribution of the Reynolds shear stress for different values of the pitch between $p/h = 2.67$ and $p/h = 6.00$ in steps of $p/h = 0.67$ at ${\text{Re}}_{{\text{d}}} = { }1.6\, \times \,105$. Also shown in Fig. 7 are the streamline patterns as computed from the mean velocity vectors. A large recirculation zone at the downstream side of the cavity can be seen for all values of the pitch. It stretches in axial direction with increasing pitch and covers most of the cavity area. A much smaller secondary recirculation zone is present in the upstream corner of the cavity. For $p/h \approx 4$ (p = 30 mm), the core flow starts to enter the cavity area, moving further into the cavity with increasing pitch. The location of the center of the major recirculation region does not change in the axial direction with varying pitch. However, its location does change in wall-normal direction, with initially an increase in wall-normal position followed by a slight decrease from $p/h = 4.00 - 4.67$.

Fig. 7

Distribution of the Reynolds shear stress $- \overline{{\rho u^{\prime } v^{\prime } }}$ for values of the pitch between $p/h = 2.67$ $\left( {p = 20\,{\text{mm}}} \right)$ and $p/h = 6.00$ $\left( {p = 45\,{\text{mm}}} \right)$ in steps of 5 mm at ${\text{Re}}_{{\text{d}}} = 1.6 \times 10^{5}$. The bulk flow is from left to right. All dimensions are in mm. White lines represent streamlines

3.3 Spatially averaged mean velocity and Reynolds shear stress

In the fully developed region, the mean flow and Reynolds shear stress distributions were spatially averaged in the axial direction over one or more full pitch lengths. Figure 8 shows the spatially-averaged axial mean velocity profiles for six different pitch values at ${\text{Re}}_{{\text{d}}} = 1.6 \times 10^{5} .$ The maximum axial mean velocity occurs at the pipe centerline and increases with increasing pitch. This is consistent with a shift from a mean velocity profile with very steep gradients at rib height and shallow gradients further toward the core (for small pitch) to a mean velocity profile with less steep gradients near rib height but extending much further toward the core (for large pitch). The mean axial velocity becomes zero at approximately half the rib height for all values of the pitch and thus becomes negative in the region below that. Note that the axial mean velocity profiles do not resolve the thin viscous region where the mean velocity approaches zero at the wall.

Fig. 8

Effect of pitch on the spatially-averaged axial mean velocity for ${\text{Re}}_{{\text{d}}} = 1.6 \times 10^{5}$. The dashed lines represent profiles of the axial mean velocity at 25% (blue), 50% (green), and 75% (red) of the cavity width, see Fig. 6

Figure 9 shows the spatially-averaged Reynolds shear stress for six different pitch values at ${\text{Re}}_{{\text{d}}} = { 1}.{6} \times {1}0^{{5}}$. For all pitch values, the profiles appear to increase linearly from zero at the pipe centerline to a maximum close to the rib crest. However, the subsequent decrease in the profiles toward zero inside the cavities appears to strongly depend on the pitch, similar to the findings that have been reported by Coceal et al. (2006) for staggered and aligned arrays of cubical obstacles mounted on a flat wall.

Fig. 9

Effect of pitch on the spatially averaged Reynolds shear stress for ${\text{Re}}_{{\text{d}}} = { }1.6\, \times \,10^5$. The dashed lines represent profiles of the Reynolds shear stress at 25% (blue), 50% (green), and 75% (red) of the cavity width, see Fig. 6

From the Reynolds shear stress and the gradient of the axial mean velocity, the effective mixing length $l_{{\text{m}}}$ can be computed as:

$$ l_{{\text{m}}} = \frac{{\left( {\overline{{u^{\prime } v^{\prime } }} } \right)^{1/2} }}{{{\text{d}}\overline{u}/{\text{d}}y}}. $$

(6)

Figure 10 shows the resulting values of the mixing length $l_{{\text{m}}}$ as a function of wall distance for two different values of the pitch. Following the arguments by Coceal et al. (2006), assuming a linear relation of the effective mixing length with the wall normal coordinate, $y$ , expressed by the relation

$$ l_{{\text{m}}} = {\upkappa}\left( {y - d_{{\text{h}}} } \right), $$

(7)

is equivalent to fitting a logarithmic mean velocity profile with the parameters ${\upkappa }$ and $d_{{\text{h}}}$, which are the von Kármán constant and displacement height, respectively. Castro (2009) and Leonardi and Castro (2010) argued that the von Kármán constant ${\upkappa }$ might not be a constant in flows with large wall roughness. In the present study, the effective mixing length expression in Eq. (7) is fitted to the measured values determined from Eq. (6) in two different ways: (1) assuming the von Kármán constant has the standard value ${\upkappa } = 0.41$ with the displacement height $d_{{\text{h}}}$ variable, and (2) assuming both ${\upkappa }$ and $d_{{\text{h}}}$ are variable. The magenta lines in Fig. 10 are the least-squares fits of Eq. (7) to the linear region of the mixing length data for a fixed value of the von Kármán constant, ${\upkappa } = 0.41$, and variable displacement height $d_{{\text{h}}}$. The green dashed lines represent the least-squares fits when both ${\upkappa }$ and $d_{{\text{h}}}$ are assumed to be variables.

Fig. 10

Effective mixing length $l_{m}$ as a function of wall distance for $p/h=2.67$ (top) and $p/h=5.33$ (bottom) at Reynolds number ${\text{Re}}_{{\text{d}}} = { 1}.{6}\, \times \,{1}0^{{5}}$. The right-hand side shows a zoom-in of the relevant region. The green dashed lines represent the least-squares fit of Eq. (7) to the linear region of the mixing length data. The magenta line is the least-squares fit for a fixed value of the von Kármán constant, ${\upkappa } = { }0.41$

It can be seen in Fig. 10 that the fitting process that treats both ${\upkappa }$ and $d_{{\text{h}}}$ as variables yields the most accurate results, especially for the larger values of the pitch. It is also observed in Fig. 10 that the linear region of the effective mixing length $l_{{\text{m}}}$ occupies only a small portion of the flow. This is consistent with the expectation that the logarithmic region of the mean velocity profile does not extend far toward the centerline of the pipe or within the cavity region.

Figure 11 (top) shows the values of the von Kármán constant ${\upkappa }$ resulting from the two different fitting procedures. The corresponding values for the dimensionless displacement height $d_{{\text{h}}} /h$ are shown in Fig. 11 (bottom). Significant scatter is observed in the results for both parameters. However, an increase in the value of ${\upkappa }$ with increasing pitch is evident. The dimensionless displacement height $d_{{\text{h}}} /h$ is larger than 1 for the smallest value of the dimensionless pitch $p/h$, consistent with the findings of Coleman et al. (2007). For increasing values of the pitch the displacement height is either continuously decreasing (for ${\upkappa } = 0.41$) or the displacement height is close to the rib height (for variable ${\upkappa }$). The decrease in the displacement height with increasing pitch is also consistent with the results reported by Coleman et al. (2007). The obtained values of ${\upkappa }$ and $d_{{\text{h}}}$ are used as input parameters for the expression of the mean velocity profile for a rough wall given by (see Perry et al. 1969 or Jackson 1981)

$$ u^{ + } \left( y \right) = \frac{1}{{\upkappa }}\ln \left( {y^{ + } - d_{{\text{h}}}^{ + } } \right) + {\text{C}} - \Delta u^{ + } , $$

(8)

where $d_{{\text{h}}}^{ + } = d_{{\text{h}}} u_{\tau } /\nu$. Equation (8) has two independent unknowns, i.e., the friction velocity $u_{\tau }$ and the roughness function $\Delta u^{ + }$. The values of these unknowns then follow from a least-squares fit to the logarithmic region.

Fig. 11

The values of the von Kármán constant ${\upkappa }$ (top) and the dimensionless displacement height ${d}_{\mathrm{h}}/h$ (bottom) as a function of the dimensionless pitch $p/h$. The green symbols pertain to the results obtained from the fitting process by using the standard value of the von Kármán constant, i.e. ${\upkappa } = 0.41$. The blue symbols show the results obtained when the value of ${\upkappa }$ was optimized as part of the fitting process

Figure 12 shows the thus found values of the roughness function in terms of the additive constant $F$ defined as

$$ F = C - \Delta u^{ + } + \frac{1}{{\upkappa }}\ln \left( {h^{ + } } \right), $$

(9)

where $\left( {h^{ + } = hu_{\tau } /\nu } \right)$ as a function of the dimensionless pitch $p/h$ for three different Reynolds numbers (colored spheres). The black symbols are the results reported by Coleman et al. (2007) for the turbulent flow through an open channel with height $H$ where the bottom wall is equipped with two-dimensional square ribs with relative roughness height $h/H$. In the present experiment, the relative roughness height $\left( {h/D = 0.154} \right)$ is significantly larger than that considered by Coleman et al. (2007), but the use of a variable value of the von Kármán constant ${\upkappa }$ enables the application of Eq. (8) to adequately describe the mean flow profiles despite the much larger relative roughness.

Fig. 12

The values of the additive constant F as a function of the dimensionless pitch $p/h$. The colored spheres correspond to the three Reynolds numbers considered in the present study (blue: ${\text{Re}}_{{\text{d}}} = { 4}.{3}\, \times \,{1}0^{{4}}$; green: ${\text{Re}}_{{\text{d}}} = { 1}.{6}\, \times \,{1}0^{{5}}$; red: ${\text{Re}}_{{\text{d}}} = { 2}.{5}\, \times \,{1}0^{{5}}$). The black symbols correspond to the results for rectangular ribs placed on the bottom of an open channel with water height $H$ (Coleman et al. 2007). Solid spheres: $h/H=0.09$, open squares & triangles: $h/H=0.1$, open circles: $h/H=0.06.$ The solid line represents the theoretical limit for $h/H=0$

Apart from the roughness function, the least-squares fit of the mean velocity profile given by Eq. (8) to the measured mean velocities also yields the value of the friction velocity $u_{\tau }$. Figure 13 illustrates the resulting fits for $p/h = 4.00$ (with ${\upkappa } = 0.46$) and for $p/h = 6.0$ (with ${\upkappa } = 0.64$). Once the friction velocity $u_{\tau }$ is known, the total friction can be determined using the height at which the computed wall shear stress acts as the effective radius rather than the pipe radius $R = D/2$. This is logically the same height as the displacement height $d_{{\text{h}}}$, which is by definition the virtual origin of the logarithmic layer. In accordance with the method described in Coceal et al. (2006), the effective wall shear stress acting on the pipe surface $\tau_{0}$, is obtained by extrapolating from a distance $d_{{\text{h}}}$ to the wall. The effective friction velocity $u_{\tau }^{*}$ then follows from:

$$ u_{\tau }^{*} = u_{\tau } \left( {R/\left( {R - d_{{\text{h}}} } \right)} \right)^{1/2} . $$

(10)

This gives the friction factor as $f_{{\text{D}}} = 8\left( {u_{\tau }^{*} /V_{{\text{D}}} } \right)^{2}$. Figure 14 shows the computed friction factor $f_{D}$ for all considered values of the pitch and three different Reynolds numbers. Also shown are the friction factors as determined from the pressure measurements (reproduced from Fig. 5). The agreement between the two data sets is satisfactory up to a pitch of $p/h = 4.67$ (p = 35 mm), with the friction factor based on the PIV measurements only slightly underestimating the friction factor based on the pressure measurements (Fig. 13). For larger pitch values, the friction factors determined from the PIV measurements are significantly lower than those determined from the pressure measurements. This may be the result of the increasing spatial variation of the mean velocity profiles and the Reynolds shear stress profiles within the cavity for increasing values of the pitch as can be seen in Figs. 8 and 9.

Fig. 13

Fit of the mean velocity profile given by Eq. (8) to the measured mean velocities for $p/h=4.00$ with ${\upkappa } = 0.46$ (top) and for $p/h=6.0$ with ${\upkappa } = 0.64$ (bottom)

Fig. 14

The friction factor ${f}_{\mathrm{D}}$ as a function of the dimensionless pitch $p/h$. The open spheres represent the results that follow from the pressure loss measurements; the red $\left( {{\text{Re}}_{{\text{d}}} = { }4.3\, \times \,10^4} \right)$, green $\left( {{\text{Re}}_{{\text{d}}} = { }1.6\, \times \,10^5} \right)$ and blue $\left( {{\text{Re}}_{{\text{d}}} = { }2.5\, \times \,10^5} \right)$ solid spheres follow from the fit of the mean velocity profile, Eq. (8), to the experimental data

4 Conclusion

The pressure loss, mean flow, and turbulence statistics were determined for pipe flow where the pipe wall was equipped with roughness elements in the form of repeated ribs with a square cross section and relative height $h/D = 0.154$. The measurements were carried out for a Reynolds number of ${\text{Re}}_{{\text{D}}} = 1.6 \times 10^{5}$ and the pitch to roughness height values varied between $p/h = 2.7$ and $p/h = 6.0.$

The axially averaged Reynolds shear stress and axially averaged velocity profiles were used to determine the mixing length, which is then used to derive the displacement height and the von Kármán constant ${\upkappa }$. The latter is not considered to be a constant but allowed to vary with the pitch. This resulted in relatively large deviations of ${\upkappa }$ from the commonly accepted value of approximately 0.41, but the agreement of the logarithmic region of the measured mean velocity profiles with the fitted velocity profile according to the theory for rough-walled flows was much better.

The use of a non-universal interpretation of ${\upkappa }$ enables the common parametrization of a rough-wall flow to be extended to larger values of the relative roughness height $h/D$. However, care must be taken to use and interpret the resulting parameters, since the friction factor derived from the fitted velocity profile does not match the measured friction factor when the rib spacing increases beyond $p/h \approx 5$. One may speculate on the physical mechanism leading to the increasing values of ${\upkappa }$ with increasing values of the relative pitch $p/h$. One remark is that in the range of relative pitch values considered in this work, the friction factor still strongly increases with relative pitch, rather than decreasing as it would for k-type roughness. Also, the mixing length in the core of the flow, as shown in Fig. 10, has clearly increased for the higher pitch values, indicating that throughout the tube the turbulent mixing process has changed.