1 Introduction

Vortices in all sizes and scales, from tiny coherent vortical structures in turbulent flows up to mesoscale dimensions, are the substantial ingredients of complex flow phenomena. Due to their fundamental importance in fluid dynamics, their general behavior and interactions in vortex systems have been analyzed thoroughly in numerous theoretical, experimental and numerical studies over the past decades, see, e.g., Saffman and Baker (1979); Widnall (1975); Leweke et al. (2016). Vortices play an important role in many engineering applications, such as the straight vortex pair trailing from large aircraft or helical vortex systems generated behind helicopter or wind turbine rotors. The persistence of those vortex systems is often associated with unwanted consequences, such as the wake vortex hazard for following aircraft (Rossow and James 2000) or blade–vortex interactions causing noise emissions and structural vibrations for helicopters (Yu 2000). In these situations, a rapid breakdown of the vortex systems is considered beneficial, and mechanisms such as instabilities are of interest to destabilize concentrated vortex structures. These instability phenomena can be separated into two groups, cooperative instabilities affecting systems consisting of two or more vortices, and instabilities that occur in a single vortex under certain external flow conditions. For both straight and curved vortices, the cooperative instabilities split into long- and short-wave phenomena, when relating the wavelength of the unstable perturbations to the vortex core diameter (Leweke et al. 2016). Widnall (1972), Gupta and Loewy (1974) and Okulov (2004) provided theoretical analyses of the long-wavelength instabilities of multiple interlaced helical vortices, and corresponding experimental work was performed by Quaranta et al. (2019). Long-wavelength instabilities provoke deformations of the entire vortex structure with minimal impact on the vortex core. In comparison, the short-wavelength mechanisms mainly arise within the core regions and lead to an accelerated core growth.

Short-wavelength phenomena in helical vortex systems include elliptical (Moore and Saffman 1975; Kerswell 2002) and curvature instabilities (Hattori and Fukumoto 2014). Leweke et al. (2014) showed experimental evidence of their presence within helical vortex systems. Additional theoretical and numerical studies evaluated the influence of various vortex parameters, such as axial flow (Roy et al. 2008) and torsion of the cores (Blanco-Rodríguez and Le Dizès 2016), on the instability growth rates. In addition, the presence of short-wavelength instabilities has an effect on the vortex merging phenomena, which occurs for closely spaced vortices of equal rotational sense. After merging, the resulting vortex exhibits a widened core and decreased peak vorticity, in comparison to its predecessor vortices (Meunier et al. 2005). Short-wavelength instabilities further enhance these outcomes (Meunier et al. 2005). Vortex merging combined with the occurrence of these phenomena represents a possible scenario for a fast decay of concentrated vortex systems.

Besides cooperative instabilities, a single vortex can also be affected by other mechanisms that are independent of the presence of other concentrated vortices. One example is the vortex breakdown phenomenon, which consists in the bursting of a concentrated vortex due to an external destabilizing agent, such as an axial pressure gradient, see Escudier (1988) and Delery (1994) for comprehensive reviews. Another instability phenomenon affecting vortices is the centrifugal instability. This mechanism occurs in vortices whose radial circulation gradient changes sign with increasing distance from the vortex center. An accumulation of opposite-signed vorticity in the vicinity of the vortex core is the reason for this behavior. The physical origin of this instability mechanism and methods to determine the instability growth rates is described in the theoretical work of Bayly (1988) and Billant and Gallaire (2005, 2013).

The present work investigates interaction phenomena in closely spaced helical vortex pairs. One global objective is to discover configurations enforcing instabilities which disrupt the system of concentrated blade tip vortices in the wake of a rotor. It was expected that this system is mainly affected by cooperative instabilities, which depend on the initial characteristics of the flow. However, previous experimental studies revealed that the evolution of certain helical vortex pairs was dominated by centrifugal instabilities (Schröder et al. 2021, 2021). The unstable pairs exhibited an immediate pronounced core growth and rapidly merged into a single vortex. The physical origin of the centrifugal instability affecting the vortices is still unclear. One hypothesis includes the presence of the vorticity layer of opposite sign than the one of the tip vortices, resulting from the particular radial bound circulation distribution along the blade. The additional tip vortex might capture parts of this vorticity sheet and transport it to the tip vortex pair shortly after emerging from the trailing edge. The influence of blade trailing shear layers on the vortex wake of rotors in hover operation has recently been studied experimentally by Wolf et al. (2019) and Schwarz et al. (2022). They observed the formation of secondary vortex structures surrounding the primary vortices as a result of shear layer interaction with preceding tip vortices. Similar structures had also been observed in numerical studies (Jain 2018; Abras et al. 2019, 2020). However, before the first experimental evidence given in Wolf et al. (2019), it was unclear if those structures are an actual physical phenomenon or a numerical artifact.

Fig. 1
figure 1

Geometry of the additional fin mounted on the pressure side to create the second tip vortex. The parameters shown in (a) are held constant, whereas those shown in (b) are varied in this study

Full size image

More recently, snapshots of preliminary volumetric velocity measurements conducted with a simplified single-bladed rotor equipped with a tip fin confirmed the existence of similar structures in the helical tip vortex pair generated by this rotor configuration (Schröder et al. 2022). In order to further analyze the three-dimensional instability effects on these vortex pairs and their temporal evolution, time-resolved volumetric Lagrangian particle tracking (TR-LPT) measurements for different fin configurations are performed for the present contribution. Additional dye visualizations give a qualitative impression of the wake structure. In order to determine the influence of the trailing shear layer on the instability formation and the presence of secondary structures, a newly designed blade geometry with a qualitatively different spanwise circulation distribution is also investigated and compared with the initial design. Preliminary phase-averaged planar particle image velocimetry (2C-PIV) is carried out to examine the characteristics of the shear layers for the two designs without the fin modification to allow comparison with the theoretically predicted radial circulation distributions.

The paper is organized as follows. The blade tip modifications, the two blade geometries and the experimental setup used for the TR-LPT, 2C-PIV and dye visualizations are presented in Sect. 2. The results of the experimental measurements are shown in Sect. 3, where both blade designs are compared and several different vortex pairs are analyzed in detail. We end conclusions and an outlook on future work in Sect. 4.

2 Experimental measurements

Two different blade geometries were investigated under identical external flow conditions in the large recirculating water tunnel of the Institute of Aerospace Systems with a test section of 1.5 m width, 1 m height and 6.5 m length. Both rotors were equipped with a single blade and were operated in conditions near hover. The rotor radius is \(R=240\) mm for both geometries. Due to the enclosed test section, a small free-stream velocity of \(u_\infty =11.4\) cm/s is required to prevent the flow from developing recirculation regions near the blade tips affecting the vortex systems. The nominal rotation rate was set to \(f=1\) Hz, which results in a tip chord-based Reynolds number \(Re = 2\pi fRc/\nu =120\),000 (c: constant blade chord; \(\nu\): kinematic viscosity) and a tip speed ratio of \(\Lambda =2\pi fR/u_\infty =13\). The rotor is mounted on a shaft having a length of 1.8 rotor diameters, driven through a gear box by a motor outside the test section.

The helical vortex pair is generated by a special tip geometry used for both blades. A perpendicular fin with a NACA0012 cross section is mounted on the pressure side of the blade close to the tip region. The developing vortex system is influenced by the geometric specifications of the fin (radial position d, height h, chord \(c_f\) and angle of attack \(a_f\)), see Fig. 1. The rotation axis for the fin is located at 25% of the blade chord c.

Fig. 2
figure 2

Radial distributions of geometric twist (orange) and corresponding theoretical circulation (blue) for the initial design (index ‘1’, dashed lines) and the new design (index ‘2’, solid lines). Shaded segments represent the hub and transition regions

Full size image

2.1 Rotor geometry

The difference between both blade designs lies mainly in their bound circulation distributions. The initial blade design, in the following referenced as blade 1, originated from preliminary fixed wing measurements (Schröder et al. 2022), investigating the general functionality of the fin as a vortex generator and the effects of the geometric parameters on the vortex system. Transferring the findings for the fixed wing to the rotating system was the targeted outcome of the following blade design process. The cross section has a NACA0012 profile with a slight geometric twist along the radial coordinate to allow for operation in hover conditions. For simplicity, no aerodynamic twist was included in the design (the effective angle of attack is constant along the blade), the focus  lay  on the vortex generation process. Sufficient spatial resolution of the velocity measurements, especially in the core region, is crucial for an accurate determination of the characteristic parameters through the optical measurement system. Therefore, it was decided to set the chord length to \(c=80\) mm to guarantee a sufficiently large initial vortex core size, which typically scales on the tip chord. The chord is kept constant for the outer 75% of the blade radius. Due to these geometric specifications, the radial circulation distribution of the initial blade is characterized by an almost linear growth with increasing radius, until reaching a maximum close to the tip. In order to analyze the effect of the circulation distribution (and the resulting shear layer propagating downstream) on the vortex system and its stability, a second blade was designed with a significantly different qualitative distribution. Comparable to wind turbine blades, the target was a nearly constant circulation over most of the blade span, with a steep in- and decrease in the hub and tip regions, respectively. The emerging tip vortex strength is mainly determined by the circulation maximum close to the blade tip. The new design (blade 2) aimed at having a similar maximum value as the initial blade, to allow for a pertinent comparison. A combination of aerodynamic and geometric twist enabled a constant chord of \(c=80\) mm for the new design as well. Two cross section profiles were used for the new geometry: a SD7062 profile (Selig 1995) in the hub region due to its good lift performance at low Reynolds numbers and again a NACA0012 profile in the tip region. Between the outer profiles, new profile geometries were interpolated to allow for a smooth geometric transition. The corresponding lift and drag data of the new profile geometries were evaluated using XFOIL (Drela 1989). Figure 2 shows the geometric angle of attack \(\theta\) over the radial coordinate for both blade designs, as well as the corresponding theoretical circulation distributions.

For both blades, a variety of fin configurations were analyzed, chosen on the basis of a previous parameter study using planar PIV measurements (Schröder et al. 2021). All configurations were manufactured via rapid prototyping  on a stereolithography printer. An overview of the different geometric and external flow parameters used in the experiments is given in Table 1. As a reference, both designs are also investigated without additional fin (hereafter referred as unmodified blades).

Table 1 External flow and geometric parameters for both blade designs and tip configurations used in the experiments
Full size table
Fig. 3
figure 3

a Schematic of the experimental setup for the time-resolved volumetric Lagrangian particle tracking measurements (isometric view). b Global coordinate system and positioning of the measurement volume and plane used for the TR-LPT and planar PIV measurements, respectively

Full size image

2.2 High-speed particle tracking velocimetry

Time-resolved Lagrangian particle tracking measurements (TR-LPT) were carried for out for both blade designs with different fin configurations using the “Shake-The-Box” (STB) method introduced by Schanz et al. (2016) to analyze both the three-dimensional characteristics and the temporal evolution of the vortex interaction process.

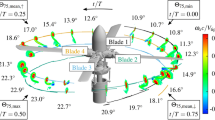
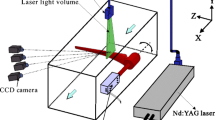
Figure 3a displays a schematic of the linear camera setup applied for the measurements. The global coordinate system introduced for subsequent data analysis is found in Fig. 3b, showing also the position of the measurement volume and plane with respect to the blade. Four high-speed cameras (Phantom v2640), operated at their full sensor resolution of \(2048\times 1920\) pixels, were used to acquire the particle images at a recording frequency of \(f_{\textrm{rec}}=1\) kHz. Following the recommendation given by Schröder and Schanz (2023), the outermost cameras had an angle of 90\(^{\circ }\), which allows appropriate projections for multicamera systems in volumetric particle tracking measurements. In order to avoid pixel-locking errors (Raffel et al. 2018) during the data evaluation, which might reduce the reconstruction fidelity of the tracking algorithm, peak locking filters were installed in front of the camera sensors. Synchronized triggering was obtained using an optical encoder mounted on the rotor shaft. Water-filled prisms and Scheimpflug adapters minimized optical aberrations and astigmatisms resulting in blurred particle images. For the outermost cameras (Cam 1 & Cam 4), lenses with 200 mm focal length were used; the lenses of the inner cameras have a focal length of 100 mm. An f-number of 16 was set for all lenses to ensure a suitable depth of focus over the entire volume. A high-speed laser (Photron DM30-527-DH) with an energy output of 30 mJ per pulse was used for flow illumination; the laser was positioned below the water tunnel. The beam was expanded using the Volume Optics Module from LaVision. Both optics and laser were installed on adjustable linear axes allowing accurate positioning with respect to the rotor. The center of the measurement volume, whose dimensions are 100 mm \(\times\) 100 mm with a depth of 80 mm, was positioned directly below the rotor axis. As a consequence of the self-induced velocities and the free-stream flow, the vortex pair is located within the measurement volume only for a limited time span (phase interval of \(\Delta \varphi \approx 50^{\circ }\)), which makes a complete time-resolved recording of the same vortex pair for one rotor revolution an impossible task. To account for the vortex motion, the rotor position is also adjustable (\(\Delta x, \Delta y\)) through linear axes. In total, 8 different rotor phases, \(\varphi =[10^{\circ }, 60^{\circ }, 110^{\circ }, 160^{\circ }, 210^{\circ }, 260^{\circ }, 310^{\circ }, 360^{\circ }]\), were recorded for various fin configurations on both blade designs to track the vortex evolution. The flow was seeded with cubic polyamide particles of mean diameter 50 \(\upmu\)m and density \(1.016\;\textrm{g}/\textrm{cm}^3\). A two-level target positioned in multiple planes perpendicular to the volume depth was used for calibration of the camera system. In order to account for the high sensitivity of volumetric measurement techniques and the need of a highly accurate calibration, a subsequent volume self-calibration (VSC) introduced by Wieneke (2008, 2018) was performed, combined with the calculation of an optical transfer function (OTF) (Schanz et al. 2013). The particle shapes in the different subvolumes vary due to altering imaging conditions, this is taken into account by the OTF to improve the track reconstruction. The complete calibration procedure, the recording and the subsequent processing of the particle images  were carried out using the commercial PIV/PTV software DaVis 10.2.1. Post-processing of the data was performed by in-house algorithms.

2.3 Planar particle image velocimetry

Planar particle image velocimetry measurements are performed to investigate the vorticity sheet behind both rotor blade designs without the fin modification. Using the installed linear axes, the measurement plane is positioned as close to the rotor as possible to acquire the flow field immediately behind the trailing edge (Fig. 3b). Images were acquired using a single camera (Imager sCMOS, \(2048\times 2048\) pixels), the installed rotary encoder ensured accurate phase-triggered recording. Flow illumination was carried out with a double-pulsed laser providing an effective pulse energy of 120 mJ and appropriate light sheet optics. Three fields of view of 120 mm \(\times\) 120 mm were acquired to cover the entire shear layer from tip to hub. For each measurement, 400 frames were recorded. Calibration, recording and processing were done in DaVis 8.4. The obtained data were  also evaluated by in-house algorithms.

2.4 Dye visualizations

Accompanying dye visualizations were conducted for a qualitative impression of the wake in the near field. Fluorescent dye activated by ultraviolet light was injected into the flow via internal channels in the models. A membrane pump adjusted the volumetric flow rate of the dye solution to match the blade tip speed based on the rotational rate of the rotor. Images were recorded by means of two high-speed cameras (Phantom v2640) from different perspectives.

3 Results

Fig. 4
figure 4

Contours of the  phase-averaged azimuthal vorticity component directly behind the trailing edge of the unmodified rotor blades. a Blade 1; b blade 2

Full size image
Fig. 5
figure 5

Dye visualizations of the tip vortex evolution of both unmodified rotor blades. a Blade 1; b blade 2

Full size image

3.1 Wake characteristics

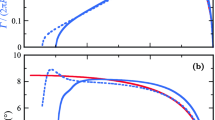
The measurements of the unmodified blade geometries are used to investigate the wake characteristics and circulation distributions for both blade designs. In order to analyze the vorticity sheet behind the blades, the planar PIV measurements performed in the trailing edge plane are evaluated. The outer parts close to the tip vortex are particularly relevant, in view of the expected influence of the secondary vortex. Figure 4 shows the averaged contours of the azimuthal vorticity component for the initial (left) and new (right) blade determined from the velocity data obtained with PIV. Both geometries generate a concentrated tip vortex structure combined with a shear layer containing both positive and negative vorticity regions. The corresponding dye visualizations are presented in Fig. 5. Both tip vortices retain their concentrated structure and show no indication of any unstable behavior. The small variations in the helix pitch hint at different induced axial velocities, which corresponds to the theoretically predicted circulation distributions. The velocity fields are used to deduce the radial distribution of bound circulation on the blades, and the result is displayed in Fig. 6. Comparison with the theoretical calculations in the design process shows good agreement for the maxima for both geometries, but slight deviations in the tip vortex regions. It should be pointed out that the distributions obtained with this method are not able to reflect the exact physical distribution along the radial coordinate. Due to the displacement of the measurement plane with respect to the rotor axis (compare Fig. 3b), the influence of the shaft boundary layer is not taken into account. The presence of the boundary layer combined with the hub vortex should result in a strong decrease of the circulation distribution in vicinity of the hub. Nevertheless, the employed methodology is able to identify the qualitative difference between the circulation distributions, and therefore the vorticity layers generated by both blade designs. As expected, the shear layer of the new blade 2 exhibits almost equal amounts of positive and negative vorticity layers, causing a small increase of the bound circulation moving inwards from the tip vortex. This is in strong contrast to the shear layer generated by the initial blade 1, which is dominated by counter-rotating vorticity in relation to the tip vortex, resulting in a reduced circulation closer to the hub. The pronounced geometric twist of the new design (see Fig. 2) causes a slightly convex shear layer distribution.

Fig. 6
figure 6

Radial circulation distribution for both blade designs. Solid lines represent the theoretical values, dashed lines show the experimental distributions, determined from measurements in the trailing edge plane. The distributions of blade 1 are shown in blue the red lines correspond to blade 2. Shaded segments represent the hub and transition regions

Full size image

The measured wake characteristics show the desired differences between both blade designs. The effect of the resulting shear layers on the instability is investigated in the following sections.

3.2 Vortex pair evolution

The evolution of the vortex pairs and the instability effects are captured by the TR-LPT measurements. All of the following experimental results were generated by blades equipped with the additional fin, we start with the analysis of blade 1. All calculated particle fields obtained by the STB processing are transformed to uniform Cartesian grids applying the VIC+ (‘Vortex-In-Cell plus’) methodology introduced by Schneiders and Scarano (2016). The significant advantage of VIC+ in comparison to other reconstruction techniques is its reduced sensitivity to seeding density, thus allowing reconstructions with high accuracy even in flow regions with low seeding concentration (Schneiders and Scarano 2016).

The reconstructed Cartesian grids have a spacing of 22 volumetric pixels, which corresponds to approximately 1.6 mm. Previous stereoscopic PIV measurements had shown that the smallest initial vortex core diameters are \(a_\textrm{min}\approx 0.05c\) (Schröder et al. 2021). Accordingly, the reconstruction results in a spatial resolution of at least 5 independent vectors per vortex core radius. The velocity reconstruction allows the calculation of characteristic vortical flow quantities, such as the vorticity, and \(Q-\) and \(\lambda _2\)-parameters (Jeong and Hussain 1995).

Fig. 7
figure 7

Vortex evolution for blade 1 illustrated by isosurfaces (\(\omega _{z,n,\textrm{iso}}\)) and contours of the normalized vorticity (z-component, x-y slice extracted at \(z/R=0\)) for two configurations with \(\alpha _f=14^{\circ }\) and \(h/c=0.3\). (a-d) \(d/c=0.2\); (e-h) \(d/c=0.3\). The view direction is changed for (h)

Full size image

Previous measurements performed with blade 1 had shown that fin configurations close to the tip (\(d/c=0.2\)) are particularly affected by instabilities resulting in a rapid core growth and vortex merging (Schröder et al. 2021). Choosing fin angles of \(\alpha _f=14^{\circ }\) and \(\alpha _f=16^{\circ }\) produces initial circulation ratios between fin and tip vortex of \(\Gamma _{f,\textrm{SPIV}}/\Gamma _{t,\textrm{SPIV}}\approx 1\), which is assumed ideal for the subsequent merging process (Meunier et al. 2005). The configurations with a slightly increased fin distance (\(d/c=0.3\)) generate a weaker fin vortex, due to a decrease in its effective angle of attack.

Table 2 Circulation ratios between fin and tip vortex of different parameter configurations for blade 1
Full size table
Fig. 8
figure 8

Shear layer distribution around the vortex pair at \(\varphi =60^{\circ }\) for the same configurations as shown in Fig. 7: \(\alpha _f=14^{\circ }\), \(h/c=0.3\). a \(d/c=0.2\); b \(d/c=0.3\)). Isosurfaces show positive (green, \(\omega _{z,n,\textrm{iso}}=5\)) and negative (blue, \(\omega _{z,n,\textrm{iso}}=-1\)) normalized azimuthal vorticity

Full size image

The circulation values are also evaluated for the volumetric measurements by analyzing each extracted flow field in planes perpendicular to the z-direction. For each slice, the minima of the \(\lambda _2\)-parameter define the centers of the primary vortices. Based on their positions, the vortex separation distance b is calculated and chosen as the diameter of the circular area around each vortex for the circulation evaluation. A projection of the velocity fields onto a local polar grid \((\rho ,\phi )\) is used for the analysis. For each instantaneous volume, the obtained values are averaged in the z-direction to determine the circulation ratio between tip and fin vortex. The ratios of the vortex pairs generated by the initial blade 1 are given in Table 2. As expected, an increased distance to the tip results in slightly weaker fin vortices, due to the reduced effective angle of attack caused by the decreased rotational velocity component. Compared to the values obtained from the previous SPIV measurements, the circulation ratios from the time-resolved measurements are slightly increased, due to the absence of averaging the frames before the evaluation. The determined relations confirm that fin angles of \(\alpha _f=14^{\circ }\) and \(\alpha _f=16^{\circ }\) generate initial ratios of approximately 1 or even higher. Consequently, these configurations were chosen for subsequent investigations with blade 2.

Despite the small difference between configurations with \(d/c=0.2\) and \(d/c=0.3\), the evolution of the corresponding vortex pairs is strongly different. Figure 7 visualizes the evolution of two typical vortex pairs, both configurations having a fin angle \(\alpha _f=14^{\circ }\) and a fin height \(h/c=0.3\). The tip distance is varied; Fig. 7a–d has a distance of \(d/c=0.2\), and Fig. 7e–h displays the outcome for \(d/c=0.3\). Isosurfaces of the normalized vorticity (z-component) \(\omega _{z,n}=\omega _{z}c/(2\pi fR)\) reveal the vortex geometry, the blade leaves the measurement volumes in negative z-direction. The contours show distributions of the vorticity in slices extracted from the middle of the corresponding volumes. At a rotor phase of \(\varphi =20^{\circ }\), the initial vortex pair in Fig. 7a is already affected by three-dimensional perturbations, observable as small wavy core deformations. In contrast, only the fin vortex exhibits a similar behavior for the configuration in Fig. 7e. With increasing rotor phase, the amplitudes of these perturbations grow, resulting in highly disturbed cores for Fig. 7b. In this phase, the critical merging ratio between the vortex core radii a and the core distance b (see Leweke et al. (2016); Meunier and Leweke (2001)) is exceeded for certain regions along the core, due to a reduced separation distance b and the pronounced growth of the vortex core radii a, causing the onset of merging. A detailed description of the core evolution and the development of a/b is given in Schröder et al. (2021). The merging process is visible in Fig. 7c-d). A highly disturbed structure is formed, distinct cores are not observed anymore. The vorticity, which was initially concentrated in both distinct vortex cores, is spread out into a larger region. Due to the conservation of angular momentum, the peak vorticity values steadily decline as the merging progresses, displayed in the development of the extracted contours. In comparison, the evolution of the second configuration in Fig. 7f–h proceeds differently. Here, only the fin vortex is influenced by instability effects, leading to its eventual collapse. The tip vortex retains its structure during the entire period and is still detectable at a rotor phase of \(\varphi =230^{\circ }\) in Fig. 7h. The presence of the destabilized fin vortex causes a weakening of the tip vortex and a combined slight growth of the vortex core radius, though a complete merging is not observed. After the disintegration of the fin vortex, the dispersed vorticity is wrapped around the tip vortex, comparable to a partial merging process as described in Dritschel and Waugh (1992); Brandt and Nomura (2010). For these cases, the tip vortex stabilizes after the partial merging is completed and continues propagating downstream. The core growth is now solely governed by viscous diffusion, resulting in small core growth rates. After a complete rotor revolution, a concentrated tip vortex is still observed, which is in strong contrast to the merging outcome for the first case with \(d/c=0.2\). For those cases, the disturbed structure stabilizes after the merging is completed and results in an extremely widened vortex core (by a factor 5 compared to a vortex of the same age generated by a blade without fin, compare Schröder et al. (2021)) and a drastically reduced peak vorticity.

Increasing the fin angle to \(\alpha _f=16^{\circ }\) results in a very similar development of the generated vortex pairs despite the slightly changed circulation ratios. The initial separation distance appears to be crucial for the instability affecting both vortices, or solely the fin vortex.

For all configurations, the fin vortices are strong enough to entrain and relocate parts of the shear layer to the vicinity of the tip vortex. This effect is illustrated in Fig. 8 for the same configuration as shown in Fig. 7 at a rotor phase \(\varphi =60^{\circ }\), using isosurfaces of positive and negative vorticity. In both cases, portions of the shear layer are wrapped around the fin vortex and transported in the region between both vortices.

Table 3 Circulation ratios between fin and tip vortex of different parameter configurations for blade 2
Full size table
Fig. 9
figure 9

Radial circulation profiles for tip (blue) and fin vortex (red) of the configuration \(h/c=0.2\), \(d/c=0.2\), \(\alpha _f=14^{\circ }\) for both blades. The single tip vortex profile obtained from an unmodified blade is shown in black. Data extracted for a rotor phase \(\varphi =20^{\circ }\)

Full size image
Fig. 10
figure 10

Dye visualizations of the wake evolution for blades equipped with an additional fin ( \(h/c=0.2\), \(d/c=0.2\), \(\alpha _f=14^{\circ }\)). a Blade 1; b blade 2

Full size image
Fig. 11
figure 11

Vortex evolution for blade 2 illustrated by isosurfaces (\(\omega _{z,n,\textrm{iso}}\)) and contours of the normalized vorticity (z-component, x-y slice extracted at \(z/R=0\)) for two configurations with \(\alpha _f=14^{\circ }\) and \(h/c=0.3\). a–d \(d/c=0.2\); e–h \(d/c=0.3\)

Full size image

In comparison to the vortex pair evolutions observed for configurations based on blade 1, the corresponding cases for blade 2 are remarkably different. It was expected that the fin parameter combinations results in similar circulation ratios as for blade 1. However, the circulation analysis for blade 2 reveals that the circulation ratios, presented in Table 3, are notably lower than the corresponding values for blade 1. Even for combinations close to the tip with high angles of attack \((\alpha _f=[14^{\circ },16^{\circ }]\), \(d/c=0.2)\), the fin vortex reaches only 50–60% of the tip vortex strength. Investigation of the individual vortices shows that the fin vortex is weaker in comparison to blade 1, and in addition the tip vortex is considerably stronger for blade 2 resulting in the decrease of \(\Gamma _{f}/\Gamma _{t}\). Figure 9 displays examples of extracted radial circulation profiles for tip and fin vortex generated by the configuration with \(h/c=0.2\), \(d/c=0.2\), \(\alpha _f=14^{\circ }\) for both blades; the data is extracted at a rotor phase \(\varphi =20^{\circ }\). As a reference, the profile for the single tip vortex generated by the corresponding unmodified blade is also plotted. For both blades, the addition of the fin generates a higher total circulation (combined tip and fin vortex) in comparison to the reference. The dye visualizations displayed in Fig. 10 qualitatively illustrate the differences in the evolution of both vortex pairs. No merging process is visible for blade 2; the tip vortex retains its concentrated structure and shows no evidence of external disturbances. In contrast, both vortices for blade 1 are affected by perturbations immediately after leaving the trailing edge and ultimately form a single vortex with a strongly widened core, consistent with the analysis presented in Fig. 7a–d.

Unfortunately, the differences in the circulation ratios complicate a direct comparison between the evolution of the generated vortex pairs with respect to the instability effects. The imbalance in vortex strength favors a partial merging process. Disturbances affecting the weaker fin vortex are likely caused by the presence of the much stronger tip vortex, whose induced strain rips it apart, and not related to any instability effect. Typical quantitative vortex pair evolutions for blade 2 are shown in Fig. 11, the vortex pairs are generated by the same fin parameter configurations as in Fig. 7. The vortex pair initially rotates, similar to the development seen for blade 1, until the weaker fin vortex is disrupted by the influence of the dominant tip vortex. In Fig. 11d and h, a distinct fin vortex is no longer observable, its disrupted structure is entangled around the tip vortex. For both configurations, the vortex structure of the tip vortex indicates no clear sign of an instability influence. The concentrated structure persists until a rotor phase of \(\varphi =230^{\circ }\). A conclusive statement on the influence of the shear layer trailing from the inner blade on the occurrence of centrifugal instabilities of the tip vortices based on the current data is not possible, due to the lack of vortex pairs with equal strength for blade 2.

3.3 Secondary structures

Fig. 12
figure 12

Formation and evolution of secondary structures between the vortex cores for different fin parameter combinations of blade 1 in different rotor phases: a–c \(h/c=0.2\), \(d/c=0.2\), \(\alpha _f=14^{\circ }\), d–f \(h/c=0.2\), \(d/c=0.2\), \(\alpha _f=16^{\circ }\), g–i \(h/c=0.3\), \(d/c=0.2\), \(\alpha _f=14^{\circ }\), j–l \(h/c=0.3\), \(d/c=0.2\), \(\alpha _f=16^{\circ }\). Isosurfaces show the normalized z-component of the vorticity (green, \(\omega _{z,n,\textrm{iso}}\)) and the total vorticity (orange, \(\omega _{\textrm{tot},n,\textrm{iso}}\))

Full size image

The unstable configurations found for blade 1 are analyzed in detail to gain insight into the instability development and potential formation of secondary structures. The vortex development displayed in Fig. 7 for blade 1 indicates the effects of the centrifugal instability on the vortex core geometry. Theoretical analyses of centrifugally unstable vortices predict wavy perturbations of the core structure, combined with the occurrence of secondary vortex structures in the vicinity of the cores. For the special case of an unstable vortex pair, the secondary structures are expected to appear in an S-shaped structure between both primary cores. Given their expected spatial orientation with respect to the primary vortex axes (perpendicular, dominated by x- and y-components of the vorticity), the total vorticity is suited to reveal secondary structures in the measurement volumes. Figure 12 shows the formation of secondary structures and their development for the investigated configurations of blade 1, vortex pairs with circulation ratios \(\Gamma _{f}/\Gamma _t\approx 1\) or even higher. Isosurfaces of the azimuthal (green) vorticity allow one to visualize the primary vortex cores, the secondary vortices are shown using isosurfaces of the total vorticity (orange). The presence of these structures appears to be linked to the instability strength affecting the vortex pair. In the case of two unstable vortices, as in Fig. 12a–c, d–f, the formation of the secondary structures is visible immediately after the vortex pair leaves the trailing edge. With increasing rotor phase and increasingly perturbed primary cores, the geometries of the secondary structures evolve into more chaotic states, until they fully entangle both primary cores at a rotor phase of \(\varphi =90^{\circ }\).

The configurations with a tip distance of \(d/c=0.3\) are characterized by a stable tip vortex and an unstable fin vortex. This feature is also reflected by the occurrence of secondary structures, which are primarily formed in the vicinity of the fin vortices, compare Fig. 12g–l. With an increasingly irregular fin vortex at rotor phases \(\varphi =90^{\circ }\), certain structures start to stretch out toward the tip vortices. However, the tip vortex remains in a stable state for both configurations, the disruptive influence of the structures is too weak to affect the cores in a notable manner.

Fig. 13
figure 13

Examples for configurations with a notably weaker tip vortex and thus strongly reduced occurrence of secondary structures having similar strength as the primary vortex cores a Blade 1, \(h/c=0.2\), \(d/c=0.3\), \(\alpha _f=10^{\circ }\), b Blade 1, \(h/c=0.2\), \(d/c=0.3\), \(\alpha _f=16^{\circ }\), c Blade 2, \(h/c=0.3\), \(d/c=0.2\), \(\alpha _f=14^{\circ }\), d Blade 2 \(h/c=0.3\), \(d/c=0.2\), \(\alpha _f=16^{\circ }\). Isosurfaces show the normalized z-component of the vorticity (green, \(\omega _{z,n,\textrm{iso}}\)) and the total vorticity (orange, \(\omega _{\textrm{tot},n,\textrm{iso}}\))

Full size image

In vortex pairs with a considerably weaker fin vortex, secondary structures of similar strength as the primary vortices are not observed, compare Fig. 13. In related numerical work investigating the characteristics of secondary structures in hovering rotor wakes, Bodling and Potsdam (2022) showed that, in their configuration, the origin of those structures is connected to the entrainment portions of the blade shear layer around the corresponding tip vortex. The break-up of the shear layer into coherent structures forms the secondary vortices. An experimental confirmation of this mechanism was given by Schwarz et al. (2022). The tip modification presented in this study further enhances this transport process, due to the presence of a second vortex generated by the fin. Its initial position further downstream additionally increases the entrainment potential, which explains the prompt detection of the secondary structures after both vortices leave the trailing edge. Consequently, weaker fin vortices have a reduced entrainment capability for a shear layer redistribution, which inhibits the formation of secondary structures.

Since the fin vortices generated by blade 2 are significantly weaker than their counterparts of blade 1, the effect of a different shear layer distribution on both instability and secondary structure formation is not soundly established. The blade geometry needs to be redesigned to generate pairs of equally strong vortices to determine a link between these phenomena.

4 Conclusions

A comprehensive experimental study of various helical vortex pairs was performed with water tunnel experiments. The vortex pairs were generated using a one-bladed rotor in hovering conditions. The blade tip is equipped with a parametric fin on the pressure side to generate the second vortex. The main goal of this modification is a beneficial interaction between the closely spaced vortices, which eventually leads to a vortex merging process resulting in a tip vortex with a larger core radius and a decreased peak vorticity. Subsequent fluid–structure interactions and the connected negative effects, such as vibrations and noise generation, can possibly be reduced in this way. Time-resolved volumetric Lagrangian particle tracking velocimetry measurements were carried out to capture the temporal development of the vortex cores and their interaction. Several vortex combinations are affected by the presence of centrifugal instabilities enforcing a rapid core growth and accelerating the merging. Low initial separation distances between the vortex centers and a strong fin vortex appear to prompt the occurrence of the instability, which causes the formation of secondary vortex structures in the vicinity of the primary pair. Their development is captured in the volumetric velocity data. Similar structures have been documented in related numerical and experimental work investigating hovering rotors with conventional blade designs (Wolf et al. 2019; Schwarz et al. 2022; Bodling and Potsdam 2022). The interaction between tip vortex and the trailing vorticity layer of the blade is believed to cause the formation of these structures. The initial position of the fin vortex with respect to the blade tip yields a strong potential for relocating the vorticity layer around the tip vortices (depending on the vortex strength), which explains the pronounced occurrence of secondary structures for this special case. To determine the connection between the vorticity layer characteristics and instability effects, a second blade design with a qualitatively different radial circulation distribution was also investigated. Unfortunately, the tip vortex formed by the new design was too strong, and generating vortex pairs of nearly equal strength was not possible. The much stronger tip vortices rapidly disrupted the weaker fin vortices, and no instability effect was observed. Consequently, the hypothesis that the origin of the instability formation is found in the vorticity layer characteristics remains unclear. To address this issue in future measurement campaigns, the second blade design will be modified to reduce the initial tip vortex strength. Supporting numerical investigations to verify the resulting radial circulation distributions and determine the drag characteristics of the fin are also planned.