1 Introduction

Understanding fluid behavior under different conditions and obtaining reliable results from numerical simulations rely heavily on thermophysical properties of materials. A significant thermophysical property in describing material behavior is surface tension. It is essential to processes involving liquids with free surface, disintegration of liquid jets (Stückrad et al. 1993), atomization (Henein et al. 2017), welding and in the determination of the direction of Marangoni convections in melt pools (Kou 2002; Brillo and Egry 2005), additive manufacturing and many related simulations (Francois et al. 2017; Chouhan et al. 2022). Surface tension is highly sensitive to temperature (Palmer 1976; Nogi et al. 1986) and can be altered by the smallest of impurities and contaminations (Passerone et al. 1990; Mills and Su 2013). Many reliable methods can be used to determine the value of surface tension in liquids, some of which include the sessile drop method, maximum bubble pressure method, pendant drop and drop weight (Keene 1993a, b; Drelich et al. 2002; Egry et al. 2010; Mills and Su 2013). These methods, however accurate, require contact with the liquid in question over extended periods of time. For the cases of liquids at low temperatures, this is standard practice. The problem arises when attempting to determine the surface tension in liquids at higher temperatures (above 500 K), as they can easily engage in chemical reactions through contact with the measurement equipment. This problem has been solved by developing non-contact methods for high temperature liquids, e.g., molten metals (Keene 1993a, b). In this study, Rayleigh’s equation has been revisited (Rayleigh 1879) to determine surface tension of molten metals using oscillating droplets. For a laminar, incompressible flow with constant density the Rayleigh frequency is defined as:

$$\omega_{{\text{n}}}^{2} = n\left( {n - 1} \right)\left( {n + 2} \right)\frac{\sigma }{{\rho_{{{\text{drop}}}} R_{{{\text{drop}}}}^{3} }}$$
(1)

which is a description of the eigenfrequencies of an oscillating droplet with radius \({R}_{\mathrm{drop}}\), density \({\rho }_{\mathrm{drop}}\), surface tension \(\sigma\) and oscillation mode number \(n\). The mode of interest is \({\text{n}} = { }2\), which corresponds to a pure prolate to oblate oscillation of a spheroid with deformations in vertical and horizontal direction (Tsamopoulos and Brown 1982). For this mode of oscillation Eq. (1) is reduced to:

$$\omega_{2}^{2} = \frac{8\sigma }{{\rho_{{{\text{drop}}}} R_{{{\text{drop}}}}^{3} }}$$
(2)

This equation is valid for incompressible liquids with low viscosity and at small oscillation amplitudes. For metal droplets, small amplitudes are frequently defined in literature as droplets having an initial deformation (aspect ratio) of smaller than 10% (Soda et al. 1978).

The oscillating droplet method has been used to determine surface tension for several decades and has been successfully demonstrated in microgravity by Egry et al. (1995), Egry et al. (1999), Fujii et al. (2000), Mohr et al. (2019a, b), on the International Space Station (ISS) by Mohr et al. (2019a, b), and in parabolic flights (Chen and Overfelt 1998; Wunderlich 2008). These environments provide the ideal experimental conditions due to absence of a gravitational force on the droplet. However, they impose restrictions regarding cost, effort and choice of material.

Limited research is available on oscillating droplets of molten metal in free-fall. Few examples include the study by Moradian and Mostaghimi (2008), in which they used an inductively coupled plasma torch to heat rods of pure copper and nickel to observe the droplets forming at the end of the rod and their oscillations in free-fall in an inert argon atmosphere after detachment from the rod. Their findings show reasonable agreement with the literature. In another study by Matsumoto et al. (2005) an electromagnetic levitator is used to levitate and melt a sample of pure copper. The levitator is then turned off, causing the droplet to experience free-fall over a short distance. The oscillations of the drop were analyzed and the surface tension was measured without any correction terms. Their results also showed good agreement with literature.

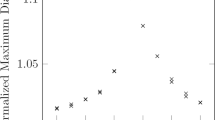
Other aspects to consider are the effect of droplet size and initial deformation on the surface tension predictions. These effects were closely investigated in studies by Tsamopoulos and Brown (1982) and Chen and Overfelt (1998). Tsamopoulos and Brown observed a quadratic decrease in frequency with increasing droplet initial deformation, as a consequence of nonlinear flow dynamics. Their findings are valid for a time-dependent, irrotational and incompressible motion of an inviscid drop. The analytical solution of their study is reproduced in Fig. 1a and compared to the numerical results by Foote (1973). On the x-axis, the major-to-minor axis ratio (a/b) is plotted, while the y-axis shows the deviation from the Rayleigh frequency. The analytical solutions are in good agreement with numerical computations.

Fig. 1
figure 1

a Comparison of the analytical solution of Tsamopoulos and Brown (1982) with the numerical results of Foote (1973). Foote used a droplet with the following characteristics: \({R}_{\mathrm{drop}}\) = 0.06 cm, \(\nu\) = 0.06 cm2s−1, \(\sigma\)= 75 mN m−1 and \(\rho\)= 1 g cm−3. b Comparison of the frequency predictions of Rayleigh’s equation to measured oscillations as a function of droplet diameter by Chen and Overfelt (1998). Droplet mass of the previous study is converted to droplet diameter using a density value of 7.81 g cm−3 from Harrison et al. (1977), Brillo and Egry (2003)

Full size image

Chen and Overfelt measured the surface tension of molten nickel onboard a parabolic flight. Figure 1b shows their frequency measurements in comparison with the predictions of Rayleigh’s equation for a nickel droplet with a surface tension of 1.78 Nm−1. It can be observed that at diameters of above 3 mm, the experimental measurements deviate rapidly from theoretical predictions.

Table 1 provides an overview of the environment and the sample size used in some of the aforementioned studies. In many of these experiments the droplet diameter varies between 3 and 8 mm. Based on the deviation of measurements from theory at such large diameters, Rayleigh’s theory seems invalid for these droplets. Therefore, the development of a technique to generate smaller droplets is beneficial.

Table 1 A selection of studies and their measurement environment and droplet diameter
Full size table

In addition to the effects of droplet size and initial deformation, the atmosphere in which the measurement takes place has a considerable impact on surface tension. A study by Saravanan et al. (2002) showed a significant decrease in surface tension under an atmosphere of nitrogen + 4% hydrogen at temperatures above 1100 K. Measurement methods such as electromagnetic levitation require observations over several minutes or longer to achieve the desired data to determine surface tension. This prolonged exposure to a possibly contaminated atmosphere increases the chances of the droplet engaging in unwanted chemical reactions with the surroundings, resulting in lower values of surface tension caused by atmospheric impurities.

This study proposes the utilization of a molten metal droplet generator, introduced by Imani Moqadam et al. (2019a), which operates on the drop-on-demand principle and can be used to create oscillating droplets for the determination of surface tension in molten metals. This generator has the ability to produce several thousand droplets within a single experiment and allows for the adjustment of droplet diameter between 0.3 and 2 mm, which is more compatible with Rayleigh’s theoretical work. Moreover, a measurement time of less than 20 ms helps reduce the effects of unwanted contamination. Examining several droplets at the same temperature provides a reliable error margin for the measurements. The suitability of this droplet generator for the aforementioned measurements is evaluated through various numerical and experimental investigations, which will be discussed in detail in the following sections.

2 Methodology

2.1 Numerical model

Here, the goal is to examine the extent to which the Rayleigh equation can be used to determine surface tension for our experimental cases. The effect of gravity, tilt and asymmetry of the droplet on the resulting frequency have been examined. For the numerical computations the Computational Fluid Dynamics (CFD) module of COMSOL Multiphysics 5.6 was utilized to model the droplet and the surrounding gas. Both the liquid and the gas phase are considered laminar, incompressible and isothermal with constant density. The Navier–Stokes equations for this flow were solved in conjunction with the boundary conditions listed in Table 3. The two main boundary conditions that need to be satisfied are: the continuity of velocity and the continuity of shear stress. The former indicates that the velocity components perpendicular to the interface must be continuous across the interface. The latter implies that the tangential stress components at any point on one side of the interface must be equal to the tangential stress components at the same point on the other side of the interface. Figure 2 displays the schematics of the defined geometry and the boundary conditions, marked with numbers corresponding to equations in Table 3. Case (I) through (IV) are three-dimensional and case (V) and its variations are two-dimensional. The used approach is based on an Arbitrary Lagrangian–Eulerian (ALE) formulation, which tracks the interface between the two laminar fluids using a moving mesh method. The corresponding equations were solved with a segregated solver in the 3D and with a fully coupled approach in the 2D case. Different geometries were used for each case of the simulations, starting with an asymmetric droplet and simplifying down to an ellipsoidal droplet, followed by a two-dimensional axially-symmetric ellipse. Case (I) consists of an asymmetrical three-dimensional droplet subject to gravity. Case (II) has the same geometry with an exception of a tilt angle of 20° and is also subject to gravity. In case (III) the asymmetric droplet is replaced by a symmetric ellipsoid of the same volume. Case (IV) is a repetition of case (III) minus the effect of gravity. Case (V) is the two-dimensional version of case (III) and (IV). Table 2 gives an overview of all study parameters. Note that the droplet geometry in cases (I) and (II) is a combination of two half-ellipsoids. The minor axis of the larger half-ellipsoid is equal to the major axis of the smaller half-ellipsoid. The axis lengths are given in Table 3, with subscripts i and ii. The length of the gas domain is adapted in each case depending on gravity and initial velocity. The reference pressure and temperature are set to 1 atm and 293.15 K, respectively. Dynamic viscosity of nitrogen is assumed 1.4 × 10–5 Pa s with a density of 1.250 kg m−3. Density and dynamic viscosity of copper are set to 7900 kg m−3 and 4 × 10–3 Pa s, respectively (Assael et al. 2010). Surface tension of copper is set to 1.29 N m−1 (Schmitz et al. 2009). The outer edges of the gas domain are defined as an open boundary. A fluid–fluid interface is defined at the boundary of the two phases. Table 3 summarizes the boundary conditions used in the model. Table 4 includes the final mesh resolution values.

Fig. 2
figure 2

Geometry of the model for different cases. Case (I) to (IV) are in 3D and Case (V) and its variations are in 2D. The corresponding boundaries are numbered in case (V). Boundaries are identical in all cases.  Condition number 1 (axial symmetry) does not apply to 3D cases

Full size image
Table 2 Summary of the study parameters and cases
Full size table
Table 3 Boundary conditions used in the model
Full size table
Table 4 Mesh resolution in the 3D and the 2D case
Full size table

2.2 Experimental setup and parameters

A drop on demand droplet generator is used to create droplets of molten metal. The generator is equipped with an induction coil and a crucible with an opening at the bottom. The sample is melted using the induction coil. The temperature of the melt is measured with a type B thermocouple. The droplet generation assembly is located inside a stainless-steel cylindrical tower, purged constantly with an inert gas. An additional vacuum nozzle helps remove the oxygen from the crucible prior to the experiment. After a slight vacuum is created, the crucible is purged with argon. This process is repeated 3–4 times to insure low levels of oxygen inside the crucible. The oxygen value of 50 ppm is measured inside the tower, in close proximity to the crucible. This value decreases with increasing crucible temperature throughout the experiment to values as low as 10 ppm, due to the formation of carbon dioxide.

The droplets are created with a pneumatic drop on demand principle and the aim is to produce a single oscillating droplet. However, experiments have shown that a longer pressure pulse, results in a generation mode between ideal single droplets and a continuous jet mode, producing 3–5 droplets at a time. The last droplet to exit the crucible typically has a larger initial deformation and lower initial velocity. This allows for more time to capture images of the droplet in motion. The droplet generation process triggers a high-speed camera (iX cameras, i -speed 210) and a CCD-camera (the imaging source, DFK 38GX267). High speed images are used to determine the oscillation frequency of the produced droplets and CCD images to determine the droplet diameter with higher resolution. Each pixel is equal to 1.34 × 10−5 m and 2.85 × 10–6 m in case of the high-speed and CCD camera, respectively. The CCD camera has an internal delay of a few milliseconds (depending on the droplet generation mode and initial velocity) to capture the droplet at its spherical form. Figure 3a shows the schematics of the droplet generator assembly. Figure 3b displays the actual generator as the droplets leave the crucible. Pure copper (Cu 99.99%, Goodfellow GmbH) was chosen for validation of the method. The sample was in the form of granulated copper and was cleaned with ethanol and rinsed with water and dried prior to the experiments.

Fig. 3
figure 3

a An Illustration of the droplet generator  and b the actual droplet generator and a produced droplet (b)

Full size image

3 Analysis

3.1 Simulation data

The change in projection area of the droplet over the symmetry plane is extracted and the oscillation frequency is determined based on two separate methods: (a) a Fast Fourier Transform (FFT) and (b) fitting of a sine function with the method of least squares. The frequency resolution of the used FFT analysis (approx. 50 Hz) proved to be insufficient in this study; however, it can be used to determine the mode of oscillation based on the number of peaks in the spectrum. The extracted frequency from the sine function is used in Eq. (2) along with the equilibrium (spherical) diameter of the droplet and the input density to determine the surface tension.

3.2 Experimental data

The change in droplet projection area over time is extracted from the captured high-speed images using an image analysis algorithm. In this algorithm, the images are imported, cropped and binarized to provide a clear droplet edge. The major and minor axes of the droplet in each image are measured and droplets with an initial deformation of under 5% (a/b < 1.05) are used to determine the droplet volume with the assumption of symmetry. The frame rate of the recordings is between 4000 and 5200 frames per second (fps). The droplet spends 10–15 ms in the frame, depending on its initial velocity. Droplets with low initial velocity are preferred, since they allow more observation time and thus more data points. The same method as in 3.1 is applied to the resulting area over time to extract the frequency. The frequency and volume are used in Eq. (2) with density values from the literature to calculate surface tension at each temperature.

4 Results and discussion

4.1 Simulation results

4.1.1 Three-dimensional

4.1.1.1 Mesh independence study

In order to establish the independency of the results from the grid resolution, a mesh sensitivity study was performed. The geometry used for this sensitivity study-case (I) is described in Table 2, which consists of an asymmetrical droplet subject to gravity, with an initial deformation of 1.5. This geometry was chosen for the analysis due to its relative complexity in comparison with other geometries in this study. The results of the independence study are displayed in Fig. 4a. The diagram shows the oscillation frequency of the projection area of the droplet over different element counts. Due to the initial deformation of 1.5, analytical solutions of Tsamopoulos suggest a frequency, which is 5% lower than the ideal Rayleigh frequency (which is equal to 347 Hz for \({{D}}_\text{drop}\)=1.3 mm). The reduced frequency (329 Hz) is shown as a line in Fig. 4a. The element count was increased, until stabilization of results was achieved. At the final chosen resolution, a frequency of 337 Hz was measured. This corresponds to a 2% deviation from analytical predictions. Due to a strong increase in computational effort and minimal change in the results, further mesh refinement was unnecessary beyond this point. Figure 4b shows half of the final meshed domain with an increased element count at the edges for better interface-tracking. The final element count is presented in Table 4. A typical droplet shape at the time of detachment from a nozzle under terrestrial conditions is included in Fig. 4c to further clarify the choice of geometry. To further investigate the applicability of the chosen ALE approach for this case, a check of the conservation of droplet volume was performed. A maximum change of mere 0.03% was observed, which could be due to discretization errors and the remeshing process and can be neglected. A graphical representation is included in the supplementary data.

Fig. 4
figure 4

a Mesh independence study in 3D, b the final resolution of the grid and c a typical droplet shape at the time of detachment from a nozzle

Full size image
4.1.1.2 Effect of tilt angle

When producing droplets with the droplet generator, droplets may exit the crucible with a slight tilt angle (between 1° and 10°), which might result in droplet rotation over time. In order to examine the effect of the tilt angle on the oscillation pattern of an asymmetrical droplet, an initial tilt angle of 20° from the vertical position was assigned to the droplet. This value is deliberately larger than the realistic angle of rotation of the droplets in order to examine the resulting changes in oscillation in extreme cases.

In Fig. 5, the simulated droplets are compared to copper droplets produced experimentally. The first and second row are a comparison of vertical droplets and the droplets on the third and fourth row are slightly tilted. In addition to the contour of the oscillating droplet, the velocity vectors inside the droplet domain are plotted in this figure. The color bar represents the velocity magnitude in ms−1. It can be observed that the droplet core has little to no engagement in the oscillatory motion and the movement mostly occurs at the droplet edges (Fig. 6). When a small droplet oscillates at low initial deformations, the motion is primarily confined to the droplet’s periphery due to the interaction between surface tension and viscosity. Surface tension generates a restoring force that acts to return the droplet to its equilibrium shape and is strongest where the curvature of the droplet’s surface is greatest, i.e., at the edges. Viscosity, on the other hand, creates a damping effect that opposes the motion of the droplet and is greater at the droplet’s center. This interaction results in the oscillation of a droplet being primarily localized to its periphery, with relatively little motion at the droplet’s core. The simulated droplets accurately replicate the oscillation behavior of the physical droplets. Figure 6a illustrates the oscillation pattern of two types of asymmetrical droplets, one tilted and one vertical over a 20 ms timespan. The results indicate that the tilt angle has minimal impact on the oscillation frequency, enabling the analysis of droplets oscillating in the second mode, even when tilted, for the calculation of surface tension. It is noteworthy, that this was only examined for a tilted droplet in free-fall. Tilted droplets with initial velocity might display a different oscillation pattern over longer observation periods.

Fig. 5
figure 5

Simulated droplets in comparison with experimentally produced droplets. The tilt angle of the droplet is deliberately chosen larger than the realistic rotation angle to examine an extreme case. The diameters of simulated droplets and experimental droplets vary slightly. The color bar gives an overview of the magnitude of the velocities inside the droplet. The oscillating motion of the droplet is mostly concentrated at droplet edges and less at the droplet core

Full size image
Fig. 6
figure 6

a Oscillation pattern of an asymmetrical tilted droplet and an asymmetrical vertical droplet in comparison and b oscillation pattern of an asymmetric tilted droplet from three different view angles on the same plane. Both graphs display simulation results

Full size image
Fig. 7
figure 7

a Comparison of the oscillation of an asymmetric droplet with a symmetric droplet in free-fall and b comparison of the oscillation of a symmetric droplet subject to gravity with a droplet subject to no gravity. Both graphs display simulation results

Full size image
4.1.1.3 Effect of viewing angle

When measuring the oscillation of droplets, it is important to account for the effect of camera’s perspective. To assess the impact of this factor, a series of images were generated from the tilted simulated droplet in the previous section as observed from three different angles within the same plane. This was done to determine whether unidirectional imaging is sufficient for determining the correct oscillation frequency. Images were created at observation angles of 0°, 45° and 90°. The change in the projection area over time for all three angles was extracted using the image analysis algorithm, described in Sect. 3. The patterns of oscillation are plotted in Fig. 6b. All three patterns display a similar oscillation frequency. At an observation angle of 90°, a faster damping of the oscillation is visible. This finding has potential implications for determining the viscosity of oscillating droplets and requires further investigation in future studies. The frequency of the oscillation at all angles remains consistent, indicating that the camera angle has minimal impact on the measured droplet oscillation. These results confirm that a unidirectional view of the droplet suffices in determining accurate frequencies.

4.1.1.4 Effect of asymmetry and gravity

In order to evaluate the impact of slight asymmetry on droplet oscillation patterns, simulations of a symmetrical droplet with the same volume as the previously studied asymmetric droplets were conducted. The results are presented in Fig. 7a. The oscillation patterns exhibited a high degree of similarity. The difference in resulting frequencies (337 and 341 Hz) was less than 2%. In this context, the effect of gravity was investigated by comparing two droplets, one subject to gravity and one gravity-free. Figure 7b shows a comparison of the oscillation pattern of the two. An absence of a noteworthy distinction within 20 ms is observed. Based on this finding, experiments can be carried out with the proposed droplet generator under terrestrial conditions to determine surface tension.

Fig. 8
figure 8

a Mesh independency study for the two-dimensional droplet and b final resolution of the two-dimensional grid

Full size image

4.1.2 Two-dimensional

4.1.2.1 Mesh independency study

A study on mesh independence was also conducted for the two-dimensional case. The droplet from case (V) was chosen for this investigation and different mesh resolutions were employed along with two distinct initial deformations (1.005 and 1.5). The smaller initial deformation was selected to ensure that the resolution is sufficient for accurately capturing even the smallest surface motions of the droplet. The analysis was repeated with a larger initial deformation to confirm the stability of the solution under greater deformations. The results of both analyses can be seen in Fig. 8a. The figure depicts the change in the oscillation frequency with increasing number of elements, along with two lines representing Rayleigh’s frequency (at small aspect ratios) and analytical predictions of frequency by Tsamopoulos and Brown (1982) for larger deformations. The stabilized frequency for the droplet with a smaller initial deformation shows a very slight deviation from Rayleigh’s frequency. This confirms that the Rayleigh’s equation is best applicable at very small initial deformations. It is apparent that the droplet with a smaller initial deformation requires more refinement in the grid resolution before stabilization is achieved. Conversely, the droplet with a larger deformation attains stability at an earlier stage, rendering further increases in the element count unnecessary. The final mesh resolution of the two-dimensional case can be seen in Fig. 8b. A finer mesh resolution is selected at the droplet edges to enable finer details of motion at the interface. The final element count is presented in Table 4. Conservation of volume was also confirmed in the 2D case (see supplementary data).

4.1.2.2 Effect of initial deformation

After the sensitivity analysis was concluded, the effect of initial deformation or aspect ratio on the frequency was investigated. To achieve different aspect ratios, the major and minor axes of the ellipse in case (V) were varied while keeping the overall volume of the droplet constant for each of the inspected diameters. The results of this comparison are displayed in Fig. 9. The diagram shows the deviation from Rayleigh’s frequency \({\omega }_{0}\) in percent over different aspect ratios. The analytical results of Tsamopoulos and Brown (1982) are also included in the diagram. Good agreement is observed between the studies until an aspect ratio of 1.3. Beyond this point the effect of droplet size becomes more apparent. The reduction in frequency with increasing aspect ratio is more prominent in larger droplets, due to the larger mass and inertia. Such droplets require a longer time to complete one oscillation and have a lower natural frequency. This further emphasizes the significance of using smaller droplets to estimate surface tension values. The slight discrepancy, observed between this study and results of Tsamopoulos and Brown (1982) could be due to a lower Ohnesorge number of metallic melts, as a result of the domination of surface forces over volume forces in comparison with aqueous liquids. On the other hand, larger initial deformations contribute to internal friction by causing movement in a larger portion of the drop, ergo increasing volume forces and decreasing the deviation from literature.

Fig. 9
figure 9

Change in Rayleigh’s frequency \({\omega }_{0}\) for different aspect ratios based on the analytical solutions of (Tsamopoulos and Brown 1982) and their comparison to the numerical results of the current study

Full size image
4.1.2.3 Effect of initial velocity and gravity

The force balance on a droplet falling vertically in a gaseous medium is defined as:

Inertial force Fi = Gravitational force Fg − Buoyant force Fb − Drag force FD

$$\frac{{{\text{d}u}}}{{{\text{d}t}}} \left[ {\rho_{{\text{l}}} \frac{\pi }{6}D_{{{\text{drop}}}}^{3} } \right] = g\left[ {\rho_{{\text{l}}} \frac{\pi }{6}D_{{{\text{drop}}}}^{3} } \right] - g\left[ {\rho_{{\text{g}}} \frac{\pi }{6}D_{{{\text{drop}}}}^{3} } \right] - \frac{{u^{2} }}{2}\left[ { \rho_{{\text{g}}} \frac{\pi }{4} D_{drop}^{2} C_{{\text{d}}} } \right]$$
(3)

Neglecting the buoyancy term due to the significant difference in density, the temporal development of the droplet velocity can be written as:

$$a_{d} = \frac{{\text{d}u}}{{\text{d}t}} = g -\underbrace{\left[ \frac{3}{4} \left( \frac{{\rho_{\text{g}}}}{{\rho_{\text{l}}}} \right) \frac{1}{{D_{\text{drop}}}} C_{\text{d}}\right]u^{2}}_{\text{Decceleration due to drag}}$$
(4)

which is calculated using the drag coefficient \({C}_{\mathrm{d}}\) introduced by Schiller and Naumann (Schiller and Naumann 1935) for Reynolds number in the range 1 < Re < 800:

$$C_{d} = \frac{24}{{{\text{Re}}}}\left( {1 + 0.15{\text{Re}}^{0.687} } \right)$$
(5)

With \({\rho }_{\mathrm{l}}\) and \({\rho }_{\mathrm{g}}\) being the density of liquid (droplet) and gas, respectively.

The Reynolds number, computed for this study has a range of 6 (for a droplet of 1 mm in free-fall) to 114 (for a 3 mm droplet with an initial velocity of 0.5 ms−1 in free-fall). The flow around an oscillation droplet is a strongly transient situation. Not only is the projection area changing, but also the resulting drag coefficient. As a consequence, the drag coefficient of a sphere as a characteristic, averaged value has been used to address mechanisms introduced by the relative velocity. According to Hölzer and Sommerfeld (2008), the change of drag coefficient due to deformation in the Reynolds number range of interest is negligible.

In order to observe the combined effect of gravity, initial velocity and their correlation with initial deformation, three droplets of one, two and three millimeters in diameter were simulated, each with initial velocities of 0, 0.1, 0.3 and 0.5 ms−1. The simulations were repeated with and without the effect of gravity.

Figure 10 displays the change in oscillation frequency over the deceleration due to drag with increasing velocity and diameter. Droplet diameters correlate with the marker size in the graph. In Fig. 10a, the ideal case closest to Rayleigh’s predictions with no drag and no initial velocity is displayed in the upper left corner. With increasing size and velocity, the change in frequency becomes more apparent. The highest deceleration can be observed in the case of droplets with 1 mm diameter at highest velocities. Figure 10b displays the same phenomena in case of a larger aspect ratio. It can be seen that at higher initial deformations, increasing size and velocity have little effect on the oscillation frequency. These findings help to determine the experimental conditions, under which the Rayleigh equation is applicable in the presence of gravity.

Fig. 10
figure 10

Change in frequency for increased droplet size and velocity for initial deformations of a 1.005 and b 1.5 for droplets subject to 0 g (hollow graph markers) and 1 g (filled graph markers). Droplet sizes correlate with marker size

Full size image

Moreover, based on the works of Taylor (Taylor 1934), a droplet subject to steady flow undergoes a drag induced deformation, \(\delta_{{\text{d}}}\) which depends on the viscosity ratio of droplet to medium, \(k\) and the Weber number, \({\text{We}} = {{\rho_{{\text{l}}} u^{2} D_{{{\text{drop}}}} } \mathord{\left/ {\vphantom {{\rho_{{\text{l}}} u^{2} D_{{{\text{drop}}}} } \sigma }} \right. \kern-0pt} \sigma }\). The deformation \(\delta_{{\text{d}}}\) can be written as:

$$\delta_{{\text{d}}} = \frac{a - b}{{a + b}} = {\text{We}}\;\frac{{\left( {19k + 16} \right)}}{{\left( {16k + 16} \right)}}$$
(6)

with \(a\) and \(b\) being the major and minor axes of the deformed droplet.

Figure 11 shows this drag induced aspect ratio (Eq. (6) solved for a/b) over the drag effect for three droplet sizes and velocities. It can be observed that the drag induced aspect ratio has a closer value to the smaller initial deformation (1.005) of the droplets in Fig. 10a, which means that the chances of interaction of the two deformations are higher than with larger initial deformations. The larger the droplet size, the higher the drag induced aspect ratio at a fixed drag induced deceleration will become. In smaller droplets, this effect is considered negligible. As a result, using higher aspect ratios with small droplets is recommended.

Fig. 11
figure 11

Drag induced aspect ratio (a/b) based on the study by Taylor (1934) for three droplet sizes (1, 2, 3 mm) and velocities. Droplet sizes correlate with marker sizes

Full size image

4.2 Experimental results

Droplets of copper were produced using the droplet generator at temperatures between 1400 and 1620 K in an inert argon atmosphere. The graphite crucible had a nozzle diameter of 820 μm. Figure 12a displays the oscillation pattern of a droplet at 1406 K and the result of the corresponding FFT-analysis in frequency spectrum. Additionally, the method of least squares was used to fit a sine function to the data with an adjusted R-squared value of above 0.98, displayed in Fig. 12b. The frequency acquired through fitting is 2.6% higher that the estimation of the FFT-analysis, which could be a result of the analysis resolution. In this case, the analysis can resolve frequency components that are spaced at least 55 Hz apart (5175 fps/94 images). Frequencies determined through fitting were used in further calculations of this study. The sample droplet has a volume of 5.12 × 10–10 m3, which was calculated assuming symmetry. Density values were estimated for each temperature based on the study by Assael et al. (2010). Possible variation of droplet temperature within the measurement period (< 20 ms) and possible temperature gradients inside the sample were neglected. The aspect ratio was monitored for each droplet over the course of the oscillation and can be seen in Fig. 13a for the aforementioned sample droplet. The largest aspect ratio observed in each oscillation was used to correct the frequency for each droplet individually. The correction was made according to the simulation results of this study (Fig. 9). Calculated surface tension values are plotted along with the literature values in Fig. 13b. Each data point represents the average value over 5 droplets measured at the same temperature. The droplets have a diameter of 1 mm with a tolerance of ± 10%. The error bars represent the standard deviation. The droplet volume was determined using the average values of the volume, when the droplet had an aspect ratio of 1.05 and lower. This indicates less than 5% deformation and is the closest shape to a sphere.

Fig. 12
figure 12

a The oscillation pattern of a sample droplet of copper over time and the corresponding frequency. b An additional fitted sine function to corroborate the result of the FFT-analysis. 2.6% difference in frequencies possibly due to FFT analysis resolution

Full size image
Fig. 13
figure 13

a The aspect ratio of the sample droplet and droplet images before and after image analysis. The circled aspect ratio is the largest in the oscillation and is used to correct the frequency to compensate for the effect of initial deformation. b Surface tension of molten copper with respect to temperature. Corrections are made to the value of frequency based on initial deformation of droplets

Full size image

The calculated surface tension results shown in Fig. 13b correlate with temperature as follows:

$$\sigma \, [{\text{mN}}\,{\text{m}}^{{ - {1}}} ] \, = { 13}0{7}{-}0.{22 }\left( {{\text{T}} - {1356}} \right) \, \left( {\text{T in K}} \right)$$
(7)

This applies to temperatures between 1400 and 1620 K. The displayed values in Fig. 13b are corrected based on initial aspect ratio.

4.2.1 Error analysis

The two main parameters and possible sources of error to be determined for use in the Rayleigh equation are droplet diameter and oscillation frequency. Each droplet is analyzed individually, in order to reduce the error introduced by difference in droplet sizes. A 4% error could be caused in volume determination by image analysis, due to error in droplet edge detection. A higher resolution camera could help reduce this uncertainty. Due to the relatively low resolution of the FFT-analysis, an optimization through fitting of a harmonic oscillator function is applied for more accurate frequency analysis. The difference between the frequency determined by the FFT and by fitting are typically up to 5%. Recording images with a higher fps could help increase the FFT resolution and reveal possible further peaks.

A droplet cooling model, as introduced by Imani Moqadam et al. (2019b) is used to calculate the temperature loss of a 1 mm droplet (typical droplet size in this work) after exiting the crucible in an argon and nitrogen atmosphere. The change in temperature after 20 ms (typical measurement time < 20 ms) is between 5 and 7 K for nitrogen and argon, accordingly. This is consistent with the observations made by Moradian and Mostaghimi (2008) with the use of a pyrometer over a similar falling distance. Thus, the temperature losses of the droplet at such high temperatures can be neglected. A graphical representation is included in the supplementary data. Note that droplets with higher temperature are especially challenging to analyze due to the brightness and the halo at the edge. This could lead to overestimations and could explain the larger standard deviation visible at 1620 K in Fig. 13b.

Guthrie and Iida (1993) showed that by differentiating the Eötvös law (a relationship between absolute temperature and surface tension) over temperature, one could obtain the temperature coefficient of surface tension. This coefficient is equal to − 0.28 mNm−1 K−1 and is achieved with the use of some simplifying factors and is strongly dependent on the assumed decrease in density over temperature. In spite of the simplifications of theory, the slope of the linear regression, determined in the current study is equal to − 0.22 mNm−1 K−1 (27% difference). In industrial applications, nitrogen is the preferred inert gas due to economic reasons. Nevertheless, simulations were performed to reveal possible deviations in surface tension, when using argon instead of nitrogen. The results for higher aspect ratios (1.5) show a mere 0.14% deviation from the base case (nitrogen). A graphical representation is included in the supplementary data. Taking the errors of volume and frequency determination into account, Eq. (7) could be written as:

$$\sigma \, [{\text{mN}}\,{\text{m}}^{{ - {1}}} ] \, = \, \left( {{13}0{7 } \pm { 98}} \right) \, {-} \, \left( {0.{22 } \pm \, 0.0{15}} \right) \, \left( {{\text{T}} - {1356}} \right) \, \left( {\text{T in K}} \right).$$
(8)

5 Summary and conclusion

A drop on demand droplet generator is proposed for creating oscillating droplets in free-fall. The frequency of these oscillations can be used in conjunction with Rayleigh’s theories to determine surface tension. Numerical models proved the applicability of the method in determination of surface tension. It was concluded from the three-dimensional models that the tilt angle of an asymmetric droplet has little impact on the oscillation pattern when compared to a vertical asymmetric droplet. A tilted droplet can therefore be analyzed; however, it must be oscillating in the second mode. It was observed that gravity and slight asymmetry cause an error of less than 3 percent in surface tension calculation and do not significantly impact the validity of the method. It was also concluded that the observation angle of the asymmetric droplet has no significant effect on the extracted frequency. Based on this finding, further analysis of the droplet dynamics can be done using a two-dimensional model, with significantly lower computational effort. It was concluded that the droplet initial deformation is inversely proportional to the decrease in oscillation frequency. At lower initial deformations and with smaller droplets, the drag induced aspect ratio has a more pronounced effect on the oscillation frequency. At higher aspect ratios these effects are negligible. It was concluded that smaller droplets with a 20% initial deformation are suitable for the experimental analysis. In such droplets, the deformation is small enough to produce reasonable results with Rayleigh’s theories but also large enough to not be affected by the drag disturbances. To validate, the surface tension of molten copper was measured over a temperature range of 1400 and 1620 K and corrected based on initial deformation. The linear relation can be written as σ [mN m−1] = (1307 ± 98) − (0.22 ± 0.015) (T−1356) (T in K).