1 Introduction

Aerodynamic designs of the future need to combat and thrive in time-varying, unsteady environments. These conditions commonly arise because of the kinematic motion of the flyers themselves (Hodara et al. 2016; Liu et al. 2020) or alternatively, due to the unsteady nature of the atmospheric boundary layer (Watkins et al. 2010; White et al. 2012). Such rapidly changing conditions are a special concern for micro aerial vehicles (MAVs) because of the high ratio between the velocity of the flow disturbance and their comparatively low flight speed (Watkins et al. 2006; Andreu-Angulo et al. 2020). Moreover, these unsteady affects are not confined to the small scale but equally extend to wind and water turbines (Sequeira and Miller 2014), where unsteady loading increases the structural requirements of turbine blades and causes fatigue failure due to cyclic loading.

Common to most unsteady wing flow scenarios is a rapidly evolving flowfield, where the separating boundary layers feed leading (LEV) and trailing (TEV) edge vortices, which grow and subsequently shed, initiating a cascade of ever changing flow states. Simultaneously, the arising time-varying force magnitude can readily exceed the steady-state equivalent (Farren 1935; Bennett 1970; Sane and Dickinson 2001) and thereby sets the stage for catastrophic events.

To remedy these potent adverse effects and instead harness the power of unsteady flow, recent research has centred on understanding how and why the time varying flowfield behaves the way it does (Eldredge and Jones 2019). Low order models (LOM) are especially dependent on such insight, since these are in many cases designed by reducing the governing equations to simple linear formulations that can be solved at a low computational cost. To achieve this, the underlying physics are split up into a series of separate components, where a simple model is used to approximate each individual contribution (Babinsky and Stevens 2016). To ensure that the individual parts of an LOM complement each other and arrive at a suitable force prediction, an accurate understanding of the force development process is necessary. Moreover, LOMs ideally limit their analysis to only the most dominant flow features in order to save resources. Being able to quantify whether a flow structure has a strong or negligible contribution to the overall force can therefore help decide whether it should feature in a LOM or if it can instead be ignored. Two common examples of this conundrum could be whether the deflected path taken by a vortex as it passes a wing needs to be modelled or whether gust shear layer deflection during a body-gust encounter (Gehlert and Babinsky 2021b) creates a sufficient force to warrant its inclusion in an LOM.

From a more global perspective, understanding how flow structures influence the force can help interpret experimental or computational results. As an example, Martínez-Muriel and Flores (2020) found that the peak force experienced by a wing, as externally created vortices of various sizes and strengths pass by at different distances, scales with the average velocity induced on the wing by the vortex. In situations like this, knowledge of how a particular flow structure affects the force can be useful to provide a more holistic understanding of why certain patterns exist and importantly, what their limitations may be.

To determine the significance of individual flow features, it is necessary to quantify their contribution to the overall force experienced by an object. Unfortunately, force balance measurements cannot readily provide such detailed information as only the total force can be retrieved. It is at this point that the development of particle image velocimetry (PIV) comes into use. Analysing the flowfield information provided by PIV allows not only the determination of the overall force, as described, for example, by the overview of Rival and van Oudheusden (2017), but it also permits a breakdown of the force into individual contributions. A particularly useful approach is based on the impulse theory developed by, amongst others, Wu (1981). Here the force is evaluated by assessing the development of the vorticity field. In its basic form, however, only the total force acting within the domain can be identified rather than individual contributions. Building on Wu’s formulation, Noca et al. (1997, 1999) limited the necessary analysis to a finite domain by introducing surface integrals along the control volume boundary. However, the limitation remains that only the total force within the domain can be identified. Bai et al. (2014) expand on this to recover the force acting on a single object within a multi-body flow system, Kang et al. (2018) extend this further still. They propose a ‘minimum domain impulse theory’ to isolate the forces, using only a limited region of the flowfield without the need for surface integrals along domain boundaries. Still however, this does not allow for an individual force contribution due to a specific flow phenomenon to be determined. Li and Wu (2018) make progress in this respect by developing vortex force maps that relate the force created by a vortex to its position and velocity. This framework evaluates each element of vorticity individually, allowing for general solutions that are independent of the surrounding flow. However, when capturing the force due to an individual region of vorticity to for example determine whether it should be modeled by a LOM, the external flow plays a crucial role and must therefore be part of the analysis. Further progress is made in this regard by Menon and Mittal (2020), who develop an approach to better understand how the unsteady force acting on a body is generated. They show that the majority of the force of an oscillating cylinder is due to a kinematic contribution, a vorticity-induced force as well as due to viscous effects and thereby help shed light on the underlying force producing mechanisms.

Whether we are developing LOMs or trying to simplify the flowfield to better understand its intricacies, one method that has shown success in the past is to recreate the true viscous flowfield using potential flow. Here, the flowfield can be understood to be composed of a superposition of individual flow elements. As such, we model free vorticity as a collection of point vortices and the boundary layer as a superposition of individual vortex sheets (Saffman 1992; Eldredge 2010; Graham et al. 2017; Gehlert and Babinsky 2021a), where the rate of change of each component of vorticity links to a force (Lamb 1932).

In light of this, the aim of this paper is to construct a framework that relies on the principles of superposition, vortex sheets and elements of free vorticity to approximate the force to a first order in two-dimensional, incompressible, unsteady flow due to an isolated region of vorticity. This decomposition of forces would allow experimentalists, modelers and designers to better understand their results, track what flow features need to constitute their LOM or gain insight into ‘designing’ a preferred flow scenario that should be aimed for.

This objective is achieved by expanding Wu’s impulse formulation and subsequently decomposing the force into its constituent parts, whilst viewing the complete flowfield as a distribution of vorticity. As an additional benefit, the derived formulation will also make it possible to recover the force acting on a single object part of a multi-body flowfield. Subsequently the framework is applied to create a force heat map that visualises the relative force created by a LEV if it were to be positioned at a respective point in space compared to if this vorticity were to reside within the boundary layer. Through this we aim to provide an example of how a designer might gain insight as to where ideally they would like to position the LEV to achieve a certain force outcome.

2 Unsteady force decomposition

A force acting within a domain can be linked to the rate of change of momentum of the fluid. In the case of a counter-rotating vortex pair of equal strength as depicted in Fig. 1, which could represent the bound and starting vortex of a surging wing, Lamb (1932) shows that the impulse created in 2-dimensional flow is given by

$$\begin{aligned} I = \rho {\varGamma } d, \end{aligned}$$
(1)

where \(\rho\) is the fluid density, \({\varGamma }\) is the circulation of each vortex and d is the distance separating the vortices. The momentum or impulse of the fluid changes when these vortices move apart or when their strength changes. The force, F, is therefore the time rate of change of the impulse I,

$$\begin{aligned} F = \rho \, \Big ( \underbrace{ {\varGamma } \dot{d}}_{\textrm{motion}} +\underbrace{d \dot{\varGamma } }_{\textrm{creation}} \Big ), \end{aligned}$$
(2)

where the first term describes the force contribution created by the relative motion between the two vortices, whilst the second is due to a change in vortex strength.

Fig. 1
figure 1

Counter-rotating vortex pair

Full size image

A real flowfield cannot always be grouped into pairs of counter-rotating vortices, however, the same theoretical approach can nonetheless be applied; for example by considering the flow to consist of many incremental vortex pairs, where their effect is summed.Footnote 1 This is the basis of the impulse approach, where Wu’s (Wu 1981) implementation of this concept can be illustrated, without loss of generality, by assuming the ‘body’ of interest to be a circular cylinder. Consider a 2-dimensional flowfield, where a single cylinder is traveling horizontally in a region \(R_L\), and enclosed by a boundary \(B_L\) far away, as illustrated in Fig. 2.

Fig. 2
figure 2

Schematic illustration of a flowfield containing a translating cylinder as well as cylinder-shed \(\omega ^{\text {shed}}\) and external vorticity \(\omega ^{\text {ext}}\)

Full size image

The flowfield consists of cylinder-shed and external vorticity, where the latter could be created by a localised region of moving fluid such as a gust. The complete vorticity field is assumed to be contained within \(R_L\), yielding

$$\begin{aligned} \int _{R_L} \omega \, dR= 0. \end{aligned}$$
(3)

Furthermore, the flow is otherwise quiescent, such that the velocity on the boundary \(B_L\) is zero. The aerodynamic force acting within the domain \(B_L\) is

$$\begin{aligned} \textbf{F}_{\textbf{a}} = -\rho \left( \frac{d}{dt}\int _{R_L} \textbf{r} \times \omega \, dR - \frac{d}{dt} \int _{R_{b}} \textbf{U}_{b} \, dR \right) , \end{aligned}$$
(4)

where \(\rho\) is the density of the fluid and for simplicity is assumed to be constant throughout and \(\textbf{r}\) is the position vector. \(R_{b}\) represents the region occupied by the cylinder, and \(\textbf{U}_{b}\) is the instantaneous velocity vector of the cylinder. The first term on the right of Eq. 4 is the force arising from the rate of change of vorticity. The second term is a ‘force correction’ and is required because Wu assumes that fluid is distributed evenly throughout the entire flowfield, including the region occupied by the cylinder. Acceleration of the cylinder causes the fluid within it to also accelerate to match the body velocity and thereby creates a contribution to the change in momentum. This change is captured by the vortex moment derived by Wu and thus needs to removed in order to recover the true aerodynamic force acting on the cylinder.

The work by Wu can now be expanded to calculate the force due to a specific flow structure. As a starting point, Eq. 4 is applied to a horizontally traveling cylinder and re-written in terms of lift and drag yields,

$$\begin{aligned} L&= \rho \frac{d}{dt} \int _{R_L} I_y \, dR\nonumber \\ D&= -\rho \frac{d}{dt} \int _{R_L} I_x\, dR + \rho \frac{d}{dt} \int _{R_{b}} U_{b} \, dR. \end{aligned}$$
(5)

where \(I_y\) and \(I_x\) represent the impulse, such that

$$\begin{aligned} I_y = x \omega , \qquad I_x = y \omega . \end{aligned}$$
(6)

We proceed by making use of the fact that in potential flow we can ‘construct’ the complete flowfield by superposing individual flow solutions that are based on vortex elements. Thus we can represent the viscous flowfield in potential flow terms, where we choose to split the flowfield vorticity into three sets. The first group consists of vorticity shed by the cylinder, \(\omega ^{\text {shed}}\), as schematically indicated in Fig. 2. The second group includes external vorticity that is not created by the cylinder, \(\omega ^{\text {ext}}\). This vorticity could arise through a sudden local acceleration of flow, for example a gust. The last group contains the boundary layer vorticity, \(\omega ^b\), attached to the cylinder surface. The complete vorticity field is therefore given as:

$$\begin{aligned} \omega = \omega ^b + \omega ^{\text {shed}} + \omega ^{\text {ext}}. \end{aligned}$$
(7)

Once the vorticity field is split up into the three groups, the force expressed in Eq. 5 can be re-written as,

$$\begin{aligned} L&= \rho \int _{B_b} \underbrace{\frac{d I_y^b }{dt}}_{\textrm{boundary} \ \textrm{layer}}dl\nonumber \\&\quad + \rho \int _{R_L} \bigg (\!\!\!\!\!\!\!\!\!\overbrace{\frac{d I_y^{\text {shed}}}{dt}}^{\textrm{cylinder}\text {-}\textrm{shed}\ \textrm{vorticity}} \!\!\!\!\!\!\!\!+\!\!\!\!\!\!\underbrace{\frac{d I_y^{\text {ext}} }{dt}}_{\textrm{external} \ \textrm{vorticity}}\!\!\!\!\bigg ) \, dR, \nonumber \\ D&= -\rho \int _{B_b} \underbrace{\frac{d I_x^b }{dt}}_{\textrm{boundary} \ \textrm{layer}} dl \nonumber \\&\quad - \rho \int _{R_L} \bigg (\!\!\!\!\!\!\!\!\!\overbrace{\frac{d I_x^{\text {shed}}}{dt}}^{\text{cylinder-shed vorticity}} \!\!\!\!\!\!\!\!+\!\!\!\!\!\!\underbrace{\frac{d I_x^{\text {ext}} }{dt}}_{\textrm{external} \ \textrm{vorticity}}\!\!\!\!\bigg ) \, dR \nonumber \\&\quad + {\rho \frac{d}{dt} \int _{R_{b}} U_{b} \, dR,} \end{aligned}$$
(8)

where

$$\begin{aligned} I_y^b&= x \gamma ^b, \qquad I_y^{\text {shed}} = x \omega ^{\text {shed}}, \qquad I_y^{\text {ext}} = x \omega ^{\text {ext}} \nonumber \\ I_x^b&= y \gamma ^b, \qquad I_x^{\text {shed}} = y \omega ^{\text {shed}}, \qquad I_x^{\text {ext}} = y \omega ^{\text {ext}}. \end{aligned}$$
(9)

We note that similar to the approach used in previous studies (Corkery et al. 2019; Gehlert and Babinsky 2021a), boundary layer vorticity is replaced by a vortex sheet \(\gamma ^b\) located on the body surface, as permitted by the potential flow framework and illustrated in Fig. 3. The first integral in Eq. 8 is performed over the cylinder surface \(B_b\), whilst the second acts on the area of the remaining flowfield. The time derivative has been taken into the integral and the impulse (\(I_x, \, I_y\)) is grouped according to the sets of vorticity. In order to simplify the explanation and to reduce the length of any subsequent equations, all further manipulations are only applied to the lift force, but of course remain equally applicable to drag.

Fig. 3
figure 3

Vortex sheet enforcing the no-penetration condition on a body surface

Full size image

The time derivatives in Eq. 8 can now be expanded to reveal force contributions due to the movement and creation of vorticity.

$$\begin{aligned} L&= \rho \int _{B_b} \Bigg (\overbrace{\underbrace{\gamma ^b \frac{dx}{dt}}_{\textrm{motion}} + \underbrace{x \frac{d\gamma ^b}{dt}}_{\textrm{creation}}}^{\textrm{boundary} \ \textrm{layer}} \Bigg ) \, dl \nonumber \\&\quad + \rho \int _{R_L} \Bigg (\overbrace{\underbrace{\omega ^{\text {shed}} \frac{dx}{dt}}_{\textrm{advection}} + \underbrace{x\frac{d\omega ^{\text {shed}}}{dt}}_{\textrm{creation}}}^{\textrm{shed}\ \textrm{vorticity}} +\overbrace{\underbrace{\omega ^{\text {ext}}\frac{dx}{dt}}_{\textrm{advection}} + \underbrace{x\frac{d\omega ^{\text {ext}}}{dt}}_{\textrm{creation}}} ^{\textrm{external}\ \textrm{vorticity}} \Bigg ) \, dR. \end{aligned}$$
(10)

The change in position of \(\gamma ^b\) is linked to the kinematic motion of the cylinder and is therefore labelled as ‘motion’ in Eq. 10.Footnote 2 Shed and external vorticity are free to move under the influence of the local flow velocity and the corresponding terms are therefore labelled as ‘advection’. The force due to the rate of change of strength of vorticity is marked as ‘creation’.

Each vortex element, regardless of whether it is part of the boundary layer vortex sheet or whether it resides elsewhere in the flowfield, induces a velocity according to the Biot-Savart law,

$$\begin{aligned} u_{\theta } = \frac{\int _{R_{el}} \omega \,dR}{2 \pi r}, \end{aligned}$$
(11)

where \(R_{el}\) is the region associated with a vortex element and r is the distance between the vortex element and a position in the flowfield at which the velocity is induced. The infinite velocities created when r approaches zero are avoided in real viscous flow through the presence of a viscous vortex core. The flow velocity at any point in the flowfield is therefore a superposition of the velocities induced by each vortex element. Thus the velocity field, \(U_{field}\), can be decomposed into a contribution from the boundary layer vortex sheet \(U_{\gamma ^b}\), a contribution from shed vorticity \(U_{\omega ^{\text {shed}}}\) and a contribution from any externally created vorticity \(U_{\omega ^{\text {ext}}}\),

$$\begin{aligned} U_{field} = U_{\gamma ^b} + U_{\omega ^{\text {shed}}} + U_{\omega ^{\text {ext}}}. \end{aligned}$$
(12)

Equation 10 can now be re-cast with the velocity, which advects the free vorticity, split up into its three contributions,

$$\begin{aligned} L&= \rho \int _{B_b} \overbrace{\frac{d I_y^b}{dt}}^{\textrm{change}\ \textrm{of}\ \textrm{boundary}\ \textrm{layer}} dl\nonumber \\&\quad + \rho \int _{R_L} \Bigg (\overbrace{ x \frac{d \omega ^{\text {shed}}}{dt}}^{\textrm{new}\ \textrm{vorticity} \ \textrm{shed}} + \overbrace{ x \frac{d \omega ^{\text {ext}}}{dt}}^{\textrm{creation}\ \textrm{ext}. \ \textrm{vorticity}} \nonumber \\&\quad + \underbrace{U_{\gamma ^b} \left( \omega ^{\text {shed}} + \omega ^{\text {ext}} \right) }_{\textrm{advection}\ \textrm{by} \ \textrm{boundary}\ \textrm{layer}} + \underbrace{ U_{\omega ^{\text {shed}}} \left( \omega ^{\text {shed}} + \omega ^{\text {ext}} \right) }_{\textrm{advection}\ \textrm{by} \ \textrm{shed}\ \textrm{vorticity}} \nonumber \\&\quad + \underbrace{ U_{\omega ^{\text {ext}}} \left( \omega ^{\text {shed}} + \omega ^{\text {ext}} \right) }_{\textrm{advection}\ \textrm{by} \ \textrm{ext}.\ \textrm{vorticity}} \Bigg ) \, dR. \end{aligned}$$
(13)

Equation 13 describes the change in momentum and thus the total lift force on the fluid within the control volume. To simplify the formulation, the impulse due to the rate of change of position and strength of \(\gamma ^b\) is written as one term because the vortex sheet elements move with the cylinder surface and develop in accordance with the requirement to ‘mirror’ the vorticity in the flowfield rather than advect freely. The remaining two terms of the first line of Eq. 13 are due to new vorticity being shed from the cylinder and any changes in strength of external vorticity. The three terms on the second line of Eq. 13 are due to the advection of free vorticity, caused either by other elements of free vorticity or the boundary layer.

To isolate the force acting on the cylinder and to simplify the expression, a number of terms can be removed from Eq. 13. Saffman (1992) shows that two vortices advecting freely under the influence of each other do not generate a force. This is because they do not create a net change in momentum. Therefore, the last two terms in Eq. 13 can be excluded. Since the cylinder cannot be responsible for the creation term associated with external vorticity (third term on the first line in Eq. 13), this can also be removed. Implicitly, a change in strength and position of external vorticity still affects the force acting on the cylinder, since this external vorticity impacts the boundary layer vortex sheet created on the cylinder surface. After removing the respective terms, the lift force experienced by the cylinder becomes

$$\begin{aligned} L_{\text {cyl}}&= \rho \int _{B_b} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \underbrace{\frac{d I_y^b}{dt}}_{\textrm{change} \ \textrm{of}\ \textrm{bound}.\ \textrm{layer}} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!dl\nonumber \\&\quad + \rho \int _{R_L} \Bigg (\underbrace{U_{\gamma ^b} \left( \omega ^{\text {shed}} + \omega ^{\text {ext}}\right) }_{\textrm{advection}} +\underbrace{x \frac{d \omega ^{\text {shed}}}{dt} }_{\textrm{creation}}\Bigg )\, dR. \end{aligned}$$
(14)

The force acting on the cylinder is therefore only dependent on the rate of change of the boundary layer impulse, the creation of new vorticity (ie. vorticity shed by the cylinder) and the advection of surrounding vorticity by the cylinder boundary layer. In the latter, the description ‘surrounding vorticity’ includes all shed vorticity coming from either the cylinder or any other body as well as the vorticity located within the boundary layer of any external object; in short, any vorticity located within the surrounding flowfield. It is mathematically accounted for by the advection term in Eq. 14.

Kang et al. (2018) rigorously extended Wu’s impulse formulation to show that the force affecting a body can be computed by only analysing a finite domain around the body of interest. As such, it becomes possible to determine the force acting on an individual object immersed in a multi-body flowfield. On the surface, their formulation looks different to Eq. 14, however, upon expansion and after subsequent simplification, the formulation proposed by Kang et al. recovers Eq. 14. This therefore suggests that Eq. 14 is equally applicable to multi-body flowfields, where the total force on each individual body can be recovered. To illustrate the use of Eq. 14 further, Appendix A and B apply the result to a steady and accelerating freestream to recover some common theoretical results.

Before attempting to recover the force due to a specific flow feature, it is worth reminding ourselves that we consider the boundary layer vortex sheet, \(\gamma ^b\), to be composed of a number of individual contributions where each enforces the no-throughflow condition on the body surface due to a related flow feature. A first component is created by the kinematic motion of the cylinder \(\gamma ^{\text {nc}}_{\text {am}}\) and can be linked to the added mass force experienced during acceleration (Eldredge 2010). We refer to this as a non-circulatory vortex sheet (\(.^{\text {nc}}\)) due to its net circulation being zero (Saffman 1992; Corkery et al. 2019). A further contribution to \(\gamma ^b\) comes from free vorticity in the flowfield. Each element of free vorticity results from vorticity not attached to the body, ie. floating ‘freely’ in the field and induces a velocity on the body surface according to the Biot-Savart law and thus requires a respective vortex sheet contribution to enforce no-throughflow on body surface (Graham et al. 2017). We choose to group this free vorticity into a first component that was shed by the cylinder itself and a second that consisted of externally created vorticity. Here we let \(\gamma ^{c}_ \text {shed}\) represent the former and \(\gamma ^{\text {nc}}_{\text {ext}}\) the later, the vortex sheet contribution due to externally created vorticity. Depending on the intent of a particular investigation, shed and external vorticity could subsequently be broken down into more specific regions of vorticity, such as LEVs or TEVs, where the related vortex sheets on the body surface enforce the no-penetration condition due to these specific regions of vorticity. Moreover, since we can use a distribution of vorticity, ie. a vortex sheet to represent an object, the region of external vorticity \(\omega _{\text {ext}}\) can equally represent a further body residing in the flowfield.

To approximate the lift arising from an external flow feature, or resulting from a surrounding body, to a first order, we first identify the force component due to the rate of change of the impulse \(dI^{\text {ext}} /dt\) created by the development of its respective vortex sheet contribution \(\gamma ^{\text {nc}}_{\text {ext}}\). A second force contribution comes from the advection of this external vorticity. More specifically, the force contribution arises because of the motion induced by the boundary layer vorticity. The effect is quantitatively described by the multiplication of the flow velocity induced by the boundary layer vortex sheet \(U_{\gamma ^b}\) and the strength of the free vorticity \(\omega ^{\text {ext}}\). It is worth noting that we do not account for changes in the way vorticity sheds from the cylinder due to this external flow feature, nor for any fundamental and systemic modifications to the flowfield dynamics which may introduce second order force effects. The total force due to an external region of vorticity, such as for example a vortex or a gust shear layer, is therefore

$$\begin{aligned} L_{\text {ext}} = \underbrace{\rho \int _{B_b}\frac{dI_y^{\gamma ^{\text {nc}}_{\text {ext}}}}{dt} dl}_{\textrm{rate}\ \textrm{of}\ \textrm{change}\ \textrm{of}\ \gamma ^{\text {nc}}_{\text {ext}}} +\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\overbrace{\rho \int _{R_{L}} U_{\gamma ^b} \omega ^{\text {ext}} dR}^{\textrm{advection}\ \textrm{of}\ \textrm{ext}.\ \textrm{vorticity} \ \textrm{by}\ \textrm{boundary}\ \textrm{layer}}, \end{aligned}$$
(15)

where

$$\begin{aligned} I_y^{\gamma ^{\text {nc}}_{\text {ext}}}= x\gamma ^{\text {nc}}_{\text {ext}}. \end{aligned}$$
(16)

A schematic illustration of the two contributions to the force, the variation of \(\gamma ^{\text {nc}}_{\text {ext}}\) and the advection of the external vortex, causing it to deflect around the cylinder, are shown in Fig. 4.

Fig. 4
figure 4

Time variation of \({\gamma ^{\text {nc}}_{\text {ext}}}\) and deflection of a free vortex as this passes by a cylinder

Full size image

Furthermore, it is worth mentioning that the second term in Eq. 15 could equally be written as the negative of the multiplication of the velocity induced by the external region of vorticity \(U_{\omega ^{\text {ext}}}\) with the boundary layer vortex sheet \(\gamma ^b\), due to the reciprocal relationship between the two,

$$\begin{aligned} \int _{R_L} U_{\gamma ^b} \omega ^{\text {ext}} \, dR= - \int _{B_b} U_{\omega ^{\text {ext}}} \gamma ^b \, dl. \end{aligned}$$
(17)

The derivation discussed above uses a cylinder as the body of interest but there is of course no conceptual difference between for example, a lift-generating spinning cylinder or any other lifting body. This therefore allows us to revisit the work by Martínez-Muriel and Flores (2020) who studied a wing encountering a vortical gust. The authors observed that the peak force experienced by the wing was dependent on the average velocity induced onto the wing by the passing vortex. Equation 17 confirms this experimental observation, since it relates the created force to the velocity induced onto the boundary layer vortex sheet by the free vortex.

3 Experimental force isolation

3.1 Experimental set-up

To explore the proposed theoretical concepts, the towing tank facility at the University of Cambridge is used to investigate the multi-body flowfield around a simultaneously accelerated cylinder and plate as well as around an, in-isolation surging and pitching NACA-0021 wing.

3.1.1 Multi-body flowfield-cylinder and plate

The 9 m long and 1 m wide tank is filled with water up to a depth of 0.8 m. The cylinder is vertically mounted to a force balance, which connects to a servo motor driven carriage that moves along the length of the tank, as shown in Fig. 5. The cylinder is 0.06 m in diameter, D, and 0.48 m long. The clear transparent acrylic is painted matte black everywhere apart from a small region around the midspan to allow the laser sheet to pass through. A skim plate is mounted flush with the top of the cylinder and acts as a mirror plane, extending the effective aspect ratio to 16.

Fig. 5
figure 5

Experimental set-up

Full size image

Two different flat plate wings are alternately mounted to the skim plate and move in unison with the cylinder. Wing 1 has a chord length c of 0.045 m and is set at an angle of attack \(\alpha\) of 40 degrees, whilst the chord length of wing 2 is 0.09 m and positioned such that \(\alpha = 22^{\circ }\). The leading edges of the wings are offset by \(l_x\) and \(l_y\) from the cylinder centre and their thickness t is 3 mm. Both are painted matte black to reduce reflections from the laser.

Fig. 6
figure 6

Experimental cylinder and cylinder and flat plate wing cases

Full size image

Three different tests are performed, as presented in Table 1 and schematically illustrated in Fig. 6. In the first test case, the cylinder is linearly accelerated in isolation over a distance \(s_{\text {acc}}\) of two diameters to a final velocity \(u_\infty\) of 0.43 ms\(^{-1}\), reaching a Reynolds number Re of 20 000. In the second case, the cylinder kinematics are unchanged and wing 1 is mounted a short distance downstream. For the final test case, the linear acceleration is performed over half a cylinder diameter and \(u_\infty = 0.22\) ms\(^{-1}\), such that the cylinder-based Reynolds number is 10 000, whilst wing 2 is now mounted just downstream of the cylinder.

Table 1 Overview of multi-body test cases
Full size table

3.1.2 NACA-0021 wing

To explore the idea of force heat maps, the flow and force response around a matte black painted, rapid prototyped NACA0021 wing, as schematically illustrated in Fig. 7, is also investigated. The upper end of the wing is in line with the water surface and is fitted with a circular endplate, which itself sits inside a circular opening within the skim plate to reduce 3-dimensional effects. The wing chord length is 0.1 m and three carbon fibre rods extend along its 0.48 m long span to improve the structural rigidity. The wing begins surging from a stationary start at zero angle of incidence and accelerates to a terminal velocity of 0.13 \(ms^{-1}\) (\(Re = 10 \, 000\)) within 0.2 chords whilst pitching to 45 degrees at an angular velocity of 0.66 rad/s.

Fig. 7
figure 7

NACA-00021 wing

Full size image

3.1.3 Data acquisition

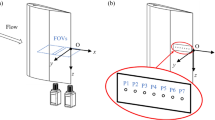
Planar particle image velocimetry is conducted to assess the flow. Titanium dioxide particles are illuminated by a Nd:YLF 527 nm laser and two high-speed Phantom M310 cameras are positioned in a dual-camera arrangement to ensure optical access to all regions of the flowfield. The sampling rate is between 400 and 800 Hz and 6 runs are conducted from which an ensemble average is obtained. The cross-correlation process, using the commercial LaVision Flowmaster 2D system, features an adaptive interrogation window with a size of \(16 \times 16\) pixels during its final pass with an overlap of 50 % leading to a final vector spacing of 1.8 \(\times\) 1.8 mm. Missing data due to laser reflections close to the cylinder and plate surface are recovered by interpolating between the tracked cylinder and plate surface velocities and the external flowfield (Gehlert and Babinsky 2021a).

To reduce the errors in the PIV measurements, the size of the particle diameters as seen by the cameras is adjusted to be greater than 2 pixels. This minimises peak-locking effects, which can otherwise dominate the root-mean-square (RMS) velocity error estimation (Westerweel 1997). For the presented data sets, the error is approximated to be around 1 % (Raffel et al. 1998). Further to this, the shift of the correlation peak, when a correlation window is mapped back to its original position based on its velocity vector, provides a further error contribution (Wieneke 2015). The related uncertainty is 2 % for the multi-body flowfield in regions of interest, once the repeated measurements are accounted for, which reduce the error by \(1/\sqrt{N}\), where N is the number of repeats (Adrian and Westerweel 2011). The total uncertainty in the PIV velocity measurements is therefore 3 %.

The forces acting on the cylinder are recorded with a Flow Dynamics two-component load cell. This is capable of force measurements in the range of \(\pm 50\) N with a resolution of 0.01 N and is calibrated in situ. The carriage position is obtained using an electro-optical sensor with a resolution of 1 mm. The velocity is determined through numerical differentiation of the position data, whilst the acceleration is measured by an ADXL335 3-component micro-electromechanical accelerometer mounted to the carriage. All measurements are sampled at a rate of 3 kHz.

The force data are averaged over 6 runs and a zero phase shift averaging window is applied to reduce the effects of electrical noise and vibrations. The standard random error relative to the peak mean force is below 2 %.

3.2 Force on an individual object - experimental implementation

In Eq. 14, the force acting on a body is broken down into its underlying constituent parts. This makes it possible to recover the force acting on a single object, even when the surrounding flowfield is populated with externally created vorticity. This external vorticity may come in the form of a freely drifting vortex pair or alternatively, it may be created within the boundary layer of external objects, which are also present within the flowfield, and any vorticity that these have shed. Focusing on the latter as an example, if the vorticity created by all objects is clearly distinguishable and does not mix, it may be tempting to draw a boundary around each individual object as well as its vorticity, as shown in Fig. 8, and simply apply the impulse method to this region in order to obtain the individual forces. Equation 14 however clearly demonstrate that the calculation is more involved. Since it is possible to use a force balance to measure the force acting on a single object, we first test our derived force formulation, Eq. 14, on this simple multi-body problem.

Fig. 8
figure 8

Schematic illustration of the tempting (yet incorrect) approach to calculating the force acting on a single object, part of a multi-body flowfield, by only considering the impulse created by the vorticity associated with the individual object

Full size image

Imagine a flowfield consisting of a circular cylinder surrounded by shed and externally created vorticity. A direct application of Eq. 14, to identify the force acting on the cylinder, can be cumbersome in an experimental setting. This is because the strength and position of newly shed vorticity must be explicitly identified in order to calculate the creation term in Eq. 14. For some geometries this may be easier, for example a flat plate at a high incidence, where vorticity is only shed at the leading and trailing edges. However, for more general bodies such as a circular cylinder, the unsteady separation point moves along the surface and it is therefore difficult to identify the exact position of unsteady separation as well as the magnitude of shed vorticity (Gehlert and Babinsky 2020, 2021a). To circumvent the necessity to explicitly identify these, we use a modified approach that in essence, is identical to that given by Eq. 14.

The vorticity field is grouped into a region associated with the cylinder, \(R_{\text {cyl}}\), as well as into a further area that encloses the externally created vorticity, \(R_{\text {ext}}\), as shown in Fig. 9.

Fig. 9
figure 9

Schematic illustration of a flowfield grouped into two sections: one encompasses cylinder-related vorticity \(\omega ^{\text {cyl}}\) and a second includes only external vorticity \(\omega ^{\text {ext}}\)

Full size image

To compute the force acting on the cylinder, the impulse

$$\begin{aligned} I_y^{\text {cyl}} = x\omega ^{\text {cyl}} \end{aligned}$$
(18)

is evaluated directly from the measured vorticity field associated with the cylinder. \(\omega ^{\text {cyl}}\) represents both the cylinder boundary layer as well as any cylinder-shed vorticity. Thereafter, the velocity induced by \(\omega ^{\text {cyl}}\) at the location of the external vorticity is computed. This determines the relative advection of the external vorticity, which in turn is responsible for an additional force according to Eq. 14. From this it follows that the total lift force acting on the cylinder is,

$$\begin{aligned} L = \int _{R_{\text {cyl}}} \bigg (\underbrace{\frac{d \, I_y^{\text {cyl}}}{dt} }_{\textrm{impulse}} + \underbrace{U_{\omega ^{\text {cyl}}} \omega ^{\text {ext}}}_{\textrm{advection}} \bigg ) \, dR , \qquad I_y^{\text {cyl}} = x\omega ^{\text {cyl}}. \end{aligned}$$
(19)

It is worth noting that, as stated earlier, this result is effectively the same as that given by Eq. 14. In fact, Eq. 14 can be recovered from Eq. 19 by expanding the time derivative, splitting up the advection of the free vorticity into the individual induced velocity contributions and by removing the force components due to free vorticity advecting itself.

In practice when applied to PIV data, Eq. 19 can be implemented by computing \(I_y^{\text {cyl}}\) for each element of vorticity associated with the cyinder at each time step first and taking the time derivative thereafter to compute the impulse component, whilst the advection term is found by multiplying the strength of external vorticity by the velocity induced through cylinder-associated vorticity.

Moreover, it is not essential to fully resolve the boundary layer, instead missing velocity vectors in close proximity to the surface can be recovered by linearly interpolating between the measured velocity field and the known surface velocity of the object (Gehlert and Babinsky 2021a). This preserves the magnitude of vorticity located in the boundary layer. The wall normal distribution of vorticity is not correctly captured, however, if the reflections only extend a couple of millimetres into the flowfield data, then the associated error is small.

4 Multi-body force response

4.1 Cylinder in isolation

The first experimental case to be explored is that of a cylinder translating in isolation. This is used as a benchmark test case to determine the accuracy of the force calculation when the original impulse formulation derived by Wu (1981) is applied to the PIV data. A number of vorticity snapshots of the flowfield around the accelerating cylinder are presented in Fig. 10. Initially, vorticity resides only within the boundary layer. As the cylinder continues to accelerate, vorticity sheds as a shear layer from the top and bottom surface of the cylinder and rolls up into two distinct vortices.

Fig. 10
figure 10

Vorticity contours around a translating cylinder, case 1

Full size image

The lift and drag coefficients, \(C_l\) and \(C_d\), measured by the force balance as well as those calculated by applying the impulse method to any vorticity located within the flowfield are presented in Fig. 11. The added mass force contribution is also shown. This is determined according to

$$\begin{aligned} F_{\text {am}} = \rho \pi a^2 \frac{dU}{dt}, \end{aligned}$$
(20)

using the measured cylinder acceleration (Brennen 1982). It can be seen that \(C_l\) remains very close to zero throughout the motion and that the force balance and impulse method results are in a good agreement. Furthermore, it is encouraging to see that the drag coefficient is initially dominated by the added mass force. This is expected, because early on, no vorticity has been shed and the force therefore solely comes from the added mass force contribution. With greater translation distance, \(C_d\) begins to rise as vorticity sheds from either side of the cylinder. Once more, a very good match is observed between the force balance data and \(C_d\) obtained using the impulse method. The results therefore confirm that the impulse method is able to provide a good indication of the forces acting on the cylinder. That is, that the resolution and quality of the PIV data are sufficient to compute the forces.

Fig. 11
figure 11

Force history, case 1

Full size image

4.2 Circular cylinder in vicinity of a small flat plate wing

Having demonstrated that the PIV data is of sufficient quality to enable force calculations, we now consider a scenario where a circular cylinder is placed in close proximity to a lifting body. The development of the unsteady flowfield around the simultaneously accelerating circular cylinder and flat plate wing is shown in Fig. 12. Vorticity is shed from the leading and trailing edges of the plate, where a pronounced leading edge vortex forms and grows in size as the translation distance increases. At the same time, vorticity is shed from either side of the cylinder, where the unsteady separation differs between the top and bottom cylinder surface due to the influence of the plate.

Fig. 12
figure 12

Vorticity contours of the cylinder and plate, case 2. The dashed line marks the region within which vorticity is associated with the cylinder

Full size image

The lift and drag force coefficients acting on the cylinder are shown in Fig. 13. In contrast to the cylinder surging in isolation, \(C_l\) no longer remains zero but gradually becomes negative until \(s/D = 2\). As before, the drag coefficient is initially dominated by the added mass contribution and then rises gradually as vorticity is shed from the cylinder and the plate. The forces are now recovered from the PIV measurements by applying Eq. 19 to the flowfield data. The conventional impulse method is applied to the flowfield within the dashed loop, encircling the cylinder and its associated vorticity. This resulting ‘impulse’ contribution (blue circles) is then added to the force component created by the ‘advection’ term (green circles) originating from cylinder vorticity advecting any vorticity external to the dashed boundary. Here, the velocity induced by the cylinder is found by applying the Biot-Savart law to any vorticity residing within the dashed loop which groups cylinder-associated vorticity. The final result (red crosses) is in good agreement with the force balance measurements (black line) throughout the captured translation distance.

It can be seen that the ‘impulse’ and ‘advection’ contributions are of similar magnitude, highlighting that both components are required for an accurate force calculation. Whilst \(C_l\) sees a greater contribution from the ‘advection’ term, \(C_d\) is dominated by the force calculated from the ‘impulse’ component. This makes sense, since the u-velocity component induced by plate and cylinder vorticity on each other is greater than the induced v-velocity.

Fig. 13
figure 13

Force history, case 2

Full size image

4.3 Circular cylinder in vicinity of a large flat plate wing

To test the proposed force formulation in a further flow environment, a large flat plate wing is placed next to the circular cylinder, whilst the Reynolds number is reduced to 10 000 and the acceleration is increased such that it occurs over 0.5 D.

A selection of snapshots of the vorticity field are shown in Fig. 14. A leading edge vortex forms on the plate and remains close to the leading edge as acceleration begins, whilst small discrete vortices are shed from the trailing edge throughout. At the same time, two distinct vortices develop on either side of the cylinder, where the influence of the plate once more leads to an asymmetric development.

Fig. 14
figure 14

Vorticity contours of the cylinder and plate, case 3. The dashed line marks the region within which vorticity is associated with the cylinder

Full size image

The cylinder’s force history is shown Fig. 15. The rapid acceleration creates a strong added mass force that is clearly visible in the recorded data. Furthermore, the flow remains largely attached during initial translation and as acceleration ceases, \(C_d\) drops accordingly. With the onset of separation from the cylinder around \(s/D \approx 0.7\), the drag coefficient increases once more as the force begins to be affected by shed vorticity. The development of \(C_l\) on the other hand is much less dramatic and it is marginally negative until \(s/D \approx 1.4\), after which it becomes positive.

Figure 15 also shows the forces computed from PIV. Both the ‘impulse’ (blue circles) and ‘advection’ term (green triangles) of Eq. 19 contribute to \(C_l\), and the sum of both (red crosses) matches the force balance measurements well. In contrast, the contribution from the ‘advection’ term is almost negligible for \(C_d\) due to the direction of the induced velocity, which is mainly aligned with the x-axis. The majority of its contribution therefore affects \(C_l\) rather than \(C_d\). Once more, a very good match between the drag force balance data and \(C_d\) calculated from the vorticity field is achieved. The small discrepancy in the peak drag force during acceleration is most likely caused by vibrations of the flat plate.

Fig. 15
figure 15

Force history, case 3

Full size image

5 Vortex force heat map

With the help of the framework outlined in Sect. 2, we now construct a force heat map to evaluate the positional effect of a vortex, comprising of vorticity otherwise residing within the attached boundary layer, on the force generated by the wing. In order to compute the impact of this hypothetial vortex, we require the instantaneous kinematics of the wing as well as the location of any non-vortex vorticity. To get a sense of the strength and location of the latter, we could either use PIV, capturing the specific moment in time that we wish to examine, or alternatively use an unsteady panel method, where vorticity is released from the wing surface into the flow at each time step. Once we have established the flowfield that is to be investigated using our preferred method, we can then iteratively place the free vortex at each grid position around the wing, as schematically illustrated in Fig. 16, and calculate the force created by it using Eq. 15. This free vortex could for example be the LEV of a wing and we will use this as an example of how the proposed method can be used to better understand an unsteady flowfield.

LEV is close to the wing. Since the force is the time differential of the impulse, a wrong identification of LEV and boundary layer vorticity would lead to extremely noisy results. Future studies could focus on achieving a very high spatial PIV resolution of the leading edge of the of the wing, the LEV and the boundary layer vorticity, which may allow for a clear distinction between LEV and boundary layer vorticity to be made and thus enable a successful force recovery.

Fig. 16
figure 16

Schematic illustration of iteratively placing a free vortex (which could for example be a LEV) on grid points to compute the force heat map

Full size image

To reconcile this theoretical approach aimed to decipher how a flow structure, in this case the LEV, contributes to the force, we create a sequence of force heat maps for the pitching and translating wing described in Sect. 3.1.2. To do so, we represent the wing as a series of 500 panels, each with a vortex and collocation point located one quarter and three quarters along. Using a panel method code (Spalart 1988) where the no-through flow condition is enforced at each collocation point, the boundary layer vortex sheet is computed at each time step. To represent the wake, a vortex is released from the trailing edge at each time step, where its strength is derived by evaluating the sum of the vorticity flux at the trailing edge on the upper and lower surface of the wing (Gehlert and Babinsky 2020). To avoid any numerical inaccuracies due to the finite discretization around the sharp trailing edge, a vorticity flux average is computed using a length equivalent to 2.5 % of the chord. As the simulation advances, all free point vortices advect according to their respective induced velocities and thereby represent the ever-changing unsteady flowfield.

Once the panel method simulation reaches the desired points in time at which we want to evaluate the positional effect of the LEV, the simulation is stopped and the hypothetical vortex is placed around the wing, where its strength is informed from PIV. In turn, the boundary layer vortex sheet is modified accordingly for each LEV location to continue to satisfy the no-through flow condition in the presence of the LEV. It is worth noting that in a real viscous flowfield, LEV circulation is distributed over a finite area and not confined to a single point in space, as it is during our simulation. The positional coordinate of the vortex heat map therefore acts as a centre-of-mass-like representation of vortex position.

Three force heat maps are shown as the background of the vorticity plots in Fig. 17. If we look at areas where a LEV is likely to reside, the force maps demonstrate that when the LEV is located close to the upper surface of the wing, the LEV force contribution, compared to if the same amount of circulation was stored in the boundary layer, is less detrimental than if it is located further away. Moreover, close to the leading edge and at a sufficient LEV circulation strength, final plot on the right, a positive contribution to the lift is noticeable. The two regions towards the trailing edge showing both a significant increase and decrease in lift should be viewed cautiously as the close proximity between the virtual LEV and the trailing edge vorticity can lead to unphysical results.

Fig. 17
figure 17

Force response and vortex heat map as well as matching vorticity contours at selected set-points

Full size image

The effect that LEV position has on the force can be distilled down to predominately originating from the magnitude and direction of the velocity that is induced onto the LEV by the boundary layer vortex sheet. When the LEV is either very close to the wing or very strong, its mirror image or vortex sheet contribution, which forms part of the boundary layer vortex sheet, induces a strong negative (right to left) velocity onto the LEV according to the Biot-Savart law (Saffman 1992). If this induced velocity is greater than the speed at which the wing is travelling, then the LEV moves further upstream than it would otherwise have if the equivalent circulation was confined to the boundary layer and thus creates a stronger impulse and higher lift force. Conversely, the opposite is the case if the velocity induced onto the LEV is less than that of the translating wing, as this causes the distance between the positively signed TEV and the negative circulation contained with the LEV to be less than if the negative circulation were to reside within the boundary layer and thus yields a lower lift force.

To relate the force heat maps to the actual force experienced by the wing, we can use the force history plotted towards the top of Fig. 17. The force reaches a maximum \(C_l\) of 3.34 at \(s/c = 1.19\), where it consists of a circulatory force due to shed vorticity as well as an added-mass force contribution due to the combined pitch and surge kinematics of the wing (Limacher 2021; Andreu-Angulo and Babinsky 2022). Upon reaching a constant angle of attack at \(s/c = 1.5\), the latter ceases to contribute and the force acting on the wing is now only a function of the circulatory force created by shed vorticity. Coincidentally, no leading edge vorticity has shed up to this point and only begins forming a LEV once the pitching motion has stopped. This allows us to compare \(C_l\) at \(s/c = 1.5\) to the three instances for which we have created the force heat maps, as any variation in \(C_l\) must have come from the evolution of leading and trailing edge vorticity. Observing the LEV vortex location in reference to the force heat map shows the LEV to move away from the wing and to propagate into regions that are associated with a more negative \(\varDelta C_l\), where the suggested magnitude is approximately in line with the reduction in force shown by the force trace.

Whilst the presented example may have been quite intuitive to forecast and therefore did not perhaps require a force heat map approach, unsteady flows can be significantly more complex with multiple sources of flow disturbances and sources of vorticity obfuscating the picture. Here a force heat map would instead be able to shed light on the underlying intricacies.

Moreover, a further next application of the theory proposed in Sect. 2 could be to isolate the force due to the LEV for all time instances rather than at select intervals. In the present case study this was unfortunately not possible due to the limited PIV resolution which prevents an accurate distinction between LEV and boundary layer vorticity in regions where the LEV is located close to the wing. If the data permits a clear isolation of the vortex in question, in this case the LEV, then its time resolved unsteady force contribution could be computed providing further insight into the unsteady mechanisms at play.

6 Conclusion

A force formulation is proposed that expands the impulse method developed by Wu (1981), which is only able to compute the total force acting within the flow domain, to instead isolate the force created by an individual flow feature or body. It does this by identifying the core contributions to the force using the vorticity field in two-dimensions, for unsteady and incompressible flows. A by-product of this is that it enables the forces acting on a single object immersed in a multi-body flowfield to be found. Since it is easily possible to compare force calculations to force balance measurements of a single object part of such a multi-body flowfield, the proposed theory is tested by extracting the forces on a cylinder located in close proximity to a flat plate wing. The lift and drag forces are successfully recovered for as long as there is no significant mixing of vorticity and the flow remains sufficiently two-dimensional. The proposed force theory is subsequently used to create a force heat map evaluating the positional effect that a leading edge vortex has on the force. We recover the expected result, that when the leading edge vortex has drifted away from the wing it lowers the force experienced by the wing in comparison with if the same amount of circulation were to reside within the boundary layer. This example is used to showcase the force heat map in a simple scenario and aims to promote its application to more intricate and complex flow scenarios where it can enable a deeper insight into the underlying physics.