On the characterization of bias errors in defocusing-based 3D particle tracking velocimetry for microfluidics

Abstract

In this work, we provide a systematic theoretical and experimental characterization of bias errors in defocusing particle tracking (DPT) methods based on a single calibration function, with respect to microfluidic applications, in which it is not possible to use calibration targets inside the measurement volume. This approach is widely used in microfluidic experiments, but bias errors are often neglected and to date only few works reported empirical procedures to compensate for that. A systematic characterization of the impact of such error in DPT measurements is still lacking. We show that the field curvature aberration and the refractive index mismatch are the main sources of bias error in these applications. We present a correction methodology for the bias error based on the determination of a reference surface, and in addition we propose a procedure based on a reference measurement of a Poiseuille flow to determine the reference surface on microfluidic channels with constant cross section. We discuss the impact of the refractive index mismatch and how to correctly compensate for it. We validated our methodology and quantified the bias errors on 10 different experimental setups, using different working fluids, materials, geometries, and microscope objective lenses ranging from 5$\times$ to 40$\times$ magnification. Our results indicate that the impact of this type of bias errors is in general not predictable and must be evaluated case by case. The proposed methodology allows to estimate and minimize the bias error in most microfluidic setups and is suitable for any single-camera DPT approach.

1 Introduction

Defocusing is a well-known concept in photography: objects lying in proximity of the focal plane of the optical system appear sharp or in focus in the image, whereas more distant objects appear blurred or out of focus. The degree of defocusing is proportional to the objects’ distance from the focal plane, thus encoding information about their out-of-plane position. This concept was used in experimental fluid mechanics already in the early 1990s to obtain the three-dimensional (3D) coordinates of tracer particles from single-camera recordings (Willert and Gharib 1992; Stolz and Köhler 1994).

Since then, a large variety of approaches have been proposed to read out efficiently the defocusing information, for instance using a measurement of the particle image diameter (Stolz and Köhler 1994; Speidel et al. 2003; Afik 2015), a pinhole mask (Willert and Gharib 1992; Pereira and Gharib 2002), or a controlled astigmatic aberration induced by a cylindrical lens (Kao and Verkman 1994; Cierpka et al. 2010). More recently, pattern recognition algorithms based on cross-correlation (Barnkob et al. 2015) or neural networks (König et al. 2020; Lammertse et al. 2022) have been used as well. We will generally refer to all these methods as defocusing particle tracking (DPT).

DPT methods found a large field of application in microfluidics where normally only a single optical access through the microscope objective is available and the multi-camera approaches commonly used in turbulence and large-scale facilities are not applicable (Schanz et al. 2016; Raffel et al. 2018). For instance, they have been used for velocimetry measurements inside evaporating droplets (Rossi et al. 2019), acoustic streaming flows (Qiu et al. 2019; Sachs et al. 2022), electrolyte convection (Tschulik et al. 2011), and for tracking bacteria (Taute et al. 2015).

DPT methods rely on a calibration procedure to map the defocusing degree of a particle image to the respective out-of-plane coordinate. In microfluidic applications, the calibration is typically performed on fixed particles (e.g., stuck to a wall) changing the focus of the microscope. Bias errors can occur if the mapping obtained from the calibration is different from the actual mapping in the experiments, for instance due to unwanted aberrations, misalignment, or modified optical conditions. It is worth mentioning that some of these bias errors, such for instance the ones due to refractive index mismatch, are not present if a calibration target could be inserted and displaced inside the measurement volume (Hain and Kähler 2006), however, this is often not possible in microfluidic experiments due to the limited accessibility and the small scale environment.

Many DPT measurement approaches currently used and developed in the literature rely on a single defocusing calibration function for the entire field of view (FOV), but this assumption is not always valid, especially if a cylindrical lens is used or the measurements are performed across a large field of view (FOV) (Cierpka et al. 2011). An empirical procedure to overcome this problem in wall-bounded volumes has been proposed by Fuchs et al. (2016) considering reference particle images moving in proximity of the wall. A similar approach was followed by Rossi and Barnkob (2020) considering tracer particles sedimented on the bottom wall. However, these approaches do not consider the impact of a misalignment of the reference wall or the effect of refraction across different media. In general, a systematic characterization of bias errors in this type of DPT measurements and their impact on the final uncertainty is still missing.

In this work, we intend to fill this gap by a thorough theoretical and experimental characterization of such bias errors. The main sources of bias errors are discussed in Sect. 2, and in Sect. 3 we propose a theoretical framework to obtain a correction method for biased systems. The impact of the bias errors in DPT measurements is characterized experimentally for the different setups in Sect. 4. The results are presented and discussed Sect. 5, whereas the conclusions are given in Sect. 6.

2 Bias error in DPT

Fig. 1

a Impact of the field curvature aberration in a standard imaging system, including: object plane, lens, image plane ($z \propto y^2$) and camera CCD. b Effect of light refraction patterns in a standard microfluidics setup, including the ray tracing with and without refraction

We consider DPT approaches performed on monodispersed particles, with a single calibration function obtained by scanning a reference particle with the microscope focus, using a distortion-free microscope objective, and in microfluidic devices with planar optical accesses. Under these conditions, verified in the majority of DPT applications in microfluidics, the field curvature aberration and refraction effects can be considered the main contributions to the bias error. Perspective errors usually present in volumetric particle image velocimetry measurements (Raffel et al. 2018) are negligible for the optical arrangements considered here (Rossi and Barnkob 2020).

2.1 Field curvature

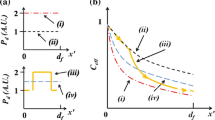
When imaging through curved lenses, the field curvature causes a geometrical distortion between the object and the image plane i.e., transforms front-parallel planar surfaces into curved image surfaces, as shown in Fig. 1a (Born and Wolf 1975). The mathematical description of this problem is given by the primary Seidel aberrations, which shows that the in-focus position in the image space of a given planar object varies with the squared distance to the optical axis (i.e., $z \propto x^2 + y^2$).

Due to the generally curved surface of microscope objective lenses, this phenomenon is commonly present in DPT measurements: Particles sitting on a flat plane perpendicular to the optical axis and expected to have the same defocusing pattern, will show instead different patterns giving biased measured positions (Fig. 1a). A practical approach to map the field curvature is to use a second-order polynomial surface to fit measured positions of particles lying on a flat plane.

Astigmatic systems, which are also often used in DPT measurements, do not feature a single focal plane and as a result the field curvature will vary with the distance to the objective lens (Born and Wolf  1975). Since the measurement depth is usually small with respect to the length scale of this variation, we assume an invariant field curvature described as

$$\begin{aligned} z = ax^2 + by^2 + cxy. \end{aligned}$$

(1)

where a, b, and c are coefficients to be determined experimentally.

2.2 Refraction

In DPT measurements, the light emitted by tracer particles travels through different media: the working fluid, the wall of the microfluidics device and immersion medium of the lens. Since these components have typically different refractive indices (i.e., refractive index mismatch, RIM), the light rays are deflected at each interface according to Snell’s law of refraction:

$$\begin{aligned} n_\text {i}\sin \theta _\text {i} = n_\text {g}\sin \theta _\text {g} = n_\text {f}\sin \theta _\text {f}, \end{aligned}$$

(2)

with $n_\text {i}$, $n_\text {g}$, and $n_\text {f}$ as the refractive indices, and $\theta _\text {i}$, $\theta _\text {g}$, and $\theta _\text {f}$ as the angles of incidence in the immersion medium of the lens, the wall of the microchannel, and working fluid, respectively.

As a consequence, the focal plane of the objective lens will be shifted from $z_\text {i}$ to $z_\text {f}$, as shown in the schematic of Fig. 1b, and according to the following equation (Kim and Liu 2004)

$$\begin{aligned} z_\text {f} = k_\text {1} z_\text {i} + k_\text {2} t_\text {wall}, \end{aligned}$$

(3)

where the $t_\text {wall}$ is the thickness of the bottom wall of the microfluidics device and the scaling factors $k_\text {1}$ and $k_\text {2}$ are given by

$$\begin{aligned} k_\text {1} = \sqrt{\frac{n_\text {f}^2 - (n_\text {i} \text {sin}\theta _\text {i})^2}{n_\text {i}^2 - (n_\text {i} \text {sin}\theta _\text {i} )^2}}, \end{aligned}$$

(4)

$$\begin{aligned} k_2 = \sqrt{\frac{n_\text {f}^2 - (n_\text {i} \text {sin} \theta _\text {i})^2}{n_\text {i}^2 - (n_\text {i} \text {sin} \theta _\text {i})^2}} - \sqrt{\frac{n_\text {f}^2 - (n_\text {g} \text {sin} \theta _\text {i})^2}{n_\text {g}^2 - (n_\text {i} \text {sin} \theta _\text {i})^2}}. \end{aligned}$$

(5)

Using small angle approximation ($\sin \theta \approx 0$) (Rossi et al. 2012), the shift of the focal plane from Eq. (3) is simplified to

$$\begin{aligned} z_\text {f} \approx \frac{n_\text {f}}{n_\text {i}} z_\text {i} + (\frac{n_\text {f}}{n_\text {i}} - \frac{n_\text {f}}{n_\text {g}}) t_\text {wall}. \end{aligned}$$

(6)

For DPT measurements, we need to consider the depth-distance between particles when refraction is present $\Delta z_\text {f}$. Using Eq. (6) to obtain $\Delta z_\text {f}$, the constant terms depending on the thickness of the wall $t_\text {wall}$ cancel out and $\Delta z_\text {f}$ takes the following form

$$\begin{aligned} \Delta z_\text {f} \approx \frac{n_\text {f}}{n_\text {i}} \Delta z_\text {i}. \end{aligned}$$

(7)

The above Eq. (7) expresses the scaling factor due to the RIM as the ratio between the refractive indexes of the fluid $n_\text {f}$ and immersion medium of the lens $n_\text {i}$, henceforth k. In the present work, the validity of this assumption in DPT measurements is verified with systematic experiments (Sects. 3.2 and 5.3).

3 Methodology

3.1 Theoretical framework

For each detected particle, a DPT evaluation returns a position vector ${\textbf {X}}$ defined by three non-dimensional coordinates (X, Y, Z). The in-plane coordinates X and Y represent the particle position projected into the two-dimensional image plane and are scaled with the side length of the camera pixel divided by the magnification. Practically, the non-dimensional values of X and Y are equivalent to values given in pixel units. The out-of-plane coordinate Z defines the depth particle position, and it will be here scaled with the total depth of the measurement volume h, thus having values between 0 and 1. It should be noted that h is the actual depth of the measurement volume which is obtained from the depth covered by the calibration images, corrected with the scaling factor due to RIM. We will come back to this point later.

To obtain physically meaningful results, we need to project the non-dimensional coordinates into the physical space using a suitable mapping function ${\textbf {x}} = T({\textbf {X}})$.

For unbiased systems, a linear mapping can be used

$$\begin{aligned} {\textbf {x}} = M {\textbf {X}} = \begin{bmatrix} d_\text {px}/M_x &{} 0 &{} 0\\ 0 &{} d_\text {px}/M_y &{} 0\\ 0 &{} 0 &{} h \end{bmatrix}{} {\textbf {X}}, \end{aligned}$$

(8)

where $d_\text {px}$ is the side length of the camera pixel, and $M_x$ and $M_y$ are the magnifications in the x and y direction, respectively (with $M_x=M_y$ for non-astigmatic systems).

For a biased system, a generic formulation of the mapping function can be given by

$$\begin{aligned} {\textbf {x}} = R M \cdot ( {\textbf {X}} - {\textbf {C}}), \end{aligned}$$

(9)

where M is the linear mapping in Eq. (8), ${\textbf {C}}$ is the translation vector due to the field curvature, and R is a rotation matrix that will be discussed later.

Fig. 2

Schematic of the methodology used to corrected the bias errors in DPT measurement, including the reference surface F(X, Y), reference plane H(X, Y), orientation vectors (${\textbf {i}}$, ${\textbf {j}}$, ${\textbf {k}}$) used to the rotation and the optical axis

Now, to derive experimentally the expression for C, we can consider a reference plane in the measurement volume. This could be a flat wall as in Rossi and Barnkob (2020) or the symmetry plane of a Poiseuille flow as proposed in Sect. 3.2. Following the analysis in Sect. 2, such plane in the non-dimensional coordinates will appear as a second-order polynomial surface

$$\begin{aligned} F(X, Y) = p_{20}X^2 + p_{02}Y^2 + p_{11}X Y + p_{10}X + p_{01}Y, \end{aligned}$$

(10)

where we omitted the constant term, since it can always be eliminated by setting the origin so that $F(0,0) = 0$.

Considering the field curvature described by Eq. (1), it is easy to show that the tangent plane to F(X, Y) at the point where the field curvature is null (i.e., $(X,Y)=(0,0)$) is given by

$$\begin{aligned} H(X,Y) = p_{10}X + p_{01}Y, \end{aligned}$$

(11)

and corresponds to the projection of the reference plane in the non-dimensional coordinates if no aberrations were present. Thus, the difference between F(X, Y) and H(X, Y) represents the contribution from the field curvature and can be used to define the translation vector C as

$$\begin{aligned} {\textbf {C}}(X,Y) = \begin{bmatrix} 0\\ 0 \\ p_{20}X^2 + p_{02}Y^2 +p_{11}XY \end{bmatrix}. \end{aligned}$$

(12)

Finally, from H(X, Y), properly scaled, it is straightforward to identify the normal unit vector ${\textbf {k}}$, which describes the tilt of the reference plane with respect to the optical axis as shown in Fig. 2. The corresponding orthogonal unit vectors ${\textbf {i}}$ and ${\textbf {j}}$ lying on the reference plane, can be oriented arbitrarily, for instance pointing ${\textbf {i}}$ in the flow direction as described in Sect. 3.2. The three orthogonal orientation vectors define the rotation matrix R

$$\begin{aligned} R = \left[ {\textbf {i}} \mid {\textbf {j}} \mid {\textbf {k}} \right] ^T \end{aligned}$$

(13)

used in Eq. (9). Although not strictly necessary to correct the bias error, it is useful to introduce the rotation matrix R in the mapping function to align the measurements with the reference plane.

Fig. 3

Different steps used to determine the reference surface F(X, Y) from a Poiseuille flow measurement. a–c field curvature along the Y direction, including the decomposition of the velocity information into N bins, estimation of the points of maximum velocity and fitting to a parabolic equation Z(Y). d–f Estimation of the reference surface F(X, Y), including relocating the individual particle trajectories in depth according to Z(Y) and fitting the relocated particle trajectories to Eq. (10) to obtain F(X, Y)

3.2 Determination of the reference surface from a Poiseuille flow

The reference surface F(X, Y) has been obtained in previous publications by looking at particles sitting in proximity of a flat wall (Fuchs et al. 2016; Rossi and Barnkob 2020). Here, we introduce an alternative approach based on a reference measurement of a Poiseuille flow. We believe that, when applicable, this approach offers a series of advantages: (i) a Poiseuille flow can easily be established in most microfluidic experiments using a microchannel with constant cross section, (ii) a large amount of measurement points across the FOV can be collected in a short time, and (iii) F(X, Y) is calculated from particle trajectories measured in the center of the microchannel, where the uncertainty is typically smaller than for particles close to the wall (Barnkob et al. 2015). Furthermore, it can provide a direct measurement of the scaling factor k for the RIM correction, as discussed in Sect. 5.3.

To derive F(X, Y) from the measurement of a Poiseuille flow, we propose the following methodology, graphically summarized in Fig. 3a–f. First, we set the reference frame so that X and Y are aligned with the stream-wise and transverse direction of the Poiseuille flow, respectively. Then, we slice the measurement volume along the Y direction into N bins and determine for each bin the velocity profile along the Z direction from the average velocity and mid-position of each trajectory (Fig. 3a). A parabola is fitted to each individual velocity profile to extract the position of the maximum velocity in each bin ($Y_N,Z_N$) (Fig. 3b). Notice that in microchannels with a symmetrical cross section (e.g., rectangular or square channels), the maximum velocity lies on a flat plane, thus ($Y_N,Z_N$) represents a curve that can be seen as the intersection between F(X, Y) and the YZ plane. Following the discussion from Sect. 3.1, we use a parabolic equation to map it: $Z(Y) = a Y^2 + b Y + c$, see Fig. 3c. Finally, each individual particle trajectory is relocated in depth using the parabolic fit Z(Y), see Fig. 3d–e. In this way, the 3D measured particle trajectories are moulded into a single surface which we can fit with (Eq. (10)) using a robust least-squares fit to determine the reference surface F(X, Y), see Fig. 3f. It should be noted that the theory developed in Sect. (3.1) requires that (X,Y) = (0,0) coincides with the optical axis. Here, we assume that the center of the image corresponds to the optical axis. We will discuss the consequences of possible differences in the actual position of the optical axis in Sect. (5.2).

4 Experimental system

4.1 Experimental setup

The general schematic of the experimental setup is shown in Fig. 4a. A microchannel was placed on the working stage of an epi-fluorescent inverted microscope coupled with a recording camera and LED backlight. For the present measurements, we used two different configurations. The first one consisted of a custom-made microscope equipped with a high-sensitivity sCMOS camera (pco.edge 5.5, PCO GmbH). For this setup, the optical system included a M = $5\times$, NA = 0.13 objective lens (EC EPIPlan, Zeiss AG), with a cylindrical lens $f_\text {cyl} = 500$ mm (LJ1144RM-A, Thorlabs Inc.) placed in front of the camera sensor. This system was used to perform measurements in a borosilicate glass capillary with rectangular cross section $w_\text {ch}\times h_\text {ch}=2000\times 200$ $\mu$m$^2$ (3520-050, VitroCom Inc.) and nominal thickness of 140 $\mu$m, see Fig.  4c(i). The FOV in the X and Y directions was 2560 and 2000 pixels, respectively.

Fig. 4

Overview of the experimental setup, GDPT calibration image stacks and optical systems. a Schematic of the experimental setup; b Calibration image stacks using fixed particles on top and bottom of the microchannel; c All test cases including microchannel cross section dimensions ($w_{\text {ch}} \times h_{\text {ch}}$) and lens systems (magnification M and numerical aperture NA)

The second configuration consisted of an inverted microscope (Leica DM IL LED, Leica GmbH) equipped with a high-speed camera (HighSpeedStar 4 G, LaVision GmbH). This system was operated with two objective lenses: M = $20\times$, NA = 0.4 (NPlan Epi, Leica GmbH) and M = $40\times$, NA = 0.55 (NPlan L, Leica GmbH). For the astigmatic measurements, the same type of cylindrical lens (LJ1144RM-A, Thorlabs Inc.) was placed in front of the camera sensor. Two different microchannels with rectangular cross section ($w_\text {ch}\times h_\text {ch}$) were observed with this configuration: $50\times 50$ $\mu$m$^2$ (CS-10000087, Darwin Microfluidics) and $800\times 20$ $\mu$m$^2$ (CS-10000109, Darwin Microfluidics), with a corresponding FOV in the measurements of 1024 $\times$ 256 pixels and 1024 $\times$ 1024 pixels, respectively. The microchannels are made of a rigid polymer (Topas COC) with bottom wall thickness of 140 $\mu$m. In some measurements, a microscope glass with 1 mm thickness (D100001, Deltalab) was placed under the microchannel, see Fig. 4c (ii)–(iii).

The flow was seeded with fluorescent polystyrene tracer particles with 9.9 $\mu$m or 2.5 $\mu$m diameter (ex/em 530/607 nm, PS-FluoRed, MicroParticles GmbH). All configurations used a backlight illumination provided by a high-power green LED (SolisC525C, Thorlabs Inc.) and a filter cube for fluorescence imaging (Excitation: BP 525/50 nm; Dichroic: 570nm and Emission: 620/60 nm).

4.2 Calibration images

From the combination of the different setups, we obtained a total of twelve independent configurations (lens-microchannel-fluid/particles) that were tested in this work (Fig. 4c (i)–(iii)). For each configuration, the corresponding measurement volume was mapped with a calibration stack of images (Rossi and Barnkob  2020). The calibration stack was obtained by taking images of particles stuck to the top or bottom wall of the microchannel, and modifying their defocusing patterns by moving the microscope objective, as shown in Fig. 4b. The step size was set to 2 $\mu$m for the $5\times$ lens, and to 1 $\mu$m for all the other cases.

Table 1 Summary of the Poiseuille test cases including dimensions of the microchannel cross section ($w_\text {ch}$ $\times$ $h_\text {ch}$), thickness of the bottom wall ($t_\text {wall}$), lens system, diameter of the tracer particles ($d_\text {p}$), working fluid, height of the measurement volume (h) and estimated error at a distance X/Y=1000 pixels from the optical axis, calculated from the field curvature $p_\text {20}$,  $p_\text {02}$ (see Eq. (10)). The astigmatic optical configurations are indicated by (A)

4.3 Fluid properties

In these experiments, two types of fluids were used. A solution of distilled (DI) water at 24,%wt. Optiprep (OptiPrep $^TM$ Density Gradient Medium, Sigma-Aldrich), with density $\rho$ = 1102.1 kg/m$^3$ and refractive index $n_\text {f}$ = 1.351, and a solution of DI-water at 25 %wt. of urea (Thermo Scientific $^TM$ Urea, Thermo Fisher Scientific Inc.), with $\rho$ = 1064.6 kg/m$^3$ and $n_\text {f}$ = 1.352. The refractive index of the fluids was measured using a refractometer (Abbe 60, Bellingam & Stanley) working at the mean sodium D wavelength (589.6 nm). The refractive index at 293.15 K, $n_t^D$, was measured, with a reproducibility of 0.010 % and an accuracy of 0.035 %. All measurements were done in five replicate runs and buoyancy corrections were applied. Additionally, to confirm the density matching between working fluid and tracer particles, the fluid density was characterized using a vibrating tube densimeter (DSA-5000, Anton Paar). The standard uncertainty of measurement was found to be $u(\rho ) = 0.30$  kg$\cdot$m$^{-3}$ and the expanded uncertainty at a 95 % confidence level ($k = 2$) is $U(\rho ) = 0.46$ kg$\cdot$m$^{-3}$.

4.4 Poiseuille flow measurements

The Poiseuille flow was measured in total for eight different experimental configurations. For each optical arrangement the measurement depth h was larger than the depth of the microchannel $h_\text {ch}$, hence no scanning procedures were needed. To check data reproducibility, the flow was recorded three times in a row for each configuration. In the 2000 x 20 $\mu$m$^2$ microchannel, a flow rate of 50 $\mu$l/min was imposed with a syringe pump (Legato110, KD Scientific). Each recording consisted of 250 frames taken at 25 frames per second (fps). For the other microchannels, the Poiseuille flow was imposed by hydrostatic pressure, by setting a height offset between the inlet and the collection reservoir. In each measurement 2500 images were recorded at 50 fps. The configurations for the different test cases, including the estimated coefficients ($p_\text {20}$,  $p_\text {02}$) associated with the field curvature are summarized in Table 1 and will be discussed in details in Sects. 5.1 and 5.3. The experimental images were processed using the open-sourc software DefocusTracker (Barnkob and Rossi  2021), based on the general defocusing particle tracking (GDPT) method, available at https://gitlab.com/defocustracking.

Fig. 5

Comparison of the field curvature for different optical setups, including the raw (i) and corrected particle cloud (ii) from the Poiseuille flow measurements, the mean absolute error $\epsilon _Z$ along the depth-coordinate (iii); the contribution from the field curvature is given by ${\epsilon _Z}_\text {fc}$. a Lens system: $\times 20/0.4$; b Lens system: $\times 20/0.4$ (A); c $\times 40/0.55$. All measurements were performed in a microchannel with cross-sectional area of $w_\text {ch}\times h_\text {ch} = 50 \times 50$ $\mu$m$^2$

5 Results and discussion

5.1 Bias error from the field curvature

We determined the field curvature using a reference surface obtained from the measurement of a Poiseuille flow as described in Sect. 3.2. The second order fitting coefficients $p_{20}$ and $p_{02}$ from the reference surface are used as evaluation parameters. It should be noted that the error from the field curvature at a distance of $X/Y=1000$ pixels from the optical axis corresponds to $p_{20}/p_{02}\times 10^6$ (see Eq. (10)). The values of $p_{20}$ and $p_{02}$ for each optical configuration are reported in Table 1 and are the average from three consecutive measurements.

A major assumption on our methodology is to consider the field curvature to be the same along the optical axis (Sects. 2.1 and 3). This assumption can be verified by comparing the measured particle trajectories before and after the field curvature correction. For each measured trajectory, we can calculate an error $\epsilon _Z$ according to

$$\begin{aligned} \epsilon _Z (Z_\text {traj}) = \frac{\sum _{i=1}^{N_\text {traj}} \mid Z_\text {traj} - Z_i \mid }{N_\text {traj}}, \end{aligned}$$

(14)

where $Z_\text {traj}$ is the Z-coordinate at $X\approx 0$, and $Z_i$ represents the collection of $N_\text {traj}$ that compose a given trajectory. After correction, the error $\epsilon _Z$ should contain only contributions due to the random error, whereas before correction the contribution due to the bias error is also included. If the field curvature is indeed constant, its contribution at the various depth positions is equal, and hence the variation of the error due to the field curvature ${\epsilon _Z}_\text {fc}$ through the measurement volume should be constant (with ${\epsilon _Z}_\text {fc}$ calculated as the difference between $\epsilon _Z$ before and after correction).

Figure 5a–c shows the raw dataset (i), corrected dataset (ii), and the mean absolute error $\epsilon _Z$ including the contribution from the field curvature ${\epsilon _Z}_\text {fc}$ (iii), for several optical configurations. The results show that the contribution from the field curvature (${\epsilon _Z}_\text {fc}$) to the measurement error is independent of the depth position, as hypothesized. Similar results were also found in the remaining setups.

It is also interesting to notice the effect of the cylindrical lens in the field curvature, comparing the astigmatic and non-astigmatic cases shown in Table 1 ($w_\text {ch}\times h_\text {ch} = 800 \times 20$ $\mu$m$^2$). On one hand, for the non-astigmatic optical system we determined a field curvature with similar values for $p_{20}$ and $p_{02}$, as a consequence of the axis-symmetry of the lens system. On the other hand, as we introduce the cylindrical lens in the astigmatic case, it breaks the overall symmetry of the lens system and the curvature of one axis is modified ($p_{02} \ll p_{20}$). A similar behaviour can be observed for the experiments within the microchannel with cross-sectional area of $w_\text {ch}\times h_\text {ch} = 2000 \times 200$ $\mu$m$^2$. Here, the cylindrical lens was rotated 90 degrees from the first to the second optical configuration which therefore results in a different direction of the maximum curvature. The field curvature aberration is also found to be different for each optical arrangement and no clear patterns between individual characteristics of the lens systems has emerged (Table 1).

Fig. 6

Impact of the field curvature on the estimated depth-coordinate Z from a DPT evaluation as function of the distance Y from the optical axis. The associated error ${\epsilon _Z}_\text {fc}$ as indicated by the colormap. a Lens system $\times$5/0.13 (A), microchannel: $w_\text {ch}\times h_\text {ch}=2000\times 200$ $\mu$m$^2$. b Lens system $\times$20/0.4 (A), microchannel: $w_\text {ch}\times h_\text {ch}=50\times 50$ $\mu$m$^2$. c Lens system $\times$20/0.4, microchannel: $w_\text {ch}\times h_\text {ch}=800\times 20$ $\mu$m$^2$

The impact of the field curvature on a DPT measurement depends also on the size of the FOV. Fig. 6 shows the evolution of three different curvatures from Table 1 as function of the distance Y to the optical axis at $Y=0$. A field curvature with $p_{02}=-0.274\times 10^{-6}$ will give a bias error of 27 % the height of the measurement volume h at 1000 pixels distance from the optical axis (Fig. 6c), whereas if $p_{02}=-0.032\times 10^{-6}$ the error reduces down to 3 % (Fig. 5 a(i)). On the other hand, if we consider a narrower FOV e.g., $Y<100$ pixels, the impact of field curvature becomes negligible. In such cases, the proposed methodology is not able to interpret the small curvatures, hence the null entries in Table 1.

In sum, the present analysis shows that the impact of the field curvature is an individual characteristic of each optical system and experimental setup, and accordingly it must be evaluated case by case.

Finally, the estimation of the reference surface F(X, Y) from the Poiseuille flow (Fig. 7b) was compared to the surface estimated with sedimented particles (Fig. 7a). As for the latter, a set of reference surfaces $F_n(X,Y)$ was obtained from the measurement of the sedimented particles at n different focus position. The final surface F(X, Y) in Fig. 7a is determined from the average of all fits at the different depth positions. Here, we considered a single experimental configuration with astigmatic lens system, corresponding to Fig. 4c(iii). Whereas the estimated curvature along the Y-direction is similar for the two methods, a different value is estimated for the curvature along the X-direction. This discrepancy is most likely due to a different distribution of data points across the FOV. In particular, since the Poiseuille flow allows to collect a larger amount of data points more evenly spread across the FOV, it is reasonable to expect a more reliable result with this approach.

Fig. 7

Estimated field curvature F(X, Y). a sedimented particles on the bottom of the microchannel b Poiseuille flow: particle trajectories. Microchannel: $w_\text {ch}\times h_\text {ch}=800\times 20$ $\mu$m$^2$; Fluid: DI-water with 25 wt.$\%$ Urea ($n_{\text {f}}=1.352$); Lens system: $\times$20/0.4 (A). The colormap represents the value of the estimated F(X,Y) in the considered FOV

5.2 Tilt of the reference plane

We showed in Sect. 3.1 that the bias error encountered in this type of DPT measurements is essentially a combination of the field curvature aberration and the tilt of the reference plane with respect to the optical axis. If the tilt is neglected, a systematic error will also occur in the in-plane directions, proportional to the cosine of the tilt angle and the depth position of the particle. Furthermore, to calculate the tilt angle in Sect. 3.1, we made the assumption that the optical axis is located at the center of the image (see Fig. 2), but a slight misalignment can clearly occur in experimental systems. To quantify the impact of the tilt angle and misalignment of the optical axis we used here Monte Carlo simulations.

Fig. 8

Estimated maximum bias error in the corrected particle coordinates along the Z- and X-direction from the Monte-Carlo simulations, obtained with and without the tilt correction. a Error in the X-axis as function of the tilt angle $\theta$, including the error in the position of the optical axis $\epsilon _\text {OA}$. b-c Error in Z-axis as function of the tilt angle $\theta$ for small field curvature ($p_{20}$, $p_{02}=-0.03\times 10^{-6}$ and $p_{20}$) and large field curvature ($p_{20}$, $p_{02}=-0.28\times 10^{-6}$), respectively

The conditions in the simulations were chosen to match experimental the test cases in Table 1 with a microchannel cross section of $800\times 20$ $\mu$m$^2$. The imposed field curvature was defined according to the highest and lowest value detected in our experiments: $p_{20}$, $p_{02}=-0.03\times 10^{-6}$ and $p_{20}$, $p_{02}=-0.28\times 10^{-6}$. For simplicity and without loss of generality, the tilt was only imposed on the Y-axis ($\theta$) and varied from 0.025 to 3 degrees. The error ($\epsilon _{OA}$) in the position of the optical axis was varied from 20 to 100 pixels along the X direction.

For each case (different $\theta$ and OA), 19674 particle coordinates moving into a Poiseuille flow with a maximum displacement of 17.6 pixels were randomly created inside the measurement volume. The selected tilt and field curvature were applied to the simulated measurements. The coordinate positions obtained in this way were then corrected by applying the methodologies proposed in Sect. 3, with and without the tilt correction (i.e., directly subtracting F(X, Y) to the Z coordinates). The error was calculated as the difference between the true and corrected coordinates. The maximum error for each case is reported in Fig. 8.

As expected, the simulations show that the full correction with no error in the optical axis (tilt corr. and $\epsilon _{OA}=0$) is able to eliminate the bias error for both X- and Z-directions and the remaining error is essentially due to random noise in the simulation and in the numerical procedure used to estimate the field curvature and rotation. If the tilt correction is neglected, the in-plane error $\text {max}\{\epsilon _X\}$ rapidly increases (Fig. 8a), however for tilt angles $\theta <3$ deg it remain below 2 pixels, which is non-negligible but still very small on the FOV of 870$\times$820 pixels (used in the simulations). On the other hand, for a large field curvature, the tilt correction can have a detrimental effect on the accuracy of the correction, if the optical axis is not lying on the image center.

Overall, the Monte Carlo simulations show that the interplay between tilting and field curvature is not trivial. While including the tilt angle in the correction is clearly beneficial for small field curvature, it is not so straightforward for larger field curvature. Given the relatively small error occurring in the in-plane direction, a possible strategy is to neglect the tilt angle correction and simply subtract the reference F(X, Y) to the data.

5.3 Refractive index mismatch

In general, the bias error due to refraction arises since the defocused particle images in the calibration and in the experiments originate from distinct optical paths. Calibration data are typically taken on static particles, while moving the microscope objective at different depth positions. Measurements are taken with a static objective and particles moving across a volume. As a consequence of the RIM, the calibration depth $h'$ calculated as the difference between higher and lower position of the microscope objective will be different from the actual measurement depth h during experiments. In practice, the scaling factor $k = h/h'$ is normally approximated to $k= n_\text {f}/n_\text {i}$ as discussed in Sect. 2.2. In this section, we verify this approximation for the scaling factor in different optical configurations and two working fluids with known refractive index. Besides, we evaluate if the calibration images can be obtained from sedimented particles or if this is an oversimplification of the problem.

Fig. 9

Methods to estimate the experimental height of the microchannel $h'_{\text {ch}}$ from image stacks: focus measure (FM) and DPT. a Objective lens M = $5\times$, NA = 0.13 (A) with glass thickness $t_g\,=\,140$ $\mu$m. b Objective lens M = $40\times$, NA = 0.55 with glass thickness $t_g=1140$ $\mu$m

We estimated the scaling factor k for the optical setups summarized in Table 1 using the ratio between the nominal $h_\text {ch}$ height of the microchannel and a measured value $h'_\text {ch}$ obtained with three different experimental approaches. Since we used air-immersed lenses ($n_\text {i}=1$), the measured scaling factor could be considered as a measured effective refractive index of the fluid, henceforth $n_\text {eff}$

$$\begin{aligned} n_\text {eff} = \frac{ h_\text {ch} }{ h'_\text {ch} }. \end{aligned}$$

(15)

The first approach to obtain the experimental heights is based on particles stuck to the bottom and top wall of the microchannels. In total, we recorded two pairs of particles for each optical setup and microchannel, scanned through different focus positions. The chosen particles were adjacent and near the optical axis to minimize the contribution from the field curvature. Examples of the particle images can be seen in Fig. 9a–b (i), where $P_\text {T}$ denotes the particle on the top wall, and $P_\text {B}$ the particle on the bottom. Following the work of Rossi et al. (2012), the experimental height was determined using a focus function, specifically the Tenengrad function (Yeo et al. 1993). With this approach, we obtain for each case two curves representing the value of the focus function for the bottom- (dark-blue markers) and top-wall particle (light-blue markers) at different focus position of the microscope, as shown in Fig. 9a–b (i). The height is estimated based on distance between the two maxima i.e.,  the two focal positions. Note that the two local maxima observed in Fig. 9a(i) are due to the use of a cylindrical lens in the optical arrangement.

A second approach, based on the same stacks of images, consists of a direct determination of the depth coordinate of the adjacent particles with a DPT measurement and calculate the channel height as the difference between the two coordinates $h'_\text {ch} = z'_\text {T}-z'_\text {B}$. The height values should then remain constant across different focus positions as shown in Fig 9a–b (ii). In particular, the observed fluctuations of $h'_\text {ch}$ are within $2\,\%$ of measurement volume which is typically the uncertainty for this type of measurement (Barnkob and Rossi 2020) and no additional systematic effects can be observed. Similar results were also found for the other optical configurations and demonstrate that the scaling due to RIM is constant across the measurement volume.

Finally, a third approach is based on the measurement of a Poiseuille flow. The z-coordinate of the top and bottom walls are extrapolated from the velocity profiles assuming no-slip boundary condition at the wall, and $h'_\text {ch}$ determined from the difference of the two coordinates.

Figure 10 shows a comparison of the estimated $n_\text {eff}$ obtained with the three different methods, normalized with the actual refractive index of the working fluid $n_\text {f}$ and as a function of the lens systems. The error associated to the measurement of the microchannel height $h'_\text {ch}$ was estimated by taking the nominal microchannel height $h_\text {ch}$ as ground true value, and it was found to be between $1.2\,\%$ and $3.2\,\%$ for all considered cases.

Fig. 10

Comparison between the refractive index of the fluid $n_\text {eff}$ obtained with focus measure (FM) and DPT (image stack and Poiseuille flow) and the actual refractive index $n_\text {f}$. The results include different lenses $\times$5/0.13, $\times$20/0.4 and $\times$40/0.55 and optical systems: astigmatic (A) and non-astigmatic

In general, the estimated refractive index of the fluid $n_\text {eff}$ corresponds to the actual refractive index $n_\text {f}$ for the three methods within a small measurement error. Hence, on one hand, the approximation used for the scaling factor k holds for DPT measurements. On the other hand, the three methods lead to equivalent results. Besides, the results reveal that the impact of the bottom wall thickness $t_\text {wall}$ does not contribute significantly to the RIM.

6 Conclusion

We provided a characterization of the bias errors of DPT measurements in microfluidic experiments, in which a single calibration function obtained with a focus scanning procedure is used. We presented a theoretical model to describe the bias error based on the field curvature aberration of the lens, the tilt of the wall of the microfluidic device with respect to the optical axis, and refractive index mismatch of different media between the tracer particles and the lens. We showed that the bias error can be mapped and corrected using a reference surface, which can be obtained looking at particles close to a wall, as done previously. In addition, we proposed an approached based on a reference measurement of a Poiseuille flow, suitable for microfluidic experiments inside microchannels with constant cross section, that allows the determination of the reference surface from a large number of measurement points evenly distributed across the entire FOV.

We tested and validated the model and correction methodologies on different microfluidic setups with different optics (magnification from 5$\times$ to 40$\times$), working fluids, and microchannel dimensions. The results are in good agreement with the model but the magnitude of the bias error has a large variability: While being negligible for some setups, we could observe an error up to 27 % of the measurement volume depth across the FOV. The study on refractive index mismatch confirms that the value of the scaling factor to be used to account for it corresponds with a good approximation to the refractive index of the working fluid.