1 Introduction

Spraying of liquids is widely used in industry, pharmacy, agriculture and construction. In virtually all spray applications, the resulting droplet size is an essential parameter. In agriculture, for example, the size of droplets sprayed over crops for pest control determines their efficacy (Hislop 1987); large drops are likely to bounce off (Lake 1977; Hoffman et al. 2021), while small droplets can cause environmental pollution due to airborne spray drift (Reichenberger et al. 2007; Stainier et al. 2006; Matthews 2008). An optimal drop size would therefore be 150 um; however, as the nozzles always produce polydisperse drop sizes, a mean drop size is chosen as to be able to control the amount of small droplets within well-defined limits. Kooij et al. (2018). Another example where droplet sizes are important is for inkjet printing, where there is a clear relation between the size of an ink drop and the printed dot after spreading and drying (Heilmann and Lindqvist 2000). This also applies to spray painting (Hicks and Senser 1995). In drug delivery by inhalation, the drop size distribution plays a crucial role, as droplets smaller than 3 \(\mu\)m are ejected during exhalation, while droplets larger than 10 \(\mu\)m are trapped in the respiratory system (Babinsky and Sojka 2002). Droplet size control is also important for fuel injection, firefighting, de-icing, etc. Lefebvre and McDonell (2017); Bayvel (2019). For all these applications, a good understanding of what determines the drop size is essential, allowing to control the droplet size and thereby increase the efficiency of the spraying process.

Most sprays are formed by breaking up a liquid jet or sheet from a spray nozzle; the desired drop size is achieved by selecting the right nozzle size and spraying pressure. Recent studies of the breakup of liquid sheets show that the droplet size depends on nozzle geometry, flow rate and surface tension, both for simple fluids (Kooij et al. 2018) and for more complex liquids containing surfactants and adjuvants (Sijs et al. 2021; Sijs and Bonn 2020). Other research shows that the average droplet size can also be predicted when spraying dilute solutions of flexible polymers (Gaillard et al. 2021), which are known to profoundly affect the flow behavior of water (Bonn and Meunier 1997).

Much prior research has been done for sprays that produce a liquid sheet, often called flat fan nozzles. These do, however, produce a wide drop size distribution, with consequently many small drops that are associated with large amounts of spray drift: the smallest drops are blown away by the wind and deposited outside the desired area of application. For the specific example of agricultural spraying, in general additional measures have to be taken to avoid pollution with pesticides: the usual way to prevent spray drift is by choosing a spray nozzle that produces large drop sizes (Nuyttens et al. 2007). The best drift reduction is achieved by Venturi nozzles, also called air-induction nozzles. In their simplest form, Venturi nozzles are conventional flat fan nozzles to which a mixing chamber is added with a small hole in the side; the fluid flow decreases the pressure inside this chamber, causing air to be sucked in and mixed with the fluid (Dafsari et al. 2021). As a result, the liquid sheet contains ‘holes’ that are believed to facilitate its breakup, leading to shorter breakup length of the liquid sheet and larger drops (Opfer et al. 2013). Bang et al. (2023) show that holes in the sheet of a pressure-swirl atomizer result in the breakup of an intact film. In particular, if 50% of the sheet consists of holes, it will result in a complete breakup of the swirling sheet, according to percolation theory. Klostermann et al. (2016) show that diluted polyether siloxane emulsions cause the nucleation of holes in the liquid sheets, which leads to earlier breakup and on average bigger droplets. In a paper of Ellis et al. (2002), the effects of the Venturi throat diameter and the size of the final orifice were investigated. It was concluded that the droplet size was affected mostly by the final orifice size and only slightly by the air intake. However, there is to date no quantitative understanding about what determines the drop sizes in Venturi nozzles and hence, how they can reduce drift. As Venturi nozzles are also important in other applications such as industrial tank cleaning, we investigate here whether the recent progress in understanding spraying can also be used to understand this type of nozzles. We therefore study different Venturi nozzles for various pressures and fluids properties, to determine what sets the mean droplet size, and how this relates with what is already known about standard flat fan nozzles.

2 Droplet formation

Droplet formation from sprays (Villermaux 2007) or jets (Villermaux et al. 2004) results from the breakup of so-called ligaments: thread-like liquid structures that form from the jet or sheet. For high enough velocities, waves will appear on the surface of the liquid sheet due to friction with the surrounding air (Squire 1953). The amplitude of this Squire instability will grow in amplitude, causing thickness modulations of the sheet that will eventually cause it to break. Fragments of a well-defined size, the Squire wavelength, will be created from the breaking sheet, which can be observed in Fig. 1. These fragments form ligaments due to the Rayleigh–Taylor instability, which is the internal instability of the sheet accelerated perpendicular to its own plane (Sharp 1983). The ligaments will subsequently break up into droplets; this happens because of the Rayleigh–Plateau instability that is driven by surface tension (Plateau 1873; Strutt and Rayleigh 1878).

Fig. 1
figure 1

Two high-speed photographs of the Venturi TDXL 11004 nozzle, at a pressure of 1 bar (left) and 5 bar (right). First the Squire waves occur, which break into fragments. These fragments form ligaments which break up into droplets

Full size image

For flat fan nozzles, there are two relevant dimensionless parameters (Kooij et al. 2018):

$$\begin{aligned} \alpha = \rho _{air} / \rho _{liquid} \qquad \qquad \text{ and } \qquad \qquad We = \rho _{liquid} v^2 b / \sigma , \end{aligned}$$
(1)

where, \(\alpha\) is the air liquid density ratio, We the Weber number in the range 800–10 000, \(\sigma\) the surface tension, v the liquid velocity, and b the characteristic size of the flat fan nozzle, i.e., derived from the hydraulic area, \(b = \sqrt{2 A_{hyd} / 3 \pi }\).

Using mass conservation and the fact that the median droplet size is proportional to the diameter of the ligaments, the final drop size for sprays can be determined from the competition between liquid inertia and surface tension (Kooij et al. 2018), which in terms of the Weber number and geometry of the nozzle gives:

$$\begin{aligned} D_{50} = C b \alpha ^{-1/6} We^{-1/3}, \end{aligned}$$
(2)

where \(D_{50}\) is the median diameter, and C a constant of order unity. This equation then allows to predict the average drop size from the spraying parameters (Kooij et al. 2018).

3 Experiments

We study the breakup of water and ethanol-water spray solutions (to control the surface tension) for different Venturi nozzles. The droplet size distributions are measured using laser diffraction (Malvern Spraytec). When the laser beam of the Spraytec hits a droplet, part of the light will be diffracted, at a diffraction angle that is inversely proportional to the size of the droplet. Assuming the droplets to be spherical, Mie theory then allows to determine the droplet size distribution from the diffraction pattern (Swithenbank et al. 1976; Dayal et al. 2004). The laser beam is placed 60 cm below the nozzle, where, for all nozzles, pressures and fluid parameters, no further breakup occurs and the drops are to a very good approximation spherical (Sijs et al. 2021).

The Spraytec can measure drops in a range of 0.1 \(\mu\)m to 2000 \(\mu\)m. All measurements take at least 30 s, and the average scattering data are used to determine the droplet size distribution. The error within this measurement is maximally a few percent, and comparable to or smaller than the symbols in the plots. The principle of the Spraytec for droplet measurements has been well established in comparison with other methods, and in the case of the Venturi nozzles, where there may be air inclusions in the droplets, the Spraytec gives a more reliable result than Phase Doppler Particle Analysis (PDPA) (Sijs et al. 2021).

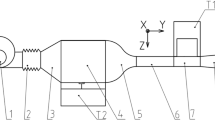
Table 1 Nozzles used to produce droplets of various sizes. Nozzle areas near the inlet (\(A_{inlet}\)) and outlet (\(A_{orifice}\)) are measured using a microscope. Liquids are water, and in the case of Airmix 11003, also an ethanol mixture (\(\sigma\) = 38.0 mN/m)
Full size table

We test different types of nozzles, both traditional flat fan and Venturi, from different brands, as listed in Table 1. Figure 2 illustrates the Venturi principle, indicating air inlet, mixing chamber and the difference between the inlet (\(A_{inlet}\)) and outlet opening (\(A_{orifice}\)). The Agrotop TDXL 11003 nozzle shown in this picture consists of a flat fan (TDXL 11003 cap, grey) mounted on a mixing chamber (blue). Without the mixing chamber, the TDXL 11003 cap functions as a regular flat fan nozzle, allowing to directly observe the effect of the air injection. All Venturi nozzles are sprayed at liquid pressures in the range 2–5 bar, where specifically for the Agrotop Airmix 11003 we also change the surface tension of the fluid to 38.0 mN/m, by using a mixture of 20% ethanol in water. The surface tension was measured by collecting sprayed sample and use the pendant drop method from Kruss for an accurate measurement of the surface tension. The air intake has been considered in detail previously by Butler-Ellis and collaborators (Butler et al. 2002) who measured the air intake of the Venturi nozzles and found it to depend mainly on the venturi throat (air inlet) diameter and flow rate. For the nozzles, we are considering here, the Venturi throat nozzle varies between typically 1.3 mm for the Airmix AI11003 nozzle to 1.6 mm for the Agrotop TDXL 11003 nozzle. For the flow rates probed here, the results of Butler-Ellis et al. then show that the air intake is between 18-28% (in volume) of the liquid flow rate.

Fig. 2
figure 2

Left: Agrotop TDXL 11003 spray nozzle based on the Venturi or air-induction principle to create larger droplets than flat fan nozzles. The center image shows where the liquid is injected into the nozzle. It is forced through the small inlet opening shown top left (\(A_{inlet}\)). The right picture shows a schematic representation of the air inlet and air/liquid mixing chamber (note that the exact formation of air bubbles has not been investigated and could therefore differ from the figure). After mixing, the liquid enters the spray tip and passes through the opening shown bottom left (\(A_{orifice}\))

Full size image

The radial liquid velocity in the liquid sheet in the first 5 cm from the nozzle is measured by tracking tracer particles in the liquid. We used silver-coated hollow glass spheres with a diameter of 100 \(\mu m\). A high-speed movie is made zooming in on the first 5 cm of the sheet, and a Python script is used to find the particles trajectory. The velocities of the spheres are then determined for different nozzles and pressures. For each measurement, at least 30 spheres are tracked at various places in the liquid sheet. We find no significant difference in sheet velocity between the different locations, as observed before (Gaillard et al. 2021).

4 Mean drop size

Fig. 3
figure 3

Median diameter \(D_{50}\) against \(b \alpha ^{-1/6} We^{-1/3}\) for Venturi (filled symbols) and flat fan (open symbols) nozzles, where b is calculated using the hydraulic area, \(A_{hyd}\). Red dotted line is Eq. 2

Full size image

If we plot drop sizes produced by all nozzles according to Kooij et al. (2018), and Eq. 2, we find that the Venturi nozzles deviate from the expected behavior (Fig. 3). We next investigate how to understand and predict the drop size produced by this type of nozzle.

Fig. 4
figure 4

a Flow rate q of the nozzles as a function of \(\sqrt{2\Delta p/\rho }\), where \(\Delta p\) is the pressure difference and \(\rho\) the density of the liquid. Solid lines are linear fits with slope equaling the effective nozzle area (\(A_{hyd}\)) of the opening of the nozzle. b Log-log plot of \(D_{50}\) divided by \(A_{hyd}\) as a function of flow rate for all nozzles. This figure shows that, though all lines have a slope of −2/3, the Venturi nozzles are shifted as for those nozzles the hydraulic area is not the correct characteristic length scale

Full size image

For flat fan nozzles, the effective hydraulic area (\(A_{hyd}\)) is an important parameter, as it sets the characteristic nozzle size and thereby, determines the mean droplet diameter. From Bernoulli and the assumption that \(v = q / A\), where q is the flow rate and A the area of the nozzle, one finds \(q = C_d \cdot A \cdot \sqrt{2\Delta p/\rho }\), where the discharge coefficient \(C_d\) accounts for losses and is typically in the range of \(0.9< C_d < 1\) for flat fan nozzles (Kooij et al. 2018). The effective hydraulic area can be defined as \(A_{hyd} = C_d \cdot A\). Figure 4a shows the flow rate of all nozzles plotted against \(\sqrt{2\Delta p/\rho }\), where, according to Bernoulli, the effective hydraulic area is the slope of the fit. It can be seen that there is no significant difference in hydraulic area between for example a Teejet XR 11003 flat fan and the corresponding Venturi nozzle Airmix 11003. This reflects the fact that the ’03’ in ’11003’ is a measure of the flow rate, according to the nomenclature of the International Organisation for Standardisation (ISO). If we then plot the mean droplet size divided by the hydraulic area against the flow rate, all nozzles and pressures would collapse if the Venturi nozzles scale similarly as flat fan nozzles. Figure 4b shows that this is not the case. From Eqs. 1 and 2, we know that \(D_{50} \sim We^{-1/3} \sim q^{-2/3}\) and Fig. 4b indicates that this slope of indeed −2/3 holds, but that for Venturi nozzles there is a shift towards larger drop sizes, meaning that the hydraulic area does not appear to be the correct parameter to unify the two types of nozzles. That the slopes in Fig. 4b correspond, suggesting that the characteristic length scale in the We number is not directly given by the hydraulic area of the nozzle.

Fig. 5
figure 5

a Measured velocity of the liquid sheet as a function of \(\sqrt{2\Delta p/\rho }\). For the Bernoulli equation \(v = q/A_{hyd}\) and therefore \(v_{measured} = \sqrt{2\Delta p/\rho }\) (blue solid line has slope 1). b The effective Bernoulli pressure \(P_{eff} = 1/2 \rho v^2\), with \(v = q/A_{hyd}\), plotted against the real spraying pressure

Full size image

Figure 5a shows the measured velocity of the liquid sheet, which is, according to the Bernoulli equation, equal to \(q/A_{hyd}\), is plotted against \(\sqrt{2\Delta p/\rho }\). The Teejet XR flat fan nozzle data (open symbols) fall on the blue solid line with slope 1, which is the Bernoulli equation \(v_{measured} = \sqrt{2\Delta p/\rho }\). The Venturi nozzles (filled symbols), on the other hand, do not fall on the line, meaning that the simple Bernoulli equation does not apply. We argue that this is due to the way the nozzles are designed. For normal flat fan nozzles, the main pressure drop is over the final nozzle that produces the spray. For Venturi nozzles, there is first a small opening area that determines the flow (\(A_{inlet}\)), subsequently the liquid enters a mixing chamber where the water mixes with air, before it leaves the nozzle by the orifice area (\(A_{orifice}\)). The mixing chamber creates an extra pressure drop, reducing the velocity of the liquid sheet that comes out of the final orifice, leading to larger drops, as described before by Nuyttens et al. (2009). The ’holes’ in the sheet therefore have no significant effect on the larger drops. The simple Bernoulli equation used for flat fan nozzles is therefore not valid for the Venturi nozzles, because the flow rate is not simply determined by the hydraulic resistance of the nozzle. The real, effective, pressure before the orifice of a Venturi nozzle can be calculated from the flow rate and the orifice opening: \(P_{eff} = 1/2 \rho v^2\), with \(v = q/A_{orifice}\). If we plot this against the spraying pressure, we clearly see the extra pressure drop for Venturi nozzles, while for standard nozzles the effective pressure is the same as the applied pressure (Fig. 5b).

This means that the main effect of the Venturi chamber is to make the effective spraying pressure smaller. As an example: for an Airmix 11003 Venturi nozzle at a spraying pressure of 5 bar, the effective pressure before the orifice is 1.2 bar; this of course gives large droplets, for this example the mean droplet size becomes 259 \(\mu\)m. We can compare this with a normal flat fan nozzle, with the same orifice opening (e.g., a Teejet XR 11006): at a spraying pressure of 1.2 bar, this gives a mean droplet size of 255 \(\mu\)m, very similar to the Venturi nozzle.

Fig. 6
figure 6

a Measured velocity of the liquid sheet as a function of calculated velocity, using the orifice area of the nozzle (\(A_{orifice}\)). The line represents \(v_{measured} = v_{calculated}\). Note that if one would use \(A_{hyd}\) instead, the calculated velocity would be incorrect due to the high losses for the Venturi nozzles, i.e., \(C_{d}< 1\). b Mean droplet size plotted against \(b \alpha ^{-1/6} We^{-1/3}\) (Eq. 2) for all nozzles using \(A_{orifice}\) instead of \(A_{hyd}\). The dotted red line has slope 1.95

Full size image

In Fig. 6a, the measured velocity of the sheet is plotted against the calculated velocity using the orifice area (\(A_{orifice}\)). Both flat fan and Venturi nozzles fall on the dotted red line that correspondents with \(v_{measured} = v_{calculated}\). This means that the orifice area is what determines the liquid flow and that the mixed air is not responsible for significant extra flow. If we now return to the Kooij et al. (2018) method to plot the mean droplet size and use the measured orifice area of the nozzle for the velocity and the characteristic length b in Eq. 2, we find that all data collapse as can be seen in Fig. 6b, for both Venturi, sprayed with water and water-ethanol mixture, and flat fan nozzles. It can be seen that the data points of TDXL 11003 (Venturi) and TDXL 11003 cap (flat fan), which by definition have the same \(A_{orifice}\), fall on the line with \(C=1.95\), meaning that the presence of a mixing chamber does not influence the droplet size. The same holds for TDXL 11004 and the TDXL 11004 with the TDXL 11003 cap, where the flow remains constant and only the orifice area changes. These data points also collapse onto the solid line. If we compare the data for the flat fan and the Venturi nozzles, we see that the Venturi nozzle is generally slightly above the flat fan nozzles. The air drawn into the mixing chamber therefore does cause a very small difference in droplet size, but this is generally negligible compared to the effect of the modified pressure drop. The last data point for the Albuz AVI 11003 and TDXL 11004 deviates somewhat from the prediction. These points correspond in fact to the lowest spraying pressure; at too low pressures, the spray is not well developed and the water flows away around the nozzle.

This means that predicting the average droplet size produced by Venturi nozzles requires an additional parameter compared to the case of flat fan nozzles: the pressure drop over the Venturi chamber. Our measurements also indicate that a Venturi nozzle has no additional added value in terms of drift reduction and droplet size compared to a flat fan. The Venturi Airmix 11003 nozzle for example does have a similar orifice area as the Teejet XR 11006 flat fan nozzle, implying that the same flow rate gives similar mean droplet sizes. We conclude that the Venturi effect in itself does not have a significant effect on droplet sizes. There is simply an extra pressure drop that is created in the mixing chamber of the nozzle that results in a lower effective spraying pressure than the one being applied. This in turn reduces the velocity of the sheet, resulting in larger droplets and thus less drift. A change in orifice size and/or lowering the injection pressure can simply lead to larger droplets, but this would also change the amount of water that will be sprayed per unit of time. In general, for agricultural spraying the goal is to spray a certain amount of water per hectare within a given time frame, To reduce drift, while keeping the same operating pressure and flow rate, one can directly replace for instance a regular 11003 flat fan nozzle by its equivalent, the 11003 Airmix (Venturi) nozzle. The Airmix nozzle has a larger orifice opening, which besides larger droplets, would normally also lead to a larger flow. However, the built-in pressure drop ensures the same flow rate as the 11003 flat fan nozzle, while increasing the droplet size.

5 Shape of the droplet size distributions

Figure 7 shows a few typical measured drop size distributions for the Airmix 11003 nozzle at different spraying pressures. The comparison with the Teejet XR 11003, a normal flat fan nozzle shows the effect of air injection: the average drop size is larger, and much larger drops are produced.

Fig. 7
figure 7

Droplet size distributions for a normal flat flan nozzle (Teejet) and a Venturi nozzle (Airmix) for different spraying pressures

Full size image
Fig. 8
figure 8

Normalized droplet size distribution of different nozzles rescaled with the mean droplet size. The data are well described by a compound gamma function (black line)

Full size image

Beyond the mean droplet size for Venturi nozzles, the distribution around the mean is just as important. Villermaux (2007) has shown that the compound gamma distribution best describes the droplet size distribution for such sprays. As discussed in Section II, a liquid sheet breaks down into ligaments of different diameters and corrugation. A very corrugated ligament will break up into a wide range of droplet sizes, because the instantaneous diameter of the ligament determines the final droplet size. The same applies to differences in average diameters between ligaments (Kooij et al. 2018). The two-parameter compound gamma function accounts for these two different parameters, i.e., the ligament diameter and the ligament corrugations, and describes the distribution as (Villermaux and Bossa 2011)

$$\begin{aligned} {\mathscr {P}}_{m,n}\left( x = \frac{d}{\langle d \rangle } \right) = \frac{2 ( mn )^{\frac{m+n}{2}} x ^{\frac{m+n}{2}-1}}{\Gamma (m)\Gamma (n)} {\mathscr {K}}_{m-n}\left( 2\sqrt{mnx}\right) , \end{aligned}$$
(3)

with \({\mathscr {K}}\) the modified Bessel function of the second kind and \(d /, (\langle d \rangle )\) the droplet size normalized by the mean diameter. The parameter n sets the ligament corrugation and m the order of the ligament size distribution. When rescaling the distribution by the mean droplet size, the data of different nozzles and pressures collapse onto a single curve, as can be observed in Fig. 8, with the black line the best fit of the compound gamma function. It can be seen that the shape of the droplet size distribution is similar for both flat fan and Venturi nozzles for different pressures. For all nozzles, the ligaments are very corrugated (\(n = 5\)) with a broad range of sizes (\(m = 6\)). For spraying, it is important to have as few small droplets (\(<100 \mu\)m) as possible to prevent unwanted drift. However, larger droplets will result in less coverage, as they are more likely to bounce off the crop leaves. Figure 8 shows that all distributions have a similar shape when rescaled with the mean droplet size, meaning that Venturi nozzles are only able to reduce drift by increasing the mean droplet size, something that could also be accomplished by using a larger nozzle opening or reducing pressure for regular nozzles.

6 Conclusion

We looked at how a Venturi spray nozzle, commonly used to ensure larger droplets than produced by flat fans, influences droplet size by spraying liquids using both types of nozzles at different pressures. We showed that the Bernoulli equation, which can be used for simple nozzles to predict the droplet size, does not apply to the Venturi nozzles because the mixing with air in the separate chamber before the nozzle leads to an extra pressure drop. Thus, for Venturi nozzles, the hydraulic area cannot be used to describe the final liquid sheet thickness and velocity and the resulting droplet distribution.

If we take the extra pressure drop into account and use the real orifice area instead of the hydraulic area, the prediction for the droplet size by Kooij et al. (2018) (Eq. 2) also holds for Venturi nozzles. Even when we only adjust the orifice area or the flow (by changing the pressure) of a Venturi nozzle, Eq. 2 still holds and all nozzles drop size data collapse onto the same curve. This means that we can predict the droplet size knowing the flow (or the pressure and nozzle characteristics), the orifice area and the sprayed liquid.

By considering not the droplet size but the droplet size normalized by the mean, we also show that the size distribution of flat fan nozzles and Venturi nozzles are identical within the experimental resolution. The rescaled droplet size distributions of both types of nozzles at different pressures all fall on the same curve described by a compound gamma function. This indicates that although Venturi nozzles have been introduced to reduce droplet drift by increasing droplet size, they produce exactly the same droplet size distributions as flat fan nozzles. Instead, the injection of air only reduces the effective spraying pressure, resulting in larger droplets. This, however, can just as well be obtained by using different nozzle sizes without air injection.