1 Introduction

When the angle of attack of an airfoil is sufficiently high, the flow over the suction side is no longer able to overcome the adverse pressure gradient and separates, leading to a state of stall (Jones 1934). Such a situation is commonly encountered over a large range of engineering applications, such as for turbine blades or landing aircraft. Stall is characterized by an abrupt change in the hydrodynamic forces imparted on the body and the generation of excess far field noise (Brooks et al. 1989; Lacagnina et al. 2019). The latter is a subject of long-lasting interest due to the undesirably high noise levels and has motivated efforts to model such generation (Brooks et al. 1989; Moreau et al. 2009) and determine the relevant mechanisms, such as using direct microphone measurements (Lacagnina et al. 2019; Zang et al. 2021) or through numerical simulation (Turner and Kim 2020) or both (Moreau et al. 2009).

Early studies on dipole noise generation near or in stalled conditions have highlighted the importance of the trailing edge (TE) as an efficient source (Amiet 1976). Such is also the case for example in tonal noise generation (Roger and Moreau 2010; Pröbsting et al. 2014). A notable difference arises from the attached to stalled flow regimes, whereby an abrupt increase in low-frequency noise content has been observed (Brooks et al. 1989; Moreau and Roger 2005; Mayer et al. 2020). This mirrors similar low-frequency phenomena observed in the flow features themselves (Zaman et al. 1989; Yarusevych et al. 2009).

The degree and manner to which the features of the flow (i.e. the velocity fields) generate noise remains an open area of research. Recent progress was reported by Lacagnina et al. (2019) whom used simultaneous particle image velocimetry (PIV) measurements with near and far-field microphones of a NACA 0012 for analysis. At near-stall conditions they found high coherence between the TE pressure and the noise at mid-range frequencies (termed “light stall” by Moreau et al. 2009) attributed to shear layer instabilities. At deep stall the same coherence was identified instead at low frequencies associated to bluff body shedding. Similar findings were also recently reported by Raus et al. (2021). In addition, Raus et al. (2021) found the transition to lower-frequency noise was more gradual for cambered airfoils than symmetric.

Microphone arrays are not the only way of obtaining estimates of far-field noise. One may instead invoke the use of an appropriate acoustic analogy (Lighthill 1954; Curle 1955). In the past decade, the use of particle image velocimetry (PIV) to determine pressure fields (Laskari et al. 2016; Van Gent et al. 2017) and resulting far-field noise using acoustic analogies has been thoroughly demonstrated in cavity flows (Larsson et al. 2004; Koschatzky et al. 2011a, b) and recently via tomographic PIV in open jet flow (Ragni et al. 2022). Such an approach has also been used for noise generation of rod-airfoils (Lorenzoni et al. 2012), Gurney flaps (Zhang et al. 2018), and even undulatory swimmers (Wagenhoffer et al. 2021). Nickels et al. (2020) used an acoustic analogy in combination with stochastic estimation via pressure transducers to estimate noise in a turbulent wall jet. Despite this progress, there is a lack of experimental work dedicated to using time-resolved PIV specifically in the turbulent flow of static stalled airfoils to determine far-field noise mechanisms.

The present work seeks to fill this knowledge gap by leveraging spatial information from time-resolved PIV fields correlated to the temporal behavior of the far-field acoustics. The goal is to identify the time-varying flow structures responsible for noise generation in static stall. In Sect. 2, the experimental methodology and chosen parameter space will be introduced. The pressure reconstruction methodology and implementation of Curle’s acoustic analogy to extract the far-field noise is presented in Sect. 3. In Sect. 4, a data-driven framework to elucidate noise generation mechanisms in the velocity fields will be introduced. Finally, discussion and conclusions are drawn in Sect. 5.

2 Particle image velocimetry experiment

Time-resolved particle image velocimetry (PIV) data were collected in the University of Southampton water flume facility, featuring a test section 6.75 m long, a span of 1.2 m and water depth of 0.5 m. A NACA 0012 airfoil of chord length \(c=15\) cm and span \(s_{tot}=70\) cm was fixed vertically in the center of the span of the flume immediately following the contraction into the test section. The portion of the span that was submerged was \(s=48.3\) cm. PIV imaging was performed in the stream-wise surface-normal (x-y) plane as illustrated in Fig. 1. An overhead carriage system was employed to allow precise control of the angle of attack \(\alpha\). Angles of attack \(\alpha =4^{\circ },13^{\circ }\), and \(15^{\circ }\) are considered at a chord-based Reynolds number \(Re_c=U_{\infty }c/\nu \approx 7.1\times 10^4\) (with \(U_{\infty }=0.5\) m/s the free stream velocity, and \(\nu =1\times 10^{-6}\) m\(^2\)/s the kinematic viscosity) were explored corresponding to a variety of stall conditions. An overview of the experimental cases is presented in Table 1. We note that various flow regimes reported in Table 1 were determined both via visual inspection as well as from spectra of the proper orthogonal decomposition (not shown for brevity).

Table 1 Data sets considered in this work at \(\textrm{Re}_c=7.1\times 10^4\). Lift coefficients \(C_L=L/\frac{1}{2}\rho U_{\infty }^2sc\) (with L the mean lift) are reported from simultaneous load cell data
Full size table

A high-speed Nd:YLF laser (527 nm Litron) was directed inwards from either side of the facility to simultaneously illuminate the pressure, suction, and trailing regions of the airfoil and three 4 megapixel (2560 x 1600 pixels) high-speed Phantom Veo 640-S cameras mounting 105 mm Ex Sigma lenses (f# 5.6) were synchronized to capture the flow field surrounding the plane of the airfoil. Caution was exercised to ensure the laser sheets were aligned within the same plane, with an estimated sheet thickness of 2 mm at the location of the foil mid-chord. For additional insight, force measurements were also collected using a six-axis force/torque load cell (ATI Delta IP65) mounted to the airfoil and synchronized to the PIV acquisition using an NI USB-6251 DAQ.

Fig. 1
figure 1

Diagram (not to scale) of the experimental setup in the water channel facility to perform high-speed PIV (a). The pseudo-colour of velocity magnitude for the NACA 0012 at \(\alpha =4^{\circ }\) is presented in (b) with the individual fields of view: (Blue dot line) suction side, (Green dot line) pressure side, (Red line) trailing region

Full size image

The flow was seeded with Vestosint 2157 polyamide particles of nominal diameter \(55\,{\upmu }\hbox {m}\) until a satisfactory seeding density was obtained. For each case simultaneous high-speed images were collected across cameras at a frequency of 1 kHz and stored until memory limitations were reached, resulting in 5.367 s of continuous data. Five runs were repeated resulting in 26.84 s of data for each case, corresponding to approximately 90 eddy turnover times \(T_L=c/U_{\infty }\). The raw images of each camera were individually processed with background subtraction and Gaussian high-pass filtering with a filter width of 10 pixels to isolate the high-frequency particle reflections. Multi-pass planar PIV was performed using a verified in-house Matlab code with 3 passes per window size and square windows decreasing from 64 by 64 pixels, to 32 by 32 pixels, to 24 by 24 pixels with 50% overlap. The final vector spacing was \(\Delta x=0.83\) mm corresponding to 181 vectors spanning the airfoil chord. PIV outliers were replaced using robust principle component analysis (Scherl et al. 2020) with the sparsity parameter at the theoretical optimum of \(\lambda _s=1\) and the inexact augmented Lagrangian method for iterative convergence (Lin et al. 2010; Sobral et al. 2016).

Prior to each measurement case, a calibration image spanning all three cameras was collected using a target aligned with the laser sheet plane. The overlap across the fields of view within the calibration images was used for reference positions to stitch the velocity fields together (Raffel et al. 1998). The stitching was performed on the calibrated vector fields using a hamming window for blending. To account for the unequal PIV grid sizes, the PIV vectors of the highest resolution grids (the suction and pressure fields of view) were bi-linearly interpolated to the lowest resolution grid (the trailing field of view) to avoid spatial up-sampling during stitching. Due to the airfoil extending downwards in the direction of the upward-facing cameras, a visual occlusion was produced on the pressure side of the airfoil, preventing PIV measurements close to the surface. In addition to the foil cross section, the occluded region was masked in the final vector fields. Surface profiles on the pressure side reported hereafter were taken from the nearest available points along the mask.

Upon inspection of the time-resolved data, several anomalous high-frequency spectral peaks were observed in both the forces and velocity fields. It was determined that such a peak was likely due to a mechanical vibration within the overhead carriage system used to mount the airfoil. To avoid this artifact, all forces and velocity fields were temporally filtered to 10 Hz using a Gaussian low-pass filter. This limits the scope of the temporal analysis of the present work to frequencies f below a non-dimensional frequency \(f^{\star }=f c/U_{\infty } \le 3\). As such, the present work may be considered a low-frequency analysis of aerodynamic noise compared to most studies focused on microphone-based wind-tunnel measurements typically in the range of \(O(10^2\)–\(10^4)\) Hz (or \(f^{\star }\) of \(O(10^0\)–\(10^2\)), Mayer et al. 2020). This is not problematic for the goals of the present study, as stall mechanisms have been demonstrated to enhance low-frequency content specifically (Moreau and Roger 2005; Mayer et al. 2020).

3 Methodology

3.1 Pressure reconstruction

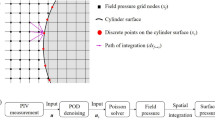
To extract the far-field acoustics, it is first necessary to determine the instantaneous pressure. Planar pressure fields were reconstructed from the instantaneous velocity fields using a Poisson solver approach (De Kat and Van Oudheusden 2012; Laskari et al. 2016) for which the divergence of Navier–Stokes momentum equations is invoked:

$$\begin{aligned} \nabla ^2p = -\rho {\varvec{\nabla }}\cdot \big (\frac{\partial {\varvec{u}}}{\partial t}+{\varvec{u}}\cdot {\varvec{\nabla }}{\varvec{u}}-\nu \nabla ^2{\varvec{u}} \big ) \end{aligned}$$
(1)

where \({\varvec{u}}\) is the instantaneous velocity vector, p is the pressure and \(\rho\) is the (constant) density. Neumann boundary conditions were applied on the inlet, outlet, and suction (upper) boundaries of the domain and Dirichlet boundary conditions were employed using Bernoulli’s equation in the free stream on the pressure (lower) domain boundary. The application of Dirichlet boundary conditions on both the suction and pressure boundaries was also tested, but was found to give slightly worse agreement in comparison to numerical simulations that will be discussed shortly. This is likely due to separation phenomena partially invalidating the assumption of irrotational flow near the suction boundary. The unsteady velocity term was directly computed from the time-resolved Eulerian fields (Jakobsen et al. 1997) using finite differences. Good agreement using central differences up to sixth order was found; therefore, second-order gradients were opted for in favor of processing speed. Spatial derivatives were also computed using second-order central differences.

Fig. 2
figure 2

Surface pressure coefficients \(C_p=P/\frac{1}{2}\rho U_{\infty }^2\) for \(\alpha =4^{\circ }\) (a), \(13^{\circ }\) (b), and \(15^{\circ }\) (c) from the PIV data (solid), RANS (dash-dot), and RANS \(\in \Omega _{PIV}\) (dashed). The standard deviation of the pressure coefficient on the suction side is shown in (d) for all three cases

Full size image

To provide a comparison for the pressure reconstructions a two-dimensional Reynolds-averaged Navier–Stokes (RANS) simulation was performed using OpenFOAM software. The simulation utilized a k-\(\omega\) shear stress transport (SST) closure model. A standard C-type domain and grid geometry was chosen with a horizontal and vertical extent of 20 chords lengths. The simulation properties (e.g. kinematic viscosity, inlet velocity, chord length) were chosen to match identically those of the experiment. The comparison between the surface pressure coefficient \(C_p=P/\frac{1}{2}\rho U_{\infty }^2\) (with P the mean pressure) in the PIV and RANS is shown in Fig. 2. The agreement in the attached case (Fig. 2a) is qualitatively comparable, but with quantitative discrepancies on the suction side particularly at the leading edge (LE) where the PIV underestimated the suction peak. At higher angles of attack (Fig. 2b,c) the PIV was found to closely compare in the magnitude of the surface pressure on the suction side, but again struggled to capture the suction peak at the leading edge. The difficulty of the PIV in capturing pressure near the leading edge is likely due to the thin boundary layers that require exceedingly high spatial resolution.

Naturally, it is important to investigate whether and how inaccuracies in the mean pressure on the suction side impacts the time-varying behavior critical for estimating the far-field noise. This is assessed via the standard deviation of the surface pressure coefficient on the suction side plotted in Fig. 2d. The magnitude of \(C_{p,std}\) compares well with results previously reported in the literature via measurements (Sicot et al. 2006; Lee et al. 2013) and simulations (Golubev et al. 2016). The erratic behaviour of \(C_{p,std}\) for the attached case (\(\alpha =4^{\circ }\)) near the LE is likely measurement bias error. As mentioned previously, the effective resolution at the leading edge relative to the developing boundary layer is low. This issue is less problematic for the stalled cases (the focus of the present work) which do not exhibit such discontinuities in \(C_{p,std}\) and have a greater effective resolution since the boundary layer separates in these cases. Taken together, the results of Fig. 2 lend confidence for the application of the Poisson solver to capture the fluctuating pressure fields necessary for the noise extrapolation.

3.2 Curle’s acoustic analogy for dipole sources

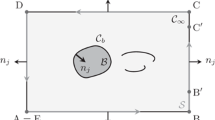
The far-field acoustics surrounding the airfoil physically belongs to a domain much too large to measure directly via experiment. Therefore, Curle’s acoustic analogy is adopted (Curle 1955) utilizing the pressure fluctuations obtained from the PIV to estimate the far-field noise. Following the work of Larsson et al. (2004), the original solution presented by Curle is modified and the far-field dipole noise emanating from the surface of the airfoil are isolated in the surface integral (see also Koschatzky et al. 2011a):

$$\begin{aligned} p_a({\varvec{x}},t)-p_{a,0}=\frac{1}{4\pi }\int _S l_i n_j \big (\frac{\dot{p}\delta _{ij}}{a_0 r} \big )\vert_{t-\frac{r}{a_0}}\textrm{d}S({\varvec{y}}) \end{aligned}$$
(2)

where \(p_a\) is the acoustic pressure and \(p_{a,0}\) the steady far-field pressure, \(l_i\) is the listener unit vector pointing from the source to the listener position, \(n_j\) is the surface normal unit vector, \(\dot{p}=\partial p/\partial t\) is the unsteady pressure, \(a_0\) is the speed of sound, \(r=|y_i-x_i\vert\) is the distance to the listener position \(x_i\) from the source \(y_i\), and the surface S is the airfoil surface. The integrand is evaluated at the retarded time \(t-r/a_0\). Quadrupole sources are ignored in the estimation of the acoustic fluctuations, as the Mach number is sufficiently low in the present case (Curle 1955). A similar result was confirmed in the work of Larsson et al. (2004) for an open cavity flow. For stalled airfoils, previous work suggests the dipole sources are likewise dominant (Moreau et al. 2009; Laratro et al. 2014).

Fig. 3
figure 3

Unit vectors \(n_j\) and \(l_i\) at two values of \(\theta\) used for the integration of Eq. 2 defined on the mask surface for the case at \(\alpha =15^{\circ }\) with every tenth unit vector shown. The inset focused at the LE shows every unit vector

Full size image

To carry out the integration, surface normal vectors were defined at each PIV vector location along the mask of the airfoils for all cases considered. A Savitsky–Golay filter was employed for smoothly varying surface normal estimates shown in Fig. 3. This was found to be necessary particularly near the LE with significant curvature. The unsteady pressure \(\dot{p}\) along the surface of the airfoil was obtained directly through finite second-order temporal differences of the pressure. To reduce noise, a sliding average was used to smooth the unsteady pressure estimates with a width of 25 ms, corresponding to a non-dimensional frequency \(f^{\star }=12\). This does not impact the acoustic frequencies of interest in the present study that are restricted to \(f^{\star }\le 3\).

Listener positions are selected in a semi-circular array of positions at a specified radius from the airfoil mid-chord position for \(0^{\circ }\le \theta \le 180^{\circ }\) spanning the suction side of the airfoil at \(N=30\) locations. Here, \(\theta =0^{\circ }\) is defined with respect to the LE at each angle of attack (not with respect to the direction of free stream velocity). The listener distance \(r=a_0/f_{\textrm{min}}\) is selected to automatically satisfy the far-field approximation for the frequencies of interest, where \(f_{\textrm{min}}=0.19\) Hz is the lowest resolved frequency. We remark that the far-field approximation in not consequential for the relative frequency content of \(p_a({\varvec{x}},t)\) but does impact the magnitude linearly with increasing r (Eq. 2). The choice of r is therefore inconsequential for the correlation-based analysis that is the focus of the present study. For reference, the resulting difference between a typical wind-tunnel choice of \(r=10 c\) and the chosen r of this study is 74.4 dB.

3.3 Data-driven structure detection

To elucidate flow structures responsible for the dipole noise generation, the spectral Linear Stochastic Estimation (sLSE) is leveraged between the instantaneous velocity fields and the far-field acoustic pressure (Tinney et al. 2006). Specifically, the sLSE is performed between the acoustic fluctuations at each listener position and the coefficients of the modes of the velocity fields via the proper orthogonal decomposition (POD; Sirovich 1987). In the following we present a brief outline on the application of this technique for the present analysis. The reader is referred to, e.g. Taylor and Glauser (2004) and Podvin et al. (2018) for more details on combining POD with LSE. The POD is performed on the fluctuating velocity vectors \(u_i'\) as

$$\begin{aligned} u_i'({\varvec{x}},t)=\sum _{k=1}^{K_{tot}}a_k(t)\phi _k({\varvec{x}}) \end{aligned}$$
(3)

where k is the mode number, \(K_{tot}\) is the total number of modes, \(a_k(t)\) is the k-th instantaneous POD coefficient, and \(\phi _k\) the k-th orthogonal spatial mode. For the present study \(K_{tot}=1075\) modes are used to generate the POD basis and up to \(K=30\) modes are retained for the sLSE analysis, as higher modes were not found to impact the results for all cases.

In the present context, the sLSE leverages the temporal cross-correlation between the mode coefficients and the acoustic fluctuations to obtain the portion of the velocity fields most correlated to the noise. Following the work of Tinney et al. (2006), two matrices are defined as

$$\begin{aligned} W_{ij} = \begin{bmatrix} \langle p_{a,1}p_{a,1} \rangle &{} \ldots &{} \langle p_{a,N}p_{a,1} \rangle \\ \vdots &{} \ddots &{} \vdots \\ \langle p_{a,1}p_{a,N} \rangle &{} \ldots &{} \langle p_{a,N}p_{a,N} \rangle \end{bmatrix}, V_{ij} = \begin{bmatrix} \langle a_1 p_{a,1} \rangle &{} \ldots &{} \langle a_K p_{a,1} \rangle \\ \vdots &{} \ddots &{} \vdots \\ \langle a_1 p_{a,N} \rangle &{} \ldots &{} \langle a_K p_{a,N} \rangle \end{bmatrix} \end{aligned}$$
(4)

where the angled brackets \(\langle \cdot \rangle\) denote ensemble averaging and N is the total number of listener positions. These two matrices are used to obtain the spectral LSE coefficients as

$$\begin{aligned} B_{kj}(f) = W_{jk}(f)^{-1}V_{ji}(f) \end{aligned}$$
(5)

where \(W_{jk}(f)=\{W_{jk}(t)\}\) and \(V_{ji}(f)=\{V_{ji}(t)\}\) are the Fourier transforms of (4) and the dependence on f implies the Fourier domain. In practice the sLSE coefficients are obtained for each run individually and ensemble averaged for each case. The estimated POD coefficients are then calculated in each run as

$$\begin{aligned} \tilde{A}_{ki}=\{B_{kj}(f)P_{a,ji}(f)\}^* \end{aligned}$$
(6)

where \(P_{a,ji}(f)\) is the Fourier transform of the matrix of acoustic fluctuations of size \([N\times n_t]\) where \(n_t\) is the number of times steps in the run, \(\{\cdot \}^*\) denotes the inverse Fourier transform, and \(\tilde{A}_{ki}\) is the matrix of estimated POD coefficients of size \([K\times n_t]\). The velocity fields correlated with the acoustic fluctuations are then reconstructed via

$$\begin{aligned} \tilde{u}_i'({\varvec{x}},t)=\sum _{k=1}^{K_{tot}}\tilde{a}_k(t)\phi _k({\varvec{x}}) \end{aligned}$$
(7)

where \(\tilde{a}_k(t)\) is the k-th mode coefficient and time instant of the matrix \(\tilde{A}_{ki}\). The main advantage of performing the LSE in the Fourier domain is the automatic incorporation of time delays in the estimation of the LSE coefficients (Tinney et al. 2006).

4 Results

4.1 Acoustic extrapolation

Fig. 4
figure 4

Overall sound power level (OASPL) (a) and orientation-averaged sound power spectra (b) with \(p_0=10^{-6}\) Pa. The vertical dashed line indicates the location of \(St= f^{\star }\sin \alpha =0.1\) and 0.2 corresponding to a range of bluff-body vortex shedding frequencies

Full size image

The results of the acoustic extrapolation via Curle’s analogy are reported in Fig. 4. The overall sound power level (OASPL) in Fig. 4a shows the expected increase in noise at the onset of stall. The variation with listener angle indicates that the noise directivity is largely driven by the geometry of the airfoil, i.e. the alignment of \(l_i\) and \(n_j\), with maximum noise level at \(\theta =90^{\circ }\) (normal to the airfoil chord) in all cases. Only the case at \(\alpha =15^{\circ }\) exhibits a notable asymmetry with approximately 2 dB more sound power for \(\theta >120^{\circ }\) (in proximity to the TE) with respect to \(\theta <60^{\circ }\) (in proximity to the LE). No significant differences in the shape of the distributions were found after considering band-limited directivity.

The spectra reported in Fig. 4b are obtained using Welch’s method with a Hamming window in 3 segments of equal length with 50% overlap and averaged over all orientations and runs. Both stalled cases exhibit significant broad-band noise indicative of turbulence. A range of bluff-body shedding frequencies at Strouhal numbers \(St\equiv f^{\star }\sin \alpha\) between 0.1 and 0.2 is indicated in the figure to delineate between bluff-body shedding related frequencies and shear-layer flapping at higher frequencies (Derakhshandeh and Alam 2019). Here we focus on the two cases in stall as this is the focus of this manuscript (in addition, the attached case contains likely unphysical variations at the LE, see Fig. 2d). Both stalled cases exhibit local peaks in the bluff-body shedding range and the shear-layer flapping range (indicated by the arrows in the figure), though these peaks do not necessarily coincide between cases. These peaks suggest that both shear layer flapping and bluff body shedding mechanisms play a role in noise generation in both transient and deep stall (Lacagnina et al. 2019).

4.2 Correlated flow structures

Fig. 5
figure 5

Contours of the turbulent kinetic energy normalized using the maximum of the fluctuating velocity fields (dotted) and the acoustic-correlated fluctuating velocity fields (solid) for \(\alpha =13^{\circ }\) and \(\alpha =15^{\circ }\). Contours levels are drawn at 0.5 (outer) and 0.75 (inner)

Full size image

Having quantified the directivity and spectral content, we turn our attention to the relationship between structures in the velocity field and the generation of noise using the framework presented in Sect. 3.3. To investigate spatial distribution of structures correlated to the noise, the planar turbulent kinetic energy for the fluctuating velocity fields \(q({\varvec{x}})=\frac{1}{2}\langle u_i'u_i'\rangle\) and for the acoustic-correlated fluctuating velocity fields \(\tilde{q}({\varvec{x}})=\frac{1}{2}\langle \tilde{u}_i'\tilde{u}_i'\rangle\) is plotted in Fig. 5. Here, the contours are shown relative to the maximum value of each quantity. It is therefore important to note the relative magnitude \(\tilde{q}_{\textrm{max}}/q_{\textrm{max}}=0.16,0.30\) for the \(\alpha =13^{\circ },15^{\circ }\) cases, respectively. In other words, at its maximum roughly 16% and 30% of the energy of the fluctuating velocity fields was found to correlate with the far-field noise for each case.

The contours of \(\tilde{q}({\varvec{x}})\) concentrate in two areas. First, in the shear layer but shifted downstream, i.e. closer to the TE, with respect to the contours of \(q({\varvec{x}})\). This contour is elongated along the shear layer, with a clear maximum shortly downstream of the TE location in both cases. For the case in deep stall, another maximum is seen in the shear layer further upstream. Second, contours appear in close proximity to the TE itself. This is likely related to the bluff body shedding alternating at the TE and in the shear layer. The location of the contours of \(\tilde{q}({\varvec{x}})\) in proximity to the TE reflects the tendency of the TE to scatter noise efficiently, consistent with the results of Lacagnina et al. (2019) and Mayer et al. (2020).

4.3 Analysis of extreme events

Fig. 6
figure 6

Instantaneous acoustic fluctuation (right axis, blue line) at \(\theta =90^{\circ }\) normalized by its standard deviation \(\sigma _{p_a}\) plotted over 2.5 s with simultaneous noise-correlated pod coefficients \(\tilde{a}_k/\sqrt{K_{tot}}\) (left axis) where k is the mode number for \(\alpha =13^{\circ }\) (a). Segments used to identify local maxima and minima are highlighted in bold lines. The conditional averages of the noise-correlated POD coefficients across all runs performed relative to the acoustic extrema are shown for local maxima (b) and minima (c). The vertical dash-dot lines are for reference to Fig. 7

Full size image

It is of further interest to isolate the structures in the velocity field that are responsible for the most intense acoustic fluctuations. To this end, we present a conditional analysis of the acoustic-correlated POD coefficients. The acoustic fluctuations are segmented based on a threshold chosen to be \(\pm 2\) standard deviations. (The ensuing results were found not to be qualitatively sensitive to this threshold down to \(\pm 1\) standard deviation.) This is chosen to isolate the top 5% most intense fluctuations by magnitude. In Fig. 6a, a time segment of 2.5 s of data is shown for the case at \(\alpha =13^{\circ }\). This particular segment reveals three instants of positive extreme events and two negative extreme events, however the overall number of peaks for both was found to be approximately equal across all runs for each case.

The conditional analysis was carried out by identifying the local maximum and minimum within each time segment of intense acoustic fluctuations. At the extrema, the time lag \(\tau\) is defined to be zero and the average of the first five POD coefficients is tabulated at all maxima and minima, respectively. (We note that beyond five modes the conditional averages were found to be negligibly small, and therefore restrict to just the first five.) The time lag is shifted at all possible temporal bins across \(\pm 0.5\tau /T_L\) in order to capture the evolution of the velocity fields leading up to and immediately following intense acoustic fluctuations. From Fig. 6b, c, the conditional averages for the \(\alpha =13^{\circ }\) case, it is evident that most of the variation in the conditional POD coefficients is in the range \(\tau /T_L=\pm 0.2\).

Fig. 7
figure 7

Conditional fluctuating velocity fields at \(\alpha =13^{\circ }\) based on noise-correlated POD modes \(\tilde{a}_k\) relative to local maxima (a,c,e,g,i) and minima (b,d,f,h,j) in the acoustic fluctuations for time lags corresponding to the dashed vertical lines of Fig. 6 (\(\tau /T_L=-0.2,-0.1,0,0.1,0.2\) from top to bottom) denoted by the dashed borders. For clarity, every fifteenth velocity vector is shown

Full size image

The fluctuating velocity fields conditioned on local maxima and minima for the case at \(\alpha =13^{\circ }\) are shown in Fig. 7 at time lags indicated in Figs. 6b, c. It can be seen that the structures leading to local maxima and local minima in the acoustic fluctuations are almost mirrored. For the local maxima, a downwash of fast-moving fluid can be seen originating in the shear layer above the trailing edge. At \(\tau =0\) (panel e), a simultaneous low-speed structure at the incipient shear layer emerges. Together, these structures manifest a diverging pattern of slow and fast-moving fluid at the incipient shear layer and above the trailing edge. At the trailing edge itself, the fluid is seen to be low-speed.

The opposite action is seen to occur for the local minima. An upwash of slow-moving fluid can be seen originating in the shear layer above the trailing edge. At \(\tau =0\) (panel f), a simultaneous high-speed structure at the incipient shear layer emerges. These structures manifest a converging pattern of fast and slow-moving fluid at the incipient shear layer and above the trailing edge. The behaviour at the TE is likewise opposite to the local maxima. This can be seen in the contours of out-of-plane vorticity \(\tilde{\omega }_3=\frac{\partial \tilde{v'}}{\partial x}-\frac{\partial \tilde{u'}}{\partial y}\) as well, with the sign of the vorticity flipping between the maxima and the minima.

Fig. 8
figure 8

Conditional fluctuating velocity fields at \(\alpha =15^{\circ }\) based on noise-correlated POD modes \(\tilde{a}_k\) relative to local maxima (a,c,e,g,i) and minima (b,d,f,h,j) in the acoustic fluctuations (time lags \(\tau /T_L=-0.2,-0.1,0,0.1,0.2\) from top to bottom). For clarity, every fifteenth velocity vector is shown

Full size image

The conditional fields for the case at \(\alpha =15^{\circ }\) are shown in Fig. 8. Despite this case being well beyond transient stall and firmly in a state of deep stall originating at the LE, the qualitative structure of the fluctuating velocity fields correlated to extreme noise events is remarkably similar to the \(\alpha =13^{\circ }\) case. The magnitude of the out-of-plane vorticity is seen to comparatively increase particularly at \(\tau =0\). In addition, likely due to the larger region of separation, the downwash and upwash structures appear to occupy a comparatively larger area.

A small difference of note between the two cases can be seen at the largest presented time lag of \(\tau /T_L=0.2\) (panels i and j of Figs. 7 and 8). For the case in transitional stall at \(\alpha =13^{\circ }\), the acoustic minima (panel i) no longer appears to mirror the maxima (panel j), unlike for the case in deep stall at \(\alpha =15^{\circ }\). Taking into account the changes relative to the previous time lag (\(\tau /T_L=0.1\)) this suggests an asymmetry exists in transitional stall such that the structures associated to the acoustic minima are not as long-lived as the maxima.

5 Conclusions

We have presented an analysis of planar time-resolved PIV data in the flow of a stalled NACA 0012 airfoil at \(\textrm{Re}_c=7.1\times 10^4\). The planar pressure fields were reconstructed from the time-resolved velocity fields and used to extrapolate the far-field dipole acoustics emanating from the surface of the foil via Curle’s analogy. A data-driven framework utilizing the POD in combination with spectral LSE was leveraged to correlate the time-varying structures of the velocity fields to the far-field noise. In particular, this study focuses on low-frequencies (\(f^{\star }=f\frac{c}{U_{\infty }}\le 3\)) that are known to increase dramatically at the onset of stall (Moreau and Roger 2005; Turner and Kim 2020; Mayer et al. 2020).

The acoustic extrapolation revealed a broad range of frequencies in the far-field noise for the stalled cases, consistent with broad-spectrum turbulence. Local peaks were observed both within the bluff-body vortex shedding range and within the shear-layer flapping range. The sLSE revealed the energy of the structures correlated to the noise to be on the order of 10–20% of the energy of the fluctuating velocity fields. Their concentration in space was found to be in proximity to the TE, centered in the shear layer. This is consistent with the beam-forming results of Mayer et al. (2020), whom also found the noise generation to be dominant at the TE. In deep stall (\(\alpha =15^{\circ }\)), a second smaller peak is seen in the incipient shear layer, possibly due to the shear-layer flapping mechanism (Lacagnina et al. 2019).

A further analysis of the extrema of the acoustic fluctuations revealed a conditional structure in the velocity fields in transient and deep stall. A large diverging flow structure at the TE and incipient shear layer and, oppositely, a converging flow structure are seen at local maxima and minima, respectively.

It is important to stress that the conditional structures themselves do not generate quadrupole noise, rather it is their footprint on the unsteady pressure at the surface of the airfoil that generates extreme dipole noise. Future efforts for noise mitigation may benefit from insight on the spatial organization of these structures to inspire reduction strategies and control.