Uncertainty and validation of unsteady pressure-sensitive paint measurements of acoustic fields under aero engine-like conditions

Abstract

Fast response pressure-sensitive paint (PSP) allows optical measurements of pressure fluctuations on a surface with high spatial and temporal resolution. This technique is evaluated for aeroacoustic measurements inside an aeroacoustic wind tunnel (AWT). The AWT is a test rig especially designed for investigating the excitation and propagation of sound under conditions typical for turbomachinery. The aim of this work is to compare the results of sound pressure measurements of tonal sound fields in a circular duct conducted with PSP and microphone arrays in order to assess the applicability of PSP in turbomachinery acoustics applications. A data analysis process is presented, which projects the camera image of the PSP data onto a given surface. To analyze the spatial pressure fluctuations, the PSP data are transformed in the frequency domain using pixel-wise fast Fourier transform. Measurements with a mean Mach number up to 0.109 and 5 kHz excitation frequency are conducted. An acoustic mode generator is used to excite the sound field with specific circumferential mode order. The pressure fluctuations obtained with the PSP measurement visualize the measured acoustic field well and allow early interpretation. The pressures of PSP and microphones are in good agreement; for example, the maximum detected deviation in pressure at 2700 Hz is 30 Pa. A preview on using radial mode analysis to decompose the acoustic field, measured by PSP, into acoustic modes is provided. The results are confirmed by a decomposition using conventional arrays of flush-mounted microphones.

Graphical Abstract

1 Introduction

In the research of aeroacoustics, aeroelasticity, and unsteady flows, the experimental investigation of unsteady pressure is indispensable for the understanding of noise sources, noise propagation, and other phenomena. Typically, sound pressure is measured at discrete positions with microphones installed flush with the surface. For measurements in turbomachinery, it is a common approach to decompose the measured acoustic field in specific acoustic modes, which allow a detailed analysis of the acoustics. To accomplish a sufficiently extensive resolution of the sound field for the modal decomposition, either a large number of sensors is needed or the positioning of the sensors must be varied during the measurement with a traversing unit; see (Tapken et al. 2006) and Tapken et al. (2011). This is limited, costly, and requires high instrumentation resources. Furthermore, the reduction of sensors through the use of a traversing system is only valid if stationary aerodynamic boundary conditions and a temporally homogeneous sound field may be assumed.

Pressure-sensitive paint is an established measurement technique for the investigation of the steady and unsteady pressure distribution on a surface with a high spatial and temporal resolution. The high spatial resolution, only limited by the pixel resolution of the camera, augments the detail of analyses of unsteady pressure fluctuations on surfaces. This can be used on an inner duct wall to investigate the acoustic propagation simultaneously over a large area or on a blade surface to identify noise sources or aeroelastic forcing throughout the entire blade surface. Therefore, this measurement technique has high potential for achieving a better understanding of aeroacoustic and aeroelastic phenomena in turbomachinery. However, acoustic measurements using PSP are particularly challenging since PSP senses absolute pressure and the acoustic pressure fluctuations are several orders of magnitude lower than the ambient pressure, as stated by Gregory et al. (2014). To assess whether PSP is a viable option despite this challenge, PSP is applied to the inner casing wall of an AWT and the unsteady pressure induced by an acoustic mode generator unit is measured. Microphone measurements on the PSP surface and on a rotatable segment upstream are compared to the PSP measurement results. Measurements with up to 9 kg/s mass flow rate and 5000 Hz excitation frequency are conducted. First steps toward a mode decomposition using PSP data are presented.

1.1 Basic principles of pressure-sensitive paint

Pressure-sensitive paint is an optical pressure measurement technique based on a photo-physical phenomenon of luminophores. Exciting the paint with light at a certain wavelength, the luminophores in the paint emit light with longer wavelength. An alternate method through which the luminophore can lose the absorbed energy is oxygen quenching, a process through which the energy from the excited luminophore is transferred to a nearby oxygen molecule without emitting a photon in the visible spectrum. Since the probability of oxygen quenching is dependent on the oxygen concentration at the paint’s surface, which is proportional to the pressure, the luminous intensity of the PSP is directly correlated with the surface pressure.

The intensity method is used in this work, which requires a continuous ultraviolet (UV) illumination of the paint. The intensity of the light emission is measured with a camera and further analyzed. Details of the measurement technique are given in Liu et al. (2021).

1.2 Application of fast response pressure-sensitive paint with low-pressure fluctuations

Acoustic measurements with PSP in turbomachinery applications are especially challenging due to the high frequencies and the low-pressure fluctuations compared to the high ambient pressure level. Previous measurements conducted inside the AWT by Bartelt et al. (2013) and Mumcu et al. (2018) reached sound pressure levels (SPLs) of up to 136 dB (126 Pa). The absolute pressure change in that case is only $0.126\%$ with an ambient pressure of approximately $10^5$ Pa. This requires further data analysis of the PSP data to improve the signal-to-noise ratio (SNR).

The first attempts at measuring spatially resolved acoustic fluctuations were made by Gregory et al. (2006), using a 14-bit charge-coupled device (CCD)-camera to record the intensity changes of a standing wave in a rectangular cavity induced by a compression driver. The compression driver induced a standing wave with a frequency of 1.3 kHz. In this test, fast response polymer/ceramic (PC)-PSP was coated on the back plate of the cavity and excited by a pulsed UV-LED. To increase the SNR, phase averaging of 200 images is performed and the intensity of 10-pixel square area is mean averaged. The resulting PSP data is compared to an analytic solution and one fast response pressure sensor. The minimum detectable pressure by PSP in this test was 115.8 dB (12.3 Pa).

Pastuhoff et al. (2013) investigated a fluctuating low-amplitude pressure field on the side of a square cylinder; the said field was decomposed using singular value decomposition (SVD) and only dominant modes were considered for the transformation back into the time domain to improve the SNR. In order to investigate multi-frequency phenomena, different data analysis methods were applied. (Alie et al. 2016) used proper orthogonal decomposition (POD), a technique related to SVD, and dynamic mode decomposition (DMD) to reduce the static noise of the optical data acquisition system. Both techniques are described in detail by Schmid (2010) and Alie et al. (2016). The experimental setup used by Alie et al. (2016), exciting standing waves inside a rectangular cavity, is a setup similar to Gregory et al. (2006), except that a second speaker is mounted at the side of the box for the distinct excitation of two different frequencies. The principles of POD and DMD are compared to each other, to the phase averaging method, and to the analytic solution. It is notable that both methods were able to separate two different modes induced simultaneously. According to Alie et al. (2016), DMD is the more robust method in discriminating between the two modes and eliminating the noise of the camera sensor.

Gößling et al. (2020) evaluated fast response polymer-ceramic type PSP developed at the German Aerospace Center DLR in Göttingen with a similar setup as Alie et al. (2016), especially for the implementation inside the AWT. Acoustic modes inside the cavity were induced with frequencies up to 4000 Hz. Using FFT and DMD data analysis, acoustic modes could be extracted from a tonal and white noise excitation with similar SNR. The minimal detectable pressure limit was 5 Pa (108 dB) at 1318 Hz. The results provide a good foundation for taking acoustic measurements inside a more complex test setup closer to aero engine application, e.g., the AWT.

2 Sound propagation in ducted flows

The sound propagation in a ducted fluid occurs in the form of acoustic modes resulting from the superposition of standing waves in the different spatial directions. In the case of circular or annular ducts, standing waves in circumferential and radial direction form an acoustic mode with the circumferential mode order m and radial mode order n under the assumption that the ducts are infinitely long or anechoic (no axial standing wave). The acoustic field consists of the superposition of all acoustic modes [m,n] propagating downstream ($.^+$) and upstream ($.^-$)

$$\begin{aligned} {\tilde{p}}(\mathbf {x},t) = \sum _{n = 0}^{\infty } \sum _{m = -\infty }^{\infty } \left( {\tilde{p}} ^+_\mathrm{{mn}}(\mathbf {x},t) + {\tilde{p}} ^-_\mathrm{{mn}}(\mathbf {x},t) \right) . \end{aligned}$$

(1)

Therein, $\mathbf {x} = [r,\Theta ,x]$ is the position inside the duct. The tonal modal acoustic field of an acoustic mode propagating down- or upstream is given by

$$\begin{aligned} {\tilde{p}}^\pm _\mathrm{{mn}}(\mathbf {x},t) = {\tilde{A}}_\mathrm{{mn}}^\pm \cdot f_\mathrm{{mn}}(r) \cdot e^{ i \left( \omega \cdot t-k_{x,\mathrm{mn}}^\pm \cdot x-m \cdot \Theta \right) } \end{aligned}$$

(2)

where ${\tilde{A}}_\mathrm{{mn}}^\pm$ is the modes’ complex amplitude, $f_\mathrm{{mn}}(r)$ is the modal radial eigenfunction and $k_{x,\mathrm{mn}}^\pm$ is the modes axial wave number. The (semi) analytical determination of the modes’ radial eigenfunction and axial wave number requires a simplified modeling approach for the mean flow. Under the assumption of a stationary isentropic mean flow at small Mach numbers, small perturbations with respect to the mean flow quantities, rigid walls and a purely axial homogeneous flow, the linearized conservation equations of fluid dynamics can be reduced to the Pridmore-Brown equation (Pridmore-Brown 1958). In the literature, more complex modeling approaches can be found, in which arbitrary radial distributions of the aerodynamic quantities can be specified (see, e.g., (Enghardt et al. 2005) and Vilenski et al. (2005)). However, the simplified modeling as a purely axially homogeneous duct is sufficiently accurate for the application presented here as the influence of radially varying distributions of the flow variables is negligible for swirl-free flows.

The solution of the Pridmore-Brown equation for a circular duct results in analytical formulations for the radial eigenfunction

$$\begin{aligned} f_\mathrm{{mn}}(r) = \frac{1}{\sqrt{F_\mathrm{{mn}}}} \cdot J_m \left( s_\mathrm{{mn}} \cdot \frac{r}{R} \right) \end{aligned}$$

(3)

and the axial wave number

$$\begin{aligned} k_{x,\mathrm{mn}}^\pm = \frac{\mathrm{He} \left( -\mathrm{Ma} \pm \sqrt{ 1-\frac{\left( 1-\mathrm{Ma}^2 \right) }{\mathrm{He}^2} s_\mathrm{{mn}}^2 } \right) }{\left( 1-\mathrm{Ma}^2 \right) R} \end{aligned}$$

(4)

respectively. Therein, $F_\mathrm{{mn}}$ is a modal normalization factor given by Tapken et al. (2006), $J_m$ is the Bessel Function of first kind and m-th order, and $s_\mathrm{{mn}}$ is the modal radial eigenvalue, which is determined such that $\partial {\tilde{p}} / \partial r (r=R) = 0$. Furthermore, $\mathrm{He} = 2 \pi R f / a^0$ is the Helmholtz number defined with the ducts shroud Radius R and the mean speed of sound $a^0$ of the flow, and Ma is the mean Mach number.

Considering Eqs. (2) and (4), it can be shown that complex axial wave numbers result in an axial damping of the sound pressure. This results in a rapid decrease of the amplitude of an acoustic mode and prevents the transport of acoustic power in the axial direction. Acoustic modes with complex axial wave numbers are labeled cut-off and are not considered in the modeling of the acoustic field, as their contribution to the acoustic field is limited spatially. We can thus define a cut-off ratio $\xi$ from the root term of eq. (4)

$$\begin{aligned} \xi = \frac{f}{f}_\mathrm{{C}} = \frac{f R}{a^0 } \frac{2 \pi }{s_\mathrm{{mn}} \sqrt{1 - \mathrm{Ma}^2} } \end{aligned}$$

(5)

that defines the ratio of the excitation frequency f to the modal cut-off frequency $f_\mathrm{C}$. Only modes with a cut-off ratio of $\xi \ge 1$ are considered in this work.

Finally, the modal sound power transported by an acoustic mode propagating in the duct is given by Hurst et al. (2019) for a purely axial flow as

$$\begin{aligned} P_\mathrm{{mn}}^\pm = \frac{\pi R^2}{\rho a^0} \frac{ \left( 1-\mathrm{Ma}^2 \right) ^2 \sqrt{1-\frac{1}{\xi ^2}} }{ \left( 1 \mp \mathrm{Ma} \sqrt{1 - \frac{1}{\xi ^2}} \right) ^2} |{\tilde{A}}_\mathrm{{mn}}^\pm |^2 \end{aligned}$$

(6)

where $\rho$ is the density of the fluid.

The complex amplitudes ${\tilde{A}}_\mathrm{{mn}}^\pm$ are determined experimentally using the radial mode decomposition described in sect. 4.3.

3 Experiment

3.1 Aeroacoustic wind tunnel

Fig. 1

Details of experimental setup for PSP measurement

The AWT was designed at the Turbomachinery and Fluid Dynamics (TFD) and is depicted in Fig. 1a. The rig consists of a settling chamber $\textcircled {1}$ covered with acoustic liners that function as an inflow silencer, a modular measurement section, and an anechoic termination $\textcircled {6}$. The designs and functions of the silencer and the anechoic termination are explained in detail by Bartelt et al. (2013).

The current design of the measurement section includes an acoustic mode generator $\textcircled {2}$, consisting of 16 loudspeakers distributed equidistantly around the circumference mounted in the casing and two instrumented traversing units $\textcircled {3}$ up- and downstream of the test specimen $\textcircled {4}$. The traversing units can be equipped with probes, microphones and other measurement devices and can be traversed 360$^\circ$. The last part of the measurement section is the diffuser section $\textcircled {5}$. The design of this setup is described in detail by Mumcu et al. (2016).

Using the acoustic mode generator, acoustic modes can be excited and superimposed on the flow in the duct. The frequency, amplitude and circumferential mode order of the dominant modes in the duct are controlled by tuning the 16 speakers relative to each other. With the current mode generator, the radial mode order cannot be controlled. Therefore, all cut-on radial mode orders of the specified circumferential mode order are excited. Additionally, only a circumferential mode order between m = −7 and 7 can be excited specifically. Higher-order modes would result in an additional excitation of spillover modes.

3.2 Experimental setup

Fig. 2

Pressure distribution of analytic mode [6,0] with field of view for setup 1 (solid line) and setup 2 (dashed line)

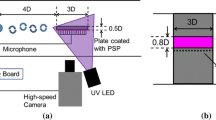
The measurement section of the AWT is modified to allow PSP measurements on the inner casing wall downstream of segment $\textcircled {4}$. An optical access for a high-speed camera (70 mm in diameter) and four UV-LEDs (55 mm in diameter) (see Fig. 1c and Fig. 1d) replaces the downstream traversing unit of the original AWT. The windows are made of borofloat 33 glass and have a max. step of 5 mm to the inner duct wall, which is 12 mm thick. Windows are used over, e.g., endoscopes to maximize the light intensity. A schematic of the PSP and reference microphone instrumentation is shown in Fig. 1b. The paint is applied on the inner duct wall over an axial length of $l_{\text {PSP}} = 220$ mm and over an angle $\theta _{\text {PSP}}= 90^\circ$. The radius of the PSP duct is $R_{\text {PSP}} = 237.7$ mm. The inner radius of the other AWT segments is $R_{\text {AWT}} = 250$ mm. The central cylindrical body has been removed to allow direct optical access to the opposite duct wall and simplify the measurement setup. The step created between PSP and AWT segment is chamfered and verified using CFD methods to remain attached retain and homogeneous axial flow in the PSP measurement section. For the in situ calibration and comparison with pressure fluctuations measured with PSP, 15 flush-mounted microphones (GRAS 46 BD) are distributed over the area coated with PSP. Fig. 1e shows the distribution of the microphones. The microphones 1-7 in axial direction define the circumferential reference $\theta = 0^\circ$, and microphones 8-15 define the axial reference $x=0$ mm. A constant temperature throughout the entire area is assumed.

Results of two different PSP setups are shown in this work:

For the first setup, the applied PC-PSP paint is developed by DLR and has a peak excitation at a wavelength of 390 nm and peak emission at 650 nm. The response time of PSP is governed by the lifetime of the luminophores, which is on the order of 15-30 µs in case of PtTFPP and by the diffusion process of oxygen to the luminophores. In order to investigate the frequency response of the paint, also with respect to temperature variation, several measurements were performed and reported in previous publication, (Gößling et al. 2020). Additionally, an analytical response model of the paint was fitted to the results. The cut-off frequency of -3dB of the DLR paint is around 6 kHz. Expected temperature variations in the AWT are found to be negligible for unsteady measurements. A high-speed camera (Photron FastCam SA-Z) is equipped with a band-pass filter, which passes light with a wavelength of 650 nm ± 10 nm. For setup 1, the equipped camera lens has a focal length of 35 mm to maximize the measured area, resulting in an image frame of 210 mm in axial direction and $80^\circ$ in circumferential direction. The investigated area is 0.070 m$^2$. The camera captures 7125 images with a frame rate of 10 kHz.

The second setup uses the commercial paint of Innovative Scientific Solutions, Inc, which is also a polymer/ceramic paint is able to detect pressure fluctuations up to 20 kHz. Further details of the paint are given in Sellers et al. (2016). The focal length of the lens is adjusted to 50 mm with the aim to improve the SNR. The emitted light intensity, which is important for the SNR, is increased by focusing the UV-LEDs on the resulting smaller area (210 mm in axial direction, $40^\circ$ in circumferential direction, 0.035 m$^2$). The camera (Photron FastCam SA-X2) captures 21839 images per measurement with a frame rate of 10 kHz. The higher number of images enhances the data analysis methods to improve SNR. The resulting field of view for both setups is illustrated in Fig. 2.

To obtain further acoustic reference data, the upstream traversing unit is equipped with two microphone arrays, each consisting of 8 microphones (GRAS 46 BD) with an equidistant axial spacing of 35 mm. The arrays $M_{\text {A1-2}}$ are located on opposite sites at the same axial position and are being traversed in the circumferential direction to sample sound pressure data over the entire circumference of the duct. Per PSP measurement, 36 equidistant circumferential positions are sampled with a frequency of 100 kHz and a duration of 5 s. Mass flow rate, static wall pressures and temperatures are measured by the systems available in the AWT.

4 Data analysis methods

Fig. 3

Data analysis methods

The process for the PSP data analysis is described in the flow chart in Fig. 3 and explained in detail below.

4.1 Preparation and projection of PSP data

For a detailed analysis of the measured spatial PSP data, it is necessary to project each pixel onto its allocated position on the duct wall. First, the image distortion created by the lens is corrected. This is done by calibrating the intrinsic camera parameters with images of a checkerboard and removing the lens distortion as described in detail by Zhang (2000).

The positions of the microphones in the image are identified in the undistorted image and used to estimate the camera’s position and orientation. This is done with a 3-D to 2-D point correspondence using the known world coordinates of the microphones within the measurement section. The method with n-points is described by Lepetit et al. (2009) and implemented in the Computer Vision Toolbox of MATLAB. A mesh is generated, discretizing the painted inner duct wall with 128x256 and 128x128 data points for test setups 1 and 2, respectively. The resulting world points of the mesh are projected on the image by

$$\begin{aligned} \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \mathbf {A} \quad \Pi \quad ^{c}\mathbf {T}_w \nonumber \\ \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{aligned}$$

(7)

using the homography described with

$$\begin{aligned} \mathbf {A} \quad \Pi ^{c}\mathbf {T}_w = \nonumber \\ \begin{bmatrix} f_x &{} 0 &{} c_x \\ 0 &{} f_y &{} c_y \\ 0 &{} 0 &{} 1 \end{bmatrix} \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \end{bmatrix} \begin{bmatrix} r_{11} &{} r_{12} &{} r_{13} &{} t_x \\ r_{21} &{} r_{22} &{} r_{23} &{} t_y \\ r_{31} &{} r_{32} &{} r_{33} &{} t_z \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$

(8)

including the focal length $f_x$ and $f_y$, the principal points $c_x$ and $c_y$, the perspective projection matrix $\mathbf {\Pi }$, and the transformation matrix $^c\mathbf {T}_w$ from world to camera frame. The intensities of the captured images are linearly interpolated on the resulting image points of the mesh. A binning of four pixels is performed in advance to increase the SNR.

4.2 Pixel-wise fast Fourier transform (FFT)

An efficient way to analyze the PSP data and enhance the SNR is to perform a fast Fourier transform (FFT) of each pixel, (Gößling et al. 2020), in this case of each projected image point. The function to calculate the FFT, included in MATLAB, is used to calculate the discrete Fourier transform (DFT) of the temporal image sequence matrix for each pixel using a FFT algorithm. To reconstruct an image of the spatial pressure fluctuation, the amplitude and phase of a specified frequency are extracted from the frequency spectrum of each pixel and rearranged into the complex matrix ${\textbf {Y}}_\mathrm {S}$. The pressure level and phase are scaled with the complex scaling factor ${\tilde{s}}$ for the specific frequency of the microphone reference measurement calculated using FFT. The microphone data are downsampled to match the sample rate of the camera for a better comparison. One mean complex scaling factor ${\tilde{s}}$ is calculated by dividing the pressure data of each microphone $\tilde{p}_{{{\text{iMic}}}}$ with the intensity fluctuations around the respective microphone $\tilde{i}_{{{\text{iMic}}}}$ at the frequency of interest. The mean value of each scaling factor is calculated. The spatial intensity fluctuation is scaled to a spatial pressure fluctuation with

$$ {\mathbf{\tilde{Y}}}_{{\text{S}}} = \tilde{s}{\mathbf{\tilde{Y}}}_{{{\text{PSP}}}} $$

(9)

for each measurement. By using one complex scaling factor at the specific frequency, the PSP pressure distribution is scaled in amplitude and phase to the reference microphone measurement.

4.3 Radial mode analysis (RMA)

A radial mode analysis (RMA) decomposes the locally sampled acoustic field into up- and downstream propagating acoustic modes such that eq. (1) is satisfied. The decomposition allows the extraction of amplitude, phase and sound power of specific modes in the sound field. In a first evaluation step, a modal decomposition into circumferential mode orders m is performed based on data at constant axial and radial positions sampled during a microphone traverse or on the PSP surface. The linear system of equations solved reads

$$\begin{aligned} {\tilde{A}}_m(r,x) = M^{-1}(\Theta ) \cdot {\tilde{p}}(r,\Theta ,x) \end{aligned}$$

(10)

where in $M(\Theta )$ is a quadratic matrix whose entries are defined as

$$\begin{aligned} M_l(\Theta _j) = e^{-i \cdot m_l \cdot \Theta _j}. \end{aligned}$$

(11)

The second evaluation step individually decomposes each circumferential mode order into up- and downstream propagating modes for each radial mode order that is cut-on according to equation (5) ($\xi \ge 1$). The method takes advantage of the fact that different radial mode orders and axial propagation directions of the same circumferential mode order have different axial wave numbers. Run-time differences of the modes at different axial positions can thus be used to further decompose the acoustic field. The linear system of equations solved is given by

$$\begin{aligned} {\tilde{A}}_\mathrm{{mn}} = N_m^{-1}(r,x) \cdot {\tilde{A}}_m(r,x) \end{aligned}$$

(12)

where in the entries of the eigenvalue matrix $N_m(r,x)$ are defined as

$$\begin{aligned} N_m(r,x_j) = f_\mathrm{{mn}}(r) \cdot e^{- i k_{x,\mathrm{mn}}^\pm x_j}. \end{aligned}$$

(13)

Further details on this algorithm and the mathematical implementation are described by Tapken et al. (2006) and Mumcu et al. (2016).

In the case of the traversed microphone array measurement, the data at different circumferential positions are not sampled simultaneously. Therefore, a phase correction with a stationary reference microphone within the PSP segment is performed. After performing a FFT of each microphone and reducing the data to complex signals at the excitation frequency, the phase correction is performed by phase-shifting every microphone by the reference microphone’s phase angle. The sound power is computed using eq. (6).

4.4 Estimation of measurement uncertainty

For the microphones instrumented in the PSP section, the standard deviation $\sigma _ \mathrm {sys}$ of the microphone itself is added to the calculated standard deviation $\sigma _ \mathrm {rep}$ based on the variations of the repeated measurements performed in the course of a traverse of the upstream traversing unit with

$$\begin{aligned} U_\mathrm{{mic}} = Z \sqrt{\sigma _ \mathrm {sys} ^2+\sigma _ \mathrm {rep} ^2}. \end{aligned}$$

(14)

The Z score $Z=1.96$ is used to account for the 95% confidence interval. The uncertainty $U_ \mathrm {rep}$ is calculated with

$$\begin{aligned} U_ \mathrm {rep} = \frac{\sigma \left( {\hat{p}} _i \right) }{\sqrt{N}}, \end{aligned}$$

(15)

calculating the standard deviation of the measured amplitude of all measurements N. Thus, it also contains the repeatability of the measurement itself. The 95% confidence interval of the PSP is calculated using the uncertainty $U_ \mathrm {band}$ of the pressure amplitude variation in a 6 mm band along the circumferential or axial direction. The width of the band is chosen to be similar to the microphone diameter. The error propagation of the microphones to the scaling of the PSP is added to the final uncertainty of the PSP measurement similar to Eq. (14). Uncertainties caused by temperature variation are neglected due to the assumption of an isothermal surface.

In accordance with the first supplement of the GUM (BIPM, Iec, IFCC, 2008), the uncertainty of the mode decomposition of the radial mode analysis (RMA) is estimated with a Monte Carlo approach. For that purpose, $10^6$ samples are generated at random in which the main input variables—the complex sound pressures of each microphone, Mach numbers and temperature—are varied stochastically and uncorrelated relative to their measurement value during the experiment within their respective measurement uncertainty. The resulting uncertainty of the complex modal amplitudes results from the deviation of the RMA results of the altered data from the unaltered data. Uncertainties in the evaluation of the sound power are determined based on a Gaussian error propagation in accordance with the GUM.

5 Measurements and results

5.1 No flow

Fig. 4

Spectrum for PSP (blue) and microphone (orange) measurement at microphone position 4, Setup 1, $m=6$, $f=1800$ Hz, $\text {Ma}=0$

During measurement 1, the sound generator is exciting a spinning mode with circumferential mode order $m=6$ at 1800 Hz. The resulting spectrum for microphone 4 and its allocated PSP reference is shown in Fig. 4. The peak at the excitation frequency of 1800 Hz is dominant in both measurements. Furthermore, the second harmonic of the excitation frequency is presented and also measured by the microphone and PSP. Since the PSP is scaled at 1800 Hz, the loss in measured amplitude at 3600 Hz is expected due to the frequency response of the paint. The noise floor of the PSP setup 1 is below 25 Pa.

Fig. 5

Comparison of PSP and microphone pressure, Setup 1, $m=6$, $f=1800$ Hz, $\text {Ma}=0$, 95% confidence interval given by error bars for the microphones and gray area for PSP

Fig. 6

Spatial pressure distribution, Setup 1, $m=6$, $f=1800$ Hz, $\text {Ma}=0$

Figure 5 shows the real and imaginary part of the complex pressure distribution at the excitation frequency measured by PSP and microphones. The phase angle is set such that $\phi = 0^\circ$ for microphone 4, which is located at $x=0$ mm and $\theta = 0^\circ$. The sinusoidal variation of the real and imaginary pressure over the circumferential direction, see Fig. 5a, with a wavelength of approximately $\theta = 60^\circ$ is dominant within the PSP and microphone data and in agreement with an excitation of an acoustic mode with circumferential mode order $m=6$. In Fig. 5c, the real and imaginary pressure of PSP and microphones are shown along the axial direction. Analyzing the measured pressure amplitude reveals an interference in circumferential and axial direction of different acoustic modes. A sinusoidal interference is visible for PSP and microphone amplitudes in the circumferential direction (see Fig. 5c) with a wavelength of approximately $\Delta \theta =30^\circ$. In axial direction (see Fig. 5d), the pressure amplitude increases. In case this interference is periodical, a full period would not be measured within the investigated axial length of 210 mm since the expected axial wavelength in this condition, calculated with eq. 4, of a circumferential mode order 6 is 0.637 m.

The 95% confidence interval of the PSP measurement is indicated with a gray area. The 95% confidence intervals of both measurement techniques are in good agreement for the real and imaginary pressure. The mean 95% confidence interval along the chosen band of the PSP is ±60 Pa in circumferential direction and ±70 Pa in axial direction.

The resulting spatial pressure distribution of the PSP data at 1800 Hz is shown in Fig. 6a. The measured pressure of the microphones is depicted at their corresponding position by circles with the same colormap as the PSP surface. A maximum pressure amplitude of 2500 Pa is observed, with a phase variation along the circumferential direction. The measured pressure distribution in Fig. 6b is similar to the expected pressure distribution of a mode with circumferential mode order 6. However, it also shows some noticeable differences. The phase fronts, which can be identified by the white lines of 0 Pa, are identified with a reduced axial component compared to the analytic solution. Furthermore, a skew of the phase front is identified in axial direction, which is distinctly visible between $-100$ mm $< x < -60$ mm. Both pressure distributions indicate interference with different acoustic modes, as already pointed out in the discussion of Fig. 5. However, the spatial pressure distribution allows further analysis and interpretation: This interference is visible within the pressure amplitude distribution shown in Fig. 6b. At $x = -100$ mm, the pressure amplitude along the investigated circumferential direction is significantly reduced. This reduced absolute pressure at a specific axial position and the reduced axial propagation is typical for the interference of an upstream and downstream traveling acoustic mode. Furthermore, there is a pattern in circumferential direction with a wavelength of about $\theta = 30^\circ$, which is indicating an interference with an acoustic mode $m=6$ with opposite circumferential rotation. This is further analyzed and discussed in Sect. 5.4.

5.2 Flow and low-frequency acoustic excitation

Fig. 7

Spectrum for PSP (blue) and microphone (orange) measurement at microphone position 4, Setup 2, $m=-6$, $f=1800$ Hz, $\text {Ma}=0.109$

The following results are measured using setup 2. The acoustic mode generator is exciting the same mode as in measurement 1 but with a decreased speaker output and counterclockwise rotation. Furthermore, the mass flow rate is set to ${\dot{m}} = 8.9$ kg/s leading to $Ma =0.109$ within the measurement section of the AWT with $R_0=250$ mm. For measurement 2, the PSP setup has been slightly changed as described in Sect. 3.2. The change of focal length results on the reduction of the area investigated (to $\vert \theta \vert =40^{\circ }$ in circumferential direction), but due to an increased UV-illumination per area to an increased SNR. This is noticed in the frequency spectrum of the PSP and microphone in Fig. 7. The noise floor is below 10 Pa. The spectrum also reveals broadband components, especially for low frequencies, due to the turbulent boundary layer. However, the tonal peak at excitation frequency is still captured well by both measurement techniques. The second harmonic is captured by the microphones but is below the noise floor of the PSP data.

Fig. 8

Comparison of PSP and microphone pressure, Setup 2, $m=-6$, $f=1800$ Hz, $\text {Ma}=0.109$, 95% confidence interval given by error bars for the microphones and gray area for PSP

Fig. 9

Spatial pressure distribution, Setup 2, $m=-6$, $f=1800$ Hz, $\text {Ma}=0.109$

Fig. 10

Spatial pressure distribution for different phase angle $\phi$ for an interval of $-110\,\text {mm}< x < 110\,\text {mm}$ and $-20^\circ< \theta < 20^\circ$ , Setup 2, $m=-6$, $f=1800$ Hz, $\text {Ma}=0.109$

Figure 7 shows the resulting pressure distribution at excitation frequency measured in the circumferential (top) and the axial (bottom) direction. The induced pressure amplitude by the acoustic mode generator at 1800 Hz has been reduced to a maximal amplitude of 150 Pa. Compared to measurement 1 without mass flow, an increased relative variation of pressure amplitude is noticed for repeated microphone measurements in measurement 2 with mass flow. These variations were unexpected before the measurement and might be induced by the PSP segment due to the diameter step or the optical access of camera and LEDs causing disturbances. Consequently, the 95% confidence interval of the microphones increases due to the observed variations between the 18 repeated measurements.

In Fig. 8a, the real and imaginary pressure is varying along the circumferential direction with a wavelength as expected for a $m=-6$ acoustic mode. Due to the reduction of the area investigated in setup 2, a full period of an acoustic mode with $m=6$ in circumferential direction, which is $60^\circ$, is not fully resolved. The pressure distribution in circumferential direction is indicating the $m=6$ mode. Similar to measurement 1, an interference with other acoustic modes at the same frequency causes local variation in pressure amplitude. A variation of pressure amplitude in both directions is detected by the PSP and microphones. In the circumferential direction, the pressure amplitude is rising from 16 Pa at $\theta = -20^\circ$ to 135 Pa at $\theta = 0^\circ$. This also explains the low maximal amplitude of real and imaginary pressure at this position. In the axial direction, the change in pressure amplitude is smaller for the investigated area. The minimal pressure amplitude of 30 Pa is measured at $x=-70$ mm by the microphone. The maximal amplitude of 146 Pa, measured by the microphone is located at $x=70$ mm. The pressure amplitude of PSP for this microphone position is 125 Pa. The deviation of 21 Pa between PSP and microphone is the highest pressure deviation observed in measurement 2. For the PSP measurement 2, the resulting mean 95% confidence interval is ±8.9 Pa in circumferential direction and ±9.2 Pa in axial direction.

In Fig. 9a, the pressure distribution of the PSP measurement 2 at 1800 Hz is shown. Fig. 9a shows the real part of the pressure distribution at $0^\circ$ phase angle for microphone 4. Due to the negative rotation of the excited mode in measurement 2, the wavefront, which can be identified by the white 0 Pa line, is sloped up to positive $\theta$ along the axial direction. The wavefront is skewed and the gradient in $\theta$-direction is reduced along the axial direction. Despite the reduced pressure amplitude and the mass flow, the mode pattern can still be recognized in the measured pressure field. The areas of positive and negative real pressure for the given phase angle are separated by a distinct 0 Pa line. In Fig. 9, the spatial PSP pressure distribution is shown. Similar to measurement 1, the pressure’s amplitude varies in both axial and circumferential directions, as shown in Fig. 6b. The surface investigated shows three areas with significantly decreased pressure amplitude, distinct in circumferential direction with pressure amplitude below 10 Pa. No axial position with significant decreased pressure over the full circumferential direction is observed. This pattern is indicating that modes with positive and negative circumferential order are interfering and compared to measurement 1, the relation between up- and downstream acoustic mode is decreased.

Figure 10 shows the real pressure distribution for different phase angles over one period. The spinning in counterclockwise direction can be observed within each phase angle step. The skewed wavefront due to the interference is noticeable for the different phase angles in PSP and microphone data.

Fig. 11

Comparison of PSP and microphone pressure, Setup 2, $m=-8/8$, $f=2900$ Hz, $\text {Ma}=0.109$, 95% confidence interval given by error bars for the microphones and gray area for PSP

Fig. 12

Spatial pressure distribution, Setup 2, $m=-8/8$, $f=2900$ Hz, $\text {Ma}=0.109$

Fig. 13

Spatial pressure distribution for different phase angle $\phi$ for an interval of $-110\,\text {mm}< x < 110\,\text {mm}$ and $-20^\circ< \theta < 20^\circ$ , Setup 2, $m=-8/8$, $f=2900$ Hz, $\text {Ma}=0.109$

5.3 Flow and high-frequency acoustic excitation

During the test, several measurements of acoustic modes with different circumferential mode order and excitation frequency were performed. Measurements 1 and 2 showed the general applicability of PSP to measure acoustic pressure distribution in turbomachinery with and without flow at 1800 Hz. In this section, higher excitation frequencies up to 5 kHz are analyzed.

For the first test, the acoustic mode generator is set to induce the circumferential mode order 8 at 2900 Hz. The generator is equipped with 16 circumferentially distributed speakers, which limit the distinct excitation to a maximum circumferential mode order of 7. Exciting the circumferential mode order 8 excites the additional spillover mode −8.

The extracted real and imaginary pressure measured by PSP and microphones for an excitation of mode 8 at 2900 Hz is shown in Fig. 11. In the circumferential direction, Fig. 11a, real and imaginary pressures of PSP are in line with the trend of the pressure measured by the microphones and follow the characteristic sinusoidal trend of expected acoustic modes. The mean 95% confidence interval of the PSP at $x=0$ mm in circumferential direction is 14 Pa. The highest deviation between PSP and microphone pressure is observed for the imaginary pressure between the microphone at $x=0$ mm and $\theta = 10^\circ$ and the PSP. This deviation exceeds the limits of the defined 95% confidence intervals of PSP and microphone. In axial direction, Fig. 11b, the pressures are within the 95% confidence intervals. The mean 95% confidence interval is slightly increased compared to the circumferential direction to 14.5 Pa.

The real pressure distribution at a phase angle of $0^\circ$, shown in Fig. 12, reveals several phase variations over the measured area. The wavelength in circumferential direction is reduced compared to measurements 1 and 2, which can be explained by the increased circumferential mode order excited. In axial direction, the wavelength also decreased to 200 mm. The decreased axial wavelength compared to measurements 1 and 2 is in line with the increased excitation frequency. A constant variation of the phase angle for all data points, as shown in Fig. 13, reveals that the mode is propagating in axial direction without significantly spinning in circumferential direction. This implies a similar pressure amplitude of mode −8 and 8. The distribution of the pressure amplitude is shown in Fig. 12b with a significant interference pattern in axial and circumferential directions. For a $\pm \theta =5^\circ$ interval starting at $\theta = 10^\circ$ and $\theta = -12.5^\circ$ and an axial position of $x=-100$ mm, the pressure amplitude is significantly reduced. The destructive interference at specific circumferential positions is in line with a decreased spinning of the modes due to a superposition of positive and negative spinning modes. At an axial position of $x=0$ mm, the pressure amplitude in axial direction is also decreased, which indicates an interference of up- and downstream propagating modes.

Fig. 14

Spatial pressure distribution for different phase angle $\phi$ for an interval of $-110\,\text {mm}< x < 110\,\text {mm}$ and $-20^\circ< \theta < 20^\circ$ , Setup 2, $m=-3$, $f=5000$ Hz, $\text {Ma}=0.109$s

The real pressure distribution for different phase angles of the measurement with an excitation frequency of 5 kHz is shown in Fig. 14. Here, the circumferential mode $m=-3$ is excited by the mode generator. The analyzed frequency is with an excitation frequency of 5 kHz and a camera sampling rate of 10 kHz at the very limit of the Nyquist–Shannon sampling theorem. However, the pressure extracted by the PSP is still similar to the pressures measured by microphones. In circumferential direction, the general trend of pressure amplitude and phase is in line with the microphones for different phase angles. In axial direction, the microphone and PSP pressure are crossing several times the 0 Pa. This is expected for an excitation frequency of 5 kHz and interference of up- and downstream traveling waves. Therefore, the general trend is captured by the PSP measurement, but due to the low sampling per period, the accuracy is decreased.

5.4 Acoustic mode decomposition using PSP data

Fig. 15

Comparison of mode decomposition between PSP data and microphones in upstream traversing unit for mode $\vert m \vert =6$, 95% confidence interval given by error bars

Fig. 16

Pressure comparison of PSP, microphones and reconstruction of identified modes, Condition 1, 95% confidence interval given by error bars for the microphones, gray area for PSP pressure and color area for PSP reconstruction

To further analyze the measured acoustic field, a radial mode analysis, described in Sect. 4.3, is applied to decompose the acoustic field into specific acoustic modes. Initial steps in performing such a decomposition using spatial pressure data from PSP measurements are presented within this section. For the PSP decomposition, the amplitudes and phases of the analytical modes with a circumferential mode order of $\vert m \vert =6$ are fitted to the PSP pressure distribution. For the calculation of the synthetic modes, the measured Mach number and static temperature from the measurement system of the AWT are used. The PSP decomposition is compared with a decomposition performed with two rotatable microphone arrays on segment 3. The setup is described in Sect. 3.2. The microphones are traversed circumferential in $\Delta \theta = 10^{\circ }$ steps.

The calculated amplitudes of the PSP decomposition are shown in Fig. 15a. The acoustic mode [6,0] excited by the acoustic mode generator is identified within the PSP pressure data with an amplitude of ${\hat{p}}^+_{6,0}=969 \pm 22$ Pa at the duct wall. The upstream propagating mode is identified with an amplitude of ${\hat{p}}^-_{6,0}=717 \pm 26$ Pa, which is 74% of the downstream amplitude. The up- and downstream propagating acoustic modes [−6,0] are fitted with an amplitude of ${\hat{p}}^-_{-6,0}=263 \pm 15$ Pa and ${\hat{p}}^-_{-6,0}=166 \pm 6$ Pa, respectively.

The resulting real and imaginary pressure of the fitted and superposed modes is shown in Fig. 16 and compared to the measured data. For the data in axial direction (see Fig. 16b), the fitted pressure is within the 95% confidence interval of the PSP measurement. In circumferential direction (see Fig. 16a), the fitted data is following the measurement, but for some circumferential positions, for example at the peak of the real pressure at $\theta =12.5^\circ$, the fitted pressure exceeds the 95% confidence interval of the PSP pressure. This deviation is assumed to result from different mode orders ($\vert m \vert \ne 6$), which are not yet included in the data fit. The deviation in pressure from the measured distribution by only fitting the acoustic modes with $\vert m \vert = 6$ indicates that other acoustic modes have an influence on the superposed pressure distribution within the PSP segment. Fitting modes with circumferential mode order $\vert m \vert < 6$ decreases the deviation in pressure between measurement and analytic fit for circumferential positions investigated with PSP, but leads to non-physically high pressures beyond the measured area. Since the measured PSP area is limited to $\Delta \theta = 80^\circ$, fitting modes with a circumferential wavelength larger than $80^\circ$ results in such non-physical modes and therefore must be excluded from the fit in this study.

The resulting pressure amplitude of the modes $\vert m \vert =6$ and $n=0$ of the microphone mode decomposition within the upstream traversing unit is shown in Fig. 15a As expected, the excited mode [6,0] traveling downstream has the highest pressure amplitude with ${\hat{p}}^+_{6,0}=808 \pm 1.8$ Pa at the casing of the unit. The mode is reflected and is propagating upstream with a pressure amplitude of ${\hat{p}}^-_{6,0}=477 \pm 1.6$ Pa. Furthermore, the upstream propagating acoustic mode [-6,0] is extracted with a pressure amplitude of ${\hat{p}}^-_{-6,0}=179 \pm 1.2$ Pa. The upstream amplitude of mode [-6,0] is higher compared to the downstream amplitude, with ${\hat{p}}^+_{-6,0}=68.38 \pm 1$ Pa. This indicates, that the mode [-6,0] is not only induced by the sound generator unit positioned upstream of segment 1, but results from reflections/interactions downstream. Modes with a different circumferential mode order and noticeable amplitude are [4,0] and [2,1] with ${\hat{p}}^+_{4,0}=87 \pm 1$ Pa and ${\hat{p}}^+_{2,1}=84 \pm 1$ Pa, respectively. Compared to the decomposition of the PSP data inside the PSP segment, the pressure amplitudes of all modes in the microphone measurement are lower. This is in line with the expectations, since the same modal sound power is inducing lower wall pressures for an increased duct radius as shown in Eq. 6. The factor to scale the wall pressure from the PSP segment to the increased duct radius of segment 3, based on constant sound power, is 0.8 for the mode ${\hat{p}}^+_{6,0}$, leading to ${\hat{p}}^+_{6,0} = 777 \pm 17$ Pa at a radius of 0.25 m. To improve the general comparability between the decomposition of PSP and microphone data in the different segments, the respective sound power of each mode is calculated and shown in Fig. 15b. The sound power is independent to the duct diameter and by assuming neither damping, nor reflection, nor mode scattering between the upstream traversing unit and the PSP segment, the sound power should be equal. The respective sound power calculated with the PSP data and the traversed microphone array is $W^+_{ [6,0], \mathrm{PSP} }=22.2 \pm 1.1$ W and $W^+_{ [6,0], \mathrm{Mic} }=24.1 \pm 0.2$ W. Since the change in diameter between the two segments and the optical access may cause reflections, the final source of the deviation between the two measurements cannot be identified with this setup. However, the RMA of the microphone array confirms the observation made by analyzing the PSP data and the decomposition of the PSP pressure distribution. All indicate interference with up-/downstream propagating mode [6,0] and up-/downstream propagating mode [-6,0] in measurement 1.

6 Conclusions

The unsteady pressure distribution on the inner duct wall within an aeroacoustic wind tunnel, which was specially designed for aeroacoustic turbomachinery investigations, is measured using pressure-sensitive paint. A detailed data analysis process is presented that projects PSP data on the allocated surface. The spatial pressure fluctuations are extracted in the frequency domain via pixel-wise FFT with a high SNR. The acoustic field induced by an acoustic mode generator as measured by PSP has been compared to local microphone pressure measurements. The following conclusions have been drawn from the experimental study:

• 1. The study shows the general applicability of PSP to measure aeroacoustic fluctuations on surfaces similar to those expected in aero engine test rigs. The spatial pressure information visualizes the measured acoustic field and allows an early interpretation of the measured phenomena.

• 2. Two different measurement setups have been tested: the first setup with paint developed by DLr and an investigated area of 0.070 m$^2$ to maximize the measured area, the second setup with commercial paint developed by ISSI and a reduced investigated area of 0.035 m$^2$ to improve the SNR. The PSP results of both setups show good agreement in pressure compared to the microphones on both cases, i.e., with and without the presence of a mean flow. For the measurement with an excitation frequency of 1800 Hz and an axial Mach number of $Ma =0.109$ (setup 2 above), the maximum deviation between PSP and microphone pressure is 21 Pa. The identified 95% confidence interval of the PSP is $\pm 8.5$ Pa in the circumferential and $\pm 11.7$ Pa in the axial direction. Measurements with an excitation frequency of 2900 Hz also agree with the observations of the microphones. The 95% confidence interval is increased to $\pm 27$ Pa in the circumferential direction and $\pm 33$ Pa in the axial direction. The maximum deviation is 30 Pa. The measurement with an excitation frequency of 5 kHz, that is at the limit of the Nyquist–Shannon theorem concerning the chosen camera sampling rate, shows the possibility to measure acoustic pressure fluctuations for such high frequencies. However, due to low sampling, the deviations and uncertainties of the measurement increase.

• 3. Initial steps to perform a radial mode analysis with spatial PSP data show the possibility of using the PSP method for more detailed aeroacoustic analyses. The extracted acoustic modes are in line with the expectations and a mode decomposition using microphones upstream of the PSP confirms the obtained results. However, for a full mode decomposition either the measured PSP area must be increased in circumferential direction or additional reference sampling points measured with microphones over the circumference must be placed and added to the decomposition. A condition number analysis for the decomposition could provide an estimate of the required additional area and sensors.

For the first time, pressure-sensitive paint has been used to measure aeroacoustic phenomena on the inner duct surface for aero engine-like acoustic fields. The results have been analyzed in detail and an initial step has been made to decompose the acoustic field using the spatially measured PSP data. The results show the potential to further use the PSP measurement technique for such aeroacoustic applications. Future PSP measurements will be performed with a central cylindrical body (hub) and blade rows.