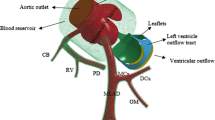
Abstract
The implantation of aortic valve prostheses is often associated with the dilation of the ascending aorta. It is well known that the modification of the fluid dynamics induced by both the prosthetic valve and aortic dilation may, in turn, promote further vessel remodelling. Besides, when the prosthesis is mechanical, a major concern is the blood cell damage and platelet activation which requires a lifelong anticoagulant therapy, which in turn is an additional significant factor of comorbidity. We analysed in vitro the combined effect of the presence of a bileaflet mechanical aortic valve and the dilation of the aortic root in patient specific laboratory models. Three model aortas with increasing degree of dilation, hosted in a mock loop reproducing the heart flow pulsatility, were investigated. The measurement of the time-resolved velocity field allowed the analysis of the general structure of the flow and shear strain-rate distribution. Additionally, the Blood Damage Indexes (BDIs) for both haemolysis and platelet activation were computed along synthetic particle trajectories. Results suggest that a feedback process can be triggered since the aortic dilation tends to decrease the shear stresses at the walls and favour blood stasis: two factors that are known to promote vessel remodelling. Secondly, the analysis of BDIs shows that aortic dilation significantly increases the damage index for haemolysis, whereas a similar effect is not shown when focusing on platelet activation.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Pathologies leading to aortic valve replacement are often associated with the risk of dilation of the ascending aorta. A typical example is the bicuspid aortic valve disease that can cause both aortic valve dysfunctions, such as stenosis or insufficiency, and ascending aorta aneurysm, which in turn may lead to dissection and rarely to rupture. Bicuspid aortic valve disease has a prevalence ranging from 1 to 2%, which makes it the most common congenital cardiac disorder (Borger et al. 2018). As a matter of fact, the consequences of bicuspid aortic valve are thought to emerge both from genetic and hemodynamic causes. The former affects the mechanical properties of the valve and arterial wall, making them particularly sensible to the altered flow patterns induced by the modified valve shape and function. Also, aortic root dilation and a larger-than-average sinotubular junction diameter are common in patients with aortic stenosis (Crawford and Roldan 2001), which is one of the most frequent heart valve diseases, with the second highest prevalence among valvular heart diseases in the general population elder than 55 years (Kanwar et al. 2018). However, the progress of the dilation is not related to the severity of the stenosis, suggesting that dilation is an early adaptive response that, however, does not always proceeds further (Crawford and Roldan 2001).
Though in the last years the use of bioprostheses has been increasingly favoured, mechanical valves are associated with a slightly lower long-term morbidity in patients aged between 50 and 70 years (Roumieh et al. 2015). Thus, mechanical valve is often the preferred option in the case of middle-aged patients (Diaz et al. 2019).
The implantation of a mechanical valve deeply alters the flow in the aortic root and the ascending aorta, with implications on the wall shear stresses (van der Palen et al. 2017; Suwa et al. 2020), possibly affecting the successive remodelling of the vessel (Steinlauf et al. 2021), and with haemolytic effects requiring a lifetime anticoagulation therapy (Vahanian et al. 2021).
From the above considerations, two main questions arise about the flow in a dilated aorta after the implantation of a mechanical valve: (1) how the general structure of the flow changes, because of the possible influences on the evolution of the dilation and the occurrence of further complications, such as dissection or rupture (Cecchi et al. 2011); (2) how the altered haemodynamics affects the haemolytic potential induced by the mechanical prosthesis (Balducci et al. 2004), since haemolysis is directly and indirectly one of the main causes of the long-term morbidity associated with the implant of the mechanical prosthetic heart valves.
Nowadays, due to the huge improvements in the diagnostic imaging technique, information relevant to the above questions can be obtained directly in vivo. Bürk et al. (2012) and Van der Palen et al. (2017) investigated the alteration of the flow in relation to the ascending aortic dilation by 4D Cardiovascular Magnetic Resonance (CMR), in order to better understand the development of the aortopathy. Ramaekers et al. (2021), with the same technique, compared the fluid dynamics of 25 patients with thoracic aortic aneurysm to 22 controls and speculated that wall shear stress modification might be a contributor to vessel remodelling and aneurysm formation. Other studies have been conducted using transoesophageal contrast echocardiography (Son et al. 2016).
However, in vivo investigations do not permit the choice and control of the geometric and functional parameters, nor allow their repeatability. Therefore, in vitro or in-silico approach is becoming more and more useful to the comprehension of the phenomena and to the interpretation of the diagnostic imaging.
In the last decades, computational fluid dynamics has been used to reproduce the phenomena occurring through the aortic valve and in the aorta with increasing accuracy. Some investigators adopted schematic geometries, Reynolds-averaged Navier–Stokes equations, and modelled the valve by prescribing the leaflet kinematics (Yokoyama et al. 2006; Alemu and Bluestein 2007). Tse et al. (2011) studied the flow within vessel geometries extracted from diagnostic imaging, while some other authors used direct numerical simulations resolving the fluid–structure interaction, thus obtaining a realistic picture of the small-scale structures playing a key role in the haemolysis (De Tullio et al. 2009). Other studies focussed on the effects of the implantation of an aortic graft both on the flow pattern and the wall stress (De Tullio et al. 2011).
Parallelly, pulse duplicators and mock aortas have been employed to investigate in the laboratory the aortic flow features in prescribed, repeatable conditions. Numerical and experimental simulations yield complementary information, and laboratory experiments have been often used for comparison with numerical simulations of cardiovascular flows (Domenichini et al. 2007; Vedula et al. 2014; Meschini et al. 2018).
Pulse duplicators initially consisted in hydraulic closed loops devoted to the evaluation the fluid dynamic performances of prosthetic valves (Björk et al. 1962; Brücker 1997). Balducci et al. (2004) investigated the flow past mechanical prosthetic valves in a rigid, geometrically schematic, model of the aortic root, using particle image velocimetry and particle tracking to evaluate the shear stresses on fluid elements. Kadem et al. (2005) focussed on the measure of the effective orifice area. Other investigators reconstructed the three-dimensional velocity field in similar aortic models by tomographic PIV (Hasler et al. 2016). In other models, a functionally realistic mock ventricle drove the flow (Querzoli et al. 2014), while other studies were based on compliant models including the coronary arteries (Querzoli et al. 2016). With the spread of the three-dimensional diagnostic imaging, the mock aortas reproduced also patient-specific geometries (Gülan et al. 2012; Bessa et al. 2021).
With the aim of investigating the effects of aortic dilation in presence of a prosthetic mechanical valve, we run a series of experiments in a pulse duplicator developed at the Fluid Mechanics Laboratory of the University of Cagliari, measuring the time-resolved velocity field in three compliant, anatomically accurate, models of the ascending aorta with increasing degree of dilation. The geometries were derived from diagnostic images. To contribute to answer to the above questions, we analysed the influence of the aortic geometry on the general flow pattern and the magnitude of the shear rate. In addition, we evaluated the Blood Damage Index (BDI) in the formulation proposed by Grigioni et al. (2005) as an indicator of the activation and damage of the blood cells. As will be shown in the following, the BDI estimates the cumulative damage that a blood cell suffers downstream of the prosthetic valve along its pathway through the ascending aorta.
2 Materials and methods
2.1 Model aortas
We compared the fluid dynamics of a normal aorta (hereafter indicated with A0, maximum diameter of 30 mm) with two dilated aortas: the first with a maximum diameter of 48 mm (hereafter indicated with A1), and the second with a maximum diameter of 64 mm (hereafter indicated with A2). The geometry of the aortas was derived from anonymised, contrast-enhanced computed tomography (CT) images of the ascending aorta chosen by the Radiology Dept. of the Brotzu Hospital (Cagliari, Italy). The CT images were segmented to select the internal lumen of the vessel and, after a post-processing procedure, a mould was realized by filament-deposition 3D printing (Fig. 1). Then, the mould was polished and brushed with several thin layers of silicon rubber until a 3-mm-thick layer was reached, so to obtain a transparent and flexible model of the aorta. The simplified geometry of the aortas, with straight axes also in the terminal part of the ascending aorta, does not include the curvature that is present in the real aortas distally to the sinotubular junction (above 2 diameters from the valve, Bessa et al. 2021). Thus, it does not reproduce the effects on the shear stresses and secondary flows (e.g. helical motion). However, this geometric difference develops in the final part of the investigated region, where the shear stresses are lower.
Pulse duplicator.
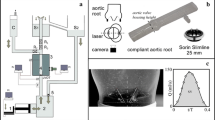
The model was inserted in a pulse duplicator developed following the general design described by Querzoli et al. (2014). The mock loop consists of a ventricular chamber (A) connected to a piston (B) driven by a linear motor which, in turn, is controlled by a personal computer according to an assigned periodic time program educed from echographic data (Cenedese et al. 2005). The resulting non-dimensional flowrates Q/Qmax (where Qmax is the maximum flow rate) measured during the experiments just upstream of the aortic valve are plotted in Fig. 2.
A schematic of the pulse duplicator is shown in Fig. 3a. The inlet of the ventricular chamber is equipped with a check valve, while the outlet is connected to the aortic model (C) through the bileaflet, prosthetic, mechanical valve (Sorin Bicarbon®, 29 mm nominal diameter) (D). The motion of the piston, together with the inlet and outlet valves, generated the pulsatile flow (Fortini et al. 2013). The model aorta was housed in a cuboidal vessel (E), with 10 mm thick Plexiglas walls, filled with water to allow undistorted optical access and compensate the internal aortic pressure during the heart cycle (Fig. 3b).
A longitudinal mid-plane of the aortic model, intersecting the non-coronary sinus of Valsalva, orthogonal to the valve leaflets, and the opposite commissure between the two coronary sinuses, was illuminated by an infrared laser (14 W in power). The light plane was 2 mm thick over the region of interest. Upstream of the aortic valve, an ultrasound flowmeter (Transonic® TS410), measured the instantaneous flowrate. Downstream of the aortic model, two adjustable resistances (R) and a vessel partially filled with air (F) reproduced the impedance of the systemic circulation. The aortic model was connected to a constant-head reservoir (G). Eventually, the circuit was closed through a second reservoir (H) that fed the ventricular chamber (the reader is referred to Susin et al. (2017) for further details).
2.2 Experimental parameters and procedures
The working fluid was water, whose kinematic viscosity is roughly one third of the blood one (depending on the haematocrit). Therefore, functional parameters were adjusted to fulfil the dynamic similarity by matching the Reynolds and Womersley numbers, which are defined as Re = DU/ν, and \(\text{Wo}=D/ \sqrt{\nu T}\), respectively (where D = 31 mm is the aortic anulus diameter, U is the mean velocity through the aortic valve, ν is the kinematic viscosity of the working fluid and T is the period of the cardiac cycle) (Querzoli et al. 2010). We reproduced a typical condition for a person at rest with a beat-rate of 70 beats per minute and a stroke volume SV = 64 ml, resulting in a cardiac output of 4.48 L per minute, Re = 940 and Wo = 17. As the geometric scale is 1:1, the dynamic similarity is guaranteed as far as the stroke volume is maintained constant (SV = 64 ml) and the period of the cardiac cycle is increased by a factor k = νb/νw, where νb and νw are the kinematic viscosity of blood and water, respectively (we assumed k = 3.5, thus the period in the model resulted T = 3.00 s).
Indicating with ρf the density of the working fluid and with ρL the leaflet density, the magnitude of fluid-dynamic forces can be estimated as \({F}_{f}\approx {\rho }_{f}{U}^{2}{D}^{2}\), the fluid inertial forces due to unsteadiness as \({F}_{i}\approx {\rho }_{f}{ D}^{3}U/T\), and the leaflet inertial force as \({F}_{L}\approx {\rho }_{L}{D}^{3}U/T\). Comparing fluid forces and leaflet inertia, we obtain two non-dimensional numbers:
and
which in our experiments are the same as in vivo because: (1) ρf does not change since the density of blood is approximately equal to that of the water, (2) ρL is the same since we use a real prosthesis, and (3) the product UT remains constant because U scales with 1/k, whereas T scales with k. As a consequence, the similarity also includes the motion of the leaflet of the valve, provided that the friction at the hinges is negligible (Querzoli et al. 2010; Vukićević et al. 2012; Verzicco 2022).
For the velocity measurement, the working fluid was seeded with pine-pollen particles, 20μ in diameter, which are neutrally buoyant, and a high-speed camera recorded 585 frames per seconds at a resolution of 1100 × 2240 pixels. Images were saved in real time on an array of solid-state hard disks during 90 successive cycles.
The fluid velocity was computed by the feature tracking velocimetry technique (Badas et al. 2020), which tracks particles features (i.e. particles) between pairs of frames: features are detected, according to the Harris corner detection algorithm, in the first frame and their displacements are computed by comparison with a window in the successive frame by minimizing the window dissimilarity measured by the Lorentzian estimator (Falchi et al. 2006; Besalduch et al. 2013, 2014). Mean velocity field and maximum shear strain-rate, S, have been computed in phase over the 90 cycles on a regular 35 × 108 grid. S is the maximum shear-rate at each given location and instant of the cardiac cycle and is obtained as \(S=\frac{1}{2}\left({s}_{1}-{s}_{2}\right)\), where s1 and s2 are the maximum and minimum eigenvalues of the strain-rate tensor, respectively (Espa et al. 2013; Fortini et al. 2015).
2.3 Blood damage index
As above mentioned, shear-induced haemolysis is a major concern in the evaluation of the consequences of mechanical prosthetic valve implantation, and several studies focussed on its evaluation both using numerical (Morbiducci et al. 2009; de Tullio et al. 2012) and laboratory simulations (Lim et al. 2001; Bellofiore and Quinlan 2011). Even with a small amount of mechanical stress, inflammatory reactions can be triggered in the cells, and it is well known that the effect is cumulative. Hence, both the instantaneous magnitude of the stress and its history are relevant to the haemolysis and platelet lysis and activation (Alemu and Bluestein 2007). We evaluated this effect by means of the semi-empirical model proposed by Grigioni et al. (2005), who introduced a non-dimensional blood damage index (BDI). They considered the relationship between the concentration of haemoglobin, Hb, released by damaged red blood cells and both the shear stress τ acting on blood and the exposure time Δt to τ:
(where a, b and C are empirically determined constants) which approximates results obtained in experiments at constant shear stress (Giersiepen et al. 1990) and extended the formulation to the general case of an erythrocyte experiencing variable shear along its trajectory in the unsteady and non-homogeneous blood flow. They remarked that trivial time integration of the former equation leads to physical incongruences (Grigioni et al. 2004), thus they developed a different formulation under the following requirements: (1) causality: exposing the blood cell to decreasing stresses cannot lead to a decreasing damage; (2) congruence with the steady case: under steady stress the index must be congruent with the above empirical law. The approach is inspired to dosimetry and assumes that the damage is a function of the so-called mechanical-stress dose, \({d}_{s}=\Delta t\bullet {\tau }^\frac{b}{a}\), experienced by a cell during a certain time interval, Δt, along its path (Grigioni et al. 2005). The cumulative effect at the N-th time step, tN, on a particle released at X0 at the beginning of the systole is estimated by the summation:
where, as above stated, a, b and C are empirically determined constants. We used the values a = 0.785, b = 2.416 and C = 3.62·10–5 proposed by Giersiepen et al. (1990) for haemolysis, and the values a = 1.3198, b = 0.6256 and C = 1·10–5 proposed by Nobili et al. (2008) for the estimation of the platelet activation (in both cases the numeric values of the constants hold for shear stresses measured in Pa and time intervals in seconds); \(\tau \left({X}_{0},t\right)=\frac{1}{2}({\sigma }_{1}\left({X}_{0},t\right)-{\sigma }_{2}\left({X}_{0},t\right))\) is the maximum shear stress on the blood cell, while σ1(X0,t) and σ2(X0,t) indicate, respectively, the maximum and minimum principal stress (Haya and Tavoularis 2017) at the location experienced at the time t by the fluid particle, initially released in X0 and ds0 is the initial mechanical dose (we assumed ds0 = 0).
We computed the maximum shear stress \(\tau ({X}_{0},t)\), along the path of 100 synthetic particles released simultaneously at the beginning of each cardiac cycle from an ideal line orthogonal to the aortic axis and located 1 mm downstream of the aortic valve stent. As a result, we generated a set of 9000 trajectories (100 particles per cycle × 90 cycles). Particle trajectories were obtained by integrating the instantaneous velocity field with a predictor–corrector scheme until particles left the investigated region, which extended up to 4 diameters downstream of the valve. The time histories of the maximum shear stress, τ(X0,t), and maximum shear-rate \(S({X}_{0},t)=\frac{1}{2}\left({s}_{1}\left({X}_{0},t\right)-{s}_{2}\left({X}_{0},t\right)\right)\) along the particle trajectories were then computed from the instantaneous gradients of the measured velocity fields (s1(X0,t) and s2(X0,t) are the maximum and minimum eigenvalues of the strain-rate tensor at time t along the trajectory of a particle initially released at X0).
The fact that synthetic trajectories are obtained from two-dimensional measurements is a limitation of the present study and, though the effect is mitigated by the fact that the plane is nearly a plane of symmetry, some underestimation of 2D shear stresses compared to 3D ones can be expected (Halser and Obrist 2018), albeit the structure of their spatial distribution is preserved. Therefore, synthetic trajectories and present results retain most of the significant characteristics of the flow field and the indications given by the blood damage index can be considered as reliable. Based on the same argument, a similar technique was used by Espa et al. (2012) in the left ventricle.
3 Results
3.1 Mean flow
Figures 4 and 5 show the phase-averaged velocity field at two salient points of the cardiac cycle in terms of streamlines and velocity magnitude made non-dimensional by the mean transvalvular velocity U. The confidence interval over the above maps, computed as \({\sigma }_{u}/\sqrt{N}\), does not exceed 10−3U (σu indicates the standard deviation of the velocity magnitudes measured in the N = 90 cycles at a given location and instant of the cycle). The first instant is at t/T = 0.12, just after the systolic peak, when the flowrate is nearly at its maximum and the three transvalvular jets (consequence of the presence of a bileaflet valve) are well developed (Fig. 4). At this stage of the cycle, the two side jets are dominant irrespective of the aortic dilatation degree. However, the aorta A1 shows the smallest intensity of the central jet. It is also worth noticing that in the case A2, due to the large volume of the aortic root, the side transvalvular jets are detached from the aortic walls and counter-rotating vortices develop both in the sinus of Valsalva and on the opposite side, at the commissure. The comparison of the maximum shear-rate distribution in the three aortas (Fig. 6) shows the important role of the valve/aortic diameter ratio, in agreement with what observed by Hasler and Obrist (2018) in schematic aortic geometries of increasing calibre in the presence of a biological prosthesis (confidence intervals \({\sigma }_{S}/\sqrt{N}\) over the maps of Fig. 6 does not exceeds 10−3 T−1). In the smaller aorta, the shear layer generated by the transvalvular jets reaches the vessel wall more proximally and generates high shear at the wall along the whole investigated area. Correspondingly, Fig. 6 shows that the shear-rate at the wall is significantly lower in the case of the dilated aortas (A1 and A2) compared to the reference case A0.
The second instant was chosen at t/T = 0.21, i.e. at the end of the systolic ejection (Fig. 5). At this time, the velocity magnitudes are much lower than before, as expected. The velocity exceeds the colour threshold, 0.5U, only where the jets, no longer fed, are extinguishing. The aorta A1 exhibits a slightly more intense central jet, which is associated with a slower closure of the valve shown also by Fig. 2. In agreement with what observed in vivo by Boussel et al. (2008), a backflow generated by the aortic compliance is apparent distally to the sinotubular junction.
3.2 Blood damage
As above mentioned, the damage of the blood depends on the forces acting on the blood cells during their path through the aortic root and both the instantaneous intensity of the shear-rate and the characteristics of the path contribute. Therefore, the modification of the aortic geometry due to the dilation has a twofold effect: on one hand, changes the instantaneous shear-rate distribution (Fig. 6); on the other hand, it changes the cell paths, which in turn change both the time and intensity of the exposition of the cells to the damaging action.
In order to evaluate this effect, we considered the maximum shear rate, S, that synthetic particles experience during their transit through the proximal aorta as a function of the time elapsed from their release at the beginning of the systole. At each given point of the cycle, we averaged over the whole set of 9000 particles. Figure 7 shows < S > ·T during two cardiac cycles for the three tested aortas (angle brackets indicate the average over the set of particle trajectories). The average, though not representing possible intense events along particular trajectories, gives a concise, general picture. During the first cycle, the values of shear-rate attained in the three tested cases are similar, with a slight predominance of the maximum average shear-rate reached by the most dilated aorta (A2), presumably because of the larger extent of relatively high shear-rate regions present in the aortic root. The situation is completely different during the second cardiac cycle, when the non-dilated aorta (A0) gives markedly higher shear-rate values.
The reason can be found in the characteristics of the flow distally to the sinotubular junction, where most of particles move during the second cardiac cycle after their release. As a matter of fact, in the non-dilated aorta (A0), the distal diameter is smaller and velocity gradients are higher compared to the dilated geometries (A1 and A2). However, in the reference case (i.e. the non-dilated aorta), the washout is more efficient, so that most of particles are quickly transported far downstream away from the zones of high shear-rate, as witnessed by the fact that < S > in the case A0 becomes lower than in the other test cases after 1.3 T.
The significant role of the aortic dilation in the washout of the aortic root is confirmed by Fig. 8, showing the fraction of particles present in the region of interest (the region extending from the valve to 4 diameters downstream) as function of time. In the most dilated aorta (A2), almost 50% of the particles still persists in the region of interest after eight cardiac cycles, whereas in the case A0, a single cycle is enough to reduce the fraction of the remaining particles to 20%. An intermediate behaviour is shown by the case of 48-mm-diameter aorta (A1). Visual inspection of the trajectories shows that the particles that remain for several cycles in the aortic root are trapped in the recirculating vortexes developing in the sinuses of Valsalva (in the aorta A0) or in other regions of stasis close to the vessel walls (in the aortas A1 and A2).
The combined analysis of the plots of Figs. 7 and 8 constitutes the phenomenological basis of interpretation of the behaviour of the Blood Damage Index both for haemolysis and platelet activation.
In Fig. 9, the blood damage index for haemolysis, the Blood Damage Index averaged in phase over the whole set of particles, < BDIe > , is plotted as a function of the non-dimensional time. As expected, irrespective of the aortic geometry, most of the damage is accumulated during the first or two systolic ejections, whereas the contribution of the successive ejections is decreasing. Particles released in the aorta A2 accumulated the largest damage during the first cycle after their release.
However, during the cycles from the second on, the fraction of particles persisting in the investigation region of the aorta A0 accumulates a huge amount of damage because of the higher shear-rates found in the portion of the particle path downstream of the sinotubular junction. Thus, at the end of the considered time, the aorta A0 attains the highest value of BDIe. The interpretation is supported also by the probability density distribution of the BDIe values experienced by the particles (Fig. 10).
In the case of the geometry A0, the probability density has a peak for the lower values of the BDIe, due to the large fraction of particles leaving the aortic root in a short time, before accumulating a significant amount of damage. However, the right tail of the distribution is the higher, corresponding to the small fraction of particles travelling close to the walls, that reach high damage levels and give a decisive contribution to the average BDIe value displayed in Fig. 9.
The scenario is different when focusing on platelet activation (Fig. 11), where the low/intermediate values of shear stresses have the predominant effect. In that case, the higher fraction of particles persisting for long time in the aortic root—exposed to the solicitations of the transvalvular jets and aortic root vortexes—has the predominant effect. Thus, the more dilated is the aorta the higher is the value of < BDIp > . In that case, the probability density function is multimodal irrespective of the geometry (Fig. 12). The multiple peaks are likely associated with the number of cycles of residence in the aortic root. Again, the normal aorta (A0) exhibits the highest probability peak at the smallest value of blood damage index (BDIp = 0.18·10–5), corresponding to the large fraction of particles leaving the aortic root in a single cycle. The second peak (BDIp = 0.47·10–5) is representative of the particles residing in the aortic root for two cycles. However, in this case, the high right-tail of the distribution is completely absent, resulting in a low average blood damage index.
The aorta A1 exhibits three peaks (BDIp equal to 0.16·10–5, 0.42·10–5 and 0.66·10–5) of decreasing probability, corresponding to particles residing in the aortic root for one, two, or three cycles, respectively. The distribution of the aorta A2 has also a similar structure. However, the third peak is broad and shifted towards much higher values (BDIp = 1.6·10–5). It corresponds to the relatively high fraction of particles remaining in the region of interest longer that two cycles, and it is responsible for the large final value of BDIp in the aorta A2.
4 Discussion
Aortic dilatation is often correlated to the implantation of mechanical prosthetic valves, and both vessel geometry and alteration of the flow by the prosthetic valve have significant effects on the evolution of the cardiovascular pathologies (Von Knobelsdorff-Brenkenhoff et al. 2010). In agreement with what observed in vivo by Burk et al. (2012), a compared analysis of the flow patterns in the three investigated aortas shows that the increased size of the aortic root tends to detach the transvalvular jet from the walls (panels A1 and A2 in Fig. 4), thus decreasing the magnitude of the shear stresses and, if the dilation increases enough, allowing the development of large recirculating vortexes (panel A2 in Fig. 4) at the wall, which are regions of potential blood stasis. The above phenomena can be part of a feedback process since modification of wall shear stress and blood stasis are known to potentially promote vascular remodelling (Boussel et al. 2008) and vessel wall weakening (Steinlauf et al. 2021). Additionally, we observe that the aortic root geometry affects the transvalvular flow, remodulating the three jets produced by the bileaflet valve with a decrease in the intensity of the central jet in the case A1.
The alteration in the flow structure in the aortic root also influences haemolysis and platelet activation by changing both the blood element paths and the shear-rate values. As a matter of fact, when focusing on haemolysis, the decrease in the wall shear stress magnitude due to the increased vessel diameter (panel A2 in Fig. 6 and Fig. 7) prevails on the longer time the blood cells remain in the proximal aorta (Fig. 8), thus both dilated aortas, A1 and A2, yield a lower BDIe compared to the reference case, A0, (Fig. 9).
The opposite happens when considering the platelet activation: in that case, the dilation of the aorta further increases the phenomenon of platelet activation, which is yet significantly promoted by the presence of the mechanical valve (Fig. 11).
5 Conclusions
We analysed in vitro the combined effect of the presence of a bileaflet mechanical aortic valve and the dilation of the aortic root in patient specific laboratory models. Present results suggest that a feedback process can be triggered because the aortic dilation tends to decrease the shear stresses at the vessel wall and favour blood stasis: two factors which are known to promote vessel remodelling (Bürk et al. 2012). On the other hand, the analysis of the blood damage index suggests that the aortic dilation is more significant for platelet activation compared to haemolysis.
References
Alemu Y, Bluestein D (2007) Flow-induced platelet activation and damage accumulation in a mechanical heart valve: numerical studies. Artif Organs 31:677–688. https://doi.org/10.1111/j.1525-1594.2007.00446.x
Badas MG, Ferrari S, Garau M et al (2020) On the flow past an array of two-dimensional street canyons between slender buildings. Boundary-Layer Meteorol 174:251–273. https://doi.org/10.1007/s10546-019-00484-x
Balducci A, Grigioni M, Querzoli G et al (2004) Investigation of the flow field downstream of an artificial heart valve by means of PIV and PTV. Exp Fluids 36:204–213. https://doi.org/10.1007/s00348-003-0744-4
Bellofiore A, Quinlan NJ (2011) High-Resolution measurement of the unsteady velocity field to evaluate blood damage induced by a mechanical heart valve. Ann Biomed Eng 39:2417–2429. https://doi.org/10.1007/s10439-011-0329-y
Besalduch LA, Badas MG, Ferrari S, Querzoli G (2013) Experimental Studies for the characterization of the mixing processes in negative buoyant jets. EPJ Web Conf 45:01012. https://doi.org/10.1051/epjconf/20134501012
Besalduch LA, Badas MG, Ferrari S, Querzoli G (2014) On the near field behavior of inclined negatively buoyant jets. EPJ Web Conf 67:02007. https://doi.org/10.1051/epjconf/20146702007
Bessa GM, Fernandes LS, Gomes BAA, Azevedo LFA (2021) Influence of aortic valve tilt angle on flow patterns in the ascending aorta. Exp Fluids 62:113. https://doi.org/10.1007/s00348-021-03199-3
Björk VO, Intonti F, Meissl A (1962) A mechanical pulse duplicator for testing prosthetic mitral and aortic valves. Thorax 17:280–283
Borger MA, Fedak PWM, Stephens EH et al (2018) The American association for thoracic surgery consensus guidelines on bicuspid aortic valve–related aortopathy: full online-only version. J Thorac Cardiovasc Surg 156:e41–e74. https://doi.org/10.1016/j.jtcvs.2018.02.115
Boussel L, Rayz V, McCulloch C et al (2008) Aneurysm growth occurs at region of low wall shear stress. Stroke 39:2997–3002. https://doi.org/10.1161/STROKEAHA.108.521617
Brücker C (1997) Dual-camera DPIV for flow studies past artificial heart valves. Exp Fluids 22:496–506. https://doi.org/10.1007/s003480050077
Bürk J, Blanke P, Stankovic Z et al (2012) Evaluation of 3D blood flow patterns and wall shear stress in the normal and dilated thoracic aorta using flow-sensitive 4D CMR. J Cardiovasc Magn Reson 14:84. https://doi.org/10.1186/1532-429X-14-84
Cecchi E, Giglioli C, Valente S et al (2011) Role of hemodynamic shear stress in cardiovascular disease. Atherosclerosis 214:249–256. https://doi.org/10.1016/j.atherosclerosis.2010.09.008
Cenedese A, Prete ZD, Miozzi M, Querzoli G (2005) A laboratory investigation of the flow in the left ventricle of a human heart with prosthetic, tilting-disk valves. Exp Fluids 39:322–335. https://doi.org/10.1007/s00348-005-1006-4
Crawford MH, Roldan CA (2001) Prevalence of aortic root dilatation and small aortic roots in valvular aortic stenosis. Am J Cardiol 87:1311–1313. https://doi.org/10.1016/S0002-9149(01)01530-2
De Tullio MD, Cristallo A, Balaras E, Verzicco R (2009) Direct numerical simulation of the pulsatile flow through an aortic bileaflet mechanical heart valve. J Fluid Mech 622:259–290. https://doi.org/10.1017/S0022112008005156
De Tullio MD, Pedrizzetti G, Verzicco R (2011) On the effect of aortic root geometry on the coronary entry-flow after a bileaflet mechanical heart valve implant: a numerical study. Acta Mech 216:147–163. https://doi.org/10.1007/s00707-010-0361-2
de Tullio MD, Nam J, Pascazio G et al (2012) Computational prediction of mechanical hemolysis in aortic valved prostheses. Eur J Mech B Fluids 35:47–53. https://doi.org/10.1016/j.euromechflu.2012.01.009
Diaz R, Hernandez-Vaquero D, Alvarez-Cabo R et al (2019) Long-term outcomes of mechanical versus biological aortic valve prosthesis: Systematic review and meta-analysis. J Thorac Cardiovasc Surg 158:706-714.e18. https://doi.org/10.1016/j.jtcvs.2018.10.146
Domenichini F, Querzoli G, Cenedese A, Pedrizzetti G (2007) Combined experimental and numerical analysis of the flow structure into the left ventricle. J Biomech 40:1988–1994. https://doi.org/10.1016/j.jbiomech.2006.09.024
Espa S, Badas MG, Fortini S et al (2012) A Lagrangian investigation of the flow inside the left ventricle. Eur J Mech B Fluids 35:9–19. https://doi.org/10.1016/j.euromechflu.2012.01.015
Espa S, Fortini S, Querzoli G, Cenedese A (2013) Flow field evolution in a laboratory model of the left ventricle. J vis 16:323–330. https://doi.org/10.1007/s12650-013-0179-9
Falchi M, Querzoli G, Romano GP (2006) Robust evaluation of the dissimilarity between interrogation windows in image velocimetry. Exp Fluids 41:279–293. https://doi.org/10.1007/s00348-006-0148-3
Fortini S, Querzoli G, Espa S, Cenedese A (2013) Three-dimensional structure of the flow inside the left ventricle of the human heart. Exp Fluids 54:1–9. https://doi.org/10.1007/s00348-013-1609-0
Fortini S, Espa S, Querzoli G, Cenedese A (2015) Turbulence investigation in a laboratory model of the ascending aorta. J Turbul 16:208–224. https://doi.org/10.1080/14685248.2014.982248
Giersiepen M, Wurzinger LJ, Opitz R, Reul H (1990) Estimation of shear stress-related blood damage in heart valve prostheses - in Vitro comparison of 25 aortic valves. Int J Artif Organs 13:300–306. https://doi.org/10.1177/039139889001300507
Grigioni M, Morbiducci U, D’Avenio G et al (2005) A novel formulation for blood trauma prediction by a modified power-law mathematical model. Biomech Model Mechanobiol 4:249–260. https://doi.org/10.1007/s10237-005-0005-y
Grigioni M, Daniele C, Morbiducci U, D’Avenio G, Di Benedetto G, Barbaro V (2004) The power-law mathematical model for blood damage Prediction: analytical developments and physical inconsistencies. Artif Organs 28(5):467–475. https://doi.org/10.1111/j.1525-1594.2004.00015.x
Gülan U, Lüthi B, Holzner M et al (2012) Experimental study of aortic flow in the ascending aorta via particle tracking velocimetry. Exp Fluids 53:1469–1485. https://doi.org/10.1007/s00348-012-1371-8
Hasler D, Obrist D (2018) Three-dimensional flow structures past a bio-prosthetic valve in an in-vitro model of the aortic root. PLoS ONE 13:e0194384. https://doi.org/10.1371/journal.pone.0194384
Hasler D, Landolt A, Obrist D (2016) Tomographic PIV behind a prosthetic heart valve. Exp Fluids 57:80. https://doi.org/10.1007/s00348-016-2158-0
Haya L, Tavoularis S (2017) Comparison of in vitro flows past a mechanical heart valve in anatomical and axisymmetric aorta models. Exp Fluids 58:73. https://doi.org/10.1007/s00348-017-2361-7
Kadem L, Knapp Y, Pibarot P et al (2005) A new experimental method for the determination of the effective orifice area based on the acoustical source term. Exp Fluids 39:1051. https://doi.org/10.1007/s00348-005-0038-0
Kanwar A, Thaden JJ, Nkomo VT (2018) Management of Patients With Aortic Valve Stenosis. Mayo Clin Proc 93:488–508. https://doi.org/10.1016/j.mayocp.2018.01.020
Lim WL, Chew YT, Chew TC, Low HT (2001) Pulsatile flow studies of a porcine bioprosthetic aortic valve in vitro: PIV measurements and shear-induced blood damage. J Biomech 34:1417–1427. https://doi.org/10.1016/S0021-9290(01)00132-4
Meschini V, de Tullio MD, Querzoli G, Verzicco R (2018) Flow structure in healthy and pathological left ventricles with natural and prosthetic mitral valves. J Fluid Mech 834:271–307. https://doi.org/10.1017/jfm.2017.725
Morbiducci U, Ponzini R, Nobili M et al (2009) Blood damage safety of prosthetic heart valves. Shear-induced platelet activation and local flow dynamics: A fluid–structure interaction approach. J Biomech 42:1952–1960. https://doi.org/10.1016/j.jbiomech.2009.05.014
Nobili M, Sheriff J, Morbiducci U et al (2008) Platelet activation due to hemodynamic shear stresses: damage accumulation model and comparison to in vitro measurements. ASAIO J 54:64–72. https://doi.org/10.1097/MAT.0b013e31815d6898
Querzoli G, Fortini S, Espa S et al (2014) Fluid dynamics of aortic root dilation in Marfan syndrome. J Biomech 47:3120–3128. https://doi.org/10.1016/j.jbiomech.2014.06.025
Querzoli G, Fortini S, Espa S, Melchionna S (2016) A laboratory model of the aortic root flow including the coronary arteries. Exp Fluids 57:134. https://doi.org/10.1007/s00348-016-2221-x
Querzoli G, Fortini S, Cenedese A (2010) Effect of the prosthetic mitral valve on vortex dynamics and turbulence of the left ventricular flow. Physics of Fluids (1994-present) 22:041901. https://doi.org/10.1063/1.3371720
Ramaekers MJFG, Adriaans BP, Juffermans JF et al (2021) Characterization of ascending aortic flow in patients with degenerative aneurysms: A 4D flow magnetic resonance study. Invest Radiol 56:494–500. https://doi.org/10.1097/RLI.0000000000000768
Roumieh M, Ius F, Tudorache I et al (2015) Comparison between biological and mechanical aortic valve prostheses in middle-aged patients matched through propensity score analysis: long-term results. Eur J Cardiothorac Surg 48:129–136. https://doi.org/10.1093/ejcts/ezu392
Son J-W, Hong G-R, Hong W et al (2016) Differences in aortic vortex flow pattern between normal and patients with stroke: qualitative and quantitative assessment using transesophageal contrast echocardiography. Int J Cardiovasc Imaging 32:45–52. https://doi.org/10.1007/s10554-015-0818-4
Steinlauf S, Hazan Shenberger S, Halak M et al (2021) Aortic arch aneurysm repair – Unsteady hemodynamics and perfusion at different heart rates. J Biomech 121:110351. https://doi.org/10.1016/j.jbiomech.2021.110351
Susin FM, Espa S, Toninato R et al (2017) Integrated strategy for in vitro characterization of a bileaflet mechanical aortic valve. Biomed Eng Online 16:29. https://doi.org/10.1186/s12938-017-0314-2
Suwa K, Rahman OA, Bollache E et al (2020) Effect of aortic valve disease on 3D hemodynamics in patients with aortic dilation and trileaflet aortic valve morphology. J Magn Reson Imaging 51:481–491. https://doi.org/10.1002/jmri.26804
Tse KM, Chiu P, Lee HP, Ho P (2011) Investigation of hemodynamics in the development of dissecting aneurysm within patient-specific dissecting aneurismal aortas using computational fluid dynamics (CFD) simulations. J Biomech 44:827–836. https://doi.org/10.1016/j.jbiomech.2010.12.014
Vahanian A, Beyersdorf F, Praz F et al (2021) 2021 ESC/EACTS Guidelines for the management of valvular heart disease: Developed by the Task Force for the management of valvular heart disease of the European Society of Cardiology (ESC) and the European Association for Cardio-Thoracic Surgery (EACTS). European Heart J. https://doi.org/10.1093/eurheartj/ehab395
van der Palen RLF, Barker AJ, Bollache E et al (2017) Altered aortic 3D hemodynamics and geometry in pediatric Marfan syndrome patients. J Cardiovasc Magn Reson 19:30. https://doi.org/10.1186/s12968-017-0345-7
Verzicco R (2022) Electro-fluid-mechanics of the heart. J Fluid Mech. https://doi.org/10.1017/jfm.2022.272
Vedula V, Fortini S, Seo J-H et al (2014) Computational modeling and validation of intraventricular flow in a simple model of the left ventricle. Theor Comput Fluid Dyn 28:589–604. https://doi.org/10.1007/s00162-014-0335-4
Von Knobelsdorff-Brenkenhoff F, Rudolph A, Wassmuth R et al (2010) Aortic dilatation in patients with prosthetic aortic valve: Comparison of MRI and echocardiography. J Heart Valve Dis 19:349–356
Vukićević M, Fortini S, Querzoli G et al (2012) Experimental study of an asymmetric heart valve prototype. Eur J Mech B Fluids 35:54–60. https://doi.org/10.1016/j.euromechflu.2012.01.014
Yokoyama Y, Medart D, Hormes M et al (2006) CFD simulation of a novel bileaflet mechanical heart valve prosthesis - an estimation of the Venturi passage formed by the leaflets. Int J Artif Organs 29:1132–1139. https://doi.org/10.1177/039139880602901206
Acknowledgements
The present paper is partially funded by the Ministero dell'Università e Ricerca (Italy) within the PRIN2017 Project n. 2017A889FP. The authors are grateful to Antonio Mascia for his valuable help in the realization of the experimental set-up and to Elena Sica and Matteo Pibiri for their valuable contribution in all the phases of the experimental work.
Funding
Open access funding provided by Università degli Studi di Cagliari within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Querzoli, G., Badas, M.G., Ferrari, S. et al. Fluid dynamics and blood damage in the dilated ascending aorta after mechanical prosthetic valve implantation: an in vitro study. Exp Fluids 63, 144 (2022). https://doi.org/10.1007/s00348-022-03490-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-022-03490-x