Reconstruction of the deterministic turbulent boundary layer for the study of aerofoil self-noise mechanisms

Abstract

In the experimental aeroacoustics, it is always a challenge to study the far-field radiation and near field hydrodynamics simultaneously, and be able to firmly establish the causality between them. The main objective of this paper is to present an experimental technique that can exploit the deterministic turbulent boundary layer generated under a base flow of either mildly separated or laminar boundary layer to either disrupt an existing acoustic scattering mechanism, or reconstruct a new acoustic scattering scenario to enable the ensemble-averaging and wavelet analysis to study the aerofoil trailing edge noise source mechanisms in the spatial, temporal and frequency domains. One of the main attractions of this technique is that the experimental tool does not need to be extremely high fidelity as a priori in order to fully capture the pseudo time-resolved boundary layer instability or turbulent structures. In one of the case studies presented here, roll-up vortices of the order of $\sim$ kHz can be captured accurately by a 15-Hz PIV. A single hot-wire probe is also demonstrated to be capable of reconstructing the turbulent/coherent structures in a spatio−temporal domain. The proposed experimental technique can be extended to other self-noise scenarios when the aerofoil trailing edge is subjected to different flow control treatments, such as the porous structure, surface texture, or finlet, whose mechanisms are largely not understood very well at present.

Graphical abstract

1 Introduction

Self-noise generated from rotor blades in aircraft engine and high-lift devices in airframes contributes significantly to the overall aviation noise. It is therefore important to identify and understand the noise sources, which are mostly hydrodynamic in origin, in order to be able to reduce them effectively and mitigate their adverse effects. Depending upon the Reynolds number (Re), angle of attack (AoA) and level of inflow turbulence intensity, the self-noise radiated from the trailing edge of lifting surfaces may have highly variable spectral characteristics (Brooks et al. 1989). For example, when the main flow is of low to moderate Reynolds number with minimal turbulence level in the freestream, the unstable laminar boundary layer interacting with the trailing edge would produce the so-called laminar instability tonal noise that typically comprises a broadband spectral ‘hump’ of comparatively narrow frequency bandwidth and/or very narrowband tones of large pressure amplitude (Paterson et al. 1975; Arbey and Bataille 1983; Pröbsting et al. 2014). When the Reynolds number is high, small disturbances to the boundary layer can be amplified and transformed to a bypass transition mechanism. In this scenario, a fully developed turbulent boundary layer is likely to be present at the trailing edge, where broadband noise can be scattered into the far-field (Roger and Moreau 2004). In summary, aerofoil self-noise and its spectral characteristics are largely governed by the state of the boundary layer at the trailing edge.

Many studies on the physical mechanisms of the laminar instability tonal noise and turbulent broadband noise rely on the statistical analysis of the boundary layer, such as the mean, standard deviation, power spectral density and so on. Experimental methods involving cross-correlation study in the time domain between the near field unsteady pressures or velocities and far-field acoustic pressure have sometimes been used to study the tonal noise mechanism, which is underpinned predominantly by the two-dimensional Tollmien–Schlichting disturbances. In the case of a fully developed boundary layer where the turbulent fluctuations are homogeneous, coherence study in the frequency domain could be conducted to measure the spectral “likeness” between the near field hydrodynamic fluctuations and far-field acoustic pressure fluctuations. Some of the advanced studies also aspire to capture the time-resolved two-dimensional instabilities, or three-dimensional coherent structures in a volumetrical space to uncover the noise mechanisms. To achieve these, expensive techniques/tools such as the time-resolved planar/tomographic particle image velocimetry (PIV) (Pröbsting et al. 2014; Avallone et al. 2016) or direct numerical simulation (DNS) (Jones and Sandberg 2012; Sandberg and Sandham 2008) may have to be adopted.

Table 1 Description of the test cases performed in this study

This paper presents a novel and low-cost experimental technique to enable the studies of the aerofoil self-noise mechanisms in the spatial and temporal domains, including the spectral characteristics as a function of time. The essence is to generate a “deterministic turbulent boundary layer” convecting over the trailing edge regions, which allows the ensemble-averaging analysis (in space and time domains) and the wavelet analysis (in frequency and time domains) to reconstruct the acoustic scattering scenario. To demonstrate the robustness and potential of this technique, two aerofoil self-noise scenarios as summarised in Table 1 will be examined: (1) Use the deterministic turbulent boundary layer to momentarily “destroy” an aeroacoustics feedback loop pertaining to a laminar aerofoil, and then allow the “re-generation” process to take place in order to enable a tracking in space and time for the entire evolution process of the laminar instability tonal noise and flow field. (2) Use the deterministic turbulent boundary layer to reconstruct the spatio and temporal evolutions of turbulent structures when convecting over a serrated trailing edge of an aerofoil. Section 2 provides some backgrounds of the “turbulent spot”, which is the basic element for a deterministic turbulent boundary layer. Section 3 contains a detailed description of the experimental methods developed in this study. More specifically, the generation of the deterministic turbulent boundary layer is discussed comprehensively in Sect. 3.2. The experimental techniques and the wavelent analysis technique are included in Sect. 3.3. General characteristics of the generated deterministic turbulent boundary layer is discussed in Sect. 4. The results pertaining to the two case studies in Table 1 are discussed in Sects. 5.1 and 5.2. Finally, the paper concludes in Sect. 6.

Fig. 1

The averaged shape of a turbulent spot in a plan view (Schubauer and Klebanoff 1956), and b elevation view (Gad-El-Hak et al. 1981). c 3D rendering illustrating the evolution of a half-turbulent spot (Chong and Zhong 2005). z and y represent the spanwise and wall-normal directions, respectively, where $z=0$ refers to the plane of symmetry of the spot. The main flow direction is from left to right for a and b, and from northeast to southwest for c

2 Fully-developed turbulent wedge by streamwise coalescence of turbulent spots

The essence of the technique developed here is to replicate the process of natural formation of ‘packets’ of turbulence, known as the turbulent spots seen in the later stage of boundary layer transition. It is normally observed that at this stage, individual turbulent spots begin to appear randomly (in both space and time) and intermittently.

2.1 Fundamental structures of single turbulent spot

After the turbulent spot was discovered by Emmons (1951), Schubauer and Klebanoff (1956) carried out a more systematic investigation on the general shape, propagation rates and spreading angles of spots that were artificially triggered in an otherwise laminar boundary layer on a flat plate. Figure 1a illustrates a turbulent spot’s shape in plan view, which has a distinct arrowhead shape. At zero pressure gradient the leading edge of the spot is found to propagate at a rate of 88% to that of the freestream velocity, whereas the trailing edge only propagates at about 50% of the freestream velocity. Because of the difference in propagation rates between the leading and trailing edges, the spot grows in the streamwise direction as it propagates downstream. On the other hand, the spot was also found to grow in the spanwise direction. Schubauer and Klebanoff (1956) found the spreading angle of the spot to be approximately $10^\circ$ half-angle, as depicted by $\alpha$ in the figure.

When viewed in elevation view of a turbulent spot at the plane of symmetry, such as the one shown in Fig. 1b, Gad-El-Hak et al. (1981) propose five distinct regions:

• 1. Region I represents the head of the spot and it exhibits a substantial ‘overhang’ over Region II. The foremost edge of the overhang is always situated at approximately one laminar boundary layer thickness above the plate (Wygnanski et al. 1976). This overhang will also grow longitudinally with streamwise distance.

• 2. Although the flow in Region II is still laminar, it is very unstable and is ready to breakdown. Examination by Gad-El-Hak et al. (1981) reveals that new turbulence is always added in Region II, which accounts for the streamwise growth of the spot.

• 3. Region III is regarded as the centre of a turbulent spot, and is dynamically very similar to the classical turbulent boundary layer on a flat plate. Indeed, most studies confirmed the similarity of wall-normal growth rates between turbulent spot (in Region III) and turbulent boundary layer (Head and Bandyopadhyay 1981).

• 4. The most downstream part of a turbulent spot in Region IV is also where the maximum shear stress is located. Turbulent activity in this region is mainly the interaction with the laminar boundary layer and the potential flows.

• 5. Finally, there is a highly stable, ‘becalmed’ region in Region V where boundary layer passes over Region V will not undergo any transition to turbulence. Wygnanski et al. (1976) found that velocity profiles in Region V are much fuller, i.e. more stable than the laminar profile upstream of the turbulent spot. The boundary layer in Region V is also thinner than the local Blasius profile.

2.2 Streamwise coalescence of turbulent spots to become a turbulent wedge

After their initial appearance, turbulent spots will undergo a growth in the wall-normal, spanwise and streamwise directions as they propagate downstream. This is shown in Fig. 1c following the works from Chong and Zhong (2005). The figure demonstrates some isosurface contours of the ensemble-averaged turbulent velocity for a visualisation of the spatial-temporal growths of a turbulent spot. The isosurfaces are constructed by an application of criterion of $\widehat{u^{\prime }}=0.04$, where $\widehat{u^{\prime }}$ is the ensemble-averaged root-mean-square velocity fluctuations to be defined in Sect. 4. This criterion has successfully been adopted to identify the boundary of turbulent spots in the past (Coles and Barker 1975; Katz et al. 1990). The streamwise growth is mainly governed by the difference in the propagation rates at the leading and trailing edges of the turbulent spot (to be demonstrated in Sect. 4), causing the spot to stretch as it propagates downstream (Schubauer and Klebanoff 1956). Growth in the wall-normal direction occurs when the smaller scale turbulent eddies within the turbulent spot entrain the high momentum irrotational fluid from the freestream into the turbulent spot (Corrsin and Kistler 1954). The lateral, or spanwise, growth is due to the destabilisation of the fluid surrounding the spot. Essentially, the turbulent eddies within the spot induce perturbations into the surrounding unstable laminar boundary layer, which then grow rapidly and eventually break down, inducing new turbulence (Gad-El-Hak et al. 1981). From this mechanism, turbulent spots are characterised by the spreading half-angle of $9^{\circ }{-}10^{\circ }$ under the condition of zero streamwise pressure gradient. The half-angle will normally increase or decrease under the adverse or favourable pressure gradients, respectively (Gostelow et al. 1996). Due to these growths, the individual turbulent spots, sometimes referred to as the ‘building blocks’ of the turbulent boundary layer, begin to interact with each other at a sufficient distance downstream. The extent of transitional boundary layer can be described by the turbulence intermittency factor $\gamma$, or the fraction of time for which the boundary layer is turbulent (Mayle 1999), which covers the range of $0<\gamma <1$. Through the process of interaction, individual spots exchange momentum and eventually coalesce completely into a fully turbulent boundary layer, reaching the intermittency factor of $\gamma =1$.

Fig. 2

a Near wall velocity fluctuations measured by a surface-mounted hot film sensor when $f_{\mathrm {trig}}=13$ HZ and 120 Hz, b power spectral density of the velocity fluctuation when $f_{\mathrm {trig}}=120$ Hz, c surface heat transfer h contour when $f_{\mathrm {trig}}=120$ Hz

In Chong and Zhong (2013), turbulent spots are artificially created in a flat plate boundary layer by an open-circuit wind tunnel with a closed test section of 200 $\times$ 460 mm cross-sectional area at freestream velocity of 28 ms$^{-1}$. The flow condition created a Blasius type boundary layer that dominates most of the plate surface of dimension of 200 $\times$ 750 mm. In order to trigger the turbulent spots, a loudspeaker was attached to the back of the flat plate underneath a 0.5 mm pinhole, which is located at 188 mm downstream of the leading edge. A surface-mounted hot film sensor placed at 160 mm downstream of the loudspeaker and temperature-sensitive liquid crystal coated on the entire flat plate surface are both employed to study the footprint of the turbulent spots. Figure 2a shows the near wall velocity fluctuations as a function of time measured by the surface-mounted hot film sensor when the spots are generated at $f_{\mathrm {trig}} = 13$ and 120 Hz, respectively. Note that $f_{\mathrm {trig}}$ is the spot triggering frequency for the square wave input to the loudspeaker. When $f_{\mathrm {trig}} = 13$ Hz, the velocity fluctuations exhibit a periodic responses of laminar and turbulent flow. This is a clear indication that the generated turbulent spots, though deterministic, are still isolated and not yet fully merged.

When $f_{\mathrm {trig}} = 120$ Hz, the large fluctuations combined with the stationary nature of the velocity fluctuations give a qualitative impression that a fully developed turbulent boundary layer, or turbulent wedge, has been produced. Indeed, when performing a Fourier transform of the velocity fluctuations, the resulting power spectral density in Fig. 2b demonstrates a decay rate of $\sim f^{-5/3}$ at the mid frequency range. Figure 2c shows the heat transfer h contour of the turbulent wedge as a result of the spot merging when $f_{\mathrm {trig}} = 120$ Hz. The heat transfer coefficient, h, determined from the liquid crystal is approximately 76 W/m$^{2}$ K at the fully turbulent region near the centre line. The theoretical (Kays and Crawford 1980) value of h for a fully developed turbulent boundary layer with an unheated flat plate leading edge is calculated as 82 W/m$^{2}$ K at the same location. This indicates that the artificially generated turbulent spots, which bear the same spectral and turbulence characteristics as a turbulent boundary layer, can be further exploited for the study of the self-noise mechanism. Despite successfully reconstructed the turbulent sources in the spatial domain, the generated turbulent wedge is unable to reconstruct the time-resolved growth of the turbulence. A different methodology to generate a deterministic turbulent boundary layer suitable for the current purpose has to be devised, which will be discussed in Sect. 3.2.

3 Experimental methodology

Information about the research facility is provided in Sect. 3.1. Methods for the generation of the deterministic turbulent boundary layers will be discussed in Sect. 3.2. Other topics that will be covered in Sect. 3.3 include the experimental measurement techniques, such as the far-field noise measurements, hot-wire anemometry and particle image velocimetry, as well as the wavelet analysis technique.

After the successful reconstruction of the deterministic turbulent boundary layers on the aerofoil surfaces, they will then be utilised in two very different case studies involving different aerofoil self-noise mechanisms. Comparison of the objectives, flow and geometrical conditions between the two cases can be found in Table 1.

3.1 Research facility

The experimental results presented in this paper are acquired in an aeroacoustics research facility at Brunel University London. The facility consists of an open-jet wind tunnel placed inside an anechoic chamber. It is specially designed for the study of aerodynamic noise produced by aerofoils placed in low-to-moderate speed flows. A detailed description of its design and performance is provided in Vathylakis et al. (2014).

The operational limit of the wind tunnel is 80 ms$^{-1}$, although most operations take place at flow velocities ranging between 10 and 60 ms$^{-1}$. These velocities are achieved by passing the flow through a nozzle with a contraction ratio of 25:1. The low turbulence flow exiting the nozzle contains a turbulence intensity of $0.1-0.2\%$ inside the potential core of the jet across majority of the speeds. A low level of freestream turbulence intensity is particularly favourable for the experimental methods developed in this study, which requires the absence of bypass transition as a prerequisite.

Fig. 3

Photographs of the aeroacoustics wind tunnel facility: a outside of the anechoic chamber, b inside the anechoic chamber with a PIV system: 1. Optical imaging system, 2. Wind tunnel nozzle exit, 3. NACA 0012 aerofoil, 4. Traverse mechanism, 5. Laser optics, 6. Litron Lasers Nano T 135-15 PIV Nd:YAG laser, 7. Laser power supply unit

The configuration of the aeroacoustics facility is illustrated in Fig. 3. The open jet wind tunnel consists a rectangular nozzle of 0.1 m (height) and 0.3 m (width). The airflow is produced by a 30 kW AC-driven centrifugal fan, before passing through a 10 m long silencer to attenuate the extraneous noise within the ducts. From there, the airflow travels towards a set of flow conditioning devices (honeycomb and woven wire mesh screens) for straightening and turbulence dissipation, after which it is accelerated by the nozzle and eventually discharged into an anechoic chamber with dimensions of 4 m (width) by 5 m (length) by 3.4 m (height).

The exit airflow velocity is measured by a Furness Controls FCO510 micromanometer to determine the gauge pressure between the nozzle inlet static pressure and the atmospheric pressure. The velocity of the exit airflow is controlled by digitally adjusting the centrifugal fan’s rotations per minute (RPM), which can achieve a velocity resolution of about 0.1 ms$^{-1}$ for steady operation. The exit jet from the open nozzle is discharged directly to outside of the anechoic chamber through a lined ventilation duct opposite to the nozzle (Vathylakis et al. 2014). This facilitates a fast establishment of the steady global flow field inside the anechoic chamber to ensure the boundary layer growth on the aerofoil surface, hence the spectral characteristics of the far-field noise, to remain consistent and constant over time.

Fig. 4

Internal features of the NACA 0008 aerofoil: a main body, b close-up view of the speaker housing and the miniature loudspeakers, c cross-sectional view of an individual miniature loudspeaker. Note that the exploded view only shows the spanwise array of the miniature loudspeakers at the aerofoil’s bottom surface. This aerofoil model is used in the Case 2 (Sect. 5.2)

3.2 Generation of the deterministic turbulent boundary layers by spanwise coalescence of turbulent spots

The key to achieve a “deterministic” turbulent boundary layer would depend on the ability to generate the turbulent spots artificially in a correct manner, and be able to control the growth of them. Section 2 describes the formation of turbulent wedges by streamwise coalescence of turbulent spots. However, it is still equivalent to a conventional boundary layer tripping method, i.e. either by an isolated disturbance, or a zigzag turbulator. It is difficult for a streamwise coalescence mode to enable the reconstruction of the temporal development of turbulence structures, which is the aim of this study. Rather, it has to be achieved by the spanwise coalescence mode. In this section, the deterministic turbulent boundary layer can be formed by simultaneously inducing several closely positioned individual turbulent spots in a spanwise array, each of which is generated by introducing a low-magnitude, localised disturbance into an otherwise undisturbed (ideally laminar) boundary layer that develops over the aerofoil surface. One example of the disturbance source is the air jet generated by the displacement of the diaphragm of miniature loudspeakers, which in turn forces the air through an orifice oriented perpendicularly to the aerofoil surface. Figure 4 depicts a NACA 0008 aerofoil instrumented by such configuration, which is adopted in the Case 2. Provided that the magnitude of the air jet is sufficiently large and additional momentum is transferred into the boundary layer, turbulent spots can be induced. This particular turbulent spot generation method has been employed previously by many researchers (Gostelow et al. 1996; Glezer et al. 1989; Wygnanski et al. 1976; Chong and Zhong 2006).

The air jets that provide the initial disturbances for the generation of turbulent spots are simultaneously discharged in sync from the spanwise arrays of twenty-five 0.5 mm diameter orifices with $\Delta s^{\prime } = 11$ mm, all of which are located at 24% of the aerofoil chord from the leading edge. Note that $\Delta s^{\prime }$ is the spanwise separation distance between the successive orifices (see Fig. 4b), where the lower limit of which is obviously dictated by the size of the loudspeaker choice. The aerofoil chord, C, is 0.15 m under a sharp trailing edge (baseline) configuration. The system described above will generate an array of individual turbulent spots that gradually grow in the streamwise, spanwise and wall-normal directions as they propagate downstream. At some downstream distances, the individual turbulent spots will begin to mutually interact and eventually coalesce to form a uniform array of deterministic turbulent flow. Note that the spanwise array of loudspeakers are present on both the aerofoil’s upper and lower sides where they are both triggered simultaneously during the experiments.

It is important to recognise that the streamwise location of the spanwise array has to satisfy two conflicting requirements. On one hand, perturbations to the otherwise laminar boundary layer need to be sufficiently downstream to ensure that they can trigger the bypass transition. On the other hand, to ensure a full coalescence of the triggered turbulent spots at the trailing edge, it is preferred to place the spanwise array sufficiently upstream. The following describes the procedures of determining the optimal streamwise location for the spanwise array.

• 1. Determine the streamwise location where the maximum thickness of the aerofoil occurs. For the aerofoil used here, it is at 30% chord. This location can be regarded as the first iteration point that still satisfies the first requirement as described above.

• 2. Next, estimation of the turbulent spot spanwise growth, such as the half spreading angle $\alpha$, can be attempted. Readers can refer to Gostelow et al. (1996) for a summary of the responses in $\alpha$ subjected to different levels of favourable and adverse pressure gradients. For simplicity, $\alpha =10^\circ$ can be assumed despite the fact that the actual value might be slightly higher due to the presence of low level of adverse pressure gradient across the aft part of the NACA 0008. Note that the footprint of a turbulent spot convecting downstream will resemble an isosceles triangular shape (see Fig. 2c).

• 3. To satisfy the second requirement as described previously, the spanwise array is preferably situated at a streamwise location either close to or less than 30% of the chord from the leading edge. Since $\Delta s^{\prime } = 11$ mm, the half width of the base edge pertaining to the isosceles triangular that resembles the turbulent spot’s footprint at the aerofoil trailing edge should be at least $2\times \Delta s^{\prime }$, i.e. $\approx 22$ mm, to ensure a full merging of the turbulent spots across the span. A simple trigonometry calculation confirms that placing the spanwise array at 24$\%$ of the aerofoil chord from the leading edge represents an acceptable compromise that satisfy both requirements.

The miniature loudspeakers used to produce the air jets are driven by a remotely placed signal amplifier that is externally triggered by a Teledyne Lecroy WaveStation 2012 waveform generator producing a $f_{\mathrm {trig}} = 12$ Hz square pulse waveform signal. The pulse duration is set to 1.7 milliseconds (ms). The responses of the miniature loudspeakers to the impulse input, and the ensuing air jet discharging from the orifices, could exhibit a decaying impulse nature. However, this has no bearing to the current study that focuses on generating a deterministic turbulent boundary layer near the trailing edge region. Nevertheless, the rising edge of the square pulse can still be used as a reference for the ensemble phase-averaging of the flow and acoustic measurement data. More discussion about this will be provided in Sect. 4.

Fig. 5

a NACA 0012 aerofoil and its main features: 1—air supply (lower aerofoil half); 2—air supply (upper aerofoil half); 3—system of bifurcated internal channels; 4—0.5 mm diameter orifice; $\Delta s^{\prime }$—spacing between individual orifices, b main components of the system: 1—external supply of pressurised air; 2—mechanical pressure regulator; 3—solenoid valves; 4—external power supply; 5—specially designed solenoid valve control system; 6—aerofoil and its associated components; blue—pneumatic line, red—electrical line. This aerofoil model is used in the Case 1 (Sect. 5.1)

The repetitive pulsation of the diaphragms undergoing the operation described above means that the lifespan of the miniature loudspeakers could be short, thus needing replacement from time to time. Another triggering method that has a different principle is also developed here. This method has a low maintenance requirement, and is also capable of producing very consistent turbulent spots. The particular system is adopted in Case 1, which is shown in Fig. 5. It consists of several components: (1) external supply of pressurised air; (2) mechanical pressure regulator; (3) solenoid valves; (4) external power supply; (5) specially designed solenoid valve control system; (6) aerofoil and its associated components. The aerofoil is a NACA 0012 type and is fabricated by a 3D Systems Viper Si2 SLA type 3D printer that enables a much greater design flexibility and incorporation of intricate design features into the aerofoil with relative ease. The most notable feature of the aerofoil is a system of internal channels (having a diameter $d_i$ of 1.4 mm) embedded within the aerofoil body. Figure 5 demonstrates the design of such channel system, where a bifurcation of a single channel results in a spanwise distribution of thirty-two orifices. The opening diameter of these orifices is $d_o = 0.5$ mm, and positioned at 0.27C from the leading edge of the aerofoil. Note that the aerofoil chord C is also 0.15 m. The spanwise spacing between successive orifice is set at $\Delta s^{\prime } = 8.5$ mm ($\Delta s^{\prime }/C = 0.057$). Similar to the loudspeaker configuration described earlier, the spanwise arrays of orifices driven by the solenoid valve system are also installed on both sides of the aerofoil. It is important to ensure that no internal flow blockage occurs due to the possibility of imperfection in the SLA printing. To investigate this, the printed aerofoil can be placed in a water bath, where each internal flow passage is connected to a high-pressure compressed air. This allows a visual examination of small air bubble emerging from each orifices.

The external air supply is initially pressurised at $p_{\mathrm {as}}=10$ bar, hence a mechanical pressure regulator is used to reduce the pressure to $p_{{\mathrm {as}},1} = 0.3$ bar. The supplied air is then fed to two SMC VQ-20 one-way solenoid valves that are connected to a remotely placed DC-power supply operated at a voltage of $E_{\mathrm {ps}}=120$ V (due to the low power of the solenoid valves, the current is typically in the range of $I_{\mathrm {ps}}=0.06$ A). The power supply is coupled with a control system that consists a Teledyne Lecroy WaveStation 2012 waveform generator and a specially designed electronic circuit that enables an accurate and individualised delivery of electric power to each solenoid valves. These valves can therefore be opened at a desired repetition rate $f_{\mathrm {trig}}$ and for a required duration $t_{\mathrm {trig}}$. As the valves are opened for a controlled duration, the air at a regulated pressure is allowed to flow freely through the valves and into two supply tubes until it is split into four separate branches that are assigned to either the top or the bottom half of the aerofoil. It is designed such that the upper and lower aerofoil halves can be operated independently. The airflow from each branch is fed into the connecting ports of the aerofoil from which it can be distributed across the system of internal channels. These channels then lead to a spanwise distribution of thirty-two orifices on the aerofoil surface. Finally, the pressurised air discharged from the orifices will generate an air jet at each orifice exit. It should also be noted that a time delay $\Delta t_d$ between the instance the pressurised air is initially released from the supply and the instance when it enters the boundary layer through the orifice is accounted for in the data-processing routines. Therefore all the results presented in Sect. 5.1 already contain this correction.

Once the air jet is discharged from the orifice, it generates a disturbance within the otherwise undisturbed boundary layer, hence inducing an array of turbulent spots. The spots will eventually coalesce fully to produce a deterministic turbulent boundary layer following the same principle described earlier in this section. The quality of the deterministic turbulent boundary layer has been evaluated by assessing the uniformity of its spanwise distribution, i.e. ideally, the deterministic turbulent boundary layer should maintain identical properties along its entire spanwise extent. This is indeed confirmed in Fig. 12a–c of Juknevicius and Chong (2019). An important aerofoil design consideration is emphasised here. Generally, a smaller spacing between orifices $\Delta s^{\prime }$ is desirable, since it will entail a denser distribution of the turbulent spots. Essentially, a denser spanwise distribution of the spots will cause an earlier onset of the process by which turbulent spots undergo a full merging in the spanwise direction. As a result, the required longitudinal distance for the formation of the deterministic turbulent boundary layer is reduced. In the opposite scenario where the distribution of orifices is too coarse (i.e. $\Delta s^{\prime }$ is too large), the turbulent spots might not be able to undergo a full merging process before reaching the trailing edge, hence a uniform deterministic turbulent boundary layer cannot be produced. Note that this design consideration has been taken into account for both the NACA 0008 and NACA 0012 aerofoils used in Case 1 and Case 2, respectively.

In order to generate turbulent spots comparable to those seen in other studies (Chong and Zhong 2005; Schubauer and Klebanoff 1956; Corrsin and Kistler 1954; Gad-El-Hak et al. 1981; Gostelow et al. 1996; Glezer et al. 1989; Wygnanski et al. 1976), the air jet discharged from the orifices on the wall surfaces has to be carefully controlled by adjusting two main parameters: the jet magnitude and the jet duration $t_{\mathrm {trig}}$. While the jet magnitude is controlled by adjusting the pressure of the supplied air $p_{{\mathrm {as}},1}$, the jet duration, $t_{\mathrm {trig}}$, is controlled by varying the width of the square pulse waveform signal (produced by the waveform generator) that is used to trigger the opening of the solenoid valves. For the experiments where the NACA 0012 aerofoil is used, the jet (and hence the deterministic turbulent boundary layer) is produced at a repetition rate of $f_{\mathrm {trig}} = 7.5$ Hz. Providing that this technique is used in tandem with a PIV system, the rising edge of the square pulse is also used as a phase reference for the phase-averaged PIV flow measurements. More detailed explanation of the phase-averaged PIV measurement technique employed in this study is provided in Sect. 3.3.2.

3.3 Measurement techniques

This section provides detailed description of the experimental measurement techniques that are employed in this research, which can be broadly categorised as the far-field noise measurement, particle image velocimetry and hot-wire anemometry. The followings cover the hardware, data acquisition parameters and their settings, and some data processing methods.

3.3.1 Acoustic measurements in case 1 and case 2

The acoustic measurements are recorded from the $\frac{1}{2}$-inch G.R.A.S. 46AE pre-polarised free-field condenser microphones that have a typical sensitivity of 41.45 mV/Pa ($\pm\,\, 0.08$ dB) and a dynamic range of 17 dB(A) to 138 dB (ref. $20\ \upmu$Pa). A typical spectrum of the G.R.A.S. 46AE microphone frequency response is flat within ± 1 dB between 5 Hz and 10 kHz, which will be suitable for acoustic measurements in the anechoic chamber environment. The microphone signal is amplified by the G.R.A.S. 12AX power modules. A G.R.A.S. 42AB pistonphone is used to calibrate the microphones.

Inside the anechoic chamber, eight G.R.A.S. 46AE microphones are permanently positioned in a polar arc arrangement, which covers polar angles $\theta$ between $50^\circ$ and $120^\circ$, with an interval of every $10^\circ$. Each microphone is positioned at a distance of approximately 1 m from the mid-span of the aerofoil trailing edge. For the study of Case 1, only the microphone at $\theta =90^\circ$ is used for the measurement of the Sound Pressure Level. For the Case 2, the polar array is not used. Instead, two G.R.A.S. 46AE microphones are placed at polar angles of $\theta =\pm 90^\circ$, but with a smaller separation distance of 0.315 m above and below the mid-span of the aerofoil trailing edge, respectively.

The acoustic measurement data are collected using a National Instruments LabView DAQ interface and a National Instruments 16-bit data acquisition system with a built-in anti-aliasing filter. The entirety of the noise data collected throughout this project is acquired at a sampling frequency, $f_s = 40$ kHz. When acquiring the “stationary” acoustic data, i.e. in the absence of the deterministic turbulent boundary layer, the sampling duration is set at 20 s for both Case 1 and Case 2. The data are then fast Fourier transform to obtain the power spectral density. On the other hand, the perturbation of the deterministic turbulent boundary layer on the aerofoil trailing edge will result in a non-stationary acoustic radiation in the temporal domain. Therefore, wavelet analysis is used to investigate the temporal variations of the energy content and frequency spectrum of the far-field acoustic pressure fluctuations caused by the passage of the deterministic turbulent boundary layer over an aerofoil trailing edge. The acoustic signal is acquired at the sampling duration of $t_s=40$ and 26 s for Case 1 and Case 2, respectively. The strategy to use different sampling duration $t_s$ is to ensure that both cases generate roughly the same deterministic events. Due to the different repetition rates $f_{\mathrm {trig}}$ adopted ($f_{\mathrm {trig}} = 7.5$ Hz for Case 1, and $f_{\mathrm {trig}} =12$ Hz for Case 2), sampling duration of 40 s for Case 1 and 26 s for Case 2 will produce 300 and 312 deterministic events, respectively. The analysis of the non-stationary acoustic data will use the continuous wavelet transform (CWT) method, where a basic working principle of which will be described in Sect. 3.3.4.

Fig. 6

Schematic illustrations of a plan view, b side view, for the PIV experimental set-up used in Case 1 (Sect. 5.1)

3.3.2 PIV measurements in case 1

Figure 6 illustrates the experimental set-up for the Case 1. The coordinate system of x, y and z shown in the figure represents the streamwise, wall-normal and spanwise directions, respectively. A PIV system is used to collect data describing the flow field around the trailing edge of a NACA 0012 aerofoil. Apart from the advantage of being a non-intrusive system, a PIV is essential for the study of the laminar instability tonal noise because it is heavily dependent on the laminar separation bubble. It is also noteworthy that the dominant flow structure of the Tollmien-Schlichting waves renders the use of a planar, two-dimensional PIV (2D PIV) system adequate to reconstruct a pseudo time-resolved flow field.

The illumination of the seeding particle is achieved by a Litron Lasers Nano T 135-15 PIV, Nd:YAG 135 mJ/pulse laser (marked as 6 in Fig. 3). Laser optics (5 in Fig. 3) are used to generate a laser sheet with a thickness of approximately 1.5 mm and a width of 45 mm. Each laser pulse has the duration of approximately 6 ns, and the time separation between two consecutive pulses is set to $\Delta t=7.3\ \upmu$s at $U_\infty =22$ ms$^{-1}$. The flow is seeded with the Palas DEHS (dioctyl sebacate) particles that have a mean diameter of $0.2{-}0.3\ \upmu$m. The particles are dispersed by a TSI 9307 atomiser by an operating pressure of approximately 1.5 bar.

Particle images are obtained from an optical imaging system (marked as 1 in Fig. 3) that consists a TSI PowerView Plus 4MP-LS CCD camera with a resolution of $2352 \times 1760$ pixels, and a pixel pitch of 5.5 $\upmu$m per pixel and a frame rate of 16 frames per second. The camera is equipped with a Nikon UV-Nikkor 105 mm lens that are operated at a focal ratio of f/5.6. At the optical magnification $M_C = 0.5$, the field of view (or the flow measurement domain) covers an area of approximately $27.5 \times 21$ mm$^{2}$, yielding a digital imaging resolution of 85 pixels/mm. The illumination and image-acquisition systems are synchronised by the LaserPulse 610036 synchroniser. The latter is also connected to a Teledyne Lecroy WaveStation 2012 waveform generator that provides a signal that acts as an external trigger for the data acquisition. The images are acquired at an acquisition frequency of 7.5 Hz. A special manual traverse mechanism (marked as 4 in Fig. 3) is designed and manufactured, which enables a robust and repeatable placement of the PIV imaging and laser illumination systems.

A total of 1500 and 500 instantaneous image pairs are obtained for the investigation of the time-averaged and phase-averaged flow properties, respectively. For the time-averaged flow analysis, images are processed from an iterative multi-grid multi-pass technique with image deformation, and the final window size of $32 \times 16$ pixels ($0.376 \times 0.188$ mm) with a 50% overlap is used. These combinations eventually result in a vector spacing of 0.188 and 0.094 mm in the streamwise x and wall-normal y directions, respectively. For the phase-averaged flow analysis, images are processed by a recursive Nyquist processing method, where the same window size and physical spacing as above are maintained. An interrogation window with an aspect ratio of 2:1 is employed to improve the spatial resolution in the wall-normal direction and to account for the large velocity gradients within the boundary layer.

Fig. 7

Schematic illustrations of a plan view, b side view, for the hot-wire experimental set-up used in Case 2 (Sect. 5.2)

3.3.3 Hot-wire measurements in case 2

Figure 7 illustrates the experimental set-up for the Case 2, which entails an experimental condition of lower Reynolds number. Kevlar working section is utilised, and the coordinate system is also shown. To achieve a good signal-to-noise ratio for the far-field such that the turbulent broadband self-noise can be captured accurately, the microphones need to be placed at a relatively close distance from the hydrodynamic sources as described in Sect. 3.3.1. In order to avoid contamination from the jet noise produced by an open nozzle that would otherwise be prominent when the far-field microphones are nearby, the use of Kevlar working section ensures that only thin boundary layer is present at the wall when transitioning from the nozzle to the Kevlar wall.

The Kevlar walls consists of a main frame made by extruded aluminium (type 6082-T6) bars having a cross section of 10 mm $\times$ 10 mm, and an aramid fabric lined over the aluminium frame. Following the design considerations outlined by Devenport et al. (2013), Kevlar® 120 aramid fabric in plain weave with a mass per unit area of 60 gm$^{-2}$ is stretched over the aluminium frames under the tension of approximately 1500 Nm$^{-1}$ to produce a Kevlar lining.

The turbulent flow measurement tool is based on the hot-wire anemometry. During the study, both single- and x-wire are utilised, depending on the requirements. The single-wire probe (Dantec 55P11) is used to measure the longitudinal velocity component u, and it is normally operated at an overheat ratio of 1.8 to maximise the velocity sensitivity. The x-wire (Dantec 55P61), on the other hand, is operated at a lower overheat ratio of 1.4 to minimise the thermal interference between the two wires. The x-wire, depending on its radial orientation against the incoming flow, is used to measure either the u and v (wall-normal velocity component), or u and w (spanwise velocity component), simultaneously. Both the single- and x-wire probes are heated by a multi-channel Dantec 55N80 Constant Temperature Anemometer (CTA). According to the quoted values from the manufacturer, when operated in CTA mode, both the 55P11 and 55P61 could reach up to 400 kHz for the frequency responses. The analogue signals from the CTA are digitised by a 12-bit TSI ADCPCI A/D card. For both the two-dimensional and three-dimensional flow domain measurements, the hot-wire probe is attached to a model TSI-ISEL T3D three-axis traverse system with a movement accuracy of $\pm 0.01$ mm. The traverse is connected to a remotely placed personal computer that controls both the traverse and the data acquisition software (TSI ThermalPro).

Before the x-wire probe is used for the turbulence measurements, a full velocity versus yaw angle calibration technique described by Browne et al. (1988) is employed to convert the voltage readings into velocities. This calibration method reduces the potential error incurred by the different sensitivity of the yaw factor to the velocity. Ambient temperature correction is applied to the acquired voltages.

For the cases when the hot-wire flow measurements are taken simultaneously with the far-field noise measurements, both the acoustic and hot-wire signals are sampled at $f_s = 40$ kHz to resolve the turbulent structures. For other cases where only the large eddy is needed to reconstruct the three-dimensional flow field, the hot-wire data are sampled at $f_s = 5$ kHz. This sampling rate, though lower, is still capable of capturing the turbulent flow features associated with the deterministic turbulent boundary layer accurately. The obvious advantage is that it will not result in excessively large amount of dataset. Typically, dataset of a single measurement point contains 131,072 samples and velocity signatures of approximately 310 individual turbulent spots.

3.3.4 Wavelet analysis

Wavelet analysis can be used for the analysis of non-stationary processes and for estimating the power of any arbitrary signal as a function of time. A brief discussion of the analysis method is given here. An arbitrary discrete time series $\xi (t)$ that describes the variation of acoustic pressure (or velocity fluctuation) is first assumed. Note that $\xi (t)$ is characterised by equal time spacing of $\delta _t$ between each sample. The continuous wavelet transform (CWT) of such time series is defined by its convolution with a scaled and translated wavelet function $\Psi$, which is given by:

$$\begin{aligned} W(s,t_{n}) = \sum \limits _{n^{\prime }=0}^{N-1} \xi (t_{n^{\prime }}) \Psi^{*} \left[ \frac{(n^{\prime }-n)\delta _{t}}{s}\right] , \end{aligned}$$

(1)

where s is the wavelet scale (or the dilation factor), $t_n=\frac{n}{f_s}$ with $n = 0 \cdots (N-1)$, and $(^*)$ indicates the complex conjugate. As the scale s of the wavelet is varied (also referred to as the wavelet dilation) and the wavelet is translated along the localised time index n, it is possible to determine the amplitude of any features versus their scale and to show the variation of this amplitude with time.

In the present study, the Morlet wavelet is chosen as the mother wavelet in the analysis due to its common use in similar applications. The wavelet (normalised to produce unit energy) is described by:

$$\begin{aligned} \Psi (\eta ) = \left( \frac{\delta _t}{s} \right) ^{\frac{1}{2}} \Psi _\circ (\eta ) = \left( \frac{\delta _t}{s} \right) ^{\frac{1}{2}} \pi ^{-\frac{1}{4}} e^{i\omega _\circ \eta } e^{-\frac{\eta ^2}{2}}, \end{aligned}$$

(2)

where $\eta$ is the non-dimensional time, and $\omega _\circ$ is the non-dimensional frequency.

Morlet wavelet is complex valued, hence the wavelet coefficients will be a complex function. Their amplitude is given by the modulus |X|, as well as the phase by $\text {tan}^{-1} \left( \frac{\Im \{X\}}{\Re \{X\}}\right)$, where $\Im$ indicates the imaginary and $\Re$ the real part of the wavelet coefficient. A comparison of the results obtained from the wavelet transform to those obtained from the Fourier transform is enabled by determining the wavelet pseudo frequency, f, using the following relationship:

$$\begin{aligned} f = \frac{\omega _\circ +\sqrt{2+\omega _\circ ^2}}{4\pi s}. \end{aligned}$$

(3)

The wavelet coefficients, $c_w$, are then used to calculate the scaled average wavelet coefficients, given by:

$$\begin{aligned} c_w = 10\ \text {log}_{10}(c_e), \end{aligned}$$

(4)

where $c_e$ is the mean wavelet coefficient. They are calculated using the following data reduction routine:

• 1. Assume an arbitrary discrete time series $\xi (t)$ that represents n successive and periodic occurrences of noise and/or velocity fluctuation variations induced by either: a) The deterministic turbulent boundary layer’s passage over the aerofoil trailing edge; or b) The interaction between the deterministic turbulent boundary layer and the mechanism responsible for the self-noise production. The overall time series $\xi (t)$ is fragmented into sections, each describing one individual occurrence of the noise or velocity fluctuation variations.

• 2. A continuous wavelet transform of each section is computed using the method described earlier.

• 3. The obtained wavelet coefficients of each section are assembled into an ensemble, and then ensemble-averaged to obtain the mean wavelet coefficients $c_e$.

The results obtained from such analysis will be presented later. The principal idea behind the use of this technique is to provide a mean to describe the temporal variations in the acoustic pressure and velocity fluctuations caused by the perturbations from the deterministic turbulent boundary layer to the flow field at the vicinity of the aerofoil trailing edge.

4 Characterisation of the deterministic turbulent boundary layer

Both the PIV and hot-wire anemometry techniques described in Sect. 3.3 are capable of reconstructing the deterministic turbulent boundary layers and their interaction with the aerofoil trailing edge in the spatio and temporal domains. A major advantage of choosing a PIV is the enabling of field measurement, although it also comes with a necessity to perform the measurements at multiple phases in the time series with respect to the triggering source in order to reconstruct the turbulent structures in the temporal domain. The opposite is true for the hot-wire anemometry, which has a very high frequency response at each measurement point, but effort is also needed to map out the three-dimensional flow field. This section will discuss some of the data analysis techniques from the acquired noise and flow data. Data analysis methods common to the individual turbulent spot are adopted for the investigation of the deterministic turbulent boundary layer.

Fig. 8

a Coloured lines represent an ensemble of instantaneous velocity signals made up of 310 individual turbulent spots. The solid black line represents the ensemble-averaged velocity $<u>$. b Ensemble-averaged velocity signatures at different wall-normal y locations from the aerofoil surface

Considering the case when the velocity fluctuation at a particular location (x, y, z) near the aerofoil trailing edge is measured by a hot-wire probe, the data are typically made up of 131,072 samples that contain the entire velocity signatures pertaining to 310 individual deterministic turbulent boundary layer passage time events. The rising edge of the square pulse used to drive the miniature loudspeakers can represent the time of its origin ($t = 0$ ms). It is also employed to locate the signal of each individual passage of the deterministic turbulent boundary layer to enable the generation of an ensemble of them. This is demonstrated by the coloured lines in Fig. 8a. The ensemble is then averaged to obtain the mean velocity signature $\left\langle u(x,y,z,t) \right\rangle$, as a function of time t, pertaining to the deterministic turbulent boundary layer. The $\left\langle u(x,y,z,t) \right\rangle$ is depicted by the black line in Fig. 8a. Typical mean velocity signatures measured across several wall-normal y locations from the surface, but at the same (x, z), are shown in Fig. 8b. Each line contains the local perturbation event by the deterministic turbulent boundary layer. Therefore, the deterministic turbulent boundary layer can be fully reconstructed in the spatial and temporal domains by mapping out the volumetric flow field in (x, y, z, t).

The velocity perturbation, which measures the momentum excess or deficit, is a useful quantity to characterise the deterministic turbulent boundary layer. If the temporal variation of the ensemble-averaged streamwise velocity component is denoted by $\left\langle u(x,y,z,t) \right\rangle$, then the velocity perturbation $\widetilde{u}$, non-dimensionalised by the local freestream velocity, can be expressed by:

$$\begin{aligned} \widetilde{u}(x,y,z,t) = \frac{\left\langle u(x,y,z,t) \right\rangle -u_L(x,y,z)}{U_\infty (x,z)}, \end{aligned}$$

(5)

where t is the time whose origin coincides with the rising edge of the triggering pulse, $u_L$ is the local velocities of the undisturbed flow and $U_\infty$ is the velocity of the freestream flow.

Similarly, the temporal variation of the ensemble-averaged root-mean-square r.m.s velocity fluctuations, $\widehat{u^{\prime }}$, can be determined by:

$$\begin{aligned} \widehat{u^{\prime }} (x,y,z,t) = \frac{\sqrt{\frac{1}{N} \sum \nolimits _{i=1}^{N} \left[ u_i(x,y,z,t) -\left\langle u(x,y,z,t) \right\rangle \right] ^2}}{U_\infty (x,z)}, \end{aligned}$$

(6)

where N is the number of realisations. Note that Eqs. 5 and 6, which describe the $\widetilde{u}$ and $\widehat{u^{\prime }}$, respectively, are also applicable to other velocity components, i.e. v and w. Finally, the temporal variations of the Reynolds shear stress $\widehat{u^{\prime } v^{\prime }}$ can be calculated from the following equation:

$$\begin{aligned}&\widehat{u^{\prime } v^{\prime }} (x,y,z,t) \nonumber \\&\quad =\frac{\frac{1}{N}\sum \limits _{i=1}^{N} \left\{ \left[ u_i(x,y,z,t) -\left\langle u(x,y,z,t) \right\rangle \right] .\left[ v_i(x,y,z,t) -\left\langle v(x,y,z,t) \right\rangle \right] \right\} }{U^2_\infty (x,z)}. \end{aligned}$$

(7)

Fig. 9

Contour plots of a velocity perturbation $\widetilde{u}$, and b root mean square velocity fluctuation $\widehat{u^{\prime }}$, of a turbulent spot

The reduced data allow each measurement point to be assembled to generate contour plots of velocity perturbation in the time domain, such as the example in Fig. 9a, which was measured at $x/C = 0.94$. The contour plot represents changes in the flow momentum induced by the deterministic turbulent boundary layer relative to the local undisturbed flow, where positive or negative values denote momentum increase or decrease, respectively. Similarly, the velocity fluctuation contour is interpreted as the changes in the turbulence intensity level of the flow, which is illustrated in Fig. 9b. Non-dimensional time scale $t^{\prime \prime }$ is also shown alongside the dimensional t. Definition of $t^{\prime \prime }$ will be provided in Sect. 5.2.

Closer examination of the velocity perturbation contour demonstrates a structure that is similar to a typical turbulent spot, thus indicates that the deterministic turbulent boundary layer formed by a coalescence of side-by-side turbulent spots has been successfully generated. The spatio and temporal domains that are dominated by levels associated with $\tilde{u} \approx 0$ denote the unperturbed laminar field. The general structure of a turbulent spot can be described by four distinctive regions: (A) the near wall region that is dominated by high level of positive perturbations, i.e. $\tilde{u} > 0$, and (B) the outer region where the velocity perturbations are predominantly negative. These two characteristics reflect very well of a typical turbulent boundary layer velocity profile that exhibits near wall velocity excess and outer layer velocity deficit. At some intermediate heights from the surface, the turbulent spot will encounter both positive and negative perturbations along its length. The third significant region is the “leading edge overhang” of the turbulent spot in (C). Here, the leading edge overhang is formed by the upstream ‘ejections’ of turbulent fluid with sufficient energy from the near wall region to beyond the edge of the laminar boundary layer. Although the ejected turbulent fluid propagates faster than the main body of the turbulent spot, it has no self-regeneration mechanism outside the boundary layer so it will gradually decay and join the nose of the turbulent spot to form an overhang. Another important feature pertaining to a turbulent spot that is discernible from the velocity perturbation contour is the presence of (D) “becalmed region” that corresponds to a slow recovery of velocity at the aft of each turbulent spot. The becalmed region is formed by the downstream ‘sweeping’ of high momentum fluid from the freestream towards the near wall of the turbulent spot’s trailing edge. From the perspective of the velocity perturbation, it is difficult to distinguish the boundary between the becalmed region and the trailing edge of a turbulent spot. Note that the latter can only be defined by identifying the turbulent and non-turbulent interface. As already mentioned earlier, the becalmed region has a fuller velocity profile that is even more stable than the local laminar boundary layer.

The turbulent part of the deterministic turbulent boundary layer is illustrated in Fig. 9b. The structure of the turbulent spot delineated by the turbulence intensity is generally well defined, where salient features such as the spot’s leading edge, including its overhang, maximum height, and trailing edge are distinguishable. The becalmed region can no longer be discernible from the r.m.s velocity fluctuation contour owing to its characteristics of high momentum excess and extremely low residue turbulence. The r.m.s velocity fluctuation contour shows that the main body of the deterministic turbulent boundary layer is characterised by a very high turbulence intensities between $10{-}14\%$ (red colour). The presence of a primary turbulence intensity within a deterministic turbulent boundary layer is consistent with Gad-El-Hak et al. (1981) and Glezer et al. (1989) who observe the presence of a dominant mechanism for the destabilisation of the surrounding laminar boundary layer in order to sustain the growth of the turbulence.

Fig. 10

Time variations of the a velocity signal of u, b detection function D(x, y, z, t), c smoothing function c(x, y, z, t) and d indicator function I(x, y, z, t)

It is important to have a systematic algorithm to be able to detect the arrival of the deterministic turbulent boundary layer to the region of interest accurately. Here, an algorithm developed by Clark et al. (1993) is used to detect the interfaces that separate the deterministic turbulent boundary layer from the surrounding non-turbulent flow.

The detection process used in the present study is illustrated in Fig. 10. The instantaneous velocity signal of the streamwise velocity u indicates that the passage of the deterministic turbulent boundary layer exhibits an abrupt increase in velocity from the non-turbulent to turbulent level. The high frequency fluctuations associated with turbulence within the deterministic turbulent boundary layer are then accentuated by a detection function D(x, y, z, t):

$$\begin{aligned} D(x,y,z,t)=m(x,y,z,t)\left( \frac{\partial u(x,y,z,t)}{\partial t} \right) ^2, \end{aligned}$$

(8)

where m(x, y, z, t) is the normalised velocity signal magnitude, which is given by:

$$\begin{aligned} m(x,y,z,t)=\frac{u(x,y,z,t)-u_{\mathrm{min}}}{u_{\mathrm{max}}-u_{\mathrm{min}}}. \end{aligned}$$

(9)

The derivative of the velocity signal is calculated using the central difference scheme:

$$\begin{aligned} \frac{\partial u(x,y,z,t)}{\partial t}=\frac{u^{i+1}-u^{i-1}}{2\Delta t}. \end{aligned}$$

(10)

The criterion function c(x, y, z, t) is obtained by smoothing the detection function:

$$\begin{aligned} c(x,y,z,t=i\Delta t)=\frac{(\Delta t)^2}{1+(\tau _s/\Delta t)} \sum \limits _{j=i-(\tau _s/2\Delta t)}^{j=i +(\tau _s/2\Delta t)}w_j.D(x,y,z,j\Delta t) \end{aligned}$$

(11)

in order to eliminate zero-crossings in the detection function. In Eq. 11, $\tau _s$ is the smoothing period and the weighting factor $w_j$ is given by:

$$\begin{aligned} w_j=\mathrm{exp} \left[ -\left( \frac{0.625}{\tau _s/\Delta t} \right)\, |j-i|\right]. \end{aligned}$$

(12)

Finally, the indicator function is given by:

$$\begin{aligned} I(x,y,z,t) ={\left\{ \begin{array}{ll} 1, &{} \text {if velocity signal is turbulent} \\ 0, &{} \text {if velocity signal is non-turbulent.} \end{array}\right. } \end{aligned}$$

(13)

The algorithm identifies the turbulent and non-turbulent portions of the velocity signal produced by each passage of the deterministic turbulent boundary layer by applying a threshold value to the smoothed criterion function c(x, y, z, t).

Fig. 11

Best fit of the integral time $t_{\mathrm{integral}}$ against the time of flight; $C_l$ and $C_t$ represent the leading edge and trailing edge propagation rates (as a proportion of the freestream flow velocity) of the deterministic turbulent boundary layer

The ability to identify the interfaces of the leading edge and trailing edge of the deterministic turbulent boundary layer at the spatial and temporal domains also allows the determination of the turbulence propagation rates. They can be obtained by plotting the “time of flight” against the “integral arrival time” of the deterministic turbulent boundary layer. The time of flight is described as the time that the leading or trailing edge of the deterministic turbulent boundary layer takes to convect from a known reference location, $x_{\mathrm{ref}}$, to the location where measurements are being taken. The integral arrival time is the time that the deterministic turbulent boundary layer requires to cover the same distance at the local freestream velocity, which is given by:

$$\begin{aligned} t_{\mathrm{integral}}=\int _{x_{\mathrm{ref}}}^{x} \frac{dx}{U_\infty (x,z)}. \end{aligned}$$

(14)

The slopes of the best fit lines then determine the propagation rates as a proportion of the local freestream velocity. Figure 11 shows the typical propagation rates for the leading edge $C_l$ and trailing edge $C_t$ determined from the method described above. In this example, the difference in the $C_l$ and $C_t$ reflects the streamwise growth of the deterministic turbulent boundary layer.

Fig. 12

a Sound pressure level spectrum of the instability tonal noise calculated by the Fourier transform in the absence of perturbation by the deterministic turbulent boundary layer, b scalogram of the scaled acoustic wavelet coefficients $c_w$ without perturbation by the deterministic turbulent boundary layer, c scalogram of the scaled acoustic wavelet coefficients $c_w$ perturbed by the deterministic turbulent boundary layer

5 Demonstration of method

As discussed in Sect. 1, and summarised in Table 1, this paper aims to demonstrate that the deterministic turbulent boundary layer can either be used to disrupt an existing acoustic scattering mechanism, or reconstruct a new acoustic scattering scenario to enable the ensemble-averaging analysis (in space and time domains) and the wavelet analysis (in frequency and time domains) in the study of aerofoil self-noise mechanisms. To demonstrate the robustness of this technique, two aerofoil self-noise scenarios will be examined. The next two subsections contain key results for each scenario. It is worth acknowledged that the 2D and 3D pseudo time-resolved flow structures to be presented in Sects. 5.1 and 5.2 are obtained from basic experimental tools (15 Hz-rated 2D-planar PIV and hot-wire anemometry, respectively).

5.1 Case 1: Evolution of the laminar instability tonal noise for aerofoil

In this noise scattering scenario, the primary role of the deterministic turbulent boundary layer is to disrupt the pre-existence of the aeroacoustics feedback loop, which will allow the study of the evolution of the laminar instability tonal noise spectral, i.e. the frequency component, as a function of time. Using a NACA 0012 aerofoil at freestream velocity of 22 ms$^{-1}$ ($\text {Reynolds number} = 2.2\times 10^5$) and an effective angle of attack of 1.65$^\circ$, Fig. 12a shows the far-field power spectral density of the aerofoil instability noise without the perturbation from the deterministic turbulent boundary layer. Owing to the stationary nature of the acoustic signals, conventional Fourier transform method is employed to calculate the power spectral density. The figure showcases several features that are expected from the laminar instability radiation, such as the tonal hump whose peak is located at approximately 1 kHz, and multiple narrowband tones that yield a constant frequency spacing $\Delta f = 98$ Hz between the adjacent tones.

Using the same raw acoustic data, but now employing the wavelet analysis technique described in Sect. 3.3.4, the radiation coefficient $c_w$ in Fig. 12b captures the tonal hump accurately, whose dominant frequency of 1 kHz coincides with that of Fig. 12a. As mentioned earlier, the stationary nature of the acoustic signals would entail little variation of the radiation coefficient as a function of time, t.

When the deterministic turbulent boundary layer is triggered at $t=0$ ms, it will convect downstream and perturb the otherwise separated boundary layer near the trailing edge of the aerofoil pressure side. This will then force a time-evolution of the radiation acoustic spectra that feature distinctly different characteristics, as shown in Fig. 12c. Zone I represents the initial temporal range of the pre-arrival of the deterministic turbulent boundary layer to the trailing edge, whose radiation coefficient is similar to the unperturbed one in Fig. 12b. Zone II represents the temporal range where the radiation of the laminar instability noise ceases to exist due to the suppression of the separation bubble by the deterministic turbulent boundary layer that has reached the trailing edge. Zones III and IV illustrate the regeneration of the laminar instability tonal noise after the deterministic turbulent boundary layer leaves the trailing edge and into the wake. The radiated acoustics then reach its pinnacle at Zone V, and settle in Zone VI. Eventually, it will return to the original unperturbed value similar to that of Zone I. Note that the non-dimensional time $t^{\prime }$ is also shown alongside. Here $t^{\prime } = t/t_\circ$, where $t_\circ = 47.4$ ms as this reference time represents the start of Zone V, where the most intense regeneration phase commences. In what follows, discussion of the temporal development of the near field hydrodynamics and far-field acoustics will mainly be based on the non-dimensional time $t^{\prime }$.

Phase measurements of the flow fields are conducted by the PIV system described in Sect. 3.3.2. The rising edge of the input square pulse waveform signal is used as a trigger for the acquisition of the PIV image pairs. This signal is also used to simultaneously trigger the deterministic turbulent boundary layer that will convect downstream on the aerofoil surface and eventually enter the PIV field of view as depicted in Fig. 6. By adjusting the $\Delta t_p$, which is the time delay between the rising edge of the square pulse and the acquisition of the PIV image pairs, the deterministic turbulent boundary layer can be captured at the desired phase of its development. At each phase, an ensemble of 500 PIV image pairs are captured to obtain an equal number of instantaneous vector fields. The calculation of the ensemble-average then provides the mean flow field as a function of time. Therefore, providing that a sufficient number of the mean flow field realisations are obtained, the spatio-temporal development of the deterministic turbulent boundary layer can be reconstructed. During the experiments, the parameter $\Delta t_p$ is varied between 26 and 70 ms at increments of 0.1 ms, yielding more than 400 phase-averaged vector fields that can be used to describe the complete passage of the time-resolved (10 kHz) deterministic turbulent boundary layer across the entire flow measurement domain.

By implementing the method described above, some new phenomena responsible for the generation of the laminar instability tonal noise have been uncovered. However, they will be reported elsewhere as they are out of scope with the current paper. To be aligned with the main objectives of this paper, only some salient features are chosen in the discussion below. More specifically, the deterministic turbulent boundary layer is measured by a low speed PIV for its capabilities to “disrupt” the acoustic scattering phase (Zone II), and subsequently “enable” the acoustic regeneration phase (Zone V). The readers are reminded that, although the smallest time step for the flow fields measured in this study is $\Delta t = 0.1$ ms ($\Delta t^{\prime }=0.002$), some of the results presented in the subsequent discussions are separated by a coarser time step in order to retain only the most salient features.

Fig. 13

Evolution of the $v_{\mathrm{r.m.s}}$ flow fields in the $y-x$ plane pertaining to Zone II at $t=26.2,\ 28.2,\ 30.2,\ 32.2,\ 34.2$ and 36.2 ms ($t^{\prime }=0.55,\ 0.59,\ 0.64,\ 0.68,\ 0.72$ and 0.76). The main flow direction is from left to right. The turbulent flow field at a particular time instance t is compared against the corresponding acoustic wavelet coefficient $c_w(f,t)$ in the embedded figure

5.1.1 Disrupting phase

Initially, the instability tonal noise is produced by a fully established aeroacoustics mechanism and remains consistent across the entirety of the Zone I. Figure 13 shows the temporal variation of the vertical velocity fluctuation $v_{\mathrm{r.m.s.}}$ fields ($y-x$ plane) in the disruption phase Zone II at $t=26.2,\ 28.2,\ 30.2,\ 32.2,\ 34.2$ and 36.2 ms, equivalent to $t^{\prime }=0.55,\ 0.59,\ 0.64,\ 0.68,\ 0.72$ and 0.76. The turbulent flow field at a particular time instance $t^{\prime }$ is compared against the corresponding acoustic wavelet coefficient $c_w(f,t^{\prime })$ in the embedded sub-figures. At $t^{\prime }=0.55$, the radiated tonal noise is at its relative maximum and essentially maintains the same level as in the case of an undisturbed flow (at $t^{\prime }=0$) in Zone I. The flow field at this instance represents the moment just prior to the arrival of the deterministic turbulent boundary layer to the region of separated bubble near the trailing edge. At this instance, the flow field is still relatively unchanged, or at best only perturbed slightly, as indicated by the lack of significant changes in terms of both the noise radiation and the flow field properties. It is also worth mentioning that the highest turbulence level is found at the near wake region, a phenomenon that is also captured by others (Pröbsting et al. 2014; Nakano et al. 2005; Chong and Joseph 2009) for naturally occurred laminar instability tonal noise. According to some (Pröbsting et al. 2014; Nakano et al. 2005), the highly turbulent flow at the near wake is likely to be caused by the intense vortex shedding that originates at the aerofoil surface due to the roll-up of vortices in the vicinity of the laminar separation region, and ultimately transforms into wake vortex shedding. This point will be discussed again in Sect. 5.1.2.

As the deterministic turbulent boundary layer progresses downstream, for example at $t^{\prime }=0.59$, the radiated noise level begins to decrease. At this time instance, a large portion of the flow domain at the trailing edge's pressure surface is occupied by a turbulent flow as indicated by the enhanced $v_{\mathrm{r.m.s.}}$ level. Such occurrence reflects the encompassing of the turbulent part of the deterministic turbulent boundary layer, which can suppress the separation bubble near the trailing edge, and subsequently reduce the turbulence level at the near wake. Interestingly, the turbulence level of the deterministic turbulent boundary layer, which at $t^{\prime }=0.59$ is still located at the aerofoil pressure surface, is significantly lower than the high turbulence at the near wake observed earlier at $t^{\prime }=0.55$. This strongly indicates that the laminar instability tonal noise, which is typically very loud, is generated at the near wake. The demise of the high turbulence at the near wake at $t^{\prime }=0.59$ marks the start of the reduction of the instability tonal noise radiation.

The trend of steady reduction in the radiated noise level continues afterwards. As demonstrated by the $v_{\mathrm{r.m.s.}}$ flow fields between $0.59 \le t^{\prime } \le 0.76$, the deterministic turbulent boundary layer continues to propagate downstream with its main body (the turbulent part) eventually leaves the trailing edge at $t^{\prime } \approx 0.64$. From this point onward, the becalmed region takes over and represents the dominant feature on the trailing edge surface until itself also leaves the trailing edge at $t^{\prime } \approx 0.76$. Between $0.68 \le t^{\prime } \le 0.76$ the boundary layer at the pressure side trailing edge undergoes a re-laminarisation process without any trace of reversed flow. The strong stability and high momentum imposed by the becalmed region also lead to a near complete suppression of the near wake turbulence. The arrival of the becalmed region induces a further decline in the level of noise radiation, reaching the lowest level of the entire time domain at $t^{\prime }=0.76$, marking the time instance when the instability tonal noise mechanism ceases to function entirely.

Fig. 14

a Results enabled by the deterministic turbulent boundary layer technique that shows the vortex roll-up sequence ($\Delta t$ = 0.4 ms, or $\Delta t^{\prime }=0.008$) measured by a low-speed 15 Hz PIV for a NACA 0012 at 22 ms$^{-1}$ and 1.65$^\circ$ effective angle of attack. b Sequence of three instantaneous velocity fields measured by a high speed time-resolved PIV for a NACA 0012 at 24 ms$^{-1}$ and 1.5$^\circ$ effective angle of attack (Pröbsting et al. 2014)

5.1.2 Regeneration phase

The regeneration phase begins in Zone III. Within this zone, the separation bubble will gradually reappear and grow in size. As the bubble’s size is growing, the turbulence intensity level at the near wake also increases and reaches the level similar to Zone I. This seemingly close correlation between the bubble size and near wake turbulence level has already been established in Zone III, well before the first appearance of the roll-up vortices in Zone V. Therefore, contrary to the conclusion by others who studied the naturally occurred instability tonal noise (Pröbsting et al. 2014; Nakano et al. 2005), the deterministic turbulent boundary layer technique reveals that the high turbulent flow at the near wake is established by the separation bubble. It is then reinforced and enhanced by the roll-up vortices that will occur later.

Flow results pertaining to Zone V is discussed here, which are shown in Fig. 14a for the contours of total velocity $\sqrt{u^2+v^2}$. In this figure, the sequence of the presented flow fields in Zone V, where $\Delta t = 0.4$ ms ($\Delta t^{\prime }=0.008$), have a much smaller time step than those presented in Fig. 13 for the Zone II. The roll-up of the vortical structures can be vividly demonstrated near the aerofoil trailing edge. The temporal spacing between the roll-up vortex pair at the trailing edge is found to be about 1.1 ms, which corresponds to a frequency of 909 Hz and close to the radiated tonal hump obtained from both the fast Fourier transform and wavelet analysis (Fig. 12). This corroborates with the previous findings from Pröbsting et al. (2014), which are based on high speed time-resolved PIV that can produce instantaneous flow fields of approximately 0.17 ms temporal resolution. An example from their paper is reprinted in Fig. 14b, where the experimental conditions of 24 ms$^{-1}$ and effective angle of attack of 1.5$^\circ$ are similar to the present study. Sequences of roll-up vortical structures are also vividly shown in their instantaneous flow fields at both the trailing edge's suction and pressure surfaces. The comparison in Fig. 14, therefore, demonstrates that the experimental techniques developed in this study that require only the basic experimental tools can still capture the pseudo time-resolved flow structures accurately.

Fig. 15

Contours of the deterministic turbulent boundary layers at 0.5 mm upstream of the aerofoil trailing edge. The horizontal and vertical dashed lines indicate the aerofoil camber line, and the deterministic turbulent boundary layer time of arrival, respectively

5.2 Case 2: turbulent structures triggered by the serrated trailing edge aerofoil

In this acoustical scattering scenario, the focus is to study the mechanisms of aerofoil self-noise reduction by a serrated trailing edge. Unlike the case study discussed in Sect. 5.1, which uses the deterministic turbulent boundary layer to perturb the pre-existing aeroacoustics feedback loop, it is now served as the tracer to enable the study of the interaction between the turbulent noise sources and the serrated trailing edge. Note that all the results presented in this section are acquired by a single x-wire probe that measures the longitudinal $u^{\prime }$ and vertical $v^{\prime }$ components of the fluctuating velocity.

A NACA 0008 aerofoil is placed at zero degree angle of attack at Re = $0.95 \times 10^5$. The current study employs an experimental technique that would benefit from a pre-existence of homogeneous flow conditions on both the upper and lower sides of the aerofoil. A carefully designed experimental set-up is performed to ensure that a mirror image of the deterministic turbulent boundary layer is achieved at both sides of the trailing edge. This can ensure that any flow behaviours uncovered in the analysis are solely due to the physical presence of the trailing edge serrations only. As shown in Fig. 15 for the contour of streamwise velocity perturbation $\tilde{u}$, a strong mirror image (structure, size and characteristics) for the deterministic turbulent boundary layers has been achieved. The times of arrival between them (marked by the vertical dashed line) are the same on both sides. Therefore, the deterministic turbulent boundary layers generated here are expected to execute a simultaneous aeroacoustics response at the trailing edge.

Temporal development of the hydrodynamic near field and acoustic far field in Case 2 is represented by the following non-dimensional form:

$$\begin{aligned} t^{\prime \prime }=\frac{t\cdot \overline{U}_\infty }{l}, \end{aligned}$$

(15)

where l represents the longitudinal distance between the loudspeakers and aerofoil trailing edge, and

$$\begin{aligned} \overline{U}_\infty = \frac{1}{2}\left( C_l+C_t \right) \cdot U_\infty . \end{aligned}$$

(16)

$C_l$ and $C_t$ represent the leading edge celerity and trailing edge celerity for a turbulent spot, respectively, as determined in Fig. 11. Essentially, $\overline{U}_\infty$ represents the average convection speed of a turbulent spot. Note that $t^{\prime \prime } = 1$ should be interpreted as the time instance when the main body of the turbulent spot, not its leading edge, reaches the aerofoil trailing edge.

Fig. 16

Results enabled by the deterministic turbulent boundary layer technique that shows the sequence of perturbed coherent-liked structure near a serrated trailing edge measured by a hot wire probe for a NACA 0008 at $0.95 \times 10^5$ and $0^\circ$ angle of attack. The red and blue structures denote the positive $(+2\%)$ and negative $(-2\%)$ velocity perturbations, respectively. Each sub-figure is indicated by both the dimensional t, as well as the non-dimensional $t^{\prime \prime }$ inside the parenthesis

Based on the deterministic turbulent boundary layers depicted in Fig. 15, a sequence of perturbed, coherent-liked structures can be reconstructed in a 3D space when it convects over a serrated trailing edge, which is shown in Fig. 16. Unlike in Fig. 1c, which depicts a turbulent spot by a frozen turbulence assumption in the ($y-z-t$) space, Fig. 16 represents a true temporal variation of turbulent spot in the ($x-y-z$) space. The isometric surfaces in Fig. 16 are described by the ensemble-averaged velocity perturbation, as defined in Eq. 5. The interface between the laminar and turbulent region is identified by employing a threshold of $\pm 2\%$ velocity perturbation (Coles and Barker 1975; Katz et al. 1990). Although the temporal resolution of the coherent structures in their spatial development is resolved at $\Delta t=0.2$ ms $(\Delta t^{\prime \prime }=0.01)$ in the current study, the time steps between the structures shown in Fig. 16 are chosen to be larger and they do not follow a particular pattern in order to show only the salient features. The arrival of the deterministic turbulent boundary layer to the serrated trailing edge is marked by two scenarios: momentum deficit (negative perturbation) at the outer layer, and momentum excess (positive perturbation) at the near wall, both of which are homogeneous across the span. The outer layer structure is shorter in the overall longitudinal length, and will disappear out of view faster than the near wall, high momentum excess structure that is also contributed by the becalmed region at the rear. Interestingly, new structures manifested by a periodic appearance of the positive and negative perturbations can be observed at $t^{\prime \prime } \geq 2.27$, which occur after the main body of the deterministic turbulent boundary layer left the serration tip. A conjecture is made that these are related to the streamwise vortical structures reported in other studies (Chong and Vathylakis 2015; Avallone et al. 2016), although at present we are unable to confirm this because of the absence of the vorticity data. If a triple hot-wire probe or low-speed stereoscopic PIV experimental tool is used in the future, it is possible to perform the vortex visualisation to reconstruct the coherent structures in the spatial and temporal domains, much in a similar capacity as a tomographic, time-resolved PIV.

Fig. 17

Illustrations of the $x-z$ plane at $y_p=0.6$ mm above the baseline and serrated trailing edge, respectively, for the wavelet analysis of the wall normal velocity fluctuation $v^{\prime }$. ’REF’ indicates the location of the reference point

The isosurface plots in Fig. 16 are useful for the visualisation of the overall turbulent structure. More in depth analysis of the turbulence behavioural changes subjected to the serrated trailing edge can focus on the internal “slices” of the isosurfaces. As an example, data of the velocity fluctuations can be presented in the $x-z$ plane that covers an area of $6 \times 9\ \text {mm}^2$ and $6 \times 24\ \text {mm}^2$ at $y_p=0.6$ mm for the baseline and serrated trailing edges, respectively, as illustrated in Fig. 17. Definition of the $y_p$ can be found in the figure. Data of the velocity fluctuations pertaining to these planes will be analysed in the time and frequency domains in conjunction with the radiated acoustic field. Details will be provided next.

Fig. 18

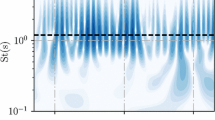
CWT scalogram depicting the temporal variation of the real part of the a, b scaled wavelet coefficients $c_w=10\text {log}_{10}(c_e)$ of the instantaneous acoustic pressure, c, d integrated wavelet coefficients $c_{w\ (v^{\prime }{}^*)}$ of the fluctuating part of the wall normal velocity component $v^{\prime }$ in the $x-z$ plane at $y_p$ = 0.6 mm

The continuous wavelet transform (CWT) technique is applied to convert the signal from the time domain to the time-frequency domain using the method described in Sect. 3.3.4. The results of the wavelet decomposition are presented by the scalogram illustrated in Fig. 18. The use of the CWT approach on both the acoustic and flow data enables a direct correlation study between the pseudo time-resolved spatial flow field near the trailing edge, and the resulting radiated noise spectrum at a given time instance $t^{\prime \prime }$. It is worth mentioning that the “source time” needs to be taken into account during the correlation study. Essentially, the “source time” is the time at which the acoustic noise source radiates acoustic waves and then arrives at the measurement location. The conversion of the acoustic signal time domain to the source time is therefore made by introducing a time delay due to the propagation of sound waves from the trailing edge to the microphone in the data processing routines. This correction makes it possible to draw a direct relation between the acoustic and flow measurement data regardless of the microphone location.

The far-field acoustic pressure is presented in terms of the scaled average wavelet coefficients $c_w(f,t^{\prime \prime })$ as the temporal variation in the spectra of the acoustic pressure emitted by both the straight or serrated trailing edges. The $c_w(f,t^{\prime \prime })$ contour pertaining to the baseline trailing edge in Fig. 18a identifies two pronounced regions of noise radiation, namely region i and region ii, in the frequency range of approximately $120< f < 500$ Hz and temporal range of approximately $0.69< t^{\prime \prime } < 1.76$. It is important to recognise that both regions i and ii are produced as a result of the interaction between the deterministic turbulent boundary layer and the trailing edge.

Compared to the trailing edge noise radiation at region i, region ii encompasses a higher frequency range, but a lower temporal range. Region ii also contains a comparatively higher amplitude in the radiated trailing edge noise, which is prominent at $f=340$ Hz. When the serrated trailing edge is used, the corresponding noise radiation $c_w(f,t^{\prime \prime })$ in Fig. 18b exhibits an overall similar radiation pattern underpinned by the two distinct regions. The most prominent result is related to the region ii, which is marked by a significant reduction in the noise amplitude ($\approx 2$ dB). This provides a clear evidence that the wavelet method employed here can successfully replicate the trailing edge noise reduction by serration. Three representative time instances for the region ii are indicated: 1) $t_1 = 18$ ms (0.83), which is designated as just before the significant noise is radiated by the aerofoil trailing edge; 2) $t_2 = 22.8$ ms (1.05), which is designated as the peak radiation of the trailing edge noise; 3) $t_3 = 25.6$ ms (1.18), which is designated as when the noise radiation returns to the initial and undisturbed state. All three time instances are indicated by the vertical dashed lines. It should be noted that, despite the difference in the scattering edges between the baseline and serration cases, the difference in $t_2$ between them are only $0.3\%$. Therefore a single representative value is retained for the $t_2$.

Region i for both the baseline and serrated trailing edges encompasses a very similar footprint in the time and frequency domains, as well as the amplitude of the radiated noise level. A lack of distinct changes in this region indicate that the responsible flow structure has not been altered significantly by the serrated trailing edge. A detailed examination reveals two characteristics with regard to the region i. First, the arrival of its prominence only occurs at the time instance of approximately $t_2$, which is later than the trailing edge noise radiation that already began at $t_1$ in region ii. Second, the radiation of region i continues at $t > t_3$, i.e. beyond the time limit of region ii. It is conjectured that region i could be the result of an interaction between the two deterministic turbulent boundary layers that arrive at the trailing edge from the opposite sides of the aerofoil, and eventually merge in the near-wake. This merging process of two highly turbulent flow could be the source of the noise radiation in region i.

Following the discussion of the acoustic wavelet $c_w(f,t^{\prime \prime })$, a separate time-frequency analysis of the flow field can be carried out to correlate them both. Out of the many flow parameters measured in the boundary layer, the wall-normal velocity fluctuations represent one of the most dominant sources for the trailing edge noise radiation according to the expression of the unsteady wall pressure wavenumber-frequency spectrum by Blake (1986) and Parchen (1998). Similar to the wavelet analysis of the acoustic data, a Morlet wavelet transformation is applied to every data point of the wall normal velocity fluctuations within the $x-z$ planes as defined in Fig. 17. The calculation produces a set of wavelet coefficients $c_{w(v^{\prime })}(f,t^{\prime \prime },x,z)$ for $v^{\prime }$ in the frequency, time and space.

The $c_{w(v^{\prime })}(f,t^{\prime \prime },x,z)$ can be further reduced to contain only information on the frequency and time:

$$\begin{aligned} c_{w(v^{\prime \,*})}(f,t^{\prime \prime })=\frac{\iint c_{w(v^{\prime })} (f,t^{\prime \prime },x,z) \,dx \,dz}{\Delta x \Delta z}. \end{aligned}$$

(17)

The integrated wavelet $c_{w(v^{\prime \,*})}(f,t^{\prime \prime })$ for both the baseline and serrated trailing edges, which are shown in Fig. 18c and d, respectively, can now be compared against their acoustic wavelets $c_w(f,t^{\prime \prime })$ counterparts directly.

The baseline trailing edge is first considered. Figure 18c indicates that significant level of $c_{w(v^{\prime \,*})}(f,t^{\prime \prime })$ is found at $t_1< t < t_3$, where both the maximum noise radiation at region ii and maximum $v^{\prime }$ occur at $t_2$. These reactions in the turbulence field as a response to the interaction with the deterministic turbulent boundary layer correlate well, in both the frequency and time domains, with the acoustic field shown in Fig. 18a. A gradual rolling-off, and subsequently a complete diminishing of the $c_{w(v^{\prime \,*})}(f,t^{\prime \prime })$ can be observed for the periods after $t_3$. Overall, the characteristics described above confirm that any occurrence of a significant level of $v^{\prime }$ should coincide with the turbulent boundary layer−trailing edge broadband noise radiation. The spectral characteristics between them are also similar. The application of wavelet analysis method to the $v^{\prime }$ can appropriately capture the frequency, temporal, and amplitude characteristics of the turbulence field that directly contribute to the production of the trailing edge noise.

When considering the serrated trailing edge, the correlation between the flow field turbulence $c_{w(v^{\prime \,*})} (f,t^{\prime \prime })$ in Fig. 18d and region ii of the acoustic response $c_w(f,t^{\prime \prime })$ in Fig. 18b is strong. It is also immediately apparent that the magnitude of the $c_{w(v^{\prime \,*})}(f,t^{\prime \prime })$ is significantly lower than that produced by the baseline trailing edge at the same time and frequency domains. Therefore, noise reduction by the serrated trailing edge is corroborated by the reduction in the turbulence flow field.

Another observation is that the footprints of the turbulence field in the frequency and time domains correlate well with the acoustic field in region ii only. Considering that the turbulence fields in this case do not consider the wake region (see Fig. 17), the results suggest that the noise radiation at region i is not directly contributed by the boundary layer interactions with the trailing edge surface. Rather, it could be produced by other hydrodynamic processes, such as the turbulent wake merging as was conjectured previously.

Although this paper is intended primarily to demonstrate the robustness of the deterministic turbulent boundary layer method for the study of aerofoil trailing edge noise mechanism, the results presented in this section confirm that the serrated edge can affect significantly the growth of the turbulent flow, which can directly link to the reduction of the trailing edge noise. Additional results from this study also reveal that the reduction of the turbulence level in Fig. 18d is caused by the mixing with a dominant streamwise vortical structure at each sawtooth. More in depth discussion about this topic will be reported elsewhere. We believe that the manipulation and reduction of turbulence flow field by a serrated edge also contributes to the reduction of broadband trailing edge self-noise, and it may coexist with the acoustical destructive interference mechanism promoted by Howe (1991) and Lyu et al. (2016). Future research efforts are needed to reconcile these two mechanisms.

6 Conclusions and outlooks

The main objective of the current work is to develop an experimental technique that can exploit the deterministic turbulent boundary layer generated under a base flow of either mildly separated or laminar boundary layer to study the aerofoil self-noise source mechanisms in the spatial, temporal and frequency domains. One of the main attractions of this technique is that the experimental tool does not need to be extremely high fidelity as a priori in order to be able to capture the pseudo time-resolved boundary layer instability or turbulent structures. For examples, the dynamics of the roll-up vortices of the order of $\sim$ kHz can be resolved by a 15-Hz PIV. Another example is the reconstruction of turbulent/coherent structures in space and time by a single hot wire probe. In other words, the proposed technique can provide very high spatial and temporal resolutions. Obviously, the reliance on the ensemble (or phase) averaging technique by the current method would inevitably smear out the finest and smallest turbulence eddies, which represents a limit on the reconstruction of the turbulence structure. For the aeroacoustics purposes, such as the study of the trailing edge noise mechanisms, the main turbulent energy-containing structure that are predominantly influential at the low and mid frequency regions can still be reconstructed accurately by the proposed experimental technique. The very fine turbulence structures, on the other hand, are usually only relevant at high frequency, and therefore less important from the aeroacoustics’ point of view.

The proposed experimental technique can be extended to other self-noise scenarios when the aerofoil trailing edge is subjected to different flow control treatments, such as the porous structure, surface texture, or finlet, whose mechanisms are largely not understood very well at present. Similarly, deterministic turbulence in free flow can also be generated by the active turbulence grid method. Applying the same principle of spatio–temporal capturing of the hydrodynamic field and acoustic far-field, the proposed technique can be extended to the turbulence–leading edge interaction noise.