Utilizing APTV to investigate the dynamics of polydisperse suspension flows beyond the dilute regime

Abstract

We present a methodology that allows to measure the dynamics of polydisperse suspension flows by means of Astigmatism Particle Tracking Velocimetry (APTV). Measurements are successfully performed with tridisperse suspensions flows in a square duct of up to $\varPhi =9.1\%$ particle volume fraction. Using a refractive index matching technique, a small amount of the particles ($\varPhi =0.08\%$) is labeled with fluorescent dye to be visible to the camera during the particle tracking procedure. Calibration measurements are performed for ten different particles diameters $d_p$ ranging from $d_p= {15}\upmu \mathrm{m}$ to $d_p= {260}\,\upmu \mathrm{m}$. It is shown that Euclidean calibration curves of different $d_p$ overlap outside the focal planes, which induces ambiguities in a polydisperse APTV measurement. In the present approach, this ambiguity can be overcome utilizing the light intensity of a particle image which increases sharply with $d_p$. In this way, extended Euclidean calibration curves can be generated for each particle group which are spatially separated through the light intensity which serves as an additional calibration parameter (Brockmann et al. in Exp Fluids 61(2):67, 2020). The extended Euclidean calibration allows to simultaneously differentiate particles of different sizes and determine their 3D location. This facilitates to investigate the migration behavior of mono- and tridisperse suspension flows which we demonstrate here for square duct flows with cross-sectional areas of $0.6\times 0.6\,\mathrm{mm}^2$ and $0.4\times 0.4\,\mathrm{mm}^2$ at bulk Reynolds numbers of $\mathrm{Re}_b \approx 20$ and $\mathrm{Re}_b \approx 40$ for particle volume fractions of $\varPhi =0.08\%$ and $\varPhi =9.1\%$. At $\varPhi =0.08\%$ and $\mathrm{Re}_b=20$, we observe particles to arrange themselves in a ring-like formation inside the capillary, henceforth referred to as Pseudo Segré Silberberg Annulus (PSSA), with no significant differences between mono- and polydisperse suspension particle distributions. At $\varPhi =9.1\%$, particles in monodisperse suspensions scatter around the PSSA. This scattering decreases when $d_p$ increases or $Re_b$ increases from 20 to 40. Striking differences are observed in polydisperse suspensions. Large particles (${60}\,\upmu \mathrm{m}$) scatter significantly less around the PSSA in the polydisperse case compared to a monodisperse suspension of the same overall volume fraction. In contrast, small and intermediate particles ( ${30}\,\upmu \mathrm{m}$, ${40}\,\upmu \mathrm{m}$) are repelled by larger particles resulting in regions of high concentration close to the channel walls which can be only observed in the polydisperse case.

Graphical abstract

1 Introduction

Suspension flows of rigid particles are found in numerous natural and technical settings. These are for instance the flow of blood cells, sediment transport in rivers, mudslides or inkjet printing (Morris 2020). In fact, the vast majority of these flows is polydisperse, while monodisperse suspensions are rather an exception. Therefore, understanding the underlying physics of polydisperse suspension flows is of high interest for both fundamental research and technical applications. One of the most interesting phenomena encountered in such flows is the effect of size segregation (Lyon and Leal 1998; Blahout et al. 2020). In laminar flows, particle segregation is usually the result of particle migration dynamics normal to the streamline orientation. In general, two mechanisms are well known that can cause particle migration in suspension flows and potentially lead to size segregation: Shear-induced migration and inertial migration.

Shear-induced migration emerges from particle interactions in concentrated monodisperse suspensions. At low particle Reynolds numbers ($\mathrm{Re}_p<< 1$), it leads to a migration of particles from regions of high shear rate to regions of low shear rate (Leighton and Acrivos 1987; Guazzelli and Morris 2011). If brownian motion of particles comes into play, the rate of migration depends on the Peclet number in such scenarios (Frank et al. 2003; Semwogerere et al. 2007; Kang and Mirbod 2020). Moreover, while shear-induced migration is usually associated with higher volume fractions, experimental evidence for shear-induced migration was also reported at volume fractions of $\varPhi <4\%$ (Brown et al. 2009; Abbas et al. 2014).

In polydisperse suspensions, migration speed of particles varies. In bidisperse suspensions, it was observed that larger particles migrate faster to the regions of low shear and screen off smaller particles which induces a size segregation. Likewise, it was also found that smaller particles migrate faster and screen off larger particles if their volume fraction is considerably higher (Husband et al. 1994; Lyon and Leal 1998; Semwogerere and Weeks 2008; Chun et al. 2019). Thereby, the overall rate of migration seems to be reduced in a bidisperse suspension compared to a monodisperse suspension such that concentration profiles develop slower (Gao et al. 2009; Van Dinther et al. 2013; Chun et al. 2019).

Inertial migration instead results from the interaction of individual particles with the ambient fluid, usually at higher particle Reynolds numbers ($\mathrm{Re}_p\gtrapprox 0.1$). Thereby, the particle experiences lift forces which induce a particle drift lateral to the main flow direction. The migration motion of a particle comes to a hold at its so-called equilibrium position (EP) where particle forces are balanced. In pipe-flows, this equilibrium position has an annular shape and is widely known as the Segré-Silberberg effect (Segre and Silberberg 1962; Matas et al. 2004; Choi and Lee 2010). Besides this, Segré-Silberberg annulus at certain conditions also an additonal inner annulus can appear (Matas et al. 2004; Morita et al. 2017). In square channels, a variety of equilibrium positions exist. Here, particles first lateral migrate on a square-shaped Pseudo Segré-Silberberg Annulus (PSSA) and then migrate cross-laterally to the channel faces. At higher Reynolds numbers, particles collect on additional EPs in the corners or at intermediate positions (Choi et al. 2011; Miura et al. 2014; Nakagawa et al. 2015; Shichi et al. 2017). Thereby, the rate of migration at which particles migrate to the EPs depends on the particle size. In fact, particles of different size experience different lift forces and therefore different lateral drift velocities (Martel and Toner 2014; Zhang et al. 2016).

Furthermore, the recent study of Udono (2020) showed that increasing particle volume fraction can give rise to hydrodynamic particle interactions resulting in a breakdown of distinct inertial focusing such that particles scatter around the EP.

Even though shear-induced and inertial migration are usually associated with different Reynolds numbers, they can also simultaneously affect the distribution of particles (Han et al. 1999; Abbas et al. 2014).

In fact, recent studies revealed that the interplay of shear induced-migration and inertial migration may result in complex particle distribution patterns and affect the bulk flow. This accounts for flows in straight channels (Kazerooni et al. 2017; Chun and Jung 2021) as well as asymmetric T-junctions (Manoorkar et al. 2018). For instance, in the latter case, the coupling of both migration mechanisms results in a strikingly different ratios of fluid and particle flow rate in the two junction branches depending on particle volume fraction and Reynolds number.

Numerical studies show for suspension flows in square ducts that monodisperse suspension particles scatter increasingly around the inertial EP as the volume fraction increases from $\varPhi =0.4\%$ to 10% up to the point where particles are distributed homogenously across the whole cross section for $\varPhi =20\%$ and a Reynolds number of $\mathrm{Re}_b=550$ (Kazerooni et al. 2017). Furthermore, at $\mathrm{Re}_b=140$ and $\varPhi =20\%$, particles were observed to migrate to the duct center which is typical for shear-induced migration, although the particle Reynolds number was significantly higher than usually associated with this migration mechanism $(\mathrm{Re}_p=1.7)$. The authors further observed that the presence of particles induces secondary cross-stream motions in the duct cross section. The magnitude of this secondary flows first increases with increasing $\varPhi$ and then decreases again as $\varPhi$ increases further and is about of 0.2% to 0.4% of the bulk velocity.

Recently, Chun and Jung (2021) numerically investigated the particle distribution of mono- and bidisperse suspensions resulting from the interplay of shear-induced and inertial migration for $0.003\le \mathrm{Re}_p\le 0.94$ at $\varPhi =20\%$ in linear shear flow. At $\mathrm{Re}_p\ge 0.078$, smaller particles enriched in the mid plane, while larger particles maintained a uniform distribution. While the distribution of small particles was found to be unchanged in bidisperse suspensions, their presence leads to a strikingly different distribution of large particles compared to the monodisperse case that became pronounced with increasing $\mathrm{Re}_p$. To our knowledge, the work of Chun and Jung (2021) is the only work considering polydisperse suspensions at finite Reynolds numbers and so far no experimental work has been performed in shear flows at finite Reynolds numbers comparable to the work of Kazerooni et al. (2017).

This may be related to the opaque nature of suspension flows at higher volume fractions such that usually sophisticated measurement techniques such as positron Emission Particle Tracking (Barigou 2004; Liu and Barigou 2015), Magnetic Resonance Imaging (Han et al. 1999; Hampton et al. 1997) or modified Laser Doppler Velocimetry (Lyon and Leal 1998) are employed which makes the experiments costly and time consuming. An alternative to these sophisticated techniques is to employ the refractive index matching (RIM) technique and utilize optical methods. Optical methods facilitate high temporal and spatial resolution and are available in virtually all laboratories (Poelma 2020; Tropea et al. 2007). For instance, recently refractive index matching (RIM) technique has been successfully employed to measure the particle trajectories in symmetric T-channels using two synchronized high speed cameras (Manoorkar and Morris 2021).

Another challenge is that geometries with high length over width aspect ratios are required for migration effects resulting in developed concentration profiles. This demands for large setups when performed on the macroscale (Hampton et al. 1997; Shichi et al. 2017). Therefore, experiments in the present paper are performed in a microscale setup and Astigmatism Particle Tracking Velocimetry (APTV) is utilized to extract the three-dimensional particle positions and velocities.

APTV is a single camera technique, where astigmatism is introduced into the optical path resulting in a specific deformation of the particle image depending on the depth position of particles. A detailed overview on APTV, its applications and its background is given by Cierpka and Kähler (2012). While APTV is commonly applied on small tracer particles ($d_p< {5}\,\upmu \mathrm{m}$) to measure fluid motion, recently the technique is extended to larger particles and applied on suspension flow problems. Using APTV, Blahout et al. (2020) investigated the fractionation of $d_p= {3.55}\,\upmu \mathrm{m}$ and $d_p= {9.87}\,\upmu \mathrm{m}$ particles at very low particle concentrations inside a serpentine channel. Distinguishing large and small particles by their individual astigmatism characteristics, they were able to simultaneously measure the motion of both particle species. Koenig et al. (2020) applied APTV on a laminar bidisperse suspension flow of ${2.5}\,\upmu \mathrm{m}$ and ${5}\,\upmu \mathrm{m}$ particles in a rectangular channel and observed that the calibration curve for both particle species overlaps close to the focal planes which causes ambiguities. They solved this problem by using a cascaded convolutional neural network algorithm to distinguish between different particle species and could successfully validate their approach. Brockmann et al. (2020) developed an adapted APTV procedure, referred to as Ball Lens Astigmatism Particle Tracking Velocimetry (BLAPTV), for large transparent particles and showed that calibration curve shape, maximum light intensity, depth reconstruction accuracy and the measurement volume depth depend on $d_p$. They also extended the Euclidean calibration approach developed by Cierpka et al. (2010) by additionally considering the light intensity of particles as a calibration parameter. Further, the recent work of Brockmann and Hussong (2021) successfully applied APTV to measure particle dynamics in neutrally buoyant suspensions of up to $\varPhi =19.9\%$ using a RIM technique. To compensate the effect of optical distortions induced by suspension particles, they adapted an interpolation procedure developed by Brockmann et al. (2020) and validated their method in a channel flow.

In the present study, based on the extended Euclidean calibration (EEC) of Brockmann et al. (2020), we develop an APTV procedure which can be applied to polydisperse suspensions at high volume fractions. We utilize the EEC for a proper differentiation between the different particles sizes. Combining this EEC calibration together with RIM, we successfully investigate particle migration in both mono- and tridisperse suspension duct flows at volume fractions of $\varPhi =9.1\%$.

2 Experimental setup

We employ two experimental configurations for investigating the mono- and polydisperse particle dynamics by means of APTV. In setup 1, the optical path is perpendicular to the main flow direction (see Fig. 1), while in setup 2, the optical path is parallel to the main flow direction as shown in Fig. 2. Setup 1 and setup 2 will be hereafter referred to as Lateral View Setup (LVS) and Front View Setup (FVS), respectively. As in APTV, the largest position reconstruction error occurs in the out-of-plane direction, the LVS allows to perform the experiments with a high accuracy in the velocity profile reconstruction. In contrast, the FVS faciliates a high accuracy in determining the cross-sectional particle distribution. Additionally, to the astigmatic measurements, we perform stigmatic measurements without a cylindrical lens in the FVS for validation of particle distributions reconstructed over the cross-sectional area by means of APTV.

2.1 Setup 1: lateral view setup (LVS)

Setup 1 consists of a custom built microscope based on a tube (Infinity Photo Optical InfiniTube Special) illuminated with a 2.4 W High Power LED (Thorlabs SOLIS-525C) featuring a peak wavelength of $\lambda = {525}\,\mathrm{nm}$. For directing the light through the objective and filtering the fluorescence signal, a filter cube (Thorlabs DFM1/M) with a dichroic mirror and two band-pass filters is installed in the optical path. For image-recording a 12-bit, $1280\times 800$ pixel CMOS high-speed camera (Phantom Miro Lab 110, Vision Research) with $20\times {20}\upmu \mathrm{m}^2$ pixel size is used. A schematic drawing of the experimental setup is shown in Fig. 1. Measurements are performed with a Nikon Cfi60 objective lens of $M=10\times$ magnification. Using a resolution of $512\times 384$ pixels, the field of view spans $992\times {744}\upmu \mathrm{m}^2$. To introduce astigmatism, a cylindrical lens with a focal length of $f_{cyl}= {150}\,\mathrm{mm}$ is placed in front of the camera sensor, generating two spatially separated focal planes with a measured distance of approximately ${110}\,\upmu \mathrm{m}$ for a refractive index of air ($n_o=1$). A similar configuration has been already used by Brockmann et al. (2020) with a bright field illumination and Brockmann and Hussong (2021) with a constant wave laser. For the present experiments, square duct capillaries (VitroCom) with a cross-sectional area of $H\times W= 400\times {400}\upmu \mathrm{m}^2$ and $600\times {600}\upmu \mathrm{m}^2$ and a length of $L= {500}\,\mathrm{mm}$, 600 mm, respectively, were utilized. Velocity profiles were measured 450 mm downstream of the channel entrance such that a minimum ratio of $L/H\approx 750$ was ensured. The flow is generated with a high pressure syringe pump (LA-800, Landgraf HLL GmbH) and a 10 mL syringe (Braun GmbH). For reducing the reflections by the curved channel corners of the capillary, the capillary is submerged into glycerol. For obtaining a density and refractive index matched suspension with PMMA particles of ${30}\,\upmu \mathrm{m}$, ${40}\,\upmu \mathrm{m}$ and ${60}\,\upmu \mathrm{m}$ diameter (Microbeads), we have used the receipe proposed by Bailey and Yoda (2003) with a ternary mixture of 26.46wt% water, 32.30 wt% glycerin and 41.24 wt% ammonium thiocyanate that has a refractive index of $n_{\text {RIM}}=1.4882$, a density of $\rho _{\text {RIM}}= {1.19}\mathrm{g}\mathrm{cm}^{-3}$ and a dynamic viscosity of $\eta _{\text {RIM}}= {4.99}\mathrm{c P}$. The refractive index was checked with a digital refractometer (DR301-95 KRUESS Optronic GmbH). The tracer particles are labeled with Rhodamine B (Carl Roth). The (bulk) solid volume fraction or particle volume fraction represents the average solid volume fraction in the fluid. It is defined as $\varPhi =V_{\text {particles}}/V_{\text {total}}$, where $V_{\text {particles}}$ is the volume of the particles and $V_{\text {total}}$ is the combined volume of liquid and particles ($V_{\text {total}}=V_{\text {particles}}+V_{\text {liquid}}$). While the bulk solid volume fraction is fixed in the experiments, the local values of $\varPhi$ (denoted as $\varPhi _\text {loc}$) may vary as a result of particle migration.

2.2 Setup 2: front view setup (FVS)

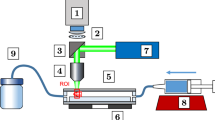
Setup 2 is schematically depicted in Fig. 2. It incorporates the identical camera, tube, filter cube, objective and syringe pump as in setup 1 but the measurement section is illuminated with a 7 W high power LED (7) (ILA iLA.LPS v3) equipped with a green LED chip ($\lambda \approx {532}\,\mathrm{nm}$). The measurements are performed with M=10$\times$ at a resolution of $512\times 512$ pixel resulting in a field of view of $992\times {992}\upmu \mathrm{m}^2$ such that the whole cross-sectional area of the capillary is captured. Measurements are performed with and without a cylindrical lens of $f_{cyl}= {150}\,mm$ placed in front of the camera sensor.

The camera and corresponding optics are aligned on the capillary centerline axis. Images are taken through a borosilicate glass coverslip (Marienfeld) with a thickness of approximately 0.13 mm and a diameter of 30 mm as depicted in Fig. 2. The camera together with LED and optical components can be precisely traversed in x, y, z direction in steps of ${1.25}\,\upmu \mathrm{m}$. The capillary is mounted on a traverse and can be positioned in steps of ${2.5}\,\upmu \mathrm{m}$ in z-direction such that the distance with respect to the glass coverslip can be adjusted. The fluid driven through the capillary is collected in a tub and drained into a container. In setup 2, experiments are performed within a square capillary of $600\times {600}\,\upmu \mathrm{m}^2$ and a length of $L= {600}\,\mathrm{mm}$. Velocity profiles were measured approximately ${250}\,\upmu \mathrm{m}$ to ${500}\,\upmu \mathrm{m}$ upstream of the capillary outlet such that a ratio of flow length to duct height of $L/H\approx 1000$ was obtained. The RIM liquid and particles used in setup 1 and 2 are identical.

Fig. 1

Sketch of setup 1 (LVS): (1) Camera, (2) Cylindrical lens and field lens, (3) Dichroic mirror with band-pass filters, (4) Microscope objective, (5) Square capillary submerged in glycerol, (6) x,y,z-Traverse, (7) High power LED, (8) Syringe Pump, (9) Bottle

Fig. 2

Sketch of setup 2 (FVS): (1) Camera, (2) Cylindrical lens and field lens, (3) Dichroic mirror with band-pass filters, (4) Microscope objective, (5) Square capillary, (6) z-Traverse, (7) High power LED, (8) Syringe Pump, (9) Bottle (10) x, y, z-Traverse (11) Coverslide (12) Tub with drainage

Fig. 3

Principle sketch of APTV. Positive z-direction refers to moving optical system to the right. a Optical system in x-z plane b Optical system in y-z plane c Resulting image

3 Calibration procedure

The principle of APTV is based on a cylindrical lens which is placed in the optical path of a microscope and generates two spatially separated focal planes $F_{xz}$ and $F_{yz}$. The images of particles which are located at a depth position midway between these planes appear circular and transform to a horizontally or vertically aligned ellipse when the particles are located closer to $F_{yz}$ or $F_{xz}$, respectively (see Figs. 3 and 5). Hence, the horizontal axis length $a_x$ and the vertical axis length $a_y$ of the particle image, viz. the particle diameter stretched in x or y direction, are a function of the particle’s depth position. The depth position will be hereafter also referred to as z position or out-of-plane position.

The variation in $a_x$ and $a_y$, with the out-of-plane position, can be described by equation (1) as derived by Cierpka et al. (2010) and based on the model of Olsen and Adrian (2000):

$$\begin{aligned} \begin{aligned}&a_i(z_i)= \\&M\sqrt{d_p^2+1.49 \lambda ^2 \left( \frac{n_0^2}{NA^2}-1\right) +4(z_i)^2 \left( \frac{n_0^2}{NA^2}-1\right) ^{-1}} \\&i=x,y \end{aligned} \end{aligned}$$

(1)

with $z_i=z-F_{iz}$ being the distance between particle and respective focal plane. The variables $d_p$, $\lambda$, $n_0$, M, NA are the particle diameter, the wavelength emitted by the particle, the refractive index of the liquid, the magnification and the numercial aperture of the objective, respectively.

Fig. 4

Plots of the axis lengths $a_x$ and $a_y$ obtained with Eq. (1) for $\lambda = {590}\mathrm{nm}$, $n_0=1$, $M=10$, $NA=0.3$ and selected values of $d_p$. White filled dots and squares indicate the $a_x$, $a_y$ values at the focal planes $F_{yz}$ and $F_{xz}$, respectively. Increasing z is associated with traversing the objective as depicted in Fig. 3. a $a_x$ (solid line) and $a_y$ (dashed line) as function of $z-z_0$ b $a_y$ as function of $a_x$

In Fig. 4a, we display $a_x$ and $a_y$ as function of $z-z_0$ obtained with Eq. (1) for different values of $d_p$. The reference position $z_0$ here refers to the scanning position where the particle is focused in $F_{xz}$. As can be seen, $a_x$ and $a_y$ first decrease down to a minimum and then increase again as $z-z_0$ increases. Thereby, the curves of $a_y$ and $a_x$ are staggered and the minimum values occur at $F_{yz}$ and $F_{xz}$, respectively. With increasing $d_p$, the values of $a_x$ and $a_y$ increase and the curvature close to the minimum decreases. Further, the total change of $a_x$ and $a_y$ becomes less pronounced as $d_p$ increases. Hence, in theory, for a given optical setup, the resolution for reconstructing the particle’s depth position decreases with increasing particle diameter $d_p$.

The difference between small and large particles becomes more clear when $a_y$ is plotted over $a_x$ as depicted in Fig. 4b. This presentation is fundamental for the Euclidean calibration procedure, which will be described later in the text. As can be seen in Fig. 4b, with increasing $d_p$, the curves are shifted toward larger values of $a_x$ and $a_y$, while at the same time, the maximum change of $a_x$ and $a_y$ over the same z-range decreases significantly. Hence, the resolution of z-position reconstruction reduces for increasing $d_p$ as concluded from Fig. 4a. Furthermore, it becomes evident from Fig. 4b that, especially for smaller $d_p$, the curves collapse outside the focal planes which are highlighted as white filled dots and squares in Fig. 4b.

For reconstructing a real particles z position depending on its $a_x$ and $a_y$ values, a calibration function, generated from recorded images, is needed. For this, we utilize the extended Euclidean calibration (EEC) procedure as developed by Brockmann et al. (2020). This calibration method requires a homogenous light distribution across the image to work properly, which we ensure by using a high power LED for illumination. In the following, we summarize the basic steps of the calibration procedure for an exemplary set of fluorescent PMMA particles of ${30}\,\upmu \mathrm{m}$ and ${60}\,\upmu \mathrm{m}$.

Fig. 5

Particle images for different $z-z_0$ obtained in calibration measurements ($n_0=1$, $M=10\times$). Particle images are not to scale. Increasing z is associated with traversing the objective as depicted in Fig. 3. a $d_p= {15}\,\upmu \mathrm{m}$ b $d_p= {60}\,\upmu \mathrm{m}$ c $d_p= {155}\,\upmu \mathrm{m}$

Fig. 6

Axis lengths $a_x$ and $a_y$ over $z-z_0$ as well as $a_y$ over $a_x$ for particles of ${30}\,\upmu \mathrm{m}$ (thin colored line) and ${60}\,\upmu \mathrm{m}$ (bold colored line) for $n_0=1$ (air) and $M=10\times$ (Setup 1). Dashed uni-color line= theoretical curve for $a_x$, solid uni-color line= theoretical curve for $a_y$, red= ${60}\,\upmu \mathrm{m}$ particles, blue= ${30}\,\upmu \mathrm{m}$ particles. a $a_x$ and $a_y$ over $z-z_0$ b $a_x$ and $a_y$ over $z-z_0$ c $a_y$ over $a_x$ d $a_y$ over $a_x$

To obtain the change of $a_x$ and $a_y$ for different particle depth positions, labeled and wall attached particles are scanned in steps of ${1.25}\,\upmu \mathrm{m}$ over a distance of ${1000}\,\upmu \mathrm{m}$. Fig. 5 shows the result of such a scan for fluorescent PMMA particles located on a glass plate. In each recorded frame, the individual particle centroids are detected by binarizing the image and applying the MATLAB function “regionprops”. The threshold for binarizing the image within this step is defined as the median of the whole image intensity. For extracting the $a_x$ and $a_y$ from the individual particle images in the next step, we employ two different approaches, which will be compared in the following.

In the binarization approach, the particle image is cropped out by a rectangular section and binarized using MATLAB’s “imbinarize”. The $a_x$ and $a_y$ values are then extracted using MATLAB “regionprops” subfunctions “major axis” and “minor axis”. For the autocorrelation method, the particle image is cropped out by a circular section around the detected particle centroid at a defined radius of $3.6 \cdot d_p/px$. Hence, the cropped particle image is autocorrelated and the isoline, where the autocorrelation coefficient is equal to $c_a$, is extracted. $a_x$ and $a_y$ are then given as the maximum x and y span of the isoline. $c_a$ is denoted as the autocorrelation coefficient as introduced by Brockmann et al. (2020) and set to $c_a=0.5184$ within this work.

Fig. 7

Maximum light intensity I of the particle image over $z-z_0$ for particles of diameter ${30}\,\upmu \mathrm{m}$ (thin colored line) and ${60}\,\upmu \mathrm{m}$ (thick colored line)

Fig. 8

Procedure of generating a calibration function ($c_a=0.518$, $c_I=0.3$, $a_D=2$ pixel $M=10\times$, $d_p= {60}\,\upmu \mathrm{m}$). Measurement perfomed on a microscope slide in air. Scale of colormap is given in 8c. a A $z-z_0$ range of scattered data is selected by light intensity I (light blue dots=$a_x$, dark blue dots=$a_y$, green dots=I, black dots=${\tilde{I}}$). b A polynominal is fitted to $a_x$ and $a_y$. c The relative position $z-z_0$ of scattered $a_x$-$a_y$ data (colored dots) is reconstructed by the 2D Euclidean distance method (black line=polynomials, red dots=outliers). d A polynomial is fitted to I data (black line). e Reconstruction of $z-z_0$ of scattered $a_x$-$a_y$-I data (colored dots) by extended Euclidean calibration (black line=polynomials, red dots=outliers)

$a_x$ and $a_y$ as function of z-$z_0$ obtained with the two aforementioned methods are displayed in Fig. 6a,b together with the theoretical curves calculated with Eq. (1). By comparing the data for $d_p= {30}\,\upmu \mathrm{m}$ (thin colored line) and $d_p= {60}\,\upmu \mathrm{m}$ (thick colored line), it can be seen that the measured $a_x$, $a_y$ values increase with increasing particle size for both the autocorrelation method and the binarization approach. Obviously, the data obtained with the autocorrelation method coincide with equation (1) inbetween the focal planes but deviate significantly from the theroetical curves outside the focal planes (Fig. 6a). In contrast, the $a_x$, $a_y$ data obtained with the binarization approach match well with the theroretical data (Fig. 6b).

In Fig. 6c,d, we show $a_y$ plotted over $a_x$ which is required for the Euclidean calibration (Cierpka et al. 2010; Brockmann et al. 2020; Brockmann and Hussong 2021). Obviously here, for both the autocorrelation and the binarization approach, the curves for the small particles (small dots) and the large particles (large dots) intersect (Fig. 6c,d). Hence, if both curves are considered together, they do provide ambiguous data in the $a_x$, $a_y$ space. In contrast, the maximum particle light intensity $I(z-z_0)$ differs significantly for both particle sizes as can be seen in Fig. 7. Hence, by combining $I(z-z_0)$ and $a_x(z-z_0)$, $a_y(z-z_0)$, an unambiguous dataset is obtained. In Sect. 4, we will use this combination of data to generate unambiguous extended Euclidean calibration curves for polydisperse suspensions. Compared to the autocorrelation approach, the binarization approach is less robust to changes in the light intensity and variations in the signal-to-noise ratio which occur in flow measurements. Hence, we restrict the following considerations to the autocorrelation method.

Fig. 9

Conventional (CEC) and extended Euclidean calibration (EEC) curves for particles of different diameters. a CECs for ${15}\upmu \mathrm{m} \le d_p\le 60\upmu \mathrm{m}$. b EECs for ${15}\upmu \mathrm{m}\le d_p\le 60\upmu \mathrm{m}$. c CECs for ${140}\upmu \mathrm{m}\le d_p \le {290}\upmu \mathrm{m}$. d EECs for ${140}\upmu \mathrm{m}\le d_p\le{290}\upmu \mathrm{m}$

In general, to obtain a calibration curve, we perform the procedure developed by Brockmann et al. (2020). In the following, we present the basic steps of the procedure applied on our data. To generate a calibration curve to be used in a velocity measurement, the calibration data of several particles randomly distributed in the field of view are required. By this individual deviations in particle shape, labeling and minor optical aberrations are accounted for statistically. In Fig. 8a, we show a set of scattered $a_x$, $a_y$ and I data obtained from 25 ${60}\,\upmu \mathrm{m}$ particles. As first step, we determine the median of $I(z-z_0)$, which is represented by the black line in Fig. 8a and referred to as ${\tilde{I}}$. Hereafter, only data points associated with $I \ge c_I \cdot {\tilde{I}}_{\text {max}}$ are evaluated and $c_I$ is referred to as the intensity coefficient. We define further an intensity threshold as $I_{thr}=c_I \cdot {\tilde{I}}_{\text {max}}$. A detailed discussion about the influence of $c_I$ is provided in Brockmann et al. 2020. Subsequently, polynomials are fitted to the $a_x$ and $a_y$ scatter data (Fig. 8a). Preliminary tests showed that a polynomial degree of at least 14 (as utilized here) is required to adapt to the different sets of calibration data that arise from different magnifications, particle sizes and processing parameters such as the autocorrelation coefficient (Brockmann and Hussong 2021). By plotting the fits of $a_y$ (denoted as $\overline{a_y}$) over the fit of $a_x$ (denoted as $\overline{a_x}$), the conventional Euclidean calibration (CEC) curve is obtained (Fig. 8c). Now the depth position of a particle can be determined by relating its measured $a_x$, $a_y$ values to a point on the calibration curve that is given by the minimum Euclidean distance and hence reading out the corresponding $z-z_0$ value (Cierpka et al. 2010). If the Euclidean distance of a $a_x$-$a_y$ pair exceeds the threshold $a_D$, it is rejected as an outlier (Brockmann et al. 2020). As the scattering distance of the data depends on magnification, pixel size of the camera and the particle size, a practical approach to estimate a reasonable value for $a_D$ is to multiply the mean distance of all $a_x$-$a_y$ data by a factor $c_D$ as proposed by Brockmann et al. (2020). In the results in Fig. 8, $a_D$ is set to 2 pixel, which provides an overall depth reconstruction uncertainty of $\sigma _{z,CEC}= {7.83}\,\upmu \mathrm{m}$ and $N\approx 8916$ valid data points for $d_p= {60}\,\upmu \mathrm{m}$ particles and the Euclidean reconstruction procedure. With $c_I=0.3$, the measurement volume depth for the given example is $\varDelta z= {606.25}\,\upmu \mathrm{m}$ such that the ratio $\sigma _{z,CEC}/\varDelta z$ is 1.29%. If a polynomial is fitted to the I scatter data as shown in Fig. 8d and denoted as ${\overline{I}}$, it can be used to generate an Extended Euclidean calibration (EEC) curve as presented in Fig. 8e. $a_x$, $a_y$, I scatter data can now be assigned to this curve by means of the three-dimensional Euclidean distance. To ensure $a_x$, $a_y$ and I are in the same order, I and ${\overline{I}}$ are normalized by $I_{\text {max}}$ and multiplied by the maximum axis length as explained by Brockmann et al. 2020. Mathematically this factor, hereafter denoted as intensity scale factor, can be defined as

$$\begin{aligned} c_{s}=\frac{\text {max}[(\text {max}(a_x)-\text {min}(a_x));(\text {max}(a_y)-\text {min}(a_y))]}{I_{\text {max}}} \end{aligned}$$

(2)

Using the EEC, an overall depth reconstruction uncertainty of $\sigma _{z,EEC}= {5.45}\,\upmu \mathrm{m}$ is achieved for the given example such that $\sigma _z/\varDelta z$ equals 0.9%. With the EEC, 8167 valid data points are obtained. It is important to note that the gain in accuracy obtained with the EEC depends on how homogeneously the light intensity is among different particles of the same size. To demonstrate this effect, synthetic $a_x$, $a_y$, I scatter data were generated around the calibration curve presented in Fig. 8. The $a_x$, $a_y$, I scatter data are randomly distributed around the calibration curve following a random Gaussian distribution (MATLAB “mvnrnd”). An exemplary set of scattered data is presented in Fig. 10a. Different data sets were investigated with different ratios of the standard deviation of I and $a_x$ (where $\sigma (a_x)=\sigma (a_y)$). Hence, the z-position was reconstructed with both the CEC and the EEC for different standard deviation of the scatter data. Fig. 10b shows the uncertainty in reconstructing the z position of the synthetic data as function of $\sigma (a_x)$. As can be seen for $\sigma (I)/\sigma (a_x)=$ 0.25, 0.5, 1 and 1.5, the extended Euclidean calibration yields a higher accuracy, compared to the conventional. Instead for $\sigma (I)/\sigma (a_x)=2$ and 3, the EEC yields a lower accuracy. For $\sigma (I)/\sigma (a_x)=1.75$, there is no significant difference in the accuracy achieved with CEC and EEC. In general, the uncertainty in reconstructing the depth position increases linearly with increased scattering (Fig. 10b) for both the CEC and EEC.

Fig. 10

Utilizing synthetic scatter data for comparison of the CEC and the EEC. The calibration curve corresponds to Fig. 8e. a Exemplary plot of synthetic scatter data around calibration curve. Data scatter around each point with a standard deviation of $\sigma (a_x)=\sigma (a_y)=\sigma (I)=$ 2 pixel. b Comparison of uncertainty in reconstructing the depth position with CEC and EEC as a function of $\sigma (a_x)$ ($\sigma (a_x)=\sigma (a_y)$) for different ratios of $\sigma (I)/\sigma (a_x)$.

4 Extended Euclidean calibration for different particle sizes

Fig. 11

Applying the extended Euclidean calibration (EEC) on mixed, scattered polydisperse calibration data. The reconstruction procedure is performed with the calibration curve for ${30}\,\upmu \mathrm{m}$ particles in a–d (black and turquoise line) and the calibration curve for ${140}\,\upmu \mathrm{m}$ particles in e-h (black and blue line). Symbols: Rejected data (gray), correct assigned data (green) and false assigned data (magenta) according to CEC or EEC. $c_a=0.51$, $c_I=0.3$, $M=10\times$. Results are exemplary for $a_D=$ 2 pixel (a–d) and $a_D=$ 4 pixel (e–h). a, c Calibration data for ${15}\upmu \mathrm{m}\le d_p\le {60}\upmu \mathrm{m}$ (a: CEC, c:EEC). b, d Histogram for ${15}\upmu \mathrm{m} \le d_p \le {60}\upmu \mathrm{m}$ (b: CEC, d:EEC). e,g) Calibration data for ${140}\upmu \mathrm{m} \le d_p \le {290}\upmu \mathrm{m}$ (e: CEC, g:EEC). f, h Histogram for ${140}\upmu \mathrm{m} \le d_p \le {290}\upmu \mathrm{m}$ (f: CEC, h:EEC)

As discussed in Sect. 3, the CEC calibration curves for particles of different size intersect outside the focal planes creating ambiguities. Hence, in a polydisperse suspension, flow particles of different size can not be assigned correctly to the calibration curve. To overcome this problem, Koenig et al. (2020) successfully employed a cascaded convolutional neural network to distiuingish between particles of different size. We use a different approach here and utilize the EEC to differentiate particle species thereby exploiting the fact that the particle light intensity increases sharply with increasing particle size. In Fig. 9, we present the CEC and the EEC curves for different smaller (${15}\upmu \mathrm{m}\le d_p \le {60}\upmu \mathrm{m}$, Microbeads) and larger particles (${140}\upmu \mathrm{m}\le d_p \le {290}\,\upmu \mathrm{m}$, Altuglas). Due to slightly different material properties, the small particles (Microbeads) provide a higher light intensity in relation to their size than the large particles (Altuglas) such that we present them separately. Here, we only present calibration curves obtained with the autocorrelation method as this method is employed in the flow measurements in Sect. 5.3. It can be seen clearly that the CEC curves intersect each other outside the focal planes. In contrast, the EEC curves are well separated from each other as the light intensity strongly correlates with $d_p$. Please note that we display the absolute value of ${\overline{I}}$ instead of the normalized ${\overline{I}}$.

In the following, we will generate a test case close to measurement conditions on which we demonstrate the application of the extended reconstruction procedure on mixed, scattered polydisperse $a_x$, $a_y$, I data. For this, the calibration data of different particle sizes are mixed, while also erroneous $a_x$, $a_y$ data are included. This erroneous data can be seen exemplary for $d_p= {60}\,\upmu \mathrm{m}$ particles in Fig. 8 outside the dashed vertical bars. This is achieved by setting $c_I$ to zero. However, the calibration curves for the individual particle sizes are still obtained with $c_I=0.3$ which corresponds to the calibration curve as shown in Fig. 8. As the calibration data are generated by a scanning procedure on static particles, the particle size as well as the out-of-plane position of each data point is known and we can evaluate the uncertainty in determining the particle size as well as the depth position. In Fig. 11a, we present the CEC curves for particles of $d_p=15, 30, 40$, ${60}\,\upmu \mathrm{m}$ as shown in Fig. 9 together with the calibration data. For this example, the reconstruction procedure was applied to the curve for ${30}\,\upmu \mathrm{m}$ particles (black and turquoise line). Data that are assigned correctly to the calibration curve for ${30}\,\upmu \mathrm{m}$ are plotted as green dots, while rejected data are gray. Data that are highlighted with magenta dots originate from $d_p=15, 40$ and ${60}\,\upmu \mathrm{m}$ particles that were erroneously assigned to the calibration curve of ${30}\,\upmu \mathrm{m}$ particles. From Fig. 11a, it can be clearly seen that the CEC procedure yields a significant amount of erroneous detections outside the focal planes, where the calibration curves overlap. The amount of erroneously assigned $d_p=15$, 40 and ${60}\,\upmu \mathrm{m}$ particles is illustrated in the histogram in Fig. 11b. However, when the EEC is used for the reconstruction procedure, it can be seen that almost all the data points are correctly assigned to the corresponding calibration curve (Fig. 11c and d). This observation also accounts for the conventional and the extended Euclidean reconstruction procedure applied on the data of larger particles ($d_p=140$, 180, 220, 260, ${290}\,\upmu \mathrm{m}$) when utilizing for instance the calibration curve for $d_p= {140}\,\upmu \mathrm{m}$ (black and blue line), as can be seen from Fig. 11g and h. In fact, the EEC allows a reliable assignment of particle images to the correct calibration curve for all individual calibration curves depicted in Fig. 11a,c,e,g. The performance of CEC and EEC greatly depends on the threshold $a_D$. To investigate the influence of $a_D$, we performed the reconstruction procedure for $a_D$ ranging from 0.25 pixel to 4 pixel for the ${15}\,\upmu \mathrm{m}$, ${30}\,\upmu \mathrm{m}$, ${40}\,\upmu \mathrm{m}$ and ${60}\,\upmu \mathrm{m}$ particles. Table 1 provides an overview of the associated results. In Table 1, erroneous detections are denoted as $N_{\text {f,EEC}}$ and $N_{\text {f,CEC}}$ for reconstruction based on EEC and CEC, respectively. Correct detections are denoted as $N_{\text {c,EEC}}$ and $N_{\text {f,EEC}}$. We further compare the efficiency of EEC and CEC by computing the factor $\frac{N_{\text {c,EEC}}}{N_{\text {c,CEC}}} \frac{\sigma _{z,\mathrm{CEC}}}{\sigma _{z,\mathrm{EEC}}}$. This factor takes into account the number of correctly assigned particles as well as the uncertainty in determining the depth position of correctly assigned particles obtained with EEC and CEC.

As can be seen, the factor assumes values higher than one for all particle sizes which means that the EEC provides more valid particles and a lower uncertainty in determining the z-position of valid particles for almost all cases. Thereby, it can clearly be seen that with increasing $a_D$, the factor $\frac{N_{\text {c,EEC}}}{N_{\text {c,CEC}}} \frac{\sigma _{z,\mathrm{CEC}}}{\sigma _{z,\mathrm{EEC}}}$ increases as well. Hence, the EEC enables higher values of $a_D$ while maintaining a reliable assignement of particle images to the calibration curve. We recall here that a homogeneous distribution of the light intensity is paramount for the accuracy of the EEC. Increasingly inhomogeneous distribution of light intensity among the different particles will increase the uncertainty of depth position reconstructing as previously shown with regard to Fig. 10.

Table 1 Comparison of CEC and EEC reconstruction applied on polydisperse calibration data. $N_{\text {c,CEC}}$ and $N_{\text {c,EEC}}$ is the number of particles assigned to the correct curve with CEC and EEC calibration, respectively. Analogous, $N_{\text {f,CEC}}$ and $N_{\text {f,EEC}}$ are the number of incorrectly assigned particles

5 Comparison of monodisperse and polydisperse Suspension dynamics

5.1 Experimental procedure

To investigate the migration behavior of mono- and tridisperse suspensions, flow measurements are performed in a square duct with $400\times {400}\upmu \mathrm{m}^2$ and $600\times {600}\upmu \mathrm{m}^2$ cross section. The suspensions are composed of RIM-liquid as proposed by Bailey and Yoda (2003) and PMMA particles (Microbeads) of ${30}\,\upmu \mathrm{m}$, ${40}\,\upmu \mathrm{m}$ and ${60}\,\upmu \mathrm{m}$ diameter. The square duct is filled with RIM-liquid and labeled particles such that the (bulk) particle volume fraction is $\varPhi =0.08\%$. Due to slight density differences between RIM-liquid and particles, particles float to the top or settle to the bottom of the channel when the residence time in the square duct exceeds several minutes. In the absence of flow, these particles act as wall markers and are used to detect the absolute position of the duct and serve to set the origin of the z-coordinate as described in Brockmann and Hussong 2021. Subsequently, the syringe pump drives a constant suspension flow rate through the square duct into a container. Prior to the actual flow measurements, calibration measurements (as described in Sect. 3) are performed on the particles at the bottom of the channel to generate calibration curves for the three particle sizes (${30}\,\upmu \mathrm{m}$, ${40}\,\upmu \mathrm{m}$ and ${60}\,\upmu \mathrm{m}$). In the FVS, the calibration was performed on particles located on the glass coverslip, shown in Fig. 2.

Brockmann and Hussong 2021 showed that slight deviations of the refractive index of particles and RIM-liquid may lead to distortions of the particle images which become severe with increasing channel height. However, the height of the present ducts ($H= {400}\,\upmu \mathrm{m}$, ${600}\,\upmu \mathrm{m}$) is much less than that of the channel ($H= {2550}\,\upmu \mathrm{m}$) used by Brockmann et al. such that the distortions can be neglected here. After calibration measurements are completed, the actual flow measurements are performed for the monodisperse and the polydisperse suspension for $\varPhi =0.08\%$ and $\varPhi =9.1\%$ for different bulk Reynolds numbers. In the polydisperse measurements, the individual volume fraction of each single species is kept equal at 1/3 of $\varPhi =0.08\%$ and $\varPhi =9.1\%$. The amount of labeled particles is always $\varPhi =0.08\%$ and considered in the total volume fraction. In case of $\varPhi =0.08\%$, the suspension only contains labeled particles, while in case of $\varPhi =9.1\%$, the suspension contains both labeled and unlabeled particles.

During the flow measurements in the LVS, the duct is scanned in steps of ${74}\,\upmu \mathrm{m}$ or ${148}\,\upmu \mathrm{m}$ and 21500 images with a resolution of $512 \times 384$ pixel (Lateral view) at 300 fps up to 8354 fps are recorded at each measurement plane. By this, depending on the duct height, data from 6 to 9 individual measurement planes are captured. In the FVS, $4 \times 16{,}500$ images with a resolution of $512\times 512$ pixel are recorded at a single measurement plane located ${250}\,\upmu \mathrm{m}$ to ${500}\,\upmu \mathrm{m}$ upstream of the channel exit. To enhance the signal-to-noise ratio, a median filter with a kernel of a 5px $\times$ 5px and a bandwidth filter filtering structures of 3 to 70 pixels in diameter is applied (Cierpka et al. 2010). In the FVS, defocussed particles in the background lead to a significant reduction in the signal-to-noise ratio. As the light intensity of 40$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$ is significantly higher than that of the 30$\,\upmu \mathrm{m}$ particles, the backgroung noise affects the image quality of the latter ones the most. Therefore, we perform the polydisperse measurements in the FVS sequentially, with only one particle size labeled at the time. Further, an additional time series subtract median filter is applied to the data recorded in the FVS. After image post-processing, the particle positions and velocities are reconstructed. Hence, the $a_x$, $a_y$ and I of all detected particles from the different measurement planes are extracted using the autocorrelation method. While the binarization method provides $a_x$, $a_y$ values close to the theoretical curves and in general yields a higher accuracy in the calibration measurements, the autocorrelation method is found to be more robust against fluctuations of the light intensity under measurement conditions as also concluded by Cierpka et al. (2010).

Thereby, particle images of all particle sizes are cropped out at a fixed radius of 30 pixel. By comparing the I scatter data from the measurement with the I calibration curve, we observe that the intensity level of the scattered data is slightly increased. The underlying reason is that during the flow measurement, a larger number of fluorescent particles is present in the picture. Furthermore, particles are distributed at different z-positions leading to superimposition of the light intensity. This effect is more pronounced for smaller particles and can be easily compensated by scaling the data with a constant factor. As the scattered data of I of the individual species are well separated (as shown in Fig. 13), this is sufficient for a proper differentiation between the species.

Fig. 12

Distribution of particles in the cross-sectional plane for the monodisperse (mono) and polydisperse (poly) suspension at $\varPhi =0.08\%$, $\mathrm{Re}_{b}=20$ and $H= {600}\,\upmu \mathrm{m}$ (measured in LVS). $N/N_{\mathrm{max}}$ = normalized number of detected particles

Hence, the $a_x$, $a_y$, I scatter data of all measurement planes are assigned to the EEC curve in order to determine the particles out-of-plane positions. In the polydisperse case, the data are compared to all three calibration curves (for 30$\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$). Thereby, the $a_x$, $a_y$, I data are automatically assigned to the correct calibration curve with the EEC reconstruction procedure as described in Sects. 3 and 4. Finally, the absolute particle positions are obtained by combining the measurement plane position and the particle-out-of-plane positions. Hence, the absolute particle positions can be computed with respect to the channel wall by considering the particle out-of-plane positions and the corresponding measurement plane position. Particle velocities are determined using a simple nearest neighbor algorithm. Outliers are removed with a median filter with a binning length of ${10}\,\upmu \mathrm{m}$ in cross-sectional direction. For obtaining averaged velocity profiles, the scattered velocity data are averaged across the horizontal center line with a binning length of ${20}\,\upmu \mathrm{m}$ with data being considered in a lateral distance of ${10}\,\upmu \mathrm{m}$ away from the centerline. The data are visualized in 2D histograms, with bins of ${10}\,\upmu \mathrm{m}$ width in x and y direction and filtered by a Gaussian filter with a filtering length of five bins (Lansey 2021). For validation of the APTV measurements, we further visualize the particle distributions directly by performing stigmatic measurements in the FVS. For this, the cylindrical lens is removed from the optical path. Hence, 16197 images with a resolution 512$\times$512 pixel at different frame rates up to 6200 fps are recorded. In the post-processing, first, the average of all images is computed. Hence, the average is subtracted from each individual image to remove the background. Then, the contrast of the individual images is enhanced by Matlab imadjust. All modified individual images are then summed up. Finally, the contrast of this summarized image is enhanced (Matlab imadjust).

5.2 Validation of Extended Euclidean calibration reconstruction procedure in dilute suspensions

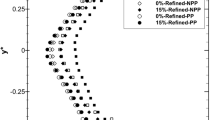
For evaluating if the EEC calibration is suitable for determining the particle distribution of an individual species in a flowing tridisperse suspension, we performed several test cases at very dilute conditions. The results of such a test case are shown in Fig. 12 where we compare the particle distributions of three monodisperse suspensions and a tridisperse suspension ($d_p= {30}\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$, 60$\,\upmu \mathrm{m}$) at $\varPhi =0.08\%$ and all particles labeled in each case. For such a low volume fraction, we assume that particle interaction does not play a role here, such that the distribution of each particle group is expected to be the same, both in the mono- and polydisperse case. In Fig. 12, the bulk Reynolds number is set to $\mathrm{Re}_b\approx 20$ and defined as $\mathrm{Re}_b=\rho _{\text {RIM}} U_b H / \mu _{\text {RIM}}$, where $U_b$ denotes the average streamwise velocity. The distribution of detected particles is displayed in normalized values and $N/N_{\mathrm{max}}$ denotes the number of particles in a bin normalized by the maximum number of particles found in all bins. The black lines represent isocontours of the theoretical velocity profile given in Shah and London (2014).

As can be seen in Fig. 12a–f, particles collect along a Pseudo Segré Silberberg Annulus (PSSA) as described by Choi et al. (2011). Evidently, the particle distribution for the monodisperse cases (Fig. 12a,c,e) and tridisperse case (Fig. 12b,d,f) are the same. For all particles sizes, the highest particle concentration is located at the centers of the channel faces, which corresponds to the Channel Face Equilibrium (CFE) positions as firstly discovered by Chun and Ladd (2006) by means of numerical simulations and experimentally shown by Di Carlo et al. (2007). This is a result of cross-lateral migration (Choi et al. 2011). Thereby, Fig. 12a,c,e or Fig. 12b,d,f clearly show that this cross-lateral migration is more pronounced for larger particles as they have a significantly larger focusing number $F_c=2 \mathrm{Re}_b (d_p/H)^2 L/H$ which is in agreement with the work of Choi et al. 2011.

In fact, the particle distributions shown in Fig. 12a,b and Fig. 12c,d are comparable to those in Fig. 2b and Fig.2c in the work of Choi et al. (2011) even though $\mathrm{Re}_b$ is slightly higher there ($\mathrm{Re}_b=23.5$ and $\mathrm{Re}_b=60$). Fig. 12e,f instead show a distribution similar to that shown in Fig. 2f in Choi et al. (2011) as well as Fig. 5a in Miura et al. (2014) even though $\mathrm{Re}_b$ (and $\mathrm{Re}_p$) are considerably higher there. Figure 12e,f show a striking similarity to Fig. 5b (for $L/H=750$ and $\mathrm{Re}_b=30$) in Shichi et al. (2017).

Overall, the particle distributions of Fig. 12a,b and Fig. 12c,d and Fig. 12e,f show an excellent agreement such that we conclude that the EEC is suitable for determining the 3D distribution of particles in polydisperse suspensions.

Furthermore, for ensuring that the species are distinguished properly when being assigned to a calibration curve, we perform an intrinsic check for all our measurements containing polydisperse tracers. Thereby, we compare the light intensity I of the individual species as a function of the reconstructed out-of-plane position $z-z_0$. Such a plot is exemplary shown in Fig. 13. As can be seen, the calibration curve and the scattered data for $d_p= {40}\,\upmu \mathrm{m}$ particles are well separated from the scattered data of $d_p= {30}\,\upmu \mathrm{m}$ particles over a distance of $\approx {347}\,\upmu \mathrm{m}$ which is almost twice the distance between the focal planes ($\varDelta F\approx {166}\,\upmu \mathrm{m}$). The data associated with the $d_p= {60}\,\upmu \mathrm{m}$ particles cover a z-range of $\approx {452}\,\upmu \mathrm{m}$ and have a much higher light intensity but are not displayed here for the sake of visualization. Please note that the data shown in Fig. 13 are multiplied with the intensity scaling factor $c_s$ (2) for $d_p= {40}\,\upmu \mathrm{m}$.

Next, we briefly demonstrate the principal difference in the accuracy of determining the particle distributions between LVS and FVS. For this in Fig. 14, we show the distribution of 30$\,\upmu \mathrm{m}$ particles at $\mathrm{Re}_b=20$ and $\varPhi =0.08\%$ in a monodisperse suspension. Comparing Fig. 14 with Fig. 12a reveals that the detected particles scatter less around the lower and upper portion of the PSSA (labeled with 1 and 2) in the measurements performed in the FVS. This is because in APTV measurements, the in-plane accuracy is higher than the out-of-plane accuracy (Cierpka et al. 2010).

Fig. 13

Light intensity as function of reconstructed $z-z_0$ of $d_p= {30}\,\upmu \mathrm{m}$ and $d_p= {40}\,\upmu \mathrm{m}$ particles corresponding to Fig. 12b,d,f. Symbols: 1 = scattered data of $d_p = {30}\,\upmu \mathrm{m}$ particles; 2 = scattered data of $d_p= {40}\,\upmu \mathrm{m}$ particles. Black line = calibration curve for $d_p= {40}\,\upmu \mathrm{m}$. Green dots = valid data associated with $d_p= {40}\,\upmu \mathrm{m}$ particles. Red dots = data that are rejected from the $d_p= {40}\,\upmu \mathrm{m}$ calibration curve

Fig. 14

Particle distribution in a dilute monodisperse suspension obtained with FVS. $d_p= {30}\,\upmu \mathrm{m}$, $\varPhi =0.08\%$, $\mathrm{Re}_b=20$, $H= {60}\,\upmu \mathrm{m}$, $L/H\approx 750$

The aforementioned scenarios considered the suitability of the proposed method for reconstructing the particle distribution along the channel. In addition, we also considered two different benchmark flows to estimate the accuracy of the method for reconstructing the particle velocity. Thereby, a special focus was to compare the accuracy obtained with the CEC and the EEC. For this, the laminar flow within a round capillary (Hagen-Poiseuille flow) as well as in a rectangular channel was investigated.

Fig. 15

Laminar flow in a round capillary. Calibration curves and scatter data ($a_x$, $a_y$, I) from different perspectives. Results are for 40$\,\upmu \mathrm{m}$ particles in a tridisperse suspension of 30$\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$. Parameters are identical for conventional Euclidean calibration (CEC) and extended Eulcidean calibration (EEC) ($c_I=0.3$, $c_a=0.518$, $a_D=1.6$ px). a Velocity scatter data (CEC) b Velocity scatter data (CEC) c 2D view (CEC) d 3D view (CEC) e 2D view (EEC) f 3D view (EEC)

Fig. 16

Measured particle velocity in a round glass capillary corresponding to data shown in Fig. 15. Tridisperse suspension with $\varPhi =0.012\%$ volume fraction with 30$\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$ at equal volume fractions. a Radial averaged measured velocity profile (CEC) b Radial averaged measured velocity profile (EEC) c Measured velocity map (CEC) d Measured velocity map (EEC) e Velocity map analytical solution

A Hagen-Poiseuille flow, of a tridisperse suspension ($d_p$ = 30$\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$, $\varPhi =0.12\%$) was measured close to the inlet ($L/D_{pipe}\approx 66$) of a pipe at a bulk Reynolds number of $\mathrm{Re}_b\approx 4.66$. By this, a laminar and fully developed velocity profile was ensured (Chen 1973; Durst et al. 2005). The inlet length is short enough to avoid significant Segré-Silberberg effect-induced particle shifts such that particles are distributed across the whole cross section. For measuring the particle velocities, the flow domain was scanned in steps of approximately 74$\,\upmu \mathrm{m}$ after the calibration measurement. The particle velocities were reconstructed using both the CEC and the EEC procedure. It should be mentioned that in case of the CEC, all data from the measurement with $I<I_{thr}$ have been removed to avoid excessive outliers biasing the data (Brockmann and Hussong 2021). Figures 15a,b exemplarily show the scatter velocity data obtained with the CEC and the EEC reconstruction procedure. As can be seen clearly, the data displayed in Fig. 15a are much more scattered compared to Fig. 15b. The underlying reason is incorrectly assigned data to the calibration curve. As explained in section 4 and shown in figure 15c, 30$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$ particle were misassigned to the 40$\,\upmu \mathrm{m}$ calibration curve. Thus, the measured in-plane velocity is assigned to a wrong depth position, which leads to an increase in the scatter in the velocity map. In contrast with the EEC, only data associated with the corresponding value of light intensity are assigned to the 40$\,\upmu \mathrm{m}$ calibration curve (Fig. 15).

Next, Fig. 16a,b shows the radial averaged velocity profile corresponding to Fig. 15a,b. Outliers have been removed using a median filter with a binning length of ${5}\,\upmu \mathrm{m}$ in radial direction. The black dots indicate the mean velocity, while the black error bars indicate the standard error of the mean. The shaded areas indicate the standard deviation of the velocity data. Thereby, green indicates data which are considered as valid, whereas red indicates data which are considered as not valid. Invalid data were identified based on the density of data points. If the density of data points in an annular segment was below half the median of the density in all annular segements, the associated data were considered as invalid. Please note that valid data points also can contain information of different particle sizes. As can be seen, the CEC procedure yields much more invalid data points compared to the EEC procedure as a consequence of 30$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$ and overlapping particles being mistakenly assigned to the 40$\,\upmu \mathrm{m}$ calibration curve. When comparing the mean of the standard deviation of the valid data points, it can be seen that the EEC procedure provides a higher accuracy ($\sigma _u/U_{b}=8.18\%$) than the CEC ($\sigma _u/U_{b}=10.04\%$).

Finally, in Figs. 16c,d, we compare the velocity maps corresponding to Fig. 15 for 40$\,\upmu \mathrm{m}$ particles. These are obtained by interpolating the scattered velocity data on a regular grid (outliers have been removed with a median filter of ${5}\,\upmu \mathrm{m}$ binning length). While both velocity maps show a good agreement with the analytical solution an important difference becomes evident close to the wall. In Fig. 16c, velocity information is available much closer to the wall compared to Fig. 16d (the dashed circle in Fig. 16c is provided as a reference). This is due the CEC (Fig. 16c) assigning a significant amount of 30$\,\upmu \mathrm{m}$ particles to the data. In fact, the radial position at which velocity information is available is essentially identical for 30$\,\upmu \mathrm{m}$ and 40$\,\upmu \mathrm{m}$ particles for the CEC. This does not reflect the reality. In pipe flows, particles experience a radial inward migration that is pronounced for larger particles, as the wall normal inertial lift force scales with $\sim \rho _f U_b d_p^6 D_h^4$ (Martel and Toner 2014). The region close to the wall depletes at first and is larger for larger particles as can be seen for instance in Choi and Lee (2010) (Fig. 4 a,d,g in their publication). This effect is captured correctly with the EEC for all particle sizes.

Next, a plane Poiseuille flow of a tridisperse suspension ($d_p = {30}\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$, $\varPhi =0.04\%$) was measured in a rectangular channel with a cross section of $1.32\times {20.1}\mathrm{mm}$ at a bulk Reynolds number of $\mathrm{Re}_b\approx 2.93$. The flow was measured close to the inlet, such that a homogenous particle distribution was maintained over the cross section. The distance from the inlet was long enough ($L/H\approx 70$), to ensure that the laminar profile was fully developed (Chen 1973; Durst et al. 2005). For measuring the particle velocities, the flow domain was scanned in steps of approximately ${148}\,\upmu \mathrm{m}$ after the calibration measurement. Hence, data were averaged in spanwise direction.

Similar to the flow in the circular capillary, the mean of the standard deviation $\sigma _U/U_{\mathrm{Bulk}}$ is significantly reduced with the EEC procedure. In particular, the mean standard deviation of the velocity is reduced by 18%, 16% and 42% for 30$\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$ particles, respectively. It may be noted that the velocity uncertainty attains the smallest value for the largest particles for both the CEC and the EEC. We assume the underlying reason is that larger particles are associated with a higher light intensity such that the associated particle images are less sensitive to the amount of background noise, which is caused by the large amount of defocused particles that are present due to the wide flow domain ($H\approx {1320}\,\upmu \mathrm{m}$). Similar to the Hagen-Poiseuille flow, the amount of erronous velocity information close to the walls is reduced with the EEC (not depicted).

Overall, the discussed benchmark cases show that the EEC can prevent wrong assignments of particle image data to calibration curves. In contrast to this, particles of different size may be erroneously assigned to the calibration curves with the CEC, which biases the obtained velocity and depth information. Overall, that the proposed method is suitable for capturing the dynamics of larger particles in millimeter and submillimeter geometries.

Fig. 17

Comparison of particle distributions in the FVS (a–f) and the LVS (g–l). $\mathrm{Re}_b\approx 20$, $H= {600}\,\upmu \mathrm{m}$ and $\varPhi =9.1\%$ for all depicted cases. The aspect ratio is $L/H\approx 750$

5.3 APTV measurements in suspensions of $9.1\%$ volume fraction

The benchmark cases discussed in Sect. 5.2 only considered dilute conditions. In this section, results from different setups and suspensions beyond the dilute regime are presented. These serve as a base for physical interpretation, but also allow a further validation of the proposed APTV technique for measuring polydisperse suspensions beyond the dilute regime.

Next, we discuss the particle distributions of mono- and tridisperse suspensions at $\varPhi =9.1\%$, determined by means of APTV, utilizing only the EEC, in both setups. For this, Figs. 17a–f and Figs. 17g–l show the particle distributions for the mono- as well as tridisperse suspension cases for $\mathrm{Re}_b\approx 20$ in a capillary of 600$\,\upmu \mathrm{m}$ height, obtained in setup 1 and setup 2.

As can be seen clearly, 30$\,\upmu \mathrm{m}$ particles are found to collect on a scattered PSSA with a significant lower concentration in the channel center in the monodisperse case (Fig. 17a,g). In the polydisperse case, the PSSA gets widened toward the wall (Fig. 17b,h). This is more pronounced in the FVS which is likely because in APTV measurements, the in-plane accuracy is higher than the out-of-plane accuracy as discussed in the previous section. A slight depletion of detected particles in vertical direction becomes evident in Fig. 17h. As the number of particles increases toward the channel bottom, we exclude optical distortions to be the underlying reason, as these would be pronounced closer to the channel bottom and would lead to a depletion of detected particles here (Brockmann and Hussong 2021). Furthermore, as will be shown later on, a depletion of detected particles toward the upper channel wall is also visible in the 400$\,\upmu \mathrm{m}$ capillary where optical distortions are expected to be less. Hence, we assume this depletion is induced by slight density mismatches leading to a sedimentation of particles. For 40$\,\upmu \mathrm{m}$, the reconstructed particle distributions (Fig. 17c,d,i,j) reveal that the particles are forced to the wall.

As can be seen from Fig. 17e, f, k, l, the particle distributions for 60$\,\upmu \mathrm{m}$ clearly show that the largest particles are more focused in the polydisperse case. This effect is more pronounced in Fig. 17l which is measured in the LVS.

Overall, these results shown in Fig. 17, generated from two different setups associated with two different perspectives, confirm that the proposed method is suitable for measuring migration phenomena in suspensions beyond the dilute regime. Even though, in the FVS, only one particle species was labeled at the time, while in the LVS, multiple particle species were labeled, the results show a good agreement. This confirms that the EEC facilitates a proper distinguishing of different particle sizes even under conditions beyond the dilute regime (in the LVS). The aforementioned observations are confirmed by our visualization experiments shown in Sect. 5.5.

Fig. 18

Distribution of particles in the cross-sectional plane for 400$\,\upmu \mathrm{m}$ square duct $\mathrm{Re}_{b}=20$ and $\mathrm{Re}_{b}=40$ for monodisperse (Mono) and polydisperse suspensions (Poly) at 9.1% volume fraction. Measured in LVS at $L/H\approx 750$

Fig. 19

Comparison of measured streamwise velocity U for monodisperse (blue) and polydisperse (red) suspensions obtained in the FVS and LVS at a volume fraction of $\varPhi =9.1\%$. Standard deviation of velocity is indicated with vertical error bars. The velocity was averaged along a stripe of 20$\,\upmu \mathrm{m}$ width along the horizontal centerline of the channel. a FVS, $d_p= {60}\,\upmu \mathrm{m}$, b FVS, $d_p= 30\,\upmu \mathrm{m}$, c LVS, $d_p= {60}\,\upmu \mathrm{m}$, d LVS, $d_p= 30\,\upmu \mathrm{m}$,

Fig. 20

Particle distribution in a monodisperse suspension visualized by summarized image series ($\mathrm{Re}_{b}\approx 20$, $H= {600}\,\upmu \mathrm{m}$, $L/H\approx 750$, $d_p= {60}\,\upmu \mathrm{m}$). Dark regions indicate particle positions. a-g) Particle concentration increasing from $\varPhi =0.08\%$ to $\varPhi =10\%$

Next, we investigate the role of the aspect ratio ($H/d_p$) on the particle distribution by using a capillary with H= 400$\,\upmu \mathrm{m}$ while keeping the particle sizes constant ( 30$\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$, 60$\,\upmu \mathrm{m}$). Further, $\mathrm{Re}_b$ is adjusted to $\mathrm{Re}_b\approx 20$ and $\mathrm{Re}_b\approx 40$. As $\mathrm{Re}_p$ scales with $\mathrm{Re}_b (d_p/H)^2$, this configuration allows us to achieve an estimated particle Reynolds number of up to $\mathrm{Re}_p=0.9$. In Fig. 18, we show particle distributions for monodisperse suspensions as well as polydisperse suspensions at $\mathrm{Re}_b\approx 20$ and $\mathrm{Re}_b\approx 40$.

At first, comparing corresponding mono- and polydisperse cases (Fig. 18a–f and Fig. 18g–l) confirms that smaller particles are closer to the wall in a polydisperse suspension compared to monodisperse suspensions while larger particles scatter less around the PSSA, as concluded for Fig. 17a,b,g,h.

Comparing Fig. 17e,k and Fig. 18c further confirms that if $\mathrm{Re}_p$ and $H/d_p$ are constant ($\mathrm{Re}_p=0.2$, $H/d_p=10$), the particle distribution is essentially the same for the monodisperse case. However, as $H/d_p$ is increased from $H/d_p=10$ to $H/d_p=13.33$ at constant $\mathrm{Re}_p$ ($\mathrm{Re}_p=0.2\approx 0.22$), the particles shift closer to the wall and deplete in the center region (Fig. 18c,g). This effect becomes also evident when comparing Fig. 18e,i ($\mathrm{Re}_p=0.4\approx 0.45$). Both, for monodisperse and polydisperse suspensions, a simultaneous increase in $\mathrm{Re}_b$ and $\mathrm{Re}_p$ results in more pronounced particle focusing at fixed $H/d_p$. A comparison of Fig. 18b,d,f and Fig. 18h,j,l confirms that an increase in $\mathrm{Re}_b$ and hence $\mathrm{Re}_p$ also leads to a stronger particle focusing of a particle species in a polydisperse suspension.

Fig. 21

Particle distributions visualized by summarized image series for mono- and polydisperse suspensions at $\varPhi =9.1\%$ and different values $\mathrm{Re}_{B}$ for a square duct with $H= {600}\,\upmu \mathrm{m}$ and $L/H\approx 750$

5.4 Velocity profiles

In this section, we discuss the velocity profiles measured in the LVS and FVS. In Fig. 19a,b and Fig. 19c,d, we show the averaged velocity profiles for 30$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$ particles measured in the LVS and FVS, respectively. The results reveal that the averaged velocity for both the monodisperse (blue dots) as well as the polydisperse suspensions (red dots) shows a good agreement with the analytical solution as given by Shah and London (2014). Merely, the averaged velocity of the 60$\,\upmu \mathrm{m}$ particles exhibits slight deviations from the analytical solution closer to the channel center even though the mean error is low (visualized by the small error bars in Fig. 19a,c). The underlying reason is that there are much less ${60}\,\upmu \mathrm{m}$ tracers than ${30}\,\upmu \mathrm{m}$ tracers in the flow and furthermore the ${60}\,\upmu \mathrm{m}$ particles deplete significantly in the center region. In fact, the averaged data points close to the center result from one or a few ${60}\,\upmu \mathrm{m}$ particles which were tracked across several frames. Hence, they enter the statistics several times. Depending on how their $a_x$, $a_y$ values deviate from the calibration curve they can bias the average. As can be seen clearly, the standard deviation (visualized by the large error bars) for the FVS method is multiple times higher than for the LVS. This was expected as the uncertainty in determining the out-of-plane position and hence the out-of-plane velocity is usually one order larger than the in-plane position and velocity (Cierpka et al. 2010, Brockmann et al. 2020). Overall, we conclude based on our results that no significant deformations of the velocity profile are induced within our parameter space for both mono- and polydisperse suspensions. For $\varPhi =10\%$ and $\mathrm{Re}_b=550$ Kazerooni et al. (2017) observed a slight blunting of the velocity profile, however significant deviations from the pure liquid flow were only observed for $\varPhi =20\%$. Our findings also coincide with the studies of Han et al. (1999) where no significant blunting of the velocity profile was observed for $\varPhi =10\%$ at comparable particle Reynolds numbers. Apart from measuring the streamwise velocity component, it would be also interesting to resolve the cross-stream secondary flows which can occur due to the presence of particles (Kazerooni et al. 2017). However, resolving these secondary flows required small tracer particles that are not affected by migration effects ($d_p< {15}\,\upmu \mathrm{m}$). However, tests showed that such particles do not provide sufficient light intensity when being excited by the LED light source. Moreover, the magnitude of the secondary flows is below 0.4% of the bulk velocity (Kazerooni et al. 2017) which is beyond the uncertainty of our method.

5.5 Visualization and physical interpretation

In this section, we present results obtained with the visualization technique to validate the migration effects described before. Furthermore, the visualization technique faciliates to easily explore a larger range of $\mathrm{Re}_b$, which allows us to gain some additional insights. For the APTV measurements increasing $\mathrm{Re}_b$ further is not possible with the current setup, as we need a minimum exposure time of $\gtrapprox {40}\upmu \mathrm{s}$ to ensure a sufficient image quality for the 30$\,\upmu \mathrm{m}$ particles. This relative large exposure time leads to motion blur at larger $\mathrm{Re}_b$ skewing the $a_x$, $a_y$ values and hence leads to bias in the velocity and the distribution information. It may be noted that the visualization technique needs optical access from the face side of the geometry. In microfluidic devices, or macroscopic geometries, this is rather an exception and optical access is mostly only available from a lateral direction.

Before discussing the effect of $\mathrm{Re}_b$, we briefly discuss the effect of increasing $\varPhi$ on the particle distribution. For this, Fig. 20 shows the particle distributions in a monodisperse suspension ($d_p= {60}\,\upmu \mathrm{m}$) at constant $\mathrm{Re}_{b}$ for $\varPhi$ increasing from 0.08% to 10%. As can be seen, in Figs. 20a-g, particles scatter increasingly around the PSSA for increasing $\varPhi$.

The results for $\varPhi =0.08\%$, 1% and 3% can be compared to the results of Udono (2020) who investigated how the particle volume fraction and associated hydrodynamic particle interactions affect the particle focussing. Even though Udono 2020 considered a higher Reynolds number ($\mathrm{Re}_b=125$), our results show a good agreement (compare Figs. 20a,b,c and Fig.7 in Udono 2020). This indicates that the increased scattering visible for $\varPhi =1\%$ and $\varPhi =3\%$ observed in the present study may result from hydrodynamic particle interaction, as will be discussed later in the text.

Moreover, Fig. 20d is qualitatively similar to the numerical results presented by Manoorkar et al. 2018 in Fig. 14a of their work (for $\mathrm{Re}_b=46$, $\varPhi =5\%$) even though $H/d_p$ equals 5 in their study.

In Fig. 21, we show particle distributions for mono- and polydisperse suspensions obtained from visualizations for $\varPhi =9.1\%$ and different $\mathrm{Re}_{b}$ ranging from 1 up to 72.86. At low Reynolds numbers ($0.99\le \mathrm{Re}_b\le 6.62$) 30$\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$, particles migrate to the center of the channel which can be attributed to shear induced migration for the monodispersed suspension. Thereby, the particles exhibit higher concentrations on the diagonal axis and the channel center. These qualitative results exhibit a similarity to those numerically obtained by Yadav et al. (2015), who investigated shear-induced migration in a Y-shaped bifurcation channel (see Fig. 7b of their publication). They concluded that a higher particle concentration at the corners originates from the lower shear rate gradients in the corner regions. In contrast, in a polydisperse suspension 60$\,\upmu \mathrm{m}$, particles exhibit a more pronounced migration to the channel center compared to the corresponding monodisperse case. On the other hand, this effect seems to be reversed for 40$\,\upmu \mathrm{m}$ particles where less particles accumulate in the center in the polydisperse case compared to the monodisperse case. This observation coincides with the finding of Semwogerere and Weeks (2008) that at equal volume fractions, larger particles migrate faster to regions of low shear and screen off smaller particles due to their lower development length. For 30$\,\upmu \mathrm{m}$ particles, no migration to the center becomes evident for the polydisperse suspension in Fig. 21a.

For $\mathrm{Re}_b \ge 19.87$, the particles distribute on a scattered PSSA in the monodisperse case which becomes more focused as $\mathrm{Re}_b$ increases (Fig. 21c–g). This confirms the observations discussed with regard to Fig. 19 and Fig. 18. The focusing of the PSSA with increasing $\mathrm{Re}_b$ is pronounced for 40$\,\upmu \mathrm{m}$ where the squared void area around the channel center increases significantly with $\mathrm{Re}_b$. An increased focusing of particles with increasing $\mathrm{Re}_b$ was also indicated by the numerical results of Manoorkar et al. (2018) (Fig. 14 of their publication). For 30$\,\upmu \mathrm{m}$, Fig. 21c-g reveals that the area around the diagonal axis features a lower particle concentration than the face centers resulting in a star-shaped particle distribution, which was similarly observed by Kazerooni et al. (2017) for $\mathrm{Re}_b=550$ and $H/d_p=18$. However, Kazerooni et al. found the highest concentration in the duct corners and not at the channel faces, which we relate to the fact that they simulated a square duct with perfectly sharp corners whereas the capillaries used within this work exhibit round corners.

The scattering around the PSSA visible in Figs. 20a–g and Figs. 21c–g results from a competition between inertial and shear-induced migration forces. On the one hand, inertial effects force particles to the equilibrium positions (EP) resulting in a high local particle concentration. On the other hand, shear-induced migration leads to a migration away from these positions which can be explained as follows: According to the diffusive flux model of Phillips et al. (1992) for shear induced migration, particle migrates from regions of high collision frequency to regions of low collision frequency. The flux related to the collision frequency ($N_c \sim d_p^2 (\varPhi ^2 \nabla {\dot{\gamma }} + \varPhi {\dot{\gamma }} \nabla \varPhi )$) depends on both $\varPhi$ and the shear rate ${\dot{\gamma }}$ and hence attains maximum values at the EP such that particles migrate away from these regions. As $\varPhi$ is increased, the collision frequency and hence shear-induced migration are enhanced resulting in an increased scattering as can be seen from Fig. 20a-g. However, when the Reynolds number increases, the inertial forces increase counteracting the shear induced migration such that the scattering is reduced as clearly visible for the 40$\,\upmu \mathrm{m}$ particles in Fig. 21c–g.

Besides shear-induced and inertial migration, hydrodynamic interactions of particles can also result in scattering around equilibrium position as shown in the aforementioned work of Udono 2020. In his simulations, Udono 2020 arranged particles in chains on the EPs. Even though the particles were initially not in touch, they repelled each other from the EPs at volume fractions about $\varPhi =1..1.7\%$ as a result of hydrodynamic interactions. As mentioned, the conditions covered by Udonos simulations are approximately comparable to Fig. 20b–c ($0.08\%\le \varPhi \le 3\%$) which leads to the conclusion that here the scattering around the EP is due to hydrodynamic interactions between particles. However, in the main body of experiments, we consider considerably higher solid volume fractions and a significantly lower Reynolds number compared to Udono 2020. In these cases, we assume the effect of particle collisions to be dominant over hydrodynamic interactions and hence shear-induced migration is the key mechanism for scattering of particles within our experiments at $\varPhi =9.1\%$.

As observed in the APTV measurements, for all investigated particle sizes, corresponding particle distributions found for the polydisperse cases are strikingly different compared to those of the monodisperse cases. For 30$\,\upmu \mathrm{m}$ and 40$\,\upmu \mathrm{m}$ particles, a significantly higher concentration close to the channel walls resulting in an outer annulus of high concentration is observed in the polydisperse case. Furthermore, a slight increase in concentration seems to exist for some $\mathrm{Re}_b$ close to the channel center forming an inner annulus of high concentration (21c-g) which was not visible in Fig. 19b,h,d,j. Similar to the APTV measurements, the 60$\,\upmu \mathrm{m}$ particles the PSSA appear to be more focused in the polydisperse case compared to the monodisperse case (Fig. 21c-g). As $\mathrm{Re}_b$ increases, the PSSA formed by 60$\,\upmu \mathrm{m}$ particles breaks up at the corners which is a indicator for cross-lateral migration forcing the particles to the CFE positions (Fig. 21c–g). The particle segregation observed in the tridisperse measurements at $\varPhi =9.1\%$ (Fig. 21c–g), Figs. 19b,d,f,h,j,l and 18b,d,f,h,j,l can be explained in analogy to the work of Semwogerere and Weeks 2008 who found that in a bidisperse suspension, the species that reaches its EP earlier (in their case region of lowest shear) screens of the other species. In our experiments, large particles experience significantly higher inertial forces such that they attain their position at the PSSA at much lower values of z/H than the smaller species. We recall here that the focusing number scales with $F_c\sim (d_p/H)^2$. Hence, larger particles quickly exhibit high concentrations closely around the PSSA. As a result, they are screening off smaller particles.

At the same time, large particles experience smaller displacements in the polydisperse case compared to the monodisperse case due to collisions as these scale with $O(d_p)$. Looking at the collision flux in the model of Philips et al. ($N_c \sim d_p^2 (\varPhi ^2 \nabla {\dot{\gamma }} + \varPhi {\dot{\gamma }} \nabla \varPhi )$) it is clear that suspensions of smaller particles exhibit smaller diffusive fluxes compared to large particles. Hence, using simple arguments, it can be assumed that the diffusive fluxes and hence the rate of migration is decreased in a polydisperse suspension which contains solely 1/3 large particles, compared to a monodisperse suspension of large particles. Therefore, the rate of shear-induced migration is lower than in the monodisperse case, leading to a decreased scattering of large particles around the PSSA.

As mentioned, all the previous results were restricted to $L/H\approx 750$ due to practical reasons. While there is no approach to estimate the development length for the simultaneous occurrence of shear-induced and inertial migration, there do exist relations to estimate it for each isolated migration phenomenon separately. The development length, required for developed inertial migration, is explained for instance in Matas et al. (2004), Choi et al. (2011) and Miura et al. (2014). Choi et al. (2011) derive $L/H=1/(2 \mathrm{Re}_b) (H/d_p)^2 \pi /B$ while Matas et al. (2004) give a relation $L/H=6\pi A^{-1} \mathrm{Re}_b^{-1} (H/d_p)^3$. These expressions are based on a balance of the viscous drag and the inertial drag force (Matas et al. 2004; Choi et al. 2011). As can be seen from Table 2, for all configurations, the lateral inertial migration for 60$\,\upmu \mathrm{m}$ is developed according to the aforementioned criteria, while for some scenarios, the inertial migration for 30$\,\upmu \mathrm{m}$ and 40$\,\upmu \mathrm{m}$ particles is not fully developed (Table 2). Nevertheless, as shown in Fig. 12a-d, for the dilute case most of the particles is collected into the PSSA, indicating that lateral migration is almost completely developed. The entry length of shear induced migration for monodisperse suspensions can be estimated based on the expression of Nott and Brady (1994). They estimated the development length as $L/H\sim \frac{1}{12 d(\varPhi )} (H/d_p)^2$, where $d_\varphi$ can be estimated as $1/3 \, \varPhi ^2 (1+0.5e^{8.8 \varphi })$ (Van Dinther et al. 2013). The estimated entry lengths for shear-induced migration are given in Table 3. As can be seen, shear-induced migration appears to be not completely developed except for 60$\,\upmu \mathrm{m}$ particles and $H= {400}\,\upmu \mathrm{m}$.

As mentioned, these considerations only account for the isolated migration phenomena. When both migration mechanisms act together, it has to be considered that inertial migration leads to high local concentrations of particles close to the PSSA ($\varPhi _\text {loc}>\varPhi$). Estimations based on the number of detected particles indicate that the local particle volume fraction can exceed the bulk volume fraction significantly (for example by a factor of 2 or 3) in our experiments. This local increase in particle concentration locally enhances the rate of shear-induced migration which roughly scales with $\sim 1/\varPhi ^2$ (and hence $\sim 1/\varPhi _\text {loc}^2$). Hence, the development length is likely to be shorter when both mechanisms act simultaneously. In general, for follow-up studies, it would be interesting to investigate the influence of L/H on the particle distribution, which is beyond the scope of the current study.

Table 2 Development length for inertial particle migration as given by Choi et al. (2011) (first two rows,$L/H=1/(2 \mathrm{Re}_b) (H/d_p)^2 \pi /B$) and Matas et al. (2004) (row 3 and 4,$L/H=6\pi A^{-1} \mathrm{Re}_b^{-1} (H/d_p)^3$) for some parametric combinations investigated in this study (Choi et al. 2011).

Table 3 Developement length $L/H\sim \frac{1}{12 d(\varPhi )} (H/d_p)^2$ for shear-induced migration according to Nott and Brady 1994

6 Discussion and conclusion

In the paper at hand, we utilize APTV to measure the particle dynamics in polydisperse suspensions containing three particles sizes of $d_p=$ 30$\,\upmu \mathrm{m}$, 40$\,\upmu \mathrm{m}$ and 60$\,\upmu \mathrm{m}$ at volume fractions of $\varPhi =0.08\%$ to $\varPhi =9.1\%$. A refractive index matching technique is used to render the suspension transparent, while just a small portion of the particles is labeled with fluorescent dye to provide a signal for the tracking procedure.

First, an extensive study on the general effect of the particle size on the calibration curves is performed where we also compare two approaches for extracting the horizontal axis lenghts $a_x$ and the vertical axis length $a_y$ of the particle image. For both methods, we observe the $a_x$, $a_y$ values to increase, as the particle size increases as predicted by the expression derived by Cierpka et al. (2010). Thereby, the data obtained with the binarizing approach are in excellent agreement with the theoretical data, while the data obtained with the autocorrelation deviate significantly from the theoretical curves beyond the focal planes. In agreement with Koenig et al. (2020), it is observed that the 2D Euclidean calibration curves for different values of $d_p$ intersect beyond the focal planes leading to ambiguities which lead to large errors when applying APTV to particles of different size. We overcome these ambiguities by utilizing an extended Euclidean calibration (EEC) procedure, exploiting the fact that the maximum light intensity of the particles increases sharply with increasing particle size. Using calibration data of nine different particles sizes ranging from 15$\,\upmu \mathrm{m}$ to 290$\,\upmu \mathrm{m}$, we show that the EEC allows a reliable differentiation of particles of different sizes.

Ultimately, utilizing the EEC, we investigate the particle migration behavior in mono- and tridisperse suspension flows in square ducts with cross-sectional areas of 400$\times$ 400$\upmu \mathrm{m}^2$ and 600$\times$ 600$\upmu \mathrm{m}^2$ at bulk Reynolds numbers of $\mathrm{Re}_b \approx 20$ and $\mathrm{Re}_b \approx 40$ and volume fractions of $\varPhi =0.08\%$ and $\varPhi =9.1\%$. At $\varPhi =0.08\%$ and $\mathrm{Re}_b=20$, we observe particles to collect onto a Pseudo Segré Silberberg Annulus (PSSA) with no significant differences between mono- and polydisperse suspensions beeing evident. At $\varPhi =9.1\%$ $\mathrm{Re}_b=20$, particles in monodisperse suspensions scatter around an annular shape with the scattering being pronounced as $d_p$ decreases. When $\mathrm{Re}_b$ is increased to $\mathrm{Re}_b=40$, the scattering decreases for all $d_p$ investigated leading to a square shaped depletion of particles close to the channel center. As $H/d_p$ is increased at constant particle Reynolds number, the particle distribution is shifted toward the channel walls and the depleted area in the channel center increases. For polydisperse suspensions, strikingly different particle migration behaviors are observed at the same values of $\mathrm{Re}_b$ and $\varPhi$. Compared to the monodisperse case, large particles (${60}\,\upmu \mathrm{m}$) are significantly more focused. In contrast, small and intermediate particles ( 30$\,\upmu \mathrm{m}$ and 40$\,\upmu \mathrm{m}$) are repelled by larger particles resulting in a region of high concentration close to the channel walls. As $\mathrm{Re}_b$ increases from $\mathrm{Re}_b=20$ to $\mathrm{Re}_b=40$, these effects become pronounced such that the focusing of large particles (${60}\,\upmu \mathrm{m}$) is further enhanced while smaller and intermediate particles become more focused close to the walls. For both the mono- and the polydisperse measurements, no significant blunting of the velocity profile becomes evident within our experiments which is in agreement for literature considering monodisperse suspensions.