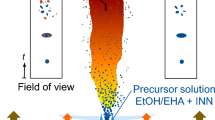
Abstract
Combusting metal precursor-laden droplets, required in spray-flame synthesis of nanomaterials, are known to undergo a rapid and disruptive disintegration, i.e., puffing and micro-explosion. In this work, imaging with high spatiotemporal resolution and image-analysis routines were developed to investigate droplet disruption in spray-flame synthesis of metal oxides. Droplet shadowgraphs were imaged on a high-speed camera. The solvent was a mixture of 35 vol% ethanol and 65 vol% 2-ethylhexanoic acid which (in some cases) was mixed with a 0.2 mol/l iron(III) nitrate nonahydrate precursor. Photometric and morphological processing identified in-focus features, estimated their size, velocity, and circularity, and discriminated regular, spherical droplets from disrupting ones. While solely regular droplets were found in the spray flame of pure solvent, with the precursor/solvent mixture, disrupting droplets were found in addition to the regular droplets. Disruption events were phenomenologically classified into puffing, comprising droplet deformation and local eruption, and micro-explosion, the violent disintegration of the droplet into multiple fragments. Puffing was found to occur much more frequently than micro-explosions. Disrupting droplets had a 32% smaller Sauter mean diameter than regular droplets, indicating that disruptions are beneficial for rapid spray evaporation. At 40 and 50 mm heights above the burner, about 8 and 6%, respectively, of the in-focus droplets are disrupting per millimeter axial distance. Thus, throughout their lifetime in the spray flame, all precursor-laden droplets are expected to experience disruption.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Advanced materials with novel or enhanced properties are often nanomaterials, and spray-flame synthesis (SFS), also known as flame spray pyrolysis (FSP), is a promising technique for creating nanomaterials (Mädler et al. 2002; Schneider et al. 2019). Metal-oxide nanoparticles are of interest in fields such as catalysis, batteries, and sensors (Teoh et al. 2010). The advantage in SFS compared to gas-phase-only synthesis is that inexpensive, low-volatility metal-precursors can be used (Strobel and Pratsinis 2011). Two major routes to particle formation in SFS can be distinguished. The droplet-to-particle route involves the precipitation of the metal precursor and its intermediates within the droplet, yielding large or hollow particles. In contrast to that in the gas-to-particle route the relevant portion of the spray is completely evaporated before particle nucleation and coagulation are initiated. The latter is usually the desired mechanism since it results in homogeneous nanopowders (Strobel and Pratsinis 2011). Thus, the evaporation of precursor-laden droplets is a key step in SFS. Optimizing the process requires in-depth understanding of droplet chemistry and physics, as well as of droplet-flow interaction.
In this context, single combusting droplets of precursor solutions have been investigated extensively. For certain precursor/solvent combinations, such as tin-2-ethylhexanoate/xylene (Rosebrock et al. 2013) and zinc-naphthenate/ethanol (EtOH) (Rosebrock et al. 2016), a rapid non-aerodynamic disruptive disintegration of the droplets with the ejection of liquid fragments was found; this is known as droplet “puffing” or “micro-explosion”. In puffing, the droplet deforms or erupts locally with the ejection of secondary droplets and vapor while droplet micro-explosion is the violent and (near-) complete disintegration of a single droplet into many fragments (Shinjo et al. 2014).
Much of the literature on non-aerodynamic droplet disruption is related to combusting droplets of fuel/water emulsions that can improve the efficiency and reduce harmful emission in internal combustion engines (Kadota and Yamasaki 2002). Also in this context, droplet disruption has been studied in single-droplet experiments (Avedisian and Andres 1978; Califano et al. 2014; Lasheras et al. 1979; Law et al. 1980; Moussa et al. 2019, 2020; Mura et al. 2014, 2010, 2012; Namba and Kimoto 2000; Suzuki et al. 2011; Watanabe et al. 2009, 2010) and simulations (Bar-Kohani et al. 2021; Fu et al. 2002; Sazhin et al. 2019, 2021, 2020; Shinjo et al. 2014; Zeng and Lee 2007). In such emulsified fuels, typically, a surfactant is added to the mixture to disperse the volatile phase (e.g., water). Single combusting droplets of binary fuel mixtures, being either solutions or blends with limited miscibility, with the components having different boiling points, were observed to undergo swelling and fragmentation (Lasheras et al. 1980, 1985; Lasheras et al. 1981a, b; Lasheras et al. 1981a, b; Mikami and Kojima 2002; Mikami et al. 1998; Wang et al. 1984; Wood et al. 1960; Yap et al. 1984). It is thought that the intense heat transfer from the flame causes the preferential and rapid vaporization of the high-volatile component from the droplet surface (Wood et al. 1960). The remaining low-volatile component, which might additionally pyrolytically decompose, increases the mixture’s viscosity. That decreases the diffusion coefficient D of the mixture thereby increasing the Lewis number \({\text{Le}} = \frac{a}{D}\), where a is the thermal diffusivity of the mixture. This can result in superheating of the remaining high-volatile component in the interior of the droplet with subsequent nucleation, bubble growth, and disruption (Wornat et al. 1994). It was found that fuel/water emulsions burn more disruptively than blends with limited miscibility or solutions (Lasheras et al. 1981a, b; Lasheras et al. 1985). Swelling of droplets before disruption was observed for solutions rather than for emulsions (Lasheras et al. 1981a, b; Wornat et al. 1994). The frequency and temporal onset of the disruption strongly depends on the difference in boiling points of the components and the concentration of the high-volatile component (Lasheras et al. 1981a, b). In the presence of convective mixing (relative gas-droplet velocities of 15–20 m/s), where mass and heat transport within the droplet are not expected to be diffusion-limited, disruptive burning was observed in single-droplet combustion of n-hexane/n-hexadecane mixtures and n-hexadecane/water emulsions (Yap et al. 1984). Even combusting droplets of pure n-decane were observed to undergo puffing (Jeong et al. 2008).
Fewer studies investigated droplet disruptions in spray flames (Fuchihata et al. 2003; Huo et al. 2014; Ismael et al. 2018; Liu et al. 2011; Mizutani and Muraoka 2001; Ochoterena et al. 2010; Sheng et al. 1994; Stodt et al. 2021, 2020; Watanabe and Okazaki 2013; Watanabe et al. 2014) where the experimental conditions are more challenging, with smaller initial droplet diameters on the order of 20 µm, droplet velocities of 100 m/s, and sometimes at high ambient pressure and temperature. High magnification is required to visualize very small liquid features, but this reduces the field of view (FOV), which in turn makes it challenging to capture the entire disruption before the droplet has left the FOV. In spray combustion of diesel/water emulsions in constant-volume vessels, small short-lived high intensity spots in the natural flame luminosity were observed and attributed to disruptive burning of single droplets (Huo et al. 2014; Ochoterena et al. 2010). Recently, isolated spots of brighter flame luminosity were also found in the outer regions of a spray flame burning iron(III) nitrate nonahydrate (INN) in EtOH and 2-ethylhexanoic acid (EHA), the flow and material system also used in this work (Stodt et al. 2020). Shadowgraphs of combusting sprays of diesel/butanol, diesel/ethanol (Liu et al. 2011), and diesel/water emulsions (Sheng et al. 1994) indicate vapor plumes erupting from the spray, an expansion of the spray or spray tip, and large-scale irregularities in the spray shape. All these features were indirectly attributed to droplet disruptions.
But only a few studies report the direct visualization of disrupting droplets in sprays (Fuchihata et al. 2003; Ismael et al. 2018; Mizutani and Muraoka 2001; Stodt et al. 2021; Watanabe and Okazaki 2013; Watanabe et al. 2014). Using dark-field schlieren imaging to visualize disrupting droplets in a spray flame of emulsified fuel, the frequency of micro-explosions was found to increase with increasing fraction of the high-volatile disperse component, i.e., water (Mizutani and Muraoka 2001). Quasi-forward Mie-scatter imaging showed disruptions in a spray flame of oil/water emulsions where a typical micro-explosion event was found to be as short as 10 µs (Fuchihata et al. 2003). Shadowgraph images of n-dodecane/water droplets in high-temperature inert gas indicated puffing and partial micro-explosions but rarely complete micro-explosions (Watanabe and Okazaki 2013). Here, events of puffing and partial micro-explosions lasted 25–80 µs and significantly reduced the droplet diameter by ejecting vapor or secondary droplets. In a spray flame of oil/water emulsion, puffing and micro-explosion were found, and they were thought to contribute to rapid evaporation and spread of fuel vapor (Watanabe et al. 2014). Recently, micro-explosions and puffing were visualized in a spray flame burning a mixture of EtOH/EHA + 0.5 mol/l INN (Stodt et al. 2021). An important outcome was that the size, shape, intensity, and number of typical ejected fragments of the disruption varied spatially throughout the flame.
Potential techniques for measuring droplet sizes and velocities include interferometric techniques such as phase Doppler interferometry (PDI) or interferometric particle imaging (IPI) (Damaschke et al. 2002; Kashdan et al. 2003). Despite its high cost and accurate-alignment requirements PDI is a widely used technique. However, PDI cannot accurately measure metrics of non-spherical particles or droplets (Damaschke et al. 1998). Thus, alternative techniques, such as particle/droplet image analysis (PDIA), are needed to directly visualize regular and disrupting droplets, characterize the degree of secondary atomization, and infer statistical data on, e.g., frequency, shape, size, and velocity (Jiang et al. 2010; Kashdan et al. 2003, 2004, 2007; Kim and Kim 1994; Koh et al. 2001; Kumar and Sahu 2020; Lecuona et al. 2000; Lee and Kim 2004; Malot and Blaisot 2000). Shadowgraphy is a suitable technique to visualize droplets in regions where the overall optical density is moderate (down to on the order of 10% transmission), as in the downstream region of sprays (Linne 2013).
This work expands on previous studies by developing imaging and post-processing techniques to visualize and discriminate regular and disrupting droplets in SFS and statistically aggregate their geometric properties for better understanding of droplet disruption. A microscope was used for high-magnification imaging with a high-speed camera and LED burst illumination to capture the small and rapid events. A robust algorithm was developed to perform automated photometric processing, identification of in-focus features, and morphological classification to infer feature size, velocity, and shape/circularity, to discriminate between regular and disrupting droplets. Example in-focus events were classified by visual inspection into puffing (droplet deformation or eruption) and complete micro-explosion. An initial statistical analysis is presented at the end of this work.
2 Methods
2.1 Spray-flame burner
Figure 1 shows a sketch of the “SpraySyn” burner, a standardized spray-flame burner for nanoparticle synthesis (Schneider et al. 2019). The liquid precursor/solvent mixture is provided through a central capillary by a syringe pump at 2 ml/min (0.26 m/s nominal exit velocity). The solvent in this study was a mixture of 35 vol% EtOH and 65 vol% 2-EHA. For the synthesis of iron oxide nanoparticles, INN was dissolved in the solvent yielding a solution with 0.2 mol/l INN. Oxygen flows at a velocity of 120 m/s [\(\dot{V}_{{{\text{O}}_{2} ,d}} = 10 {\text{slm}}\), Mach number 0.35, nozzle-exit Reynolds number 7160 (Stodt et al. 2020)] through a coaxial gap and atomizes the solvent flowing out of the capillary. A mixture of methane (\(\dot{V}_{{{\text{CH}}_{4} ,p}} = 2 {\text{slm}}\)) and oxygen (\(\dot{V}_{{{\text{O}}_{2} ,p}} = 16 {\text{slm}}\)) with an equivalence ratio of 0.25 flows with 2.3 m/s through a porous sintered bronze matrix surrounding the atomization zone, forming a flat pilot flame that stabilizes the spray flame. The entire process is shielded from the surrounding environment by a nitrogen co-flow at a velocity of 0.6 m/s (\(\dot{V}_{{{\text{N}}_{2} }} = 120 {\text{slm}}\)).
The high velocity of the oxygen dispersion-flow produces a strong shear zone at the base of the spray, yielding small and fast droplets after the shear-induced secondary atomization. At the heights above burner (HAB) considered in this work, 40 and 50 mm, PDI measurements yielded mean axial velocities of 91 and 82 m/s, and Sauter mean droplet diameters of 22.5 and 23.6 μm, respectively (Bieber et al. 2021). This poses significant experimental challenges, since the imaging not only must have high resolution in space (implying high magnification) and time (to avoid blurring), but also cover sufficient streamwise distance to observe an entire droplet-disruption event. The latter was anticipated to occur in about 20 μs, which may seem very rapid, but is a practical limit for this experiment as the droplets travel about 1.7 mm in that time.
Under the same flow conditions but with an ethanol spray flame, the average aerodynamic Weber number was found to be 0.0001 and 0.01 at 40 and 50 mm HAB, respectively (Stodt et al. 2020). These values are far below the critical Weber number of 1.04–1.18, such that secondary aerodynamic breakup of droplets is very unlikely. This is essentially because in this region of the flame both droplets and gas phase have nearly the same velocity, with insufficient shear to produce aerodynamic breakup.
2.2 High-speed high-magnification shadowgraphy
Figure 2a, b shows the optical layout and the beam path of illumination and detection. A red LED (Nichia NCSR219B-V1, peak emission wavelength 630 nm, emission-intensity full width at half maximum (FWHM) 16 nm, 1 W power at 4 V constant voltage) was pulsed with a homebuilt driver inspired by (Willert et al. 2010), and emitted light pulses of around 200 ns duration. For Köhler-type illumination, light from the LED is (nearly) collimated by an aspheric collector lens (f = 16 mm). An auxiliary lens (f = 200 mm) images the LED into the illumination-aperture plane. A bi-convex “best-form” condenser lens (f = 40 mm) then demagnifies the field aperture and illuminates the FOV homogeneously. The shadowgraphs of the droplets are imaged by a combination of a microscope lens (Mitutoyo M Plan APO 10x) and an achromatic tube lens (f = 208 mm) onto the sensor of a high-speed camera (Photron Fastcam SA-Z, 20 μm pixel size). This yields a magnification of 11.1 and a projected pixel size in the object plane of 1.8 µm/pixel. At the numerical aperture of the microscope lens of 0.28 and the LED peak intensity wavelength of 630 nm, the Abbe diffraction limit is 1.1 µm. From measurements of the modulation transfer function (MTF), we found that the imaging system’s resolution is primarily limited by the sensor’s pixel pitch and not by the imaging optics. The MTF-50% value in the object plane was measured to be at a spatial frequency of 400 line pairs per millimeter.
The full sensor of the Photron SA-Z has 1024 × 1024 pixels on a 20.48 × 20.48 mm sensor. This corresponds to a FOV of 1.8 mm ∙ 1.8 mm with the magnification of the imaging optics employed. The maximum frame rate at full sensor read-out is 20,000 frames/second (fps). An LED burst of three pulses at very high repetition rate was triggered during each frame’s exposure time, essentially “stacking” the shadowgraphs of the burst of three light pulses in one exposure. This increases the temporal resolution but decreases the contrast of the (dark) shadow to the (bright) background. Three pulses were found to yield a reasonable compromise between temporal resolution and contrast. In the measurements with precursor/solvent mixtures, each LED burst was triggered with 360 kHz while the repetition rate of the camera was 120 000 fps reading out a region of interest (ROI) of 1024 ∙128 pixels (height ∙ width). This yielded a continuous sequence of temporally equally spaced droplet shadows. In some measurements the full sensor was read at 20 000 fps, but the LED pulse rate was kept at 360 kHz, yielding discontinuous three-shadow sequences over a horizontally wider FOV. In measurements with only the solvent the frame rate of the camera was 75,000 fps with an ROI of 1024 ∙ 256 pixels while the LED was triggered with 333 kHz.
The ensemble average of many dark (background) images IBG was subtracted from ensemble-averaged bright-field images I0—images without spray—and from each raw image I of the spray. The bright-field image was then divided by the spray image such that shadowgraphs of droplets appear bright in the processed images I*:
3 Results
3.1 Disruptive evaporation events
Figure 3 shows images, obtained in the SpraySyn burner, of droplets for the solvent EtOH/EHA only and the precursor INN dissolved in EtOH/EHA. Raw images show droplets as dark shadows. However, the processing according to Eq. (1) corresponds to a signal inversion, such that droplets appear bright while the background is dark. In Fig. 3, the images with EtOH/EHA show regular droplets with diameters between 14 and 21 µm. Within one image, the spacings between the three droplet shadowgraphs are very similar, indicating very little acceleration. There is slight “smearing” in the vertical direction, indicating that the 200 ns LED pulse duration is still not quite short enough to completely “freeze” the image of the moving droplet. In the droplets’ center, most images show a dark spot, which in fact in the raw images is a bright spot. This results from the droplets acting as micro lenses that focus some of the incident light to near the center of the droplet. Sometimes the spot is faint or not visible, which we attribute to the droplet being so small that the even smaller center region cannot be resolved, or that the droplet is slightly defocused. The toroidal symmetry of the droplet shadowgraph implies that the solvent-only droplets are nearly perfectly spherical.
In contrast to this, images of droplets with EtOH/EHA + INN not only show regular, spherical droplets but also morphologies that clearly deviate from that spherical shape. The regular droplets are visually very similar to the ones from EtOH/EHA, with diameters between 13 and 20 µm and slightly lower velocities (a more quantitative analysis is presented below). The irregular droplets are sometimes stretched asymmetrically, appear as several fragments, or the images indicate the ejection of jets of liquid and possibly gaseous solvent. We attribute these irregularities to puffing and micro-explosion events. Consistent with Stodt et al. (2021), a disrupting droplet tends to appear larger than it was before the onset of disruption. However, even the smaller droplets before disruption are spatially resolved (typical examples are the two rightmost images), such that we will be able to determine their size.
The fact that micro-explosions are observed only when adding INN to the solvent EtOH/EHA might result from different causes. First, adding INN to EtOH is known to increase the liquid’s viscosity (Keller et al. 2020) which in turn lowers the mass diffusion coefficient, increases the Lewis number, and results in an increased potential for superheating the volatile components (Wornat et al. 1994). Second, internally suspended solid filaments might increase the tendency for disruption by heterogeneous nucleation (Lasheras et al. 1980). Such filaments could stem from not completely dissolved INN salt or from precipitated intermediates from decomposing INN or INN reacting with EtOH/EHA. Third, INN is a hydrate, and dissolving 0.2 mol/l INN in the solvent adds around 3.4 wt% of water which then together with EtOH may form the dispersed phase in an emulsion with the EHA. Consistent with Stodt et al. (2019), photographs of such samples (0.2 mol/l INN in EtOH/EHA) at ambient temperature do not provide evidence of a phase separation or an emulsion, i.e., a disperse phase in the sample. However, the miscibility of the liquid mixture might decrease with increasing temperature, potentially resulting in liquid–liquid separation. As discussed in the Introduction, such emulsions are known to favor droplet disruption, because the high-volatile components (water + EtOH) are already spatially concentrated, increasing the likelihood for disruptive burning and disintegration.
Localized flame luminosity is observed in only very few of the images, while in the vast majority there is neither a dark (because of the color inversion) trail along the droplet path, as would be expected from a continuously burning droplet, nor dark spots that would be attributable to a flash-like sudden increase in luminosity. There are, however, image-wide variations in the background intensity. (These variations happen to be slight in the examples in Fig. 3, but Fig. 5 illustrates them more clearly.) This may indicate that as opposed to the single-droplet experiments, where necessarily each droplet is burning singly, the dominant spray combustion mode here is group combustion. (The droplet concentrations are about 1.6 and 0.5 mm−3 resulting in average interdroplet spacings of 0.6 and 2 mm at 40 and 50 mm HAB, respectively.) It is also possible that our detection with its exposure time on the order of 10 μs is not sensitive enough, despite the efficient light collection afforded by the numerical aperture of 0.28.
The fact that regular and disrupting droplets are both found within the probe volume suggests that it would be useful to be able to discriminate the two. Also, the few example images in Fig. 3 were selected as “in-focus” by visual inspection of many candidate images. However, for a systematic analysis of thousands of images such visual (i.e., human) confirmation of focus is not reasonable. Therefore, image processing was developed that identifies in-focus features, estimates the geometric properties of the features, and determines whether a feature is a regular or disrupting droplet.
3.2 Image analysis
Figure 4 shows the flowchart for the image processing and analysis algorithm. Raw images are background-corrected and flat-field corrected according to Eq. (1). In a second step a Sobel operator is applied to the images to find sharp edges associated with in-focus features. This operator determines the magnitude of the intensity gradient at each pixel. Then, the image is binarized by thresholding at a gradient magnitude value of 0.03, which visually yielded good results. (There is some interdependence of depth of field, threshold value, and detection sensitivity, as described below.) These high-gradient edge features are then dilated and filled (MATLAB R2021b functions imdilate and imfill with the binarized image as input) in the next step.
The exterior boundaries of filled objects then define a single in-focus feature. All individual in-focus features in an image are then labeled (MATLAB functions bwboundaries and regionprops) for further processing in the shape classification. Within the smallest rectangle enclosing the thresholded pixels of each labeled feature, intensity-based thresholding according to Otsu’s method (Otsu 1979) is applied to the flat-field corrected images I*. This yields the actual area of each feature more accurately than the gradient-based thresholding that was used to find it. From the area, A, the area-equivalent diameter, d, is calculated:
Since the contrast-transfer function deteriorates with increasing spatial frequency, small droplets are expected to have over-proportionally less Sobel-edge pixels than larger ones. A constant threshold on the number of edge pixels would thus bias the in-focus features toward larger droplets. To counter this bias, features in which the number of Sobel-edge pixels are below a size-dependent minimum are discarded. The size-dependent minimum number of edge pixels was determined in separate bench-top measurements in which images of a microscope slide with opaque circular dots (NG1 Patterson Globes and Circles) were acquired at different distances from the focal plane (results not shown here), as described in (Kashdan et al. 2003, 2007; Kim and Kim 1994). The dot images were processed according to the flowchart in Fig. 4 until the intensity-based thresholding. For each dot size, ranging from 10 to 144 µm in diameter, and each distance from the focal plane, the number of edge pixels was determined. With that information a fit was found that approximates the minimum number of edge pixels as a function of the droplet diameter. The function was found to validate features ± 42.5 µm from the focal plane as “in-focus”. Features with less than the minimum number of edge pixels are discarded as “out-of-focus”. Features covering less than two pixels (corresponding to an area-equivalent diameter of 2.8 µm) are also discarded. Then, area, A, perimeter, P, velocity, v, and circularity, S of each feature are determined. The circularity is defined as
In the next part, features are discriminated into regular and disrupting droplets. Since the convection of the flow is mostly vertical, it is likely that single features, illuminated three times, are found within a small horizontal distance. Thus, in a first step, features that are less than 50 columns away from each other are grouped. Further classification is based on four metrics, the number of features N, the circularity S, the pairwise distance between two features L, and the feature area A. If exactly three features are in such a group, the circularity of all features is above 0.7 (a circle has a circularity of S = 1, and, for example, a square has a circularity of S = 0.78) or the difference in area is less than 15%, and the difference between the pairwise vertical distances is less than 15%, the group is classified as a regular droplet illuminated three times. If the pairwise distances are not similar, it is a disrupting droplet (potentially showing the ejection of two secondary droplets). If more than three features are found or the requirements on circularity and area difference are not fulfilled, the group is classified to show a disruption. If exactly two features are found in a group, the circularity of both is above 0.7 or the difference in area less than 15%, the features represent a regular droplet. If their separation is less than 25 pixels, it is a disrupting droplet (ejection of one secondary droplet). A single feature with a circularity above 0.7 is a regular droplet. If the pairwise distances (of exactly three features in a group) or the features’ areas (of two or three features in a group) are similar (within 15% difference), these distances and LED pulse rate are used to calculate the velocity. Judged against visual inspection of the images, accuracies of 93 and 87% were determined for the algorithm in identifying regular and disrupting droplets, respectively.
At 40 and 50 mm HAB the processing classifies around 13.8 and 11.1% of the in-focus features as disrupting droplets, respectively. Since the FOV is 1.8 mm tall, this means that 7.7 and 6.2% of the in-focus droplets undergo puffing or micro-explosion per millimeter axial distance. Therefore, a first important statistical result from the image analysis is that along the 80 mm length of the flame all droplets are expected to undergo puffing or micro-explosion.
3.3 Classification of droplet-disruption events
After this algorithmic discrimination between regular and disrupting droplets, in some of the images the latter were further classified by visual inspection into puffing and micro-explosion. Puffing was further sub-divided into the phenomena of “droplet deformation” and “droplet eruption”. The former describes an obvious deviation from sphericity of the droplets, while the latter refers to the local rupture of the droplet surface and thus the apparent ejection of secondary droplets and/or vapor. Figure 5 shows a set of images for each class of droplet deformation, eruption, and micro-explosion. The variation in brightness throughout the images in Fig. 5a results from the large-scale variations in background flame luminosity discussed in Sect. 3.1.
Figure 5a shows 13 puffing events of the first class, droplet deformation. The images show strong perturbations in the droplet shape throughout the three-illumination sequence, comprising a time of only 5.6 µs. Images 3, 7, 10, 11, and 12 show droplets either elongating or “bending”. The bent droplet in the center of image 12 shows a surface rupture in the bottom left and the apparent ejection of fine secondary droplets and potentially vapor followed by the ejection of secondary droplets toward the left and right in the subsequent third illumination. Images 5, 6, 8, and 13 show the sudden swelling of the droplets, most likely from the rapid growth of a gas bubble within the droplet’s interior. Image 13 indicates an expansion of the droplet diameter from about 11 µm in the second to 20 µm in the third illumination (i.e., within 2.8 µs), corresponding to a rate of expansion in the radius of 1.6 m/s and an increase of the volume by a factor of six. In images 6 and 8 the droplet strongly deforms into what appears to be a flattened structure after swelling. Most likely, whether a droplet swells and remains mostly spherical, or deforms to a highly non-spherical shape depends on the position of the bubble nucleation sites within the droplet. While nucleation and growth of a bubble near the droplet’s center cause an isotropic expansion of the droplet, nucleation and growth near the surface result in strong deformation and potentially local surface rupture (Shinjo et al. 2014).
Figure 5b shows 10 images of droplet eruption. In this class of events, the droplet surface locally bursts, and one or more secondary droplets are ejected. Potentially, droplet deformation precedes droplet eruption. The blue arrows label the ejection of secondary droplets that move away from the parent droplet with time. Most images, like 2, 6, and 9, show a significant deformation of the droplet before the ejection of one or more secondary droplets. Image 2 shows a partial micro-explosion in which large parts of the droplet’s surface burst into multiple droplets. From images 4, 5, 7, 8, and 11, the velocity of the secondary droplets relative to the parent droplet’s velocity can be estimated to about 2–3 m/s.
Figure 5c mostly shows fragments of droplets which remain after a micro-explosion, while only image 3 shows the event itself. The first illumination in image 3 shows a large swollen droplet and the second illumination secondary droplets after micro-explosion. The fact that we mostly see fragments of micro-explosions at 50 mm HAB indicates that the event of a micro-explosion is very short and potentially happens further upstream in the spray flame. Micro-explosion fragments were found much less frequently than puffing, consistent with the findings of Watanabe and Okazaki (Watanabe and Okazaki 2013). In contrast, qualitative results from single-droplet experiments (Li et al. 2019; Rosebrock et al. 2013, 2016) suggest the more violent micro-explosion is the dominant disintegration mechanism. Such single-droplet experiments typically use larger initial droplets (on the order of 100 µm diameter) (Rosebrock et al. 2016) than found in our spray. Also, residence times before disruption are significantly longer (on the order of 1.5–5 ms) for these idealized experiments than in the spray (on the order of 500 µs) (Rosebrock et al. 2016). In a theoretical model of precursor-laden vaporizing single droplets, Ren et al. (2021) determine the ratio of the precursor-evaporation rate and the decomposition rate. They find that this ratio significantly increases with decreasing droplet size due to increasing time scales of thermal and mass diffusion. Thus, in small droplets less precursor decomposing could theoretically yield a less viscous shell, thus a lower Lewis number, as well as less precipitate, and potentially a more moderate disruption.
Finally, Fig. 6 shows puffing and micro-explosion at 40 and 50 mm HAB from multiple consecutive images. Image series 1 at 40 mm HAB shows an initially regular droplet that undergoes a puffing event with droplet deformation between 0 and 8.4 µs. At 11.2 µs, the droplet appears to have reformed into a spherical shape, before undergoing a weak micro-explosion starting at 14 µs that ends in the fragmentation of the parent droplet into two droplets of similar size between 19.6 and 22.4 µs, and the ejection of a secondary droplet to the left at 25.2 µs. The image series 2 shows a spherical droplet until 5.6 µs that then rapidly swells and bursts first near the top, then forming a pointed tip in the bottom that may indicate the ejection of fine droplets and presumably vapor. In image series 3, the droplet bends at 5.6 µs and swells before it disintegrates into two fragments between 8.4 and 11.2 µs. In series 4, the droplet shows a local surface rupture and the ejection of fine droplets at 2.8 µs before it first horizontally flattens, then swells (by about a factor of three in volume) and micro-explodes between 8.4 and 11.2 µs. These timescales are generally consistent with Fuchihata et al. (2003) who found a 25 µm diameter droplet of oil/water emulsion completely disintegrating in a micro-explosion lasting 10 µs. Similarly, Watanabe et al. (2014) observed multiple puffing and micro-explosions for a single droplet of water/oil emulsions with a diameter around 20 µm. Recently, Stodt et al. (2021) also observed multiple disintegration phenomena of a single droplet of EtOH/EHA + INN in the SpraySyn burner, lasting for about 32 µs.
Image series 1 at 50 mm HAB shows multiple puffing events of a droplet. Between 2.8 and 11.2 µs, single secondary droplets are ejected to different sides by the parent droplet. At 5.6 and 14 µs the droplet appears significantly swollen but does not micro-explode, most likely due to some local surface rupture. The second series at 50 mm HAB indicates slower puffing with the ejection of a secondary droplet to the left. Consistent with the results from Stodt et al. (2021), the parent droplet undergoes a rotation, here counterclockwise, which might result from radial momentum induced by puffing and shear stress.
3.4 Statistical analysis
Figure 7 shows frequency histograms of the area-equivalent diameters of regular and disrupting droplets at 40 and 50 mm HAB. Also indicated are Sauter mean diameters (SMD, d32), velocities, as well as log-normal fits to the data. At 40 mm HAB, the histograms comprise data from 1122 and 225 regular and disrupting droplets, respectively, and at 50 mm HAB from 3999 and 813 regular and disrupting droplets, respectively. The histograms show that disrupting droplets are significantly smaller than regular droplets and have a 36 and 28% lower SMD than regular droplets at 40 and 50 mm HAB, respectively. Note that this does not imply that a certain size class of droplets predominantly experiences disruption. To clarify that individual droplets must be followed throughout their evaporation history to assess whether they are disrupting, as shown in Fig. 6. However, the current sample size of these images is not sufficient for reliable, more detailed statistics.
The size distributions for both regular and disrupting droplets are well-approximated by a log-normal distribution, i.e., the disruptions qualitatively maintain the initial distribution characteristics. As opposed to that Stodt et al. (2020) found a bimodal frequency distribution of the droplet diameter at 50 mm HAB, which they attributed to droplet disruptions. Their measurements were in a very similar flame on the SpraySyn burner (but their precursor concentration, 0.5 mol/l INN in EtOH/EHA, was 2.5 times higher than ours). However, they measured droplet sizes with PDI where aspherical droplets either are not measured accurately or rejected in automatic signal processing. Better statistics from our droplet imaging will be needed to clarify these differences in the size distributions.
The mean axial velocity is about 7.7% higher and 5.5% lower for disrupting than for regular droplets at 40 and 50 mm HAB, respectively. Therefore, the droplet velocity and thus their past residence time in the high-temperature region appears not to be clearly correlated to droplet disruptions in the probe volume. However, since droplet disruption creates smaller droplets, it reduces the downstream survival time of the droplets due to evaporation. In the mean over both regular and disrupting droplets, the axial velocities are 92 and 81 m/s at 40 and 50 mm, respectively. This is in very good agreement with the PDI-based values of 91 and 82 m/s from Bieber et al. (2021). At the two HAB, our overall mean droplet SMDs are 19 and 19.8 µm and these are also consistent with the 22.5 and 23.6 µm from Bieber et al. (2021). Our overall arithmetic mean diameters are 14.7 and 15.4 µm, consistent with the 12.5 and 16 µm reported by Stodt et al. (2020) at these two heights.
4 Conclusions and future work
Shadowgraphy imaging with high spatiotemporal resolution was used to visualize regular and disrupting droplets in spray flames burning mixtures of 35% ethanol (EtOH) and 65% 2-ethylhexanoic acid (EHA) as well as mixtures of EtOH/EHA + 0.2 mol/l iron(III) nitrate nonahydrate (INN). With EtOH/EHA only, solely regular, spherical, droplets were found, while with EtOH/EHA + 0.2 mol/l INN at 40 and 50 mm height above burner (HAB) droplet puffing and micro-explosion were observed along with regular droplets.
An algorithm was developed to automatically find in-focus features (the depth of field, which is 85 µm here, and the field of view then constitute the probe volume), infer morphologic metrics such as size, velocity, and shape, and discriminate regular droplets from disrupting droplets, the latter undergoing puffing or micro-explosions. It was found that in the probe volume between 11 and 14% of the in-focus droplets are undergoing disruption while the rest are regular spherical droplets. Extrapolated from the admittedly limited database, we conclude that in this flame droplet disruption is not an exception but the rule. Most disruption events are “puffing”, where the droplet deforms or swells due to bubble growth and then bursts locally with or without the visible ejection of secondary droplets and vapor. Other images show a more violent disintegration of the droplet into many secondary drops, a “micro-explosion”, which is sometimes only a few microseconds short. Consecutive images indicate that a single droplet can be subject to several puffing and micro-explosion phenomena, each significantly reducing the droplet diameter. The area-equivalent diameter of disrupting droplets was found to follow a log-normal probability distribution, as did the diameter of regular droplets. But the distribution of the former is shifted toward smaller diameters with respect to the latter, the Sauter mean diameter of disrupting droplets being 32% smaller than that of regular droplets. Regular and disrupting droplets’ axial velocities were found to be very similar and consistent with phase Doppler interferometry results from the literature.
This work has established a method to investigate puffing and micro-explosion phenomena in spray-flame synthesis of nanomaterials. In future work, the diagnostics and processing tools developed here will be applied to the entire spray flame to statistically investigate the occurrence of puffing and micro-explosion along the axial and radial dimensions of the spray flame. Also, the influence of different solvents and precursors on puffing and micro-explosion will be studied. The existing image-analysis routines will be extended to also classify the disruption event (micro-explosion of puffing) and infer further parameters such as number and relative velocity of secondary droplets and the evaporation rate during disruption. The existing imaging technique can be complemented by different schemes, such as dark-field or scattering techniques which may yield better contrast in some situations. One may infer from this work that droplet size has a role in the probability of a droplet disruption—this is also a topic for further investigation.
Change history
04 June 2022
A Correction to this paper has been published: https://doi.org/10.1007/s00348-022-03440-7
References
Avedisian CT, Andres RP (1978) Bubble nucleation in superheated liquid–liquid emulsions. J Colloid Interface Sci 64:438–453. https://doi.org/10.1016/0021-9797(78)90386-7
Bar-Kohani T, Antonov D, Strizhak PA, Sazhin SS (2021) Nucleation inception due to conductive heating of composite droplets: experimental observations and modelling. In: 15th international conference on liquid atomization and spray systems (ICLASS), Edinburgh, UK
Bieber M, Al-Khatib M, Fröde F et al (2021) Influence of angled dispersion gas on coaxial atomization, spray and flame formation in the context of spray-flame synthesis of nanoparticles. Exp Fluids. https://doi.org/10.1007/s00348-021-03196-6
Califano V, Calabria R, Massoli P (2014) Experimental evaluation of the effect of emulsion stability on micro-explosion phenomena for water-in-oil emulsions. Fuel 117:87–94. https://doi.org/10.1016/j.fuel.2013.08.073
Damaschke N, Gouesbet G, Gréhan G, Mignon H, Tropea C (1998) Response of phase doppler anemometer systems to nonspherical droplets. Appl Opt 37:1752–1761. https://doi.org/10.1364/AO.37.001752
Damaschke N, Nobach H, Tropea C (2002) Optical limits of particle concentration for multi-dimensional particle sizing techniques in fluid mechanics. Exp Fluids 32:143–152. https://doi.org/10.1007/s00348-001-0371-x
Fu WB, Hou LY, Wang L, Ma FH (2002) A unified model for the micro-explosion of emulsified droplets of oil and water. Fuel Process Technol 79:107–119. https://doi.org/10.1016/S0378-3820(02)00106-6
Fuchihata M, Ida T, Mizutani Y (2003) Observation of microexplosion in light oil-water emulsion spray flame. Trans Jpn Soc Mech Eng B 69:1503–1508. https://doi.org/10.1299/kikaib.69.1503
Huo M, Lin S, Liu H, Lee CF (2014) Study on the spray and combustion characteristics of water–emulsified diesel. Fuel 123:218–229. https://doi.org/10.1016/j.fuel.2013.12.035
Ismael M, Heikal MR, Aziz AAR et al (2018) Investigation of puffing and micro-explosion of water-in-diesel emulsion spray using shadow imaging. Energies 11:2281. https://doi.org/10.3390/en11092281
Jeong I, Lee K-H, Kim J (2008) Characteristics of auto-ignition and micro-explosion behavior of a single droplet of water-in-fuel. J Mech Sci 22:148–156. https://doi.org/10.1007/s12206-007-1018-5
Jiang Y, Jeon HY, Tian L, Bode LE (2010) Measuring particle size distribution using LED-illumination. Int J Multiph Flow 36:193–201. https://doi.org/10.1016/j.ijmultiphaseflow.2009.11.004
Kadota T, Yamasaki H (2002) Recent advances in the combustion of water fuel emulsion. Prog Energy Combust Sci 28:385–404. https://doi.org/10.1016/S0360-1285(02)00005-9
Kashdan J, Shrimpton J, Whybrew A (2003) Two-phase flow characterization by automated digital image analysis. Part 1: fundamental principles and calibration of the technique. Part Part Syst Charact 20:387–397. https://doi.org/10.1002/ppsc.200300897
Kashdan JT, Shrimpton JS, Whybrew A (2004) Two-phase flow characterization by automated digital image analysis. Part 2: application of PDIA for sizing sprays. Part Part Syst Charact 21:15–23. https://doi.org/10.1002/ppsc.200400898
Kashdan JT, Shrimpton JS, Whybrew A (2007) A digital image analysis technique for quantitative characterisation of high-speed sprays. Opt Lasers Eng 45:106–115. https://doi.org/10.1016/j.optlaseng.2006.03.006
Keller A, Wlokas I, Kohns M, Hasse H (2020) Thermophysical properties of solutions of Iron(III) nitrate-nonahydrate in mixtures of ethanol and water. J Chem Eng Data 65:3519–3527. https://doi.org/10.1021/acs.jced.0c00105
Kim KS, Kim S-S (1994) Drop sizing and depth-of-field correction in TV imaging. At Sprays 4:65–78. https://doi.org/10.1615/AtomizSpr.v4.i1.30
Koh K, Kim J, Lee S (2001) Determination of in-focus criteria and depth of field in image processing of spray particles. At Sprays 11:317–333. https://doi.org/10.1615/AtomizSpr.v11.i4.20
Kumar A, Sahu S (2020) Liquid jet disintegration memory effect on downstream spray fluctuations in a coaxial twin-fluid injector. Phys Fluids 32:73302. https://doi.org/10.1063/5.0009188
Lasheras J, Fernandez-Pello A, Dryer F (1979) Initial observations on the free droplet combustion characteristics of water-in-fuel emulsions. Combust Sci Technol 21:1–14. https://doi.org/10.1080/00102207908946913
Lasheras J, Fernandez-Pello A, Dryer F (1980) Experimental observation on the disruptive combustion of free droplets of multicomponent fuels. Combust Sci Technol 22:195–209. https://doi.org/10.1080/00102208008952383
Lasheras JC, Fernandez-Pello AC, Dryer FL (1981a) On the disruptive burning of free droplets of alcohol/n-paraffin solutions and emulsions. Symp Combust Proc 18:293–305. https://doi.org/10.1016/S0082-0784(81)80035-5
Lasheras JC, Kennedy IM, Dryer FL (1981b) Burning of distillate fuel droplets containing alcohol or water: effect of additive concentration. Combust Sci Technol 26:161–169. https://doi.org/10.1080/00102208108946956
Lasheras JC, Yap LT, Dryer FL (1985) Effect of the ambient pressure on the explosive burning of emulsified and multicomponent fuel droplets. Symp Combust Proc 20:1761–1772. https://doi.org/10.1016/S0082-0784(85)80673-1
Law CK, Lee CH, Srinivasan N (1980) Combustion characteristics of water-in-oil emulsion droplets. Combust Flame 37:125–143. https://doi.org/10.1016/0010-2180(80)90080-2
Lecuona A, Sosa PA, Rodriguez PA, Zequeira R (2000) Volumetric characterization of dispersed two phase flows by digital image analysis. Meas Sci Technol 11:1152. https://doi.org/10.1088/0957-0233/11/8/309
Lee S, Kim Y-D (2004) Sizing of spray particles using image processing techniques. J Mech Sci 18:879–894. https://doi.org/10.1007/BF02990860
Li H, Rosebrock CD, Wu Y, Wriedt T, Mädler L (2019) Single droplet combustion of precursor/solvent solutions for nanoparticle production: optical diagnostics on single isolated burning droplets with micro-explosions. Proc Combust Inst 37:1203–1211. https://doi.org/10.1016/j.proci.2018.06.133
Linne M (2013) Imaging in the optically dense regions of a spray: a review of developing techniques. Prog Energy Combust Sci 39:403–440. https://doi.org/10.1016/j.pecs.2013.06.001
Liu H, Lee C-f, Huo M, Yao M (2011) Comparison of ethanol and butanol as additives in soybean biodiesel using a constant volume combustion chamber. Energy Fuels 25:1837–1846. https://doi.org/10.1021/ef200111g
Mädler L, Kammler HK, Mueller R, Pratsinis SE (2002) Controlled synthesis of nanostructured particles by flame spray pyrolysis. J Aerosol Sci 33:369–389. https://doi.org/10.1016/S0021-8502(01)00159-8
Malot H, Blaisot J-B (2000) Droplet size distribution and sphericity measurements of low-density sprays through image analysis. Part Part Syst Char 17:146–158. https://doi.org/10.1088/0957-0233/21/2/025501
Mikami M, Kojima N (2002) An experimental and modeling study on stochastic aspects of microexplosion of binary-fuel droplets. Proc Combust Inst 29:551–559. https://doi.org/10.1016/S1540-7489(02)80071-2
Mikami M, Yagi T, Kojima N (1998) Occurrence probability of microexplosion in droplet combustion of miscible binary fuels. Symp Combust Proc 27:1933–1941. https://doi.org/10.1016/S0082-0784(98)80037-4
Mizutani Y, Muraoka M (2001) In situ observation of microexplosion of emulsion droplets in spray flames. At Sprays 11:12. https://doi.org/10.1615/AtomizSpr.v11.i5.30
Moussa O, Francelino D, Tarlet D, Massoli P, Bellettre J (2019) Insight of a water-in-oil emulsion drop under leidenfrost heating using laser-induced fluorescence optical diagnostics. At Sprays 29:1–17. https://doi.org/10.1615/AtomizSpr.2019029233
Moussa O, Tarlet D, Massoli P, Bellettre J (2020) Investigation on the conditions leading to the micro-explosion of emulsified fuel droplet using two colors LIF method. Exp Therm Fluid Sci 116:110106. https://doi.org/10.1016/j.expthermflusci.2020.110106
Mura E, Josset C, Loubar K, Huchet G, Bellettre J (2010) Effect of dispersed water droplet size in microexplosion phenomenon for water in oil emulsion. At Sprays 20:791–799. https://doi.org/10.1615/AtomizSpr.v20.i9.40
Mura E, Massoli P, Josset C, Loubar K, Bellettre J (2012) Study of the micro-explosion temperature of water in oil emulsion droplets during the leidenfrost effect. Exp Therm Fluid Sci 43:63–70. https://doi.org/10.1016/j.expthermflusci.2012.03.027
Mura E, Calabria R, Califano V, Massoli P, Bellettre J (2014) Emulsion droplet micro-explosion: analysis of two experimental approaches. Exp Therm Fluid Sci 56:69–74. https://doi.org/10.1016/j.expthermflusci.2013.11.020
Namba K, Kimoto K (2000) Ignition and combustion behavior of asphalt/water-emulsified fuels. JSME Int J Ser B 43:478–484. https://doi.org/10.1299/jsmeb.43.478
Ochoterena R, Lif A, Nydén M, Andersson S, Denbratt I (2010) Optical studies of spray development and combustion of water-in-diesel emulsion and microemulsion fuels. Fuel 89:122–132. https://doi.org/10.1016/j.fuel.2009.06.039
Otsu N (1979) A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern 9:62–66. https://doi.org/10.1109/TSMC.1979.4310076
Ren Y, Jinzhi C, Pitsch H (2021) Theoretical single-droplet model for particle formation in flame spray pyrolysis. Energy Fuels 35:1750–1759. https://doi.org/10.1021/acs.energyfuels.0c03669
Rosebrock CD, Riefler N, Wriedt T, Mädler L, Tse SD (2013) Disruptive burning of precursor/solvent droplets in flame-spray synthesis of nanoparticles. AlChE J 59:4553–4566. https://doi.org/10.1002/aic.14234
Rosebrock CD, Wriedt T, Mädler L, Wegner K (2016) The role of microexplosions in flame spray synthesis for homogeneous nanopowders from low-cost metal precursors. AlChE J 62:381–391. https://doi.org/10.1002/aic.15056
Sazhin SS, Rybdylova O, Crua C et al (2019) A simple model for puffing/micro-explosions in water-fuel emulsion droplets. Int J Heat Mass Transf 131:815–821. https://doi.org/10.1016/j.ijheatmasstransfer.2018.11.065
Sazhin SS, Bar-Kohany T, Nissar Z, Antonov D, Strizhak PA, Rybdylova OD (2020) A new approach to modelling micro-explosions in composite droplets. Int J Heat Mass Transf 161:120238. https://doi.org/10.1016/j.ijheatmasstransfer.2020.120238
Sazhin SS, Bar-Kohani T, Nissar Z, Antonov D, Strizhak PA, Rybdylova OD (2021) Micro-explosions in composite droplets: experimental observations and modelling. In: 15th international conference on liquid atomization and spray systems (ICLASS), Edinburgh, UK
Schneider F, Suleiman S, Menser J et al (2019) SpraySyn: a standardized burner configuration for nanoparticle synthesis in spray flames. Rev Sci Instrum. https://doi.org/10.1063/1.5090232
Sheng HZ, Chen L, Zhang ZP, Wu CK, An C, Cheng CQ (1994) The droplet group microexplosions in water-in-oil emulsion sprays and their effects on diesel engine combustion. Symp Combust Proc 25:175–181. https://doi.org/10.1016/S0082-0784(06)80642-9
Shinjo J, Xia J, Ganippa LC, Megaritis A (2014) Physics of puffing and microexplosion of emulsion fuel droplets. Phys Fluids 26:103302. https://doi.org/10.1063/1.4897918
Stodt MFB, Gonchikzhapov M, Kasper T, Fritsching U, Kiefer J (2019) Chemistry of iron nitrate-based precursor solutions for spray-flame synthesis. Phys Chem Chem Phys 21:24793–24801. https://doi.org/10.1039/C9CP05007H
Stodt MFB, Kiefer J, Fritsching U (2020) Drop dynamics in heterogeneous spray flames for nanoparticle synthesis. At Sprays 30:779–797. https://doi.org/10.1615/AtomizSpr.2020034819
Stodt MFB, Groeneveld JD, Mädler L, Kiefer J, Fritsching U (2021) Combustion of multi-component drops during flame spray pyrolysis. In: 15th international conference on liquid atomization and spray systems (ICLASS), Edinburgh, UK
Strobel R, Pratsinis S (2011) Effect of solvent composition on oxide morphology during flame spray pyrolysis of metal nitrates. Phys Chem Chem Phys 13:9246–9252. https://doi.org/10.1039/c0cp01416h
Suzuki Y, Harada T, Watanabe H et al (2011) Visualization of aggregation process of dispersed water droplets and the effect of aggregation on secondary atomization of emulsified fuel droplets. Proc Combust Inst 33:2063–2070. https://doi.org/10.1016/j.proci.2010.05.115
Teoh WY, Amal R, Mädler L (2010) Flame spray pyrolysis: an enabling technology for nanoparticles design and fabrication. Nanoscale 2:1324–1347. https://doi.org/10.1039/c0nr00017e
Wang CH, Liu XQ, Law CK (1984) Combustion and microexplosion of freely falling multicomponent droplets. Combust Flame 56:175–197. https://doi.org/10.1016/0010-2180(84)90036-1
Watanabe H, Okazaki K (2013) Visualization of secondary atomization in emulsified-fuel spray flow by shadow imaging. Proc Combust Inst 34:1651–1658. https://doi.org/10.1016/j.proci.2012.07.005
Watanabe H, Harada T, Matsushita Y, Aoki H, Miura T (2009) The characteristics of puffing of the carbonated emulsified fuel. Int J Heat Mass Transf 52:3676–3684. https://doi.org/10.1016/j.ijheatmasstransfer.2009.02.033
Watanabe H, Suzuki Y, Harada T, Matsushita Y, Aoki H, Miura T (2010) An experimental investigation of the breakup characteristics of secondary atomization of emulsified fuel droplet. Energy 35:806–813. https://doi.org/10.1016/j.energy.2009.08.021
Watanabe H, Shoji Y, Yamagaki T, Hayashi J, Akamatsu F, Okazaki K (2014) Observation of droplet behavior of emulsified fuel in secondary atomization in flame. J Therm Sci Technol. https://doi.org/10.1299/jtst.2014jtst0009
Willert C, Stasicki B, Klinner J, Moessner S (2010) Pulsed operation of high-power light emitting diodes for imaging flow velocimetry. Meas Sci Technol 247239:129–247. https://doi.org/10.1088/0957-0233/21/7/075402
Wood BJ, Wise H, Inami SH (1960) Heterogeneous combustion of multicomponent fuels. Combust Flame 4:235–242. https://doi.org/10.1016/S0010-2180(60)80027-2
Wornat MJ, Porter BG, Yang NYC (1994) Single droplet combustion of biomass pyrolysis oils. Energy Fuels 8:1131–1142. https://doi.org/10.1021/ef00047a018
Yap LT, Kennedy I, Dryer F (1984) Disruptive and micro-explosive combustion of free droplets in highly convective environments. Combust Sci Technol 41:291–313. https://doi.org/10.1080/00102208408923836
Zeng Y, Lee C-fF (2007) Modeling droplet breakup processes under micro-explosion conditions. Proc Combust Inst 31:2185–2193. https://doi.org/10.1016/j.proci.2006.07.237
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was supported by the German Research Foundation (DFG) within the Priority Program SPP 1980 SpraySyn under project number 447500013. The DFG Mercator Fellowship held by Greg Smallwood is supported by project number 374957702.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known financial or non-financial conflict of interest interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jüngst, N., Smallwood, G.J. & Kaiser, S.A. Visualization and image analysis of droplet puffing and micro-explosion in spray-flame synthesis of iron oxide nanoparticles. Exp Fluids 63, 60 (2022). https://doi.org/10.1007/s00348-022-03411-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-022-03411-y