Experimental investigation of the pre–Darcy regime

Abstract

The validity of Darcy’s law at very low Reynolds numbers is discussed controversially in literature, as some authors propose a pre–Darcy flow regime below some critical Reynolds number. The scope of this work is to investigate this problem experimentally. Therefore, a packing of glass spheres is perfused by different glycerin–water solutions. A linear behaviour between the flow velocity and the pressure drop through the packed spheres is found in the complete investigated range of Reynolds number ${Re}_{d'}$, based on the mean-pore diameter $d'$ and mean-pore velocity $v'$ with $10^{-9} \le {Re}_{d'} \le 10^{-1}$. This contradicts the results of different authors like Fand et al. (1987) or Kececioglu and Jiang (1994), postulating a pre–Darcy regime for ${Re}_{d'} \le 2.8 \cdot 10^{-6}$ or ${Re}_{d'} \le 0.13$, respectively.

Graphical abstract

1 Introduction

For the flow of a fluid through a porous medium, a pressure gradient is necessary. A creeping flow can be described by the law of Darcy (1856). The pressure loss due to the friction at the pore walls proves to be proportional to the speed of the flow. For sufficiently large Reynolds numbers, inertial effects come into play. Hence, Darcy’s law loses its validity, and the data follow the law of Forchheimer (1926). In literature, the transition to inertia has been extensively investigated and appears to be generally accepted. For similarly long times, a limit of Darcy’s law for sufficiently small Reynolds numbers has been discussed. Not only that different authors give different Reynolds number limits for this transition but also in a review article, Kutilek (1972) lists twelve different qualitative deviations from the linear Darcy behaviour. Before taking a closer look in the literature, the definition of some basic quantities appears helpful.

2 Basics

A porous medium consists of a solid and of pores, which are non–solid regions. A variable for the averaged description is the porosity.

$$\begin{aligned} \varepsilon =\frac{V_e}{V_{tot}}=1-\frac{V_s}{V_{tot}}, \end{aligned}$$

(1)

which is the ratio of empty volume $V_e$ and total volume $V_{tot}$. The total volume can also be expressed by using the solid volume $V_s$. The appropriate characteristic length scale for a flow through a porous medium should be the mean pore diameter $d'$. If the porous medium is a packed bed of spheres, like in this work, $d'$ can be related to the diameter $d_p$ of the spherical particles. The specific surface $s_s$ of a spherical particle is

$$\begin{aligned} s_s=\frac{\text {surface of sphere}}{\text {volume of sphere}}=\frac{\pi d_p^2}{\frac{\pi }{6}d_p^3}=\frac{6}{d_p}. \end{aligned}$$

(2)

The specific surface of a packed bed $s_p$ can be computed by multiplying with the solid fraction $(1-\varepsilon )$, i.e.

$$\begin{aligned} s_p=s_s(1-\varepsilon ). \end{aligned}$$

(3)

The specific surface area of the total porous medium is the common specific area of the spheres and the pores. Therefore, the specific surface of a pore is

$$\begin{aligned} s_{pore}=\frac{s_p}{\varepsilon }. \end{aligned}$$

(4)

The characteristic pore length is $d'$ is determined by the definition of the equivalent diameter of Coulson and Richardson (1993) as

$$\begin{aligned} d' = \frac{1}{s_{pore}} = \frac{\varepsilon }{s_p}=\frac{1}{6}\frac{\varepsilon }{(1-\varepsilon )}d_p. \end{aligned}$$

(5)

If the porous medium is located in a tube with the cross–sectional area A, and if a flow of an incompressible fluid with the volumetric flow rate ${\dot{V}}$ exists through the porous medium, two different definitions of the velocity are common: (i) The so–called superficial velocity $v_s$ corresponds to the mean flow velocity through the empty tube without the porous medium. (ii) Alternatively, the so–called mean pore velocity $v'$ can be engaged. Hence, we have

$$\begin{aligned} v_s=\frac{{\dot{V}}}{A}; \quad v'=\frac{{\dot{V}}}{A\varepsilon }=\frac{v_s}{\varepsilon }. \end{aligned}$$

(6)

If fluid flows through a porous medium, it experiences a flow resistance. The French civil engineer Darcy (1856) discovered a linear correlation between the flow rate and the pressure loss $\varDelta p$ along the length L within the porous medium. This has led to Darcy’s law

$$\begin{aligned} {v_s}=-\frac{k}{\eta }\frac{\varDelta p}{L}, \end{aligned}$$

(7)

with the superficial velocity $v_s$, the dynamic viscosity $\eta$, pressure p, and the proportionality factor k, usually termed permeability. Several conditions must be met for applicability, namely

• Newtonian fluid,

• Single–phase flow,

• Constant fluid properties,

• Inert porous medium,

• Fixed position of particles,

• Steady flow,

• Creeping flow.

The theoretical determination of the permeability is based on the capillary model, according to which the porous medium is traversed by a number of identical pore channels (Carman 1937). According to Hagen–Poiseuille Poiseuille (1840), the velocity v is given in an empty tube with the diameter $d_t$ as

$$\begin{aligned} v=\frac{d_t^2}{32 \eta }\frac{-\varDelta p}{L}. \end{aligned}$$

(8)

A transfer to the pore velocity gives

$$\begin{aligned} v'={\frac{d'^2}{K' \eta }}\frac{-\varDelta p}{L'} = \underbrace{\frac{1}{K''}\frac{\varepsilon ^2}{s_s^2(1-\varepsilon )^2}}_{k\varepsilon ^{-1}}\cdot \frac{1}{\eta }\frac{-\varDelta p}{L}, \end{aligned}$$

(9)

with a proportionality factor $K'$ and the length of the pore channels $L'$, which is generally not the length of the porous bed L. The proportionality factor $K''$ takes the influence of this difference into account and can be combined with $K'$ via $L'\cdot K'=L \cdot K''$. This is the so–called Kozeny constant, the value of which is $K''\approx 5$ in most experiments. This results in the well–known Carman–Kozeny equation (cf. Coulson and Richardson 1993, Carman 1937), i.e.

$$\begin{aligned} k\approx \frac{1}{180}\frac{\varepsilon ^3}{(1-\varepsilon )^2}d_p^2. \end{aligned}$$

(10)

This equation is valid for a creeping flow, whereas the flow regimes, in general, can be categorized by the Reynolds number. The Reynolds number is the ratio of inertial and frictional forces and is defined in this work as

$$\begin{aligned} Re_{d'}=\frac{\varrho v' d'}{\eta }=\frac{v_s \varrho d_p}{6\eta (1-\varepsilon )}=\frac{1}{6(1-\varepsilon )}\underbrace{\frac{\rho d_p v_s}{\eta }}_{Re_{d_p}}, \end{aligned}$$

(11)

with the density of the fluid $\varrho$. Using the Carman–Kozeny Eq. (10), a direct correlation can be made with the usual definition of the Reynolds number $Re_k$ (cf. Kececioglu and Jiang 1994, Civan 2011) for flows through porous media, which reads as

$$\begin{aligned} Re_k = \frac{v'\varrho }{\eta }\sqrt{\frac{k}{\varepsilon }} = \frac{1}{\sqrt{5}}Re_{d'} . \end{aligned}$$

(12)

Figure 1 shows schematically the different flow regimes in porous media according to Fand et al. (1987). Plotted is the qualitative dependence of the Kozeny constant $K''$, i.e.

$$\begin{aligned} K''=-\frac{\varDelta p}{L}\frac{1}{\eta v'}\frac{\varepsilon ^2}{(1-\varepsilon )^2s_s^2} \end{aligned}$$

(13)

against the Reynolds number $Re_{d_p}$. A horizontal line can be expected in this diagram if Darcy’s law is applicable. Further, if the horizontal line is at $K''= 5$, this proves the validity of the Carman–Kozeny equation. As expected, for greater Reynolds numbers $Re_{d_p} > 2.3$ in laminar flow, inertial effects are no longer negligible, and the flow even gets turbulent for even larger Reynolds numbers. The deviation for very small Reynolds numbers from Darcy’s law appears rather unexpected. This is the so–called pre–Darcy regime, which is proposed by various authors. Since no uniform behaviour in the pre–Darcy regime and various critical Reynolds numbers for the transition to the pre–Darcy regime are proposed, some authors doubt its existence and assume measurement errors or other physical or chemical effects instead.

Fig. 1

Flow regimes in porous media according to Fand et al. (1987)

3 Literature

Kutilek (1972) reviews literature on the flow of water within soils. According to Darcy’s law, a plot of the superficial velocity $v_s$ against the applied pressure gradient $\nabla p$ should follow a straight line through the origin. Kutilek (1972) lists 12 different forms of deviations from this behaviour, as summarized in Fig. 2. If a fluid flows through natural porous materials, a dissolution of solid components may occur if the retention time is long enough. Fluid and solid may even develop a complete dissolution. This could explain deviations from Darcy’s law, since on the one hand, the viscosity of the fluid, and on the other hand, the structure of the porous medium may change. For example, Russel and Swartzendruber (1971) report a pre–Darcy regime for the flow of water through swellable mixtures of sand, clay, and loam. Further, Miller-Brownlie (1919) finds a threshold pressure gradient for the onset of subsoil water flows, and Prada and Civan (1999) for saturated brine flowing through stones and a packing of sand. In Fig. 2, the flow behaviour is, e.g., of type $\textcircled {\small {A}}$ – $\textcircled {\small {G}}$.

Fig. 2

Pre–Darcy flow behaviour in the form of superficial velocity against the pressure gradient

In literature, there are more publications on pre–Darcy behaviour. Pre–Darcy behaviour appears to play a major role in the extraction of crude oil. For example, von Engelhardt and Tunn (1954) observe pre–Darcy behaviour of distilled water flowing through clay–containing sandstones of types $\textcircled {\small {H}}$ – $\textcircled {\small {K}}$, and of water with dissolved NaCl of types $\textcircled {\small {E}}$, $\textcircled {\small {G}}$, $\textcircled {\small {J}}$. They suspect a connection with the binding of water to clay minerals due to dipole forces and the osmotic equilibrium. The size of pores and pore throats in stones is of the order of some tens of nanometers. Therefore, the cross-sectional constrictions due to the so-called connate water, adhering to the pore walls, cannot be neglected.

Siddiqui et al. (2016) choose an organic fluid and consolidated petroleum rocks to experimentally investigate into the pre–Darcy regime. They find pre–Darcy behaviour of types $\textcircled {\small {B}}$ and $\textcircled {\small {C}}$. This combination of organic liquid and porous medium is used to avoid polar interactions, associated with aqueous fluids. They detect critical velocities below which their data depart from a linear Darcy behaviour and instead follow a power–law behaviour. Different porous materials reveal an increasing critical velocity with increased permeability. The authors attribute this pre–Darcy behaviour to an interaction between the organic liquid and the consolidated porous medium. Wang and Sheng (2017) review several publications with regard to the pre–Darcy flow regime, and particularly to the liquid threshold pressure gradient. These authors divide the flow regimes into (i) a non–linear flow regime (non–Darcy flow) for low-pressure gradients and (ii) a linear flow regime (Darcy flow) for higher pressure gradients. However, they conclude that the concept of a threshold pressure gradient is a misinterpretation of experimental data. In detail, all experimental data do not really approach a point of zero velocity, and hence, in the absence of true data, any extrapolation leads to a non–zero pressure gradient, without any physical meaning.

Deviations from Darcy’s law are also observed in beds of impermeable and inert stones and sand. Dudgeon (1966) finds deviations of type $\textcircled {\small {B}}$ for coarse materials such as rinsed sand, river gravel, and blue metal. The critical Reynolds number for the onset of pre–Darcy behaviour is found in the range $Re_{d_p} \simeq \{8\cdot 10^{-4}; 0.4\}$. Dudgeon (1966) also performs experiments with glass marbles of three diameters in the range 16–29 mm. In this case, he does not find a pre–Darcy regime, presumably because the Reynolds number is rather large. Li et al. (2017) detect a pre–Darcy regime of type $\textcircled {\small {B}}$ or $\textcircled {\small {C}}$ for water flowing through the packing of rinsed sand of five mean particle diameters in the range 1.075–3.17 mm. Yang et al. (2017) report similar experiments with water flowing through the packing of various sands and crushed quartz, with mean particle diameters in the range 0.0375–7.125 mm. Special care is taken to ensure a sufficiently large diameter of the tube, such that the wall effect appears negligible. The authors observe types $\textcircled {\small {F}}$ and $\textcircled {\small {G}}$ for the flow behaviour and report the onset of the pre–Darcy regime for Reynolds numbers in the range $Re_{d_p} \simeq \{0.019; 2.39\}$.

Farmani et al. (2018) present a thorough literature review of research into the pre–Darcy regime. Moreover, they investigate the flow through a sand packing, with three mean particle sizes in the range 0.15–3.0 mm. They use different liquids and gases and find pre–Darcy behaviour for all fluids, in detail, all types of behaviour according to Kutilek (1972) have been found, except types $\textcircled {\small {I}}$ and $\textcircled {\small {J}}$. The onset of the Darcy regime is found to depend on the particle size and the fluid, it occurs in the range $Re_{d_p} \simeq \{ 10^{-4};10^{-2}\}$. Hao et al. (2008) and Wei et al. (2009) observe more obvious deviations to the Darcy–flow regime for porous media with extremely low permeability, (e.g., with $k\approx 10^{-15} m^2$). Farmani et al. (2018) suspect that a decreasing ratio of $(\eta / k)$ increases the Reynolds number for the onset of the Darcy regime, i.e., for a porous medium with very low permeability (e.g., $k \simeq 10^{-14} \mathrm {m^2}$) and a very viscous liquid (e.g., $\eta \simeq 1$ mPas), the onset of the Darcy regime would occur for $Re_{d_p} < 10^{-8}$. This (critical) Reynolds number is several orders of magnitudes smaller than any Reynolds number at the transition from pre–Darcy to Darcy behaviour reported by other authors. The authors also report on problems with mobile fines and entrapped air in their porous medium during the experiments.

Interestingly, several publications also report on pre–Darcy flow regimes for packed beds of glass or metal spheres. Soni et al. (1978) find Darcy’s law valid only in a range $Re_{d_p} > 0.08$, for water flows through packed beds of glass beads with five mean diameters in the range 0.149–1.19 mm. Fand et al. (1987) also conduct experiments for water flowing through beds of spheres with three mean diameters in the range 2.098–4.029 mm. They find that for $Re_{d_p} \le 2.3$ their experimental results significantly depart from Darcy’s law and, therefore, assume the existence of a pre–Darcy flow regime. As the focus in their investigation is on the transition to Forchheimer flow, their experiments only cover the range $Re_{d_p} \ge 1$. Kececioglu and Jiang (1994) let water flow through packed beds of spherical glass beads with mean diameters of 3. mm and 6. mm. They observe a pre–Darcy regime with $35 \%$ higher volumetric flow rates than expected for $Re_{d_p} < 0.58$. Bağcı et al. (2014) also use water flowing through packed beds of steel spheres with diameters of 1. mm and 3. mm, and report pre–Darcy flow regimes of type $\textcircled {\small {G}}$ for $Re_{d_p} < 9.65$ and $Re_{d_p} < 0.72$, respectively. Dukhan et al. (2014) find a strong pre–Darcy effect of type $\textcircled {\small {B}}$ for Reynolds numbers in the range $Re_k \le 0.4$. In their experiments, water flows through a metal foam with a porosity of 87.6 % and the flow resistance appears to be three times higher than expected. Kundu et al. (2016) use mono–disperse spherical glass beads with three mean diameters in the range 2.5 – 5. mm, and beds of particles with a poly–disperse distribution, the fluid is distilled water. They observe the onset of the pre–Darcy flow regime of type $\textcircled {\small {B}}$ for Reynolds numbers in the range $Re_{k} \le 5 \cdot 10^{-3}$.

Similar work for tubes is conducted by Farkas et al. (1999). These authors have investigated the flow of ethylene glycol through a chromatographic column, filled with porous particles of 5–10 $\upmu$m diameter. They find Darcy’s law to be applicable in their complete range of Reynolds numbers, namely within $10^{-6} \le Re_{d_p} \le 10^{-4}$. Also, Yang et al. (2011) address the range of small Reynolds numbers by having de–ionized water flowing through microtubes of inner diameters $d_t=\{2.5, 5, 7.5, 10 \}$ $\upmu{\text{m}}$. These inner diameters $d_t$ coincide with the typical range of pore diameters in stones. However, they find the flow resistance depending nonlinearly on the Reynolds number $Re_{d_t}$ in the range $Re_{d_t} < 10^{-3}$. An overview of the critical Reynolds numbers found by various authors is shown in Table 1.

Table 1 Critical Reynolds numbers for the onset of the pre–Darcy regime, together with porous medium, published by several authors

3.1 Explanations for deviations from Darcy behaviour

Possible physical, chemical, or biological reasons for a deviation from Darcy's behaviour are collected in the following list. In most cases, these reasons are linked to changes of the properties of the fluid or/and the porous medium. Hence, it remains unclear whether these changes of properties really justify the appearance of a new flow regime.

• Compaction/re-arrangement of porous structure (consolidated/unconsolidated) (cf. Sherwood and Meeten 1997; Kutilek 1972);

• Temperature fluctuations may, e.g., alter the viscosity;

• Bacterial growth within the liquid or the porous structure (cf. Gupta and Swartzendruber 1962);

• Entrapped gas in the porous medium (cf. Kutilek 1972);

• Initial contamination of fluid with (fine) particles (dirt effect, cf. Kutilek 1972);

• (Electro–) osmotic effects (cf. Bolt and Groenevelt 1969);

• Dissolution of solid from porous structure, modifying fluid viscosity (cf. Stieß 2009);

• Fine particles within liquid or dissolution of solid from porous structure, forming a suspension of different viscosity (cf. Stieß 2009).

Kutilek (1972) relates some types of pre–Darcy behaviour to specific causes. Namely, swelling of the porous medium ($\textcircled {\small {B}}$, $\textcircled {\small {C}}$, $\textcircled {\small {H}}$, $\textcircled {\small {K}}$, $\textcircled {\small {L}}$) and movement of particles ($\textcircled {\small {B}}$, $\textcircled {\small {C}}$, $\textcircled {\small {K}}$, and $\textcircled {\small {L}}$). Another cause may be an adhering liquid layer von Engelhardt and Tunn (1954) on the particle surface, the so–called connate water. This would reduce the available cross–sectional area for the flow. This effect should depend on the properties of the solid and liquid in contact and on the ratio of the adhering film thickness and the pore diameter. However, no dependency on the Reynolds number can be expected. Due to the few layers of adhering molecules, this effect cannot explain the observed pre–Darcy behaviour in course–particle porous structures. Another potential cause may be the wall effect. As particles close to a wall are not distributed homogeneously and forced into a specific order, any packed bed will be loosened near the wall. However, the wall effect onto the velocity profile appears negligible for spherical mono–disperse particles, e.g., in a tube, provided the diameter of the tube is ten times larger than the particle diameter, i.e., $d_t > 10 d_p$ (Bey and Eigenberger 1997).

To summarize, it appears that several effects may alter the flow through porous media. The porous medium which can be defined most precisely is a packed bed of spheres. In such a medium, also the existence of a pre–Darcy regime is observed in the literature. This is why an investigation into the pre–Darcy flow regime in packed beds of spheres appears rewarding and it is chosen as the scope of our present work.

4 Experiments

This section presents the experimental setup and the materials and measuring instruments used. Since usually negligible, systematic errors may also lead to significant deviations from Darcy’s law and generate (apparent) pre–Darcy behaviour in the investigated flow, the filling of the measuring section with the porous medium and the liquid, as well as the measuring procedure, are also described here.

4.1 Experimental setup

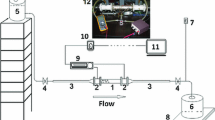
The experimental setup is schematically shown in Fig. 3. The slight oil–contaminated compressed air from a 6 bar compressed–air line is filtered to a residual oil content of less than 0.01 mg/$m^3$ using an ultra–fine filter LFMA-D-MIDI-DA (Festo), followed by a pressure reducer Kendall Model 10 (Fairchild) to adjust the overpressure to 0.02–2 bar. This pressure loads a 100-liter steel pressure vessel of the type V 100 D (B. Braun + Diessel Biotech GmbH, C1), which is partially filled with the working liquid. Parallel to the measuring section, the pressure drop across the porous bed is recorded with two differential pressure gauges. The ball valve V1 is used to shut off the compressed air network, the manual valve V2 to vent the pressure vessel. The conical valve V3 at the outlet of the tank is used for shut-off, and the volumetric flow rate is controlled by the pressure reducer. The liquid flows through a tube with the packed bed. The pressure difference is measured directly in front of, and directly behind the tube with the porous bed. The used sensors are for greater pressure differences up to $\varDelta p = 10^5$ Pa the HBM DDA PD1 / 1 (Hottinger Baldwin Messtechnik GmbH, PDIR1), and for smaller pressure differences up to $\varDelta p$ = 6200 Pa the Rosemount 3051CD (Emerson, PDIR2). With the valve V4, an unsteady flow can be discharged into the container C3, before starting the measurements. During a measurement, the liquid flows into the plastic measuring cup (C2) of volume V = 1 liter. It is located on the enclosed fine-scale Sartorius LE1003S (Sartorius AG, WIR) with a maximal load of $m_{max}$ = 1010 g and an accuracy of $\varDelta m$ = 0.001 g. From the time–resolved mass measurement (measurement frequency 4 Hz), the volumetric flow rate is determined. The combined temperature (TIR) and humidity sensor (MIR) DKRF400 (Driesen+Kern GmbH, accuracy better than $\pm 0.5 \%$, respectively better than $\approx 2 \%$ ), is inside the enclosure C2, to monitor the environmental parameters. In order for the measurement to be carried out at a low humidity and constant temperature, the experimental setup is located in a room with temperature control and dehumidification.

Fig. 3

Schematic experimental setup

4.2 Beads

The porous bed is realized by a PMMA tube, filled with spherical glass beads. To remove any water, the glass beads are initially dried in a drying oven at 100$^\circ$C for several hours and are stored hermetically sealed. The laser diffraction particle–size analyzer Mastersizer 3000 (Malvern Instruments Ltd., accuracy better than ± 0.6 %) has been used to determine the particle–size distribution, plotted in Fig. 4. For these measurements, the glass beads have been dispersed and well mixed in water, before they have entered the cuvette of the Mastersizer. The median value is $d_{P,50,3} = 113$ $\upmu$m. The particle–size distribution can mathematically be approximated by

$$\begin{aligned} p_{d_{P}}= & {} 0.16499\cdot \exp \left( 1-\frac{d_p-120.137}{37.701}\right. \nonumber \\&\left. -\exp {\left( -\frac{d_p-120.137}{37.701}\right) }\right) -0.00174. \end{aligned}$$

(14)

Fig. 4

Particle–size distribution

4.3 Measurement section

The glass beads are filled into a tube made of PMMA with a length of $L=220$ mm and an inner diameter of $d_t = 40$ mm. As for $d_t/d_p = 350\gg 10$, wall effects can safely be neglected. To prevent the glass beads from leaving the tube, a wire gauze is glued into the inlet and outlet of the tube. The mesh width of $w=80$ $\upmu$m is slightly larger than the diameter of the smallest particle fraction. Nevertheless, for ${w}/{d_p}<7$, particles start to arch over holes (Stieß 2009). Here, this should be the case even for the smallest particles, i.e., for

$$\begin{aligned} \frac{w}{d_{p,min}}\approx \frac{80~\mathrm {\mu m}}{45~\mathrm {\mu m}} \approx 1.8 < 7. \end{aligned}$$

(15)

The porosity can be calculated by measuring the masses (i) of the tube filled with the beads ($m_{TB}$), (ii) of the tube filled with beads and the working liquid ($m_{TBF}$), (iii) of the tube filled with the working liquid ($m_{TF}$), and (iv) of the empty tube ($m_{T}$), via

$$\begin{aligned} \varepsilon =\frac{m_{TBF}-m_{TB}}{m_{TF}-m_T}. \end{aligned}$$

(16)

During the experiments, an overpressure acts on the inner surface of the tube. This could lead to a (small) deformation of the tube and, thus, to an increase of the cross–sectional area for the flow. The increase of the radius is experimentally checked by using a chromatic confocal measurement sensor, namely CHRocodile S (Precitec). The distance to the sensor is measured both without applying a pressure and with applying the highest pressure of 1 bar, to get a worst–case estimate. This is done for five evenly–distributed measuring points along the tube length. The radius of the tube increases at most by 2.5 $\upmu$m, which corresponds to an increase of the area by 0.025 %. This deviation is in the range of the precision of the sensor. Hence, this deviation appears to be negligible.

4.4 Fluids

In order to realize a wide range of Reynolds numbers, three Newtonian liquids of different viscosities are used. These are, as already used by several other authors, (i) de–ionized water, (ii) $75~\%$ glycerin mixed with de–ionized water, and (iii) glycerin of $98.5~\%$ purity, as already recommended by Farkas et al. (1999). Glycerin is a bactericidal liquid, which prevents any problems due to bacterial growth Szymanowska-Powalowska (2015). A big drawback of glycerin is its deliquescence. If glycerin absorbs water from the ambient air, its material properties change significantly. KC–drying beads of type ORANGE CHAMELEON 2050 (BASF Catalysts GmbH) are used to keep the moisture constant, 1.5 kg are inside the hermetically–sealed pressure vessel and 200 g inside the closed measurement chamber of the scale. To check its operational reliability, 100 g glycerin are filled into the measurement chamber, wetting nearly the complete weighing surface of the balance. The mass of the liquid increases due to deliquescence every hour by less than 1 mg, which is below $1\%$ of the lowest expected mass flow rate.

The liquid properties, depending on temperature $\vartheta$, are measured. An Ubbelohde viscosimeter (mgw Lauda Viscotimer S, accuracy better than ±1%) is used to determine the viscosity correlation and the dynamical mechanical analyzer DMA 45 (Mettler/Anton Paar, accuracy better than ±1%) for the density correlation. The obtained correlations are

$$\begin{aligned} \eta _{G98.5\%}= & {} 5.7856\exp {(-0.084\vartheta )}, \quad \quad R^2=0.998, \end{aligned}$$

(17)

$$\begin{aligned} \varrho _{G98.5\%}= & {} -0.600 \vartheta + 1.27\cdot 10^3, \quad \quad R^2=0.994, \end{aligned}$$

(18)

$$\begin{aligned} \eta _{G75\%}= & {} 0.1107\exp {(-0.054\vartheta )}, \quad \quad R^2=0.990, \end{aligned}$$

(19)

$$\begin{aligned} \varrho _{G75\%}= & {} -0.585 \vartheta + 1206.6, \quad \quad R^2=1.000, \end{aligned}$$

(20)

while $\vartheta$ denotes temperature in units of $^\circ$C. The density data for $\varrho _{G75\%}$ have been taken from Bosart and Snoddy (1928).

4.5 Filling procedure

To avoid entrapped gas, the porous packing is filled by a displacement flow of the liquid before it is mounted into the experimental setup. For this, the porous packing is positioned vertically and filled with the working liquid by applying the pressure difference $\varDelta p = 10^5$ Pa. After 8 hours, the porous packing is completely filled with glycerine and is then reinstalled horizontally in the test rig so that any rising gas bubbles remain observable. After every measurement campaign, the porous packing is disassembled, cleaned with de–ionized water, and dried.

4.6 Measuring procedure

Although the experiment is set up in an air–conditioned laboratory, the room temperature varies in the range 22.5 $\pm 1.5^{\circ }$C due to the fluctuation of the outside temperature in summer and winter. This alters the viscosity by up to ± 15 %, e.g., for the 98.5 wt%–glycerin solution. In contrast, changes in density are much smaller with ± 0.1 %. Therefore, the mean value of the temperature prevailing during the measurement of one data point is used for the calculation of the liquid properties. The working liquid may absorb water from the compressed air, which also could change the viscosity. Therefore, the viscosity of the working liquid is measured after each measurement campaign, leading to an increase of the viscosity by $+0.07$ %, which is below the measurement precision. To avoid an increase in the mass of glycerin in the weighing chamber due to absorbed water from the air, the air humidity is controlled to be in equilibrium with the glycerin. The drip off of a single droplet into the weighting chamber may last a few hours for the lowest flow rates. Therefore, it is important to choose the correct measurement interval between two such events, as shown in Fig. 5. At least the drip off of 20 drops is evaluated for each data point, to decrease uncertainty. This may last from twenty minutes to three days for each data point.

Fig. 5

Scheme of the correct (solid line) and incorrect (dotted and dashed lines) intervals for the measurement

During each measurement campaign, the velocity is changed by setting the pressure gradient across the packing. If the pressure gradient is increased, a rearrangement of the particles could be the consequence. This could alter the permeability due to a change in the inner structure of the porous packing. To reduce this effect, each measurement campaign starts with the greatest pressure gradient. Further consolidation did not appear necessary, as the deviations caused by it are shown to be negligible. Due to the experimental setup, the measured pressure drop is a sum of the losses due to the porous medium and due to the flow through the rest of the experimental setup. The magnitude of the pressure drop due to the porous packing is estimated by using the law of Carman–Kozeny (10). The losses due to the empty tube and the rest of the setup are estimated by using Bernoulli’s equation, taking into account all losses due to friction and losses due to inflow and outflow, due to the curvature of the tubes, and due to the wire gauze. In summary, the pressure drop due to the flow through the porous medium is found to be three orders of magnitude greater than the pressure drop due to the flow through the rest of the experimental setup.

5 Results

Following the aforementioned measuring procedure (cf. Sect. 4.6), we have conducted several measuring campaigns. After the initial flow of large Reynolds number for consolidation of the bed, our regular measurements are conducted with stepwise decreasing Reynolds numbers, using the experimental setup and procedures. In a number of measurements, we have found apparent non–Darcy behaviour. However, we have identified in all these cases the respective reason for this apparent non–Darcy behaviour and have consequently eliminated these reasons within the next measuring campaign. Typical reasons for such deviations from Darcy’s law have been (i) a poor preparation of the experiment (campaign 0) and non–accurate evaluation of the experimental data (campaign 1, campaign 2). With appropriate preparation of the experiment and correct evaluation of the experimental data, Darcy’s behaviour is found in all cases even in the range of the smallest Reynolds numbers (campaign 1, campaign 2), with deviations from Darcy’s law lying well below the accuracy of measurement.

In contrast, in the literature a pre–Darcy behaviour is reported for substantially larger Reynolds numbers summarized in Table 1. Several authors report pre-Darcy behaviour for Reynolds numbers up to eight orders of magnitude above the Reynolds number range in both campaign 1 and campaign 2. This is discussed in more detail in the 5.2 and 5.3 sections.

To confirm our findings, we have additionally conducted measurements with a Glycerin–water mixture of lower viscosity (campaign 3) and with de–ionized water (campaign 4). Table 2 summarizes the parameters of all campaigns and compares the mean measured permeability with the mean theoretical permeability. For all campaigns, starting with campaign 1, the mean deviation is found to be below 1 %.

Table 2 Porosity, working liquid, experimental, theoretical (Karman–Cozeny) permeability, and deviation for each measurement campaign

5.1 Preliminary measurements (campaign 0)

Several preliminary experiments were carried out in order to enhance both the measurement procedure and the experimental setup. Some observed deviations from Darcy’s law appeared to be linked to typical pre–Darcy flow types, as summarized by Kutilek (1972) in Fig. 2.

The superficial velocity $v_s$ is plotted in Fig. 6 over the pressure drop (dp/dx) along the measurement section. Both, experimental and theoretical data are compared, whereas the theoretical data are calculated from the pressure drop in a porous medium via Eqs. (7) and (10). The measured pressure drop for the empty tube (cross symbols) agrees perfectly with the theoretical values (dashed line). In contrast, the measured pressure drop with the porous packing (plus symbols) shows clear deviations from the theory (filled squares, solid line). The difference of both, experimental and theoretical data, obviously features an offset of both curves and a non–linear behaviour of the experimental data, particularly for small pressure drops. The experimental behaviour could even be attributed to some types of a pre–Darcy regime, given in Fig. 2. As already discussed in Sect. 4.6, from Fig. 6 we reinsure that the (total) pressure drop of the tube with porous packing is measured three orders of magnitude larger than the (total) pressure drop of the empty tube. This means, that the total pressure drop could be taken, at good accuracy, from the pressure drop along with the porous packing.

In fact, a closer inspection of the experimental situation reveals, that a small amount of entrapped air is present in the porous packing, which could be seen through the transparent tube walls (cf. Fig. 7). This occurs because the (initial) displacement flow for filling the tube and the built–in porous packing with the working liquid was arranged horizontally. The entrapped air bubbles can even move through the porous packing and cause – due to their lower viscosity – a lower pressure drop. As the pressure increases, the bubbles shrink and occupy a smaller volume, i.e., this effect appears to be weaker for larger pressure. Consequently, such a behaviour does not agree with Darcy’s law for a single liquid phase. These observations lead to the conclusion, that the (initial) displacement flow should be oriented vertically from bottom to top, and slow, as already described in Sect. 4.5.

Fig. 6

Preliminary measurements: measured pressure drop without porous packing (empty tube, symbols $\times$), compared to theoretical data (dashed line); measured pressure drop with porous packing (and entrapped air (symbols +)), compared to theoretical pressure drop for porous packing (filled squares) and total pressure drop (solid line)

Fig. 7

Entrapped air bubbles in the porous packing

5.2 Campaign 1

Even if we avoid all imperfections from the filling procedure, we still may encounter deviations from Darcy’s law, as can be recognized from a close inspection of Fig. 8, particularly at low-pressure gradients. To evaluate these measurements more accurately, it appears helpful to plot the Kozeny constant $K''$ as a function of the Reynolds number, as done in Fig. 9. In this plot, data points on a horizontal line reflect a linear relationship between the pressure gradient and the superficial flow velocity, which means that Darcy’s law is valid. If, further, that constant is $K'' \simeq 5$, also the law of Carman–Kozeny is valid.

Fig. 8

Superficial velocity against pressure gradient, data of campaign 1 for 98.5 % glycerin

For larger Reynolds numbers, all measured data appear to be in a range $4.8 \le K'' \le 5.2$, i.e., around $K'' \simeq 5$, as expected. In contrast, for Reynolds numbers $Re_{d'} \le 0.5\cdot 10^{-7}$, a strong decrease of the Kozeny constant $K''$ is visible from the data of the HBM pressure sensor (plus symbols), while the data from the Rosemount pressure sensor (cross symbols) remain in the expected range. A closer inspection of both pressure sensors reveals, that a re–calibration appears necessary in some cases even after a few hours. In the present case, the HBM pressure sensor developed an offset of 738 Pa within about four hours. Such a (small) offset, of course, appears to be responsible for (larger) errors at low pressures. In the present case, a re–calibration of the pressure sensor gives more accurate data, as presented in Fig. 9 in the form of the circle symbols. With these corrected data, all measurements remain within the expected range of the Kozeny constant $K''$, i.e., the deviation from $K'' = 5$ remains smaller than 4.6 %. As a consequence, all pressure sensors are calibrated before the start of each measurement series, even if the measurement series are on the same day.

Fig. 9

Kozeny constant $K''$ against Reynolds number $Re_{d'}$, data of campaign 1 for 98.5 % glycerin. Sensor HBM (symbols +), sensor Rosemount (symbols $\times$), offset–corrected HBM sensor (symbols o)

5.3 Campaign 2

The results from campaign 2 are plotted in Fig. 10. Although, the coefficient of determination is $R^2=0.9989$, some deviations from Darcy’s (ideal) law are obvious: the measured data (plus symbols) in some ranges of the pressure gradient deviate from the straight line. While the temperature within the laboratory is controlled at an accuracy of about $\pm 1.5^o C$, it appears that these deviations are caused by the temperature–dependent viscosity of the working liquid. This becomes obvious if we use the measured temperature of the working liquid to precisely calculate its true viscosity. The resulting (dashed) line in Fig. 10 now reflects the data point (plus symbols) almost perfectly. In other words, it appears not sufficient to rely on the “constant” laboratory temperature, but instead, the precise temperature of the working liquid must be measured before and after entering the porous bed to determine the precise (mean) viscosity of the working liquid. These two temperatures typically differ by less than $0.1^o C$.

The small visible discrepancies in Fig. 10 make clear, that plotting the superficial velocity $v_s$ over the pressure gradient (dp/dx), as in Fig. 10, is not ideal to recognize such deviations from Darcy’s law. Instead, plotting the Kozeny constant $K''$ over the Reynolds number $Re_{d'}$ appears to be a more sensitive way to evaluate the measured data. This is done in Fig. 11. We recognize that $K''$ exhibits some scatter of amplitude $4.87 \le K'' \le 5.12$, particularly at low Reynolds numbers (cross symbols). At larger Reynolds numbers, though, the scatter is $4.97 \le K'' \le 5.05$ only (plus symbols). The different symbols refer to pressure gauges of different sensitivity. Further, the horizontal dashed lines in Fig. 11 give the deviation of $\pm 2 \%$ from the (ideal) value $K'' = 5$. To summarize, all measured deviations from $K'' = 5$ remain below $\pm 2.6 \%$, while the mean deviation is below $\pm 0.7 \%$.

Fig. 10

Superficial velocity against pressure gradient, data of campaign 2 for 98.5 % glycerin. Darcy’s law (solid line), measurements (symbols +), temperature–corrected Darcy’s law (dashed line)

Fig. 11

Kozeny constant $K''$ against Reynolds number $Re_{d'}$, temperature–corrected data of campaign 2 for 98.5 % glycerin. Sensor HBM (symbols +), sensor Rosemount (symbols x). Dashed lines give deviations of $\pm 2 \%$ from $K'' = 5$

5.4 Campaigns 3 and 4, larger Reynolds numbers

Within the investigated range of lower Reynolds numbers $1.1 \cdot 10^{-9} \le Re_{d'} \le 3 \cdot 10^{-7}$, so far no indication of pre–Darcy effects has been observed (cf. sections 5.1–5.3). As various types of pre–Darcy behaviour show a linear correlation between pressure gradient and superficial velocity (cf. Fig. 2, $\textcircled {\small {J}}$ and $\textcircled {\small {K}}$) in this range, it appears reasonable to also analyze the range of larger Reynolds numbers carefully. To bridge this gap, two additional experiments are performed. To obtain smaller viscosities, and hence larger Reynolds numbers, we use a mixture of 75 % glycerin and de–ionized water as working liquid. To keep the amount of water in the working liquid constant, any water evaporation must be avoided. Therefore, we modify the experimental setup at two places, namely we cover the working liquid both in the measuring cup and in the pressure vessel with a layer of rapeseed oil. This proves to minimize water evaporation, while the rapeseed oil itself does show only an evaporative mass flux smaller than 1 % of the mass flux of the working liquid.

The results of campaign 3 are presented in Fig. 12. Once more, within the complete range of Reynolds numbers, $4.4 \cdot 10^{-7} \le Re_{d'} \le 1.5 \cdot 10^{-4}$, the Kozeny constant remains around $K'' \simeq 5$. The mean deviation from $K'' = 5$ is about 1.1 %, the maximal deviation is 3.1 %. Hence, all data from this experimental campaign 3 indicate, that no pre–Darcy effects can be observed in the above range of larger Reynolds numbers.

Fig. 12

Kozeny constant $K''$ against Reynolds number $Re_{d'}$, data of campaign 3 for 75 % glycerin, sensor Rosemount (symbols x) and HBM (symbols +). Dashed lines give deviation of $\pm 2 \%$ from $K'' = 5$

For even larger Reynolds numbers, we use pure de–ionized water as the working liquid. The corresponding results are shown in Fig. 13. Also within this range $1.65 \cdot 10^{-3} \le Re_{d'} \le 0.19$, the Kozeny constant remains around $K'' \simeq 5$. In detail, the mean deviation of the measured values from the ideal value $K'' = 5$ is 0.49 %, and the maximal deviation is 3.7 %. Hence, also in this range of larger Reynolds numbers, there is no indication of any pre–Darcy behaviour. Though, if the Reynolds number is increased further, the inertial effect comes into play and we do expect that Darcy’s law is no longer valid. This transition is expected around $Re_{d'} \simeq 2.3$ (cf. Fig. 1), it goes along with a distinctive increase of the Kozeny constant $K''$.

Fig. 13

Kozeny constant $K''$ against Reynolds number $Re_{d'}$, data of campaign 4 for pure water, sensor Rosemount (symbols x), and sensor HBM (symbols +). Dashed lines give deviation of $\pm 2 \%$ from $K'' = 5$

6 Comparison to literature

The appearance of the pre–Darcy regime is often attributed to low Reynolds numbers. Therefore, in Fig. 14 we summarize our experimental findings with regard to the Kozeny constant, plotted as a function of the Reynolds number. In this figure, two horizontal dashed lines mark deviations of $\pm 5 \%$ from a Kozeny constant of $K'' = 5$. For $K'' \simeq$ constant, the data indicate that Darcy’s law is valid. Even though our experimental data show some scatter for smaller Reynolds numbers, in all cases the deviation from $K'' = 5$ remains smaller than 5 %. In other words, all our data points are closed to a constant for all Reynolds numbers down to $Re_{d'} = 1.6 \cdot 10^{-9}$. In view of the uncertainties present in all experiments, this is a remarkable result. For orientation, vertical lines mark the onset of the pre–Darcy regime, published by several authors. The lowest value for the onset of the pre–Darcy regime in literature is $Re_{d'}\approx 10^{-5}$ (cf. Fand et al. (1987)). In contrast, our experimental data clearly show the validity of Darcy’s law down to Reynolds numbers, four orders of magnitude smaller.

Fig. 14

Kozeny constant $K''$ against Reynolds number $Re_{d'}$ for campaigns 1–4. Dashed lines: deviation of $\pm 5 \%$ from a Kozeny constant of $K'' = 5$

Recently, Farmani et al. (2018) derived a correlation for the onset of the pre–Darcy regime. In detail, for a number of liquids, these authors infer experimentally the range of Reynolds numbers, for which pre–Darcy behaviour can be observed. The test liquids include water, a condensate, n–hexane, and n–heptane, the porous bed consists of (Persian Gulf) sand of three different (mean) particle diameters in the range 0.15–0.3 mm and permeabilities in the range 0.8–2.53 $\cdot 10^{-12} \mathrm {m^2}$. According to these authors, the onset of the pre–Darcy regime depends on the ratio of dynamic viscosity and permeability $(\eta /k)$. In Fig. 15 the data points for which these authors have found the onset of pre–Darcy behaviour are depicted as plus symbols. For comparison, we have also inferred and plotted a trendline (dashed curve), which allows to extrapolate to larger values of the ratio $(\eta /k)$. This trendline follows

$$\begin{aligned} Re_{crit}=1.11056\cdot 10^{-16}\cdot \left( \frac{\eta }{k}\right) ^{-2.1886}. \end{aligned}$$

(21)

In contrast, in our present experiments, we do not find any indication for the onset of pre–Darcy behaviour. Hence, our data points in Fig. 15 (various open symbols) represent Darcy's behaviour! Moreover, our data points are at least one order of magnitude below the above correlation, not yet showing any pre–Darcy behaviour. This demonstrates that the correlation derived by Farmani et al. (2018) is not transferable to our situation, and therefore not generally valid.

Fig. 15

Data points from Farmani et al. (2018) for the onset of pre–Darcy behaviour in various liquids (symbols +) in comparison to our present data (various open symbols)

7 Summary and outlook

We have investigated the (possible) onset of the pre–Darcy flow regime experimentally. Therefore, mixtures of Glycelrol and water are used as working liquids, in order to obtain a wide range of Reynolds numbers, namely $1.6 \cdot 10^{-9} \le Re_{d'} \le 0.19$. Careful control of the working liquid temperature and of moisture, in conjunction with temperature-dependent liquid properties, allows for high accuracy.

We demonstrate that in all experiments the pressure drop along the measurement section, i.e., the tube filled with porous packing, is dominated to more than 99 % by the pressure drop due to the flow through the porous medium, and the contribution due to the tube can safely be neglected. Deviations from Darcy’s law have been observed, but in all cases could be attributed to imperfections of the experimental conditions: (i) An non–perfect filling procedure could result in entrapped gas bubbles within the porous medium, altering the pressure drop. (ii) Variations of the laboratory temperature may lead to non–accurate liquid properties, which need to be corrected. (iii) At low Reynolds numbers, a small offset of the pressure transducers could lead to apparent deviations from Darcy’s law. More frequent calibration, though, captures a flow that follows Darcy’s law down to Reynolds numbers of $Re_{d'} = 1.6 \cdot 10^{-9}$. This Reynolds number is four orders of magnitude smaller than the lowest Reynolds number published in the literature for the onset of the pre–Darcy regime. (iv) Finally, our experimental data demonstrate that a recently–published limit by Farmani et al. (2018) for Darcy’s law does not hold, as our experimental results prove that Darcy’s law remains valid for Reynolds numbers well below this limit.

Our experimental setup and measuring techniques appear to be fairly accurate, as all experimental data are highly reproducible and consistently show a Darcy behaviour in the complete investigated range of Reynolds numbers. In future efforts, the influence of dissolved salt could be addressed, as several authors propose that an (electro–) osmotic effect could be responsible for pre–Darcy behaviour. Hence, the influence of connate liquid within porous media could be investigated, also extending to smaller particles in the porous packing.