Superhydrophobic drag reduction in turbulent flows: a critical review

Abstract

Superhydrophobic (SHPo) surfaces have been investigated vigorously since around 2000 due in large part to their unique potential for hydrodynamic frictional drag reduction without any energy or material input. The mechanisms and key factors affecting SHPo drag reduction have become relatively well understood for laminar flows by around 2010, as has been reviewed before [Lee et al. Exp Fluids 57:176 (2016)], but the progress for turbulent flows has been rather tortuous. While improved flow tests made positive SHPo drag reduction in fully turbulent flows more regular since around 2010, such a success in a natural, open water environment was reported only in 2020 [Xu et al. Phys Rev Appl 13:034056 (2020b)]. In this article, we review studies from the literature about turbulent flows over SHPo surfaces, with a focus on experimental studies. We summarize the key knowledge obtained, including the drag-reduction mechanism in the turbulent regime, the effect of the surface roughness morphology, and the fate and role of the plastron. This review is aimed to help guide the design and application of SHPo surfaces for drag reduction in the large-scale turbulent flows of field conditions.

Graphic abstract

1 Introduction

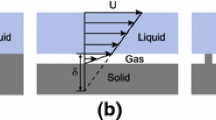
A superhydrophobic (SHPo) surface, which typically consists of a micro- and/or nanoscale roughness treated chemically to be hydrophobic, is well known to trap pockets or a layer of air [called plastron (Brocher 1912)] between the roughness elements when submerged under water. Instead of the conventional no-slip boundary condition imposed on fluid–solid interfaces for viscous flows, the partial fluid–fluid (e.g., water–air) interfaces on the SHPo surface would result in an effective slip, as illustrated in Fig. 1a. Following the Navier slip model, the slip is typically quantified as a slip length ($\lambda$) obtained by virtually extrapolating the slip velocity (u_s) below the surface (y = 0) as ${u}_{s} = \lambda {\left.(\partial u/\partial y)\right|}_{y=0}$. Found capable of achieving $\lambda \gtrsim {\varvec{O}}(10) {\mu} {\mathrm{m}}$ (Ou et al. 2004; Choi and Kim 2006; Truesdell et al. 2006; Lee et al. 2008), which is large enough to modify the dynamics of common bulk water flows considering their viscous sublayer thickness would typically range around ${\varvec{O}}(10-100) {\mu} {\text{m}}$ (Yeginbayeva and Atlar 2018), the SHPo surfaces have been widely investigated as a promising tool for flow control, especially hydrodynamic drag reduction. Drag reduction in large systems of turbulent flows is of particular interest, considering the significant practical benefits expected from the curtailment of energy consumption and pollutant emission in oceanic transportation, long-range liquid transport pipe systems, and others (van den Berg et al. 2007; Ceccio 2010; Murai 2014; Park et al. 2014; Gose et al. 2018; Bullee et al. 2020; Xu et al. 2020b).

Fig. 1

Definitions of parameters relevant to the liquid flow over a SHPo surface: a Velocity distribution on a SHPo surface, showing a slip velocity (u_s) and an effective slip length (λ). b Water on an organized roughness with vertical sidewalls, illustrating the air–water interface on or in the roughness elements. The roughness is usually defined with the roughness height (k), roughness width (w), and roughness pitch (P). To address the intermediate wetting states, here we introduce new parameters to reflect how much the air–water interface penetrates into the roughness: wetted roughness height (h) and interface width (s) with the degree of wetting expressed by the subscript 0, 1, 2, and wet. Note w = s (except s_wet = 0) for this particular roughness. c Water on a random roughness, defining the average roughness height (k_a) and average roughness pitch (P_a), which is the same as the average roughness width (w_a), along with the average wetted roughness height (h_a) and average interface width (s_a) with the subscript 0, 1, 2, and wet. Overall, note the dewetted condition with the air–water interfaces pinned on the roughness tops (i.e., subscript = 0), which is commonly (albeit rather casually) referred to as the Cassie–Baxter state, is well defined for truncated (including organized) roughness surfaces but poorly defined for random roughness surfaces, whose tops have varying height

During the past two decades, a plethora of research has been performed to study turbulent drag reduction over a SHPo surface experimentally and numerically. Experimental studies were done for both internal (e.g., channel) and external (e.g., boundary layer) flows under various types of flow geometries, using predominantly water tunnels. While numerical results suggested consistently that a substantial turbulent drag reduction could be achieved with a SHPo surface (Min and Kim 2004; Fukagata et al. 2006; Martell et al. 2009; Park et al. 2013; Rastegari and Akhavan 2015; Jung et al. 2016; Im and Lee 2017), experimental results did not converge to any clear trend. Some reported a consistent drag reduction (Daniello et al. 2009; Park et al. 2014; Li et al. 2020a, b), while others showed little drag reduction or even drag increase (Zhao et al. 2007; Peguero and Breuer 2009; Aljallis et al. 2013; Gose et al. 2018). Although this discrepancy might have been partially caused by the measurement techniques, we believe the main culprit has been a deteriorated or depleted plastron, looking back with the updated knowledge we have today (Lee et al. 2016). The plastron is easily lost by the increased shear stress (Wexler et al. 2015a), inertia, and velocity (pressure) fluctuation (Piao and Park 2015; Seo et al. 2015) of turbulent flows especially at high Reynolds numbers, in addition to the hydrostatic pressure and air diffusion (Samaha et al. 2012a; Xu et al. 2014; Xiang et al. 2016; Ling et al. 2017; Kim and Park 2019) that are important for laminar flows as well. In typical marine applications, for example, friction Reynolds number, ${\mathrm{Re}}_{\tau }=\delta {u}_{\tau }/\nu$, is at least ${\varvec{O}}({10}^{3})$, where $\delta$ is a boundary-layer thickness, $\nu$ is the kinematic viscosity of the fluid, and ${u}_{\tau } (=\sqrt{{\tau }_{w}/\rho })$ is the frictional velocity (${\tau }_{w}$: shear stress at the wall; $\rho$: fluid density). Considering that plastron is what allows drag reduction and that its stability and loss dynamics are affected by the roughness morphology of SHPo surfaces, it is only natural that the amount and longevity of drag reduction have been reported to depend on the type of roughness, such as organized (e.g., Park et al. 2014) versus random (e.g., Rajappan et al. 2019), as well as wetting-resistant provisions, such as hierarchical (e.g., Jung and Bhushan 2010; Tanvir Ahmmed and Kietzig 2016) and reentrant (e.g., Xu et al. 2020b) structures.

In laminar flows, the drag reduction can be mainly determined by the slip length of the SHPo surface and the geometry of the given flow over the surface. For example, a significant reduction in skin friction drag can be obtained if the slip length is comparable to the characteristic length of the given flow geometry (Ou et al. 2004; Choi et al. 2006a, b; Lee et al. 2016), implying that the mechanism of drag reduction can be explained solely by the slip length and the flow length scale. In addition, the slip length can be predicted from the morphology of the surface roughness (Lauga and Stone 2003; Ybert et al. 2007; Lee et al. 2008) as far as the plastron exists in an appropriate condition (Lee et al. 2016). However, currently the drag reduction cannot be determined for a given SHPo surface in turbulent flows. First, there is a wide range of scales in turbulence to affect the skin friction drag, making it hard to establish a universal relation between the drag reduction and slip length of a SHPo surface in turbulent flows, despite some suggestions from numerical studies (Fukagata et al. 2006; Park et al. 2013; Jung et al. 2016; Rastegari and Akhavan 2019). It is commonly understood that the viscous length scale (${l}_{v}= \nu /{u}_{\tau }$) can represent the reference length scale (note: ${l}_{v}$ decreases as the Reynolds number increases) and constitute the criteria for turbulent drag reduction together with the slip length (Park et al. 2013, 2014; Bidkar et al. 2014; Ling et al. 2016; Gose et al. 2018; Fairhall et al. 2019; Xu et al. 2021). This scaling strategy, i.e., normalization in wall unit, is based on the knowledge that the mechanism of drag reduction in a turbulent flow involves not only the effective slip at the solid wall (a direct effect) but also the suppression of near-wall turbulence structures (an indirect effect). However, the experiments in turbulent flows have been much more challenging than those in laminar flows because the plastron is much more easily disrupted and depleted in turbulent flows. Despite the difficulty, experimental studies of SHPo drag reduction in turbulent flows have also started to report successful (i.e., positive) drag reduction more consistently in recent years (Daniello et al. 2009; Bidkar et al. 2014; Park et al. 2014; Rajappan et al. 2019; Li et al. 2020a, b), following the path experienced earlier for laminar flows (Lee et al. 2016). Furthermore, successful SHPo drag reduction in fully turbulent flows have recently been reported in ‘open water’ (defined in Sect. 2.1), validating the SHPo drag reduction in field (Xu et al. 2020b) or field-like (Xu et al. 2021) conditions. Compared with most laboratory flow systems (e.g., water tunnel), where the water flowing over a SHPo surface happened to be (e.g., some water tunnels) or designed to be (e.g., Taylor–Couette flow) favorable to plastron by being supersaturated with air or circumventing the shear-induced drainage of air, respectively, the undersaturated water below the free surface of the open water (e.g., seawater and towing tank) is unfavorable to plastron, imposing a fundamental challenge against SHPo drag reduction. Furthermore, if the open water is in a typical field condition of natural environment, as tested by Xu et al. (2020b), the water contains numerous chemical (e.g., surfactant) and particulate contaminants and presents additional uncertainties (e.g., temperature and salinity), most of which work against the plastron and SHPo drag reduction. Note the challenges presented by the field condition of natural environment cannot be fully tested by laboratory experiments. While towing tank provides the open water and mimics the nature in terms of hydrostatic pressure and air saturation, which most laboratory flow systems cannot, it does not pose the chemical, particulate, and other environmental challenges.

With the successful open water tests including an actual marine condition in place (Xu et al. 2020b) that realized the central concept of reducing the friction drag using a SHPo surface for practical applications, we conclude it is time to collect the results of turbulent SHPo drag reduction in the literature and draw out some useful lessons, especially in association with the key issues discussed above. Since the existence and condition of plastron are more difficult to maintain and complicated to measure, respectively, in turbulent flows compared with laminar flows, it is essential to discuss the effects of roughness morphology and Reynolds number on the plastron. Building on the reviews about SHPo surfaces in the literature that addressed the issues related to turbulent flows (Rothstein 2010; Golovin et al. 2016), this review focuses mostly on the experimental approaches and aims to provide a guideline to help the readers develop SHPo surfaces appropriate for their own targeted applications.

This review is organized as follows. Section 2 reports the lessons learned by scrutinizing the comprehensive data of SHPo drag reduction experiments in turbulent flows collected from the literature, followed by Sect. 3 that discusses the mechanism of turbulent drag reduction. Then, Sect. 4 examines the efforts to apply the SHPo surfaces to the challenging conditions of a speeding boat on seawater. After Sect. 5 raises critical issues that need to be tackled to realize practical applications, Sect. 6 presents the summary and future outlook.

2 Experiments of drag reduction on SHPo surfaces in turbulent flows

In this section, we collect the data from the experimental efforts in the literature to investigate the SHPo drag reduction in turbulent flows. Readers will find that the results are quite scattered under the wide range of the SHPo surface morphologies, turbulent flow types, flow systems, and measurement techniques, not revealing clear and common trends, although the scatter has subsided in recent years. Considering the close connection between the state of plastron during the flow tests and the SHPo drag reduction, more often than not we will discuss or speculate the state of plastron when reviewing the reported results of SHPo drag reduction.

2.1 Plastron and flow facilities

While the existence of plastron is an essential premise for SHPo drag reduction, in reality the plastron is easily lost under common water flows. It is a fundamental challenge that a large (long) air–water interface, e.g., s in Fig. 1b and c, which is needed for a large drag reduction, would, unfortunately, imperil the trapped air in the first place. The plastron is vulnerable also to many environmental variables, making the replication of laboratory results in field conditions especially difficult. Multiple factors cause or accelerate the plastron depletion and make the rough hydrophobic surface transition from the initial dewetted or Cassie–Baxter state, which may reduce the friction drag, to the eventual fully wetted or Wenzel state, which will likely increase the friction drag. In nature, where the water below the free surface is undersaturated with air, the plastron becomes more vulnerable as the hydrostatic pressure increases with the immersion depth, following the Henry’s law (Lei et al. 2010; Samaha et al. 2012a; Lv et al. 2014; Xu et al. 2014). In addition, if the water flows with an appreciable speed, the shear stress (Wang et al. 2015; Waxler et al. 2015a) and pressure fluctuation (Piao and Park 2015; Seo et al. 2015) may deplete the plastron dynamically, making high Reynolds number flows exceedingly more challenging for the plastron to survive, as the scarcity of successful SHPo drag reduction at high Reynolds number flows in the literature indicates. Furthermore, even when the plastron is intact, the surfactants in the flowing water (e.g., diffused out from the synthesized surface or naturally existing in the environmental water) may immobilize the water–air interface and deteriorate or negate the drag reduction (Kim & Hidrovo 2012; Peaudecerf et al. 2017; Song et al. 2018; Landel et al. 2020; Li et al. 2020a, b). The stability of plastron will be further discussed in Sect. 4.1. Unlike the numerical simulation, experimental studies have to deal with the above factors that compromise the plastron and hinder drag reduction.

For flow experiments with SHPo surfaces, the importance of plastron poses unique differences between different flow systems as they determine flow geometries and water conditions. For water tunnel, for example, while the pressure and air concentration of the water in the test section are usually not important for conventional surfaces (except having to suppress the cloud of bubbles in water if excessive), such water conditions are critically important for SHPo surfaces as they affect the drag-reducing performance directly. If the water pressure is below the surrounding air pressure, the SHPo surface will enjoy an overgrown plastron and produce an overly optimistic drag reductions, as explained in Xu et al. (2021). If used in a realistic condition, such as in lake or ocean water which is at or above the atmospheric pressure, the same SHPo surface will produce a smaller drag reduction or even a drag increase. On the other hand, if the water pressure happens to be high in the test section, water tunnel experiments may produce overly pessimistic drag reduction. This importance of water condition compels us to categorize the flow systems somewhat differently for SHPo drag reduction studies from the convention. Flow systems may be a closed system, as many water tunnels are, or an open system, such as water flume. To represent the water most commonly considered for SHPo drag reduction, such as ocean or lake, Xu et al. (2020b) used the term ‘open water.’ Open water refers to the water that has been exposed to the ambient long enough in time so that the dissolved air is in equilibrium with the ambient air. Good examples would be lake and ocean water in natural environment and towing tank among laboratory facilities. Note the open water differs from the water flowing in open channel or flume, which is open to but likely not in full equilibrium with the surrounding air. To help the readers determine (or speculate if unclear) how favorable certain experiments could have been for plastron—uniquely important for SHPo drag reduction experiments but so far not adequately addressed or observed in most studies, the types of facility setup that creates the flows (e.g., water tunnel and towing tank) are noted in Table 1 as well as the types of flow over the SHPo surface (e.g., boundary layer flow and channel flow).

Table 1 Experimental studies on the SHPo drag reduction in turbulent flows presented with key parameters useful for comparisons

2.2 Comprehensive collection of experimental data

Table 1 summarizes the experimental studies of SHPo drag reduction in turbulent flows available in the literature. For the past two decades, experiments were extensively performed mostly for canonical wall-bounded turbulent flows, whether external flows (i.e., boundary-layer flows) or internal flows (e.g., channel flows and Taylor–Couette flows), with the Reynolds number based on its characteristic scale (L) ranging ${\mathrm{Re}}_{L}={10}^{3}-{10}^{7}$. Since the definition (or size) of a characteristic scale depends on the flow geometry, it is not proper to compare the drag reduction results by different studies simply based on ${\mathrm{Re}}_{L}$. To overcome the problem, the frictional Reynolds number (${\mathrm{Re}}_{\tau }$) based on the viscous length scale is shown as well (some are estimated using certain related information found in the corresponding reference), ranging ${\mathrm{Re}}_{\tau }$ up to 7000. For the SHPo surfaces, majority of the studies used randomly distributed roughness morphology made by spray coating or chemical etching for convenience and scalability, and a relatively small number of studies adopted well-defined and ordered morphology such as grooves (trenches, ridges) and posts that require precision machining such as photolithography. An exemplary picture of the SHPo surfaces employed is shown for each reference, if reported, in Table 1 to let the readers identify the type of SHPo surfaces quickly for each study.

2.3 Organized roughness morphology

As for the SHPo surfaces with organized morphology, which helps provide the physical insights into the relationship between the surface morphology and the flow behavior, mostly microgrooves and some microposts as depicted in Fig. 1b were fabricated and tested. For example, Henoch et al. (2006) measured the drag variation of a SHPo surface with an array of tall posts spaced in nanoscale (400 nm in diameter and 1.25 μm in periodicity, ${w}^{+}\approx 0.03$) in boundary-layer flows inside a water tunnel. While drag reductions as large as 50% were achieved in laminar flows, the drag reduction decreased to 10% when the flow became turbulent. The particle image velocimetry (PIV) measurement by Woolford et al. (2009) showed how the direction of an effective slip over the grooves affects the turbulent channel flow at ${\mathrm{Re}}_{H}=4.8\times {10}^{3}-{10}^{4}$, where H is the channel height. The SHPo surface with longitudinal grooves (i.e., grooves aligned to the streamwise direction) with GF = 0.8 produced less turbulence (by about 11%) than the smooth surface, but the same surface with transverse grooves (i.e., the grooves aligned transverse to the streamwise direction) increased the turbulence by 6.5%. Daniello et al. (2009) measured the pressure drop in turbulent channel flows with a SHPo surface having longitudinal grooves at Re_H = 2000–9500 by using a millimeter-scale channel height. While keeping the gas fraction as 50% (GF = 0.5), they varied the space width (w) of the groove. Although there was no discernible drag reduction in a laminar regime, a significant drag reduction occurred in turbulent regime at Re_H > 3000. Furthermore, the rate of drag reduction tended to increase as Re_H increased. They suggested that for an effective drag reduction in turbulent flows, the space width of the groove should be comparable to the thickness of a typical viscous sublayer in TBL flows, that is ${w}^{+}=w/{l}_{v}\approx 5.0$ in wall unit (see Fig. 1b for the definition of roughness parameters). As addressed earlier, the viscous length scale (${l}_{v}= \nu /{u}_{\tau }$) generally decreases as the Reynolds number increases. Thus, the increase in the Reynolds number can allow the given groove width to work more effectively for drag reduction, as far as the plastron can be well retained despite the increased shear and turbulence. Later, Park et al. (2014) used longitudinally grooved SHPo surfaces monolithically fabricated on floating elements and flexure beams, following the silicon microlithographic process developed by Sun et al. (2015), to directly measure the skin-friction drag in TBL flows in a water tunnel, and achieved a drag reduction as high as 75% (or ~ 65% after compensating for the effect of small sample size, following Park (2015)) with GF = 0.97 at ${\mathrm{Re}}_{\tau }=250$ (or ${\mathrm{Re}}_{x}= {10}^{5}-{10}^{6}$, where x denotes the local position in the streamwise direction), which corresponds to ${w}^{+}\approx 0.9$. The amount of drag reduction increased exponentially with gas fraction at GF > 0.9, following the same trend found in laminar flows (Lee et al. 2016). On the other hand, Van Buren and Smits (2017) tested a SHPo surface with longitudinal grooves (${w}^{+}\approx 10-80$) in a Taylor–Couette (TC) flow and measured the variation of frictional torque corresponding to ${\mathrm{Re}}_{L}=6000-11000$, where L is the gap between two concentric cylinders. Note, however, the longitudinal grooves in concentric flows are infinitely long, artificially overcoming the shear drainage effect that is inevitable in practical conditions. Over the range of the Reynolds number, they obtained the maximum drag reduction rate of about 45% with ${w}^{+}\approx 35$. Within the range of Reynolds number, the drag reduction ratio generally increased with increase in Reynolds number. However, the trend was not simple and changed depending on the groove width (w). Very recently, Xu et al. (2021) have shown that a drag reduction up to about 30% can be achieved using similar longitudinally grooved SHPo surfaces in a high-speed towing tank experiment with GF = 0.9 and ${\mathrm{Re}}_{\tau }= 2000-5800$, which corresponds to ${w}^{+}=4.0-16.0$. They visualized the partial loss of plastron occurring at high Reynolds numbers of ${\mathrm{Re}}_{\tau }>4000$, which deteriorated the drag reduction performance, as will be discussed in more detail in Sects. 2.6 and 2.7.

2.4 Random roughness morphology

Although the well-ordered morphology has the advantage to show the correlation between the roughness morphology and the flow behaviors more clearly, currently it is not possible in practice to produce such organized SHPo surfaces over a relatively large surface area. Thus, many researches prepared a SHPo surface with random shape and distribution of roughness elements and tested them in various flow conditions. Zhao et al. (2007) used an anodic oxidation method to make a large SHPo plate of aluminum and measured the turbulent friction force acting on it in a water tunnel. However, they did not observe any significant drag reduction in the turbulent regime. Aljallis et al. (2013) applied a sprayable hydrophobic silica nanoparticles coating (now commercially available as NeverWet®) on an aluminum plate (1.2 m × 0.6 m) and tested in a high-speed towing tank. They measured the friction drag over ${\mathrm{Re}}_{L}={10}^{5}-{10}^{7}$ (L: plate length) and obtained the drag reduction as much as about 30% on the SHPo plate with a high gas fraction (i.e., thick plastron). As the Re_L increased, however, the amount of drag reduction decreased and a slight drag increase was measured at higher Re_L. This was explained by the wetting (depletion of trapped air) of the surface that effectively increased the surface roughness (consult Fig. 1c). By measuring the velocity field over the same type of SHPo surface, Zhang et al. (2015b) measured drag reduction of 10–24% in a TBL flow at ${\mathrm{Re}}_{\tau }=300-500$, while Hokmabad & Ghaemi (2016) measured a slight (3–5%) increase in the near-wall mean velocity profile (i.e., slip) on the SHPo surface compared to a smooth surface in a channel flow (Re_H = 9600). Bidkar et al. (2014) measured drag reduction on a SHPo surface of random-textured roughness coated with fluorosilane (FAS, according to the authors) in a TBL flow at relatively high Reynolds numbers (${\mathrm{Re}}_{\tau }=2000-4000$). They obtained 20–30% of drag reduction and remarked that the non-dimensional surface roughness ${k}^{+}={R}_{\mathrm{avg}}/{l}_{v}$, where ${R}_{\mathrm{avg}}=(\int {h}_{a}dx)/S$ (S: length of the sample) is the arithmetic average roughness height (Farshad and Pesacreta 2003; Bidkar et al. 2014, see Fig. 1c), should be much (at least by one order of magnitude) smaller than the viscous sublayer thickness in wall unit for a successful drag reduction. Srinivasan et al. (2015) tested a similar SHPo surface in TC flow up to ${\mathrm{Re}}_{\Omega }=r{i\Omega g}/\nu = 8\times {10}^{4}$ (equivalent to ${\mathrm{Re}}_{L}$), where $\Omega$ is the rotational speed, r_i is the radius of inner cylinder, and g is the gap between inner and outer cylinders of the TC setup. The drag reduction increased as the Reynolds number increased (about 22% at the highest ${\mathrm{Re}}_{\Omega }$ tested). Importantly, a greater drag reduction was obtained when the SHPo surface was not fully submerged so that the plastron was connected to the surrounding air and well maintained. Ling et al. (2016) performed a digital holographic microscopy to measure the drag in TBL flows (${\mathrm{Re}}_{\tau }=700-4500$) over several SHPo surfaces with varying random-texture characteristics. About 35% of drag reduction was measured along with a clear slip velocity when the root mean square of roughness height in wall unit was smaller than unity, i.e., ${k}_{\mathrm{rms}}^{+}$ $=\sqrt{\int {h}^{2}dx}/S$ < 1.0. However, about 10% of drag increase was obtained when the roughness increased to ${k}_{\mathrm{rms}}^{+}>1.0$. Even in the case of smaller roughness (${k}_{\mathrm{rms}}^{+}<1.0)$, the turbulence in the inner part of the boundary layer was found enhanced compared with the smooth surface. Gose et al. (2018) applied four different morphologies of random textures to the turbulent channel flow at ${\mathrm{Re}}_{H}=1\times {10}^{4}-3\times {10}^{4}$ and obtained a wide variation in drag—from 90% drag reduction to 90% drag increase, depending on the roughness characteristics. To consider the intermediate wetting transition, i.e., between the full Cassie–Baxter and Wenzel states, occurring at a high-Re flow, they suggested a scaling relation between the drag reduction and the product of roughness height (${k}^{+}$) and contact-angle hysteresis (i.e., the difference between the advancing and receding contact angles of water on the surface) at high pressure; both the roughness height and contact-angle hysteresis should be minimized to achieve an appreciable turbulent drag reduction. Relatedly, note in this review we have introduced the degree of wetting or air–water interface penetration in defining the roughness parameters of SHPo surface, as illustrated in Fig. 1b and c, to account for the intermediate wetting.

2.5 Roughness morphology and plastron

Although the existence of plastron is an essential premise for SHPo drag reduction in the first place, most of the early studies did not pay proper attention to the condition of plastron during the experiments, contributing to the widely scattered data in the literature even for laminar flows (Lee et al. 2016). In fact, it is not possible to fully understand or analyze experimental data of SHPo drag reduction without well-documented states of plastron throughout the reported experiments. Despite the lack of full information on the plastron state for most experimental studies of turbulent SHPo drag reduction, Table 1 still reveals a general trend that SHPo surfaces with longitudinal grooves resulted in a drag reduction most consistently, while those with random roughness produced less consistent results including drag increase. For example, considering most random roughness surfaces have roughness scale in the range below 10 μm or ${\varvec{O}}(1) {\mu} {\text{m}}$, which would lead to a relatively small slip length of $\lambda ={\varvec{O}}(1) {\mu} {\text{m}}$ or smaller, the surprisingly large drag reductions measured on them in many reports are likely by the plastron overgrown during the flow experiments. The air–water interfaces on the overgrown plastron would be much larger than the roughness scale, i.e., ${s}_{a,0}\gg {P}_{a}$ in Fig. 1c, resulting in a much larger slip length than predictable from the roughness scale, i.e., $\lambda \gg {P}_{a}$. This deviation was unmistakable even for the simpler experiments in laminar flows; see Fig. 6b in Lee et al. (2016). As a good example of the overgrown plastron in turbulent flows, Li et al. (2020a, b) used a confocal microscope image to reveal the air–water interface between water–asperity contact points (corresponding to ${s}_{a,0}$ in Fig. 1c), which would determine the slip length ($\lambda \sim {s}_{a,0})$, is much larger than the geometric roughness value (${P}_{a}\sim {k}_{a}$) of the given surface, i.e., ${(\lambda \sim s}_{a,0}\gg {P}_{a}$), in their water tunnel experiments. Conversely, on the same surfaces the plastron may be thinned down (corresponding to ${s}_{a,1}$ and ${s}_{a,2}$ in Fig. 1c) under different flow conditions, such as the open water of natural environment where the water is mostly undersaturated. In such unfavorable but more realistic conditions, the effective slip length would become smaller than the expected from the roughness scale, i.e., ${(\lambda \sim s}_{a,2}\ll {P}_{a}$), in a fashion opposite to how the overgrown plastron increased the effective slip length. In addition and importantly, the asperities of roughness that impale into the water would increase the drag, negating or even overtaking the plastron-based drag reduction, especially in turbulent regime (Aljallis et al. 2013; Xu et al. 2020b, 2021). In contrast, on well-defined morphologies the plastron would not be overgrown or thinned down much, as illustrated in Fig. 1b, whether the flow condition is favorable or unfavorable to the plastron, respectively, as far as the plastron exists. Note not only the slip interface width would remain constant throughout the intermediate states, i.e., ${s}_{1}$ and ${s}_{2}$ in Fig. 1b, but also the intermediate states are typically only transient anyway. Furthermore, the asperities that impale into the water would not create a form drag if the morphology is of longitudinal grooves. Much of the varying conditions of the flow that would change the thickness of plastron (i.e., slip interface width and morphology impalement height) on random morphologies would only change the curvature of water–air interfaces (not shown in Fig. 1 for simplicity) on organized morphologies. Since the curvature of pinned interfaces does not affect the slip length much (Lee et al. 2016), the organized morphologies provide a consistent slip length, explaining why longitudinal grooves resulted in more consistent drag reduction data than random roughness surfaces.

As the importance of plastron became better understood over the years, most of the recent experimental studies checked its existence during the flow tests, commonly by looking for the bright silvery sheen that appears due to the total internal reflection of light on the air–water interface. However, while it indicates the existence of plastron, the bright appearance does not inform the thickness of plastron. Even for organized morphologies, on which the plastron is more stable and the resulting slip stays more constant than on the random roughness, an appreciable deviation is expected if the air–water interfaces depin from the top of asperities and slide down in between them (Lee et al. 2016; see also Fig. 1b), suggesting the importance of keeping a proper plastron with pinned interfaces for successful drag reduction. Analytical studies and empirical evidences indicate that minute details of roughness asperities may affect the pinning of air–water interface and, thus, the status of plastron, which determines how slippery the surface is for overlying flows, e.g., slip length. Generally, sharp edges, including reentrant edges (Xu et al. 2020b), help keep the interface pinned on top of the roughness feature longer under unfavorable conditions until the onset of wetting starts to compromise the slip effect. Recently, Yu et al. (2021) developed a convenient (only with naked eyes) observation technique that can detect the depinning of interface, not just the existence of plastron, on microgrooves, making the monitoring of the plastron status throughout flow experiments more practical.

2.6 Drag reduction vs. slip length

Although highly relevant to design SHPo surfaces for applications, the correlation between the slip length and drag reduction for turbulent flows has been studied mostly by numerical simulations, lacking experimental corroboration. Despite the difficulty, however, organized roughness morphologies, such as the longitudinal grooves, could provide a useful physical insight into the correlation. For example, testing in TBL flows in a water tunnel, Park et al. (2014) measured how the drag ratio (i.e., drag on a sample surface relative to that on a smooth surface) on longitudinal grooves decreases (i.e., drag reduction increases) with increase in gas fraction (GF) and also with the pitch (P) of the groove. Although the drag reduction in turbulent flows is not solely determined by the slip length (see Sect. 3 for detailed discussion), the trend of increasing drag reduction with increase in GF and P was attributed to the slip length ($\lambda$) that increases with increase in GF and P, similar to the trend in laminar flows (Lee et al. 2016). Testing in a Taylor–Couette flow, Srinivasan et al. (2015) measured the drag reduction on spray-coated random roughness and suggested a scaling that the skin-friction coefficient (c_f) would follow ${c}_{f} \sim 1/{({\lambda }_{s}^{+})}^{2}$, where ${\lambda }_{s}^{+}={\lambda }_{s}{u}_{\tau }/\nu$ is the streamwise slip (${\lambda }_{s}$) expressed in wall unit, also attributing the drag reduction to the increased slip length, especially expressed in wall unit. This scaling trend is corroborated by the numerical studies (Fukagata et al. 2006; Busse et al. 2012; Park et al. 2013; Jung et al. 2016), as plotted in Fig. 2, which also includes the results from the TBL flows performed in a water tunnel (Park et al. 2014) (after compensating for the effect of small size), underneath a motorboat (Xu et al. 2020b), and in towing tank (Xu et al. 2021). The results of the TC flows by Hu et al. (2017) and Van Buren and Smits (2017) are not plotted because we could not deduce their values of ${u}_{\tau }$ from the reported data. The data sets that involved deteriorated plastron (existing in the boat and towing tank studies) are excluded in the graph for a fair comparison with the numerical data, which assumed a perfect plastron. While the water tunnel and towing tank data show the relationship between the drag ratio and dimensionless slip length that resembles the numerical predictions, the boat data show a scatter. The scatter for the boat test is not surprising if one considers the uncontrollable flow conditions of the field tests. Here, the streamwise slip length (${\lambda }_{s}$) was estimated using the analytical relationship confirmed for laminar flows $\frac{{\lambda }_{s}}{P}=-\frac{1}{\pi }ln\left[\mathrm{cos}\frac{\pi GF}{2}\right]$ (Lauga and Stone 2003; Lee et al. 2008), and the slip length in wall unit (${\lambda }_{s}^{+}$) was estimated using the friction velocity (${u}_{\tau }$) obtained from the corresponding Reynolds numbers.

Fig. 2

Drag ratio with respect to the streamwise slip length in wall unit (${\lambda }_{s}^{+}$) in turbulent flows reported for SHPo surfaces with longitudinal grooves (LG) and random roughness (Ra). Since there are only a few experimental reports in the literature presentable in this graph properly, the numerical reports are included to provide valuable references. NUM: numerical simulation; EXP: experiment; Slip: effective slip length imposed, i.e., without regard to roughness morphology

2.7 Drag reduction vs. Reynolds number

Figure 3 shows all the drag reduction results experimentally obtained on SHPo surfaces in turbulent flows, following Table 1. The data are presented in the form of drag ratio as function of the friction Reynolds number (${\mathrm{Re}}_{\tau }$). It should be noted that the effect of roughness size is not explicitly compared in the figure because the main goal is to show the effect of ${\mathrm{Re}}_{\tau }$ for a given SHPo surface. The drag ratio is widely scattered in the range between around 0.3 (i.e., drag reduction by 70%) and nearly 1.5 (i.e., drag increase by 50%) over the Reynolds numbers up to ${\mathrm{Re}}_{\tau } \simeq 7000$. The broad spectrum of the data is attributed to the plastron highly disturbed by the stronger inertia (and agitation) and shear stress in turbulent flows, as well as to the different mechanism of drag reduction, compared with laminar flows (see Sect. 3 for details). The drag ratio is also substantially dependent on the type of roughness morphology, such as organized vs. random roughness, as well as the size and shape of the morphology. Some studies confirmed the increase in the drag reduction, i.e., decrease in drag ratio, with an increase in ${\mathrm{Re}}_{\uptau }$ (Daniello et al. 2009; Srinivasan et al. 2015; Zhang et al. 2015b; Rajappan et al. 2019; Li et al. 2020a, b; Xu et al. 2020b, 2021), agreeing with the numerical and theoretical predictions (Min and Kim 2004; Fukagata et al. 2006; Park et al. 2013). All of them visually confirmed the existence of plastron during the experiments. However, other studies reported the opposite trends. For example, the drag reduction effect diminished, i.e., drag ratio increased, with an increase in ${\mathrm{Re}}_{\tau }$ and even became negative (i.e., drag ratio > 1.0) at high Reynolds numbers (Aljallis et al. 2013; Ling et al. 2016; Xu et al. 2020b, 2021), which was explained with increased wetting and hydrodynamic roughness at higher Reynolds number (${\mathrm{Re}}_{\tau }\gtrsim 2000$). Most of them reported observation of diminished or depleted plastron at high speeds. Note two of the above studies (Xu et al. 2020b, 2021) predictably confirmed both the positive and negative trend by testing longitudinally grooved and random roughness surfaces side by side simultaneously in given flows.

Fig. 3

Experimentally obtained turbulent drag reduction data of Table 1 plotted as drag ratio vs. frictional Reynolds number (${\mathrm{Re}}_{\tau }$), separated by roughness types or flow types: a all of the available data; b data for longitudinal grooves (LG) and transverse grooves (TG); c data for posts (Po) and random roughness (Ra); d data for channel flows in water tunnel; e data for TBL flows in water tunnel; f data for TC flows in TC setup; g data for TBL flows in open water

To review the effect of slip directions on the turbulent drag reduction, the drag ratio on the SHPo surfaces with longitudinal grooves (LG) and random roughness (Ra) is plotted separately in Fig. 3b and c, respectively. Additionally, the data for transverse grooves (TG) are plotted along with LG in Fig. 3b, and the data for posts (Po) are with Ra in Fig. 3). Figure 3b shows all the longitudinal groove (LG) surfaces produced a drag reduction (drag ratio < 1.0) consistently, although the degree of reduction varies significantly. Unlike those who tested one or several surfaces at one Reynolds number (Woodford et al. 2009; Park et al. 2014; Gose et al. 2020), those who tested a given surface over a range of Reynolds numbers (Daniello et al. 2009; Xu et al. 2020b, 2021) found the drag ratio would decrease as the frictional Reynolds number increases, corroborating the numerical studies (Fukagata et al. 2006; Martell et al. 2010; Park et al. 2013; Lee et al. 2015). The reversed tendency (i.e., drag increase with Reynolds number) at ${\mathrm{Re}}_{\tau }\gtrsim 4000$ in Xu et al. (2021), drawn with a lighter color, was caused by the shear-driven wetting (Wexler et al. 2015a), not by any flow mechanism. In contrast, Fig. 3c shows that the drag ratio data on the random roughness (Ra) surfaces were scattered significantly. Despite the large scatter, we can see a slight trend that the drag ratio would generally increase as the frictional Reynolds number increases, contradicting the numerical studies. The results suggest that the effect of the streamwise slip was compromised or overshadowed by the equal spanwise slip due to the non-directionality of the randomly arranged surface morphology. However, it also suggests that the hydrodynamic roughness effect becomes dominant on random textures (Ling et al. 2016), which are also more prone to wetting, and added a significant drag (Aljallis et al. 2013). While included, the surfaces of transverse grooves (TG) in Fig. 3b and posts (Po) in Fig. 3c have not produced enough data to allow us to discuss the correlation between the drag ratio and the frictional Reynolds number. Posts are considered to be closer to random roughness than longitudinal grooves in terms of slip directions although their truncated roughness height belongs to organized roughness in terms of hydrodynamic roughness.

The reasons for the more favorable drag reduction on LG than on Ra above can also be understood by two aspects: the effect of slip direction and the stability of plastron in flows. The slip on a SHPo surface is the most effective when it is aligned to the flow direction. Any slip not in the streamwise direction is known to mitigate the drag-reduction performance (Min and Kim 2004; Fukagata et al. 2006; Busse and Sandham 2012), and the mitigation becomes more severe as the Reynolds number (or the slip length in wall unit) increases. For grooved SHPo surfaces in a laminar flow, the slip length along the transverse direction is generally a half of that along the streamwise direction as analytically predicted (Lauga and Stone 2003) and experimentally confirmed (Lee et al. 2016). However, as alluded earlier, the effects of the flow direction on the slip length and drag are not as simple in turbulent flows. For example, Woolford et al. (2009) reported a drag reduction of about 11% on longitudinal grooves (P = 32 μm; GF = 80%) placed in streamwise direction but a drag increase of 6.5% in transverse direction. Although the favorability of streamwise direction over transverse direction is common for both laminar and turbulent flows, the experimental data for turbulent flows are still scarce to reveal any quantifiable comparison. For the plastron stability in flows, the random-textured roughness is known to be generally more vulnerable to the depletion than the well-organized roughness. Aljallis et al. (2013), Xu et al. (2020b), and Xu et al. (2021) visually confirmed the partial loss of plastron on their SHPo plate with the loss being more pronounced at higher flow speeds, which impart a larger shear stress on the plastron. This partial loss is illustrated with the subscript 1 and 2 in Fig. 1c. In addition, as the Reynolds number increases, the corresponding viscous length scale (${l}_{v}= \nu /{u}_{\tau }$) becomes smaller, making the dimensionless length scales of a given roughness geometry, ${P}_{a}^{+}={P}_{a}/{l}_{v}$ ~ ${k}_{a}^{+}={k}_{a}/{l}_{v}$, larger and inducing a drag increase once the average wetted roughness height in wall unit (${h}_{a}^{+}$) becomes large enough to become hydrodynamically rough (Bidkar et al. 2014). Note a stronger turbulent flow not only increases the wetted roughness height ${h}_{a}$ by thinning the plastron but additionally makes the increased ${h}_{a}$ hydrodynamically even rougher by decreasing the viscous length scale. This issue will be discussed more in Sect. 3.2. In comparison, for organized textures, such as grooves and posts, the wetted roughness height ($h$) in wall unit would be quite small, i.e., ${h}^{+}$ $\lesssim$ O(1), and considered to be hydrodynamically smooth (Nikuradse 1933) as far as the air–water interface is pinned (much more persistently than the random textures) at the texture top edges, i.e., ${h}_{o}$ in Fig. 1b. Lastly, although the increased pressure (or its fluctuation) in a high-Re turbulent flow would promote sagging of the air–water interface and accelerate its depinning (Kim and Park 2019), the effect of decreased slip length by the curved interface (Crowdy 2016) is considered much smaller compared with the negative effect by the above roughness effect. Unlike the random roughness surfaces, where a significant wetting would lead to an overall drag increase, the longitudinal grooves still produced an overall drag reduction of an appreciable amount (~10%) even when around a half of surface was found wetted (Xu et al. 2021), likely because of less roughness height effect. Based on the studies reported until today and especially the studies that predictably confirmed both of the opposite trends in same flows (Xu et al. 2020b, 2021), we believe the drag ratio would decrease (i.e., drag reduction would increase) with increase in ${\mathrm{Re}}_{\tau }$ on a given SHPo surface as predicted by most numerical studies, as far as the plastron is properly maintained. The contradicting trend found with most of the random roughness surfaces is most likely and simply by their lack of ability to maintain the plastron rather than by any fluid dynamic mechanism, as explained in Aljallis et al. (2013).

As suggested in Sect. 2.1, the effect of flow geometry on SHPo drag reduction, including the trend of drag ratio with ${\mathrm{Re}}_{\uptau }$, tends to be greater in turbulent flows than in laminar flows. For channel flows in water tunnel, obtained for ${\mathrm{Re}}_{\tau }<1000$ as shown in Fig. 3d, the drag ratio (especially for Ra) tends to increase with increase in ${\mathrm{Re}}_{\tau }$. As the Reynolds number increases, the plastron would thin down and the wetted roughness height would increase, i.e., ${h}_{a,0}\to {h}_{a,1}\to {h}_{a,2}$ in Fig. 1c, degrading the drag-reducing capability of the surface. For TBL flows in water tunnel, obtained mostly for ${\mathrm{Re}}_{\tau }<2000$ as shown in Fig. 3e, meaningful drag reductions are obtained up to ${\mathrm{Re}}_{\tau }\simeq 5000$, showing drag ratio decreasing with increase in ${\mathrm{Re}}_{\tau }$. For Taylor–Couette (TC) flows, obtained for ${\mathrm{Re}}_{\tau }<4000$ as shown in Fig. 3f, drag ratio is shown to decrease with ${\mathrm{Re}}_{\tau }$. Compared with most other flows, TC flow can provide a uniquely favorable environment to keep the plastron, for example, by connecting the plastron to the outside air or circumventing the shear drainage effect. Finally, for TBL flows in open water shown in Fig. 3g, the data were obtained in a wider range of ${\mathrm{Re}}_{\tau }$ (= 1000–7000), and the dependency of LG and Ra on ${\mathrm{Re}}_{\tau }$ is clearly distinguished. Since the water in open water environment (e.g., towing tank and boat) is saturated or undersaturated with air, not providing the supersaturated water or any other favorable condition the laboratory flows may generate whether intentionally or unintentionally, the advantage of LG over Ra is unmistakably evident. Before the wetting transition occurs by high ${\mathrm{Re}}_{\tau }$, i.e., at ${\mathrm{Re}}_{\tau }$ < 5000, the decrease of drag ratio with increase in ${\mathrm{Re}}_{\tau }$ agrees with the prediction by numerical studies (Min and Kim 2004; Fukagata et al. 2006; Park et al. 2013), emphasizing the importance of keeping the plastron to achieve the drag reduction.

2.8 Turbulent drag reduction on liquid-infused surfaces

Slippery liquid-infused porous surface (SLIPS), or more generally liquid- or lubricant-infused surface (LIS), is a hydrophobized textured surface with its texture filled with a low-surface-energy liquid (Wong et al. 2011), in contrast to the SHPo surface whose texture is filled with a gas. The use of liquid instead of gas makes the lubricating layer significantly more robust against the loss by molecular diffusion or pressure difference across the interface—the main advantage of LIS compared with SHPo surfaces. Although the infused liquid on LIS cannot provide the very small viscosity ratio (~ 1/50 for air-to-water) the concept of SHPo drag reduction is footed on, various studies have nevertheless explored LIS for drag reduction, anticipating the liquid–liquid interface between the infused liquid (typically oil) and the bulk liquid flow would lead to a drag reduction. While not effective in laminar flows, where drag reduction is solely by the viscosity ratio, LIS was found capable of an appreciable drag reduction in turbulent flows. However, the large viscosity (typically similar to or larger than water) of the lubricants that are acceptable for LIS generally results in a smaller slip length and drag reduction compared with the air-filled SHPo surface for the same roughness geometry, as reported by Arenas et al. (2019) and Chang et al. (2019). There have been only a few successful experiments to test LIS in turbulent flows. Rosenberg et al. (2016) tested the LIS of longitudinal grooves (a spiral to be exact) in turbulent TC flows and obtained a drag reduction up to 14%. In a follow-up study, Van Buren & Smits (2017) tested the LIS with improved longitudinal grooves in turbulent TC flows and obtained a drag reduction up to 35%. The optimal width of fluid–fluid interface (groove width) that led to the maximum drag reduction was found to be ${w}^{+}\simeq 35$, which is significantly larger compared with the SHPo surface in other flows; we will discuss this issue in Sect. 3. Importantly, note all the experiments that reported an appreciable drag reduction with LIS (Rosenberg et al. 2016; Van Buren and Smits 2017) were performed in TC system, which uniquely avoids the shear-driven loss of the infused fluid, whether liquid or air, but such a loss is most likely unavoidable in most practical applications, unfortunately. While more stable against diffusion and pressure, the liquid lubricant on LIS is generally more susceptible to the shear-driven drainage (Wexler et al. 2015a; Fu et al. 2019), compared with the air plastron on SHPo surfaces. Several strategies have been proposed to enhance the oil retention for LIS (Lee et al. 2019; Chen et al. 2020), but despite the general improvement they fall far short of overcoming the high shear expected in common drag reduction applications. In employing a LIS for hydrodynamic drag reduction, it should be noted that the ratio of oil viscosity to the bulk fluid flow is an important parameter to determine the functionality, and an effective drag reduction cannot be expected in laminar flows if the infused fluid is more viscous than the bulk fluid. Although the LIS has not been widely tested in turbulent flows and more data are required, it is expected that the effective drag reduction can be obtained in the case of a turbulent flow due to the additional effects such as the modification of the flow structures similarly to the SHPo surfaces, as suggested by recent numerical studies (Fu et al. 2017; Arenas et al. 2019; Chang et al. 2019).

3 Mechanism of drag reduction on SHPo surfaces in turbulent flows

The mechanism of turbulent drag reduction on a SHPo surface has been mostly investigated by the numerical studies, which modeled the SHPo surface typically as a flat wall consisting of solid–water and air–water interfaces with a directional or non-directional slip. In comparison, experimental results, while invaluable to advance the field, have not provided enough information necessary to study the mechanism in earnest mainly due to the difficulty of measuring or controlling the air–water interface during test runs. However, it is still informative to collect the experimental data in the literature and discuss the overall tendencies. Here, we summarize the common understanding from the numerical results first to help the readers interpret the findings from the experimental studies.

3.1 Modification of the turbulent flow structure

Earlier numerical studies showed that the direct slip effect from the air–water interface alone would not be enough to explain the higher skin-friction drag reductions obtained in turbulent flows than those in laminar flows on the same surfaces (i.e., same slip length). They revealed that the near-wall turbulence structure (i.e., the streaky structures with a higher streamwise vorticity) would be suppressed significantly on the SHPo surface (Fig. 4a), and the suppression would be induced more by the streamwise slip (${\lambda }_{s}$) than spanwise slip (${\lambda }_{z}$) (Min and Kim 2004; Busse and Sandham 2012; Park et al. 2013; Jelly et al. 2014). A spanwise slip (${\lambda }_{z}$) was reported to strengthen the dynamics of streamwise streaky structures, mitigating the slip effect and even resulting in an overall drag increase (Min and Kim 2004; Fukagata et al. 2006). Based on the experiments with a grooved SHPo surface in a turbulent channel flow (${\mathrm{Re}}_{\tau }= 180$), Woolford et al. (2009) reported a drag reduction of 11% when the grooves were parallel to the flow direction but a drag increase of 6.5% when they were transverse to the flow direction. According to the numerical study of Seo and Mani (2016), while combining ${\lambda }_{s}$ and ${\lambda }_{z}$ would be justified for moderate values of GF, the use of a single effective slip length to represent a SHPo surface needs to be amended for a large GF (> 90%) where the contribution of ${\lambda }_{z}$ is large. Based on a direct numerical simulation of turbulent channel flows with a SHPo surface, Rastegari and Akhavan (2015) suggested that the drag reduction ratio could be modeled as ${u}_{s}/{u}_{bulk}+\Delta \varepsilon$, where ${u}_{s}$ and ${u}_{bulk}$ denote the slip velocity and bulk velocity in an uncontrolled channel flow, respectively. Here, ${u}_{s}/{u}_{bulk}$ and $\Delta \varepsilon$ represent the contributions by the direct slip effect and by the turbulence modification, respectively. Their results indicated that the contribution of turbulence modification to the drag reduction is positive (although not more than 20% of the total drag reduction) in the case of longitudinal grooves but negative in the cases of transverse grooves and posts, even resulting in an overall drag increase for transverse grooves. Considering the resemblance to the posts (even though posts have a uniform height), which do not have a preferential direction of slip, random roughness surfaces are expected to perform similarly to the post surfaces in terms of directional drag reduction in turbulent flows as far as the non-uniform height is small enough to be considered hydrodynamically smooth. The reduction of turbulence production on SHPo surfaces was attributed to the suppression of near-wall turbulence structures (Jelly et al. 2014; Im and Lee 2017), making the turbulence intensity and Reynolds stress also reduced near the SHPo surface. On the other hand, Martell et al. (2010) claimed that the near-wall structures should simply be shifted upward (away) from the wall by the SHPo surface, which could also lead to the drag reduction.

Fig. 4

Suppression of turbulence on LG SHPo surfaces. a Contours of streamwise vorticity shown in y–z plane for turbulent channel flow in x direction (i.e., flowing into the page) at ${\mathrm{Re}}_{\tau }= 590$: smooth walls (left) and SHPo walls of LG with 93.75% GF and pitch in wall unit P⁺ = 220 (right) (Park et al. 2013). b Displacement readings of a smooth and SHPo surface of LG with P = 50 μm and 90% GF in a TBL flow at ${\mathrm{Re}}_{\tau }= 250.$ The optical images (left) show the floating element before and during the flow to compare the smooth and SHPo surface, and the graph (right) shows temporal displacements of the two surfaces (Park et al. 2014). c Contour of turbulent kinetic energy (TKE) and velocity vectors in a turbulent pipe flow with a SHPo surface of LG with 50% GF at ${\mathrm{Re}}_{\tau }= 180$ (Im and Lee 2017). All figures are reproduced from each reference noted

The evidence of turbulence suppression on a SHPo surface has also been provided by several experimental studies. Based on the decomposition of time-resolved velocity measurements, it was found that the event of bursting in the near-wall region was reduced on a SHPo surface with random roughness (Haibao et al. 2015; Tian et al. 2015). Hokmabad and Ghaemi (2016) compared the flows over random-roughness SHPo surfaces with and without the plastron, using a PIV measurement. When the surface had the plastron, the vortex dynamics of sweep and ejection was suppressed, and the spanwise distance between low and high speed streaks increased. They also explained that the drag reduction by the streamwise slip can be opposed by the spanwise slip that enhances the spanwise turbulent intensities (measured 6% higher than the smooth surface). When the surface lost the plastron, on the other hand, the wetted surface had a negligible slip effect on the flow. The wetted roughness did not result in drag increase because the roughness height was smaller than the viscous sublayer thickness, i.e., the wetted surface was hydrodynamically smooth. Using a direct comparative shear sensor, Park et al. (2014) and Xu et al. (2020b) observed that the fluctuating displacement of the floating element covered with a SHPo surface was reduced significantly compared to the smooth counterpart (Fig. 4b), indicating that the velocity fluctuation was also suppressed on the SHPo surface.

Numerical studies also showed that the direct slip effect would increase the mean velocity ($\overline{u }$) by the amount of slip velocity (u_s) (Min and Kim 2004; Martell et al. 2009; Seo and Mani 2016; Alamé and Mahesh 2019; Fairhall et al. 2019), and the differential velocity profiles in wall unit, ${\overline{u} }^{+}-{u}_{s}^{+}=(\overline{u }-{u}_{s})/{u}_{\tau }$, would collapse to a single curve for different values of u_s if the SHPo surface is assumed to have only a streamwise slip (Min and Kim 2004). When a roughness morphology that would lead to both streamwise and spanwise slip is considered, ${\overline{u} }^{+}-{u}_{s}^{+}$ would collapse to a single curve only very close to the wall (i.e., in the viscous sublayer) and would not collapse outside the viscous sublayer (Alamé and Mahesh 2019; Fairhall et al. 2019). While the differential velocity profile follows the log-law of a turbulent boundary layer, i.e., ${\overline{u} }^{+}-{u}_{s}^{+}={\kappa }^{-1}\mathrm{ln}{y}^{+}+B$, the constant B would vary depending on the roughness features such as the slip direction and GF. Min and Kim (2004) also showed that in drag-increasing cases, the spanwise slip would cause the ${\overline{u} }^{+}-{u}_{s}^{+}$ value to decrease in buffer and log layers. Similarly, Fairhall et al. (2019) claimed that the slip effect would not directly modify the dynamics of the turbulence. Instead, they suggested that the drag on the SHPo surface should be determined by the increase in the mean velocity by the effective slip and the enhancement in the turbulence structure by the roughness. Since the effects of the streamwise and spanwise slips oppose each other (i.e., the former increases but the latter decreases the mean-velocity profile), the amount of drag reduction is expected to be a combination of the two opposing effects. When the transverse width of the air–water (shear-free) interface on longitudinal grooves is too large (${w}^{+}\gtrsim 25$), the turbulence is enhanced by the nonlinear interaction between the slip-induced flow and the underlying turbulence (i.e., background turbulence in the bulk water flow), increasing the Reynolds stress and decreasing the mean velocity, i.e., increasing the drag. Experimentally, Zhang et al. (2015a) reported that the increase in the mean velocity was accompanied by the drag reduction on a SHPo surface. Using a digital holographic microscopy, Ling et al. (2016) also measured the increase in the mean-velocity profile in the drag-reducing case of a randomly distributed roughness.

In addition, numerical studies suggested the generation of a secondary flow structure consisting of pairs of counter-rotating streamwise vortices at the top edges of roughness, i.e., boundary between slip and no-slip surfaces (Fig. 4c) (Jelly et al. 2014; Türk et al. 2014; Im and Lee 2017; Costantini et al. 2018). Jelly et al. (2014), and claimed that this secondary flow should increase the drag on the solid–water portion (i.e., no-slip boundary condition) of the surface. Türk et al. (2014) showed that, if the width of a slip interface was too large, e.g., ${w}^{+}> 20$, the slip length of the SHPo surface under a turbulent flow became smaller than that under a laminar flow due to the enhanced mixing by the secondary vortical structure. Im and Lee (2017) compared the effect of alternating streamwise strips of no-slip and slip boundary conditions in pipe (i.e., circular) and channel (i.e., two parallel plates) flows. In both the flow geometries, the secondary vortical structure was found, while it was stronger in a pipe than in a channel due to the enhanced spanwise slip in the pipe geometry. They decomposed the energy budget and explained that the secondary flow would be driven and maintained by the gradient of Reynolds stress (Prandtl’s secondary flow of the second kind). In a similar pipe flow, Costantini et al. (2018) showed that the direct effect of surface slip on the increase of flow rate would be much stronger than the decrease of flow rate caused by the secondary flow structure. So far, the secondary flow structures and their role in the turbulence modification on SHPo surfaces have not been experimentally measured.

While most numerical studies utilized a SHPo surface consisting of flat air–water interfaces flush with flat solid surfaces, which resembles the organized roughness of grooves or posts, Alamé and Mahesh (2019) performed a direct numerical simulation of a turbulent channel flow (${\mathrm{Re}}_{\tau }=180$) with a random-textured roughness whose profiles were generated from a three-dimensional surface profile measurement of real surfaces. Although all the air–water interfaces between the roughness walls were assumed to be flat (i.e., similar to Fig. 1c), they were able to examine the roughness effect by changing the average height of the wetted roughness, i.e., by varying ${{h}_{a}}^{+}$. The result suggested that two counteracting effects—the slip interface effect (reduction of turbulence) and the roughness asperities effect (enhancement of turbulence)—compete each other depending on the roughness height, which was not addressed in other simulations that modeled organized roughness. When the roughness effect was not significant, the time-averaged velocity increased by the amount of slip velocity, following the law of the wall. However, when the roughness effect was significant, the roughness caused the velocity distribution to deviate from the above. For many asperities that impale the water significantly and create large ${{h}_{a}}^{+}$, one should consider the high stagnation pressure induced in front of the wetted asperities and the lower pressure behind them. This causes a significant pressure fluctuation (Seo et al. 2015), which would result in a non-negligible form (pressure) drag and wetting transition (Piao and Park 2015). Considering these competing effects, Alamé and Mahesh (2019) suggested that the increase in the bulk (mean) velocity, which includes the information of slip velocity and variation in the Reynolds stress, instead of slip velocity alone, should be a better indicator of drag reduction in turbulent flows.

3.2 Dependence on the roughness morphology

The mechanism of the turbulent flow modification by the SHPo surface indicates that the drag reduction is determined by not simply the roughness parameters but also their wetted variants. Note, while the roughness parameters are determined by the SHPo surface, the wetted roughness parameters are determined by the flow condition as well as the SHPo surface. Let us consider the opposite effects of the air–water interface and wetted roughness that are two main wetted roughness parameters. A larger interface width ($s$) would increase the slip length and reduce drag, while a larger wetted roughness height ($h$) would generate an additional turbulence and increase drag. Considering the important and opposing roles of $s$ and $h$, it would be helpful to analyze how the drag ratio is affected by these two wetted roughness parameters normalized in wall unit, ${s}^{+}$ and ${h}^{+}$. However, because $s$ and $h$ are rarely measured and reported in the literature, in Fig. 5 the drag ratio is plotted as function of w⁺ and k⁺ instead. For the cases of organized roughness collected in Fig. 5a, the roughness height (k) rarely causes any wetted roughness height ($h$), i.e., ${h}_{0}= 0$, because the roughness top has a uniform height and the air–water interfaces are pinned there, i.e., subscript 0 in Fig. 1b. Since k would not affect the drag ratio, the roughness width (w⁺) was used as the representative length scale. For longitudinal grooves (LG), where w⁺ was tested up to about 16, the drag ratio was shown to decrease (i.e., drag reduction increases) with increase in w⁺ up to ${w}^{+}\simeq 10$. The reversed trend (i.e., drag ratio increasing with w⁺) found for ${w}^{+}\gtrsim 10-30$ may be caused by the wetting that occurred when the air–water interface became large, as speculated by Van Buren and Smits (2017) and visually corroborated and quantitatively (albeit indirectly) supported by Xu et al. (2021). Recall the reversed trend was also predicted by the secondary vortical structure, as reported by the numerical studies of Türk et al. (2014) and others in the previous subsection. Further studies will be necessary to understand the reversed trend more conclusively. For the case of posts (Po), the number of available experimental data is too small to draw a trend, but the numerical studies of Fairhall et al. (2019) showed that an excessive spanwise slip (${w}^{+}\gtrsim 25$) would increase the drag. The negative drag reduction (i.e., drag ratio > 1) for the sole case of transverse grooves (TG) at ${w}^{+}\simeq 1.0$ was likely because the spanwise slip (${\lambda }_{s}$) was larger than the streamwise slip (${\lambda }_{z}$), following numerical and theoretical studies. Although the lateral scale of solid–water interface (P-w in Fig. 1b) would also affect the drag ratio via the gas fraction (GF), Fig. 5a does not include it for simplicity. Furthermore, even when the air–water interfaces are pinned on the roughness tops, note the flow near the composite wall should experience no-slip (on solid) and slip (on air) boundary conditions alternately.

Fig. 5

Drag ratio of SHPo surfaces as function of roughness scales normalized in wall unit: a For the organized roughness (LG, TG, and Po), the interface width ($s$) (i.e., slip interface lateral scale) would be a key data that determines the drag ratio. However, the roughness width ($w$) (i.e., geometric lateral scale) is used here because most studies report $w$ and $w\cong s$; b For the random roughness (Ra), the average wetted roughness height (${h}_{a}$) (i.e., wetted roughness vertical scale) would be a key data that determines the drag ratio. However, the average roughness height (${k}_{a}$) (i.e., geometric vertical scale) is used here despite the disparity (i.e., ${k}_{a}\ne {h}_{a}$) because ${h}_{a}$ is rarely reported in the literature

So far, most of the experimental studies have employed random-textured SHPo surfaces because of the convenience and scalability in preparing large-area SHPo surfaces. Although most random textures have random roughness in both horizontal and vertical directions (Fig. 1c), one of them may be used to represent the roughness, unless the randomness is directional. Since the air–water interfaces would move up or down as illustrated in Fig. 1c, some studies such as Ling et al. (2016) considered the roughness above the air–water interfaces, which is similar to the wetted roughness height ($h$) defined in Fig. 1c. However, because $h$ is difficult to obtain and rarely reported in the literature, we will use the roughness height ($k$) in its dimensionless form (${k}^{+}$) as an available alternative for Fig. 5b as was used in Table 1. The results of random roughness morphologies collected in Fig. 5b show that the drag ratio is consistently below unity (i.e., positive drag reduction) at small roughness height ${k}^{+}$, gradually increases with increase in ${k}^{+}$, and may become larger than unity (i.e., more drag than smooth surface) at ${k}^{+}>1.0$, confirming that the effect of vertical roughness counteracts the slip effect of lateral air–water interface. Bidkar et al. (2014) suggested that the roughness height should be much smaller than the thickness of a viscous sublayer, i.e., ${k}^{+}\ll 5.0$, for a successful drag reduction; if not, the drag ratio would decrease less or even become larger than unity. Similarly, Ling et al. (2016) observed a transition from drag reduction (where a viscous stress dominates the total stress) to drag increase (where a Reynolds stress dominates) when the root mean square of roughness height was ${k}_{rms}^{+}\simeq 1.0$ (${k}_{rms}^{+}$ and ${k}^{+}$ have the same order of magnitude for the SHPo surfaces used in the literature). When ${k}_{rms}^{+}>1.0$, the velocity profiles were similar to those over a typical (i.e., no trapped air) rough-wall turbulent boundary layer. Using micro-particle tracking velocimetry and particle image velocimetry, Abu Rowin et al. (2017) showed that the drag reduction on a random roughness SHPo surface (${k}_{rms}^{+}\simeq 0.1$) was caused mainly by the reduction of a viscous wall shear stress with a negligible change in the Reynolds stress.

As a strategy to design an effective SHPo surface with random-textured roughness, Gose et al. (2018) suggested that the product of contact angle hysteresis under a high pressure (~ O(10³) Pa) condition ($\Delta {\theta }^{HP}$) and non-dimensional roughness height (k⁺) should be minimized to have a significant drag reduction, as replotted in Fig. 6. Note the drag ratio is as small as ~ 0.1 for $\Delta {\theta }^{HP}{k}^{+}$ ~ 2 and as large as ~ 1.9 for $\Delta {\theta }^{HP}{k}^{+}$ ~ 80. Rajappan et al. (2019), on the other hand, proposed the following three conditions for the effective turbulent drag reduction on random roughness: (i) large mean horizontal spacing between roughness asperities (analogous to w), (ii) small vertical roughness, i.e., ${k}_{rms}$ < ${l}_{v}$ (viscous length scale), and (iii) hierarchical structure of roughness morphology (to help resist the wetting transition). For high-speed turbulent flows (i.e., small ${l}_{v}$), it is critically important but exceedingly difficult to assure $k$ is small enough to prevent turbulence as well as w is large enough to induce a large enough slip to affect the bulk flow, if a random roughness should be used. Interestingly, it was found that the drag reduction increased when the random roughness was aligned along the streamwise direction, mimicking the longitudinal grooves (Ling et al. 2016).

Fig. 6

Drag ratio plotted versus the product of the non-dimensional roughness (k⁺) and the contact angle hysteresis ($\Delta {\theta }^{HP}$) at higher pressure (370 Pa). Replotted using the data from Gose et al. (2018). Symbols denote the different type of random roughness considered

3.3 Utilities other than the skin-friction drag reduction

Aside from the skin-friction drag reduction, a combination of the opposing two effects of the lateral slip interface and the vertical surface roughness would be useful in some flow controls, such as the mixing, heat transfer, and flow separation, which can benefit from the enhanced turbulence. Within some limited range of roughness size, for example, the surface roughness is known to be beneficial to control the flow around bluff body, like a sphere and circular cylinder, for the purpose of delaying flow separation and reducing the pressure drag (Achenbach 1971; Choi et al. 2006a, b; Choi et al. 2008). However, the surface roughness (when it is comparable to or larger than the thickness of a viscous sublayer) would increase the frictional drag of a turbulent flow in most cases except the riblet of an optimal configuration (Jimenez 2004). Using spray-coated hydrophobic nanoparticles and roughened Teflon surface, Kim et al. (2015) reduced the recirculation bubble in the wake of a circular cylinder by 40%, achieving a drag reduction of 10%. They showed that the rough hydrophobic surface enhanced the turbulence in the flows above the circular cylinder and along the separating shear layers, delaying the flow separation and encouraging the early vortex roll-up. Opposite to the streamwise slip preferred for the skin-friction drag reduction, the roughness texture transverse to the flow direction (spanwise slip) was more effective than that aligned to the flow (streamwise slip) for the case. For example, flow over the TG experiences the no-slip and slip conditions alternatively along the flow direction, which tends to amplify the nonlinear process of turbulent stress production (Costantini et al. 2018). A similar mechanism was also confirmed to be effective in the flow control around a hydrofoil (Lee et al. 2018). It is also interesting to note that the SHPo surface could reduce the turbulent kinetic energy by about 20% in the wake of a rotating blade (Choi et al. 2019). As the rotor surface was modified to be SHPo, the accumulation and shedding of vorticity from the rotating blade surface was delayed or became weaker to disturb the organized vortex structure in the wake, reducing the velocity fluctuation without a significant loss of a momentum (thrust). This suggests that the SHPo surface can also be a potential strategy for reducing the flow-induced noise from a turbomachinery.

4 Drag reduction on SHPo surfaces in turbulent flows of field condition

Ultimately, the most anticipated goal of the SHPo drag reduction research has been to serve common water vessels traveling in a real-world aquatic environment. Although it is rather obvious that the air lubrication on SHP surfaces would reduce the friction drag on them moving in water, two main questions are posed before opening the door for real-life applications: (i) would the drag reduction be large enough to be practical? and (ii) would the manufactured surface function as a SHPo surface, i.e., would the plastron persist, in the actual service conditions? The first question was answered positively through the analytical and experimental studies in laminar flows. The second question, however, is still being addressed with no clear solution yet. As a matter of fact, the question of plastron viability in practical conditions has not been appreciated properly until somewhat recently. Lee et al. (2016) identified the issue of air concentration level in water as the main reason for the discrepancy between the lab experiments and field conditions. Considering the importance of plastron for SHPo drag reduction and the utilities of SHPo reduction in real applications, in this section we review the plastron stability (longevity) first before covering the recent success of achieving appreciable drag reductions in turbulent flows on open seawater in a natural environment.

4.1 Assessment of plastron stability

After a SHPo surface is immersed under water, air is trapped on its roughness to form a plastron so that the surface is in a dewetted (Cassie–Baxter) state. The loss of plastron, or transition from a dewetted (Cassie–Baxter) to wetted (Wenzel) state, on the SHPo surface starts with the air–water interface deflecting into the roughness (Patankar 2010; Papadopoulos et al. 2013; Xu et al. 2014; Piao and Park 2015; Kim and Park 2019). The concave deflection occurs as the hydrostatic pressure of water is countered by the capillary force of the air–water interface pinned on the asperity (roughness) top. If the local contact angle of water on sidewall of roughness exceeds the advancing contact angle, the interface is depinned (freed) from the asperity top and slides into the roughness, starting the wetting transition. If the roughness is organized as shown in Fig. 1b as an example, a critical hydrostatic pressure, under which a full plastron (i.e., the air–water interface pinned on the asperity tops) can be retained as shown with ${h}_{0}$, is predictable from the given texture geometry. If the hydrostatic pressure is higher than the critical value, the surface will go through the unstable states (${h}_{1}$ and with ${h}_{2}$) relatively fast to become fully wetted (${h}_{\mathrm{wet}}$). On the other hand, if the roughness is random as shown in Fig. 1c as an example, there would be no specific critical hydrostatic pressure. Instead, the plastron would become gradually thinner under increasing hydrostatic pressure, and its dynamics can be predicted only in average or statistically. Note the intermediate states (${h}_{a,1}$ and ${h}_{a,2}$) tend to be stable; as the hydrostatic pressure increases, the interface slides deeper into the roughness, increasing the capillary force to balance the increased hydrostatic pressure. Under a static condition, i.e., without any bulk flow, it was investigated how long the SHPo surfaces could retain the plastron (Bobji et al. 2009; Poetes et al. 2010; Emami et al. 2013; Xu et al. 2014) or how the plastron would respond to increasing hydrostatic pressure (Lei et al. 2010; Samaha et al. 2012a; Lv et al. 2014) (Fig. 7). Optical techniques have mostly been used to monitor the wetting transition, measuring the difference in the reflected light intensities or diffraction patterns depending on the media (solid or gas). When assessing the plastron longevity, the diffusion rate of the trapped air into the bulk water (Henry’s law) is important, which is closely related to the condition of bulk flow and roughness geometry. For example, the plastron longevity associated with the diffusion is proportional to the roughness height, but inversely proportional to the spacing between roughness asperities (Emami et al. 2013; Hemeda and Tafreshi 2014). On the other hand, Poetes et al. (2010) showed that the mass transfer rate by the diffusion was exponentially proportional to the immersion depth, i.e., hydrostatic pressure. From the theoretical formulation on the plastron longevity against the diffusion for groove geometry, Emami et al. (2013) showed that a shallower cavity (smaller k) would keep the full plastron better against the hydrostatic pressure than a deeper cavity (larger k) because a smaller air volume is compressed more than a larger air volume under the same pressure. However, once depinning occurs, the shallow cavity would be fully wetted faster than the deeper cavity. Xu et al. (2014) experimentally validated the critical hydrostatic pressure against the depinning by performing long-term experiments under a near-ideal condition with no environmental fluctuation. Below the critical pressure (or in water shallower than the critical immersion depth), the plastron was proven to last indefinitely (tested up to 50 days). The inevitability of plastron loss by diffusion on SHPo surfaces except in a small range of conditions (as proven by Xu et al. 2014) motivated the exploration of LIS for drag reduction.

Fig. 7

Longevity of plastron. a Images of air pockets over time on a random roughness under water. Bright spot indicates the existence of air pockets (Bobji et al. 2009). b The air–water interface in a groove (147 μm wide, 85 μm deep, and 1 mm long) viewed from side over time (left) and the lowest point of the curved interface measured over time in the microgroove placed shallower (red) and deeper (black) than the critical immersion depth (right) (Xu et al. 2014). All figures are reproduced from the cited references

When there is a bulk liquid flow over the SHPo surface, the shear (velocity gradient) stress on the interface would further promote the wetting. Using LIS with an oil lubricator, Wexler et al. (2015a) investigated the mechanism of oil drainage dynamics in longitudinal grooves and determined the shear stress would limit the oil length to a certain maximum value; any excess oil would be drained out by the shear stress. They suggested dividing a groove into multiple shorter ones to prevent the oil loss and experimentally demonstrated in a subsequent study (Wexler et al. 2015b). Liu et al. (2016) suggested that the lubricating liquid with a lower viscosity would be more resistant to the shear-induced drainage, which would favor the SHPo surface (i.e., with an air lubricator) over LIS. A shear-induced drainage of air was indeed found during the drag reduction experiments with longitudinal-groove SHPo surfaces in high-speed (i.e., large shear stress) towing tank (Xu et al. 2021). Samaha et al. (2012b) visually quantified the longevity of air pockets on a polystyrene fibrous-coated SHPo surface by shooting a waterjet on it to mimic a bulk flow. They found that the population of the air pockets decreased promptly when the flow rate increased. At high Reynolds numbers, not only the shear stress but also the pressure fluctuation by turbulence promotes the wetting. It is worth noting that low-viscosity lubricators (e.g., air), which tend to diffuse fast (Probstein 1994), would suffer from the diffusion-based loss (e.g., SHPo surfaces losing the plastron), while high-viscosity lubricator (e.g., oil) would suffer from the shear-based loss (e.g., LIS surfaces losing the infused oil). Conversely, the SHPo surfaces are relatively robust but not completely immune to the shear-based plastron loss, and the LISs are considerably stable but not completely free from the diffusion-based loss. For example, if your application involves significantly undersaturated water, avoid SHPo surfaces; if it involves high speed flows, avoid LISs.

By modeling the air diffusion process of a plastron as a nonlinear oscillator system, Piao & Park (2015) theoretically investigated the effect of fluctuating water pressure (i.e., unsteady pressure difference across the air–water interface) on the longevity of plastron formed on a micrometer-scale groove. The plastron became more susceptible to the pressure fluctuation to cause the depinning as the groove width and the fluctuation amplitude increased, while higher fluctuating frequency (below the mechanical resonance frequency) mitigated the negative effect slightly by enhancing the viscous damping effect. It was suggested that the interplay between the air compression by fluctuating water pressure and the water impalement by gas diffusion should determine the response of plastron to the unsteady environment.

In addition, several studies tried to measure (visualize) the temporal variation of the air–water interface shape on individual cavities (Fig. 8), using a direct optical imaging (Xu et al. 2014; Ling et al. 2017), confocal laser scanning microscopy (CLSM) (Lv et al. 2014; Xiang et al. 2016), and reflection interference contrast microscopy (RICM) (Kim and Park 2019). The CLSM technique has a high spatial resolution but low temporal resolution, whereas a direct optical imaging can provide a higher temporal resolution with a lower spatial resolution. Since the RICM method captures the image of the whole region of interest simultaneously, it is possible to visualize the three-dimensional dynamics. Based on the measured interface profiles, in general, two variables are used to quantify the gas diffusion characteristics from plastron: the invasion coefficient and diffusion length. The invasion coefficient indicates the volumetric rate of dissolution in terms of a partial pressure difference (Emami et al. 2013; Hemeda and Tafreshi 2014; Piao and Park 2015), and the diffusion length represents the thickness of a concentration boundary layer (Lv et al. 2014; Xu et al. 2014; Ling et al. 2017; Kim and Park 2019). As for the SHPo surfaces under a flowing condition, a few studies measured the diffusion length (diffusion occurs faster when the diffusion length is smaller). By normalizing the characteristic length of a system ($\xi$) with the diffusion length ($l$) in defining the Sherwood number as ${\mathrm{Sh}}_{\xi }=\xi /l$ (a higher Sh indicates a faster diffusion), Xiang et al. (2016) proposed ${\mathrm{Sh}}_{H} \sim { \mathrm{Re}}_{H}^{1/3}$ for the SHPo surface with a hole roughness morphology in laminar channel flows of $2<{\mathrm{Re}}_{H}<17$, where channel height (H) is the characteristic length. Ling et al. (2017), on the other hand, proposed ${\mathrm{Sh}}_{{\delta }_{m}}={\delta }_{m}/l \sim { \mathrm{Re}}_{\tau }^{0.913}$ for the SHPo surface with TG (w ~ 100 μm) in transitional and turbulent boundary layer flows ($500<{\mathrm{Re}}_{{\delta }_{m}}<2300$), where ${\delta }_{m}$ is a momentum thickness, i.e., the inner scale of a boundary layer. They suggested that the diffusion of trapped air should be accelerated as the Reynolds number of the bulk flow increases. The accelerated diffusion of the trapped air with increased Reynolds number can be another reason that increased the drag ratio with the increased Reynolds number reported in some experimental studies of SHPo drag reduction in turbulent flows. The recent study of Kim & Park (2019) tried to decompose the stages of wetting process in detail, and established the relation between the diffusion length and interface shape, based on the measurements of temporally varying three-dimensional meniscus on longitudinal and transverse grooves, as well as posts, in turbulent channel flows. They used Sherwood number ${\mathrm{Sh}}_{{l}_{o}}={l}_{o}/l$, where the diffusion length measured in a static condition of the channel (${l}_{o}$) (i.e., measured separately in stagnant water) was chosen as the characteristic length, so that the effect of turbulent flow might be clearly captured. When the interface was pinned to the roughness edges, with meniscus changing from convex to concave curvature, the Sherwood number scaled as ${\mathrm{Sh}}_{{l}_{o}} \sim {(2d/w)}^{1/3}\bullet {e}^{-\mathrm{cos}\theta }$, where d and w are the half channel height and the roughness width (same scale as s), respectively, and $\theta$ is the contact angle between the interface and sidewall of the roughness. Once the depinning started (i.e., $\theta$ reaches a critical value), the diffusion was accelerated to ${\mathrm{Sh}}_{{l}_{o}} \sim {\mathrm{Pe}}^{3/4}$, where the Peclet number is defined as the ratio of characteristic shear rate (U/w) to the diffusion rate, $\mathrm{Pe}=(U/w){(2d)}^{2}/{D}_{G}$, where U is the bulk velocity of channel flow and D_G is the diffusion coefficient of air. Both suggest that the diffusion should be faster when the roughness width (w) is greater, agreeing with the theoretical predictions (Xu et al. 2014).

Fig. 8

Evolution of the air–water interface on or in a cavity. a Sequential sagging interface on a transverse groove (100 μm wide) in a turbulent channel flow (Ling et al. 2017). b Meniscus shape on a hole (50 μm diameter) at 5 (or 15) min after immersion under a different pressure, measured with a CLSM method (Lv et al. 2014). c Temporal variation of three-dimensional interface on longitudinal groove and hole in a turbulent channel flow, measured with a RICM method (Kim and Park 2019). All figures are reproduced from each reference noted

4.2 The first success of drag reduction in turbulent flows on open water of natural environment

A few studies applied a SHPo surface onto a miniature ship model and tested in an open water (Fukuda et al. 2000; Jiang et al. 2011; Dong et al. 2013; Zhang et al. 2015c; Wang et al. 2018). However, the miniature ship models were in laminar flows or transitional flows at best, and did not provide the information necessary to assess the feasibility of SHPo surfaces for drag reduction in realistic turbulent flow conditions. Considering the lack of successful SHPo drag reduction under fully turbulent flows in realistic (field) condition despite the many successful results using lab facilities, the recent successful demonstration of drag reduction (~ 30%) with a SHPo surface attached underneath a 4-m-long passenger motorboat cruising on the sea water (Xu et al. 2020b), as shown in Fig. 9, is quite encouraging. A SHPo surface (40 × 70 mm²) was installed underneath the boat close to the stern so that the surface experiences the local flow at high Reynolds number. The test was performed at 5–10 knots (2.6–5.1 m/s), which placed the sample surface at ${\mathrm{Re}}_{\tau }=3600-5800$ (which loosely corresponded to ${\mathrm{Re}}_{x}=4.5-6.5\times {10}^{6}$). For the roughness morphology of a SHPo surface, they tested longitudinal grooves (pitch P of 50, 100, and 200 μm, with 90% GF) as well as a random roughness, which is essentially the same as those used in Aljallis et al. (2013), Zhang et al. (2015b), and Hokmabad and Ghaemi (2016), for a comparison. To enhance the plastron stability, the top edges of the grooves were made to be re-entrant by developing a new but simple microfabrication process. The re-entrant edges increased (nearly doubled) the capillary force of the air–water interfaces against the pressure forces from the water, increasing (also nearly doubling) the critical immersion depth and extending the plastron lifetime if wetting is to occur (Emami et al. 2013; Xu et al. 2014). The drag ratio on the SHPo surface was measured against a smooth (no-slip) surface placed right next to it on a custom-developed shear comparator (Xu et al. 2020a) shown in Fig. 9b. The shear comparator was designed to directly and simultaneously compare the shear forces acting on two different surfaces experiencing the same flow. The sensor consists of two floating elements (surfaces) in a side-by-side arrangement, which displace only along the streamwise direction in proportion to the shear stress on them. The displacements of the two surface samples are measured simultaneously through an optical interference encoder. The floating elements are suspended by flexure beams machined monolithically from a marine-grade aluminum plate, and their mechanical resonance is designed to not affect the measurement. The uncertainty analysis showed less than 10% deviation in measurement, and the accuracy and scalability of this sensor were validated in different flow setups, including water and wind tunnels. Designed on the concept of comparative skin-friction measurement, which was demonstrated by developing a small silicon-based micro-electro-mechanical (MEMS) device (Park et al. 2014; Sun et al. 2015), this metal shear comparator was successfully used for high-speed towing-tank experiments as well (Xu et al. 2021) and may be ordered through University of California, Los Angeles (UCLA). The plastron on the SHPo surface was also monitored (visualized) with a custom-built underwater camera system, as shown in Fig. 9d. The motorboat was retrofitted to accommodate the required instrumentations, as shown in Fig. 9a.

Fig. 9

Drag reduction study with a longitudinally grooved SHPo surface attached underneath a passenger motorboat (Xu et al. 2020b). a Picture and schematic cross-section view of a boat retrofitted for the field test. b Top view (left) and cross-sectional view (right) of direct shear comparator (Xu et al. 2020a), not drawn to scale. c Temporal variation of the shear forces on smooth and SHPo (P = 100 μm and 90% GF) surfaces. d Representative images of SHPo surfaces during boat tests. The groove SHPo surface (P = 50 μm and 90% GF, or P50-GF90) maintained a full plastron at high speed (3.1 m/s). However, the one with random roughness surface (Random) showed a significant loss of air, as indicated by the numerous dark specks in the inset at high speed (3.9 m/s)

The results of the study (Xu et al. 2020b) are included in Table 1 and Fig. 3, together with all the data from the laboratory experiments in the literature. The SHPo surface with longitudinal grooves produced a consistent drag reduction as well as a trend that the drag ratio decreases with increase in Reynolds number, agreeing with the results of the well-controlled laboratory experiments and numerical simulations. Among the tested groove surfaces, the cases with 100 μm pitch provided the most stable drag reduction of approximately 30% across the tested Reynolds number range. The surface with 50 μm pitch maintained plastron well but provided smaller drag reductions (understandably, considering a smaller slip length on a smaller pitch). On the other hand, although the surface with 200 μm pitch produced a larger drag reduction (40%) when plastron was retained, the plastron was compromised on the surface in most runs. As shown in Fig. 9c, the drag reduction on the SHPo surface was clearly observed during the stage of cruising. However, with the random-textured roughness, the drag increased in the high-Re regime, resembling the trend reported using similar surfaces in a towing tank by Aljallis et al. (2013). Agreeing with Aljallis et al. (2013), the drag increase was attributed to the loss of plastron, as visualized with the underwater camera in Fig. 9d, which showed the thick plastron formed at the stationary condition would disappear as the boat speed increases. In contrast, on the SHPo surface with longitudinal grooves of the reentrant edge, the plastron was clearly observed to be stably maintained on the surface even at the high speeds. The field demonstration also confirmed the general trend drawn from the collection of laboratory experiments.

5 Further issues for practical applications

Although the successful demonstration in a field condition (Xu et al. 2020b) is encouraging, there are still numerous challenges to overcome for practical applications. The first main challenge is the effects of environmental factors on the viability of plastron. For natural environment, in addition to the negative effect of surfactant mentioned in Sect. 2.1, contamination of the air–water interface by micro-organisms in the water is also a concern. Although SHPo surfaces demonstrated the efficacy for anti-biofouling (Hizal et al. 2017; Luan et al. 2018), the micro-organisms such as bacteria or biosurfactants produced by the marine micro-organisms can populate over time on the air–water interface (Zhang et al. 2013), immobilizing the meniscus to reduce the slip effect and accelerate the wetting transition. Hokmabad & Ghaemi (2017) experimentally investigated the effect of solid contaminants in the flow and found that the collisions of the particles to the air–water interface reduced the plastron lifetime by approximately 50%. For seawater, Ochanda et al. (2012) studied the change in the plastron longevity on a SHPo surface with fibrous coatings while varying the salinity in the water, showing that the wetting transition is accelerated in salt solution compared with deionized water. They pointed out two contradictory influences of salinity. The increase in salt concentration is beneficial for plastron stability by reducing the rate of air dissolution into water but detrimental by lowering the air–water surface tension due to the Na⁺ and Cl⁻ ions accumulating at the interface. While the slower air dissolution would increase the lifetime of the plastron, the lowered surface tension would mitigate the hydrophobicity of the SHPo surface. It was suggested that detrimental effect of the lowered surface tension is larger than the beneficial effect of the slowed air loss. The second main challenge is the viability of plastron in high speed flows. The large shear (velocity gradient) at the wall can drain the plastron out of the surface roughness (Aljallis et al. 2013; Xu et al. 2021) if one considers the shear-induced drainage of oil for LIS (Wexler et al. 2015a; Liu et al. 2016). The fluctuating (unsteady) pressure (velocity) field in the water compromises the plastron stability as well (Piao and Park 2015; Seo et al. 2015).

Many passive and active methods have been explored to elongate the lifetime of plastron and sustain the drag reduction; see Lee et al. (2016) for a review. A promising passive strategy, as also addressed earlier, is to adopt hierarchical SHPo surfaces. Lee and Kim (2009) showed that the roughness width (w) acceptable under a given hydrostatic pressure can be increased by adding nanoscale roughness on the sidewall of microscale roughness. Carlborg and van der Wijngaart (2011) devised a sub-channel under the SHPo surface so that the air pockets could automatically be compressed by a water flow in the sub-channel. To augment or replace the passive mechanisms, active or on-demand mechanisms have been devised to replenish gas when it is lost. Carlborg et al. (2008) connected the SHPo surface to the external tank outside the microchannel. The de-wetted surface survived the water pressure up to 60 kPa. To supply the pressurized air from the bottom, Ling et al. (2016) installed a porous backing plate under their SHPo surface during the flow test. Lee and Kim (2011) have developed a semi-active mechanism that can replenish the lost plastron autonomously. A self-triggered and self-limiting gas generation mechanism was imbedded monolithically in the SHPo surface. If water intrudes the microstructures by plastron loss at any location and time, a gas is generated automatically by electrolysis; after the generated gas restores the plastron, the electrolysis stops automatically to shut off the power consumption. Recently, Xu et al. (2020c) have improved this self-regulated method to make it self-powered as well, eliminating the need for any external power. Other active methods include vapor generation by Leidenfrost effect (Vakarelski et al. 2012, 2014; Saranadhi et al. 2016), catalyst-mediated gas generation (Panchanathan et al. 2018), and air injection onto a surface resembling Salvinia leaf (Xiang et al. 2020). While some of the passive and active methods proved to be helpful to extend the plastron lifetime in a well-defined laboratory environment, their effectiveness in real environments with limited controllability remains to be studied or demonstrated.

As a different approach to compensate for the degradation of a SHPo surface, hybrid methods of introducing gas (bubbles) into the bulk flow have been also explored. Bullee et al. (2020) combined the bubbly flow and a random-roughness SHPo surface in a turbulent Taylor–Couette flow to investigate their complementary interaction for drag reduction. While the drag increased by about 14% on a smooth surface in a bubbly flow by the extension of the log layer in the velocity profile (roughness effect), the drag decreased by up to 5% on a SHPo surface in the same bubbly flow, overcoming the roughness effect. Although it was claimed that the gas bubbles introduced into the flow would enhance the sustainability and amount of plastron and hence reduce the drag on the random-roughness SHPo surface (Fukuda et al. 2000; Du et al. 2017), the exact mechanism of interaction was not found, although one can speculate the bubbles in the flow replenish the air pockets. Jeong and Park (2015) experimentally showed that rising air bubbles attach and slide on a SHPo vertical wall without merging with the plastron unless the thin water layer present between the surface and bubble (${d}_{l}$) becomes thinner than O(1) μm. Following the theoretical relation of ${d}_{l}\sim {({\mu }_{l}{\rho }_{l}{v}_{l}{v}_{g})}^{0.5}{d}_{g}^{2}{\sigma }^{-1}{\Delta t}^{-0.5}$ for the critical thickness in their study (${\mu }_{l}$: viscosity of water, ${\rho }_{l}$: density of water, ${v}_{l}$: velocity of water, ${v}_{g}$: velocity of bubble, ${d}_{g}$: bubble diameter, $\sigma$: surface tension of water, and $\Delta t$: time duration at which the bubble resides on the surface), the product of ${v}_{l}{v}_{g}/\Delta t$ should be smaller than O(1) for the bubble of ${d}_{g} \sim {\varvec{O}}(100)$ μm, for example, to have a chance to merge into the air layer on the SHPo surface. Numerous bubbles were seen to pass by the SHPo surface during the boat test by Xu et al. (2020b). Because the water flowed past the entire boat length in just a few seconds (< 1 s at the highest speed tested), only micrometer-scale bubbles had a possibility to merge and replenish the plastron.

Even after the most promising design (condition) of the surface texture for SHPo drag reduction is found (currently, it is thought to be longitudinal grooves with reentrant top edge), another practical issue is how to produce the SHPo surface over a large area of desired shapes and curvatures at high rate and low cost. While there have been many approaches, most methods employed to fabricate the scalable SHPo surface were limited to random-roughness morphology (Xue et al. 2010). However, there are on-going efforts that show a potential for mass production of large-area SHPo surfaces with organized-roughness morphology, including roll-to-roll imprinting (Ahn and Guo 2009; Dong et al. 2018) and hot embossing (Li et al. 2018; Wang et al. 2020; Xu et al. 2020c). In particular, Xu et al. (2020c) have developed a one-step hot-embossing process to fabricate the self-powered SHPo surfaces out of a Teflon FEP film, which can restore the depleted plastron autonomously in a self-limiting and self-powered fashion. Lastly, while it is rather conclusive that SHPo surfaces with a proper plastron would reduce the friction drag, their effect on other aspects of performance needs to be studied for each application. For example, it is unclear how the slippery surfaces covered with a plastron would affect the overall hydrodynamics and maneuverability of an entire vessel, such as speedboat. Would SHPo surfaces enhance or undermine them; if the latter, would the net effective positive enough? How about hydrofoils and propellers? While these issues can be investigated theoretically and numerically any time, fabrication of a large SHPo surface with the roughness proven to function (i.e., maintain a proper plastron) in field conditions should precede before serious flow experiments are launched.

6 Summary and outlooks

Although hydrodynamic drag reduction using SHPo surface has attained a great attention for its potential for economic and environmental benefits of global scale, its field demonstration has not materialized until very recently. Because one of the reasons for the painfully tortuous progress was the seemingly contradicting experimental results in the literature, in this review we have provided a comprehensive analysis of the data collected from the experimental studies performed for the skin-friction drag reduction on SHPo surfaces in turbulent flows. While many different surface morphologies and fabrication methods have been developed for SHPo surfaces during the past two decades, there has not been much effort to understand and develop flow experiments adequate or ideal for SHPo drag reduction, which demands certain requirements not considered in traditional flow-test facilities. Considering a plastron is essential to sustain SHPo drag reduction, one can now see many of the early experiments did not pay enough attention to the state of plastron during the flow tests. The collected data of all experimental studies in turbulent flows indicated a general but clear trend that SHPo surfaces with an organized roughness of longitudinal grooves led to a successful drag reduction with more consistency and a larger reduction than those with random roughness. The reported mechanisms of turbulent drag reduction on SHPo surfaces have also been summarized to reveal the trends how the frictional Reynolds number and the roughness scale in wall unit affect the SHPo drag reduction. While SHPo surfaces with longitudinal grooves revealed a tendency of enhanced drag reduction with increase in frictional Reynolds number in a decent range up to ${\mathrm{Re}}_{\tau }\simeq 6000$, corroborating most numerical studies, those with other roughness morphologies showed a somewhat opposite trend of deteriorating drag reduction or even drag increase as the Reynolds number increases. The random-roughness morphology is understood to suffer from the negative effect of spanwise slip being identical to streamwise slip and, probably more importantly, the inability to maintain a full plastron compounded by the non-uniform asperities impaling the water.

Despite the recent success in turbulent flows in open water including the realistic condition of a cruising motorboat on seawater of natural environment, there are still numerous scientific, technical, and economic challenges to overcome before expecting, for example, water vessels covered with SHPo surfaces. In the meantime, we expect that the more consistent results reported in recent year, along with the successful demonstration in field condition, would remove the lingering doubts and spur more studies and development efforts to extend the applicability of the SHPo surface for hydrodynamic drag reduction. In addition to the skin-friction drag, SHPo surfaces are expected to find utilities for thermal and flow control. Although we focused on drag reduction here, the lessons and insights collected in this review can be readily applied to other fluids-related purposes as well including mixing enhancement and heat transfer control, not to mention the widely cited applications, such as self-cleaning, anti-fogging, anti-icing, anti-biofouling, and anti-corrosion.