Experimental characterization of mixing and flow field in the liquid plugs of gas–liquid flow in a helically coiled reactor

Abstract

Flow mixing of two miscible liquids with the addition of gas bubbles is a process often found in industrial chemical apparatus for the production of primary matter. The ongoing optimization of such processes also involves the transformation of batch to continuous mode operation. In that case, the use of helically coiled tubes is an interesting alternative, since those reactors have narrow residence time distributions, very good radial mixing properties and excellent mass transfer can be realized between gases and liquids. For these reasons, in this study the mixing of two miscible liquids with addition of air bubbles in gas–liquid flows has been characterized in a horizontal helically coiled reactor in the laminar flow regime at ${\text{Re}}_{{{\text{total}}}} = 300 \ldots 1088$. Eight different superficial liquid velocities and five superficial gas velocities were investigated. In order to characterize mixing in the liquid plugs between two bubbles, laser-induced fluorescence of resorufin was used and particle image velocimetry has been employed to characterize the flow field. Pseudo-3D-visualizations of the resorufin concentration and the Q-criterion, representing the mixing efficiency and vorticity, respectively, were established for individual liquid plugs from the time-resolved measurement results. A time-resolved mixing coefficient, as well as a mean mixing coefficient obtained from multiple liquid plugs, is calculated from the fluorescence images for all examined flow conditions. The experimental results clearly show an increase in the mixing coefficient compared to single-phase conditions, caused by the bubbles. However, distinct mixing pattern, depending on the flow structure, can be recognized on different locations inside the liquid plug. Compared to a stationary case without air bubbles, mixing is worse behind the bubbles and increases inside the plug, reaching a maximum mixing coefficient in front of the next bubble. Overall the mixing coefficient is always increased by the presence of the bubbles. Pseudo-3D-visualizations of the Q-criterion and the vorticity show the presence of secondary vortices right in front of the bubbles, shifted to the outer tube walls, and in addition to the steady Dean vortices. In small plugs, these secondary vortices appear in the whole plug and increase the mixing coefficient drastically.

Graphical Abstract

1 Introduction

Helical reactors with different shapes and sizes (Kockmann 2020) have been a subject of interest since a rather long time, due to their practical use in industry for static mixing or heat and mass transfer. The focus of most studies in the literature relies on single-phase mixing of two liquids, the flow field and pressure drop, heat transfer and investigating the influence of Reynolds, Dean, and Schmidt numbers as well as the curvature ratio on these processes, e.g. (Jiang et al. 2004; Kaufhold et al. 2012; Kumar et al. 2006; Mansour et al. 2017; Vashisth and Nigam 2008). However, mixing of two liquids in a gas–liquid multiphase flow is a common procedure in many industrial processes and has, unfortunately, gained not much attention in the literature concerning coiled tubes up to now. Jokiel et al. (2017) presented such a study for use in the hydroformulation of long-chain olefins. In this process, synthesis gas (CO and H₂) is added in the presence of a catalyst to the alkene bond of long-chain olefins. Kaiser et al. (2017) proposed a semi-batch reaction network for this reaction including a continuously working helically coiled tubular reactor. This was the motivation of for further studies concerning this subject (e.g. Jokiel et al. 2019; Mansour et al. 2020b) and also for this present experimental investigation.

The definition of flow regimes in coiled tubes bases on those of straight ones, but different phenomena occur due to the centrifugal forces acting on both bubbles and liquid. Literature draws a sharp line between bubbly flow and annular flows, but everything in between, e.g. plug and slug flows, is kept quite vague, including the fact that bubbles can occupy the whole cross section of the tubes or not. K.A. Triplett (Triplett et al. 1998) already mentioned this inconsistency in relevant data for flow pattern and their transition boundaries in 1998. First flow regime maps for gas–liquid pipe flows were established from, e.g. Hoogendoorn (1957) and Mandhane et al. (1973). Gas–liquid flows have also been investigated in straight tubes concerning bubble characteristics and flow regimes, in vertical (Furukawa and Fukano 2000) and horizontal tubes (Coleman and Gerimella 1999; Fernandes et al. 2018; Krieger et al. 2020; Zhang et al. 2020). A good database of flow maps is gathered by Awad (2012) in which he includes a variety of different flow regime maps for vertical and horizontal pipe flows. The definitions for the flow regimes differ slightly between the authors, and even modern definitions for flow regimes (Kraume 2020) offer a wide scope for interpretation. As stated later in this paper, the distinction between a sharp separation of liquid plugs by gas bubbles and gas bubbles with by-pass flow, thus a connection of the liquid plugs, is crucial, because the mixing behaviour and the flow field inside the liquid plugs change, but very difficult to establish. For horizontal helical gas–liquid reactors, to the authors’ knowledge, no extensive and precise data are available in the literature for flow field characteristics and two-phase regimes at the current state of time. Bubble creation and flow regimes for Taylor bubbles in micro-channels are shown by Cubaud and Mason (2008), but are not necessarily applicable to the flows studied here. The effect of dry bubbles, which are cylindrical bubbles with poor wall wetting, shown by Kurt et al. (2017) and Krieger et al. (2020) was not found in this study. Zhu et al. (2017) identified flow regimes for gas–liquid flows in vertical coiled tubes. One of the only flow field sketches for horizontal helical reactors on a micro-scale is shown by Kurt et al. (2017).

The study of gas–liquid flows in curved and coiled pipes has often concentrated on the measurement of residence times, and mass transfer coefficients or enhancement factors, e.g. (Kaufhold et al. 2012; Kováts et al. 2018). In addition, often vertical, but not horizontal, helical reactors have been examined, e.g. (Che et al. 2020; Colombo et al. 2015; Li et al. 2017; Liu et al. 2015; Mandal and Das 2003; Mansour et al. 2020b; Mei et al. 2020; Murai et al. 2006; Zhu et al. 2017, 2019), since accumulation of bubbles in the upper part of the coils is avoided like that. Also micro-channels with Taylor bubble experiments, e.g. (Fries and Rohr 2009; Yang et al. 2017; Zaloha et al. 2012), have been examined. The investigation of the mass transfer between the gas and liquid phase in such Taylor bubble experiments in helical reactors has shown recirculation streams inside a liquid plug occurring as triangular structures (Gaddem et al. 2021; Krieger et al. 2019) which are visible in the vertical cut along the flow direction.

Gas–liquid flows in derived coiled structures as the coiled flow inverter have been studied, for example, by (Kurt et al. 2017; Vashisth and Nigam 2009). The influence of the flow structure and regime of the two-phase flow has only been examined for micro-channels in (Zaloha et al. 2012), for a vertical helical reactor via micro-PIV in (Murai et al. 2006) and recently by visualization and X-ray tomography in (Breitenmoser et al. 2021). Numerically they have been investigated in (Falconi et al. 2016; Krieger et al. 2020; Mansour et al. 2020a). The micro-PIV in planar horizontal curved pipes performed by Zaloha et al. (2012) showed vortical structures close to the bubbles and triangular vortex structures inside the plug. Horizontally coiled reactors are only rarely used for such gas–liquid flow studies (Jokiel et al. 2017; Zheng et al. 2020), and only planar results for the gas–liquid flow field can be found in the literature to the authors’ knowledge.

The focus of this work is therefore given on the bubbles' influence on flow field and accompanying mixing behaviour in horizontal gas–liquid helical flows in the laminar flow regime, where coiled reactors are mostly used. The time-resolved mixing behaviour of two miscible liquids inside the liquid plugs is characterized experimentally by the use of planar laser-induced fluorescence (PLIF), and in addition, the flow field and vortex occurrence are measured by time-resolved particle image velocimetry (TR-PIV). The resulting images and vector maps are processed to unwound pseudo-3D visualizations of the liquid plugs, showing the time-resolved phenomena caused by the bubbles over the plug's length.

2 Experimental setup

2.1 Helix geometry

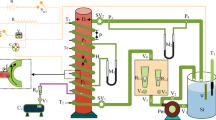
The horizontal helix reactor (Fig. 1, left) was made of FEP tube (fluorinated ethylene propylene) with an inner diameter of $d_{i} = 4\;{\text{mm}}$, a wall thickness of $s = 1\;{\text{mm}}$, a coil pitch of $p = 6$ mm and a coil diameter of $D = 42\;{\text{mm}}$ resulting from the core diameter of $d_{c} = 36\;{\text{mm}}$. The coil curvature ratio results in $\delta = d/D = 0.111$. The manufacturing process of the helix reactor was established before by Kováts et al. 2020. The FEP tube had been wound around a PVC kernel and placed into a transparent acrylic glass box (Fig. 1, right) for refractive index matching (see later). The flow through the helix comes from bottom to top, to prevent the accumulation of gas bubbles in upstream tubing and the reactor itself during the start-up process.

Fig. 1

Experimental setup: drawing of the helix (left); sketch of plexiglass tank with helical reactor (right)

2.2 Refractive index matching

In order to minimize optical distortions, especially on the curved surfaces of the tube walls, the helical reactor is placed in a rectangular tank (Fig. 1, right), filled with a liquid with the same refractive index as the FEP-tubes. The refractive index of the FEP-tubes has been studied in previous experiments (Kováts et al. 2020) and corresponds to n = 1.3405. Therefore, a mixture of glycerol and de-ionized water with a glycerol concentration of 5.25 vol% was used and controlled with a refractometer (Abbemat 200 from Anton Paar, accuracy ± 0.000100 nD).

For the mixing measurements (PLIF), the working fluid was not matched, due to chemical incompatibilities with the tracer-PLIF method. For the PIV measurements, the working fluid consisted of the same glycerol-water solution as mentioned above (see also next section).

2.3 Choice of flow conditions

In order to investigate the mixing of two aqueous liquids in a gas–liquid flow by optical measurement techniques, the flow conditions have to be chosen appropriately. Agglomeration and coalescence of air bubbles in the upper part of the horizontal coil have to be avoided. Therefore, a certain liquid flow velocity is necessary to carry the bubbles through the whole reactor. On the other hand, high Reynolds numbers lead to high mixing rates of the two miscible liquid phases, preventing from a clear analysis of the mixing process itself. The inner diameter of the reactor coil has therefore to be kept small, in order to keep the Reynolds number under 1000. Due to those limitations, this study considered total Reynolds numbers from $300 < {\text{Re}}_{{{\text{total}}}} < 1088$. Under those conditions, it was possible to investigate experimentally the influence of the bubbles on the flow field, as well as their influence on the mixing behaviour of the two miscible liquids in the liquid plugs of the reactor.

The mixing of two liquids in the gas–liquid flow has been investigated for eight different superficial liquid velocities between 0.075 and 0.251 m/s and five different superficial gas velocities between 0 and 0.0221 m/s, resulting in 40 different cases (Table 1). Their total Reynolds numbers, which is the Reynolds number of the gas and liquid phases of the two-phase flow considering incompressible gas behaviour, range from 300 to 1088. The Dean number lies between 94 and 340; thus, Dean vortices can be expected for all configurations and the regimes are situated in the region of the second mixing optimum according to Mansour et al. 2019. First, the liquid volume flow rate was regulated, and then, the gas volume flow rate was set to the distinct values, in order to create different bubble sizes and bubble frequencies. The gas content thus varied between $\varepsilon$ = 0 and $\varepsilon$ = 0.227. The parameters of all 40 investigated settings are summarized in Table 1.

Table 1 Flow parameter

Mixing is investigated in this study by PLIF using two different fluids. One is de-ionized water, and the other is de-ionized water containing the fluorescing dye resorufin (10 mg/l ± 0.1 mg/l, CAS: 34994–50-8, Sigma-Aldrich). Both liquids are set to the same flow rate (± 0.5 ml), which corresponds to half of the total liquid flow rates given in Table 1.

Thus, ideal mixing is characterized by a solution with half the dye concentration of the initial one. The influence of the dye on the physical properties of the solution can be neglected, as has been shown by previous measurements (Kováts et al. 2020).

The PIV measurements, executed separately with a refractive index matching solution of 5.25% glycerol and de-ionized water as working fluid, use fluorescent rhodamine B-doped PMMA tracer particles (mean diameter 10 µm) for the acquisition of the flow field. The glycerol water mixture used for a better distinction of the PIV-tracer particles, also changes slightly the physical properties such as the dynamic viscosity (Table 2). Therefore, the Reynolds number of the PIV experiments is slightly smaller than that of the PLIF measurements and corresponds to total Reynolds numbers between 277 and 1005. All measurements were carried out in a temperature-controlled room at 20 °C; thus, the temperature of the liquids from the storage tanks equals the room temperature T.

Table 2 Physical properties of the working fluids known from the previous measurements (Kováts et al. 2020)

2.4 Experimental apparatus and measurement systems

Figure 2 shows the main components of the experimental setup as two-dimensional flow chart. Two 110-L tanks filled with the working fluids (1a and 1b for mixing via PLIF, 2 for PIV) are situated about 3 m above the reactor with its refractive index matching box (9) in order to provide a pulsation-free inlet flow driven just by gravity. The liquid flow rate (see Table 1) is set manually with a needle valve (5) and controlled by an ultra-sonic flow meter (3). The air (see Table 1) is introduced by a control valve (Bronkhorst) (6) into the pure water side. For the mixing study, the water flow with bubbles on one side and the resorufin-water solution on the other are joined in an Y-piece (8) and enter the helix reactor from the bottom. The Y-inlet is oriented in such a way that the separation of the two liquids is orthogonal to the coil axis, which corresponds to the worst mixing case (Mansour et al. 2017). This position has been chosen to focus attention on the bubble's influence on the mixing behaviour. For the PIV measurements, only one tank has been filled with the working fluid mixture, including tracer particles (2). This tank supplied the same tubing and valve system as before, thus keeping the same pressure drop in the system before entering the helix as for the PLIF measurements. The outlet from the reactor (10) is situated on the top, to avoid air accumulation inside the helix.

Fig. 2

Experimental setup 2D-flow chart, 1a and 1b: PLIF measurements; 2: PIV measurements

Figure 3 shows the main components of the optical setup. The fluorescence of resorufin (for mixing) and rhodamine B particles (for PIV) is excited by a Nd:YAG laser at 532 nm with 10 mJ/p, formed to a light sheet of 0.5 mm thickness. The fluorescence intensities are detected at a 90° angle to the light sheet with two Imager Pro HS 4 M high-speed cameras from LaVision with a 2016 × 2016 pixel resolution, each using an AF Micro-Nikkor 60 mm-lens with a 537-nm long-pass filter for PLIF and also for PIV. A PLIF image resolution of $0.0085\;{\text{mm}}/{\text{pixel}}$ in X- and Y-direction was thus obtained. The coordinate system is fixed with the flow direction vertical to the measuring cross section, which is the X–Y-plane.

Fig. 3

Optical setup with two high-speed cameras and light sheet, top view (left), bottom view (right)

The cameras are arranged on each side of the light sheet, in order to capture the complete liquid plug in between two bubbles. This is shown in Fig. 4: as soon as a bubble enters the field of view of the first camera (top schema), the images of the second camera will be used for evaluation. Then, the bubble moves forward and a second bubble enters into the field of view of the second camera (centre schema), but the first bubble leaves the field of view of the first camera. Therefore, those images are now used for analysis. The liquid plug ends with the next incoming bubble (bottom schema).

Fig. 4

Bubble passing through the measuring cross section, blocking the camera view partially

The light sheet and field of view of the cameras are arranged to visualize the cross sections of the third turn of the helix on the top side of the coil. Previous studies of horizontal coils have shown that the Dean vortices are fully developed after the first 2 turns (Kováts et al. 2020). It has to be noted that mixing and velocity could only be measured in the liquid plugs, due to the high light distortion at the bubble surface in the film region.

First, a flow regime map was created by taking images from the top of the helix and perpendicular to the laser light-sheet. The flow regimes were identified from 1000 images over the first three coils recorded at 10 Hz by categorizing the bubbles qualitatively in shape and size.

For each set of Reynolds number and gas flow rate, 5000 images with a recording frequency of 1 kHz are taken for the PLIF measurements. For PIV measurements, 10 000 images are taken at different recording frequencies between 0.8 and 2 kHz ensuring a constant pixel shift between two consecutive images.

3 Post-processing of experimental data

The resulting images of the PLIF and PIV measurements are treated in a couple of steps with DaVis 8.4 software to obtain the concentration and velocity fields. For further calculations of the mixing coefficient and averages of the flow field, MatLab and Excel are used. The final data are then visualized in ParaView 5.6. In that way, time-resolved pseudo-3D-visualizations of the resulting mixing coefficient and flow structures inside the liquid plugs between two bubbles are obtained.

3.1 PLIF-measurements

Figure 5 shows exemplary raw PLIF images from both camera frames (front and back) of a single liquid plug, which are then treated further as explained below.

Fig. 5

Raw PLIF images with both camera frames of a single liquid plug for case 9 $\left( {u_{s,\;l} = 0.075\frac{m}{s};\; u_{s,\;g} = 0.0022\frac{m}{s}} \right)$

3.1.1 Mixing coefficient

First, a sheet and background correction of the raw images is done on a pixel-to-pixel basis with the pixel fluorescence intensity $I$ according to the following equation:

$$\overline{I} = \frac{{I - I_{0} }}{{I_{\max } - I_{0} }}$$

(1)

where $I_{0}$ represents the background intensity at the same position, obtained from the average of 200 images of the flow without resorufin. Laser sheet inhomogeneities are corrected with the sheet images, taken with the maximum resorufin fluorescence intensity $I_{\max }$ at maximum resorufin concentration. This leads to a normalized intensity $\overline{I}$ in the range of 0 and 1 for each pixel. The thus obtained normalized fluorescence intensity values have been calibrated with known resorufin concentrations. Figure 6 shows such a calibration curve, where the linearity between the fluorescence intensity and the concentration of resorufin in a range of $c_{{{\text{res}}}} < 10\frac{{{\text{mg}}}}{{\text{l}}}$ (Kováts et al. 2020) with a correlation coefficient of $k = 0.9986$ is obvious.

Fig. 6

Normalized fluorescence intensity in function of resorufin concentration for concentration calibration; black: average data points; grey: normal standard deviation

Since the normalized intensity $\overline{I}$ behaves linear with respect to the concentration, the mass fraction of resorufin corresponds directly to that. A value of $\overline{I} = 1$ corresponds to the maximum concentration, and $\overline{I} = 0$ indicates that no fluorescent tracer is present, whereas $\overline{I} = 0.5$ means ideal mixing of the two solutions, since their flow rates are equal.

From these images, after application of a geometric mask to exclude all values from and outside the tube walls, the mixing coefficient $M_{C}$ is calculated in MatLab using the following equation:

$$M_{C} = 1 - \frac{{\sum \left| {I - I_{{{\text{AVG}}}} } \right| \cdot A_{{{\text{Pixel}}}} }}{{I_{{{\text{AVG}}}} \cdot \sum A_{{{\text{Pixel}}}} }}$$

(2)

with $I$ the intensity of a single pixel, $I_{{{\text{AVG}}}}$ the average intensity of all pixels in the cross section and $A_{{{\text{Pixel}}}}$ the pixel size. Thus, a mixing coefficient of 1 means ideal mixing, and at a mixing coefficient of 0, no mixing at all has taken place. The mean mixing coefficient for one flow condition was then calculated from the average of 5000 images containing between 3 and 30 liquid plugs, depending on the plug length.

3.1.2 Pseudo-3D-visualization of mixing

The pseudo-3D-visualization is an extension of two-dimensional time-resolved images into a third dimension defined by a pseudo-distance, which is the ratio of the mean flow velocity vertical to the image plane and the recording frequency. The following equation describes the pseudo-distance between the images that is accorded as $\Delta$ Z-value to each single image: $\Delta Z = u_{{{\text{total}}}} / f_{{{\text{rec}}}} \left[ {{\text{mm}}} \right]$ and lies in the range $\Delta Z = 0.075 \ldots 0.273\;{\text{mm}}$. With the image number $i$ follows $Z = \Delta Z \cdot i \left[ {{\text{mm}}} \right]$ for the Z-coordinate. The resulting pseudo-resolution in Z-direction lies in the range $13.33 \ldots 3.66\;{\text{planes}}/{\text{mm}}$. Such representations have been produced from the individual cross-sectional intensity and velocity fields and will be used for presentation of the results in the following sections. Here a general explanation of these figures is given.

Image series corresponding to the representation of single liquid plugs have been extracted and processed in ParaView 5.6. Images from the front and back camera have been used for that in a way that the air bubbles are not appearing in the field of view (see description of Fig. 4). Thus, the complete liquid plug becomes visible, as represented exemplarily in Fig. 7 for the horizontal centre plane of a plug (${\text{case}} 9;\;u_{s,\;l} = 0.075\frac{m}{s};\;u_{s,\;g} = 0.0022\frac{m}{s}$). In this, and all following figures, the plug is represented in an unrolled manner, which means that the axial coordinate of the coil is represented as a straight line. The two successive bubbles are represented as grey regions on either side of the figure. The first images of the liquid cross section after a bubble passage in the field of view of the cameras are taken with camera 2, and their results are represented on the right side of Fig. 7; thus, the time is running from the right to the left. At a certain time (red dashed line in Fig. 7), the next bubble is arriving in the field of view of camera 2, but not yet in that of camera 1 that is situated on the other side of the light sheet. Therefore, the images of camera 1 can now be used to complete the image of the liquid plug, until the second bubble arrives in its field of view.

Fig. 7

Horizontal cut of pseudo-3D-visualization of the normalized intensity (corresponding to mass fraction) for case 9 $\left( {u_{{s,\;l}} = 0.075\frac{m}{s};\;u_{{s,\;g}} = 0.0022\frac{m}{s}} \right)$. The red line corresponds to the moment when images of the second camera are used for visualization of the plug. Flow direction is from left to right, acquisition time of the individual cross-sectional images was running from right to left

In Fig. 8, the same reconstructed liquid plug is presented in several cuts of the 3D intensity and thus mass fraction volume. Seven example cross-sectional images are shown in A, and their position in the plug is visualized with red frames. Bubble positions are visualized in grey. It is obvious from these cross-sectional images that the mixing structure changes inside a liquid plug, due to the influence of the bubbles. From this view, a vertical cut, forming the Y–Z-plane (Fig. 8B), and a horizontal cut (Fig. 8C), forming the X–Z-plane, are extracted through the centre of the tube with + Z as flow direction. The outer side of the reactor coil is at the top, and the inner side of the coil at the bottom of the images.

Fig. 8

Pseudo-3D visualization of normalized fluorescence intensity within a liquid plug (bubbles in grey) for case 9 $\left( {u_{s,l} = 0.075 m/s; u_{s,g} = 0.0022 m/s} \right)$ with cross sections (A), vertical cut (B), horizontal cut (C)

3.2 PIV measurements

Figure 9 shows exemplary raw PIV images from both camera frames (front and back) of a single liquid plug, which are then treated further as explained below.

Fig. 9

Raw PIV images with both camera frames of a single liquid plug for case 33 $\left( {u_{s,\;l} = 0.075\frac{m}{s};\; u_{s,\;g} = 0.0221\frac{m}{s}} \right)$

3.2.1 Velocity fields

In all time-resolved PIV measurements, a pixel shift of 2–3 pixels between two consecutive images was ensured. A geometric mask, in the form of the tube walls, was used to remove disturbances outside the measuring area, as, for example, reflections on the tube walls. The vector calculation is then done with a multi-pass cross-correlation with decreasing interrogation area size. They contain at least 5–7 particles and have a size of 64 × 64 pixels with 50% overlap for the first 2 passes, and 32 × 32 pixels with 50% overlap for the next 4 passes. Vector post-processing includes a median filter with allowed vector length and an iterative replacement of excluded vectors. These are interpolated from their neighbours, and an optimal smoothing is applied. Thus, a time-resolved series of velocity fields with a physical time of 5 to 12.5 s, depending on the recording frequency, is obtained. The two-dimensional PIV results have a resolution of $7.97\;{\text{vectors}}/{\text{mm}}$ in X- and Y-direction. As for the PLIF case, the images of camera 1 or 2 are treated further, in a way to obtain a complete as possible flow field in the whole liquid plugs, avoiding regions where bubbles pass in the field of view of the respective camera. Figure 10 shows exemplary final Z-vorticity fields from the raw PIV images from Fig. 9. Clearly visible are the dominant Dean vortices in the centre of the liquid plug.

Fig. 10

Vector fields with Z-vorticity from both camera frames of a single liquid plug for case 33 $\left( {u_{s,\;l} = 0.075\frac{m}{s};\; u_{s,\;g} = 0.0221\frac{m}{s}} \right)$

3.2.2 Pseudo-3D visualization of velocities, vorticity and Q-criterion

The thus obtained time-resolved series of 2D-velocities in the X–Y-cross sections have been transformed to a pseudo-3D representation of the X–Y-velocity components in the liquid slugs. As for the mixing fields, the pseudo-distance between consecutive vector fields is calculated as Z-coordinate:$Z = \Delta Z \cdot i = u_{{{\text{total}}}} / f_{{{\text{rec}}}} \cdot i \left[ {{\text{mm}}} \right]$. The pseudo-distance lies in the range $\Delta Z = 0.094 \ldots 0.136\;{\text{mm}}$. The resulting pseudo-resolution in Z-direction lies in the range $10.64 \ldots 7.35 planes/mm$. Vector image series for single liquid plugs are treated in the same way as for the PLIF results, thus forming a pseudo-3D view of the x–y velocity components. Please note that no axial z-component of the velocity has been measured here. For each data point, containing the x-velocity and y-velocity, the vorticity in Z-direction is calculated using the following equation:

$$\vec{\omega } = \nabla \times \vec{u} = \left( {\frac{{\partial u_{y} }}{\partial x} - \frac{{\partial u_{x} }}{\partial y}} \right)\overrightarrow {{e_{z} }}$$

(3)

Further, the Q-criterion is calculated based on definitions from Jeong and Hussain (1995) and Haller (2005).

Due to increased measurement uncertainty that is caused by reflections of tracer particles stuck to the tube walls, only the inner flow field up to 0.26 mm from the wall is treated in that way. For the following visualizations, the Q-criterion is shown in a range from 0.00035 to 0.05 as isosurface, with the vorticity in Z-direction from − 0.125 to 0.125 mapped on its surface to illustrate the rotational direction of the vortices. Figure 11 shows this exemplarily for case 33 ($u_{s,\;l} = 0.075\frac{m}{s}$; $u_{s,\;g} = 0.0221\frac{m}{s}$) resulting in a total Reynolds number of ${\text{Re}}_{{{\text{total}}}} = 388$. On this figure, a counter-rotating vortex pair, the Dean vortices, can be distinguished behind the previously passed bubble (back right grey cylinder), and nearly up to the following bubble (front left grey cylinder). Just in front of this arriving bubble, a differently formed vortex pair appears. The dominant Dean vortices are centred in the tube; the vortices in front of the bubbles, however, are shifted to the upper half. The changes in the flow structure inside the plug and due to the influence of the bubbles can be observed on the six cross-sectional images of the stream-lines, being represented by red frames (Fig. 11A). A horizontal projection of this 3D-representation is shown in B (Fig. 11), and a vertical projection from the top is shown in C (Fig. 11). Due to the strong and dominant Dean vortices, a top-down view as in Fig. 11C will mainly be used in the following.

Fig. 11

Pseudo-3D visualization of Q-criterion and Z-vorticity within a liquid plug (bubbles in grey) for case 33 ($u_{s,\;l} = 0.075\;{\text{m}}/{\text{s}}$; $u_{s,\;g} = 0.0221\;{\text{m}}/{\text{s}}$) with streamlines of cross sections (A), vertical projection (B), horizontal projection (C). Flow direction is from left to right, acquisition time of the individual cross-sectional images was running from right to left

4 Experimental results and discussion

4.1 Bubble characteristics

The bubble size, observed in the two-phase flow, can be divided into two cases: (1) the bubble filling the whole tube diameter as shown in Fig. 12 (filled data points, left of the red line), and (2) the bubbles are smaller than the inner tube diameter (unfilled data points, right of the red line). In the latter case, it has to be observed that the bubbles are not separating the liquid plugs sharply. For both cases, exemplary images are shown with a red frame in Fig. 12. Between those two regions, the bubble shape becomes egg-like (light blue framed region and image), which also causes an indistinct plug separation. The dark blue area represents a flow regime, in which the air content is so high and the overall flow rate so low that bubbles accumulate in the upper part of the helix reactor and an unsteady flow with very short liquid plugs occurs (dark blue). However, annular flow conditions were not detected. The purple region at higher superficial liquid velocity represents wavy bubbles (see purple framed image), where waves on the back side of the bubbles are visible. With rising superficial liquid velocities, passing the orange line from left to right, the centrifugal forces on the liquid phase surpass the buoyancy force of the gas bubbles, which leads to gas bubbles flowing on the inner side of the helix tubes, when the bubbles are smaller than the cross section (see orange framed image). In overlapping areas, bubble size and shape are more random, and the corresponding cases described before occur simultaneously. With low gas and high liquid contents, the bubbles become very small and form spherical bubbles floating in the centre of the cross section (green framed image and region). At the highest gas and liquid velocities (yellow framed region and images), the bubbles are arbitrarily shaped and only flow at the bottom of the cross section, which is the inner side of the helix coil. These bubbles become non-axisymmetric due to the centrifugal forces acting in the curved channel. The effect of bubbles, not filling the whole cross section, on mixing will be discussed later.

Fig. 12

Flow regime map for gas liquid flow in a helical reactor with $d_{i} = 4\;{\text{mm}}$ (see 2.1 for total geometry). On images in top-down view (dark blue, purple, top yellow, green, light blue, and without frame) flow direction is from bottom to top of the image, on images in front view (red, bottom yellow, orange), the flow comes towards the observer

It must be noted that all regime boundaries shown are not hard boundaries but transition areas. The image without a coloured frame in the bottom left of Fig. 12 represents all data points outside the coloured areas with fully developed bubbles, filling the cross section without any other characteristics, which was favourable for PLIF and PIV measurements. The black dashed area contains all measurement points at which PLIF and PIV measurements were taken (Table 1). This area covers a much smaller parameter space than the bubble aspect evaluation just presented before.

4.2 Mixing pattern and mixing coefficient

The experimental results, obtained for mixing, are shown in Figs. 13, 14, 15, 16, 17 and 18. The results are presented as cross-sectional images and as unwound pseudo-3D-graphics showing the time-resolved field of mass fraction in the cross section on top of the third coil. Since the inlet is located at the bottom of the tank, the measuring area, crossed by the laser light sheet, is located at 810° from the inlet. The flow direction goes always from left to right; thus, the right bubble, represented in the figures as grey area, is the first one, and the left bubble is the second one, closing the plug. In the following results, the vertical and horizontal cuts of the pseudo-3D-graphics are depicted, as presented before.

Fig. 13

Normalized intensity (≙ mass fraction w_res) in single-phase liquid–liquid mixing: cross section, vertical pseudo-3D cut, horizontal pseudo-3D cut

Fig. 14

Mass fraction w_res of resorufin for single-phase and gas liquid flow, in front of bubbles, in the centre of the liquid plug and behind bubbles

Fig. 15

Mass fraction w_res in a liquid plug between two bubbles: vertical cuts, dimensionless plug length

Fig. 16

Mass fraction w_res in a liquid plug between two bubbles: horizontal cuts, dimensionless plug length

Fig. 17

Mass fraction w_res in a liquid plug in front of a bubble: vertical cut, first 14 mm of plug

Fig. 18

Mass fraction w_res in a liquid plug in front of a bubble: horizontal cut, first 14 mm of plug

For comparison, Fig. 13 shows the single-phase mixing results with the same liquid Reynolds numbers as for the gas–liquid-liquid flow. For the single-phase case, the vertical and horizontal cuts (third and fourth column in Fig. 13) just show stratified mass fraction distributions that are due to the steady Dean vortices (second column in Fig. 13). Once these are established (after 2–3 turns), the liquids are trapped in the vortex pair and mixing is not further promoted. The red zones indicate the full mass fraction of the tracer dye resorufin and so a rather bad mixing. In green regions, a better overall mixing is achieved.

Figure 14 compares the single-phase cases cross sections with cross sections of the gas–liquid experiments 0.5 mm in front of the bubbles, in the centre of the liquid plug, and 0.5 mm behind the bubbles for the lowest and highest gas content. Due to the high mixing rates especially at high gas contents, the mass fraction of resorufin is visualized only in the range of 0.2 < w_res < 0.8 in order to create a better contrast in all subsequent figures. At low gas velocities (third column in Fig. 14) and thus higher plug lengths, the structure of mass fraction in the centre of the plugs is similar to the single-phase cases (second column in Fig. 14). Behind the bubble, the two liquid phases are almost completely separated, at a low liquid velocity (Fig. 14a). In front of the bubble, the Dean vortices are shifted downwards and an additional vortex pair appears in the top half of the cross section. However, with rising liquid velocity (Fig. 14c and e), the bubbles become smaller as shown in Fig. 12 and a stronger liquid by-pass flow takes place. Behind the bubbles diffuse mixing pattern occur. In front of the bubbles, the Dean vortices are shifted downwards as before, but no additional vortices are visible. The turquoise colour around the smaller bubbles indicates a good mixing.

At high gas velocities (fourth column in Fig. 14), the higher bubble frequency leads to smaller liquid plugs and the whole liquid plugs are very well mixed. The Dean vortices are the best visible at the highest liquid velocity (Fig. 14f). In front of the bubbles, the aforementioned secondary vortices occur in the upper half of the cross section at all liquid velocities, but with inverted direction of rotation at higher liquid velocities (Fig. 14f).

A phenomenon that is visible in the single-phase cases (Fig. 13) as well as in the gas–liquid phase (Fig. 14) is a swap of the high resorufin concentration core from right to left in the cross section of the third helix coil, around the liquid velocity of $u_{s,l} = 0.176\;{\text{m}}/{\text{s}}$ corresponding to a Reynolds number of ${\text{Re}}_{{{\text{SP}}}} = 700$. The resorufin core (red) is located on the right side of the cross section at lower liquid velocities, which is the inlet configuration, but it gets swapped to the left side at high liquid velocities.

Figures 15 and 16 show, respectively, the vertical and horizontal cuts of plugs with the lowest, centre and highest Reynolds number, combined with the lowest and highest gas velocity. The spatial location is normalized with the length of the respective plug. The secondary vortices intensify close to the left bubble and are visible in the vertical cuts as triangular structures (marked with pink dashed lines) in the upper half of the liquid plug. At low gas contents and thus longer liquid plugs, those structures only take up a small part of the entire plug (second column Fig. 15), which is ca. 10–20% of the total plug length. At high gas contents this triangular structure takes up to 90% of the liquid plug (Fig. 15b). The grey triangle in Fig. 15b and all similar following cases represent a bubble that has not left the camera view before the camera switch, due to very short plugs, as described in Fig. 4. Therefore, the camera switch was set at a point where the leaving bubble is at the same height as the next incoming bubble, which creates a triangular region, which cannot be evaluated and which corresponds to the two bubble parts seen by the respective cameras.

In the same range as the triangular structures in the vertical cut (Fig. 15, pink dashed lines), symmetrical vortex structures can be found in the horizontal cuts as well (pink dashed lines in Fig. 16). The horizontal parallel lines in the horizontal cuts represent the Dean vortices, as also shown in Fig. 13 for the single-phase case, which dominate a great portion of the liquid plugs.

The overall mixing at low liquid and gas velocities is comparatively bad, indicated by the large red and white areas in the horizontal cuts, especially behind the right bubble (Fig. 16a and f). At lower gas contents, diffuse mixing can be seen, corresponding to the smaller bubble cases as described before (Figs. 15c and e, and 16c and e, black dashed lines).

In the following, the focus will be given on the secondary vortices in front of the bubbles. Therefore, the first 14 mm of the liquid plugs in front of the bubbles is zoomed and shown, this time in a finite manner, in Figs. 17 and 18. Despite different total plug lengths and degrees of mixing, the triangular structure of the concentration profiles is similar at constant liquid velocities, which indicates a constant length of additional vortex structures in front of the bubbles, independently on the plug length. With rising liquid velocities, the structures inside the marked triangle become more complex, but stay in the same area. Figures 17e and 18 e are representative for small bubbles, whereby the occurring structures differ clearly from the others, with the deformation of the vortex structure in the horizontal and vertical cut.

The calculated mixing coefficient in function of time is represented in Fig. 19 for the smallest, centre and highest liquid surface velocities, respectively, and for no gas and the lowest and highest gas velocities. The interruptions of the curves (with gas) correspond to the passage of a bubble, when no mixing coefficient of the liquid phase can be determined. For all liquid surface velocities, it can be stated that the presence of the bubbles strongly increases the mixing coefficient. The higher the gas flow rate, the higher the mixing coefficient. Further, it can be recognized that the mixing coefficient just behind a bubble (left side of each curve segment) is much smaller than in front of the next bubble (right side of each curve segment), since the mixing coefficient increases between two bubbles. This behaviour might be due to the additional vortices observed in the mixing pattern (figures above). At high gas volume flow rates, almost perfect mixing up to $M_{c} = 0.95$ is achieved already at the measurement position, that is, the third turn of the helix, and especially for the cases with low liquid velocities and correspondingly small plug length ($u_{s,\;g} = 0.0221\;{\text{m}}/{\text{s}}$ in Fig. 19a and b). In the cases B and C (Fig. 19), with low gas velocity ($u_{s,\;g} = 0.0022\frac{{\text{m}}}{{\text{s}}}$) and bubbles smaller than the tube diameter, the mixing coefficient shows a slightly different behaviour. In these cases, the minimum mixing coefficients exist in the centre of the plug, the maxima before and behind the bubbles, resulting in a zigzag aspect of the curves.

Fig. 19

Mixing coefficient for different superficial liquid velocities, respectively, for the smallest and highest superficial gas velocity and for the single-phase case in function of time

Both, nearly unmixed zones behind the bubbles, and strong mixing due to secondary vortices in front of the bubbles, which was found in the cuts in Figs. 15 and 16, are clearly visible in the development of the mixing coefficient. The bubbles have an obvious impact on mixing compared to the single-phase case without air bubbles. The mean overall mixing coefficient in the third turn, averaged over 5000 cross-sectional images, corresponding to a physical time of 5 s and containing between 2 and 30 liquid plugs (depending on the plug length), is shown in Fig. 20 for all experimental parameters. The liquid superficial velocity has little influence on the mixing result, whereas the main increase in mixing coefficient is related to the gas superficial velocity. The single-phase case has a well-known (Mansour et al. 2019, 2020c) maximum at ${\text{Re}}_{{{\text{total}}}} = 700$, which corresponds to a superficial liquid velocity of $u_{s,\;l} = 0.1756\;{\text{m}}/{\text{s}}$, with a mixing coefficient of $M_{c} = 0.68$. The highest mixing coefficients of $M_{c} > 0.9$ in the two-phase experiments were reached with maximum gas velocity ($u_{s,\;g} = 0.0221\;{\text{m}}/{\text{s}}$) and liquid velocities of $0.075\;{\text{m}}/{\text{s}} < u_{s,\;l} < 0.176\;{\text{m}}/{\text{s}}$, corresponding to total Reynolds numbers of $388 < {\text{Re}}_{{{\text{total}}}} < 788$ (light blue region in Fig. 20).

Fig. 20

Mean mixing coefficient in function of the superficial liquid and superficial gas velocities

4.3 Flow fields and vortex structures

The following paragraph deals with the results of the PIV measurements, which were carried out with a 5.25% glycerol-water mixture as working fluid. This results in slightly lower Reynolds numbers at the same liquid velocities as in the PLIF measurements.

Figure 21 shows the streamlines for the lowest, centre and highest measured liquid velocities and lowest and highest gas velocities, compared to the single-phase flow fields. In the centre of the liquid plugs (centre images in third and fourth column of Fig. 21), the streamlines of the two-phase flow look very similar to those of the single-phase case, showing the characteristic Dean vortices. But, in the two-phase flows, depending on the location inside the liquid plugs, the flow field varies strongly. In front of the bubbles, at low liquid velocities (0.5 mm, left images in third and fourth column, first row of Fig. 21), a shifted double vortex structure is visible. This structure changes with rising liquid velocity, where the vortex cores become smaller and move away from each other, and falling gas content, where they get the form of deformed Dean vortices. For all cases, it can be stated that the streamlines straighten up vertically compared to the diagonal streamlines in the single-phase cases. Behind the bubbles (right images in third and fourth column of Fig. 21), no clear vortex cores are visible, but diverging and converging flow spots can be recognized on these 2D streamlines that show the strong 3D nature of the flow. Thus, the liquid flow behind the bubbles seems rather unstructured. These two-dimensional results show the strong dependency of the liquid flow field on the location inside the liquid plug.

Fig. 21

Streamline results of PIV measurements for single-phase and gas liquid flow, in front of bubbles, in the centre of the liquid plug and behind bubbles

To get a clearer impression of the flow structures inside the liquid plugs, the aforementioned 2D velocity results of the cross section on top of the third turn have been post-processed, as explained in Sect. 3.2. Thus, the vortical structures inside the plug can be visualized by the Q-criterion from the time-resolved measurements as unrolled pseudo-3D representations. These are presented in Figs. 22, 23, 24 and 25 as horizontal and vertical projections. Isosurfaces with Q = 0.00035–0.05 are shown, coloured with the z-vorticity in axial direction, and the bubbles location represented in grey. The flow direction goes in positive Z-direction from left to right.

Fig. 22

Top view of flow structures in plugs normalized with their length for the highest (left) and lowest (right) gas content; isosurface Q-criterion coloured by z-vorticity; bubbles in grey

Fig. 23

Top view (zoom on first 14 mm in front of a bubble) of 6 different liquid plugs for $u_{s,\;l} = 0.0753 \frac{m}{s},\; u_{s,\;g} = 0.0022 \frac{m}{s},$ Re_total = 285, Q-criterion (isosurface), vorticity (coloured surface), bubbles (grey)

Fig. 24

Top view of mean flow structure in front of a bubble, isosurface Q-criterion coloured by z-vorticity $u_{s,\;l} = 0.151\;{\text{m}}/{\text{s}}$; $u_{s,\;g} = 0.0221\;{\text{m}}/{\text{s}}$; ${\text{Re}} = 636$

Fig. 25

Top view of mean flow structures 12 mm in front of a bubble for the lowest, centre and highest liquid velocities and lowest and highest gas velocities; isosurface Q-criterion coloured by z-vorticity

Figure 22 shows such representations of exemplary liquid plugs, normalized with their plug length, for two extreme cases with highest and lowest gas content. In all cases, the flow field is dominated by the well-known Dean vortices, which are developing very near behind the bubbles, after the unstructured flow field mentioned above and reach through the whole plug. Additional vortices can be observed in front of the bubbles (left bubble in Fig. 22a) as long as the bubbles fill the whole tube cross section (see Fig. 12, left of red line). They are located in the upper half of the tube (only visible in the side view) and will be discussed in detail with the following figure. At lower gas contents, additional vortices occur behind the bubbles (right bubble in Fig. 22b). Those vortices give the impression to slip through the by-pass flow around the bubble and depend strongly on bubble shape and location. Unfortunately, it is not possible to measure directly in the by-pass flow with the described set-up, but vortices in a by-pass flow have also been described by Fernandes (Fernandes et al. 2018) for gas–liquid flows in straight horizontal pipes.

Figure 23 shows a zoom on the structure of six different, arbitrarily chosen plugs, for the same experimental parameters at $u_{s,\;l} = 0.0753\frac{m}{s}$ and $u_{s,\;g} = 0.0022\frac{m}{s}$ (Re_total = 285), for the first 14 mm in front of the bubble. These plugs have very different total plug lengths between 161.8 mm and 37.3 mm, but the vortex structure and length in front of the bubbles are strictly the same. The Dean vortices stop about 0.5 mm in front of the bubble, and an additional vortex pair, turning in the same direction as the Dean vortices, develops at a length of about 2.5 mm. This behaviour has been found also for the other measuring parameter combinations. However, in cases with low gas content, and thus small bubbles, no vortices exist in front of the bubbles, as shown in Fig. 22b.

Therefore, in the following figures, mean representations are shown for parameter comparisons that were calculated from 7 different plugs, which were at least available for all measurements, by cutting the plugs at $z = 12\;{\text{mm}}$, which is a length being available even in short liquid plugs, and averaging the velocity vectors, followed by the post-processing as described in 3.2.2.

In order to define the following terminology, the described vortices are named as shown in Fig. 24, which shows a special case containing all appearing vortex structures at once and will be discussed later. The dominant Dean vortices lie near the wall in the vertical centre of the tube. Secondary vortices are rotating in the same direction as the Dean vortices, but are clearly separated from them, while seeming attached to the following bubble and are shifted to the upper half of the tube (only visible in a side view). Tertiary vortices are counter-rotating to the previous ones, lie in the upper half of the tube and are centred to the Dean vortices. They can reach significantly deep into the liquid plug.

Figure 25 shows a co-rotating secondary vortex pair extending from 0 mm to maximum 3 mm (Fig. 25 a and b), attached in front of the bubbles and located in the centre of the upper tube half. At low gas velocities and increasing liquid velocity (Fig. 25c and e), no such secondary vortices are detected, which might be caused by the smaller bubble size. For higher gas velocities (Fig. 25d and f), at the same time long tertiary counter-rotating vortices, detached from the bubbles, appear in the centre of the tube, while the secondary vortices become smaller. The tertiary vortices reach, with increasing liquid velocity, up to 7 mm into the liquid plug.

In the special case of $u_{s,\;l} = 0.151\;{\text{m}}/{\text{s}}$; $u_{s,\;g} = 0.0221\;{\text{m}}/{\text{s}}$; ${\text{Re}} = 636$ (Fig. 24), both secondary and tertiary vortices can be recognized, while the secondary vortices are smaller compared to cases with lower liquid velocities. This leads to the assumption that the tertiary vortices supersede the secondary vortices at higher liquid velocity (here $u_{s,\;l} = 0.176\;{\text{m}}/{\text{s}}$). Such a shift in the vortex rotation direction has also been noticed in the PLIF results (left images, fourth column of Fig. 14).

The secondary vortices, mentioned above, could also be observed during the PIV measurements through particles that got stuck and agglomerated on the bubbles' surface (Fig. 26). These raw images show vortex structures on the bubble surface that are shifted to the upper wall of the tube and do not correspond to the characteristic Dean vortices. They only appear if the bubbles fill the whole tube cross section.

Fig. 26

Particles stuck on the bubble surface and visualizing the secondary vortex structures, $\Delta t = 4\;{\text{ms}}$, $u_{s,\;l} = 0.164\frac{m}{s}$, $u_{s,\;g} = 0.0022\frac{m}{s}$. The bubble is approaching the camera from left to right

4.4 Relationship between mixing and flow fields

The comparison of Fig. 25 and the mixing fields in Figs. 17 and 18 suggests that the vortex strength in the liquid plug and especially the additional vortices, appearing at higher superficial gas velocity, have a strong influence on the mixing result in the plug. Therefore, Figs. 27 and 28 show an overlay of the results from the mixing measurements and the PIV measurements and cuts in the measuring cross section at given distances from the bubbles. The mass fraction and the Q-criterion in the range Q = 0.0001…0.05, representing the vorticity in z-direction, are represented in these figures. It is important to remind that these are not simultaneous measurements and also the Reynolds number is slightly different between the mass fraction and velocity measurements.

Fig. 27

Overlay of mass fraction w_res and velocity measurements, represented by the z-vorticity on Q-criterion in the range Q = 0.0001…0.05 $\left( {u_{s,\;g} = 0.0022\frac{m}{s}} \right)$; from Fig. 17, 18 and 25

Fig. 28

Overlay of mass fraction w_res and velocity measurements, represented by the z-vorticity on Q-criterion in the range Q = 0.0001…0.05 $\left( {u_{s,\;g} = 0.0221\frac{m}{s}} \right)$; from Fig. 17, 18 and 25

Figure 27 shows the cases with the lowest gas superficial velocities. Even though mixing and flow field have been measured separately, the vortex structure shows a good agreement with the mass fraction field. Directly in front of the bubble, the Dean vortices get shifted by the secondary vortices to the top centre of the cross section, leading to a butterfly-like concentration field (first row Fig. 27). With increasing distance from the bubble, the secondary vortex pair moves downwards and finally at about 3.5 mm merges with the Dean vortices that are established in the centre of the tube. The mixing field follows this evolution, and a centred symmetric pattern appears. The low gas content at higher liquid velocities leads to smaller bubbles, which did not create secondary vortices in front of the bubbles (second and third row Fig. 27). Secondary vortices are neither visible in the concentration field, nor in the vortex structure of the flow field. Only 0.5 mm in front of the bubble a small shift of the Dean vortices downwards is visible (second row second column in Fig. 27). At the lowest gas content, the bubble shows no significant impact neither on the concentration field, nor on the flow field and vortex structure (third row in Fig. 27).

A higher gas velocity (Fig. 28) reduces the plug length and leads to better mixing, but the overall mixing pattern and flow field stay the same when comparing the second rows in Figs. 27 and 28. With rising liquid velocity (second and third row Fig. 28), the additional counter-rotating tertiary vortices, already presented in Fig. 25, appear in the top centre of the cross sections. This leads to visible additional vortices in the concentration field as well. They can be recognized in Fig. 28, as well as in Fig. 14 before, for the conditions in the second and third row and are fully developed at 2 mm in front of the bubble (white and red crosshatched areas representing the vorticity in the cross section). After some millimetres, these vortices disappear once more at about 8 mm for the two cases shown.

5 Conclusions

In this study, the effects of bubbles on the flow field and mixing in a gas–liquid–liquid flow in a helical reactor have been investigated experimentally for Reynolds numbers in the laminar flow regime and different gas contents. The flow fields have been measured by high-speed particle image velocimetry, and mixing has been characterized by high-speed planar laser-induced fluorescence. The time-resolved measurements allowed for the reconstruction of the pseudo-3D flow field and mixing pattern inside the liquid plugs.

The results showed the direct link between the appearance of well-defined vortex structures and the mixing efficiency. Especially in parameter combinations where small bubbles (d_b < d_i) occur, no additional vortices are produced in front of the bubbles, the main body of the plug is dominated by the Dean vortices, and the measured mixing coefficients are low, but always higher than the single-phase cases. Occasionally small vortices appear behind bubbles, which leads to the assumption that the vortices are situated underneath the small bubbles, not filling the hole tube diameter. This behaviour has already been investigated by Fernandes (Fernandes et al. 2018) for two-phase flows in straight horizontal pipes, in which bubbles float in the upper half of the tube (d_b < d_i).

In the case with full-sized bubbles (d_b = d_i), secondary vortices appear in front of the bubbles, which evolve to tertiary structures when increasing the Reynolds number, starting around ${\text{Re}}_{{{\text{total}}}} = 650$. These lead to high mixing coefficients, although the bubbles are followed by an unmixed portion of the initial solutions. Compared to the Dean vortices, the secondary vortices are shifted to the upper side of the helix tube wall. With higher Reynolds number, the secondary structures are reduced, but further tertiary vortices reach deeper into the liquid plug, rotating in the opposite direction and also enhancing mixing.

A high mixing coefficient can be achieved at the lowest liquid velocity of $u_{s,\;l} = 0.075\;{\text{m}}/{\text{s}}$ and the highest gas velocity of $u_{s,\;g} = 0.0221\;{\text{m}}/{\text{s}}$, corresponding to a total Reynolds number of ${\text{Re}}_{{{\text{total}}}} = 388$ and the highest measured gas content of $\varepsilon = 0.277$. In this case, the plug length is so small that the vortices in front of the bubbles dominate the plugs mixing behaviour. A similar effect happens at a liquid velocity of $u_{s,\;l} = 0.176\;{\text{m}}/{\text{s}}$ and $u_{s,\;g} = 0.0221\;{\text{m}}/{\text{s}}$ (${\text{Re}}_{{{\text{total}}}} = 788$), at which the tertiary vortices are fully developed and the liquid plugs are still short. With rising liquid velocity, the vortices grow less than the plug length; thus, the liquid plug gets dominated by the Dean vortices again and mixing becomes less pronounced, until the turbulent flow regime is reached.

These results show the clear relationship between the mixing result and flow structure. The creation of additional vortices is favourable for good mixing. Therefore, flow regimes with short liquid plug length and fully developed bubbles, filling the cross section of the tube, should be preferred, when strong mixing is necessary.

In the frame of this study, only one specific geometry has been examined. When changing the curvature ratio and pitch of the helix, different mixing results are to be expected. In single-phase flow, (Izadi et al. 2018; Kumar et al. 2006; Mansour et al. 2017) showed that mixing can be improved by increasing the curvature ratio or reducing the dimensionless pitch (Mansour et al. 2020a). However, at very low Reynolds number (very weak secondary flows), a higher pitch improves mixing due to the increased torsion. A more extensive numerical study (Mansour et al. 2019) considering 27 different geometries showed that the influence of tube diameter and pitch is more complex, depending on whether the Reynolds (Dean) number is in an optimal region (Re ≈ 35 or Re ≈ 650) or not. On the other hand, for practical devices it is also important to consider the increase in pressure drop with increasing curvature ratio. Thus, curvature ratio should be high enough to ensure strong secondary flows and efficient mixing, while at the same time not too high in order to reduce the curvature-induced pressure drop. For vertical two-phase flow, Saffari and Moosavi (2014) examined the influence of both parameters on friction with the same conclusions.

In the frame of this study, also a flow regime map for the horizontal helical reactor has been established (Fig. 12), showing the different bubble shapes and sizes for different superficial gas velocities ($u_{s,\;g} = 0.0022 \ldots 0.221 \frac{m}{s}$) and superficial liquid velocities ($u_{s,\;l} = 0.013 \ldots 1.254 \frac{m}{s}$). This map shows the great variety of different bubble aspects, depending on the flow rate of gas and liquid in a helical coil.