Abstract
State-of-the-art technologies for wind and tidal energy exploitation focus mostly on axial turbines. However, cross-flow hydrokinetic tidal turbines possess interesting features, such as higher area-based power density in array installations and shallow water, as well as a generally simpler design. Up to now, the highly unsteady flow conditions and cyclic blade stall have hindered deployment at large scales because of the resulting low single-turbine efficiency and fatigue failure challenges. Concepts exist which overcome these drawbacks by actively controlling the flow, at the cost of increased mechatronical complexity. Here, we propose a bioinspired approach with hyperflexible turbine blades. The rotor naturally adapts to the flow through deformation, reducing flow separation and stall in a passive manner. This results in higher efficiency and increased turbine lifetime through decreased structural loads, without compromising on the simplicity of the design.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
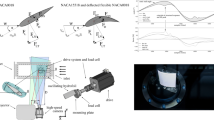
(Left) Cross-flow tidal turbine rotor. (Middle) Schematic presentation of the flow conditions in the rotor at \(\lambda =2\), expressed with velocity triangles. The vertical rotation axis leads to unsteady flow conditions featuring alternating relative velocities w and angles of attack \(\alpha\) with respect to the azimuth angle \(\theta\). (Right) Numerical simulation of a CFTT at \(\lambda =2\) (vorticity), generated with the OpenFOAM/Paraview software packages. The turbine features a complex flow field, due to the rotor dynamics. A video of the vorticity field can be accessed on the author’s website as a supplemental material. The asymmetry in the profiles displayed left and right results to their adaptation to the circumference of the turbine radius according to Maître et al. 2013.
Tidal flows represent a huge source of renewable energy, which is as of yet largely unexploited. This exploitation remains a major challenge in energy engineering, because of the conflicting requirements that must be addressed. To be competitive on the electricity market, low production costs must be achieved, which requires high efficiency and durability in order to reduce initial investment and maintenance efforts. Salt water, high levels of turbulence and underwater installation make for unfavorable construction and operation conditions. Beyond this, the fragile maritime ecosystem makes low ecological impact a necessity, requires systematic accompanying eco-engineering efforts (Bugnot et al. 2020) and a detailed investigation of the impact of the energy extraction on the flow regime (Barnier et al. 2020). For instance, dam-based installations act as a sea fauna migration border, have high ecological impact, require high initial investments and are therefore an unsatisfactory solution if one aims for a fully sustainable tidal energy exploitation. In this context, installations featuring hydrokinetic turbines are particularly attractive. However, the power density of such power plants is generally low.
Cross-flow tidal turbines (CFTTs, see Fig. 1) are now known to outperform conventional (horizontal-axis) turbines in their area-based power density (Whittlesey et al. 2010; Dabiri 2011; Brownstein et al. 2016), since positive turbine-to-turbine interaction and their rectangular plan-view area allow for denser, more efficient turbine farm installations. This is a very important advantage, since conflicting interests of nature conservation and resource exploitation have to be weighed up in order to use the few suitable areas as sensibly and efficiently as possible (Bugnot et al. 2020). CFTTs operate independently of the flow direction without requiring yaw control. Additionally, their impact on marine fauna is considered to be extremely low (Berry et al. 2019; Zhang et al. 2017; Castro-Santos and Haro 2015; Hammar et al. 2013). The hydrokinetic energy conversion leads to negligible pressure drops (the highest injury risk for fish in turbines according to Stephenson et al. 2010), and their low rotor speed and absence of guiding structures result in low probability for direct hits or crush between moving and static parts (Müller et al. 2018; Deng et al. 2007; Turnpenny et al. 2000). These ecological advantages are associated with a technological drawback—a low turbine efficiency.
2 Complex flow and rotor dynamics
2.1 Dynamic stall and turbine efficiency
CFTTs feature a complex rotor flow, dominated by dynamic stall (Laneville and Vittecoq 1986), as shown in a numerical simulation in Fig. 1 (right). Dynamic stall is characterized by alternating flow separation and reattachment on the blades, with peaking hydrodynamic loads; it is the focus of current research (Benton and Visbal 2019; Buchner et al. 2018; Miller et al. 2018). Severe structural vibrations and unsteady blade thrust lower endurance and efficiency. Numerous studies have investigated methods to overcome these effects, which doubtlessly hinder large-scale industrial applications. One approach is to continually vary the pitch angle of the blades using mechanical systems in order to control their angle of attack (Abbaszadeh et al. 2019; Liang et al. 2016; Mauri et al. 2014; Zhang et al. 2014; Lazauskas and Kirke 2012; Khalid et al. 2013). Another approach, termed angular velocity control, uses phases of rotational acceleration and deceleration in order to control the angle of attack by adjustment of the tangential velocity (Strom et al. 2016). Both methods result in higher efficiency and lower structural load peaks. The first requires complex designs, which are then prone to failure and less suitable for low-cost, low-maintenance applications. Both approaches require significant advanced control systems, with the second additionally requiring extended torque capacities of the electric drive that serves for the highly dynamic acceleration and deceleration phases.
(Left) section of a bioinspired flexible hydrofoil, displaying the solid leading edge on the left, a flexible carbon-fiber composite skeleton, surrounded by a white silicone embodiment. (Right) Hyperflexible structures adapt to the flow and can inhibit or milden dynamic stall effects. The NACA0018 shaped hydrofoils encounter significant deformation of up to 25% of the chord length. (High-speed recording image enhanced, colors inverted)
Bioinspired approaches deploying hyperflexible rotor blades have shown potential for reducing the structural loads and improving the efficiency (Descoteaux and Olivier 2021; Hoerner et al. 2019; MacPhee and Beyene 2016; Zeiner-Gundersen 2015). In the context of complex rotor flow dynamics, the additional effect of blade deformation under load and its impact on the fluid dynamics (the fluid–structure interaction, FSI) make the investigation of this phenomena particularly challenging. In this experimental study, the FSI of hyperflexible CFTT blades is visualized and fully characterized, by linking together the dynamics of hydraulic forces, blade deformation and flow field.
Through this multimethod experimental investigation, we show how hyperflexible blades effectively adapt their angle of attack dynamically and passively control the flow through deformation (see Fig. 2). Load peaks are smoothed out, and a significant reduction of the hydrodynamic structural loads is achieved simultaneously with increased turbine efficiency for specific operation points. This is obtained because flexible structures feature shorter phases of flow detachment and result in reduced wake structures. The power-producing phases are extended within the rotation period, when the stiffness of the hydrofoil is adjusted to the operational regime. At low-speed regimes, where fish compatibility is highest, we observed an efficiency increase of up 20% along with a decrease of 20% in the structural loads, as already reported in Hoerner et al. 2019, demonstrating the potential of this approach to improve the ecological and performance characteristics of future CFTT designs.
2.2 Turbine physics
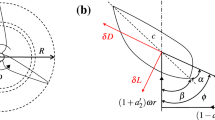
The rotor kinematics are governed by two parameters: (1) the operation point \(\lambda\) and (2) the solidity \(\sigma\). The first is given as the ratio of tangential turbine velocity \(u=\omega R\) ( \(\omega\) angular velocity, R turbine radius) to flow speed \(v_\infty\) (see Eq. (1)). The second is defined as the relation of the plan-view area of the blades to half of the turbine’s cross-section area (see Eq. (2), with n the number of blades and C the blade chord length).
The blade motion—in parts crosswise to the flow—results in an alternating angle of attack \(\alpha\) (see Eq. (3)) and an alternating relative velocity w, both functions of time and of the azimuth angle \(\Theta\) (see Fig. 1).
Because of the highly dynamic conditions, the flow remains attached at angles far exceeding the foils’ static stall angles; the maximum angle of attack \(\alpha _\text {max}\) typically reaches 30\(^\circ\).
The flow field in a real rotor is further affected by blade–blade interactions (see Fig. 1(right)) and three-dimensional effects, such as blade tip effects on the upper and lower blade ends. Hyperflexible blades further increase the system complexity, making for a difficult distinction between the influences of single parameters. For this reason, in order to generate high-resolution flow observation around the airfoil, a reduced, well-established surrogate model was deployed in the experimental campaigns presented here, where a pitching hydrofoil substitutes for a single-bladed CFTT (Ly and Chasteau 1981). It has to be mentioned that the angle of attack in the downstream part of a real rotor configuration is strongly affected by the power extraction in the upstream part. Therefore, the angles of attack are normally strongly decreased as shown by Delafin et al. 2021. However, the level of reduction depends on several factors and is unknown for the cases tested, due to the FSI mechanism with the variations of the deformable structures. In consequence, this phenomenon have been neglected. This should be kept in mind when analyzing the results.
3 Experimental approach
3.1 Model reduction
Now, the dynamic stall regime observed on the pitching hydrofoil depends on the maximum angle of incidence \(\alpha _\text {max}\) and the reduced frequency k, a measure for the ratio of the time scales of the foil motion and the flow convection (McCroskey 1981). In the light of CFTT applications, k depends on \(\lambda\) and \(\sigma\) (Laneville and Vittecoq 1986). For the surrogate model in a water channel with constant flow speed \(v_\text {ch}\), k can be expressed with respect to \(\lambda\) and the pitch frequency f (see Eqs. (7) and (8) for details):
In this way, multiple CFTT solidities and operating points can be investigated with a single oscillating foil by simply changing the pitch trajectory \(\alpha = \text {f}\;(\lambda )\), and the reduced frequency k (by varying the oscillating frequency f), since \(k=\text {f}\;(f)=\text {f}\;(\lambda ,\sigma )\).
In turn, the performance is assessed by measuring the hydrodynamic forces acting on the profile, as converted in dimensionless coefficients \(c_\text {L}\) and \(c_\text {D}\) for lift and drag (see Eqs. (10) and (11)), as well as the thrust \(c_\text {T}\) and the normal force coefficient \(c_\text {N}\):
The surrogate model does not allow for a quantitative evaluation of the power obtained on a three-dimensional turbine, especially given the large range of frequencies and operation points covered here. However, given any turbine design at one operation point, a rigorous comparison can be made between designs of different rigidities—one central aim of the study. In this case, \(c_\text {T}\) directly contributes to the power and can be used as a substitute to evaluate the turbine efficiency, while \(c_\text {N}\) characterizes structural loads, whose periodic variations lead to vibrations and causes material fatigue. Therefore, the changes in these coefficients brought by the flexible foils relative to the rigid foil (the thrust change \(c_{T}-c_{T_\text {ref}}\) and maximum load amplitude change \(c_{N_\text {max}}-c_{N_\text {max,ref}}\)) were the observed parameters used to assess performance. It is worth noting that according to Eqs. (6) and (5) when \(\alpha<\)45\(^\circ\), drag has a major influence on the blade thrust, while lift has a major influence on the structural loads. Both influences are detrimental to the turbine’s performance and endurance.
The surrogate model also allows for the installation of measurement systems around any single blade, in order to investigate the fluid–structure interaction occurring there. We deployed a light-based surface tracking (SFT) system to measure the flexible blades’ deformation in three dimensions and a 2D2C (two-dimensional, two-component) particle image velocimetry (PIV) system in order to observe the flow around the blade. The combination of the results from these two measurement campaigns, in addition to the performance improvements quantified using the force and moment measurements, provides a holistic description of the flexible-blade approach to improving CFTT performance.
3.2 Experimental setup
The experiments were performed in the closed-loop water tunnel in the LEGI labs Grenoble. Four different hydrofoils with a symmetric NACA0018 geometry (C = 66 mm) were deployed. The leading edge of the three bioinspired foils consisted of a milled aluminum piece reaching up to the first quarter of the chord, followed by a composite tail consisting of a carbon-fiber blade and a silicone embodiment (see Fig. 2). The profile stiffness was adjusted by changing the carbon-fiber blade thickness, varying from 0.3 to 0.7 mm. The fourth hydrofoil was milled entirely out of aluminum and served as the reference, corresponding to a standard rigid-blade CFTT. For each hydrofoil, the trajectory of \(\alpha = \text {f}(t)\) and the pitch frequency f were varied. A total of 64 parameter sets featuring two operating points and seven turbine solidities for four hydrofoils were investigated:
The hydrodynamic forces were captured with 1 kHz temporal resolution by means of a fully submerged six-axis load cell, placed underneath a mounting plate for the hydrofoils (see later Fig. 3). The drive system encoder returned the angle of incidence. The average flow speed of 3 and 3.5 m/s was obtained from the tunnel flow meter and led to a chord-based Reynolds number of 200,000–230,000. All signals were synchronized with the optical measurements by use of a trigger signal.
Two different measurement campaigns were designed, aiming for a full classification of the FSI. A custom high-speed, structured-light-based surface tracking technique (SFT) was deployed to measure the solid deformation. The corresponding flow field was captured with 2D2C high-speed particle image velocimetry (PIV) measurement. The masking of the highly deformable structure posed a particular challenge and was solved using classic image segmentation strategies combined with a model for the mechanical bending of the profile (Hoerner 2020). More details of the methods, data sheets and measurement uncertainty considerations are provided in Methodology section.
The two experimental setups deployed at the LEGI labs’ closed-loop water tunnel. (Left) Flow field measurements, 2D2C high-speed PIV with two lasers facing one another in order to illuminate the flow field surrounding the foil. (Middle) Deformation measurements through high-speed structured-light surface tracking. (Right) Force and torque measurements with a fully submerged six-axis load cell
4 Methodology
4.1 LEGI labs water tunnel
The LEGI labs water tunnel is a closed-loop device with a maximum discharge of 0.65 m\(^3\)/s. The turbulence intensity was found to be less than 0.5% in the core flow by means of laser Doppler anemometry measurements. The control volume is of \(1000\times350\times 280\) mm\(^3\) (\({\rm length} \times {\rm height} \times {\rm width}\)). The flow rate is determined by a propeller sensor immersed in the main pipe with \(<0.5\)% measurement uncertainty. Confinement effects may be encountered: with the rigid foil, the maximum cross-section blockage periodically reaches 12% (at \(\alpha=30\)\(^\circ\)). According to West and Apelt (1982), blockages beyond 6% are no longer negligible when considering lift measurements; however, drag is not affected. In the present study, the blockage ratio may translate into exaggerated lift values for the rigid hydrofoil in particular, translating into an underestimation of the efficiency improvement of flexible blades. This would translate into an even better performance of the flexible hydrofoil by comparison.
4.2 Experimental model
The reduced frequency k, Eq. (4), a key parameter for this study, was derived from original equations to match flow conditions in the water channel. Starting from helicopter aerodynamics (Eq. 7 left, from (McCroskey 1981)) k is re-expressed in a rotating reference frame (Eq. 7 right) and formulated as follows (Laneville and Vittecoq 1986):
With elimination of R by insertion of Eq. 1 and replacement of the angular velocity \(\omega\) by the frequency \(2\pi f\), k can finally be expressed as Eq. 4.
4.3 Force measurement
The forces were captured with a load cell of specifications given in Table 1.
A customized amplifier with an integrated first-order, low-pass hardware filter for anti-aliasing was deployed. No software-based filtering was applied to the signals displayed in the figures. The sample rate was set to 1 kHz at 16-bit discretization with a Labjack T700 DA card. The sensor was tested with standard weights (0.1–2 kg) for single-channel calibration and uncertainty tests. The nonlinearity was found to be negligible for loads \(>1\)N. Significant channel cross talk was observed, which is due to the measurement principle. The combined error from cross talk and single-channel accuracy was determined to be \(<2\%\). It was calculated with the subsequent equation. Here, as an example, calculation for the drag measurement channel (\(F_X\)) is shown. The other channels can be calculated accordingly.
where \(F_{X,Y,Z}\) and \(M_{X,Y,Z}\) are the forces and moments in the three axes in space, \(r_{X,Y,Z}\) is the single-channel uncertainty in reading, and \(c_{C_{F_{X,Y,Z}}}\) is the channel crosstalk coefficient provided by the calibration matrix of the vendor. Hysteresis effects and nonlinearity are neglected. The forces were expressed as dimensionless coefficients and then averaged over the phase angle using the subsequent equations with use of the profile surface projection s as reference:
For this, values for \(c_D\), \(c_L\) and \(\alpha\) at any time point within a period were averaged across periods. For example, in a representative period constructed with n periods for each sample j of the position feedback \(\alpha\), the period-averaged lift coefficient \(\overline{c_{L}}(\alpha _j)\) is obtained as:
The coefficients of tangential and normal force, \(c_T\) and \(c_N\) were calculated from the time-averaged values of \(\overline{c_D}\), \(\overline{c_L}\) and \(\overline{\alpha }\) with Eqs. (5 and 6).
4.4 Surface and deformation tracking
The method was implemented in the open-source PIV framework fluidimage (Augier et al. 2019) published under the CECILL-B license.Footnote 1 The measurements are based on a structured-light projection and phase angle shift due to defocusing:
where \(h_{i,j,t}\) is the height of a point of the surface in i and j direction for a sample time t, \(D'\) is the appearing distance (magnified by refraction) to the reference point, \(\Delta \phi _{i,j,t}\) is the phase angle shift, due to defocusing, \({2\pi }/{\lambda _{rec}}\) is the wave vector of the recording, \(D'_{PC}\) is the appearing distance (magnified by refraction) between projector and high-speed camera.
The method provided 4 kHz temporal and 1.5 mm spatial resolution in this setup. The averaged measurement accuracy was found to be of 0.77 mm (RMS) which corresponds to 1.17% of the profile chord length. The method, originally introduced by Takeda et al. 1982, was adapted to the case at hand and presented in detail, including validation and error assessment, in Hoerner and Bonamy 2019.
4.5 Particle image velocimetry
Two continuous lasers, positioned opposing one another in order to avoid shades, provided a light sheet with thickness 2 mm. A Phantom V2511 high-speed camera captured the fluid flow with 4 kHz and \(1280\times 800\) px\(^2\) (see Table 2 for details). The fluidimage software package was deployed for data processing. A multistep postprocessing with a final interrogation window of \(16 \times 16\) px\(^2\) and 50% overlap led to \(1.5\times 1.5\) mm\(^2\) spatial resolution in a plane section of \(120 \times 74\) mm\(^2\). Final vector fields were compared to those obtained by processing with the DaVis software package. A significant difference in the direct vicinity of the hydrofoils was found, which is considered to be a result of different mask treatment strategies. The averaged differences were found to be − 0.02 m/s, which is less than of 1% of the average flow speed. Vectors with correlation peak \(<0.3\) were rejected. The flow field was subsequently filled up by an unweighted moving average of valid vectors based on a rolling window containing four samples. This led to a final temporal resolution of 1 kHz. Further details of the method are provided in Hoerner et al. 2021. The resulting flow fields of size i, j were presented dimensionless by the velocities relative to the mean flow speed \(\bar{v}\) of the entire measurement take.
4.6 Hydrofoils
The flexible hydrofoils were designed assuming the carbon blades would deform according to the Euler–Bernoulli beam theory. Because the silicone embodiment features a Young’s modulus 100,000 times lower than that of the carbon blades, the stiffness is determined entirely by the blade (Table 3). Carbon fiber composite and silicone material specifications were determined experimentally through bending and tensile tests. Aluminum alloy properties are provided by European standards (EN -7075):
Improvements in turbine structural loading. The variations in the loads (\(c_{\text {N}_\text {max}}-c_{\text {N}_\text {min}}\),



The rigid airfoil was considered fully rigid after its deformations were found to be below the measurement uncertainty.
5 Results and discussion
5.1 Thrust and structural loads
The relative structural loads, expressed by \(c_{N_\text {max}}-c_{N_\text {max,ref}}\) and the relative thrust \(c_{T}-c_{T_\text {ref}}\) for the flexible profiles compared to the rigid reference, are shown in Fig. 4 for the full parameter study. A clear trend can be observed.
For all cases where \(\lambda=2\), the flexible profiles perform better than the rigid hydrofoil over the entire range of the stiffnesses (\(t=0.3-0.7\) mm) and for all geometries (\(k = 0.028-0.735\)). By contrast, for \(\lambda =3\), the improvements are negligible and the performance sometimes drops. However, considering the absolute variation of the hydrodynamic forces compared to the measurement uncertainty, force measurements in the \(\lambda =3\) case generally do not allow for definite conclusions (Hoerner et al. 2019).
The largest improvements are seen using the most flexible foils. The hyperflexible profile (t = 0.3 mm) outperforms the rigid profile over the entire range of the geometries in \(\lambda =2\). The profile performs best for \(k=0.028-0.341\), which correspond to low and moderate solidities.
5.2 FSI mechanisms and passive flow control
The reduction in loads and increase in thrust associated with the most flexible blades can be explored by observing deformation and fluid flow. In this way, the FSI mechanisms lying underneath these improvements can be exposed and characterized in a holistic manner. Results resulting from force and moment measurements, foil deformation, and optical flow measurement are shown subsequently in unified diagrams (see later Figs. 5 and 6). The two most relevant cases were selected, corresponding to one thin- and one robust-structured turbine, both operating at \(\lambda =2\) with the most flexible and the reference foil.
In the center of the figures, the top plot displays the angle of attack (measured according to Fig. 7), and the bottom plot displays fluid-induced forces, as a function of the phase angle \(\Theta\). The lift (solid line) and drag (dashed line) are shown for the rigid reference foil (red) and the hyperflexible profile blade (black), as obtained with the SFT setup shown in Fig. 3 (middle).
Surrounding these two diagrams are fifteen depictions of particular events of interest (numbered). For these phase angles, the corresponding flow fields from the PIV measurements are presented for both the rigid reference (bottom) and the flexible profile (top). The flow fields were obtained with the PIV setup shown in Fig. 3 (left). These two diagrams allow for a complete characterization of the passive flow control for two different rotor geometries.
It must be noted that the water tunnel velocity in both measurement campaigns was not identical, varying between 3 m/s (in the force and SFT measurements) and 3.5 m/s (for the PIV measurements). The comparability of the results is achieved by the selection of a common reduced frequency (k = 0.06 & 0.38). This guarantees flow similarity for the stall dynamics.
5.3 Thin structures: the k = 0.06 case
Figure 5 shows the FSI for a thin structure, which would be typically suited for wind turbine applications, and resulting in a low reduced frequency and a flow regime in transition from quasi-static (\(k<0.05\)) to fully dynamic. There, the solidity of \(\sigma =0.19\) will normally lead to a best efficiency point far beyond \(\lambda = 2\) (Shiono et al. 2000).
The FSI mechanism associated with the blade flexibility can be explored following points 1 to 15 around the diagram. Starting from point 1, the angle of attack continuously rises, while the flexibility leads to reductions in a lower single-digit range. A first flow separation can be observed when the rigid profile reaches the static stall angle (point 3). A characteristic curve slope for stall occurrence is observed in points 4–6 for the rigid profile, featuring a lift peak with subsequent harsh drop along with overshooting drag. A very different behavior is shown by the flexible profile. It displays maximum deformation for a phase angle corresponding to the maximum lift on the rigid foil. The flexible structure balances the flow and provides a smooth load curve with negligible drag.
This effect repeats for subsequent load/deformation variations and in particular in the second half of the oscillation period. The flow fields around the rigid profile are characterized by a fully separated flow, starting from point 5, and a large wake zone. Hysteresis effects delay the reattachment of the flow to the zero-crossing of the angle of incidence (at \(\Theta =\pi\)). The hyperflexible structure, instead, adapts to the flow. Stall is decreased, the fully detached time span is significantly shorter, along with the size of the wake structure. The drag remains moderate for the entire oscillation, along with reduced lift forces. This is beneficial for the torque, which is proportional to the cosine of drag and the sine of lift for low angles of attack, according to Eq. (5).
5.4 Robust structures: the k = 0.38 case
In structurally robust, thicker turbine structures corresponding to higher reduced frequencies, the flow conditions are fully dynamic. Figure 6 shows the flow at a reduced frequency of k = 0.38, which corresponds to a common solidity of \(\sigma =1.2\) for CFTT.
There, although the trends are similar to the previous, finer geometry, the flow regime features significantly higher hydrodynamic forces, which result in a stronger deflection of the structure. Again, the bioinspired blades’ flexibility successfully smoothens the load peaks observed on the rigid foils.
The flow fields of the rigid structure clearly show that although the stall angle is increased (a known mechanism as per (McCroskey et al. 1976; McCroskey 1981)), the flow remains detached for more than half of the period, in accordance to the findings on a full turbine rotor reported by Gorle et al. 2016. Hysteresis effects shift the phase angle for flow reattachment to the opposing pitch movement period. Here, the flexibility of the bioinspired structure again decreases these effects, so that it behaves like a cambered hydrofoil operating at lower angles of attack. The extensive drag forces measured on the rigid foil are no longer present for the flexible structure. Lift forces are significantly reduced as well. Interestingly, the coincidence of maximum flexible structure bending and maximum rigid profile load which was observed in the previous case no longer occurs. The shift, we believe, is due to mass inertial effects which delay the structural and hydrodynamic response.
6 Outlook
This in-depth visualization of the structural adaptation of the hyperflexible foils, and their influence on the flow field, demonstrates that chordwise flexibility is an appropriate means of passive flow control. The best results, which combine a reduction of 25% in structural loads along with improved blade thrust of 20% compared to an identical rigid turbine (as shown in detail in Hoerner et al. 2019) and qualitatively in accordance with the numerical results reported by Descoteaux and Olivier 2021; MacPhee and Beyene 2016, show the method’s potential for broadening the deployment of CFTT. The largest improvements occur for low-\(\lambda\) applications, which are especially relevant for ecological compatibility, as they feature lower blade strike probability.
The bioinspired blades result in reduced wake areas, which we expect will significantly affect blade–blade interactions as well as the flow field downstream of the turbine, with possible influence on the area-based power density in farm installations. Now, with the most promising design areas identified through systematic analysis using the surrogate oscillating-foil model, the path is opened for a quantitative assessment of performance, structural loads, as well as flow and wake fields on a full three-dimensional rotor.
Data availability
The data that support the findings of the study are available from the corresponding author upon request. The source code of the PIV software, the structural displacement tracking and the force measurements, comprising customized functions for processing, data acquisition and drive system control, is also available and was published along with previous publications. A single server with open access to all relevant experimental data and code related to the entire study is under construction and will be linked here and on the author’s website upon its availability.
Abbreviations
- 2D2CV:
-
Two-dimensional, two components
- BEP:
-
Best-efficiency point
- CAD:
-
Computer-aided design
- CFTT:
-
Cross-flow tidal turbine
- EN:
-
European norm
- FSI:
-
Fluid–structure interaction
- LDA:
-
Laser Doppler anemometry
- LEGI:
-
Laboratoire des Écoulements Géophysiques et Industriels
- NACA:
-
National Advisory Committee for Aeronautics
- NaN:
-
Not a Number
- PIV:
-
Particle image velocimetry
- SFT:
-
Surface tracking
- TPS:
-
Thin plate spline
- \(\alpha\) :
-
Angle of attack [\(^\circ\)]
- \(\beta\) :
-
Equivalent angle of attack [\(^\circ\)]
- \(\Delta\) :
-
Difference [–]
- \(\lambda\) :
-
Tip-speed ratio [–]
- \(\phi\) :
-
phase angle [rad]
- \(\rho\) :
-
Density [kg/m\(^3\)]
- \(\sigma\) :
-
Rotor solidity [–]
- \(\Theta\) :
-
Rotor azimuth angle [rad]
- \(\omega\) :
-
Angular velocity [rad/s]
- \(c_D\) :
-
Drag coefficient [–]
- \(c_L\) :
-
Lift coefficient [–]
- \(c_N\) :
-
Normal force coefficient [–]
- \(c_T\) :
-
Torque coefficient [–]
- f :
-
Frequency [Hz]
- h :
-
Height from SFT [m]
- k :
-
Reduced frequency [–]
- n :
-
Number of blades [–]
- r :
-
Combined relative error [%]
- t :
-
Thickness [m]
- v :
-
Absolute flow velocity [m/s]
- w :
-
Relative flow velocity [m/s]
- u :
-
Tangential velocity [m/s]
- C :
-
Blade chord length [m]
- D :
-
Distance [m]
- F :
-
Force [N]
- H:
-
Height [m]
- L:
-
Length [m]
- M :
-
Moment [Nm]
- R :
-
Turbine radius [m]
- W:
-
Width [m]
- Re:
-
Reynolds number [–]
- \(_\infty\) :
-
Free-stream condition
- \(_\text {ch}\) :
-
Water channel
- \(_\text {max}\) :
-
Maximum
- \(_\text {o}\) :
-
Oscillation
- \(_\text {rec}\) :
-
Recording
- \(\dot{}\) :
-
Temporal derivation
- \(\bar{}\) :
-
Average
- \('\) :
-
Apparent
References
Abbaszadeh S, Hoerner S, Maître T, Leidhold R (2019) Experimental investigation of an optimised pitch control for a vertical-axis turbine. IET Renew Power Gener 13:3106–3112. https://doi.org/10.1049/iet-rpg.2019.0309
Augier P, Mohanan V, Bonamy C (2019) Fluiddyn: a Python open-source framework for research and teaching in fluid dynamics by simulations, experiments and data processing. J Open Res Softw. https://doi.org/10.5334/jors.237
Barnier B, Domina A, Gulev S, Molines J-M, Maître T, Penduff T, Le Sommer J, Brasseur P, Brodeau L, Colombo P (2020) Modelling the impact of flow-driven turbine power plants on great wind-driven ocean currents and the assessment of their energy potential. Nat Energy 5:240–249. https://doi.org/10.1038/s41560-020-0580-2
Benton SI, Visbal MR (2019) The onset of dynamic stall at a high, transitional Reynolds number. J Fluid Mech 861:860–885. https://doi.org/10.1017/jfm.2018.939
Berry M, Sundberg J, Francisco F (2019) Salmonid response to a vertical axis hydrokinetic turbine in a stream aquarium. In: 13th European Wave and Tidal Energy Conference (EWTEC)
Brownstein ID, Kinzel M, Dabiri JO (2016) Performance enhancement of downstream vertical-axis wind turbines. J Renew Sustain Energy 8:053306. https://doi.org/10.1063/1.4964311
Buchner A-J, Soria J, Honnery D, Smits AJ (2018) Dynamic stall in vertical axis wind turbines: scaling and topological considerations. J Fluid Mech 841:746–766. https://doi.org/10.1017/jfm.2018.112
Bugnot AB, Mayer-Pinto M, Airoldi L, Heery EC, Johnston EL, Critchley LP, Strain EMA, Morris RL, Loke LHL, Bishop MJ, Sheehan EV, Coleman RA, Dafforn KA (2020) Current and projected global extent of marine built structures. Nat Sustain. https://doi.org/10.1038/s41893-020-00595-1
Castro-Santos T, Haro A (2015) Survival and behavioral effects of exposure to a hydrokinetic turbine on juvenile atlantic salmon and adult American shad. Estuaries Coasts 38:203–214. https://doi.org/10.1007/s12237-013-9680-6
Dabiri JO (2011) Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J Renew Sustain Energy. https://doi.org/10.1063/1.3608170
Delafin P-L, Deniset F, Astolfi JA, Hauville F (2021) Performance improvement of a darrieus tidal turbine with active variable pitch. Energies. https://doi.org/10.3390/en14030667
Deng Z, Carlson TJ, Ploskey GR, Richmond MC, Dauble DD (2007) Evaluation of blade-strike models for estimating the biological performance of Kaplan turbines. Ecol Model 208(2):165–176. https://doi.org/10.1016/j.ecolmodel.2007.05.019
Descoteaux P-O, Olivier M (2021) Performances of vertical-axis hydrokinetic turbines with chordwise-flexible blades. J Fluids Struct. https://doi.org/10.1016/j.jfluidstructs.2021.103235
Gorle JMR, Chatellier L, Pons F, Ba M (2016) Flow and performance analysis of H-Darrieus hydroturbine in a confined flow: a computational and experimental study. J Fluids Struct 66:382–402. https://doi.org/10.1016/j.jfluidstructs.2016.08.003
Hammar L, Andersson S, Eggertsen L, Haglund J, Gullström M, Ehnberg J, Molander S (2013) Hydrokinetic turbine effects on fish swimming behaviour. PloS one. https://doi.org/10.1371/journal.pone.0084141
Hoerner S (2020) Characterization of the fluid-structure interaction on a vertical axis turbine with deformable blades, PhD thesis. ISUT, University Otto-von-Guericke Magdeburg & LEGI, University Grenoble-Alpes, 2020. https://doi.org/10.25673/33025
Hoerner S, Bonamy C (2019) Structured-light-based surface measuring for application in fluid-structure interaction. Exp Fluids 60(11):168. https://doi.org/10.1007/s00348-019-2821-3
Hoerner S, Abbaszadeh S, Maître T, Cleynen O, Thévenin D (2019) Characteristics of the fluid-structure interaction within Darrieus water turbines with highly flexible blades. J Fluids Struct 88C:13–30. https://doi.org/10.1016/j.jfluidstructs.2019.04.011
Hoerner S, Kösters I, Vignal L, Cleynen O, Abbaszadeh S, Maître T, Thévenin D (2021) Cross-flow tidal turbines with highly flexible bladesexperimental flow field investigations at strong fluidstructure interactions. Energies. https://doi.org/10.3390/en14040797
Khalid S, Liang Z, Qi-hu S, Xue-Wei Z (2013) Difference between fixed and variable pitch vertical axis tidal turbine-using CFD analysis in CFX. Res J Appl Sci Eng Technol 5(1):319–325
Laneville A, Vittecoq P (1986) Dynamic stall: The case of the vertical axis wind turbine. J Solar Energy Eng Trans ASME 108:140–145. https://doi.org/10.1115/1.3268081
Lazauskas L, Kirke BK (2012) Modelling passive variable pitch cross flow hydrokinetic turbines to maximize performance and smooth operation. Renew Energy 45:41–50. https://doi.org/10.1016/j.renene.2012.02.005
Liang Y, Zhang L, Li E, Zhang F (2016) Blade pitch control of straight-bladed vertical axis wind turbine. J Central South Univ 23(5):1106–1114. https://doi.org/10.1007/s11771-016-0360-0
Ly KH, Chasteau VAL (1981) Experiments on an oscillating aerofoil and applications to wind-energy converters. J Energy 5(2):116–121. https://doi.org/10.2514/3.62511
MacPhee DW, Beyene A (2016) Fluid-structure interaction analysis of a morphing vertical axis wind turbine. J Fluids Struct 60:143–159. https://doi.org/10.1016/j.jfluidstructs.2015.10.010
Mauri M, Bayati I, Belloli M (2014) Design and realisation of a high-performance active pitch-controlled H-Darrieus VAWT for urban installations. In: 3rd Renewable Power Generation Conference. https://doi.org/10.1049/cp.2014.0930
Maître T, Amet E, Pellone C (2013) Modelling of the flow in a Darrieus water turbine: Wall grid refinement analysis and comparison with experiments. Renew Energy 51:497–512. https://doi.org/10.1016/j.renene.2012.09.030
McCroskey WJ (1981) The phenomenon of dynamic stall. Technical report, NASA TM-81264, 1981
McCroskey WJ, Carr LW, McAlister KW (1976) Dynamic stall experiments on oscillating airfoils. AIAA J 14(1):57–63. https://doi.org/10.2514/3.61332
Miller MA, Duvvuri S, Brownstein I, Lee M, Dabiri JO (2018) Vertical-axis wind turbine experiments at full dynamic similarity. J Fluid Mech. https://doi.org/10.1017/jfm.2018.197
Müller S, Cleynen O, Hoerner S, Lichtenberg N, Thévenin D (2018) Numerical analysis of the compromise between power output and fish-friendliness in a vortex power plant. J Ecohydraulics 3(2):86–98. https://doi.org/10.1080/24705357.2018.1521709
Shiono M, Suzuki K (2000) An experimental study of the characteristics of a Darrieus turbine for tidal power generation. Electr Eng Japan 132(3):38–47. https://doi.org/10.1002/1520-6416(200008)132
Stephenson JR, Gingerich AJ, Brown RS, Pflugrath BD, Deng Z, Carlson TJ, Langeslay MJ, Ahmann ML, Johnson RL, Seaburg AG (2010) Assessing barotrauma in neutrally and negatively buoyant juvenile salmonids exposed to simulated hydro-turbine passage using a mobile aquatic barotrauma laboratory. Fisheries Res 106(3):271–278. https://doi.org/10.1016/j.fishres.2010.08.006
Strom B, Brunton SL, Polagye B (2016) Intracycle angular velocity control of cross-flow turbines. Nat Energy. https://doi.org/10.1038/nenergy.2017.103
Takeda M, Ina H, Kobayashi S (1982) Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J Opt Soc Am 72(1):156–160. https://doi.org/10.1364/JOSA.72.000156
Turnpenny A, Clough S, Hanson K, Ramsay R, McEwan D (2000) Risk assessment for fish passage through small, low-head turbines. Technical report, Atomic Energy Research Establishment, Energy Technology Support Unit, New and Renewable Energy Programme, 2000
West GS, Apelt CJ (1982) The effects of tunnel blockage and aspect ratio on the mean flow past a circular cylinder with Reynolds numbers between 10\(^4\) and 10\(^5\). J Fluid Mech. https://doi.org/10.1017/s0022112082000202
Whittlesey RW, Liska S, Dabiri JO (2010) Fish schooling as a basis for vertical axis wind turbine farm design. Bioinspiration Biomim 5(3):035005. https://doi.org/10.1088/1748-3182/5/3/035005
Zeiner-Gundersen DH (2015) A novel flexible foil vertical axis turbine for river, ocean and tidal applications. Appl Energy 151:60–66. https://doi.org/10.1016/j.apenergy.2015.04.005
Zhang J, Kitazawa D, Taya S, Mizukami Y (2017) Impact assessment of marine current turbines on fish behavior using an experimental approach based on the similarity law. J Marine Sci Technol 22(2):219–230. https://doi.org/10.1007/s00773-016-0405-y
Zhang L, Liang Y, Liu X, Guo J (2014) Effect of blade pitch angle on aerodynamic performance of straight-bladed vertical axis wind turbine. J Central South Univ 21:1417–1427. https://doi.org/10.1007/s11771-014-2080-7
Acknowledgements
The authors thank Roberto Leidhold (University Otto-von-Guericke of Magdeburg), Christian-Toralf Weber (Magdeburg University of Applied Sciences) and Laure Vignal (LEGI, Grenoble) for their advice. The work of the student assistants in this project is grateful acknowledged: Iring Koesters, Yanneck Kiiski, Carsten Laddey and Stephanie Müller. The technical support of Michael Haarmann (CATLAB, Berlin), Michel Riondet and Jean-Marc Barnoud (LEGI, Grenoble), is also gratefully acknowledged.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
S.H. wrote the article. S.H. and S.A. designed the experiment, the electrical drive system control and force acquisition, acquired and processed the data. S.H. and C.B. developed the SFT method. S.H. and O.C. analyzed the results. T.M. and D.T. supervised the study. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
competing of interest
The authors declare no competing financial interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors gratefully acknowledge funding for their work from the German Federal Ministry of Education and Research, Grant Number 03WKC02B and the doctoral fellowships for the corresponding author, received from the Rosa-Luxemburg-Foundation and the Franco-German University.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hoerner, S., Abbaszadeh, S., Cleynen, O. et al. Passive flow control mechanisms with bioinspired flexible blades in cross-flow tidal turbines. Exp Fluids 62, 104 (2021). https://doi.org/10.1007/s00348-021-03186-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-021-03186-8