Abstract
The spatial and temporal resolution of a fast-response aerodynamic pressure probe (FRAP) is investigated in a benchmark flow of grid-generated turbulence. A grid with a mesh size of \(M=6.4\) mm is tested for two different free-stream velocities, hence, resulting in Reynolds numbers of \(Re_M= \{4300,12800\}\). A thorough analysis of the applicability of the underlying assumptions with regard to turbulence isotropy and homogeneity is carried out. Taylor’s frozen turbulence hypothesis is assumed for the calculation of deducible flow quantities, like the turbulent kinetic energy or the dissipation rate. Furthermore, besides the examination of statistical quantities, velocity spectra of measurements downstream of the grid are quantified. Results of a small fast-response five-hole pressure probe equipped with piezo-resistive differential pressure sensors are compared to single-wire hot-wire constant temperature anemometry data for two different wire lengths. Estimates of temporal and spatial turbulent scales (e.g., Taylor micro scale and Kolmogorov length scale) show good agreement to data in the literature but are affected by filtering effects. Especially in the energy spectra, very high bandwidth content cannot be resolved by the FRAP, which is mainly due to bandwidth limits in the temporal calibration of the FRAP and the minimal resolution of the integrated sensors.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The unsteady flow field in the wake of objects is of great interest in experimental aerodynamics. Therefore, measurement techniques that are capable of acquiring this unsteadiness can help to understand highly fluctuating phenomena. Beside optical techniques, e.g., particle image velocimetry, intrusive measurement techniques have been developed in the past decades. The best known method is hot-wire constant temperature anemometry (CTA). In order to overcome the downsides of hot-wire probes (e.g., fragility and high calibration effort), fast-response multi-hole aerodynamic probes (FRAP) have been investigated in several research groups worldwide (see, e.g., Johansen (2001) and Kupferschmied et al. (2000)). Compared to steady pressure probes, a temporal calibration of the acoustic behavior of the line-cavity system inside the probe is determined in addition to the spatial calibration (Heckmeier et al. (2019)). Due to resonance and damping effects in the acoustic system and due to the outer dimensions of the probe, both spatial and temporal filtering effects of the velocity fluctuations are expected. The measurement of turbulent flows with turbulence length and time scales (e.g., Kolmogorov length scale \(\eta\)) smaller than the corresponding probe sensing length and bandwidth is challenging. In order to quantify hot-wire probe resolution, Ashok et al. (2012) and Bailey et al. (2010) examined various hot-wire CTA probes with different wire lengths in grid-generated turbulence. Hence, in this paper, a similar wind-tunnel setup is used to characterize and validate the FRAP spatial and temporal measurement behavior. A comparison to hot-wire data and to data from the literature is conducted, since no validation with pressure probes has been carried out so far for grid-generated turbulence measurements in the literature.
In the first part of this paper, a theoretical introduction on grid-generated turbulence is given. Thereafter, general information on the calibration, the specification and assembly of the FRAP and the used hot-wire probes are discussed. The experimental setup in the wind tunnel of the Chair of Aerodynamics and Fluid Mechanics (TUM-AER) is described. In the last part, the results regarding spatial and temporal resolution of the probe are discussed and an outlook is given.
2 Grid-generated turbulence theory
As mentioned, grid-generated turbulence is well documented in the literature. Therefore, a theoretical introduction is given, before discussing the experimental results. A statistical analysis of grid-generated turbulence can be performed by evaluating higher-order moments (like second and third central statistical moment) (see Reynolds (1895); and Taylor (1935)). The nomenclature for the velocity vector is \((u_1,u_2,u_3)\), and the velocity can be expressed by its mean value and the fluctuation around the mean \(u_i=\langle u_i \rangle +u_i'\). The magnitude of the velocity vector is denoted as U. In grid-generated flows, the mean velocity component in streamwise direction is approximately the mean velocity magnitude \(\langle u_1\rangle \approx \langle U\rangle\). The degree of anisotropy DA measures if isotropy is given and relates the variances of the velocity component fluctuations \(\langle u_i'^2 \rangle\):
For an isotropic flow, the velocity component variances are similar \(\langle u_1'^2\rangle =\langle u_2'^2\rangle =\langle u_3'^2\rangle\) and DA approaches 1. For grid-generated turbulence, values \(DA>1\) are stated in the literature (see Ting (2016)). As a measure for the homogeneity, the third central moment of the velocity fluctuation can be used. When both isotropy and homogeneity can be assumed, the turbulent kinetic energy (TKE) K is approximated by the following equation:
Furthermore, the decay of turbulent kinetic energy can be expressed as a function of the normalized distance x/M downstream of the grid:
Here, \(x_0\) describes the virtual origin of the turbulent kinetic energy decay. The coefficients A and n can be fitted with measurement data. The coefficient A depends on the grid dimensions and the applied Reynolds number. According to the literature, the exponent lies between \(1.15<n<1.45\) (see Pope (2011)).
By using Taylor’s hypothesis of “frozen turbulence,” the dissipation rate \(\varepsilon\) for homogeneous, isotropic turbulence can be calculated and the spatial development of the flow can be inferred from the temporal properties. Furthermore, the dissipation rate can be approximated by assuming a homogeneous isotropic turbulent (HIT) flow. The dissipation rate \(\varepsilon\) corresponds to the decay of the TKE over time:
Hereby, turbulent length scales can be defined, which describe the size of eddies in the turbulent energy cascade. The Taylor micro scale \(\lambda\) indicates the size of the largest vortex structures in the dissipative range and can be expressed as a function of the dissipation rate \(\varepsilon\) and the kinematic viscosity \(\nu\) (Kolmogorov (1991)):
Furthermore, a turbulence Reynolds number \(Re_{\lambda }\) that is calculated with the Taylor micro scale can be used as a figure of similarity for turbulent flows and is given by:
As a measure for the lower size limit of the dissipation range, the Kolmogorov length scale \(\eta\) is defined. Here, the turbulent kinetic energy is dissipated into heat due to dominating viscous effects.
Further turbulence measures, the Kolmogorov velocity \(u_\eta\) and time scales \(\tau _\eta\), as functions of \(\varepsilon\) and \(\nu\) can be deduced by dimensional analysis:
For the spectral examination of the grid-generated turbulence, the normalized kinetic energy is calculated and shown as a function of the non-dimensional variable \(k\eta\). Hereby, the wave number k is defined as \(k=2\cdot \pi \cdot f / \langle U \rangle\). For de-noising the measured signals, the following procedure is applied on all hot-wire and FRAP signals ensuring an analogous post-processing workflow: The velocity signal is split in evenly distributed parts of \(\Delta t=1~s\) and averaged in the time domain. With a sampling rate of \(f_s=50~kHz\), this step results in \(f_s/\Delta t=50k\) averaged samples. Moreover, further filtering in the frequency domain is applied. Figure 1 shows the filtering procedure exemplary for a measurement downstream of the grid. The noisy initial signal is averaged and filtered after transformation into the frequency domain. A 1-D median filter of 20th order and a Savitzky–Golay finite impulse filter (FIR) of 1st order and a frame length of 999 Hz are further applied on the signal, using MATLAB’s inbuilt functions medfilt1 and sgolayfilt, respectively (MathWorks (2020)).
3 Experimental setup
In the first part of this section, the measurement equipment for the grid-generated turbulence investigations is explained. The focus lies on the multi-hole pressure probe. Moreover, since the pressure probe data are compared to hot-wire CTA probe measurements, the basic characteristics of the used CTA equipment are given. In the second part, the wind tunnel setup with the grid is documented. A fast-response five-hole probe, as depicted in Fig 2a, is assembled to measure the flow field downstream of the grid. The probe head of the FRAP is additive manufactured. The hemispheric probe head and the cavities for the placement of the pressure sensors are post-manufactured in a cutting step. The probe is equipped with five differential piezo-resistive pressure sensors (Meggitt Endevco 8507C-2), which are pressurized with the ambient pressure outside of the wind tunnel as reference pressure. The sensors are surrounded with a silicone tubing and pressed into the cavities in order to avoid leakage (Heckmeier et al. (2019)). The reference pressure lines of the differential transducer are merged in a manifold, so only one pressure tubing is connected to the reference pressure. The sensors are connected to NI 9237 data acquisition cards, which transmit the data to the Labview-controlled computer. The 24-bit A/D-conversion of the typical input voltage range of \(\pm 25~mV/V\) for 3.3 V excitation voltage yields a least significant bit (LSB) of \(E_{LSB}\approx 9.8~nV\), resulting in a minimal detectable pressure of around \(p_{LSB}\approx 5\cdot 10^{-4}~Pa\) depending on the linear calibration coefficient (in [Pa/V]) of the respective pressure sensor. A sketch of the measurement setup for the FRAP is shown in Fig. 3.
Before the usage of the FRAP, it has to be calibrated for (a) its spatial/aerodynamic and (b) its temporal/transient characteristic, when exposed into unknown flow fields. In the following, some details on the respective calibration process is given. Nevertheless, a more detailed description can be found in Heckmeier et al. (2019) and Heckmeier and Breitsamter (2020). When measuring the five pressures and setting them into relation in the reconstruction process, the flow properties at the probe tip can be deduced. During the spatial/aerodynamic calibration, pressure data sets for different angle combinations at various flow velocities are gathered in a free-jet calibration wind tunnel. Several hundred angle combinations are set and calibrated, resulting in a maximum reconstruction range for the FRAP of up to \(\pm 60^\circ\). The acquired pressures are processed in form of four non-dimensional calibration coefficients \(b_1\), \(b_2\), \(A_t\), and \(A_s\), which form the basis of a local interpolation approach based on Johansen et al. (2001). Here, the calibration data are divided in a low-angle and high-angle regime. The pressure port with the highest measured pressure determines the set of calibration coefficients that are used for the reconstruction. Exemplary, the definition of the high-angle regime coefficients, where one of the circumferential ports \(p_i\) measures the highest pressure, is given:
Thereby, \(p^+\) and \(p^-\) denote the pressures at the circumferential pressure ports in clockwise and counter-clockwise direction. \(\bar{q}\) denotes the pseudo-dynamic pressure, which is used to non-dimensionalize the coefficients. \(p_t\) and \(p_s\) denote the total and static pressure of the free-stream flow, respectively.
In the reconstruction procedure, the acquired data of the five pressure ports \(p_{1,T},p_{2,T},...,p_{5,T}\) are post-processed. Here, the subscript T denominates the values at the unknown test point T. The non-dimensional coefficients \(b_{1,T}\) and \(b_{2,T}\) are calculated, respectively. In the following step, a local-least square interpolation determines the quantities \(A_{t,T}\), \(A_{s,T}\) and \(\alpha _T\), \(\beta _T\) as functions of \(f(b_{1,T},b_{2,T})\). Here, \(\alpha\) and \(\beta\) denote the two flow angles. The deduced Mach number Ma can be calculated as follows (shown for the high-angle regime):
Here, c is the speed of sound, \(\kappa\) the specific heat ratio and R the specific gas constant. Lastly, the velocity components u, v and w can be calculated depending on the reconstructed quantities:
For the interpolation process in MATLAB, the built-in Delaunay triangulation function delaunayTriangulation is applied. Using its object function pointLocation, the triangle enclosing a test point and the barycentric coordinates of the test point can be determined. Thus, a fast and efficient interpolation can be ensured.
Furthermore, a temporal/transient calibration of the line-cavity system inside the probe is performed in a frequency test rig. The acoustic system is mainly dominated by resonance and attenuation. Bergh and Tijdeman (1965) analytically formulated a recursive solution for small disturbances in such systems and for tubes with small diameters compared to the tube length \(L/D\gg 1\) (laminar flow and ideal gas law is assumed). The attenuation and phase shift for the acoustic wave propagation inside a single-tube system is formulated as the complex ratio \(H(\omega )=P_{sensor}(\omega )/P_{tip}(\omega )\) and is denoted as transfer function (TF). Richards shows a different approach to describing the line-cavity system by using an analogy to electrical transmission lines (Richards (1986)). However, experiments have shown that due to imperfections in the probe manufacturing or due to a more complex probe assembly, analytic solutions can solely serve as a first guess (see Englund and Richards (1984); Wyer et al. (2012); Fioravanti et al. (2016)). Hence, the transfer function is determined experimentally in a frequency test-rig, where the investigated object (e.g., the FRAP) and a reference sensor are mounted in close proximity to each other. Furthermore, the rig contains a speaker placed directly facing the test object and the reference sensor in a distance of approximately 40 mm. It is connected to an amplifier. Acoustic modes could develop or resonate in the cavity between the loudspeaker and the test object, and thus, distort the pressure signal. For this reason, damping material is used on the one hand and the test object and reference sensor mount is rotated in several calibration runs to compensate for the modes. Sinusoidal waves are emitted and recorded at specified frequency steps (\(\Delta f=20~Hz\)), and hence, the amplitude ratio and the phase shift are obtained. For this study, the temporal calibration was performed for frequencies up to 10 kHz in order to compensate for resonance and attenuation effects (Heckmeier et al. (2019)). Figure 4 depicts the attenuation of the five line-cavity systems of the FRAP. It is clearly visible that for some higher frequency ranges, the amplitude is attenuated to \(\le 25\%\) of the initial pressure signal magnitude at the probe tip, highlighted by the red, transparent rectangle.
In the temporal reconstruction process, the time series pressure data are transformed into frequency domain with a fast Fourier-transformation (FFT) and the TF is applied on the measured data:
By applying an inverse FFT, the reconstructed pressure data at the probe tip are available and can be further processed with the spatial reconstruction as described above. Summing up, Table 1 shows the pressure probe properties including some geometric dimensions.
For the reconstruction of the flow-field properties, the measured pressures are post-processed taking the calibration data of both, temporal and spatial, calibrations into account. A high reconstruction accuracy below \(0.2^\circ\) in both flow angles and 0.1 m/s in the reconstructed velocity can be achieved, as shown in Heckmeier and Breitsamter (2020). Pretests have shown that the temporal characteristics of the probe are limited due to bandwidth restrictions of the transfer function in the temporal calibration. The speakers in the frequency test-rig ensured good quality sound emission only up to 10 kHz. Furthermore, as discussed before, the minimal resolution of the sensor and the DAQ-card \(p_{LSB}\) must be taken into account, since the expected pressure fluctuations attenuated in the line-cavity system in the higher kHz-range could be lower than the minimal resolvable pressure fluctuation. For this case, an additional digital low pass filter is applied on the pressure data before reconstruction of the flow field properties. For example, if the pressure fluctuation of sensor 1 lies in the range of \(10^{-3}~Pa\), the signal is further attenuated in the frequency range around 7 kHz of almost one order of magnitude, and thus, cannot be resolved due to the LSB-restriction mentioned before. Hence, the temporal resolution restriction comes either from the bandwidth of the temporal calibration or the minimal resolvable pressure fluctuation.
As a counterpart to pressure measurement systems, hot-wire probes are used to validate the FRAP results. A Dantec 55P11 single-wire probe with a standard wire length of \(l_{w} = 1.25~{\text{mm}}\) (see Fig. 2b) and a retrofitted, shortened probe with a wire length \(l_w=0.7~mm\) are compared (see Table 2).
The CTA hot-wire probe is operated with a Dantec StreamLine Pro constant temperature anemometer. The signal is digitized by a Data-Translation DT9836 16-bit A/D-converter. After bridge-balancing of the CTA-bridges, the probes are calibrated in the desired velocity range. The cutoff frequency inferred from a square-wave test lies above the set low-pass frequency of the CTA. In order to compensate for temperature changes during the calibration and the wind tunnel measurements, the voltages are corrected as described in Bearman (1971):
where:
The experiments on the grid-generated turbulence are conducted in the “Wind Tunnel B” (W/T-B) of TUM-AER. The low-speed wind tunnel, which is of Göttingen type (closed-loop), has a cross section of \(h \cdot b=1.20~m \cdot 1.55~m\). Turbulence intensity without the grid lies below \(Tu=1\%\). At the nozzle section, a weaved grid with a mesh size \(M= 6.4~mm\) and a wire diameter of \(d=1.6~mm\) is installed (see Fig. 5). Hence, the solidity of the mesh is \(\sigma = \left( \frac{d}{M}\right) \left( 2- \frac{d}{M}\right) =0.438\). The free-stream velocity is monitored with a Prandtl probe that is installed upstream of the grid near the nozzle. The free-stream velocities are set to match the Reynolds numbers \(Re_M=\{4300,12800\}\). For all types of probes, measurements are acquired along an x-traverse downstream of the grid. The x-positions are normalized by the mesh size M and lie between \(x/M=(20,100)\). Both hot-wire and FRAP data are sampled with a sampling frequency of \(f_s=50~kHz\). In order to account for aliasing problems, a low-pass filter below the Nyquist frequency (\(f_{lp}\le f_s/2\)) is set for both acquisition setups. The measurement time was set to \(t_s=15~s\).
4 Results and discussion of the grid-generated turbulence
In a first evaluation step, the assumptions made regarding homogeneous, isotropic turbulence are evaluated as a prerequisite for the application of Taylor’s frozen turbulence hypothesis. The stated equations in sect. 2 are only valid, if both homogeneity and isotropy are present in the flow field. In comparison with the literature, where Ashok et al. (2012) and Bailey et al. (2010) solely stated a homogeneous, isotropic flow without any validation, the usage of a fast-response five-hole probe giving the 3D velocity vector enables a closer look on the evaluation of the stated prerequisites for further grid-generated turbulence observations in this paper:
The first assumption is the homogeneity of the flow field. Hence, three measurement planes with a very fine measurement grid resolution (\(\Delta y=\Delta z=M/8=0.8~mm\)) are measured in the near wake of the grid at \(x/M=\{2, 10, 20\}\). Contour plots of the turbulence intensity Tu at the measurement planes at \(Re_M=4300\) are shown in Fig. 6. The turbulence intensity Tu is defined as:
In the near field of the grid, the flow field is very inhomogeneous due to the separation and acceleration of the flow at the grid. At \(x/M=10\), the flow field is still strongly influenced by the grid, resulting in a more homogeneous flow field at \(x/M=20\). In the backmost measurement plane in Fig. 6 at \(x/M=20\), repeat measurements indicated that turbulence intensities lie between \(Tu=0.05\) and \(Tu=0.1\), which is approximately one order of magnitude higher than the undisturbed flow at the nozzle in W/T-B at TUM-AER.
In order to investigate the assumption of isotropy, the degree of anisotropy is observed with the FRAP downstream of the grid. In Fig. 7, the degree of anisotropy and the variances of the three velocity fluctuation components are depicted. As described in the literature, the component in streamwise direction is higher compared to the lateral and vertical components. The difference is decreasing with a larger distance from the grid. From \(x/M\ge 40\), the flow gets more and more isotropic. Moreover, since the variance of the velocity component in streamwise direction \(\langle u_1'^2\rangle\) matches the variance of the velocity magnitude \(\langle U'^2\rangle\) to a very high extent (see Fig. 7b), further evaluations on grid-generated turbulence are based on the velocity magnitude and its variance, since \(\langle u_1'^2\rangle \approx \langle U'^2\rangle\). However, a certain degree of anisotropy is still present in the wake of the grid: The degree of anisotropy never falls below \(DA=1.3\). In the literature, similar values for DA have been noted for grid-generated turbulence by Ting (2016). Nevertheless, for further evaluations steps, the degree of anisotropy is seen as acceptable. For higher Reynolds numbers, the degree of anisotropy decreases as expected.
Another indication justifying the assumption of homogeneity at distances \(x/M\ge 40\) is the investigation of higher-order statistical moments of the velocity magnitude, like the non-dimensional 3rd-order moment in Fig. 8 for both Reynolds numbers. The 3rd-order statistical moment is very low and almost constant for farther downstream measurement points.
The lack of full isotropy, as seen in the discussion before, leads to the investigation of the error made when applying the HIT approximation when calculating the TKE and all deduced quantities, which is being discussed in more detail in the following: Figure 9 shows the decay of the turbulent kinetic energy K as a function of the normalized distance x/M downstream the mesh with and without the HIT approximation. Furthermore, the fit parameters when fitting the measurement data to the power law in Eq. 3 are investigated. The fitted exponent \(n=1.26\) fulfills the assumptions as mentioned in Pope (2011). Using the aforementioned approximation, the TKE is overestimated. The relative error for the TKE is more than \(40\%\) in the near wake of the mesh and decreases with increasing distance. Since Ashok et al. (2012) solely use data from a single wire CTA probe, it is assumed that they make a similar error when calculating deduced quantities in grid-generated turbulence, approximating U with \(u_1\).
As described in Eq. 4, the dissipation rate of the flow can be deduced from the spatial derivative of the velocity components variances, when assuming homogeneous, isotropic turbulence and Taylor’s frozen turbulence hypothesis. In Fig. 10a, the dissipation rate for both Reynolds number cases is displayed for a) the dissipation rate calculated with the present 3D variances, viz. without the homogeneous isotopic turbulence (HIT), and b) with the HIT approximation. Due to the described higher degree of anisotropy in the near wake, the approximation overestimates the dissipation rate throughout the full traverse in downstream direction, but still follows the estimated trend. The error made in the calculation of the Kolmogorov length scale \(\eta\) is shown in Fig. 10b. The relative error is lower compared to the dissipation rate plot, due to the fact that \(\eta \sim \varepsilon ^{1/4}\). The Kolmogorov scale is underestimated when applying the HIT-approximation. This is also important with regard to single-wire CTA-probe measurements since there this assumption also holds, as stated before by assuming \(U\approx u_1\).
a FRAP dissipation rate \(\varepsilon\) and b Kolmogorov scale \(\eta\) for \(Re_M=4300\) (red) and \(Re_M=12800\) (blue) with and without the homogeneous isotropic turbulence (HIT) approximation in eq. 4
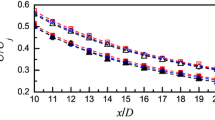
In the literature, values for the Reynolds number based on the Taylor micro scale lie in the range \(Re_\lambda =(30, 80)\) (see Ashok et al. (2012)). The measurements from the FRAP \(Re_\lambda =(20, 70)\) match the reference data. Furthermore, the Kolmogorov length scale \(\eta\), calculated as defined in Eq. 7, is shown in Fig. 11a for both Reynolds numbers. For \(Re_M=12800\), the data for both measurement techniques match very well in the entire x/M range downstream of the grid. For the lower Reynolds number, deviations between the hot-wire measurements and the FRAP occur in the far wake at distances \(x/M>80\). This is mainly due to the low velocity fluctuation magnitudes. Small velocity fluctuations around a low mean velocity correspond to even smaller pressure changes and therefore cannot be resolved appropriately. It can be seen that the Kolmogorov length scale increases with increase in distance from the grid. Furthermore, it increases with decrease in Reynolds numbers. The same trend is shown in the literature with Kolmogorov length scales of \(\eta =(0.04,0.275)~mm\) for an equivalent \(Re_M\) (see Ashok et al. (2012)). The same trend can be observed for the Taylor micro scale \(\lambda\) in Fig. 11b. For measurements farther away from the grid, larger deviations between the various probes are present for \(Re_M=4300\). Here, the absolute velocity and the respective velocity component fluctuations are very small. Hence, the fluctuations of the measured total pressure lie below \(\Delta p\ll 1~Pa\) and the probe reconstruction accuracy is influenced, which can lead to inaccurate results. For the higher Reynolds number case \(Re_M=12800\) this mismatch is less pronounced.
Figure 12 shows the local, normalized velocity variance for all probes under investigation and validation data from the literature (see Ashok et al. (2012)). The trend that the smaller the spatial filtering due to the probe size, the higher the measured variance, can be observed in both the literature and the measurement data at TUM-AER. Interestingly, the five-hole probe with a head diameter of 3 mm lies between the two single-wire probes used for validation purposes. The reason why the TUM-AER single-wire probe with a wire length of 0.7 mm lies below the 1 mm probe in the literature is due to the lack of comparability in the length to diameter ratio of the various probes. Ashok et al. used wires with smaller diameters to compensate for 3D flow effects around the hot-wire. The ratio of the wire length to the wire diameter \(l_w/d_w\) is larger by a factor of at least 2 for all measurements of Ashok et al. Ligrani and Bradshaw showed that at ratios \(l/d>200\) 3D effects are negligible and, hence, the influence of the hot-wire prongs is less prominent (Ligrani and Bradshaw (1987)). The TUM-AER hot-wire probe \(l_w/d_w\)-ratios, \(l_w/d_w=250\) and \(l_w/d_w=140\) for the standard and shortened probe, respectively, are in the same range as this lower limit. An additional reason for the deviation of the measurements from the literature to the measurements at TUM-AER is related to the differences in the flow in the wind tunnel, i.e., wind tunnel effects.
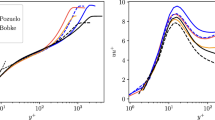
In the spectral analyses, the acquired signals are post-processed (averaging and filtering) as described in Fig. 1. Figure 13a shows kinetic energy spectra as a function of the frequency. The influence of the digital low-pass filter is visible for the FRAP data. Furthermore, the spectra approach a non-physical near constant value near the low-pass frequency of the DAQ system at \(f\approx 25~kHz\), which shows the minimal resolution restrictions of the FRAP sensors and measurement cards. In Fig. 13b, normalized kinetic energy spectra \({\hat{E}}_{kin}/(\varepsilon \nu ^5 )^{1/4}\) for the FRAP at various downstream positions as a function of \(k\eta\) at \(Re_M=12800\) are depicted. As a reference, the energy spectra for the single-wire measurement at \(x/M=\{40,60,80\}\) are given, as well. In addition, the \(k^{-5/3}\) slope in the inertial range of the energy cascade, which applies for flows with \(Re_\lambda \xrightarrow []{}\infty\), is included. After the near constant trend in the low bandwidth region, the inertial subrange is clearly visible. For flows with small Reynolds numbers \(Re_\lambda\), the exponent p of the \(k^{-p}\) dependency deviates from the ideal value of \(p=5/3\) (Pope (2011)). Due to the minimal resolution of the sensor-DAQ-system, the FRAP signals have been additionally low-pass filtered. Therefore, the inertial subrange cannot be fully resolved by the FRAP. Since the abscissa is non-dimensionalized with the Kolmogorov length scale, which increases with the distance from the grid, the cutoff value \(k\eta\) for the FRAP measurements is shifted for measurements farther downstream. In comparison, the single-wire measurement with a wire length of \(l_w=1.25~mm\) additionally resolves even smaller scales in the dissipative range of the energy cascade. A linear fit in the log–log scale between \(k\eta =[0.04,0.1]\) results in fitted exponents p for the measurements that were carried out at \(Re_\lambda \approx 50\): Following the proposed experimentally derived dependency for \(p(Re_\lambda )\) by Mydlarski and Warhaft (1998) \(p(Re_\lambda )=5/3-5.25Re_\lambda ^{-2/3}\), the exponent for FRAP and for the HW measurements are \(p_{FRAP}\approx 1.3\) and \(p_{HW}\approx 1.47\), respectively. The discrepancy between the two measurement techniques can be attributed to effects due to the filtering process and the assumptions made concerning homogeneous, isotropic flows.
In Fig. 14, the pre-multiplied energy spectra \(kE_{kin}/(\varepsilon \nu ^5 )^{1/4}\) are shown for all measured distances downstream the grid. It can be seen that the energy decreases with the distance from the grid. For all measurements, the FRAP cannot fully resolve the decay in the high bandwidth region \(k\eta > 10^{-1}\).
In the last step of the grid-generated turbulence evaluation, an equivalent wire length is calculated for the FRAP in order to make the pressure probe dimensions comparable to single-wire probes. The flow around the bluff FRAP body leads to a spatial filtering effect and, hence, can be made comparable to the spatial filtering due to the wire length of the single-wire CTA probe. Ashok et al. investigate the ratio between the wire length and the Kolmogorov length scale \(l_w/\eta\) (Ashok et al. (2012)). As a reference, Ashok et al. use a miniature hot-wire probe with a wire length \(l_w=0.06~mm\). This miniature wire size is in the same order of magnitude as the Kolmogorov scale \(l_w\sim \eta\) and spatial filtering hardly occurs. Hence, they postulate an exponential trend of the spatial filtering as a function of the ratio \(l_w/\eta\):
Here, \(U_m\) denotes the measured velocity and \(U_{hw0.06}\) the reference value measured with a miniature hot-wire probe. Consistent to the findings in Fig. 12, where the FRAP data lie nearer to the 1 mm HW than the 4 mm one from the literature, an equivalent wire length \(l_{w,equi.}\) can be found for the FRAP, when fitting the measured data to the exponential trend. Figure 15 shows the variance normalized by hot-wire variance values with a wire-length of \(l_w=0.06~mm\) (Ashok et al. (2012)) as a function of \(l_w/\eta\). For the depicted values of the FRAP, an equivalent wire length of \(l_{w,equi.}=2.0~mm\) is assumed and lies below the outer dimension of the probe tip, which reads \(d_{tip}=3~mm\).
Variance normalized by hot-wire variance values with a wire-length of \(l_w=0.06~mm\) (Ashok et al. (2012)) as a function of \(l_w/\eta\)
5 Concluding remarks
In this study, grid-generated turbulence has been investigated experimentally in a low-speed wind tunnel. Data from a fast-response multi-hole pressure probe are compared to data from single-wire CTA probes and data from the literature. The underlying assumptions of homogeneity and isotropy have been studied thoroughly. The evaluation of higher-order statistics shows a good agreement between the different measurement methods. Solely, minor deviations in regions with small velocity fluctuations around a low wind speed can be observed in the FRAP data. In the spectral investigations, the limits of the FRAP have been shown. These are mainly due to the minimal resolution of the FRAP sensors/DAQ system and the bandwidth limit of the experimentally acquired temporal calibration. Future developments concerning those issues should overcome the problems: Smaller probe dimensions could further reduce spatial and temporal filtering. Moreover, the limits of the piezo-resistive sensor should be avoided by the application of newly developed fiber-optic pressure sensors in the future. Nevertheless, the measurements have shown that the FRAP can be used for turbulence measurements. In comparison with state-of-the-arts hot wire CTA probes, FRAP offers a reduced setup time (no recurring calibration needed), the full 3D velocity vector and a more robust probe design, which can also be used in harsh environments.
References
Johansen ES (2001) Development of a fast-response multi-hole probe for unsteady and turbulent flowfields. Dissertation. Texas A&M University, Texas
Kupferschmied P, Köppel P, Gizzi W, Roduner C, Gyarmathy G (2000) Time-resolved measurements with fast-response aerodynamic probes in turbomachines. Measurement Sci Technol 11:1036–1054
Heckmeier FM, Iglesias D, Kreft S, Kienitz S, Breitsamter C (2019) Development of unsteady multi-hole pressure probes based on fiber-optic pressure sensors. Eng Res Expr 1(2):025023
Ashok A, Bailey SCC, Hultmark M, Smits AJ (2012) Hot-wire spatial resolution effects in measurements of grid-generated turbulence. Exp in Fluids 53:1713–1722
Bailey SCC, Kunkel GJ, Hultmark M, Vallikivi M, Hill JP, Meyer KA, Tsay C, Arnold CB, Smits AJ (2010) Turbulence measurements using a nanoscale thermal anemometry probe. J Fluid Mech 663:160–179
Reynolds O (1895) IV. On the dynamical theory of incompressible viscous fluids and the determination of the criterion. Philos Trans Royal Soci Lond 186:123–164
Taylor GI (1935) Statistical theory of turbulence. Proce Royal Soci A: Math, Phys and Eng Sci 151(873):421–444
Ting D (2016) Basics of Engineering Turbulence. Academic Press, Cambridge
Pope SB (2011) Turbulent flows. Cambridge University Press, Cambridge
Kolmogorov AN (1991) The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proce Royal Soci A: Mathe, Phys and Eng Sci 434(1890):9–12
MathWorks, Inc.: MATLAB Signal Processing Toolbox - User’s Guide, R2020b (2020)
Heckmeier FM, Breitsamter C (2020) Aerodynamic Probe Calibration using Gaussian Process Regression. Measurement Sci Technol 31:125301
Johansen ES, Rediniotis O, Jones G (2001) The compressible calibration of miniature multi-hole probes. Trans. ASME 123:128–38
Bergh H, Tijdeman H (1965) Theoretical and experimental results for the dynamic response of pressure measuring systems, NLR-TR F.238
Richards WB (1986) Propagation of Sound Waves in Tubes of Noncircular Cross Section. NASA Technical Paper No. 2601
Englund D, Richards WB (1984) The Infinite Line Pressure Probe. NASA Technical Memorandum No. 83582
Van de Wyer N, Brouckaert JF, Miorini RL (2012) On the Determination of the Transfer Function of Infinite Line Pressure Probes for Turbomachinery Applications. Proceedings of ASME Turbo Expo 2012: Volume 1: Aircraft Engine; Ceramics; Coal, Biomass and Alternative Fuels; Controls, Diagnostics and Instrumentation, No. GT2012-69563
Fioravanti A, Lenzi G, Ferrara G, Ferrari L (2016) Development of a fast response aerodynamic pressure probe based on a waveguide approach. J Eng Gas Turb and Power 139(3):031902
Bearman PW (1971) Corrections for the effect of ambient temperature drift on hot-wire measurements in incompressible flow. DISA Inf. 11(11):201–208
Ligrani PM, Bradshaw P (1987) Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp Fluids 5(6):407–417
Mydlarski L, Warhaft Z (1998) Passive scalar statistics in high-Péclet-number grid turbulence. Journal of Fluid Mechanics 358:135–175
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Heckmeier, F.M., Hayböck, S. & Breitsamter, C. Spatial and temporal resolution of a fast-response aerodynamic pressure probe in grid-generated turbulence. Exp Fluids 62, 44 (2021). https://doi.org/10.1007/s00348-021-03141-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-021-03141-7