Utilizing the ball lens effect for astigmatism particle tracking velocimetry

Abstract

In the present study, a simple method is developed to apply astigmatism particle tracking velocimetry (APTV) to transparent particles utilizing backlight illumination. Here, a particle acts as ball lens and bundles the light to a focal point, which is used to determine the particle’s out-of-plane position. Due to the distance between focal point and particle, additional features have to be considered in ball lens astigmatism particle tracking velocimetry (BLAPTV) compared to conventional APTV. We describe required calibration steps and perform parameter studies to show how the autocorrelation coefficient and the light exposure affect the accuracy of the method. It is found that the accuracy and robustness of the Euclidean calibration approach as also used in conventional APTV (Cierpka et al. in Meas Sci Technol 22(1):015401, 2010a) can be increased if an additional calibration curve for the light intensity of the particle’s focal point is considered. In addition, we study the influence of the particle diameter and the refractive index jump between liquid and particles on the calibration curves and the accuracy. In this way, particles of the same size, but different material, can be distinguished by their calibration curve. Furthermore, an approach is presented to account for shape changes of the calibration curve along the depth of the measurement volume. Overall, BLAPTV provides high out-of-plane particle reconstruction accuracies with respect to the particle diameter. In test cases, position uncertainties down to 1.8% of the particle diameter are achieved for particles of $d_{\mathrm{p}}={124}\,{\upmu \hbox {m}}$. The measurement technique is validated for a laminar flow in a straight rectangular channel with a cross-sectional area of $2.3 \times 30$ $\hbox {mm}^2$. Uncertainties of 0.75% for the in-plane and 2.29% for out-of-plane velocity with respect to the maximum streamwise velocity are achieved.

Graphic abstract

1 Introduction

Astigmatism particle tracking velocimetry (APTV) is a single-camera measurement technique to determine the three-dimensional displacement of suspended particles in a fluid. Since its first application to a fluid mechanics problem by Kao and Verkman (1994), it has been applied and developed further by various authors (Angarita-Jaimes et al. 2006; Chen et al. 2009; Cierpka et al. 2010a, b; Rossi and Kähler 2014). In APTV, astigmatism is introduced to create abberrated images from which the 3D particle position can be reconstructed from a 2D image. This is mostly achieved by placing a cylindrical lens into the optical path. As a single-camera approach, APTV can be applied to flow problems where multi-camera approaches fail due to imaging constraints and calibration problems (Cierpka and Kähler 2012). Whereas this is the case especially in microfluidics, APTV has been successfully applied to geometries at various length scales to investigate a wide spectrum of physical phenomena. Ragan et al. (2006) applied APTV to measure the motion of living kidney cells with a measurement volume depth of $\varDelta z={2.5}\,{\upmu \hbox {m}}$. Huang et al. (2008) applied the technique in a nanoscale environment. Using stochastic optical reconstruction microscopy, they reconstructed the position of ${200}\,{\hbox {nm}}$ beads labeled with photo-switchable molecules with a resolution of ${60}\,{\hbox {nm}}$ in the depth direction within a measurement volume of ${600}\,{\hbox {nm}}$ depth. Huang et al. (2016) could resolve the protein structures in a ${9}\,{\upmu \hbox {m}}$ spermatocyte with a depth resolution of 10–${20}\,{\hbox {nm}}$ and a measurement volume depth of ${1200}\,{\hbox {nm}}$, by using a dual objective 4Pi-microscope system with deformable mirrors to compensate for aberrations as well as an improved scanning technique. Another example of the application of APTV is the work of Muller et al. (2013). Investigating the ultrasound-induced acoustophoretic motion of microparticles, they utilized APTV in a channel with a rectangular cross section of $377 \times 157\,\upmu \hbox {m}^{2}$ and captured the trajectories of ${0.5}\,{\upmu \hbox {m}}$ and ${5}\,{\upmu \hbox {m}}$ particles to validate their analytical results. Apart from microfluidic applications, increasing efforts are undertaken to apply APTV to larger flow domains. Fuchs et al. (2014a, b) showed that APTV is suitable for measuring volumetric velocity fields in macroscopic domains of up to ${40}\,{\hbox {mm}}$ measurement volume depth. Likewise, Buchmann et al. (2014) measured the motion of ${110}\,{\upmu \hbox {m}}$ particles in a supersonic, impinging jet flow, over a measurement volume depth of ${5100}\,{\upmu \hbox {m}}$. Recently, APTV is combined with special particles to measure properties other than velocity. Segura et al. (2015) utilized non-encapsulated thermochromic liquid crystals (TLC) particles, to measure the volumetric 3D velocity- and temperature field in an evaporating droplet with a measurement volume depth of ${20}\,{\upmu \hbox {m}}$. Also, Massing et al. (2016, 2018) used luminescent polymer particles to measure the three-dimensional temperature and velocity field of a heated flow in a channel with a cross section of $2 \times {2}\,{\hbox {mm}^{2}}$. Rossi et al. (2019) investigated the phenomena of electrokinetically induced pattern formation and measured the particle concentration and velocity in a $350 \times 30\,\upmu \hbox {m}^{2}$ trapezoidal channel. To enable tracking of single particles even at higher particle concentrations, they used a mixture of differently labeled particles, among which the majority of them was invisible to the camera. For a more detailed report of the history of APTV and its different fields of application, the reader is referred to Cierpka and Kähler (2012). In the present study, we restrain ourselves to provide an overview of the reconstruction accuracies and measurement volume depths achieved in these and other publications (see Table 1 in “Appendix”).

As the performance of APTV strongly depends on the quality of defocused particle images, a central aspect is the correct selection of the imaging system and the tracer particles. Therefore, usually high-quality fluorescent particles are used, as they provide high-quality particle images, with acceptable signal-to-noise ratio (SNR) (Cierpka et al. 2010a).

However, commercially available fluorescent particles are expensive and not all sizes or materials are available. Manually coated particles may be an alternative; nonetheless, it is a challenge to ensure a sufficient, uniform and repeatable coating quality and to avoid bleeching. Furthermore, powerful monochromatic light sources such as lasers are required to excite fluorescent particles, which are an additional cost factor. Despite these challenges, only very few studies report on the use of non-fluorescent particles for APTV. One is the aforementioned work of Buchmann et al. (2014), who used a pulsed high-power LED for backlight illumination to capture the 3D motion of ${110}\,{\upmu \hbox {m}}$ opaque polyamide particles. Their error in reconstructing the particle position was about $\sigma _z={140}\,{\upmu \hbox {m}}$ which was 2.74% of the measurement volume depth. However, compared to the particle diameter, the error was relatively large ($\sigma _z/d_{\mathrm{p}} =127\%$). Segura et al. (2015) used a white light source with a circular polarization filter to excite their TLC particles and reported a relative high uncertainty of $\sigma _z/\varDelta z =8.5\%$ in reconstructing the z-position compared to laser-based APTV. They concluded it was due to the less bright particle images obtained with a white light source. Using a backlight illumination, Franchini et al. (2019) performed APTV measurements with a calibration based on fitting a 2D, generalized Gaussian distribution to each particle image. They could resolve the velocity profile of a laminar flow in a $2 \times 1.2 \times {3}\,{\hbox {mm}^{3}}$ channel covering a measurement volume depth of ${240}\,{\upmu \hbox {m}}$. Due to a low SNR, an extensive calibration procedure including measuring the background intensity of the channel in each measurement plane and sophisticated neural network algorithms were required in their study for a reliable reconstruction of the particles out-of-plane position. Apart from APTV, other single-camera approaches have been developed to measure the 3D displacement of unlabeled, transparent spheres using bright-field illumination. Ovryn and Hovenac (1993), Ovryn (2000) and Ovryn and Izen (2000) developed forward-scattering particle image velocimetry (FSPIV), where the scattering pattern of particles is exploited to determine the particles depth position. They applied the method to track $d_{\mathrm{p}}={7}\,{\upmu \hbox {m}}$ particles in the lower half of a $6 \times 48 \times {0.315}\,{\hbox {mm}^{3}}$ channel flow. Similarly, Moreno-Hernandez et al. (2011) used the central spot size of the interference pattern of a particle diffraction image to encode the out-of-plane particle position. However, they reported large position reconstruction errors for larger particles (up to 25% of the absolute position for $d_{\mathrm{p}}={15}\,{\upmu \hbox {m}}$). Here, we present a simple, low-cost APTV-based measurement technique to determine the three-dimensional displacement of transparent, non-fluorescent particles utilizing bright-field illumination. In contrast to fluorescence-based APTV, particles act as ball lens and focus the light to a focal point that is used to determine the particle’s out-of-plane position. The method provides high accuracy and is designed for high magnification and particles big in comparison with the field of view ($d_{\mathrm{p}} > {30}\,{\upmu \hbox {m}}$ and $M >10{\times }$).

2 Experimental setup

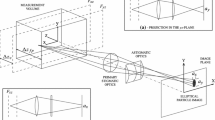
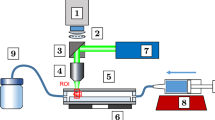
The measurement system consists of a microscope (Nikon Eclipse LV100) with a continuous backlight illumination. For image recording, two cameras are used for a comparative study. These are a 12-bit, $1280 \times 800$ pixel CMOS high-speed camera (Phantom Miro Lab 110, Vision Research) with ${20}\,{\upmu \hbox {m}}$ pixel size, as well as a 12-bit, dual frame, CCD camera (Imager ProSX 5M, LaVision GmbH) with $2456 \times 2058$ pixel and a pixel size of ${3.45}\,{\upmu \hbox {m}}$. A schematic of the full experimental setup is shown in Fig. 1. Measurements are taken with two Nikon Cfi60 objective lenses of $M = 20{\times }$ and $M = 10{\times }$ magnification. To introduce astigmatism, a cylindrical lens with a focal length of $f_{\mathrm{cyl}} = {200}\,{\hbox {mm}}$ is placed in front of the camera sensor. To investigate the influence of the magnification, the light intensity, the processing parameters and the properties of particles and liquid on the calibration curves, we build a test chamber which allows us to easily change particles or liquid. To validate the accuracy of BLAPTV for macroscopic flow applications, a plane channel flow is realized with a rectangular cross-sectional area of ${h } \times {w} =2.305 \times {30}\,{\hbox {mm}^{2}}$ and a length of ${150}\,{\hbox {mm}}$.

Fig. 1

Experimental setup: a sketch. b Photograph. (1) Camera, (2) cylindrical lens and field lens, (3) microscope objective, (4) transparent channel, (5) x, y, z-traverse, (6) mercury lamp, (7) pump, (8) tank and (9) cooling unit

3 Measurement principle

In BLAPTV, transparent particles are illuminated in bright-field mode as illustrated in Fig. 2. As the particle’s refractive index differs from the surrounding liquid, they act as ball lenses and focus the light, forming a focal point at some distance between particle and objective. A cylindrical lens, placed in front of the camera sensor, alters the light path resulting in two different focal planes for rays traveling in the xz and the yz plane. This induces astigmatism to the image of the particle’s focal point (highlighted as red dots in Fig. 2), henceforth called “focal image.” The shape of the focal image changes based on the z location of the focal point with respect to the focal planes, denoted as $F_{xz}$ and $F_{yz}$ in the object plane (see Fig. 2). The shape of the focal image is circular when the particle’s focal point is located approximately in the middle between both focal planes (see label “2” in Fig. 2), and it deforms to a vertically or horizontally stretched ellipsoid when the focal point is located closer to $F_{xz}$ or $F_{yz}$, respectively (see label “1” and “3” in Fig. 2). In comparison with the focal image, the shape change of the particle image is not significant. In fact, the particle silhouette remains almost circular as it can be seen in Fig. 3a. Hence, it is the deformation of the focal image that will be used to determine the out-of-plane position of the particles. This shape change can be quantified by extracting the information of the length of the horizontal $a_x(z)$ and the vertical axis $a_y(z)$ of the ellipsoid (see Fig. 2). Hereafter, the ratio of the major axis $\text {max}[a_x, \, a_y]$ and minor axis $\text {min}[a_x, \, a_y]$ of the focal image is referred to as aspect ratio $a(z) = \frac{\text {max}[a_x, \, a_y]}{\text {min}[a_x, \, a_y]}$. Due to this definition, the aspect ratio is always greater than one.

Fig. 2

Illustration of the measurement principle: the particle’s focal point (red dots) deforms in the image plane to a vertically or horizontally deformed ellipsoid depending on the particle’s out-of-plane position ($f_{\mathrm{p}}$ = focal length of particle)

As mentioned before, there is a distance between a particle and its focal point, viz., the particle’s focal length, which has to be considered for reconstructing the out-of-plane position of a particle. Measuring this distance is not a difficult task in a non-astigmatic (stigmatic) imaging system, as the system has only one focal plane. This can be done by scanning a stationary particle in z-direction to determine the scanning position at which the particle and its focal point are in focus. As there is no shape change of the focal image in the stigmatic case, the focal point is located in the focal plane when the focal image diameter is minimum. Note that the focal image always appears as a round bright spot in a stigmatic imaging system. For both stigmatic and astigmatic systems, the particle position along the scanning path can be found where the particle center plane is located in the focal plane ($F_{xz} = F_{yz}$). Hence, the focal length can be calculated as the difference between the particle and its focal point position, hereafter referred to as $\varDelta F_{yz} = \varDelta F_{xz}$.

However, in the presence of a cylindrical lens, the imaging system features two focal planes, and hence, the particle’s “focal length” can be determined with respect to both focal planes ($F_{xz}$ and $F_{yz}$). To determine the out-of-plane position of a particle with respect to its focal point, one can choose either $\varDelta F_{xz}$ or $\varDelta F_{yz}$ as a reference length. Preferably, the reference length should be considered which can be determined more accurately. Theoretically, $\varDelta F_{yz}$ and $\varDelta F_{xz}$ should be identical. Nonetheless, because different methods are used to determine the particle’s position and its focal points position, measured values of $\varDelta F_{yz}$ and $\varDelta F_{xz}$ may slightly differ, depending on the refractive index of liquid and particles or the magnification. Hereinafter, the particle’s focal length measured in an astigmatic system is referred to as $\varDelta F_{yz} \approx \varDelta F_{xz}$. Similar to the stigmatic optical system, $\varDelta F_{xz}$ and $\varDelta F_{yz}$ can be deducted from a scanning procedure. Here, the focal point is located in $F_{xz}$ or $F_{yz}$ when the axis length $a_x$ or $a_y$ is minimum, respectively. The particle itself is in focus when either $F_{xz}$ or $F_{yz}$ pass the particle’s center plane during the scanning procedure. Knowing these positions in the depth direction, the focal length of a particle ($\varDelta F_{xz} \approx \varDelta F_{yz}$) can be defined in an astigmatic optical system. The particle’s focal length is approximately linearly proportional to the particle diameter and can be estimated by the lensemaker’s equation (see Sect. 8).

Fig. 3

a Particle images for different depth positions z ($d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$, PMMA, z corrected for 25 wt% glycerol–water solution). b, c ROI for focus measures $f_{xz}$, $f_{yz}$. b Particle is focused on $F_{yz}$. c Particle is focused on $F_{xz}$. d Raw particle image. e Cropped particle image. f Autocorrelation map of e. g Autocorrelation isocontours (red line $c_{\mathrm{a}} =0.7$, green line $c_{\mathrm{a}} =0.4$, blue line $c_{\mathrm{a}} =0.155$)

4 Calibration measurement procedure

To determine the particle’s focal length $\varDelta F_{xz} \approx \varDelta F_{yz}$ as well as the change of the aspect ratio a(z) of the focal image, wall-attached particles are scanned in ${1}\,{\upmu \hbox {m}}$ steps typically over a range of ${500}\,{\upmu \hbox {m}}$ such that the shape change of the focal image and the focusing and defocusing of the particle itself are fully captured, as shown in Fig. 3 for a ${60}\,{\upmu \hbox {m}}$ PMMA particle with $M = 20{\times }$ magnification in a 25 wt% glycerol–water solution. Figure 3b and c shows the particle located in the focal planes $F_{yz}$ and $F_{xz}$, respectively. To determine $\varDelta F_{xz}$ and $\varDelta F_{yz},$ a focus detection algorithm based on the Tenengrad variance is applied in four regions of interest (ROI) at the edge of the particle image and delimited by the green and blue squares in Fig. 3b and c according to Pertuz et al. (2013). The computed values of the Tenengrad variance are a measure for the sharpness of an object image, hence referred to as $f_{xz}$ and $f_{yz}$. The maximum values of $f_{xz}$ (blue ROI) and $f_{yz}$ (green ROI) show that the focal planes $F_{xz}$ and $F_{yz}$ are located at the center plane of the particles, respectively. Please note that the maxima of $f_{xz}$ and $f_{yz}$ can be used to detect the particle center during a scanning procedure to define the absolute coordinate system with respect to the channel wall as will be described in Sect. 9. If the scanning procedure is continued, the particle image defocusses and the focal image is characterized by varying axis lengths $a_x$ and $a_y$ (Fig. 3a, ${-\,75}\,{\upmu \hbox {m}}< z < {+\,75}\,{\upmu \hbox {m}}$). It can be seen that the shape change of the focal image is much more pronounced than the shape change of the particle itself, which almost remains circular. $a_x(z)$ and $a_y(z)$ and their ratio a(z) are determined with an autocorrelation method as indicated in Fig. 3d–g. First, the image of the detected particle (Fig. 3d) is cropped out by the particle radius (see Fig. 3e). Hence, an autocorrelation is applied to the image section and the aspect ratio of the autocorrelation peak is determined by extracting isocontours at a fixed threshold (see Fig. 3f, g). This procedure was found to be insensitive to light intensity fluctuations (Cierpka et al. 2010a). The threshold at which the aspect ratio is determined will hereafter be referred to as autocorrelation threshold $c_{\mathrm{a}}$.

Fig. 4

Calibration measurements in water with PMMA particles of $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ ($c_{\mathrm{a}} = 0.4095$). The z-position where $a_x$ is minimum ($F_{xz}^*$) is taken as reference position $z_0$. a Without cylindrical lens for $M =20{\times }$. b With cylindrical lens for $M = 20{\times }$. c Without cylindrical lens for $M = 10{\times }$. d With cylindrical lens for $M = 10{\times }$. Symbols: black dots = a, blue dots = $f_{xz}$, green dots = $f_{yz}$ (see Fig. 3b, c), red dots = $a_y$ and orange dots = $a_x$

To illustrate the influence of the particle image size and induced astigmatism on the calibration procedure, a ${60}\,{\upmu \hbox {m}}$ PMMA particle is dispersed in water and the same scanning procedure is repeated four times at $M = 20{\times }$ and $M = 10{\times }$ with (astigmatic case) and without cylindrical lens (stigmatic case) (see Fig. 4). The z-position where $a_x(z)$ assumes its minimum value is chosen as the reference position, referred to as $z_0$ such that $a_x(z = z_0)$ assumes a minimum. As expected and shown in Fig. 4a and c, without cylindrical lens, the focal planes $F_{xz}$ and $F_{yz}$ collapse onto each other. This is why the evolution of the particle image sharpness measures $f_{xz}$ and $f_{yz}$ is identical for both magnifications (see Fig. 4a, c). $f_{xz}$ and $f_{yz}$ attain their maximum where the focal plane reaches the center of the particle (highlighted with ${F}_{xz} = {F}_{yz}$); hence, the particle itself is focused (see Fig. 4a, c). As the scanning procedure is continued further, the focal plane ($F_{xz} = F_{yz}$) passes the particle and consequently $f_{xz}$ and $f_{yz}$ decrease again, as the particle itself gets defocused. As $z - z_0$ increases more, the focal planes now get closer to the focal point of the particle. This is illustrated in the insets I1–I3 of Fig. 4a, c with the respective $z - z_0$ positions highlighted by the crosses in the plots. As the focal plane moves toward the particle’s focal point, the axis lengths of the focal image $a_y(z - z_0)$, $a_x(z - z_0)$ shown in Fig. 4a, c decrease till the focal point is located at $F_{xz}^* = F_{yz}^*$ ($z - z_0 = 0$). As no astigmatism is involved in the results presented in Fig. 4a and c, the aspect ratio $a(z - z_0)$ is constantly one. The distance between the particle and its focal point is given by $\varDelta F_{xz} = \varDelta F_{yz}$ (see Fig. 4a, c), which is ${130}\,{\upmu \hbox {m}}$ and ${119}\,{\upmu \hbox {m}}$ for the particle in Fig. 4a and c. The distance between a particle and its focal point can be estimated by the lensemaker’s equation for thick lenses. With the refractive index of the liquid $n_{\mathrm{L}}$ and of the particle $n_{\mathrm{p}}$ the focal length $f_{\mathrm{p}}$ of a ball lens, that is the particle in the present case can be expressed as (1):

$$\begin{aligned} \frac{1}{f_{\mathrm{p}}}=\frac{4 \, (n_{\mathrm{p}}-n_{\mathrm{L}})}{n_{\mathrm{L}}} \frac{\left( n_{\mathrm{p}}-\frac{n_{\mathrm{p}}-n_{\mathrm{L}}}{n_{\mathrm{L}}}\right) }{n_{\mathrm{p}} \, d_{\mathrm{p}}} \end{aligned}$$

(1)

For a PMMA particle with $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ ($n_{\mathrm{p}} = 1.49$) in water ($n_{\mathrm{L}} = 1.333$), the lensemaker’s equation (1) results in $f_{\mathrm{p}}={138}\,{\upmu \hbox {m}}$. This approximates the measured values quite well.

As mentioned before, if astigmatism is involved two focal planes coexist ($F_{xz} \ne F_{yz}$). In this case, $F_{yz}$ is shifted closer toward the camera (see Fig. 2). Thus, $f_{yz}$ assumes its peak value at a lower $z - z_0$ compared to $f_{xz}$ (see Fig. 4b, d) and the aspect ratio $a(z - z_0)$ shows its characteristic M-shape (see black curves in Fig. 4b, d). As mentioned before, the focal image appears circular in the image plane only when the focal point in the object plane is located in-between the focal planes $F_{yx}$ and $F_{zx}$, that is when $a_x = a_y$ (see Fig. 4b, d). The distance between both focal planes can be determined from Fig. 4b, d. This is equal to the distance ${F}_{xz} - {F}_{yz}$ which equals $F_{xz}^* - F_{yz}^*$ (see Fig. 4b, d). For $M = 10{\times }$ (Fig. 4d), this distance is significantly larger than for $M = 20{\times }$ (Fig. 4b). The distance between the particle and its focal point is given by $\varDelta F_{xz} \approx \varDelta F_{yz}$ that is $\varDelta F_{xz}={136}\,{\upmu \hbox {m}} \approx \varDelta F_{yz}={135.6}\,{\upmu \hbox {m}}$ for $M = 20{\times }$ and $\varDelta F_{xz}={107.33}\,{\upmu \hbox {m}} \approx \varDelta F_{yz}={94}\,{\upmu \hbox {m}}$ for $M = 10{\times }$ as depicted in Fig. 4b and d, respectively. Thus, there is a good agreement with Eq. (1) for $M = 20{\times }$. However, the discrepancy observed for $M = 10{\times }$ requires further investigations to be explained in future.

For an overview on the effect of magnification, the properties of the cylindrical lens, the distance of the focal planes on the measurement range in the context of conventional APTV, the reader is referred to Chen et al. (2009), Cierpka et al. (2010a) and Rossi and Kähler (2014).

Fig. 5

Maximum light intensity of the focal image for a $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ PMMA particle in water. Pink dots = without cylindrical lens, light blue dots = with cylindrical lens a $M = 20{\times }$. b $M = 10{\times }$. The focal planes are highlighted by the dashed lines

Fig. 6

$a_x$ as function of $a_y$ for a $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ PMMA particle in water (corresponding to Fig. 4) ($c_{\mathrm{a}} = 0.4095$). The color map indicates the out-of-plane position $z - z_0$. a $M = 20{\times }$, without cylindrical lens. b $M = 20{\times }$, with cylindrical lens. c $M = 10{\times }$, without cylindrical lens. d $M = 10{\times }$, with cylindrical lens

Figure 5a and b displays the evolution of the light intensity of the focal image for a $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ PMMA particle in water for $M = 20{\times }$ and $M = 10{\times }$, with and without cylindrical lens. For $M = 20{\times }$ the evolution of the light intensity with and without cylindrical lens remains similar (Fig. 5a). In contrast, for $M = 10{\times }$ the light intensity exhibits two peaks close to ${F}^*_{yz}$ and ${F}^*_{xz}$ when a cylindrical lens is mounted in the system (Fig. 5b). This is because the distance between the focal planes $F_{yz} - F_{xz}$ is significantly larger for $M = 10{\times }$ than for $M = 20{\times }$ (see Fig. 5a, b). Please note that the effective magnification is higher in the stigmatic case, as the distance between field lens and camera sensor is altered ($M_{\mathrm{stig}}/M_{\mathrm{astig}} \approx$ 125%). This is why for $M = 20{\times },$ the maximum light intensity is higher in the astigmatic case (see Fig. 5a). Figure 6a–d shows $a_x$ as function of $a_y$ for a $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ PMMA particle in water with $M = 20{\times }$ and $M = 10{\times }$, each with and without cylindrical lens. As can be seen, $a_x$ is directly proportional to $a_y$ in the stigmatic case (Fig. 6a, c). When astigmatism is introduced, $a_x$ plotted over $a_y$ shows a characteristic curled curve (Fig. 6b, d). Thus, every $a_y$, $a_x$ pair is associated with just one $z - z_0$ value (Fig. 6b, d). This form of representation is the base for the out-of-plane reconstruction based on the Euclidean calibration approach which will be discussed and utilized in the next section.

5 Reconstruction of the out-of-plane particle position and outlayer detection

The calibration procedure described in Sect. 4 is repeated for several particles randomly distributed over the field of view. The major steps to generate a calibration function from which the out-of-plane particle positions can be determined are illustrated in Fig. 7 for a total number of 36 calibration particles. In fact, for all results presented later in this work at least ten calibration particles have been used. In the first step, $a_x(z - z_0)$, $a_y(z - z_0)$ and the maximum intensity $I(z - z_0)$ of all focal images that are taken at different out-of-plane positions ($z - z_0$) are superimposed. Hence, the median curve of I is generated, denoted as ${\overline{I}}$ (see Fig. 7a). From the median intensity curve ${\overline{I}},$ the maximum value ${\overline{I}}_{{\mathrm{max}}}$ is determined (see Fig. 7a). The out-of-plane measurement volume depth $\varDelta z$ is determined by only considering data that fulfills the following criterion: $I \ge {\overline{I}}_{\mathrm{max}} \cdot c_{\mathrm{I}}$ (see vertical dashed lines in Fig. 7a). $c_{\mathrm{I}}$ is hereafter referred to as the intensity coefficient, and its influence on the relative measurement accuracy will be discussed in Sect. 6. In the next step, a polynomial of 14th order is fitted to the $a_x$ and $a_y$ scatter data. The resulting fitting curves $\overline{a_x}(z - z_0)$ and $\overline{a_y}(z - z_0)$ are shown in Fig. 7b. The actual calibration function now consists of three data sets, $\overline{a_x}$, $\overline{a_y}$ and $z - z_0$ which can be represented as one calibration curve with $\overline{a_x}$ plotted as function of $\overline{a_y}$, see Fig. 7c. This is known as the 2D calibration curve in APTV. For the sake of clarity, we divide the calibration curve into three equal sections A, B and C with respect to the depth position $z - z_0$. The section borders are indicated with white dots in Fig. 7b–f.

Fig. 7

Procedure of generating a calibration function. Scale of colormap in b–f is given in e. $z - z_0$ data are corrected for refractive index of a 25 wt% glycerol–water solution ($d_{\mathrm{p}}={30}\,{\upmu \hbox {m}}$, $M = 20{\times }$, $c_{\mathrm{a}} = 0.7$, $c_{\mathrm{I}} = 0.7$, $c_{\mathrm{D}} = 2$). a Selecting $z - z_0$ range of scattered data by light intensity I (light blue dots = $a_x$, dark blue dots = $a_y$, green dots = I, black line = ${\overline{I}}$). b Fitting polynomials of degree 14 to $a_x$ and $a_y$ (black line = polynomials $\overline{a_x}$, $\overline{a_y}$). c Reconstruction of $z - z_0$ of scattered $a_x\text{-}a_y$ data (colored dots) by Euclidean distance with the 2D calibration curve (black line = polynomial, red dot = outliers). d Fitting polynomials of degree 14 to I (black line = polynomial ${\overline{I}}$). e Reconstruction of $z - z_0$ of scattered $a_x\text{-}a_y\text{-}I$ data (colored dots) by Euclidean distance with the 3D calibration curve in the $a_y\text{-}a_x\text{-}I$ space (black line = polynomials). f Position reconstruction error $z' - z$ plotted over $z - z_0$ obtained with the 3D calibration curve (colored dots) and the 2D calibration curve (black dots). The uncertainty of the 2D and 3D position reconstruction procedure is $\sigma _z^*={1.71}\,{\upmu \hbox {m}}$ and $\sigma _z^*={1.18}\,{\upmu \hbox {m}}$, respectively

As mentioned before, $z_0$ is the relative z-position where $a_x$ assumes its minimum value. With these data at hand, we can reconstruct the z-position of the focal point of a particle with respect to $z_0$. Fig. 7c shows the scatter data of $a_x$ plotted as a function of $a_y$ and the calibration curve obtained from $\overline{a_x}$ plotted over $\overline{a_y}$. To determine the $z - z_0$ position, measured $a_x$, $a_y$ values are associated with a point on the calibration curve that is given by the minimum Euclidean distance (see Fig. 7c). Hence, this method is referred to as the Euclidean method and is described in detail by Cierpka et al. (2010a). If the Euclidean distance of a pair of $a_x$, $a_y$ values exceeds a certain threshold, the measurement data are rejected. This threshold will be hence referred to as $a_{\mathrm{D}}$ and is defined as the mean Euclidean distance of all $a_x$ and $a_y$ pairs of all calibration particle images multiplied by the factor $c_{\mathrm{D}}$ (2):

$$\begin{aligned} a_{\mathrm{D}} = \frac{c_{\mathrm{D}}}{N} \sum _{i=1}^{N} \text {min} \sqrt{(\overline{a_x} - a_{x,i})^2 + (\overline{a_y} - a_{y,i})^2} \end{aligned}$$

(2)

with N being the total number of the calibration particle images. For the given case, the factor is set to $c_{\mathrm{D}} = 2$ with the detected outliers indicated as red dots in Fig. 7c.

Particles may differ in terms of shape, roughness and refractive index such that their $a_x$, $a_y$, I or $z - z_0$ data deviate from the majority of the particles. Moreover, we noticed that the change of the particles light intensity can be used as additional information to encode the particles depth position. It is also observed that the calibration curve may intersect in the $a_y$, $a_x$ space resulting in a large uncertainty in estimating the depth position of a particle (see Sect. 6). To reduce such problems, we use the information of the particles light intensity as an extra parameter to increase the accuracy and robustness of the calibration procedure. In fact, using a polynomial fit of 14th degree to the I scattered data ${\overline{I}}(z - z_0)$ (see Fig. 7d), we extend the 2D ($a_y - a_x$) calibration curve to 3D $a_y\text{-}a_x\text{-}I$ space (see Fig. 7e). As for the 2D case, the $z - z_0$ position of scattered data is determined by assigning measured $a_x\text{-}a_y\text{-}I$ values to a point on the calibration curve that is given by the minimum 3D Euclidean distance (see Fig. 7e). To facilitate computation of the 3D Euclidean distance, the light intensity is transformed to the same order of magnitude as $a_y$ and $a_x$ by normalization with ${\overline{I}}_{\mathrm{max}}$ and multiplication with the maximum width or height of the 2D calibration curve. Data points which are too far away from the 3D-calibration curve are rejected as indicated with red dots in Fig. 7e. Similar to the 2D case, the threshold $a_{\mathrm{D}}$ for rejecting data is defined as the mean Euclidean distance of all $a_x$, $a_y$ and I pairs of the calibration set multiplied by a factor $c_{\mathrm{D}}$ (3):

$$\begin{aligned} a_{\mathrm{D}} = \frac{c_{\mathrm{D}}}{N} \cdot \sum _{i=1}^{N} \text {min} \sqrt{(\overline{a_x} - a_{x,i})^2 + (\overline{a_y} - a_{y,i})^2 + ({\overline{I}} - I_{i})^2} \end{aligned}$$

(3)

For the given case, the factor is set to $c_{\mathrm{D}} = 2$.

From Fig. 7c, a strong increase in the 2D calibration curve curvature becomes evident in regions A and C, while the curve is almost linear in region B. Furthermore, the arclength of A is small compared to B and C. These topological differences result in different depth position reconstruction accuracies in A, B and C as depicted with the black dots in Fig. 7f. Here, we show the difference of the reconstructed depth position $z' - z_0$ and the true scanning position $z - z_0$ ($z' - z$) as a function of $z - z_0$ (Fig. 7f). As can be seen the out-of-plane reconstruction error with the 2D calibration, curve sharply increases in regions A and C where the curvature assumes maximum values. In contrast to this, the 3D calibration curve enables a more accurate assignment of data and significantly reduces the error in regions A and C (see colored dots in Fig. 7f). This leads to a total reduction of 30% in the reconstruction uncertainty for the 3D calibration procedure in comparison with the 2D one ($\sigma _z^*={1.71}\,{\upmu \hbox {m}}$ for 2D vs $\sigma _z^*={1.18}\,{\upmu \hbox {m}}$ for 3D). Furthermore, the 3D reconstruction procedure increases the number of valid data points which are $N_{\text {valid}} = 1995$ and $N_{\text {valid}} = 2120$ (+ 6%) for the 2D and the 3D case, respectively.

With the steps mentioned above, we reconstruct the out-of-plane position of the particle’s focal point relative to $z_0$ with $\sigma _z^*$ being the associated uncertainty. To determine the absolute uncertainty in reconstructing the particle’s out-of-plane position, the uncertainty in determining the particle’s focal length $\varDelta F_{yz} \approx \varDelta F_{xz}$ has to be considered: ${\sigma }_z = \sqrt{\sigma _z^{*2}+\sigma (\varDelta F_{xz})^2}$. Therefore, the overall reconstruction accuracy of the out-of-plane particle position of a ${30}\,{\upmu \hbox {m}}$ PMMA particle in the given example is ${\sigma }_z={3.11}\,{\upmu \hbox {m}}$ and ${\sigma }_z={2.85}\,{\upmu \hbox {m}}$ for the 2D and the 3D calibration curve, respectively. A detailed analysis of the out-of-plane reconstruction accuracy for different particle sizes is given in Sect. 8.

6 The influence of the autocorrelation threshold $c_{\mathrm{a}}$ on the relative out-of-plane reconstruction accuracy

The relative out-of-plane reconstruction uncertainty $\sigma _z^*/\varDelta z$ depends on the choice of the threshold values $c_{\mathrm{a}}$ and $c_{\mathrm{I}}$. Therefore, an optimization study is performed for both threshold values $c_{\mathrm{I}}$ of the focal image light intensity and $c_{\mathrm{a}}$ of the autocorrelation. The optimization study is done with $M = 20{\times }$ and PMMA particles of $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ diameter in water. To account for the aberrations of particle images at different in-plane positions, calibration particles (here 14 particles) are randomly distributed over the whole field of view. As, the signal strength of the focal image depends on the light sensitivity of a camera, the same measurements are taken with a light-sensitive CCD camera (LaVision Imager Pro SX) and a CMOS camera (Miro 110 Phantom). To ensure comparability of both cameras, the same group of particles is used for both calibrations. For both parameter sets, we determine the optimum combination of $c_{\mathrm{a}}$ and $c_{\mathrm{I}}$ that leads to a minimum relative out-of-plane reconstruction uncertainty $\sigma _z^*/\varDelta z$ ($0< c_{\mathrm{a}} <1$ and $0< c_{\mathrm{I}} <1$). The resulting uncertainties are plotted in Fig. 8a and b as function of $c_{\mathrm{a}}$, for the optimum value of $c_{\mathrm{I}}$ for both camera types. As $c_{\mathrm{I}}$ only affects $\varDelta z$, whereas $c_{\mathrm{a}}$ affects $\sigma _z^*$ as well, we focus on discussing $c_{\mathrm{a}}$ for fixed $c_{\mathrm{I}}$.

Different light intensities are used, given here as ratio of the median image intensity of the whole image $c_{{\mathrm{med}}}$ and the maximum camera intensity $c_{{\mathrm{max}}}$, which is 8-bit (4096 counts) for both the CCD and the CMOS camera. Tests showed that the median of the whole image $c_{{\mathrm{med}}}$ is equal to the median of the background intensity without the particles. Hence, $c_{{\mathrm{med}}}/c_{{\mathrm{max}}}$ describes the normalized background illumination intensity. As we use backlight illumination, the background intensity is directly proportional to the illumination intensity. Hence, the parameter $c_{{\mathrm{med}}}/c_{{\mathrm{max}}}$ can be easily adjusted prior to the measurements by simply increasing the illumination intensity. The influence of the light intensity will be discussed in Sect. 7 in further detail.

Fig. 8

$\sigma _z^*/\varDelta z$ over $c_{\mathrm{a}}$ for different $c_{{\mathrm{med}}}/c_{{\mathrm{max}}}$. All data are presented using optimal $c_{\mathrm{I}}$ ($M = 20{\times }$, $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$, water, $c_{\mathrm{D}} = 3$). a CCD camera. b CMOS camera

Fig. 9

Calibration curves in $a_x \text{-} a_y$-space (I) and $a_x \text{-} a_y \text{-} I$-space (II) corresponding to A, B, C, D in Fig. 8b (CMOS, $c_{\mathrm{med}}/c_{\mathrm{max}} = 0.115$, $c_{\mathrm{I}} = 0.375$, $M = 20{\times }$, $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$, $c_{\mathrm{D}} = 3$, $z - z_0$ corrected for water). a $c_{\mathrm{a}} = 0.11$ (A) b $c_{\mathrm{a}} = 0.33$ (B) c $c_{\mathrm{a}} = 0.6637$ (C) d $c_{\mathrm{a}} = 0.85$ (D)

Four characteristic regions of $c_{\mathrm{a}}$ can be identified in Fig. 8a and b denoted as A–D. Obviously, a range of $c_{\mathrm{a}}$ values between $0.40< c_{\mathrm{a}} <0.75$ (denoted with C) leads to uncertainties $\sigma _z^*/\varDelta z$ below 2% for both camera types. The corresponding, optimized $c_{\mathrm{I}}$ values are given in the legend. For lower or higher values of $c_{\mathrm{a}}$ (regions denoted with A, B and D in Fig. 8), the relative out-of-plane reconstruction uncertainty sharply increases due to ambiguities in the corresponding calibration curves. This can be better understood from the calibration curves in the $a_y \text{-} a_x \text{-} I$-space as plotted in Fig. 9a–d. Here, we report the 3D calibration curves (Fig. 9a–d II) and their projections onto the $a_y \text{-} a_x$ plane (Fig. 9a–d I). Please note that Fig. 9a–d correspond to regions A–D in Fig. 8a and b. While the calibration curves shown in Fig. 9a and c are continuous without intersections, those corresponding to regions B and D in Fig. 8a and b exhibit a sharp kink (see Fig. 9b) or intersect in the $a_x \text{-} a_y \text{-} I$-space (see Fig. 9d). These characteristics lead to local ambiguities during the Euclidean reconstruction procedure and hence a sharp increase in the relative out-of-plane reconstruction uncertainty $\sigma _z^*/\varDelta z$. It may be noted that the $a_x$ and $a_y$ data are typically used in fluorescence APTV. In the present study, information on I are additionally utilized to derive 3D calibration curves for BLAPTV. Figure 9c I and II reveals that ambiguities in the 2D $a_x \text{-} a_y$ space can be avoided by this extended calibration, giving rise to an improvement evaluation accuracy with a stable $c_{\mathrm{a}}$ range of low relative out-of-plane reconstruction accuracies $\sigma _z^*/\varDelta z$ as mentioned earlier (see region C in Fig. 9a, b). Furthermore, preliminary tests (not shown here) indicate that significant improvements in the reconstruction accuracy may also be realized for fluorescence APTV by utilizing calibration curves in $a_x \text{-} a_y \text{-} I$-space. Finally, Fig. 8a and b indicates that lower light intensities corresponding to lower values of $c_{{\mathrm{med}}}/c_{{\mathrm{max}}}<0.45$ lead to a reduction in the relative out-of-plane reconstruction uncertainty $\sigma _z^*/\varDelta z$.

For the cases under investigation, the in-plane position of particles has a negligible effect on the reconstruction accuracy compared to other parameters such as $c_{\mathrm{a}}$, $c_{\mathrm{I}}$ and $c_{\mathrm{D}}$. As said before, in this study each calibration is performed using particles that are randomly distributed across the field of view. Hence, the resulting calibration curve can be considered as an averaged calibration curve. For all calibration measurements, the mean value of the depth position reconstruction error for all individual particles is monitored. The results show a negligible difference in the reconstruction accuracy with respect to the in-plane particle position and associated aberrations. However, if the 3D calibration is applied to situations where a strong gradient of I is present across the image or $a_x$ and $a_y$ depend on the in-plane particle position, the in-plane position of particles has to be taken into account as well in the calibration.

Fig. 10

Optimized parameter values associated with minimum $\sigma _z^*/\varDelta z$ plotted over $c_{{\mathrm{med}}}/c_{{\mathrm{max}}}$ obtained with the 3D (solid lines) and the 2D (dashed lines) calibration procedure ($M = 20{\times }$, $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$, water, $c_{\mathrm{D}} = 3$). a Influence of $c_{{\mathrm{med}}}/c_{{\mathrm{max}}}$ on $\sigma _z^*/\varDelta z$. b Maximum SNR as a function of $c_{{\mathrm{med}}}/c_{{\mathrm{max}}}$. c Influence of $c_{{\mathrm{med}}}/c_{{\mathrm{max}}}$ on $\varDelta z$. d Influence of $c_{\mathrm{med}}/c_{{\mathrm{max}}}$ on valid particle images $N_{\text {valid}}$. e Influence of $c_{{\mathrm{med}}}/c_{{\mathrm{max}}}$ on $c_{\mathrm{I}}$. f Influence of $c_{\mathrm{med}}/c_{{\mathrm{max}}}$ on $c_{\mathrm{a}}$

7 The effect of the light intensity

Due to the ball lens effect, the light intensity of the focal image is much higher compared to the background light intensity. Thus, the ratio of focal image and background intensity, denoted here as signal-to-noise ratio, varies for different particle materials, magnifications, particle sizes and liquid–particle combinations. It even varies with the depth position of a particle (see Sect. 9). Thus, in practice it may not be feasible to adjust the light intensity for each particle species, especially in a polydisperse suspension.

In the present section, we investigate how the relative light intensity, defined here as the ratio between median image intensity $c_{\mathrm{med}}$ and the grayscale depth (maximum counts) of the camera $c_{{\mathrm{max}}}$, influences the minimum achievable relative out-of-plane reconstruction uncertainty of a particle $\sigma _z^*/\varDelta z$ (Fig. 10a). Hence, the signal-to-noise ratios (SNR), the measurement volume depths $\varDelta z$, the number of valid data points $N_{\text {valid}}$ and the $c_{\mathrm{I}}$ and $c_{\mathrm{a}}$ values that result from the optimization study (shown in Figs. 10b–f) are discussed. From Fig. 10a, it can be seen that $\sigma _z^*/\varDelta z$ assumes a minimum around $c_{\mathrm{med}}/c_{{\mathrm{max}}} \approx 0.1$. Please note that $\sigma _z^*/\varDelta z$ assumes just slightly larger values for the CMOS camera in comparison with the CCD camera for $c_{\mathrm{med}}/c_{{\mathrm{max}}} <0.5$. This is remarkable, as the resolution of the CMOS camera is significantly lower than the resolution of the CCD camera, that is ${1.78}\,{\upmu \hbox {m}}$ and ${0.29}\,{\upmu \hbox {m}}$ per pixel at $M = 20{\times }$, respectively. For larger relative intensity values $c_{\mathrm{med}}/c_{{\mathrm{max}}}$, the relative uncertainty $\sigma _z^*/\varDelta z$ increases.

The increase in $\sigma _z^*/\varDelta z$ is accompanied with a decrease in the maximum signal-to-noise ratio (SNR) as shown in Fig. 10b. Here, the SNR is defined as the maximum intensity of the focal image (${\overline{I}}_{\text {max}}$) divided by the median of the background light intensity. As can be seen from Fig. 10b, the SNR increases with decreasing intensity $c_{\mathrm{med}}/c_{{\mathrm{max}}}$. This trend is counterintuitive and is reversed for very low values of $c_{\mathrm{med}}/c_{{\mathrm{max}}}$. As $c_{\mathrm{med}}/c_{{\mathrm{max}}}$ drops below $c_{\mathrm{med}}/c_{{\mathrm{max}}} <0.042$ for the CCD camera, the SNR decreases again due to the vanishing image contrast (Fig. 10b). On the other hand, it can be understood easily why the SNR decreases for $c_{\mathrm{med}}/c_{{\mathrm{max}}} >0.2$ and $c_{\mathrm{med}}/c_{{\mathrm{max}}} >0.4$ for the CCD and the CMOS camera, respectively. This is related to an overexposure of the focal image as indicated in Fig. 11a and b in which we display the evolution of the median light intensity of the focal image of all 14 particles ${\overline{I}}(z - z_0)$ for the CCD and CMOS camera. As the light intensity exceeds $c_{\mathrm{med}}/c_{{\mathrm{max}}} >0.236$ for the CCD and $c_{\mathrm{med}}/c_{{\mathrm{max}}} >0.45$ for the CMOS camera, the curve peak transforms into a plateau. Thus, the maximum exposure of the camera chip is reached. These limits are also indicated in Fig. 10a–f with vertical dashed lines for the CCD (blue) and CMOS (red) camera. Overall, for $c_{\mathrm{med}}/c_{{\mathrm{max}}} \le 0.6$ uncertainties $\sigma _z^*/\varDelta z$ stay below 2%, thus the measurement technique is also applicable outside the optimal range of illumination, though loosing accuracy.

Fig. 11

Median of I (${\overline{I}}$) over $z - z_0$ for different $c_{\mathrm{med}}/c_{{\mathrm{max}}}$. Horizontal lines: $c_{\mathrm{I}} \cdot {\overline{I}}_{{\mathrm{max}}}$. $M = 20{\times }$, $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$, $z - z_0$ corrected for refractive index of water. a) ${\overline{I}}$ over $z - z_0$ (CCD). b) Particle image at $c_{\mathrm{med}}/c_{{\mathrm{max}}} = 0.015$ (CCD). c) Particle image at $c_{\mathrm{med}}/c_{{\mathrm{max}}} = 0.511$ (CCD). d) ${\overline{I}}$ over $z - z_0$ (CMOS) e) Particle image at $c_{\mathrm{med}}/c_{{\mathrm{max}}} = 0.115$ (CMOS). f) Particle image at $c_{\mathrm{med}}/c_{{\mathrm{max}}} = 0.783$ (CMOS)

From Fig. 10a, a strong increase in $\sigma _z^*/\varDelta z$ also becomes evident for the CCD camera when $c_{\mathrm{med}}/c_{{\mathrm{max}}} < 0.1$. This can be better understood from Fig. 10c where the effective measurement volume depth $\varDelta z$ for BLAPTV is plotted as function of the relative light intensity. Here, $\varDelta z$ drops sharply for $c_{\mathrm{med}}/c_{{\mathrm{max}}} < 0.042$, leading to an increase in relative uncertainty $\sigma _z^*/\varDelta z$. We assume that the decrease of $\varDelta z$ originates from weaker signals of focal images with a focal point located behind or in front of the reference plane. In addition, we observed that with decreasing $c_{\mathrm{med}}/c_{{\mathrm{max}}} <0.1$ the detection of particle centers is increasingly erroneous. This leads to false $a_x$ and $a_y$ data and hence creates high uncertainties. The increasing number of misdetections for low values of $c_{\mathrm{med}}/c_{{\mathrm{max}}}$ also leads to large standard deviations of the measured particle’s focal length as will be discussed later in this section. Figure 10a and c displays the evolution of the relative uncertainty and effective measurement volume depth for a 3D calibration procedure in $a_x \text{-} a_y \text{-} I$ space (solid lines) and the 2D calibration in $a_x \text{-} a_y$ space (dashed lines). It may be noted that the 3D calibration procedure decreases the relative uncertainty and increases the effective measurement volume depth. Furthermore, utilizing a 3D calibration procedure increases the number of valid data points $N_{\text {valid}}$ up to 26% (see Fig. 10d). The minimum relative uncertainty is determined based on an optimization of the $c_{\mathrm{I}}$ and $c_{\mathrm{a}}$ combinations for all tested light intensities. These values are plotted in Fig. 10e and f. Overall, the optimal values of $c_{\mathrm{I}}$ decrease, and hence, $\varDelta z$ increases, if 3D calibration curves are utilized instead of 2D calibrations in the $a_x \text{-} a_y$ plane. Moreover, from Fig. 10f it can be seen that the optimal values of $c_{\mathrm{a}}$ differ for the CCD and CMOS camera depending on $c_{\mathrm{med}}/c_{{\mathrm{max}}}$ and they are in the range of $0.38< c_{\mathrm{a}} <0.7$ (CCD) and $0.6< c_{\mathrm{a}} <0.7$ (CMOS) for $c_{\mathrm{med}}/c_{{\mathrm{max}}}$ values below the onset of overexposure.

As discussed above, the relative light intensity has a significant influence on the accuracy of the out-of-plane particle reconstruction. This can be better understood when the effect of $c_{\mathrm{med}}/c_{{\mathrm{max}}}$ on the shape of the calibration curves is analyzed. For this, Fig. 12 depicts the calibration curves for selected values of $c_{\mathrm{a}}$ and $\varDelta z$ for both the CCD and the CMOS camera. As can be seen from Fig. 12a–d, an increase in light intensity leads to an overall decrease in the calibration curve length. Furthermore, it can be observed that the significance of this shape change depends on $c_{\mathrm{a}}$. Comparing Fig. 12a and b, a much higher deformation of the calibration curve can be seen for $c_{\mathrm{a}} = 0.118$ in comparison with $c_{\mathrm{a}} = 0.7$. Here, we conclude that if the light intensity varies significantly across the image, the particle in-plane position has to be taken explicitly into account during the calibration procedure.

Fig. 12

Influence of light intensity ($c_{\mathrm{med}}/c_{{\mathrm{max}}}$) on the calibration curve shape in the $a_x \text{-} a_y$ plane for a single particle and fixed $c_{\mathrm{a}}$ and $\varDelta z$. a CCD, $c_{\mathrm{a}} = 0.118$, $\varDelta z={130}\,{\upmu \hbox {m}}$ b CCD, $c_{\mathrm{a}} = 0.7$, $\varDelta z={112}\,{\upmu \hbox {m}}$ c CMOS, $c_{\mathrm{a}} = 0.118$, $\varDelta z={217}\,{\upmu \hbox {m}}$ d CMOS, $c_{\mathrm{a}} = 0.627$, $\varDelta z={180}\,{\upmu \hbox {m}}$

Fig. 13

Effect of increasing light intensity $c_{\text {med}}/c_{\text {max}}$ on the measured focal length of $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ PMMA particles in water for CCD and CMOS camera ($M = 20{\times }$, $c_{\mathrm{a}} = 0.7$ (CCD), $c_{\mathrm{a}} = 0.6274$ (CMOS)). The horizontal black line indicates the focal length calculated by the lensemaker’s equation (1). The vertical blue and red dotted lines highlight the onset of overexposure for the CCD and the CMOS camera, respectively

As the light intensity affects the calibration curves, the question arises if it also affects the measured focal length of the particle, which is considered to be constant in theory. Fig. 13 shows the measured values of $\varDelta F_{xz}$ and $\varDelta F_{yz}$ plotted versus $c_{\mathrm{med}}/c_{{\mathrm{max}}}$ for both the CCD and the CMOS camera. As can be seen for $0.015< c_{\mathrm{med}}/c_{{\mathrm{max}}} <0.5,$ the measured values of $\varDelta F_{xz}$ and $\varDelta F_{yz}$ are in good agreement with the lensemaker’s equation (black horizontal line). In particular, the values obtained with the CMOS camera show an excellent agreement. As already stated before, for $c_{\mathrm{med}}/c_{{\mathrm{max}}} <0.015$ the detection of the particle centers becomes increasingly erroneous, leading to a sharp increase in $\varDelta F_{xz}$ accompanied by large standard deviations of $\varDelta F_{xz}$ and $\varDelta F_{yz}$ (vertical error bars). For $c_{\mathrm{med}}/c_{{\mathrm{max}}} >0.6,$ (CMOS) measured values for $\varDelta F_{xz}$ show significant deviations from the lensemaker’s equation, yet for $\varDelta F_{yz}$ there is still a good agreement. Overall, we conclude that changes in $c_{\mathrm{med}}/c_{{\mathrm{max}}}$ have a significant effect on the shape of the calibration curves, whereas the measured focal length of the particle, as a intrinsic feature of the particle itself, remains approximately constant. We will reconsider this observation in Sect. 9.

8 Influence of particle size, material, liquid and magnification on the calibration properties

As BLAPTV is based on light being focused by particles, the optical properties of the system and the particles have an influence on the measurement technique. In this section, we present a parametric study to understand the influence of the particle diameter $d_{\mathrm{p}}$, the refractive index jump between particle and surrounding fluid $\varDelta n = n_{\mathrm{p}} - n_{\mathrm{L}}$ and the magnification M.

From the lensemaker’s equation (1), we conclude that the particle’s focal length and hence $\varDelta F_{xz} \approx \varDelta F_{yz}$ will increase linearly with increasing $d_{\mathrm{p}}$ and decreasing refractive index jump between particle and liquid ($\varDelta n = n_{\mathrm{p}} - n_{\mathrm{L}}$). As these parameters determine the aperture of the focused light behind a particle, they are expected to affect $I_{{\mathrm{max}}}$, $a_x$, $a_y$ and hence the aspect ratio $a(z - z_0)$ as a function of the out-of-plane position $z - z_0$. For the sake of comparison, the threshold for the autocorrelation and the threshold for the light intensity are kept constant in the following ($c_{\mathrm{a}} = 0.4095$, $c_{\mathrm{I}} = 0.77$). These values are found to provide satisfactory accuracy for the particle sizes and liquids discussed in this section. In Fig. 14a–c, calibration measurements for single PMMA particles of $d_{\mathrm{p}}={30}\,{\upmu \hbox {m}}$, ${60}\,{\upmu \hbox {m}}$ and ${124}\,{\upmu \hbox {m}}$ are presented for a 25 wt% glycerol–water solution at a magnification of $M = 20{\times }$. With increasing $d_{\mathrm{p}},$ a wider range of $z - z_0$ is covered by $a_y(z - z0)$ and $a_x(z - z0)$ (red and orange dots in Fig. 14a–c). This leads to an increase in measurement volume depth $\varDelta z$ as given in Fig. 15a, which can be understood from Fig. 15b. Here, the maximum focal image intensity is plotted as function of the out-of-plane position $z - z_0$. For increasing particle sizes, a larger $\varDelta z$ is determined, as a larger particle provides a sufficiently strong focal image signal over a bigger $z - z_0$ range (indicated by dashed lines). It may be noted that, for large particles the measurement volume depth $\varDelta z$ exceeds the distance between the focal planes by far ($F_{yx} - F_{xz}={21}\,{\upmu \hbox {m}}$ in Figs. 14 and 15). This is a significant difference to conventional APTV with small particles where it is assumed that the measurement range is primarily defined by the distance of the focal planes (Cierpka et al. 2010a).

Fig. 14

Effect of particle size on the axis lengths $a_y(z - z_0)$, $a_x(z - z_0)$ and measured particle focal lengths $\varDelta F_{yz}$, $\varDelta F_{xz}$. $z - z_0$ is corrected for the refractive index of a 25 wt% glycerol–water solution ($M = 20{\times }$, $c_{\mathrm{a}} = 0.4095$, $c_{\mathrm{I}} = 0.77$, CCD camera). Symbols: red dots = $a_y$, orange dots = $a_x$, green dots = $f_{yz}$, blue dots = $f_{xz}$. a $d_{\mathrm{p}}={30}\,{\upmu \hbox {m}}$ b $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ c $d_{\mathrm{p}}={124}\,{\upmu \hbox {m}}$

Figure 14a–c indicate a linear increase in the measured particle’s focal length with increasing $d_{\mathrm{p}}$, as also depicted in Fig.15c: $\varDelta F_{yz}$ (dashed lines with filled squares) and $\varDelta F_{xz}$ (bold lines with filled circles). This is in agreement with the lensemaker’s equation (1), where the particle’s focal length increases linearly with $d_{\mathrm{p}}$. However, as can be seen from Fig. 15c $\varDelta F_{yz}$ and $\varDelta F_{xz}$ deviate from the particle’s focal length obtained by the lensemaker’s equation (solid thin lines) as the refractive index of the liquid increases. While for water the agreement of measured and calculated values is quite good (red lines), obviously this is not the case when the refractive index difference between particle and liquid is increased (see Fig. 15c). As already stated in Sect. 3, here further investigations are required to understand the reasons for this discrepancy.

In general, we observe that the shape change and hence the change of the aspect ratio as function of the out-of-plane position is more pronounced with decreasing focal image size. As the size of the focal image increases with the particle size, it can be understood that the uncertainty of the out-of-plane particle reconstruction $\sigma ^*_z$ grows with the particle size as shown in Fig. 15d. Also a decrease in $\varDelta n = n_{\mathrm{p}} - n_{\mathrm{L}}$ is associated with a decrease in focal angle of light rays that are bundled by the particle. Hence, a decreased focal image deformation is observed when moving along the out-of-plane direction. Therefore, $\sigma ^*_z$ grows when $\varDelta n = n_{\mathrm{p}} - n_{\mathrm{L}}$ decreases, as shown in Fig. 15d. A further overview of measured values of $\sigma ^*_z$, $\sigma _z$, $\varDelta F_{yz}$ and $\varDelta F_{xz}$ for different particle sizes and different ratios of glycerol and water is provided in “Appendix” (see Table 3).

Fig. 15

Effect of $d_{\mathrm{p}}$ on the calibration data ($M = 20{\times }$, $c_{\mathrm{a}} = 0.4095$, $c_{\mathrm{I}} = 0.77$, $c_{\text {D}} = 3$, CCD camera). Symbols: red dots = 0 wt% ($n_{\mathrm{L}} = 1.333$), green dots = 25 wt% ($n_{\mathrm{L}} = 1.364$), dark blue dots =50 wt% ($n_{\mathrm{L}} = 1.398$) glycerol–water solution, pink dots = $d_{\mathrm{p}}={30}\,{\upmu \hbox {m}}$, light blue dots = $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$, orange dots = $d_{\mathrm{p}}={124}\,{\upmu \hbox {m}}$. a Effect of $d_{\mathrm{p}}$ and refractive index of liquid on $\varDelta z$. b Effect of $d_{\mathrm{p}}$ on $I(z - z_0)$ ($z - z_0$ corrected for refractive index of 25 wt% glycerol–water solution). c Effect of $d_{\mathrm{p}}$ on $\varDelta F_{xz}$ (solid line with filled circles), $\varDelta F_{yz}$ (dashed line with filled squares) and on the focal length $f_{\mathrm{p}}$ of a particle according to the Lensemaker’s equation (1) (solid dotted line). d Effect of $d_{\mathrm{p}}$ on $\sigma _z^*$

Fig. 16

Effect of $d_{\mathrm{p}}$ and refractive index jump on the calibration curves ($c_{\mathrm{a}} = 0.4095$, $c_{\mathrm{I}} = 0.77$, CCD camera). For $d_{\mathrm{p}}={30}\,{\upmu \hbox {m}}$ and $M = 10{\times }$ the particle and focal image size and quality are not sufficient enough for evaluating. a $M = 20{\times }$, PMMA, 25 wt% ($n_{\mathrm{L}} = 1.364$). b $M = 10{\times }$, PMMA, 25  wt% ($n_{\mathrm{L}} = 1.364$). c $M = 20{\times }$, 0 wt% ($n_{\mathrm{L}} = 1.333$), $d_{\mathrm{p}}={124}\,{\upmu \hbox {m}}$. d $M = 10{\times }$, 0 wt% ($n_{\mathrm{L}} = 1.333$), $d_{\mathrm{p}}={124}\,{\upmu \hbox {m}}$. e $M = 20{\times }$, PMMA, $d_{\mathrm{p}}={124}\,{\upmu \hbox {m}}$. f $M = 10{\times }$, PMMA, $d_{\mathrm{p}}={124}\,{\upmu \hbox {m}}$

The effect of particle size and refractive index jump on the calibration curves in the $a_y \text{-} a_x$ plane is illustrated in Fig. 16a–f. Overall, an increase in particle size, shown here for PMMA particles in a 25 wt% glycerol–water solution for two magnifications (Fig. 16a and b), leads to an increase in $a_x$ and $a_y$. Therefore, calibration curves are strongly shifted without any overlapping region. Please note that this characteristics may be utilized to assign particles to one calibration curve. Thus, it is possible to determine both the out-of-plane position of the particles and at the same time perform a size classification, if particles of the same shape and material are used. Figure 16c and d reveals that a reconstruction of out-of-plane particle positions can be also combined with a classification of particles according to their refractive index. Here, calibration curves for PS and PMMA are shown with a refractive index difference of $\varDelta n = n_{\mathrm{p}} - n_{\mathrm{L}} = 0.258$ and $\varDelta n = n_{\mathrm{p}} - n_{\mathrm{L}} = 0.154$, respectively. It may be noted that more stringent outlier criteria are required when calibration curves move closer together as it is the case for Fig. 16c and d compared to Fig. 16a and b. A change in refractive index jump can also occur when the refractive index of the liquid is varied. Figure 16e and f shows how changes of the refractive index affect the calibration curves. Different refractive indices are realized by creating different water–glycerine mixtures. When the refractive index jump between particle and fluid increases with decreasing glycerol fraction, $a_x$ and $a_y$ decrease. In the present study, refractive index changes of the liquid of $\varDelta n = 0.0307$ (for 25 wt%) and $\varDelta n = 0.064$ (for 50 wt%) are realized. Overall, it can be seen that the differences between the individual calibration curves are more pronounced for $M = 20{\times }$ compared to $M = 10{\times }$ under the depicted experimental conditions. In the present section, only an excerpt of the whole parameter study is presented. An overview of $\varDelta z$, $\varDelta F_{xz}$, $\varDelta F_{yz}$, $\sigma _z^*$, ${\sigma }_z$ for all investigated parameter combinations of $d_{\mathrm{p}}$, M, material of the particles and wt% of the glycerol–water solution is given in Table 3 of “Appendix”. For the investigated cases, ${\sigma }_z/\varDelta z$ is around 0.7-5.2% for BLAPTV (except for two cases) which is comparable to the accuracies obtained by Cierpka et al. (2010b), Buchmann et al. (2014) and Franchini et al. (2019). In the present study, the uncertainty relative to the particle diameter is in the range $1.8\%\le {\sigma }_z/d_{\mathrm{p}} \le 16\%$ (except for two cases), see Table 3 in “Appendix”. This is even below the values reported in earlier studies which are also given in Table 2 in “Appendix.”

9 Validation measurements

To demonstrate the capability of BLAPTV for flow domains with a depth beyond the submillimeter range, measurements in a plane channel flow with ${2305}\,{\upmu \hbox {m}}$ channel height are performed. For this, a 25 wt% glycerol and 75 wt% deionized water solution was seeded with $10^{-4}$%wt polystyrene particles of diameter $d_{\mathrm{p}}={80}\,{\upmu \hbox {m}}$. The solution is density matched to the particles at ${20}\,{^{\circ }}\hbox {C}$. As particles are two orders of magnitude smaller compared to the channel height, we expect them to behave as neutrally buoyant fluid tracers (Lindken et al. 2009). Despite the fact that the density of liquid and particles is matched, few particles float and stick to the top or settle at the bottom channel walls, due to small variations in the individual particle density as a result of the manufacturing process. These particles are used to determine the absolute position of the channel walls prior to the experiments. For this, the whole channel is scanned in steps of ${1}\,{\upmu \hbox {m}}$, to record particles that are located at the top and the bottom wall within the field of view, acting as “wall markers.” As mentioned in Sect. 4, the evolution of the Tenengrad sharpness measure ($f_{xz}$) is used to detect the particle center and hence the walls of the channel by considering the particle radius. The origin of the scanning coordinate is set to zero at the bottom channel wall. Hence, a volume flow rate of $3.75 \times 10^{-4}\,{\hbox {m}^{3}\hbox {s}^{-1}}$ is created using a submerged rotary pump (Barwig). The liquid is continuously recirculated and temperature regulated at 19–$20\,{{^{\circ }}\hbox {C}}$, see Fig. 1a and b. To measure the flow rate, we repeatedly measured the weight of the liquid pumped during a defined time interval. Hereafter, the mass flow rate was calculated based on the density of the glycerol–water mixture (Cheng 2008). An in situ total gap height of $H={2305}\,{\upmu \hbox {m}}$ was determined.

Fig. 17

Linear interpolation of calibration curves. Dashed line$={0}\,{\upmu \hbox {m}}$ (bottom), solid line$={2305}\,{\upmu \hbox {m}}$ (top), colored dots = valid data, red dots = rejected data. $M = 20{\times }$, $d_{\mathrm{p}}={80}\,{\upmu \hbox {m}}$, $c_{\mathrm{D}} = 2$, $c_{\mathrm{a}} = 0.7$, $c_{\mathrm{I}} = 0.575$, $z - z_0$ corrected for $n_{\mathrm{L}}$ of 25 wt% glycerol–water solution. a Scattered $a_x \text{-} a_y \text{-} I$ data and resulting 3D calibration curves. b Interpolated 3D calibration curves. c Best matching interpolated calibration curve for $z={971}\,{\upmu \hbox {m}}$ d $z_{\mathrm{int}}$ of best matching 3D calibration curves versus measurement plane position z (blue dots =interpolated, white dots=best matching, black dots =shown in c)

Prior to the actual flow measurement calibrations are performed. The resulting calibration curves and the associated scattered $a_x$, $a_y$ and I-values are presented in Fig. 17a. For particles located at the top wall ($z={2305}\,{\upmu \hbox {m}}$), $a_x$, $a_y$, I and hence the calibration curve differs from those of particles located at the bottom wall ($z={0}\,{\upmu \hbox {m}}$). As shown in Sect. 7, different light intensities result in different calibration curves for the same particle. Therefore, we assume that the shape difference of the calibration curves is a result of a change in the light intensity along the gap height.

Due to the different shapes of the calibration curves, the challenge is to find a calibration function which is valid for particles located at any z-position in-between the bottom and top channel wall. To overcome this difficulty, we interpolate the coefficients of the ${\overline{a}}_x$, ${\overline{a}}_y$ and ${\overline{I}}$ polynomials of the calibration curves as a linear function of z. In this way, intermediate calibration curves are computed, see Fig. 17b. In the present case, the measurement volume depth of the interpolated calibration curves is set to $\varDelta z={173.22}\,{\upmu \hbox {m}}$. In addition to the calibration curve, the threshold for the Euclidean distance $a_{\mathrm{D}}$ is also interpolated linearly.

Also the measured particle’s focal length $\varDelta F_{yz} \approx \varDelta F_{xz}$ differs for particles located at the top and bottom, see Table 4 in “Appendix.” As discussed in Sect. 7, the measured particle’s focal length is almost constant as light intensity is increased. Therefore, we assume the difference is related to the refractive index jump at the top channel wall. Hence, the particle’s focal length is assumed to be constant for the major part of the channel ($\varDelta F_{xz} \approx \varDelta F_{yz} =\hbox { const}$.), as the refractive index jump at the top wall comes only into play for particles closer than $\varDelta F_{yz}={177.32}\,{\upmu \hbox {m}} \approx \varDelta F_{yz}={196.29}\,{\upmu \hbox {m}}$ (see Table 4) to the channel walls. The out-of-plane position reconstruction uncertainties for the top and the bottom calibration curve are given in Table 4. As can be seen, the uncertainty of determining the particle’s z-position is decreased by 15% and 10% with a 3D calibration in comparison with a 2D calibration, while the number of valid particles is increased by 2.5% and 4.8% for the top and bottom calibration curve, respectively. It should be mentioned that a maximum position error of 0.488% of the total channel height and 14% of $d_{\mathrm{p}}$ is achieved for the 3D calibration.

During the actual flow measurements, the gap is scanned in steps of 136 micron and at each measurement plane 5300 images with a resolution of $512 \times 384$ pixel, covering a $0.93 \times {0.82}\,{\hbox {mm}^{2}}$ field of view, are recorded at 1000fps. Hence, the out-of-plane positions of particles, based on the $a_y$, $a_x$ and I data of the flow measurement, have to be determined. For this, each of the 3D calibration curves displayed in Fig. 17b is compared with the $a_x$, $a_y$ and I-values from the corresponding measurement planes. In this way, a suitable calibration curve with associated out-of-plane particle positions along the curve can be associated with the scatter data of each measurement plane. To find the most suitable calibration curve, it is checked how many pairs of $a_y$, $a_x$ and I are valid, i.e., their minimum Euclidean distance to the calibration curve is smaller than $a_{\mathrm{D}}$, as described in Sect. 5. The curve that yields the largest number of valid particles is considered as a match and selected for determining the $z - z_0$ of the $a_y$, $a_x$ and I pairs in the respective measurement plane. Figure 17c displays the best matching calibration curve (black solid line) and corresponding scatter data with valid measurement points (colored markers) and outliers (red markers) for the measurement plane located at $z={971}\,{\upmu \hbox {m}}$. Note that the interpolated $a_{\mathrm{D}}$ value corresponding to the depicted calibration curve has been used for outlier detection. Here, an interpolation of $a_{\mathrm{D}}$ is crucial as the scattering of $a_x \text{-} a_y \text{-} I$ data varies along the gap height. (Compare the scattering distance of the top and bottom curve in Fig. 17a.)

This procedure is applied to the $a_x$, $a_y$ and I data of all measurement planes, such that for each measurement plane the out-of-plane positions of the focal points are computed. Hence, the absolute particle positions can be computed with respect to the channel wall by summing up the focal points out-of-plane positions, the particles focal length ($\varDelta F_{xz}$) and the associated measurement plane position. In Fig. 17d, the interpolated coordinate $z_{\mathrm{int}}$ of the calibration curve is plotted vs. the z where the curve showed the most valid pairs and hence is considered as a match (white dots). As can be seen z versus $z_{\mathrm{int}}$ of the matching curves (white dots) approximately shows a linear behavior. This confirms the previous assumption that the shape of the calibration curves can be described as a linear function.

Fig. 18

a Particle image centroids detected within the field of view during the measurement. Green dots denote valid particle images, and red dots denote outliers. b Experimental results and analytical solution for laminar channel flow. red line = analytical solution, green dots (with error bar) = measurement, black straight line = channel walls, black dashed line = particle depletion area. The dashed lines indicate the minimum distance particles assume relative to the walls. The mean value of the streamwise velocity standard deviation along z is $\sigma _u = 0.75\%$ of $U_{\text {max}}$ ($c_{\mathrm{D}} = 2$)

Figure 18a shows a scatter plot of the position of all valid (green dots) and invalid (red dots) data in the x–y measurement plane. As can be seen, the accepted data points are well distributed across the image (Fig. 18a). This means that any in-plane particle position effect is already included in the result data, as particles across the whole field of view are accepted. Hence, the influence of the in-plane position on the Euclidean distance to the calibration curve and thus on the particle’s out-of-plane reconstruction accuracy is not significant here. It may be noted that data points at the very corners of the images are rejected as particle images intersect with the image borders and do not provide the complete focal image. Therefore, particle center points close to the FOV border do not enter the statistics.

Figure 18b shows the measured velocity profile of the plane channel flow that is obtained with the aforementioned extended calibration procedure. The velocities are calculated using a simple nearest neighbors algorithm. As is it clear from Fig. 18b, the experimentally determined velocity profile matches very well the analytical solution (red line). It may be noted that particles assume a minimum z-distance of approximately ${200}\,{\upmu \hbox {m}}$ to both top and bottom channel walls which might be due to wall-induced lift forces, which push particles away from the walls toward the channel center. Utilizing a 3D calibration procedure 7996 valid data points are obtained while in-plane velocities u, v as well as the out-of-plane velocity w could be determined with standard deviations of $\sigma _{u} = 0.75\%$, $\sigma _{v} = 0.28\%$ and $\sigma _{w} = 2.29\%$ of the maximum streamwise velocity $u_{{\mathrm{max}}}$, respectively. The same procedure with a 2D calibration and reconstruction yields $N_{\text {valid}}(2D) = 7267$ (− 10%) data points and uncertainties of $\sigma _{u} = 0.80\%$ (+ 6.1%), $\sigma _{v} = 0.27\%$ (− 3%) and $\sigma _{w} = 2.66\%$ (+ 16%) for u, v and w, respectively. If $c_{\mathrm{D}}$ is reduced to $c_{\mathrm{D}} = 1.75$ for the 3D calibration such that the number of valid particles is approximately equal ($N_{\text {valid}}(2D) = 7267 \approx N_{\text {valid}}(3D) = 7298$) uncertainties of $\sigma _{u} = 0.73\%$ (− 8%), $\sigma _{v} = 0.25\%$ (− 8%) and $\sigma _{w} = 2.05\%$ (− 30%) for u, v and w are achieved. This shows that the 3D calibration procedure provides a better accuracy and more reliable data in comparison with the 2D calibration procedure.

Overall, the accuracies obtained with the 3D as well as the 2D calibration procedure are comparable to the uncertainties obtained by Cierpka et al. (2010a), which are $\sigma _{u} = 0.9\%$ and $\sigma _{w} = 3.72\%$ of $u_{{\mathrm{max}}}$. Thus, BLAPTV shows comparable measurement accuracies compared to fluorescence-based APTV, if a proper calibration procedure as presented here is utilized.

10 Discussion and conclusion

In the present study, a method is presented to apply APTV to large transparent particles, using bright-field illumination. As particles act here as ball lens, we referred to this method as ball lens astigmatism particle tracking velocimetry (BLAPTV). Based on a parameter study on the role of the background light intensity, the particle size and the refractive index jump between particle and fluid, it was shown that BLAPTV achieves comparable measurement accuracies as conventional APTV where fluorescent particles are typically utilized. We showed how the evaluation procedure, in particular the autocorrelation coefficient $c_{\mathrm{a}}$ and the light intensity coefficient $c_{\mathrm{I}}$ affect the accuracy of the method. Furthermore, we showed that BLAPTV may be utilized to combine measurements of the 3D displacement of particles with a particle classification by either size or refractive index due to different shapes of the corresponding calibration curves. Given a proper calibration procedure, BLAPTV can provide high reconstruction accuracies with respect to the particle diameter even for large particles. To reduce the particle depth position reconstruction uncertainty, we proposed an extended calibration procedure in which the focal image intensity is used an additional parameter to the Euclidean method of Cierpka et al. (2010a) resulting in a 3D calibration curve. Uncertainties of the out-of-plane particle position reconstruction of ${\sigma }_z={2.5}\,{\upmu \hbox {m}}$ for $d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$ (${\sigma }_z/d_{\mathrm{p}} = 4.16\%$) with $M = 20{\times }$ and ${\sigma }_z={2.26}\,{\upmu \hbox {m}}$ for $d_{\mathrm{p}}={124}\,{\upmu \hbox {m}}$ (${\sigma }_z/d_{\mathrm{p}} = 1.8\%$) and $M = 20{\times }$ were reported using the 3D calibration procedure. We observed that the measurement depth $\varDelta z$ depends on the particle diameter and can exceed the distance of the focal planes significantly (up to 11.1–13.4 times for a ${124}\,{\upmu \hbox {m}}$ particle, while it is typical of the same order of magnitude in conventional APTV with small particles. We also developed a method to compensate for shape changes of the calibration curve inside a large measurement volume without the need to place a calibration target inside the measurement volume. Instead, linearly interpolated calibration curves are assigned to the measurement data in a best fit procedure to determine the out-of-plane position of particles.

Finally, we validated BLAPTV successfully by measuring a planar Poiseuille flow in a rectangular channel. Utilizing a 3D calibration procedure, we showed that the uncertainty of the measured streamwise and out-of-plane velocity can be reduced by 6.1% and 16%, respectively. Overall, the accuracies obtained in the measurement are comparable to those obtained by Cierpka et al. (2010a) for both the 2D and the 3D calibration.

As BLAPTV is an adapted version of APTV, the same postprocessing code can easily be applied to both fluorescent and transparent particles. Also measurements can be taken with the same optical setup if the light source is adapted. This is an advantage, when measurements should be taken with small fluorescent tracer particles ($d_{\mathrm{p}} \le {3}\,{\upmu \hbox {m}}$) combined with larger transparent suspension particles ($d_{\mathrm{p}} \ge {30}\,{\upmu \hbox {m}}$) with the same magnification. We conclude our observations can be transferred to conventional, fluorescent APTV, as from some experiments we know that the choice of $c_{\mathrm{a}}$ affects the reconstruction accuracy $\sigma _z$ as well in the case of fluorescent particles. Furthermore, using a 3D calibration curve has the potential to increase accuracy and robustness of conventional fluorescent APTV, because here outliers appear due to deviations in shape or coating and overlapping particles.

Appendix

See Tables 1, 2, 3 and 4.

Table 1 Accuracies achieved in the literature

Table 2 Accuracies for optimized values of $c_{\mathrm{a}}$, $c_{\mathrm{I}}$ in order to minimize $\sigma _z^*/\varDelta z$ ($d_{\mathrm{p}}={60}\,{\upmu \hbox {m}}$, $M = 20{\times }$, water, ${\sigma }_z = \sqrt{\sigma _z^{*2}+\text {min}[\sigma (\varDelta F_{xz}),\sigma (\varDelta F_{yz})]^2})$ (top two rows=CMOS camera, bottom two rows=CCD camera)

Table 3 Measured values of the performed parametric study for optimized values of $c_{\mathrm{a}}$, $c_{\mathrm{I}}$ obtained with 3D calibration procedure (top: PMMA, bottom: PS ${\sigma }_z = \sqrt{\sigma _z^{*2}+(\text {min}[\sigma (\varDelta F_{xz}),\sigma (\varDelta F_{yz})])^2})$, $c_{\mathrm{D}} = 2$)

Table 4 $\varDelta F_{xz}$, $\varDelta F_{yz}$, $\sigma _z^*$ and ${\sigma }_z$ for particles with $d_{\mathrm{p}}={80}\,{\upmu \hbox {m}}$ in a 25 wt% glycerol–water solution located at the top $z={2305}\,{\upmu \hbox {m}}$ and bottom $z={0}\,{\upmu \hbox {m}}$ of the channel ($c_{\mathrm{I}} = 0.575$, $c_{\mathrm{a}} = 0.7$, $c_{\mathrm{D}} = 2$)