Abstract
We investigate the effect of highly contrasting non-Newtonian liquid properties on the formation of liquid jets with a focused shape. By using two nozzle-free ejection techniques, mechanically impact- and laser-induced, fast jets of a highly elastic (sodium polyacrylate) and weakly elastic (xanthan-gum) diluted polymer solutions are generated. A unique high-speed effect is encountered at the jet ejection onset of the highly elastic solution. Its jet-tip speed is on average 1.4 times faster in comparison to a Newtonian (glycerin/water) and the weakly elastic liquids. We explain this effect occurring as a result of the high viscoelasticity of the sodium polyacrylate solution. Additionally, a ‘bungee jumper’ jet behaviour (Morrison and Harlen in Rheol Acta 49(6):619–632, 2010) is observed in a regime of high speed (\(10<V_j<40\) m/s) and high viscosity (\(\mu >20\) mPa s) not previously examined. We additionally characterise the viscoelastic non-breakup jet limit using the Bazilevskii et al. (Fluid Dyn 40(3):376–392, 2005) ejection criterion. Herein, the extensional rheological parameters are measured implementing a novel DoS-CaBER technique (Dinic et al. in Lab Chip 17(3):460–473, 2017). Our findings may influence results of inkjet printing technologies and recent nozzle-free ejection systems for ejecting liquids with non-Newtonian properties.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The generation of highly focused jets of complex liquids is a fundamental phenomenon and crucial for the development of advanced inkjet printing, 2D patterning and 3D additive manufacturing, of particular impact in printed electronics (Bihar et al. 2018) and bioprinting (Hölzl et al. 2016) applications. Jets are typically generated when a rapid pressure impulse is applied normal to a concave liquid–air interface which overcomes the resisting surface tension forces. The deformation of the interface leads to a thin stream of liquid with a conical (focused) shape propagating through the air. This well known phenomenon occurs due to a flow focusing mechanism of the velocity and impulsive pressure fields (Antkowiak et al. 2007; Gordillo et al. 2020). Focused jets typically appear in the bursting of bubbles at liquid interfaces (Duchemin et al. 2002; Longuet-Higgins 1983), high amplitude Faraday waves (Goodridge et al. 1999; Longuet-Higgins 2001), or the ubiquitous collapse of cavities after a drop impact on a liquid interface (Worthington and Cole 1897; Fedorchenko and Wang 2004).
Motivated by the development of a new generation of inkjet printing applications, several groups have used diluted polymeric solutions for enhancing printability and binding of 3D printed structures (de Gans et al. 2004). A diluted polymeric solution is the mixture of a Newtonian liquid with small quantities of polymer. This solution type shows complex behaviour such as shear-thinning (viscosity decrease with increasing shear-rate) and viscoelastic effects. Mun et al. (1998) and Amarouchene et al. (2001) have demonstrated how these complex properties significantly affect the jet dynamics and droplet formation.
Moreover, several ejection regimes have been investigated experimentally (Hoath et al. 2012) to identify a single drop pinch-off regime for practical applications. Bazilevskii et al. (2005), Hoath et al. (2009) observed a ‘bungee jumper’ jet behaviour as a secondary effect of drop-on-demand formation where a jet filament stretches and then retracts. This jet type was numerically predicted by Morrison and Harlen (2010) in the context of inkjet printing technology. Nonetheless, inkjet printing is still limited to the ejection of solutions with low viscosities (\(<20\) mPa s) and speeds (\(<10\) m/s).
Onuki et al. (2018) developed a method of ejecting focused viscous jets using an impulsive force and demonstrated the ejection of non-Newtonian liquids with shear-thinning and weakly elastic properties. However, the elastic mechanisms influencing the ejection of focused jets are still not well understood. To address these challenges, we investigate the jet formation of highly viscous Xanthan-gum (XG) and Sodium polyacrylate (SPA) solutions having weakly elastic and highly elastic properties, respectively. Their polymer concentrations are selected to produce the same shear-thinning properties.
We use a mechanically impact-induced method (Onuki et al. 2018) and a laser-induced method (Thoroddsen et al. 2009; Tagawa et al. 2012; Delrot et al. 2016) identifying jet-tip speed differences in the weakly elastic (XG) and highly elastic (SPA) solutions, and comparing these observations to a glycerin/water mixture (GW). We encounter an intriguing efficient speed effect occurring in the elastic (SPA) solution observed for the first time. Moreover, for the SPA liquid, we observe a non-breakup ‘bungee jumper’ jet behaviour in a regime of high speed (\(V_j>10\) m/s) and high viscosity (\(\mu >20\) mPa s).
a Shear viscosity and b first normal stress difference as a function of shear rate (\(2\times 10^{-2}<{\dot{\gamma }}\le 1\times 10^{3}\) 1/s) for glycerin/water mixture 86 wt% (blue circle), Xanthan-gum 0.35 wt% (red right-pointing triangle) and sodium polyacrylate 0.4 wt% (black diamond). The data for the Newtonian (GW) mixture are presented from the shear rate \({\dot{\gamma }}\ge 0.6\) 1/s due to the technical limitation to reach steady states using this solution. The concentrations of the polymeric solutions are chosen to match their shear-thinning behaviour while exhibiting highly contrasting elastic properties
2 Experimental methods
2.1 Liquid solutions
We use a mixture of glycerin (Sigma-Aldrich) at 86 wt% and Milli-Q water resulting in constant viscosity of 110 mPa s from shear rate \({\dot{\gamma }}\ge 0.6\) s\(^{-1}\) at 25 \(^{\circ }C\), and two polymeric solutions Xanthan-gum 0.35 wt% (Sigma-Aldrich) and Sodium polyacrylate 0.4 wt% (molecular weight \(M_w=2.1-6.6\times 10^{6}\) FUJIFILM). The polymeric solutions were prepared by using a rotatory shaker (Nissin Scientific NX-25D) at 140 RPM for a minimum of 8 h. The concentrations of the polymeric solutions give almost identical shear-thinning behaviour as observed in Fig. 1a (TA Instruments Rheometer ARES-G2). Xanthan-gum (XG) and Sodium polyacrylate (SPA) were selected due to their contrasting weakly and highly elastic properties, respectively. The magnitude of the polymer elasticity is commonly associated with the first normal stress difference (\(N_1\)) (Barnes et al. 1989). Figure 1b presents the first normal stress difference for the three liquid solutions. Note the values of \(N_1\) for GW and XG are significantly smaller than that of SPA for \({\dot{\gamma }}>100\) confirming their high elasticity contrast.
2.2 Focused jet generation
Highly focused jets are generated using two techniques, impact-induced (Onuki et al. 2018) and laser-induced (Tagawa et al. 2012). The impact-induced system illustrated in Fig. 2 uses a capillary tube of inner diameter \(D_{i}=2\) mm, outer diameter \(D_{o}=3\) mm and \(W=50\) mm in length. The tube is placed along the central axis of a rectangular container with side wall of 25 mm and 60 mm height. The container was initially filled with one solution type and then a cap with the inserted capillary tube was placed. In such condition, the air pressure inside the system is used to control the liquid volume entrapped in the capillary tube. The liquid volume inside the capillary is set at a small height \(l_{\text {cap}}=3\) mm. The total liquid height in the container \(l_{\text {top}}\simeq 40\) mm is measured between the meniscus of the liquid capillary volume and the top container liquid interface. An electro-mechanical device (ShinDengen solenoids, KGK power supply) is used to apply a short pulse impact under the rectangular container at speed \(U_0\) by direct contact of a metal rod with the liquid container. The impact generates a highly focused and fast jet emerging from the liquid interface at approximate speed \(\displaystyle V_{\text {jet}}\simeq \beta '\left( 1+ \frac{l_{\text {top}} }{ l_{\text {cap}} } \right) U_0\), with \(\beta '\) a constant determined by the concave shape of the interface and viscosity of the liquid (Onuki et al. 2018).
During jet generation experiments, the container is displaced along with the capillary. Thus, we subtract the speed of the bottom of the capillary tube to obtain the jet-tip speed from the capillary frame of reference. The jet ejection is captured by a high-speed camera (Photron SA-X) at 10000 fps, and the experimental system is backlit with a LED light (Phlox LLUB white led backlight) of dimensions \(20\times 20\) cm. The resulting images are \(384\times 1024\) pixels with resolution 28.0 \(\upmu\)m/px.
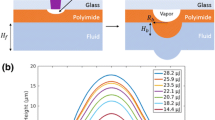
The laser-induced jet ejection system uses a laser of high energy power and short pulse duration of 6 ns (Litron-NanoPIV). A capillary tube of the same dimensions as the impact-induced system is provided (\(D_{i}=2\) mm, \(D_{o}=3\) mm and \(W=50\) mm). As illustrated in Fig. 3, the capillary is partially filled with the liquid and vertically positioned so that jets are ejected upwards. The laser beam is focused with a 10x magnification lens (Olympus SLMPLN) and directed perpendicular to the capillary tube axis at a constant distance \(H=3\) mm with respect to the position of the bottom of the liquid meniscus. Upon laser pulse radiation into the liquid bulk, a cavitation bubble and consequent pressure impulse are generated provoking the formation of a highly focused jet (Tagawa et al. 2016; Hayasaka et al. 2017). In our experiments, a ramp of output laser energy magnitudes is used ranging from 3.3 mJ to 8.8 mJ. For each energy magnitude that was applied, the experiments were performed five times. Tagawa et al. (2012) estimated that jet-tip speed of water jets is proportional to \(\displaystyle V_{\text {jet}} \simeq C_0\frac{E' (1+\beta \cos \theta )}{D_{i} H}\) where \(C_0\) is a proportionality constant with units of viscosity inverse, \(E'\) is the absorbed energy laser and \(\theta\) the internal meniscus contact angle. The parameter \(\beta\) accounts for the flow focusing effect (Peters et al. 2013). Typically, \(\beta\) is of the order of 2 for small contact angles as set in our experiments. Recently, a detailed theoretical analysis of the flow focusing effect can be found in Gordillo et al. (2020) who report a quantitative agreement with experimental results using the impact- and lased-induced ejection techniques.
The cavitation bubble and jet ejection behaviour are simultaneously captured using two fast cameras at 50000 fps (Photron SA-X2) and 30000 fps (Photron SA-X), respectively. Each camera is equipped with a lens (Nikon 105 mm) and a bandpass filter to protect the sensor from laser overexposure. For camera illumination source, we use a LED backlight (Olympus KL-1600-LED) coupled with a light diffuser (LSD diffusion angle \(80^{\circ }\)). The laser and the cameras are triggered using a pulse/delay generator (BNC 575). The resulting images are \(328\times 768\) pixels for the bubble behaviour and \(256\times 1024\) pixels for the jet propagation with resolutions 9.8 \(\upmu\)m/px and 24.6 \(\upmu\)m/px, respectively.
2.3 Liquid-wall contact angle
Before all experiments, the cut to size capillaries are treated with a plasma cleaner (SAMCO FA-1) for 60 s, which gives a contact angle between the liquid and the capillary inner glass wall of \(\theta =20^\circ \pm 4^\circ\). The error considers the angle variation due to the change of wettability properties of each liquid solution. This procedure increases the wettability properties reducing the contact angle, which generates flow focused and fast jets. The treated capillaries are used within three days after the cleaning process to maintain constant contact angle values, which degrades in time due to environmental contamination.
i. Data processing of jet ejection images to identify the jet-tip position: (a) experimental image, (b) background subtracted and greyscale normalised image, (c) black/white (binary) jet profile, and (d) overlap of original image with black/white profile, the cyan solid line indicates the limit of the jet-tip. ii. Measurement of the projected area of a cavitation bubble in Glycerin/water mixture (a) original experimental image, (b) binary bubble image, (c) the remaining white voids in image (b) are closed by using an expansion/contraction algorithm, and (d) overlapped of the original image and the inverted outline of the binary outcome (outline highlighted in red line). The solid blue lines correspond to 1 mm
2.4 Jet-tip velocity
A time sequence of jet ejection obtained from the impact- or laser-induced experiments is converted into a black/white (binary) sequence. The jet-tip position in the binary sequence and the instantaneous jet-tip speed are obtained, the last one by calculating \(V_j=\displaystyle \frac{{\text {cal}}\,\,\varDelta y}{1/{\text {fps}}}\), where cal is the calibration value from pixel to meters, \(\varDelta y\) is the displacement of the jet-tip between two consecutive frames in pixels and fps the camera frame-rate in 1/s. The binarization is performed by subtracting the greyscale background using a reference image without the jet ejection and normalising the resulting greyscale between [0, 1]. A colour bandpass filter maps the jet shape into black (0), and everything else outside the colour band is set to white (1). The limits of the bandpass filter [w, u] are obtained from each sequence image by selecting a small grey region from the background. The jet-tip position is accurately obtained by introducing a threshold \(\delta \ll w,u\) to the bandpass filter \([w-\delta ,u+\delta ]\), carefully calibrated by overlapping an original experimental image with the binary image. No smoothing methods were applied on the data processing. Figure 4-i illustrates this data processing method.
2.5 Projected area of a cavitation bubble
A projected area is obtained from an image of the growth and collapsed dynamics of the laser-induced cavitation bubble. An experimental image shown in Fig. 4ii-a is binarised using the same bandpass filter method as described above for jet profiles. However, an additional algorithm of morphological expansion and contraction is implemented (MATLAB2019a) to close the remaining voids inside the bubble profile (white voids in Fig. 4ii-b). From the closed bubble profile shown in Fig. 4ii-c, the number of pixels is counted, and the result is transformed into physical units. The example shown corresponds to a bubble with \(A=4.1\) mm\(^{2}\). For visual verification, an original experimental image and the colour inverted binary outline are overlapped in Fig. 4ii-d. For validation, a few bubble images are selected whose area is measured by hand. The comparison of these measurements (not shown here) and results using our algorithm confirms that the bubble projected area is measured to better than 5% accuracy.
3 Properties of liquid solutions by DoS-CaBER
Bazilevskii et al. (2001, 2005), McKinley (2005) showed how extensional rheological properties are crucial for the analysis of breakup of an elastic filament and droplet detachment of polymer solutions. Herein, we measure the extensional rheology properties of GW, XG and SPA solutions using dripping-onto-substrate capillary breakup elongation rheometry (DoS-CaBER), following previous works by Dinic et al. (2015, 2017) and Sur and Rothstein (2018).
The experimental setup of DoS-CaBER is shown in Fig. 5. A high-speed camera (Photron SA-Z) captures the pinch-off process of a liquid bridge. The system is backlit using a LED light (Phlox LLUB). The liquid is initially infused using a syringe pump (Harvard Apparatus Pump 11 Elite) at a flow rate of 40 \(\upmu\)l/min through a vertical nozzle (outer diameter \(2R_0 = 1.27\) mm, inner diameter \(2R_i=0.97\) mm) where a dripping drop is formed. The pump is switched off and the drop is let to fall by interia onto a glass substrate. The nozzle-substrate distance \(H_0\) is set so that an unstable liquid bridge is formed immediately after the dripped droplet contacts and spreads on the substrate. In this experiment, the aspect ratio \(H_0/2R_0\) is set to about 3. The frame rates of the high-speed camera are 1000, 5000 and 10000 fps to capture the time evolution of the neck shape of the liquid bridge of SPA, XG and GW, respectively. The resulting images are 512 \(\times\) 1024 pixels with a resolution of 3.9 \(\upmu\)m/pix. The neck radius of the liquid bridge (minimum filament radius) is obtained as a function of time R(t) from the captured images using an in-house MATLAB2019a code. Each measurement is repeated five times.
(top) Schematic diagram of the dripping-onto-substrate capillary breakup extensional rheometry (DoS-CaBER) experimental setup. A liquid is infused from a nozzle using a syringe pump where it is statically dripped onto a glass substrate. The liquid bridge formed between the nozzle-substrate undergoes a self-thinning and pinch-off dynamics. (bottom) Sequence of the thinning dynamics for a Glycerin/water 86 wt%, b Xanthan-gum 0.35 wt% and c Sodium polyacrylate 0.4 wt%. The solid blue line corresponds to 1 mm
In the case of a high viscous liquid (Newtonian), the thinning of the liquid bridge is dominated by the balance between viscous and capillary forces. In this case, the neck radius decreases linearly with time and the thinning dynamics follows a visco-capillary scaling (Papageorgiou 1998; McKinley and Tripathi 2000):
Here, \(t_p\) is the breakup time of the liquid bridge, \(\sigma\) is the surface tension and \(\mu\) the viscosity of the liquid. Figure 6 shows the neck radius evolution for GW where the later stage of neck thinning for GW shows a typical viscous decrease with time as predicted in Eq. (1). Its breakup time has a value \(t_p=46.8\) ± 8.5 ms.
Non-dimensional radius as a function of time for a XG 0.35 wt% and b SPA 0.4 wt%. The dashed lines show the fitted region obtained using Eq. (2) and corresponds to a constant extension rate. The error in the radius decay is of the order of the symbols size. The insets show the time evolution of the extension rate as a function of time for each solution. In the insets, the highlighted regions correspond to a near constant extension rate with average values of \({\dot{\varepsilon }}_{\text{XG}}=50\) ± 22 1/s and \({\dot{\varepsilon }}_{\text{SPA}}=1.6\) ± 0.4 1/s. The critical time \(t_c\) when the elasto-capillary scaling first develops have values \(t_{\text{c-XG}}=10.0\) ± 1.5 ms and \(t_{\text{c-SPA}}=235.0\) ± 20.0 ms
In the case of a viscoelastic liquid, the thinning of the liquid bridge is dominated by a balance between elastic and capillary forces. In this case, the neck radius decreases exponentially with time and the thinning dynamics follows an elasto-capillary scaling (McKinley 2005; Entov and Hinch 1997):
where \(\lambda _E\) is the extensional relaxation time and \(G_E\) is the elastic modulus. Figure 7a,b shows the neck radius evolution for XG and SPA solutions evidencing the exponential decrease with time in each case. The extension rate of the liquid bridge is calculated from \(\displaystyle {\dot{\varepsilon }} = -\frac{2}{R(t)}\frac{dR(t)}{dt}\) giving approximately constant in the exponential regime. The result is shown in the insets of Fig. 7a,b where the critical time \(t_c\) marks the beginning of the elasto-capillary scaling (shadowed region).
The relaxation time of the polymer solutions can be obtained by fitting an exponential function where \({\dot{\varepsilon }}\) is nearly constant. Thus, giving \(\lambda _{\text{E-XG}}=13.5\) ± 1.1 ms for XG and \(\lambda _{\text{E-SPA}}=502.6\) ± 72.5 ms for SPA. In Eq. (2) at \(t-t_c=0\), we define the initial neck radius \(R_{{E_0}}\) of the elasto-capillary scaling. Their values measure \(R_{{E_0{\text{-XG}}}}=362.7\) ± 17.6 \(\upmu\)m for XG and \(R_{{E_0{\text{-SPA}}}}=264.9\) ± 24.1 \(\upmu\)m for SPA.
The elastic modulus can be estimated considering the balance between the capillary pressure and the elastic stress \(\displaystyle \frac{\sigma }{R(t)} \approx G_E\left( \frac{R_*}{R(t)}\right) ^4\exp {\left( -\frac{t-t_c}{\lambda _E}\right) }\) where \(R_*=\sqrt{(R_0^2+R_i^2)/2}\) (\(R_*=565.0\) \(\upmu\)m) is the median radius (Wagner et al. 2015; Bazilevskii and Rozhkov 2018) giving,
By using surface tension values measured by the pendant drop method, the previous results for \(R_{E_0}\), \(\lambda _E\) and Eq. (3) at \(t=t_c\), the elastic modulus give \(G_{\text{E-XG}}\approx 30.0\) ± 8.8 Pa for XG and \(G_{\text{E-SPA}}\approx 11.0\) ± 6.0 Pa for SPA. Moreover, we confirm that calculating estimates of the elastic modulus for \(t > t_c\) within the elasto-capillary scaling, the results are similar to our reported values at \(t-t_c=0\) showing it a robust method. Note, the elastic modulus for XG polymer solution is larger in comparison to SPA, consequence of the stiffer XG polymer structure than that of SPA. The liquid properties are summarised in Table 1 where all reported errors correspond to one standard deviation.
a Snapshots of impact-induced jets for GW 86 wt%, XG 0.35 wt% and SPA 0.4 wt%, time zero corresponds to the meniscus position at rest one image frame before the jet is generated. The solid line at the bottom left corresponds to 1 mm. b Averaged jet-tip speed as a function of time for SPA 0.4 wt% (black diamond), XG 0.35 wt% (red triangle) and GW 86 wt% (blue circle) by using the impact-induced jet generator. The averages are calculated over five experimental data sets for each solution type where the error bar corresponds to the standard deviation. The dash-dotted line indicates zero velocity
4 Jet ejection by impact-induced generator
The glycerin/water mixture and the polymeric solutions are ejected using the mechanically impact-induced generator (Onuki et al. 2018; Tagawa and Onuki 2018). Snapshots of jet ejection are shown in Fig. 8a (see multimedia material) and the corresponding jet-tip speed as a function of time is presented in Fig. 8b. The experiments are performed setting constant liquid height parameters in the container (\(l_{\text {cap}}\), \(l_{\text {top}}\)) and applying the same impact magnitude. Each liquid type is ejected five times. The initial time \(t=0\) corresponds to a one image frame before a jet-tip is first observed emerging from the liquid meniscus. The presence of small bubbles, specially for the SPA solution, appear during consecutive jet ejections and after the system is set. These bubbles are most likely a consequence of inherent wettability characteristics of each liquid.
The results shown in Fig. 8b reveal significant differences in propagation behaviour and jet-tip speed maximum values. The jets of GW and XG propagate with initial jet-tip speeds (\(t=0.2\) ms) of \(7.8\,\pm \,0.7\) m/s and \(8.7\,\pm \,1.5\) m/s on average, respectively. The average is taken over the five experimental repetitions. The error (standard deviation) is likely consequence of vibrations originated by the collision between the solenoid rod with the liquid container, introducing deviations of the initial impact speed \(U_0\). After ejection, the jets displace along the capillary tube developing a filament shape and decreasing their speeds. Eventually, the jet filament breaks into droplets. The maximum jet-tip speed of SPA jets is on average \(14.5\,\pm \,1.5\) m/s. The SPA jet propagates until the speed decreases to zero, reaching a maximum elongation length and following a retraction where the fluid jet displaces downwards. This behaviour has been numerically predicted by Morrison and Harlen (2010) who have denominated it ‘bungee jumper’ jet.
Overall, the average difference between the jet-tip maximum speed of SPA minus the GW and XG jet maximum speeds is \(\langle \varDelta u\rangle _{\text {spa-xg/gw}}=6.3\pm 1.5\) m/s. This speed difference indicates an effect not previously reported and likely due to the viscoelasticity of the SPA solution. A further discussion of this effect is provided in Sect. 5.3. To uncover non-Newtonian effects on the jet ejection, detailed experiments using the laser-induced jet generator are performed in a wide range of impulse energies, which otherwise would be difficult to achieve using the impact generator.
5 Jet ejection by laser-induced generator
5.1 Laser-induced cavitation bubble
Averaged projected area of the cavitation bubble as a function of time for GW (blue circle), XG (red triangle) and SPA (black diamond). Here, the output energy of the laser is 6.8 mJ. The expansion of the bubble is larger for GW, while smaller differences are observed for the bubble expansion of XG and SPA. The averages are calculated over three experimental data sets for each solution type and the error bars include the deviation due to the optical deformation of the capillary tube. Simple ray-tracing calculations performed using SolidWorks2020 indicate that the bubble projected area increases by less than 12%
By focusing a laser pulse into the liquid bulk, a main cavitation bubble is generated with origin at the focusing point and surrounded by secondary bubbles of smaller sizes. Multiple cavitation bubble formation is a well-known effect due to the presence of nucleation sites originated from the natural saturation of air in the liquid and geometrical nonuniformities on the walls of the system (Apfel 1984; Mørch 2015). Although secondary cavitation effects and bubble-wall interactions may influence the ejection dynamics, our experimental observations confirm that the jet formation is qualitatively equivalent by using the impact-induced technique where cavitation events are significantly less frequent. Therefore, we address our analysis of jet ejection as a function of the laser-induced cavitation bubble maximum size. The maximum bubble volume is proportional to the energy delivered to the liquid interface. Avila et al. (2015) has compared the kinetic energy of the jet and the energy of the cavitation bubble showing a proportional relation; they then provided a scaling law to relate with the maximum bubble radius. In our investigation, the bubble volume as a parameter value is more suitable over the laser energy output because it circumvents the unknown difference between the absorbed energy by the liquid and the laser energy pulse. However, because of the high asymmetry of the bubble, for practical measurements, we use the maximum projected bubble area (see Sect. 2).
Figure 9 presents the bubble expansion as a function of time for three liquids when the output laser energy is 6.8 mJ. An average over three data sets per liquid type is presented. The GW mixture experiences the largest bubble expansion \(A_{m}=4.6\,\pm \,0.1\) mm\(^2\) which is on average 15% greater in comparison with the largest expansion XG and SPA bubbles, \(A_{m}=3.9\,\pm \,0.2\) mm\(^2\) and \(A_{m}=3.6\,\pm \,0.3\) mm\(^2\), respectively. Despite these differences in maximum bubble expansion, they occur at time \(t_m=0.23\,\pm \,0.04\) ms for all liquids, corresponding to the bubble growth time. On the other hand, the bubble collapse takes place at \(t_e=0.6\) ms for GW and \(t_e=0.46\) ms for XG and SPA, indicating an asymmetry possibly due to the influence of shear-thinning and the elastic properties of the polymeric solutions. The observation of secondary bubble expansions in the XG and SPA solutions was too noisy to be clearly captured by the image processing method.
The maximum bubble expansion indicates that \(A_{\text{m-GW}}>A_{\text{m-XG}}>A_{\text{m-SPA}}\), where the first difference can be explained due to the shear-thinning of the bubble in the XG solution, while the second difference an effect due to the high elasticity of SPA solution as its shear-thinning properties are almost identical to that of XG solution. From \(t_e\ge 0.6\) ms, the bubble in the GW solution experiences a secondary growth and collapse reaching a maximum at \(t_{2m}=0.72\) ms with \(A_{2m}=1.5\,\pm \,0.2\) mm\(^2\). These maxima cannot be identified for the XG and SPA solution. Nonetheless, this secondary growth and collapse process occurs most likely through a similar mechanism as described for the initial process (Kafiabad and Sadeghy 2010).
Detailed experiments by Bazilevskii et al. (2003) have shown that the growth and collapse of microbubbles is mainly controlled by their thermophysical properties (heat exchange). Moreover, they showed that the deceleration of bubbles created with the same experimental conditions and using a wide range of elastic polymer properties does not vary largely from the experimental errors of the parabolic-like behaviour. Consequently, we consider the jet ejection is not significantly affected by the differences of bubble collapse or rebound from each liquid solution.
5.2 Jet-tip speed as a function of time
Selected data of jet-tip speed as a function of time for a Glycerin/water mixture 86 wt%, b Xanthan-gum solution 0.35 wt% and c Sodium polyacrylate solution 0.4 wt%. The open (closed) symbols correspond to the minimum (maximum) cavitation bubble size obtained in our experiments by applying output laser energies of 4.6 mJ and 8.8 mJ, respectively
Snapshots of jet ejection as a function of time for 4.6 mJ and 8.8 mJ laser energies are shown in Fig. 10 (see multimedia material). In Fig. 10b, we observe a two-tier structure of the GW jet result of the combination of a highly-focused upper slim shape due to flow focusing from the concave initial meniscus and a lower cylindrical shape consequence of the suction of the laser-induced bubble acting on the interface. This structure of the GW jets in (a) and (b) is dynamically the same. However, due to conservation of volume, the liquid in the faster jet in (b) should move proportionally faster relative to the jet-tip speed due to its higher laser energy. This then causes the diameter of the lower cylindrical part to thicken. We find this two-tier jet dynamics qualitative similar to the one carefully investigated by Fedorchenko and Wang (2004) where jets are generated from the collapse of a concave liquid cavity formed after a drop impact.
Jets of GW and XG evolve into a slender filament shape with typical upper diameter of 200 \(\upmu\)m. The jet speed decreases significantly at later stages and the filament eventually breaks up into droplets due to surface tension driven instabilities (Castrejon-Pita et al. 2012). Initially, the SPA jet evolves in a similar manner as GW and XG solutions propagating along the capillary tube. However, after a maximum elongation is reached, the jet retracts, displacing downwards. Similar phenomenology is captured by using the impact-induced generator (see Sect. 4). Note, the maximum elongation length of the SPA jet increases with the magnitude of the output laser energy. This unique retraction behaviour is a necessary consequence of the elasticity of the SPA solution. Additionally, no breakup of the elastic jet was ever observed even at the highest applied output laser energy.
Figure 11 presents the evolution of jet-tip speed as a function of time for the minimum and maximum cavitation bubble size encountered by applying 4.6 mJ and 8.8 mJ, respectively. In all cases, the time \(t=0\) is measured when the first spark of the laser is observed. For the three liquid solutions, the ejection shows a precise maximum jet-tip speed typically reached before 0.2 ms, defined here as the peak speed. For GW and XG, the peak speed is similar in value of 12.3 m/s and 11.8 m/s for the smallest laser energy (4.6 mJ), and 27.1 m/s and 26.1 m/s for the largest laser energy (8.8 mJ), respectively, while for SPA jets the peak speed values occur at 19.2 m/s (4.6 mJ) and 34.9 m/s (8.8 mJ). By using the laser-induced method, these results confirm the more efficient SPA jet ejection behaviour as observed in Sect. 4 using the impact ejection method.
The GW and XG jet-tip speed decreases from the peak values and tends to a nearly constant speed, which we refer to as asymptotic speed. In this context, we use asymptotic with an experimental interpretation. The asymptotic speed is obtained from the last value measured within the range of image (ROI) and therefore faster jets reach proportionally faster the end of such window. Note the decay is more pronounced for jets of XG solution than GW solution. This speed decay and the observed SPA efficiency behaviour are further discussed in Sect. 5.3. On the other hand, from the peak speed, the SPA jet-tip speed decreases to zero occurring at the maximum jet elongation length, from where the jet-tip retraction (‘bungee jumper’) behaviour starts leading to negative velocities. This jet reaches a maximum retraction speed before it tends to zero.
Bazilevskii et al. (2005) suggested a theoretical criterion for whether a droplet detaches and ejects from the jet filament of a polymer solution if the ratio \(\displaystyle B=\frac{\pi a_0G_E\lambda _E^2}{4m_0}<1.45\), otherwise the jet experiences the ‘bungee jumper’ effect. In this criterion \(a_0\) is the typical diameter of the jet near the tip, \(m_0\) the expected mass of a droplet, \(G_E\) the elastic modulus and \(\lambda _E\) the breakup relaxation time.
By using the results obtained from DoS-CaBER for the elastic modulus \(G_E\) and the relaxation time \(\lambda _E\) from Table 1 (Sect. 3), while considering typical values of \(a_0\approx 200\) \(\upmu\)m and \(m_0\approx 1\) \(\upmu\)g, we can estimate the polymer property effects. Therefore, for XG the Bazilevskii criterion gives \(B_{\text{XG}}\approx 0.9\) ± 0.3, while for SPA liquid solution \(B_{\text{SPA}}\approx 436.5\) ± 240.0. The value of \(B_{\text{XG}}\) predicts a breakup behaviour in agreement to our experimental observations. On the other hand, elastic jets of SPA are on average 300 times over the Bazilevskii threshold, which we observe as a consequence of the long relaxation time of the elastic polymer, relative high molecular weight and concentration. Thus, preventing the elastic jets to break up at any given impulse energy level investigated and leading to the ‘bungee jumper’ jet effect.
5.3 Jet-tip speed as a function of maximum bubble area
Jet peak speed (black triangle) and jet asymptotic speed (black square) as a function of maximum bubble area \(A_m\) for a Glycerin/water 86 wt%, b Xanthan-gum 0.35 wt% and c jet peak speed (black triangle) and jet maximum retraction speed (inverted black triangle) for sodium polyacrylate 0.4 wt%. Each data set is linear fitted using the minimum square method (MATLAB2019a) for peak (solid line), asymptotic (dotted line) and retraction (dash dotted line) speeds
Comparison of the experimental fittings of jet-tip, asymptotic and maximum retraction speeds as a function of the maximum bubble area (obtained in Fig. 12) for GW (blue), XG (red) and SPA (black). Here, the minimum square fittings are plotted using the same energy range from 4.6 mJ to 8.8 mJ. The shadow regions correspond to their standard deviation. The following observations are noted, (i) The maximum bubble expansion for GW is on average 27% larger in comparison to XG consequence of its shear-thinning effects, whereas the bubble expansion difference between XG and SPA is less than 9.5% attributed to differences in shear-thinning and elastic properties. (ii) The decrease from jet peak speed to asymptotic speed for XG is 2.3 times larger compared with GW, which can be attributed to shear-thinning effects. (iii) The peak speed range between GW and XG is closely similar, regardless of the different range of bubble size, suggesting that peak speed can be considered independent from the shear-thinning effects of the XG solution. (iv) The peak speed of SPA is on average 1.4 times larger in comparison to GW; this efficiency phenomenon can be attributed to the high elasticity of the SPA fluid
The jet-tip peak and asymptotic speeds are obtained as a function of the maximum bubble projected area. The results for GW, XG and SPA solutions are presented in Fig. 12a–c, respectively. Typical laser output energies range from 3.3 mJ to 8.8 mJ. For each energy magnitude and solution type, the experiment is performed five times maintaining the same geometrical parameter conditions. The results, however, show variations of the jet-tip peak and asymptotic speed. At a constant laser output energy, we attribute this effect due to the differences of the size of the cavitation bubble originated from fluctuations of the absorbed energy by the liquid bulk (statistical fluctuation of nucleation sites). Hence, the pressure impulse propelling the liquid interface varies proportionally. Even though the bubble area fluctuates for the same experimental parameters, the jet-tip speed increases proportionally over the entire parameter range in all cases. For analysis, the experimental data are compared with a linear fit obtained by the minimum square method. The confidence level of the linear fittings confirms better than \(r^2=0.9\) for the peak and asymptotic jet-tip speeds where we focus our main analysis. On the other hand, the retraction speed gives \(r^2=0.3\) possibly due to larger experimental errors. All linear fits are compared in Fig. 13, where we have selected the same laser output energy range from 4.6 mJ to 8.8 mJ. A shadow region is plotted around the peak speed fitting with limit values given by the standard deviation of the data points in Fig. 12.
In Fig. 13 distinctive effects of jet ejection behaviour are observed as a consequence of using complex polymeric solutions. By comparing the largest bubble area reached, the cavitation bubble in GW mixture is 27% larger than in XG solution, while the bubble in XG is up to 9.5% larger than in SPA solution. These differences may be explained due to the shear-thinning and elastic properties of the polymeric solutions, as noted in Sect. 5.1.
The decrease from jet-tip peak speed to asymptotic speed of XG solution is on average 2.3 times larger in comparison to the GW mixture. The jet-tip speed of GW solution decreases mainly due to viscous dissipation. This deceleration effect is enhanced using the XG solution due to the increase in shear-thinning viscosity while the jet propagates along the capillary tube. The difference in jet-tip peak speed between XG and GW solution is 2.0 m/s for the smaller bubble area and 0.2 m/s for the largest bubble area, \(\langle \varDelta u\rangle _{\text{xg-gw}}=1.1\pm 1.3\) m/s on average. These small differences indicate that the onset of ejection of GW and XG can be considered equivalent. Thus, the XG solution should reach an apparent viscosity of similar order of magnitude to that of the GW solution during the initial propagation stage.
More remarkably, we observe a consistent increase in the jet peak speed of the SPA solution in comparison to the GW mixture. This speed increase is on average of 1.4 times larger or \(\langle \varDelta u\rangle _{\text {spa-gw}}=7.8\pm 1.5\) m/s average difference between SPA and GW. Note that by using the impact-induced jet generator (see Sect. 4), this difference in peak speed between the elastic and inelastic/Newtonian liquids is \(6.3\pm 1.5\) m/s. Because the polymeric solutions were prepared to yield almost identical shear-thinning behaviour while having distinct elastic properties (Fig. 1), the enhanced peak ejection speed of SPA jets ought to be the result of their highly elastic property. Overall, considering the results in Sect. 4 of impact jet generation and where cavitation is negligible, the same jet ejection behaviour is observed by using the laser jet generator. We confirm the reported phenomena is independent of the ejection technique and otherwise a direct consequence of the properties of the complex liquids investigated.
6 Conclusions and outlook
Highly viscous jets of a glycerin/water mixture (110 mPa s), weakly elastic (Xanthan-gum 0.35 wt%) and highly elastic (sodium polyacrylate 0.4 wt%) polymeric solutions were generated using a mechanically impact-induced (Onuki et al. 2018) and laser-induced (Tagawa et al. 2012) ejection methods. These methods rely on a rapid and high momentum transfer from the liquid bulk contained in a capillary tube to the concave liquid–air interface. Thus, forming a fast and slender focused conical jet with typical speeds of tens of meters per second.
The analysis of the projected area of the laser-generated cavitation bubble is influenced by the shear-thinning and elastic properties. The bubble size for XG and SPA solutions is comparatively smaller than that of GW by an average of 20%, whereas comparing the bubble size of XG and SPA solutions, their differences are smaller than 10%. Nonetheless, due to natural fluctuations of bubble cavitation phenomena compared within the same experimental conditions, these observations may differ when performing a more comprehensive analysis in a wider polymer property range (Bazilevskii et al. 2003).
We obtained the jet-tip speed as a function of time where a maximum ejection speed (peak speed) is observed for all solutions occurring within time scales of 0.2 milliseconds. For the GW and XG solutions, a decrease in jet-tip speed from the peak speed tends to a nearly asymptotic value within a few milliseconds. However, the asymptotic speed of XG is on average 2.3 times lower than that of GW, which we conclude is a consequence of the shear-thinning property of the XG solution. Further jet propagation for GW and XG solutions results in filament thinning and breakup into droplets (see multimedia material).
In contrast, after the SPA jets reach a peak speed, its propagation shows a maximum elongation followed by a retraction at the later stage. Morrison and Harlen (2010) previously reported a similar ‘bungee jumper’ jet ejection behaviour by performing numerical computations. Bazilevskii et al. (2005), Hoath et al. (2009) reported experiments of ‘bungee jumper’ like jets. However, these were observed as collapsing ligaments detaching from drop-on-demand (DOD) ejection by using inkjet printing technologies. Typical inkjet ejection speeds are lower than 10 m/s. In contrast, our reported jet-tip speeds reach up to 40 m/s. Nonetheless, by using the breakup ejection criterion theoretically obtained by Bazilevskii et al. (2005) we quantitatively characterised the breakup and non-breakup limits from our XG and SPA jets, respectively. Due to the long relaxation time, relative high molecular weight of the SPA polymer solution and jet geometry, the resulting jets are found in an extreme non-breakup regime which leads to the ‘bungee jumper’ effect.
Interestingly, we encounter complex elastic effects at the ejection onset observed for the first time. The jet-tip peak speed values for the SPA solution are consistently larger than that of GW and XG by 1.4 times on average. This efficiency effect is confirmed in both the impact- and laser-induced methods. By comparing the qualitative influence of the shear-thinning and elastic effects in the outcomes of jet and bubble behaviour, we conclude this effect is attributed to the highly elastic property of the SPA liquid undergoing a large and rapid stress deformation during its ejection.
Our jet ejection observations may be applied to not only laser- and impact-induced focused jets, but also the stretched jet induced by other methods such as the laser-induced forward transfer method (LIFT) (Turkoz et al. 2018; Theodorakos et al. 2019). Additionally, these results may shed light into the elongation and contrasting breakup/non-breakup of a jet filament using viscoelastic liquids (Entov and Hinch 1997; McKinley 2005) in extremely high elongation rate regimes.
References
Amarouchene Y, Bonn D, Meunier J, Kellay H (2001) Inhibition of the finite-time singularity during droplet fission of a polymeric fluid. Phys Rev Lett 86(16):3558
Antkowiak A, Bremond N, Le Dizès S, Villermaux E (2007) Short-term dynamics of a density interface following an impact. J Fluid Mech 577:241–250
Apfel R (1984) Acoustic cavitation inception. Ultrasonics 22(4):167–173
Avila S, Song C, Ohl CD (2015) Fast transient microjets induced by hemispherical cavitation bubbles. J Fluid Mech 767:31–51
Barnes HA, Hutton JF, Walters K (1989) An introduction to rheology, vol 3. Elsevier, New York
Bazilevskii A, Rozhkov A (2018) Splash of an elastic liquid as a rheological test of polymer solutions. Polym Sci Ser A 60(3):391–403
Bazilevskii A, Entov V, Rozhkov A (2001) Breakup of an oldroyd liquid bridge as a method for testing the rheological properties of polymer solutions. Polym Sci Ser AC/C Vysokomol Soedinen 43(7):716–726
Bazilevskii A, Meyer D, Rozhkov A (2003) Dynamics of a spherical microcavity in a polymeric liquid. Fluid Dyn 38(3):351–362
Bazilevskii A, Meyer J, Rozhkov A (2005) Dynamics and breakup of pulse microjets of polymeric liquids. Fluid Dyn 40(3):376–392
Bihar E, Wustoni S, Pappa AM, Salama KN, Baran D, Inal S (2018) A fully inkjet-printed disposable glucose sensor on paper. Flexible Electron 2(1):30
Castrejon-Pita AA, Castrejon-Pita JR, Hutchings IM (2012) Breakup of liquid filaments. Phys Rev Lett 108(7):074506
Delrot P, Modestino MA, Gallaire F, Psaltis D, Moser C (2016) Inkjet printing of viscous monodisperse microdroplets by laser-induced flow focusing. Phys Rev App 6(2):024003
de Gans BJ, Duineveld PC, Schubert US (2004) Inkjet printing of polymers: state of the art and future developments. Adv Mater 16(3):203–213
Dinic J, Zhang Y, Jimenez LN, Sharma V (2015) Extensional relaxation times of dilute, aqueous polymer solutions. ACS Macro Lett 4(7):804–808
Dinic J, Jimenez LN, Sharma V (2017) Pinch-off dynamics and dripping-onto-substrate (dos) rheometry of complex fluids. Lab Chip 17(3):460–473
Duchemin L, Popinet S, Josserand C, Zaleski S (2002) Jet formation in bubbles bursting at a free surface. Phys Fluids 14(9):3000–3008
Entov V, Hinch E (1997) Effect of a spectrum of relaxation times on the capillary thinning of a filament of elastic liquid. J Non-Newtonian Fluid Mech 72(1):31–53
Fedorchenko A, Wang AB (2004) On some common features of drop impact on liquid surfaces. Phys Fluids 16(5):1349–1365
Goodridge C, Hentschel H, Lathrop D (1999) Breaking faraday waves: critical slowing of droplet ejection rates. Phys Rev Lett 82(15):3062
Gordillo JM, Onuki H, Tagawa Y (2020) Impulsive generation of jets by flow focusing. J Fluid Mech 894:A3
Hayasaka K, Kiyama A, Tagawa Y (2017) Effects of pressure impulse and peak pressure of a shockwave on microjet velocity in a microchannel. Microfluid Nanofluid 21(11):166
Hoath SD, Hutchings IM, Martin GD, Tuladhar TR, Mackley MR, Vadillo D (2009) Links between ink rheology, drop-on-demand jet formation, and printability. J Imag Sci Technol 53(4):041208
Hoath SD, Harlen OG, Hutchings IM (2012) Jetting behavior of polymer solutions in drop-on-demand inkjet printing. J Rheol 56(5):1109–1127
Hölzl K, Lin S, Tytgat L, Van Vlierberghe S, Gu L, Ovsianikov A (2016) Bioink properties before, during and after 3d bioprinting. Biofabrication 8(3):032002
Kafiabad HA, Sadeghy K (2010) Collapse of cavitation gas bubbles in giesekus liquids. J Soc Rheol Japan 39(3):55–64
Longuet-Higgins M (1983) Bubbles, breaking waves and hyperbolic jets at a free surface. J Fluid Mech 127:103–121
Longuet-Higgins M (2001) Vertical jets from standing waves. Proc R Soc Lond Ser A Math Phys Eng Sci 457(2006):495–510
McKinley GH (2005) Visco-elasto-capillary thinning and break-up of complex fluids. In: Binding DM, Walters K (eds) Book section in rheology reviews. British Society of Rheology, Aberystwyth, Wales, pp 1–48
McKinley GH, Tripathi A (2000) How to extract the Newtonian viscosity from capillary breakup measurements in a filament rheometer. J Rheol 44(3):653–670
Mørch KA (2015) Cavitation inception from bubble nuclei. Interface Focus 5(5):20150006
Morrison NF, Harlen OG (2010) Viscoelasticity in inkjet printing. Rheol Acta 49(6):619–632
Mun RP, Byars JA, Boger DV (1998) The effects of polymer concentration and molecular weight on the breakup of laminar capillary jets. J Non-Newtonian Fluid Mech 74(1–3):285–297
Onuki H, Oi Y, Tagawa Y (2018) Microjet generator for highly viscous fluids. Phys Rev App 9(1):014035
Papageorgiou DT (1998) On the breakup of viscous liquid threads. Phys Fluids 7(7):1529
Peters IR, Tagawa Y, Oudalov N, Sun C, Prosperetti A, Lohse D, van der Meer D (2013) Highly focused supersonic microjets: numerical simulations. J Fluid Mech 719:587–605
Sur S, Rothstein J (2018) Drop breakup dynamics of dilute polymer solutions: effect of molecular weight, concentration, and viscosity. J Rheol 62(5):1245–1259
Tagawa Y, Onuki H (2018) Liquid jet discharge device and liquid jet discharge method. US Patent 2018/0133745 A1
Tagawa Y, Oudalov N, Visser CW, Peters IR, van der Meer D, Sun C, Prosperetti A, Lohse D (2012) Highly focused supersonic microjets. Phys Rev X 2(3):031002
Tagawa Y, Yamamoto S, Hayasaka K, Kameda M (2016) On pressure impulse of a laser-induced underwater shock wave. J Fluid Mech 808:5–18
Theodorakos I, Kalaitzis A, Makrygianni M, Hatziapostolou A, Kabla A, Melamed S, de la Vega F, Zergioti I (2019) Laser-induced forward transfer of high viscous, non-newtonian silver nanoparticle inks: jet dynamics and temporal evolution of the printed droplet study. Adv Eng Mater 21(10):1900605
Thoroddsen T, Takehara K, Etoh T, Ohl CD (2009) Spray and microjets produced by focusing a laser pulse into a hemispherical drop. Phys Fluids 21(11):112101
Turkoz E, Perazzo A, Kim H, Stone HA, Arnold CB (2018) Impulsively induced jets from viscoelastic films for high-resolution printing. Phys Rev Lett 120(7):074501
Wagner C, Bourouiba L, McKinley GH (2015) An analytic solution for capillary thinning and breakup of fene-p fluids. J Non-Newtonian Fluid Mech 218:53–61
Worthington A, Cole R (1897) Impact with a liquid surface, studied by the aid of instantaneous photography. Containing papers of a mathematical or physical character. Philos Trans R Soc Lond Ser A 189:137–148
Acknowledgements
We thank Professor K. Iwami for allowing us access to plasma cleaner facilities.
Funding
This work was funded by JSPS KAKENHI Grant numbers 17H01246 and 20H00223, Japan. A.F-G gratefully acknowledges funding from ANID FONDECYT Grant number 3200093, Chile.
Author information
Authors and Affiliations
Contributions
A.F-G, H.O and Y.Y have conducted the experiments and prepared the manuscript of the paper. Y.N and Y.T have contributed equally to the direction and writing of the paper.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interests.
Availability of data and material
Data and material are available on request.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary material 1 (M4V 6171 kb)
Supplementary material 2 (M4V 7549 kb)
Supplementary material 3 (M4V 7183 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Franco-Gómez, A., Onuki, H., Yokoyama, Y. et al. Effect of liquid elasticity on the behaviour of high-speed focused jets. Exp Fluids 62, 41 (2021). https://doi.org/10.1007/s00348-020-03128-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-020-03128-w