Unsteady aerodynamics of a wing in a novel small-amplitude transverse gust generator

Abstract

A novel small-amplitude high-frequency gust generator has been developed that works by oscillating a small fence on the wind tunnel wall. The gust generator produces approximately constant local angle of attack in the chordwise direction. Due to the challenges of measuring small and slightly non-uniform gust angles the gust generator was calibrated using direct lift measurements on a symmetric wing set at zero geometric angle of attack. Unsteady lift force measurements and the Theodorsen's theory were used for the dynamic calibration of the gust angle. At nonzero geometric angles of attack, if the wing’s effective angle of attack remains below the stall angle, unsteady lift closely follows the static lift curve with very small hysteresis. Beyond the stall angle, dynamic stall and larger lift hysteresis are observed. Interestingly, in this regime, if flow is separated and a separation bubble is maintained on the wing throughout the cycle then increasing frequency reduces lift hysteresis. The slope of the lift curve, averaged over the cycle, may be greater than that of attached flow. The gust response is more sensitive to maximum effective angle of attack than the reduced frequency or the reduced pitch rate. The normalized lift change is much larger for separated flows than for attached flows.

Graphic abstract

1 Introduction

Unsteady aerodynamics of wings in discrete gusts and turbulence continues to be an important area of research. Estimates of maximum loads as well as reduction of extreme loads are essential for better aircraft stability and lighter designs, which may also provide lower drag. The unsteady forces and moments are typically short in period but can be severe. A maximum reduced frequency near k = 1 (where $k=\pi fc/$ U_∞, f is the frequency, c chord length, U_∞ freestream velocity) is estimated for civil transport aircraft at cruise (Heathcote et al. 2018).

It is estimated that the von Karman turbulence spectrum can be equivalent to peak-to-peak gust amplitudes of up to 3 deg at cruise and 12 deg at take-off and landing for larger civil transport aircraft (Heathcote 2017). For discrete gusts, estimates of gust amplitude are similar. In contrast, for micro air vehicles operating in the atmospheric boundary layer the peak-to-peak gust amplitude can be much larger, due to the slower speed of aircraft, while the reduced frequency is still high (due to both small size and speed) (Gursul 2004). In this paper we focus on the unsteady aerodynamics of wings in small-amplitude gusts. It is noted that even smaller gust amplitudes (vertical velocity amplitude of 0.5% of the freestream velocity) were experimentally produced by Brion et al. (2015). One natural consequence of such small-amplitude gusts is the difficulty associated with the measurement of gust velocity. Fast response pressure probes, laser Doppler velocimetry, and particle image velocimetry (PIV) have all been employed, but typical measurement uncertainties are around 1–2% of the freestream velocity. For example, a transverse gust velocity of 2% of the freestream velocity would correspond to 1.1 deg in gust angle. Hence, it is extremely challenging to characterize gusts produced in experimental facilities. A solution to this problem is to make use of the linearized unsteady aerodynamic theory (Theodorsen 1934). For example, Brion et al. (2015) applied Theodorsen’s theory to relate the pitching amplitude of a gust generator’s oscillating vane to the gust amplitude it produced downstream. Wei et al. (2019a, b) used this theory to prescribe the motion of a gust generating airfoil which would produce smooth and symmetric gusts at high frequencies.

Various gust generators in wind and water tunnels have been used to simulate gusts. The two most important considerations are (i) two-dimensionality of the gust, and (ii) capability to operate at higher speeds in wind tunnels. There are several methods used in the literature to generate single or periodic gusts in experimental facilities. These include oscillating tunnel walls (Holmes 1973; Patel 1980), oscillating airfoils (Gilman and Bennett 1966; Booth and Yu 1986; Wilder and Telionis 1998), fixed airfoils with oscillating flaps (Jones and Moore 1972; Bicknell and Parker 1972; Parker and Bicknell 1974), rotating cylinders (Lorber and Covert 1982), and rotating slotted cylinders (Tang et al. 1996), as discussed by Wooding and Gursul (2003). These can be classified into two broad categories: (1) vortical gusts, and (2) irrotational gusts. Examples of vortical gust generators are oscillating airfoils or flaps, which produce rolled-up trailing-edge vortices. Unfortunately, vortical gusts do not maintain two-dimensionality as they are based on the generation of shear flows. In addition, oscillating airfoils or flaps are not as suitable for the higher frequencies required in wind tunnel applications.

The effect of three-dimensionality of the vortical gusts may be more significant than the tip effects and finite aspect-ratio effects studied by Massaro and Graham (2015), who theoretically predicted that the effect depends on the aspect ratio of the wing and the spanwise correlation of the turbulence. Although the correlation length of the sectional lift is larger than the correlation length of the turbulence, the degree of spanwise correlation of approaching gusts could be important in interpreting the data from nominally 2D gust generators. For example, even for nominally 2D wake flow, at a Reynolds number based on the diameter Re = 13,000 and in the intermediate wake region x/d = 20, Hayakawa and Hussain (1989) found significant three-dimensionality and estimated the spanwise scale of vortical structures around 1.8d. They concluded that the typical spanwise extent of large spanwise vortices is comparable with the local half-width of the wake.

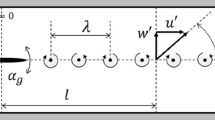
The irrotational gust generators maintain better two-dimensionality as they oscillate the freestream but do not rely on shear flows. Low turbulence level in the deflected flow and improved signal-to-noise ratio are additional advantages. However, the need for high mechanical frequency is still a limiting factor in wind tunnels. Gust generation is achieved by oscillating larger airfoils or flaps to deflect the unsteady stream (Wooding and Gursul 2003) or oscillating the walls of the test section (Holmes 1973). To overcome the limitation of high mechanical frequency, in this paper we propose a small oscillating fence in a wind tunnel (see Fig. 1). The small dimensions of the oscillating fence partially overcome the limitations of large inertia and power requirement, while still being able to deflect the freestream. To overcome the difficulties with measuring gust velocities, this novel gust generator was calibrated for “steady gusts” by recording the lift force of a symmetrical wing at varying geometric angle of attack with no gust, and then equating to the lift force of the same wing at zero angle of attack in the gust. The steady gust angles were calibrated as a function of the fence position. For “unsteady gusts”, Theodorsen’s theory was used to calibrate unsteady gust angle from the unsteady lift measurements at zero angle of attack. Then the unsteady aerodynamics of the wing was studied at nonzero angles of attack, while subjected to various gusts.

Fig. 1

a Gust generator concept, b gust fence deployment profile

2 Experimental methods

2.1 Experimental setup

The conceptual design of the gust generator, shown schematically in Fig. 1, was initially guided by steady computational fluid dynamics simulations which helped select the size and the location of the two fences to produce small gust angles with sufficient uniformity. Both fences can be actuated with the same harmonic time function to produce the angles β₁ and β₂ between zero and 90 deg. However, in this paper we kept β₁ constant at 0 or 90 deg and varied the fence angle β₂ as a periodic wave shown in Fig. 1b.

Figure 2 shows a schematic of the experimental setup. The experiments were carried out in the large wind tunnel at the University of Bath. The insets in Fig. 2 show the test section, wing, schematic of PIV setup, and the drive train of the gust fence. Two false walls inside the wind tunnel turn its octagonal working section into a 1.52 m × 1.52 m square. The walls are welded aluminium frames with riveted aluminium skins which fully house the fences when stowed (β₁ = β₂ = 0 deg) and allow a portion of the flow to bypass the working section. The fences are thin carbon fibre sandwich panels with 2 mm skins and a 5 mm foam core which span the height of the wind tunnel and deploy to a height of 107 mm from the walls. Each fence has a dedicated crank mechanism powered by a 6 kW servo motor (ABB BSM100C) via low-backlash timing belt. The cranking mechanisms are each a flywheel and pulley which drive a carriage along linear bearings in a reciprocating motion. Actuator arms on the fences are connected to the carriage via internal pushrods. A window in one of the false walls grants optical access to the test section.

Fig. 2

Model of the wind tunnel showing the wing mount structure, downstream fence $\left({\beta }_{2}\right)$ drive train and drive support structure. Detail views are of (top) working section and tunnel layout, (bottom) gust fence drive train

The wing model was a rectangular wing of 0.23 m chord, semi-aspect ratio sAR = 5 and a symmetrical NACA 0012 cross section with an extremely rigid carbon fibre semi-monocoque construction. It was supported vertically in the tunnel by a carriage mounted on air bushings which allowed the free transmission of lift into the load cell.

2.2 Force and velocity measurements

Lift measurements were taken by a one-component miniature load cell (Futek LSB200Jr—FSH00105) with a 25 lb measurement range. For steady gust measurements, 20,000 samples were taken at 1 kHz, while for unsteady gust measurements 1000 samples/cycle were taken for 50 cycles. Acquisition was performed by a National Instruments cRIO-9076 running a LabView program on the RealTime and FPGA environments, which recorded the load cell voltage alongside the servo motor’s encoder signal to obtain phase-locked measurements with respect to the position of the oscillating fence.

PIV was used to obtain the time-averaged and phase-averaged flow fields for steady and unsteady gust conditions, respectively. Flow was seeded with olive oil droplets from a TSI oil-droplet generator. Acquisition was performed by a TSI 2D-PIV system using one 8MP TSI PowerView CCD camera (3,312 × 2488 pixels) with a 50 mm lens, a Quantel Evergreen 200 mJ 15 Hz Nd:YAG laser and a TSI LaserPulse synchroniser. The laser was supported next to the wind tunnel and aligned with the mid-span plane of the wing, while the camera recorded the flow field from a traverse underneath the glass floor (see Fig. 2). For phase-averaging each image was triggered externally by the cRIO, which monitored the crank position and output a trigger pulse at the desired phase.

2.3 Steady gusts

Figure 3a shows an example of the gust angle α_g obtained from the time-averaged PIV data in the absence of the wing for k = 0, β₁ = β₂ = 90 deg. The schematic of the wing cross-section was inserted to provide a reference scale and location. Although we have focussed on a small region around the wing, there are clear nonuniformities in gust angle. Note that the schematic in Fig. 1 is drawn to scale, to reflect the relative size of the wing cross-section relative to the test section and fences. The wing cross-section is relatively small, but nevertheless the gust is not perfectly uniform across its chordline. Figure 3b shows the variation of the local gust angle over the chordline of the wing cross-section (in the absence of the wing) for steady (k = 0) as well as unsteady (k = 0.018, 0.181) gusts for β₁ = 0 deg, at the instants corresponding to the minimum β₂ = 0 deg (t/T = 0/8) and maximum β₂ = 90 deg (t/T = 4/8). Only the lowest and highest reduced frequencies are included as examples. Figure 3c shows similar information for β₁ = 90 deg. It is seen that, even for steady gusts, the chordwise gust angle shows variations of around 1 deg. This may be considered a nearly constant gust angle for a large-amplitude gust, but it is relatively large for a small-amplitude gust.

Fig. 3

a Local gust angle in the working section for $k=0, {\beta }_{1}={90}^{o}, {\beta }_{2}={90}^{o}$; chordwise gust distribution for b ${\beta }_{1}={0}^{o}$ and c ${\beta }_{1}={90}^{o}$

As can be seen in Fig. 1, the oscillating fence is just below the wing. The resulting gust angle variations are not due to a disturbance that is generated upstream and convects over the wing. It is not a travelling wave or convected gust, which was experimentally and theoretically studied using the Sears function (Wei et al. 2019a, b), instead, it could be considered as a standing wave. In our analysis we approximated the amplitude of the standing wave as constant in the streamwise direction, although small deviations exist in velocity measurements. There are similar concepts in which the disturbance has a standing-wave nature rather than a travelling wave. For example, Volpe et al (2013) used a “double wind tunnel” configuration to produce lateral gusts on a stationary model. An auxiliary wind tunnel produced the cross-flow component of the freestream. Other studies used pair of oscillating flaps (Wooding and Gursul 2003) and oscillating walls of the test section (Holmes 1973; Patel 1980) to deflect the unsteady freestream. Considering the size of the model with respect to the spatial length scale of freestream deflections as well as the location at which the disturbance is introduced, the case of Wooding and Gursul (2003) is closest to a standing wave, whereas the other two reported a wave that convects with very low velocity compared to the freestream. None of these previous facilities examined the unsteady aerodynamics of a wing in a small-amplitude transverse gust with a standing-wave nature. In terms of relevant engineering applications of this type of gust generation, small wings in very large disturbances and slow-moving gusts, and unsteady freestream variations for maneuvering wings and rotorcraft blades are highly relevant.

Figure 4 shows the variation of the chordwise-averaged gust angle $\overline{\alpha }_{g}$ as a function of the fence angle β₂ for fixed values of β₁ = 0 and 90 deg. The standard deviation (from the chordwise average) is larger for β₁ = 90 deg, which can be up to 1 deg. Keeping in mind that 1 deg causes a change in the theoretical lift coefficient of around 0.11 for an airfoil, we propose a method to calibrate the gust angle using the lift force measurements of a symmetrical wing cross-section at zero angle of attack. The current wing with the NACA 0012 cross-section was used for this purpose.

Fig. 4

Lift force-derived effective gust angle and PIV chordwise-averaged gust angle as a function of β₂ at k = 0. Error bars denote standard deviation of chordwise-average

Figure 5a shows the variation of lift coefficient as a function of wing angle of attack with the gust generator stowed (β₁ = β₂ = 0 deg). Comparison with another experimental study (Hansman and Craig 1987) for an airfoil at a similar Reynolds number as well as the theoretical lift coefficient for airfoil (assuming a slope of 2π according to the thin airfoil theory) and wing are presented. For the wing the initial slope agrees well with the lifting surface theory of wings in inviscid subsonic flow (ESDU, 2012). The variation of the lift coefficient for small angles of attack can be used to calibrate gust angles.

Fig. 5

a Static lift coefficient curve; b lift coefficient as a function of β₂ for ${\alpha }_{0}={0}^{o}$

Figure 5b shows the variation of the lift coefficient as a function of the fence angle β₂ for fixed values of β₁ = 0 and 90 deg, when the wing is set at zero angle of attack. Fitting these lift values to the baseline lift curve with no gust (Fig. 5a) yields the effective gust angle α_{g eff} as a function of fence angle (see Fig. 4). The comparison of the chordwise-averaged gust angle $\overline{\alpha }_{g}$ obtained from the PIV measurements and the effective gust angle α_{g eff} obtained from the lift measurements in Fig. 4 reveals that both have a similar trend, but there are large differences (as much as 1 deg) for the β₁ = 90 deg case.

2.4 Unsteady gusts

The dynamic calibration of the gust angle was performed using the Theodorsen’s theory as discussed earlier in the paper. The Theodorsen model of unsteady aerodynamics of a thin airfoil is based on the attached potential flow assumption and is valid for small-amplitude oscillations. As the reduced frequency in this study is small (k < 0.2), the thickness of the wing cross-section is not expected to be significant (Lysak et al. 2013, 2016). The Theodorsen model is known to agree well with experiments, even at low Reynolds numbers (Chiereghin et al. 2019). Consequently, it was also used in the prediction of operating parameters for various gust generators (Brion et al. 2015; Wei et al. 2019a, b). To ensure attached flow during the gust, we performed the experiments at zero geometric angle of attack, α₀ = 0 deg. The attached flow hypothesis was verified with PIV measurements for various cases, including at t/T = 0.5 (β₂ = 90 deg) for k = 0.018, β₁ = 0 deg and k = 0.18, β₁ = 90 deg shown in Fig. 6a.

Fig. 6

a Phase-averaged velocity magnitude contours at t/T = 0.5 for (left) $k=0.018, {\beta }_{1}={0}^{o}$ and (right) $k=0.18, {\beta }_{1}={90}^{o}$; b comparison of steady (k = 0) and phase-averaged (k = 0.018–0.18) lift coefficient as a function of ${\beta }_{2}$ and $t/T$

Theodorsen’s formula can be used to estimate the fluctuations of lift coefficient in response to a transverse gust of velocity $v={v}_{\mathrm{amp}}{e}^{i2\pi ft}$:

$${C}_{L}=2\pi \frac{v}{{U}_{\infty }} \left(C(k)+i\frac{k}{2}\right)$$

where the Theodorsen function C(k) is a complex number and i is the imaginary unit. For small gust angles, this equation becomes:

$${C}_{L}=2\pi {{\alpha }}_{g} \left(C(k)+i\frac{k}{2}\right)$$

The time history of the gust angle ${{\alpha}}_{g}$ can be calculated using the time history of the measured lift coefficient. In this paper we have assumed that the lift coefficient slope $2\pi$ can be replaced with the measured lift coefficient slope of the static wing ${C}_{L0}$ at α = 0 deg, as the wing has a high aspect ratio of AR = 10. It is reasonable to use the above equation, revised for the 3D wing, as the flow remains attached.

This method for determining the time history of gust angle was applied for α₀ = 0 deg; however, it will be shown later that the Theodorsen theory remains valid for the wing in gusts at α₀ = 5 deg. For β₁ = 0 deg and β₁ = 90 deg, Fig. 6b shows the variation of lift coefficient as a function of t/T as well as the fence angle β₂ for selected reduced frequencies. With increasing reduced frequency, increasing hysteresis as a function of fence angle β₂ and increasing phase lag as a function of t/T are observed. The lift coefficient is not sinusoidal even though the fence height sin(β₂) is sinusoidal (see Fig. 1b). The time history of the lift coefficient for each case was expressed as a Fourier series and the first four terms were kept for analysis. Each term in the Fourier series was used in the Theodorsen equation to predict its contribution to the gust angle, hence forming a Fourier series representation of the effective gust angle. Further details can be found in the thesis of the first author (Fernandez 2020). Figure 7 compares the chordwise-averaged gust angle $\bar{{\alpha }_{g}}$ obtained from PIV and the effective gust angle α_{g eff} obtained from lift measurements at similar reduced frequencies for β₁ = 0 deg (in black) and β₁ = 90 deg (in red). It is seen that, although the trends are similar, there are large discrepancies around certain phases in the cycle. All further analysis and discussion will use effective gust angle α_{g eff}. Increasing β₁ = 0 deg to β₁ = 90 deg shifts the minimum and maximum gust angles in the cycle to larger values.

Fig. 7

Comparison of effective gust angle ${\alpha }_{g \mathrm{eff}}$ from lift data and chordwise-averaged gust angle $\stackrel{-}{{\alpha }_{g}}$ from PIV for ${\beta }_{1}={0}^{o}, {90}^{o}$: a k = 0.018 (black), k = 0.017 (red), b k = 0.072 (black), k = 0.067 (red), c k = 0.126 (black), k = 0.117 (red), d k = 0.181 (black), k = 0.168 (red)

It is seen that gust amplitude decreases and phase lag increases with increasing reduced frequency. Although it is not ideal, frequency dependency is typical for all experimental gust generators. The unsteady response of the deflected freestream with respect to sinusoidal actuation of the fence is inherently similar to that of a first order system, with amplitude and phase modulation (Fernandez 2020). We estimate that the normalized time constant U_∞τ/c is around 3 for this gust generator. It is known that dynamic behaviour of the test section velocity in response to dynamic exit area variations is governed by the inertia force (to accelerate the total air mass in the wind tunnel) as well as viscous and acoustic resonance effects (Greenblatt 2016; Rennie et al. 2019). Under simplified conditions, tunnel response (velocity oscillations) can be reduced to a first order system (Greenblatt 2016). This effect results in unavoidable phase lag of the velocity with respect to the quasi-steady case. In addition, it is believed that the dynamic response of our gust generator is likely to be affected by the separation bubble induced by the oscillating fence. It is known that dynamic characteristics such as size of separation bubbles behind oscillating fences are highly dependent on the oscillation frequency (Francis et al. 1979; Miau et al. 1991). In practice the phase lag is not consequential, because it can be calibrated out and the amplitude decay can be measured to allow fair comparison. The main focus in this paper was restricted to the effect of the wing angle of attack on the gust response at a fixed gust frequency. Later we also consider the effect of the gust as a function of reduced frequency through a normalized lift response.

The gust time history shows that it is not an exact sine wave. We have not attempted to control and modify the waveform to achieve an exact sine wave, although in theory this is possible, but not always straightforward for large velocity variations (He & Williams 2020; Gursul & Ho 1992; Gursul et al. 1994). The gust waveform generally deviates from the pure sine wave more for low frequencies (see Fig. 7), although, in the worst case, the amplitude of the higher harmonics in the Fourier series was small compared to the amplitude of fundamental frequency. In our case, the amplitude of the ratio of C_L/α_g, using the method outlined above follows the same theoretical curve of Theodorsen when plotted as a function of reduced frequency k. This will be discussed later. In addition, as we are focussed on unsteady aerodynamics for small-amplitude gusts, any non-harmonic effects are likely to be small.

3 Results and discussion

3.1 Wing in steady gust

Figure 8 shows the variation of the lift coefficient for steady gusts when the wing is placed at α₀ = 0, 5, 10, and 12 deg. The x-axis is the effective angle of attack, which is defined as:

$$ \alpha_{{{\text{eff}}}} \, = \,\alpha_{0} \, + \,\alpha_{{g{\text{ eff}}}} . $$

Fig. 8

Time-averaged lift coefficient versus effective angle of attack, with accompanying pre- and post-stall flow fields at ${\alpha }_{0}={12}^{o}$

The lift coefficients in gusts were compared for β₁ = 0 deg in part (a) and for β₁ = 90 deg in part (b), with the static lift coefficient for no gust. The data for α₀ = 5, 10, and 12 deg show excellent agreement with the wing baseline case (no generator) until stall. The data for α₀ = 0 have already been used in the calibration of the gust angles as explained previously. There is a slight delay of the stall angle in steady gusts and consequently some discrepancies in the post-stall region. The differences in the stall behaviour may be due to the nonuniformity of the gust angle in the chordwise direction, which was not accounted for by the effective angle of attack in Fig. 8.

Figure 8 also shows the values of β₂ just before and just after the stall in both parts (a) and (b). The time-averaged vorticity and velocity magnitude with streamlines are consistent with the pre-stall and post-stall lift coefficients. The lift force and velocity measurements were performed at different times, separated by months, suggesting that the gusts are highly repeatable.

3.2 Wing in unsteady gusts for β ₁ = 0 deg

Figure 9a shows the variation of the lift coefficient as a function of effective angle of attack at α₀ = 0, 5, 10, and 12 deg for the lowest reduced frequency k = 0.018. Negligible unsteady effects and hysteresis are seen at α₀ = 0 and 5 deg, whereas at α₀ = 10 and 12 deg lift overshoot, which peaks near the maximum effective angle of attack, and a sudden drop characterize large hysteresis loops, similar to those of “deep dynamic stall” described by McCroskey (1982), as α_eff exceeds the static stall angle.

Fig. 9

a Phase-averaged lift coefficient loops; b phase-averaged vorticity and velocity contours at various phases, $k=0.018, {\beta }_{1}={0}^{o}$, ${\alpha }_{0}={10}^{o}$ and ${\alpha }_{0}={12}^{o}$

Open circle symbols are used in the lift loops to indicate the timing of the fence position (t/T). The exact timing of the sudden lift drop is different for α₀ = 10 and 12 deg. The lift hysteresis loops show this drop starts when the fence angle is maximum β₂ = 90 deg (t/T = 4/8) or even earlier, around t/T = 3/8, depending on the wing angle of attack α₀. Corresponding phase-averaged vorticity and velocity magnitude with streamlines are shown at selected phases in part (b). For α₀ = 10 deg, the loss of lift at t/T = 4/8 correlates well with the separation of flow between t/T = 4/8 and t/T = 5/8. However, for α₀ = 12 deg, the phase-averaged vorticity fields before and after the loss of lift (t/T = 3/8 and 4/8, respectively) do not appear very different. In contrast, a closer examination of the closed recirculating streamlines above the wing reveals that they are centered near the mid-chord and trailing-edge, respectively, which is consistent with the change in the lift force. In this case, phase-averaged closed streamline patterns (and their center) are better correlated with the lift force than the phase-averaged vorticity fields.

For this case, the reduced frequency of k = 0.018 is much smaller than both the wake vortex shedding instability (with an order of magnitude of k = O(1)) and the most unstable frequency of the separated shear layer from the leading-edge (with an order of magnitude of k = O(10)). Hence, low excitation frequencies (k = O(0.01) to O(0.1)) coupled with small amplitude do not cause the vortex lock-in phenomenon (Young and Lai, 2007) that has been documented for unsteady oscillating airfoils. This has been recognized and documented by Wernert et al. (1997) and emphasized again by Ramasamy et al. (2018). Figure 10 shows the phase-averaged streamlines at t/T = 3/8 for α₀ = 12 deg, together with three instantaneous vorticity fields at the same phase. Vortex roll-up can be identified in each of them with varying location and size. Hence, the flow is not perfectly locked-in and, therefore, not repeatable. The phase-averaged streamlines present an average picture.

Fig. 10

Phase-averaged streamline (top) and three instantaneous vorticity fields for $k=0.018, t/T =3/8, {\alpha }_{0}={12}^{o}$

When the reduced frequency is increased to k = 0.072, shown in Fig. 11, flow is mostly attached (with trailing-edge separation at some phases) for α₀ = 10 deg as seen in the vorticity and velocity fields, and the lift loop becomes almost linear with small hysteresis. On the other hand, for α₀ = 12 deg there is always flow separation, ranging from mild separation with no indication of closed streamlines to massively separated flow with large swirling regions. The maximum lift occurs when the center of the swirling region is close to the surface near the mid-chord at t/T = 4/8. For this case, the lift hysteresis loop becomes narrower than that of Fig. 9 at the same angle of attack.

Fig. 11

a Phase-averaged lift coefficient; b phase-averaged vorticity and velocity contours at various phases, $k=0.072, {\beta }_{1}={0}^{o}$, ${\alpha }_{0}={10}^{o}$ and ${\alpha }_{0}={12}^{o}$

With a further increase to k = 0.126, shown in Fig. 12, there is attached flow for all geometric angles of attack except α₀ = 12 deg. At all phases of the cycle for α₀ = 12 deg there is a swirling region with closed streamlines whose center moves over the wing. The hysteresis loop is narrower even though the swirling region is present throughout. For the highest reduced frequency k = 0.181 in Fig. 13, the hysteresis loop is the narrowest for α₀ = 12 deg. The loop is similar in shape to that of α₀ = 10 deg but with a steeper slope. This can be attributed to the existence of a swirling flow over the wing throughout the cycle, as seen in the flow fields. Although decreased hysteresis was also observed when a separation bubble exists throughout the cycle, this aspect remains to be understood better in future studies.

Fig. 12

a Phase-averaged lift coefficient; b phase-averaged vorticity and velocity contours at various phases, $k=0.126, {\beta }_{1}={0}^{o}$, ${\alpha }_{0}={12}^{o}$

Fig. 13

a Phase-averaged lift coefficient loops; b phase-averaged vorticity and velocity contours at various phases. $k=0.181, {\beta }_{1}={0}^{o}$, ${\alpha }_{0}={12}^{o}$

3.3 Wing in unsteady gusts for β ₁ = 90 deg

As increasing the β₁ from 0 to 90 deg results in an effective shift of the gust time history (see Fig. 7), some aspects of the lift and flow fields remain similar for both cases. Here we summarize the main similarities and differences. Figure 14 shows the lift loops for the smallest reduced frequency tested k = 0.017. It is seen that the case of the wing angle of attack α₀ = 10 deg results in a larger lift loop than that of α₀ = 12 deg, as the minimum and maximum effective angles of attack increase for both cases. Whereas this leads to a higher maximum lift coefficient for α₀ = 10 deg, it causes the maximum lift coefficient to be lower for α₀ = 12 deg compared to those in Fig. 9. The flow fields shown in Fig. 14b, together with the lift variation, also reveal that the timing of the sudden lift drop for α₀ = 10 deg is different in Fig. 9 (near t/T = 4/8) and Fig. 14 (near t/T = 3/8).

Fig. 14

a Phase-averaged lift coefficient loops; b phase-averaged vorticity and velocity contours at various phases, $k=0.017, {\beta }_{1}={90}^{o}$, ${\alpha }_{0}={10}^{o}$

When increasing reduced frequency to k = 0.067, shown in Fig. 15, the flow remains separated throughout the cycle for α₀ = 10 deg, in contrast with the case of a similar reduced frequency in Fig. 11, where the flow remains attached. Compared to the lower reduced frequency in Fig. 15, the lift loops are narrower. With further increase to k = 0.117, shown in Fig. 16, the lift loops at α₀ = 10 and 12 deg become narrower, while the swirling flows remain similar to Fig. 16. At the highest reduced frequency k = 0.168 in Fig. 17 the lift loops are the narrowest, with an average slope larger than those of the attached flows at α₀ = 0 and 5 deg. This is comparable to the observations made for a similar reduced frequency in Fig. 13.

Fig. 15

a Phase-averaged lift coefficient loops; b phase-averaged vorticity and velocity contours at various phases, $k=0.067, {\beta }_{1}={90}^{o}$, ${\alpha }_{0}={10}^{o}$

Fig. 16

a Phase-averaged lift coefficient loops; b phase-averaged vorticity and velocity contours at various phases, $k=0.117, {\beta }_{1}={90}^{o}$, ${\alpha }_{0}={10}^{o}$

Fig. 17

Phase-averaged lift coefficient loops for $k=0.168, {\beta }_{1}={90}^{o}$

McCroskey (1982) commented that “the unsteady stall behavior is characterized by growing hysteresis in the airloads” for pitching airfoils, yet here we find that, beyond the large hysteresis seen at low frequency, the wing in gusts experiences lower hysteresis for increasing reduced frequency. For our gust generator we have approximately constant local angle of attack in the chordwise direction, which is more similar to a plunging motion than a pitching motion. A comparison with dynamic stall of pitching airfoils (Ekaterinaris and Platzer 1998) at around k ≈ 0.2 (near our maximum in these experiments) shows that the pitching airfoils display much larger lift hysteresis at similar reduced frequencies. We also compared the shape and the extent of the hysteresis loops of our data with those of plunging airfoils (Carta 1979), and found similarly less hysteresis in both cases compared to the pitching airfoils. For a plunging airfoil it is more difficult to measure the lift force in experimental studies. This is because the inertial force due to the mass of the oscillating airfoil needs to be removed. Unfortunately, the inertial force may become much larger than the aerodynamic force with increasing frequency of the plunging oscillations. The current set up, in which the unsteady lift force on a stationary wing is measured, does not suffer from this problem. This is an advantage for the method employed in this article.

4 Discussion

As the amplitude of gust depends on the frequency in the experiments, here we compare the gust response by defining normalized lift change and dividing the amplitude of the lift coefficient with the amplitude of the gust:

$$\frac{{C}_{L \, \mathrm{amp}}}{{\alpha }_{g \,\mathrm{amp} }{C}_{L\alpha 0}}$$

Here the lift peak-to-peak amplitude ${C}_{L \,\mathrm{amp}}$ is normalized by the gust peak-to-peak amplitude, ${\alpha }_{g \,\mathrm{amp}}$, and the lift curve slope at $\alpha ={0}^{o}, {C}_{L\alpha 0}$. Figure 18a, b shows the variation of the normalized lift response as a function of reduced frequency k for β₁ = 0 and 90 deg. Here the solid line shows the Theodorsen theory for a sinusoidal gust in attached flow, which was previously used to dynamically calibrate the gust angles of the experimental gust generator at zero geometric angle of attack α₀ = 0 deg. The normalized lift change for experimentally generated gusts, calculated for α₀ = 0 deg, follows the same theoretical curve of Theodorsen for sinusoidal gusts. This implies that non-harmonic distortions of the experimental gusts have negligible effect. It is seen that the agreement between theory and experimental gusts (which are not necessarily sinusoidal and contain higher harmonics) is also good at α₀ = 5 deg for both β₁ = 0 and 90 deg if k ≥ 0.05. Even for geometric angle of attack as high as α₀ = 10 deg at β₁ = 0 deg, the normalized lift change is close to the Theodorsen’s theory. As previously discussed in the PIV results, for this combination of wing angle of attack and gust, the flow remains attached throughout the cycle, except for the smallest reduced frequency investigated k = 0.018 for which there is attached flow during part of the cycle. For the same angle of attack α₀ = 10 deg, but for β₁ = 90 deg, the normalized lift change increases rapidly until k ≈ 0.04 and then remains roughly constant at a value significantly larger than the Theodorsen’s prediction. At the largest wing angle of attack α₀ = 12 deg for both β₁ = 0 and 90 deg, the normalized lift change becomes larger than that of the attached flows if the reduced frequency k is larger than 0.02–0.04. Hence, whether the flow remains mostly attached or not is the primary factor, followed by the reduced frequency. For β₁ = 90 deg, it is noted that the normalized lift change is smaller for α₀ = 12 deg than for α₀ = 10 deg. The normalized lift-coefficient data in Fig. 18 also show uncertainty bars, which is due to the cycle-to-cycle variations of the lift force. As expected, the cycle-to-cycle variations are small for attached flows, but increase in separated flows.

Fig. 18

Lift coefficient amplitude, ${C}_{L \,\mathrm{amp}}$, normalized by gust amplitude, ${\alpha }_{g \,\mathrm{amp}}$, and the lift curve slope at $\alpha ={0}^{o}, {C}_{L\alpha 0}$, a ${\beta }_{1}={0}^{o}$, b ${\beta }_{1}={90}^{o}$; Phase lag of the lift with respect to the gust angle, c ${\beta }_{1}={0}^{o}$, (d) ${\beta }_{1}={90}^{o}$

The phase lag between the fundamental Fourier components of the lift and the gust angle is presented in Fig. 18c, d. The Theodorsen’s prediction for attached flows is also shown with solid line. As expected, the phase lag is small for attached flows, but increases substantially in separated flows near the stall or at the post-stall regimes.

Whereas the reduced frequency,

$$k=\frac{\pi fc}{{U}_{\infty }}$$

has only the frequency information, the reduced pitch rate has both the magnitude and frequency information:

$$K= \frac{{c{\left(\frac{\mathrm{d}{\alpha }_{\mathrm{eff}}}{\mathrm{d}t}\right)}_{\mathrm{max}} }}{2{U}_{\infty }}$$

Figure 19a shows the normalized lift change as a function of reduced pitch rate. The symbols are grey-level coded according to their reduced frequency. The reduced pitch rate values are generally lower than those reported in the literature (Sheng et al. 2006). This is a natural consequence of small-amplitude gusts. It is seen that the parameter K does not present an improved understanding. However, the data are divided into two groups (squares and triangles), which reveal some correlation. This grouping of the data is based on the maximum effective angle of attack with a threshold of 15.5 deg as explained below. In general, the square symbols remain below unity, and the triangular symbols are larger than unity.

Fig. 19

Non-dimensional lift amplitude versus a maximum reduced pitch rate, b maximum α_eff

McCroskey (1982) suggested that the most important parameter for the dynamic stall of a given airfoil is the maximum angle of attack. For plunging airfoils, if the motion induced angle of attack is taken into account, the maximum of the effective angle of attack (sum of the static and induced angles of attack) is well correlated with the maximum and the mean lift coefficients (Chiereghin et al. 2019) of the cycle. As previous work (McCroskey, 1982; Chiereghin et al. 2019) suggested that the most important parameter for the dynamic stall of a given airfoil is the maximum angle of attack, we searched for trends of the data in Fig. 18. This is a data-driven approach, facilitated by a physically important parameter. In Fig. 19a, it is seen that the critical value of the non-dimensional lift amplitude, which is unity and represented as a horizontal line, gives the clearest delineation between the points above and below the line, if the critical value is chosen as 15.5 deg. Consequently, we present the normalized lift change as a function of the maximum effective angle of attack for our experiments in Fig. 19b. It is seen that, when the maximum effective angle of attack is less than a critical value around 15.5 deg, the normalized lift change is always smaller than unity and the dependency on the reduced frequency is weak. The cases of max(α_eff) ≤ 15.5 deg are shown with square symbols and the rest are shown with triangular symbols. When max(α_eff) > 15.5 deg, there are large variations in the normalized lift change. For very low reduced frequencies, the normalized lift change is substantially smaller than unity, but rapidly becomes significantly larger than unity with increasing k. Hence, the critical value of the maximum effective angle of attack is the most important parameter in determining the gust response of the wing. This critical value is approximately 15.5 deg for this wing at the considered amplitudes and frequencies. The critical value of 15.5 deg is above the stall angle by a margin, which is expected to depend on the choice of airfoil profile.

An interesting presentation of the gust response is obtained when all lift measurements are plotted on the same axes against angle of attack, as shown in Fig. 20. All four geometric angles of attack for both steady and unsteady gusts, as well as the baseline ‘no gust’ curve, are included. It is seen that when max(α_eff) is smaller than around 11.5 deg, which is just below the static stall angle of the baseline wing, the gust response closely follows the static lift curve, with very small hysteresis. Above this angle of attack, the envelope of the unsteady lift increases in the vertical direction, reaching a maximum around 16.5 deg. However, at higher angles of attack the vertical extent of the lift envelope evidently decreases.

Fig. 20

Lift coefficient versus α_eff for all steady and unsteady gusts

5 Conclusions

A novel small-amplitude gust generator has been developed for wind tunnel experiments. It relies on the unsteady deflections of the freestream flow to produce a transverse velocity component. As the periodic deflection of the freestream is achieved by oscillating a small fence on the tunnel wall, it has the advantages of small inertia force and thus the capability to drive the fence oscillations at higher frequencies. The PIV measurements showed that the gust generator produces gusts of variable reduced frequency (up to around k ≈ 0.2 for the current wing), with roughly constant local gust angle along the chordwise distance. However, the small variations of the local gust angle due to slight nonuniformity can influence the unsteady aerodynamics.

To overcome the challenges in characterization of small gust angles by means of direct velocity measurements, the gust generator was calibrated by measurement of lift force for a symmetrical wing (whose lift curve is known) set at zero angle of attack and immersed in the gust. The effective gust angles obtained from these steady measurements reveal consistent trends with the chordwise-averaged gust angles obtained from the PIV measurements. Unsteady lift force measurements were used for dynamic calibration of gust angle as a function of time using Theodorsen’s theory for the wing at zero angle of attack and immersed in the gusts. The unsteady force measurements and hence the gust angle variations reveal decreasing amplitude and increasing phase lag of the gusts as the gust frequency is increased.

The unsteady aerodynamics of the wing at nonzero angles of attack and immersed in gusts was studied by means of lift force and flow field measurements. The unsteady lift force as a function of the effective angle of attack, which is the sum of the wing angle of attack and the effective gust, reveals small deviations from the static lift curve and small hysteresis for small angles of attack. At small reduced frequencies, with increasing geometric angle of attack the wing enters the post-stall region of the baseline curve, leading to lift overshoot, shedding of leading-edge vortices, sudden lift loss, and significantly increased hysteresis when compared to the attached flows. However, with further increases in the reduced frequency, the lift hysteresis becomes smaller even though the flow remains separated, but forms a swirling separation bubble over the wing throughout the cycle. The slope of the lift curve, averaged over the cycle, may be greater than that of attached flows, which is attributed to the existence of the separation bubble throughout the cycle. Depending on the wing angle of attack, gust amplitude and frequency, the flow may remain attached even in the post-stall regime of the baseline wing. The phase of the maximum lift and sudden lift loss show dependence on the same parameters.

The normalized lift change in response to gusts is much larger for separated flows than for attached flows. The gust response is better correlated with the maximum effective angle of attack than reduced frequency or reduced pitch rate. When the maximum effective angle of attack is just below the static stall angle of the baseline lift curve, the gust response closely follows the static lift curve with very small hysteresis. Above this angle of attack, high amplitude lift fluctuations with large hysteresis are possible. When the maximum effective angle of attack is greater than a critical value above the stall angle of the baseline lift curve, the normalized lift change may become substantially larger than that for attached flows.