1 Introduction

Research on unsteady aerodynamics has significantly grown in recent years due to its relevance to bio-inspired flight (Ellington et al. 1996; Birch and Dickinson 2001; Wang 2005; Muijres et al. 2008; Lentink et al. 2009; Rival et al. 2009; Videler et al. 2004; Pitt-Ford and Babinsky 2013; Wu 2011; Harbig et al. 2013; Krishna et al. 2018, 2019), underwater vehicles (Triantafyllou et al. 2000; Taylor et al. 2003; Beal et al. 2006; Fish and Lauder 2006; Borazjani and Daghooghi 2013; Mackowski and Williamson 2015, 2017), flapping-foil energy harvesters (Dabiri 2007; Kinsey and Dumas 2008; Zhu 2011; Kinsey and Dumas 2012; Xiao et al. 2012; Liu et al. 2013; Young et al. 2014; Xiao and Zhu 2014; Ramesh et al. 2015; Wu et al. 2015; Kim et al. 2017; Rostami and Armandei 2017; Su and Breuer 2019), and tidal turbine blades (Sequeira and Miller 2014; Tully and Viola 2016; Smyth and Young 2019; Dai et al. 2019; Scarlett et al. 2019; Scarlett and Viola 2020). The presence of a leading-edge vortex (LEV) in these applications gives rise to a strongly nonlinear relationship between forces and kinematics (Eldredge and Jones 2019). The LEV plays a crucial role in augmenting lift in both insect/bird flight and bio-inspired flight as well as in enhancing the efficiency of flapping-foil energy harvesters.

The applications listed above frequently experience massively separated flows due to the high angles of attack reached by the aerofoils and wings. When the flow separates, it becomes more challenging to predict the unsteady forces at play. The classical linear theory of Theodorsen (1935), based on unsteady potential flow theory is widely used to predict forces for sinusoidal aerofoil kinematics. For arbitrary kinematics, we can use the extension of Theodorsen’s theory by von Kármán and Sears (1938). For transient variations of the angle of attack, the indicial response function by Wagner (1925) provides an alternative as long as the angle variations are small. Unsteady thin-aerofoil theory (UTAT) is another potential flow model that is based on the time-stepping approach. It assumes attached flow and is applicable to arbitrary small-amplitude kinematics (Katz and Plotkin 2001; Ramesh et al. 2013). More recently, researchers proposed extensions to UTAT for solving three-dimensional problems (Boutet and Dimitriadis 2018; Bird et al. 2019).

Despite apparent violations of the theoretical assumptions, researchers have applied Theodorsen’s theory to oscillating aerofoils with flow separation. According to Brunton and Rowley (2009), Theodorsen’s theory does not agree with the results of direct numerical simulation when the geometric angle of attack of a pitching flat-plate is large (\(\alpha > 40^\circ\)) due to the flow separation and the non-planar wake. A similar observation was reported by Baik et al. (2012) for a heaving and pitching aerofoil with high pitching amplitude (\(\alpha _0 > 40^\circ\)). Liu et al. (2015) reported that the agreement with Theodorsen’s theory was only good with low oscillation amplitude and low reduced frequency for a heaving and pitching plate. For a purely plunging aerofoil, Ol et al. (2009), Kang et al. (2009) and Ramesh et al. (2014) found that Theodorsen’s theory agrees well with measured lift force despite the presence of a significant LEV and McGowan et al. (2011) explains that the trailing-edge Kutta condition and the assumption that surface vorticity is bound to the aerofoil are satisfied as long as the LEV is attached. The above review of the literature shows that there is no clear agreement on why Theodorsen’s theory provides an accurate prediction when the original assumptions are not met and on the flow condition that causes Theodorsen’s theory to fail.

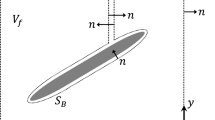
To investigate which significant force generation mechanisms Theodorsen’s theory can and cannot model, we attempt to calculate the force generation mechanisms from the fluid impulse. The concept of the fluid impulse dated back from the 19th century and was first suggested by Thomson (1868) and Thomson (1883). From Newton’s second law, we find that the force \(\varvec{F}\) on a body equals the time derivative of the impulse. For a fluid with constant density \(\rho\) and a volume of fluid \(V_\text {f}\), whose external boundaries are at infinity,

$$\begin{aligned} \varvec{F} = -\int _{V_\text {f}} \rho \frac{\text {d}\varvec{u}}{\text {d}t} \text {d}V = - \rho \frac{\text {d}}{\text {d}t} \int _{V_\text {f}} \varvec{u} \text {d}V = -\rho \frac{\text {d} \varvec{I}}{\text {d}t}, \end{aligned}$$
(1)

where

$$\begin{aligned} \varvec{I} = \int _{V_\text {f}} \varvec{u} \, \text {d}V \end{aligned}$$
(2)

is the impulse. Burgers (1920), Lighthill (1986), and Wu (1981) independently showed that the impulse is given by the sum of the integral over the fluid volume \(V_\text {f}\) of the first moment of the vorticity \(\varvec{\omega }\), and the integral over the solid surface \(S_\text {b}\) with outward unit normal \(\varvec{n}\) of the moment of tangential velocity:

$$\begin{aligned} \varvec{I} = \frac{1}{n_\text {d} - 1} \left( \int _{V_\text {f}} \varvec{x} \times \varvec{\omega } \text {d}V + \int _{S_\text {b}} \varvec{x} \times (\varvec{n} \times \varvec{u}) \, \text {d}S \right) , \end{aligned}$$
(3)

where \(n_\text {d} = 2\) and 3 in two and three dimensions, respectively, with \(\varvec{x} = (x,y)\) or \(\varvec{x} = (x,y,z)\) being the position vectors. A complete derivation and discussion is also available in Eldredge (2019, Sect. 6.2). The second term in Eq. 3 vanishes in a reference system fixed with the body. This term represents an unsteady body force equal to the difference between the forces observed in the present reference system O(x, y, z) and those observed in a reference system fixed with the body. It is proportional to the mass of the body (Koumoutsakos and Leonard 1995; Leonard and Roshko 2001) and its effect is negligible for slender bodies with small volume to surface ratio (Rival and Van Oudheusden 2017) and for a small body to fluid density ratio (Lentink 2018).

The impulse theory is based on Newton’s second law (Eq. 1) and is universally applicable to three-dimensional flow around arbitrary bluff bodies at any Reynolds number. Another advantage of the impulse theory is that it does not require pressure computations. The impulse theory is linear in vorticity such that the effect of individual vortices can be superimposed.

The impulse theory enables intuitive insights into the flow physics, which makes it an attractive basis for low-order force estimation models. Babinsky et al. (2016) developed a low-order model considering the leading-edge vortex (LEV) and the trailing-edge vortex (TEV) as a vortex pair, which was successfully applied to various unsteady aerodynamic problems (Stevens and Babinsky 2017; Stevens et al. 2017; Mancini et al. 2019). This low-order model only requires the LEV and TEV circulations, positions, and advective velocities as input. It does not require data of the vorticity in the boundary layer, which is difficult to resolve with particle image velocimetry (PIV) (Graham et al. 2017). Other promising models based on the impulse include the models by Polet et al. (2015) and Li and Wu (2015). Polet et al. (2015) estimated the circulatory force of an aerofoil undergoing a perching manoeuvre. Li and Wu (2015) developed a vortex force map method in which the impulse yields forces due to bound vorticity, free vortices, and residual vortex sheets. The latter method was extended to a high angle of attack problem (Li and Wu 2016), arbitrary aerofoils (Li and Wu 2018), and the prediction of the pitching moment (Li et al. 2020).

The aim of this study is twofold. The first aim is to verify to what extent the linear theory of Theodorsen (1935) can be adapted to accurately predict forces of large-amplitude, non-sinusoidal kinematics. To aid the interpretation of the results, we will compare the proposed adapted version of Theodorsen’s theory with unsteady thin-aerofoil theory. The second aim is to identify the force generation mechanisms that cause Theodorsen’s theory to inaccurately predict forces. This will be done by estimating the lift contribution of the LEV and TEV through a data-driven method based on the impulse theory. With this data-driven method, we will clarify the apparently conflicting conclusions of previous studies on why Theodorsen’s theory provides an accurate prediction in some separated flow conditions and not in others.

We organise the paper as follows. In Sect. 2 we describe the experimental details, the aerofoil kinematics, the lift-predictive models, and the data-driven method based on the impulse theory. In Sect. 3 we discuss the limit of applicability of the lift-predictive models and the estimation of the vortex lift by the data-driven method based on the impulse theory.

2 Methodology

2.1 Experimental setup

A schematic of the experimental rig is illustrated in Fig. 1. Experiments are performed at the SHARX water channel facility of the UNFoLD laboratory at EPFL. The channel has a test section of \(0.6~\text {m} \times 0.6~\text {m} \times 3~\text {m}\) in width, height, and length. The freestream velocity is fixed at \(U_\infty = 0.215~\text {m}~\text {s}^{-1}\). A two-dimensional NACA 0018 aerofoil is used, with the chord length \(c = 150\) mm, and the span \(b = 580\) mm, resulting in the chord-based Reynolds number \(\mathrm{{Re}} = 32,000\). A NACA 0018 aerofoil is chosen since it is structurally strong due to its thickness. Thick aerofoils are frequently used for small-scale vertical axis wind turbines (VAWTs) and tidal turbines (Payne et al. 2017; Scarlett et al. 2019). Amongst thick aerofoils, NACA 0018 is frequently used for VAWTs (Müller-Vahl et al. 2015, 2016).

Fig. 1
figure 1

Schematic of the experimental pitching aerofoil test rig

Full size image

The pitching axis is located at quarter-chord from the leading edge. The wing is placed vertically at the centre of the test section. The gap between the wingtip and the channel wall is made as small as possible (approximately 3 mm) to minimise three-dimensional effects. The pitching motions are driven by a stepper motor, monitored via an encoder.

An ATI NANO-25 IP68 6-axis force/torque sensor is used for the direct force measurement. The load cell is capable of measuring forces in the streamwise and lateral direction up to \(\pm 125\) N with a resolution of 1/48 N. Signals are recorded at 1 kHz. The forces measured in quiescent air are subtracted from those obtained in the water flow to isolate the hydrodynamic forces from the inertial forces.

The force data are filtered in three steps. The first step is a fourth-order Butterworth low-pass filter with a cutting frequency of 35 Hz. The second is a moving average of 30 points for smoothing the data. The final step is a sixth-order Chebyshev II low-pass filter with \(-\,20\) dB attenuation in the stopband. The cutoff frequency is 36 times the pitching frequency \(f_\text {p}\). This three-step filtering method is capable of preserving load spikes and it is adopted by, for instance, Granlund et al. (2011), Baik et al. (2012), Granlund et al. (2013), Ramesh et al. (2013) and Jantzen et al. (2014). A phase-average is applied over six periods. Using different numbers of periods for the phase-averaging, we find that with three or more periods the convergence error in the phase-averaged lift is smaller than 3%.

Time-resolved particle image velocimetry (TR-PIV) is conducted to measure the velocity field around the aerofoil in a horizontal cross-sectional plane 0.2 m from the water channel bottom. The measurement plane is placed at this location to reduce the influence of the free surface and the wingtip. Polyamide seeding particles (VESTOSINT 2155, Evonik Industries) are illuminated by a double-pulsed ND:YLF laser (\(\lambda = 527\) nm) (Terra PIV, Continuum). A beam splitter divides the laser beam and allows us to simultaneously illuminate both the suction and the pressure side of the aerofoil. A high-speed camera (FASTCAM SA X-2, Photron) with 1024 \(\times\) 1024 px resolution captures images at 1000 Hz. Adaptive multi-pass cross-correlation is employed to compute velocity vectors, with a final interrogation window of 48 px \(\times\) 48 px, and an overlap of 82 % (DaVis 8.4, LaVision Inc.), yielding a physical resolution of 2.4 mm or 0.016c. Outliers are detected by universal outlier detection (Westerweel and Scarano 2005) and interpolated by cubic splines.

Fig. 2
figure 2

Smoothed asymmetric triangular pitching kinematics. Shaded regions represent acceleration/deceleration parts. Refer to Eq. 4 for the detailed definition of the kinematics

Full size image

2.2 Pitching kinematics

Smoothed asymmetric triangular pitching kinematics shown in Fig. 2 are used to verify to what extent a modified version of Theodorsen’s theory (Sect. 2.3), whose original version assumes small and sinusoidal oscillations, can provide an accurate prediction of the forces. The acceleration/deceleration time is \(t_\text {a} = 0.15 T\), where \(T = f_\text {p}^{-1}\) is the pitching period. The kinematics consist of piecewise functions in which the acceleration/deceleration parts are 4th-order polynomials:

$$\begin{aligned} \alpha = {\left\{ \begin{array}{ll} {\dot{\alpha }}_1 t, &{} (0 \le t< t_1),\\ \frac{{\dot{\alpha }}_1}{2 t_\text {a}^3} (t - t_2)^4 + \frac{{\dot{\alpha }}_1}{t_\text {a}^2} (t - t_2)^3 + \alpha _0, &{} (t_1 \le t< t_2),\\ -\frac{{\dot{\alpha }}_2}{2 t_\text {a}^3} (t - t_2)^4 + \frac{{\dot{\alpha }}_2}{t_\text {a}^2} (t - t_2)^3 + \alpha _0, &{} (t_2 \le t< t_3),\\ {\dot{\alpha }}_2 (t - t_4) - \frac{{\dot{\alpha }}_2 t_\text {a}}{2} - \alpha _0, &{} (t_3 \le t< t_4),\\ \frac{{\dot{\alpha }}_2}{2 t_\text {a}^3} (t - t_5)^4 + \frac{{\dot{\alpha }}_2}{t_\text {a}^2} (t - t_5)^3 - \alpha _0, &{} (t_4 \le t< t_5),\\ -\frac{{\dot{\alpha }}_1}{2 t_\text {a}^3} (t - t_5)^4 + \frac{{\dot{\alpha }}_1}{t_\text {a}^2} (t - t_5)^3 - \alpha _0, &{} (t_5 \le t< t_6),\\ {\dot{\alpha }}_1 (t - T), &{} (t_6 \le t < T), \end{array}\right. } \end{aligned}$$
(4)

where \({\dot{\alpha }}_1\) and \({\dot{\alpha }}_2\) are pitch rates in regions \(0 \le t \le t_1\) and \(t_3 \le t \le t_4\), respectively, expressed as:

$$\begin{aligned} \begin{aligned} {\dot{\alpha }}_1&= \frac{2 \alpha _0}{\xi T - t_\text {a}},\\ {\dot{\alpha }}_2&= -\frac{2 \alpha _0}{(1 - \xi ) T - t_\text {a}}. \end{aligned} \end{aligned}$$
(5)

The amount of asymmetry is controlled by the asymmetry parameter \(\xi\) such that the maximum angle of attack \(\alpha _0\) is at \(t_2^* = 0.5\xi\). For symmetric triangular pitching, \(\xi = 0.5\). The reduced frequency \(k = \pi f_\text {p} c/U_\infty\), pitching amplitude \(\alpha _0\), and asymmetry parameter \(\xi\) are varied such that \(k \in \{0.22, 0.44, 0.66, 0.88\}\), \(\alpha _0 \in \{4^\circ , 8^\circ , 16^\circ , 32^\circ , 64^\circ \}\), and \(\xi \in \{0.5, 0.4, 0.3\}\). The relative error between the input and the angular position of the aerofoil measured by an encoder is less than 2%.

2.3 Theodorsen’s theory for high angles of attack

The classical theories of Theodorsen (1935) and von Kármán and Sears (1938) use linear potential flow theory and are developed for a flat-plate undergoing small sinusoidal oscillations in attached flow conditions. Under these conditions, the theory shows a good agreement with experimental results (Kang et al. 2009; McGowan et al. 2011; Baik et al. 2012; Liu et al. 2015; Mackowski and Williamson 2015; Cordes et al. 2017). In our experiment, the angle of attack reaches up to \(64^\circ\) and the flow becomes massively separated, which violates the expected limit of applicability. We assume that the linear theory of Theodorsen gives the normal force due to the pressure difference between the upper and lower surfaces of the aerofoil. In Theodorsen’s theory, the plate-normal unsteady force consists of the non-circulatory (also called added-mass, apparent-mass, or virtual-mass in literature) and the circulatory terms:

$$\begin{aligned} \begin{aligned} C_\text {N}^\text {TH}&= \underbrace{\frac{\pi c}{2 U_\infty ^2} \left[ {\dot{\alpha }} U_\infty - \frac{c}{2} \ddot{\alpha } (2 x_\text {p} - 1) \right] }_{\text {non-circulatory}} \\&\quad + \underbrace{\frac{2 \pi C(k)}{U_\infty } \left[ \alpha U_\infty + \frac{c}{2} {\dot{\alpha }} \left( \frac{3}{2} - 2 x_\text {p} \right) \right] }_{\text {circulatory}}. \end{aligned} \end{aligned}$$
(6)

The lift coefficient is given by:

$$\begin{aligned} C_\text {L}^\text {TH} = C_\text {N}^\text {TH} \cos \alpha . \end{aligned}$$
(7)

Here \({\dot{\alpha }}\) and \(\ddot{\alpha }\) are the pitching rate and acceleration, \(x_\text {p}\) is the location of the pitching axis from the leading-edge normalised by c, and C(k) is the Theodorsen function

$$\begin{aligned} C(k) = \frac{H_1^{(2)}(k)}{H_1^{(2)}(k) + i H_0^{(2)}(k)}, \end{aligned}$$
(8)

where \(H^{(2)}_n\) is the Hankel function of the second kind of the order n. The Theodorsen function C(k) is responsible for the effect of the wake on the vortex-sheet strength along the aerofoil. Theodorsen’s model is technically applicable for sinusoidal oscillations only. Therefore, we expanded the smoothed triangular kinematics into the first 20 Fourier harmonics. The resulting curves have less than 1 % difference from the original kinematics. Lift coefficients computed for all 20 Fourier harmonics are summed to obtain the total lift coefficient.

2.4 Unsteady thin-aerofoil theory

From the unsteady thin-aerofoil theory (UTAT), we find the normal force for a flat-plate undergoing arbitrary kinematics up to high angles of attack

$$\begin{aligned} \begin{aligned} C_\text {N}^\text {TA}&= 2 \pi \left[ \cos \alpha \left( A_0 + \frac{A_1}{2} \right) \right. \\&\quad + \left. \frac{c}{U_\infty } \left( \frac{3}{4} {\dot{A}}_0 + \frac{1}{4} {\dot{A}}_1 + \frac{1}{8} {\dot{A}}_2 \right) \right] , \end{aligned} \end{aligned}$$
(9)

where \(A_0\), \(A_1\), and \(A_2\) are the first three time-dependent Fourier coefficients of the vortex sheet strength distribution along the camber line. The only difference from the UTAT of Katz and Plotkin (2001) is \(\cos \alpha\), which arises from the chord-tangential velocity \(U_\infty \cos \alpha\) as the high angle of attack consideration (Ramesh et al. 2013). Ramesh (2020) derived the Fourier coefficients for Theodorsen’s theory as

$$\begin{aligned} \begin{aligned} A_0&= C(k) \frac{W}{U_\infty } - \frac{{\dot{\alpha }} c}{4 U_\infty }, \\ A_1&= \frac{{\dot{\alpha }}c}{2U_\infty } -2 \frac{W}{U_\infty } (C(k) - e^{-ik} S(k)),\\ A_2&= 2ikS(k) \frac{W}{U_\infty } Q_2, \end{aligned} \end{aligned}$$
(10)

where the normal downwash is

$$\begin{aligned} W = U_\infty \sin \alpha - {\dot{\alpha }} c \left( x_\text {p} - \frac{3}{4} \right) . \end{aligned}$$
(11)

To account for the large angle of attack, in the first term of Eq. 11 we use \(\sin \alpha\), whilst Ramesh (2020) used \(\alpha\). In Eqs. 10, C(k) is the Theodorsen function (see Eq. 8),

$$\begin{aligned} S(k) = \frac{2i/\pi k}{H_1^{(2)}(k) + i H_0^{(2)}(k)}, \end{aligned}$$
(12)

is the Sears function, and \(Q_2\) is a wake coefficient. The latter is defined as

$$\begin{aligned} Q_n = \int _0^\infty \exp (-ik \cosh \zeta - n\zeta )\text {d} \zeta . \end{aligned}$$
(13)

We follow the suggestions from Epps and Roesler (2018) to compute \(Q_n\). This includes using the trapezoidal numerical integration for \(n > 1\) (for \(n = 0\) and 1, analytical solutions are given), and the approximation \(Q_n \approx e^{-ik}/n\) for very small k/n.

We compute the circulatory lift as a component of the normal force and need to account for the leading-edge suction force separately. In a steady potential flow, this leading-edge suction force acts to cancel the streamwise component of the chord-normal force giving zero drag, which is known as D’Alembert’s paradox. The leading-edge suction force, which acts at the leading-edge in the chord-tangential direction, is expressed as (Ramesh et al. 2013)

$$\begin{aligned} C_\text {S} = 2 \pi A_0^2. \end{aligned}$$
(14)

The first Fourier coefficient \(A_0\) is called the leading-edge suction parameter (LESP) (Ramesh et al. 2014). Finally, we compute the lift based on the unsteady thin-aerofoil theory for harmonic kinematics (UTAT-H) as

$$\begin{aligned} C_\text {L}^\text {TA} = C_\text {N}^\text {TA} \cos \alpha + C_\text {S} \sin \alpha . \end{aligned}$$
(15)

Here, the lift is again computed for the first 20 Fourier harmonics of the kinematics.

Fig. 3
figure 3

Example of vortex identification from the PIV data

Full size image

2.5 Vortex lift

To calculate the vortex lift we consider only a concentrated pair of counter-rotating vortices with circulation \(-\varGamma\) and \(\varGamma\) in two-dimensional flow. Eq. 3 reduces to

$$\begin{aligned} \varvec{I} = \varGamma \hat{\varvec{z}} \times \varvec{d}, \end{aligned}$$
(16)

where \(\varGamma\) is the (absolute) circulation of a vortex, \(\hat{\varvec{z}}\) is the unit vector pointing normal to the plane towards the observer, and \(\varvec{d}\) is the displacement vector from the positive to the negative vortex core. Lamb (1932) originally derived this impulse for a vortex pair. From Eq. 1, we find that the force \(\varvec{F}\) in the direction orthogonal to the vector \(\varvec{d}\) is (Kim and Gharib 2011; Babinsky et al. 2016)

$$\begin{aligned} \varvec{F}= -\rho ({\dot{\varGamma }} \hat{\varvec{z}} \times \varvec{d} + \varGamma \hat{\varvec{z}} \times \dot{\varvec{d}}). \end{aligned}$$
(17)

The lift due to the LEV-TEV pair is expressed in coefficient form as

$$\begin{aligned} C_\text {L}^\text {V} = -\frac{1}{\frac{1}{2} U_\infty ^2 c} [\underbrace{{\dot{\varGamma }}(x_\text {LEV} - x_\text {TEV})}_{\text {vortex growth}} + \underbrace{\varGamma (u_\text {LEV} - u_\text {TEV})}_{\text {vortex advection}}], \end{aligned}$$
(18)

where \(u_\text {LEV}\) and \(u_\text {TEV}\) are the streamwise velocity components of the LEV and the TEV, which are at the streamwise locations \(x_\text {LEV}\) and \(x_\text {TEV}\). Their (absolute) circulation is \(\varGamma\) and their (absolute) growth rate is \({\dot{\varGamma }}\). This method does not require absolute positions and velocities but merely the relative positions and velocities of the vortices to each other and is independent of the location of the origin (Noca et al. 1999; DeVoria et al. 2014; Rival and Van Oudheusden 2017; Limacher et al. 2018; Siala and Liburdy 2019). The relative positions are more straightforward to determine than absolute positions, limiting the error. In the steady case (\({\dot{\varGamma }} = 0\), \(u_\text {LEV} = 0\), and \(u_\text {TEV} = U_\infty\) as a starting vortex), Eq. 18 yields the Kutta-Joukowski sectional lift \(\rho U_\infty \varGamma\). Eq. 18 shows that unsteady vortex lift has two contributions. The first is due to the circulation of the vortex pair and their streamwise velocities. The second is due to the rate of change of circulation and the distance between the vortices and their orientation. Babinsky et al. (2016) suggests approximating \(-(u_\text {LEV} - u_\text {TEV}) \approx 0.5 U_\infty\), \(-(x_\text {LEV} - x_\text {TEV}) \approx c \cos \alpha\), and \(\varGamma\) from the modified Wagner’s circulation model to make a reasonable prediction (Stevens and Babinsky 2017; Stevens et al. 2017). However, these approximations are limited to attached or moderately separated flows because the relative velocity between the LEV and TEV becomes nonlinear when there is a strong LEV-TEV interaction. Babinsky et al. (2016), Stevens and Babinsky (2017), Stevens et al. (2017) and Mancini et al. (2019) have successfully applied their low-order model to various unsteady aerodynamics problems in attached or moderately separated flows. The total lift is the superposition of the lift for the attached flow condition and the lift due to the vortex pair:

$$\begin{aligned} C_\text {L} = C_\text {L}^\text {TH} + C_\text {L}^\text {V}. \end{aligned}$$
(19)

This correction becomes significant when substantial trailing edge vorticity is slowed down instead of being advected downstream at approximately the freestream velocity as assumed by Theodorsen’s theory. We choose the lift of Theodorsen’s theory (Eq. 7) rather than UTAT-H (Eq. 15) to give the lift for the attached flow since it is experimentally observed by Deparday and Mulleners (2018, 2019) that the leading-edge suction force significantly drops to nearly zero after the aerofoil experiences leading-edge separation.

2.6 Vortex identification

The boundaries of LEVs and TEVs are identified by swirling strength \(\lambda _\text {ci}\) (Zhou et al. 1999), with a threshold value of 10% of the maximum \(\lambda _\text {ci}\) to identify vortices. This threshold aids separation of the vortex from the feeding shear layer, which is essential for the computation of the circulation. Figure 3 shows an example of the identified LEV and the black line, which indicates the vortex boundary. Onoue and Breuer (2016, 2017) and Wilroy et al. (2018) successfully applied this method to PIV velocity data to identify coherent vortices. The LEV and TEV cores are the centroids of their circulation distributions. The circulation of each identified vortex is computed by integration of the vorticity \(\omega\) over the area of the vortex A as \(\varGamma = \iint \omega \text {d}A\). Time derivatives (\(u_\text {LEV},~u_\text {TEV},~{\dot{\varGamma }}\)) are computed from the best fit curves of \(x_\text {LEV}\), \(x_\text {TEV}\), and \(\varGamma\).

Fig. 4
figure 4

Identified vortices in symmetric pitching case (\(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.5\)) at a \(\alpha =36^\circ \nearrow\), b \(\alpha =62^\circ \nearrow\), c \(\alpha =64^\circ \nearrow\), d \(\alpha =44^\circ \searrow\), e \(\alpha =31^\circ \searrow\), f \(\alpha =23^\circ \searrow\)

Full size image
Fig. 5
figure 5

Identified vortices in asymmetric pitching case (\(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.3\)) at a \(\alpha =36^\circ \nearrow\), b \(\alpha =62^\circ \nearrow\), c \(\alpha =64^\circ \nearrow\), d \(\alpha =44^\circ \searrow\), e \(\alpha =31^\circ \searrow\), f \(\alpha =23^\circ \searrow\)

Full size image

Figures 4 and 5 depict the contours of identified LEV and TEVs of symmetrically pitching (\(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.5\)) and asymmetrically pitching cases (\(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.3\)), respectively.

Fig. 6
figure 6

Measured lift coefficients \(C_\mathrm{L}\) of all kinematics tested: a \(\alpha _0 = 4^\circ\), \(\xi = 0.5\), b \(\alpha _0 = 4^\circ\), \(\xi = 0.4\), c \(\alpha _0 = 4^\circ\), \(\xi = 0.3\), d \(\alpha _0 = 8^\circ\), \(\xi = 0.5\), e \(\alpha _0 = 8^\circ\), \(\xi = 0.4\), f \(\alpha _0 = 8^\circ\), \(\xi = 0.3\), g \(\alpha _0 = 16^\circ\), \(\xi = 0.5\), h \(\alpha _0 = 16^\circ\), \(\xi = 0.4\), i \(\alpha _0 = 16^\circ\), \(\xi = 0.3\), j \(\alpha _0 = 32^\circ\), \(\xi = 0.5\), k \(\alpha _0 = 32^\circ\), \(\xi = 0.4\), l \(\alpha _0 = 32^\circ\), \(\xi = 0.3\), m \(\alpha _0 = 64^\circ\), \(\xi = 0.5\), n \(\alpha _0 = 64^\circ\), \(\xi = 0.4\), o \(\alpha _0 = 64^\circ\), \(\xi = 0.3\). Shaded regions represent the 95% confidence interval for the mean of six realisations. Pitching motion is depicted in grey. Markers show maximum and minimum lift coefficients. Vertical dashed lines indicate the beginning/end of deceleration/acceleration and maximum/minimum angles of attack

Full size image

3 Results

3.1 Measured lift

The phase averaged lift coefficients are presented in Fig. 6 for all tested conditions. The three columns show the three degrees of symmetry of the kinematics, and the five rows show increasing angle of attack amplitudes from \(4^\circ\) on the top to \(64^\circ\) on the bottom. The shaded regions show the 95% confidence interval for the mean of six realisations. This interval decreases with pitching amplitude as the signal to noise ratio increases.

The force peaks (indicated with a solid marker) tend to align for increasing pitching amplitudes, due to the increased effect of the non-circulatory forces. At \(\alpha _0 = 64^\circ\), the force peaks all occur at the beginning of the acceleration phase. A plateau region occurs while the angle of attack decreases until it reaches \(45^\circ\). To explain this temporal lift evolution, we will compare the experimental results with the lift prediction from Theodorsen’s theory and UTAT-H.

Fig. 7
figure 7

The effect of pitch rate on the force response: a time difference between the static stall angle and the magnitude of maximum/minimum normal force coefficients, and b magnitude of maximum/minimum normal force coefficient over the dimensionless pitch rate

Full size image

To investigate the effect of the asymmetry of the motion on the force response, we analyse the time delay \(\varDelta t_\text {s}\) for the occurrence of the normal force peaks with respect to when the static stall angle \(\alpha _\text {ss} = \pm 16^\circ\) is exceeded and the magnitude of normal force peaks. The analysis for \(\alpha _0 = 64^\circ\), \(k = \{0.22, 0.44\}\), and \(\xi = \{ 0.3, 0.4, 0.5\}\) is presented in Fig. 7. The asymmetry in the motion results in a different pitch rate for the pitch up and pitch down motion. The absolute dimensionless pitch rate \(|{\dot{\alpha }}|c/(2 U_\infty )\) is used as the governing scaling factor. Here the pitch-rate \({\dot{\alpha }}\) is either \({\dot{\alpha }}_1\) or \({\dot{\alpha }}_2\) in Eq. 5. As shown in Fig. 7a, the time delay \(\varDelta t_\text {s}\) decreases with increasing nondimensional pitch rate. The variations in the results taken from the two reduced frequencies are marginal. The time it takes to reach the lift peaks is therefore mainly dependent on the pitch rate and, to a lesser degree, on the reduced frequency.

As shown in Fig. 7b, the magnitude of the normal force coefficient increases linearly with the increasing pitch rate. This is due to the non-circulatory effect on the forces. In fact, if we regard the non-circulatory part of Theodorsen’s model (Eq. 6) for zero acceleration as a case for the constant pitch rate part of the motion, the non-circulatory part increases linearly with the pitch rate, where the slope is \((\text {d}C_\text {N} / \text {d} {\dot{\alpha }})(2 U_\infty /c) = \pi\). This approximation shows a good first agreement for the investigated pitch rates. The slope is steeper for the lower pitch rate. This could be due to the influence of changes in the circulatory part of the forces.

3.2 Comparison with theory

Fig. 8
figure 8

Amplitude of the lift coefficient of symmetric pitching aerofoils for different pitching amplitude. Markers show the measured values, solid lines represent Theodorsen’s theory (Eq. 7), and dashed lines represent UTAT-H (Eq. 15). Error bars show the 95% confidence interval for the mean of six realisations

Full size image

Figure 8 summarises the lift maxima from the experimental data and the prediction by Theodorsen’s theory and UTAT-H. Both theories tend to slightly overpredict the lift for low amplitude and low reduced frequency. We observe the same tendency for the asymmetrically pitching aerofoil. Similar results have been reported by Mackowski and Williamson (2015) who investigated a pitching NACA 0012 aerofoil at \({\mathrm{{Re}} = 17,000}\). Overall, UTAT-H shows a better agreement with the experiments at low pitching amplitudes, whereas Theodorsen’s theory shows a better agreement at high pitching amplitudes.

Fig. 9
figure 9

Temporal evolution of the lift coefficient of Theodorsen’s theory (Eq. 7), UTAT-H (Eq. 15), and the measured lift coefficients for \(\alpha _0 = 64^\circ\), \(k=0.22\) for different degrees of asymmetry a \(\xi =0.5\), b \(\xi =0.4\), and c \(\xi =0.3\). Markers show maximum and minimum lift coefficients. Shaded regions represent the 95% confidence interval for the mean of six realisations. The pitching motion is in grey

Full size image

At first glance, the linear theories are capable of accurately predicting the maximum lift at pitching amplitudes as high as \(64^\circ\) for low reduced frequencies. Under these conditions, the lift peak is governed by the non-circulatory forces. In Fig. 9, the temporal evolution of the theoretical lift predictions are compared with the phase averaged lift over a pitching period. Both Theodorsen’s theory and UTAT-H predict the lift well and the two theories show nearly the same results except for a region around the maximum angle of attack. This is due to the overpredicted leading-edge suction force by UTAT-H. Deparday and Mulleners (2018, 2019) experimentally showed that the leading-edge suction force significantly drops to nearly zero once the aerofoil experiences leading-edge separation. As shown in the next section (Sect. 3.3), the flow is massively separated in this region. For this reason, the agreement with UTAT-H is poor. The agreement is robust around the positive peak values and both the magnitude and timing of the peaks are accurately predicted. After reaching the positive peak values, both theories start to overpredict the lift. This is due to the vortex force, which will be investigated in Sect. 3.4. Kang et al. (2009), Ol et al. (2009) and Ramesh et al. (2014) also observed the overprediction by Theodorsen’s theory in the region where there is a LEV-TEV interaction, while reasonable predictions occur elsewhere even when a coherent LEV is present. Baik et al. (2012) confirmed a better prediction by setting \(C(k) = 1\) (ignoring the effect of the wake on the lift) in Theodorsen’s theory based on their observation from PIV that there is no vortex shedding into the wake during downstroke of the heaving and pitching motion. The agreement is weaker around the negative peaks for the strongly asymmetric kinematics (Fig. 9c) when the non-circulatory force is not as strong as the circulatory force.

Fig. 10
figure 10

Instantaneous dimensionless vorticity and streamlines around a symmetrically pitching aerofoil (\(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.5\)) at a \(\alpha =36^\circ \nearrow\), b \(\alpha =62^\circ \nearrow\), c \(\alpha =64^\circ \nearrow\), d \(\alpha =44^\circ \searrow\), e \(\alpha =31^\circ \searrow\), f \(\alpha =23^\circ \searrow\). Corresponding lift coefficients \(C_\mathrm{L}\) are plotted against \(\alpha\)

Full size image
Fig. 11
figure 11

Instantaneous dimensionless vorticity and streamlines around an asymmetrically pitching aerofoil (\(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.3\)) at a \(\alpha =36^\circ \nearrow\), b \(\alpha =62^\circ \nearrow\), c \(\alpha =64^\circ \nearrow\), d \(\alpha =44^\circ \searrow\), e \(\alpha =31^\circ \searrow\), f \(\alpha =23^\circ \searrow\). Corresponding lift coefficients \(C_\mathrm{L}\) are plotted against \(\alpha\)

Full size image

3.3 Flow topology

In this section, we focus on two cases: the symmetric pitch at \(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.5\), and the asymmetric pitch at \(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.3\). In these cases, we observe a nonlinear effect on the forces due to the presence of shed vortices.

Figure 10 shows streamlines and the normalised vorticity field around the symmetrically pitching aerofoil at \(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.5\). At an early stage of the LEV formation, several clockwise-rotating vortices (negative vorticity) emerge on the suction side of the aerofoil due to Kelvin–Helmholtz instability (Fig. 10a). At high angles of attack, we identify a bluff body-like vortex pattern (Fig. 10b). At this point, the LEV starts to detach. Widmann and Tropea (2017) reported two mechanisms for the onset of LEV detachment. The first mechanism is related to the secondary vortex near the leading edge. This secondary vortex is called the eruption vortex (Doligalski et al. 1994). The second mechanism is related to the flow reversal at the trailing edge. According to Widmann and Tropea (2017), the former LEV detachment mechanism occurs at high Reynolds numbers and the latter at low Reynolds numbers. The simultaneous occurrence of both the boundary layer eruption and the flow reversal at the trailing-edge can happen at the moderate Reynolds numbers \(10,000< \mathrm{{Re}} < 35,000\) (Widmann and Tropea 2017). In our case, at \(Re = 32,000\), we observe a combination of both mechanisms (Fig. 10b, c). The advection of the primary LEV [around (b) and (c) in Fig. 10] decreases lift. This decrease will be discussed in Sect. 3.4. This decrease in the lift is more gentle in the potential flow than in the experiments. In the potential flow, we do not consider the formation and shedding of the LEV. In the lift predicted by Theodorsen’s theory, the steady contribution increases until \(\alpha = 45^\circ\) (as \(C_\text {L} = 2 \pi \sin \alpha \cos \alpha\) has its maximum at \(\alpha = 45^\circ\)).

Figure 11 shows streamlines and the normalised vorticity field around the asymmetrically pitching aerofoil at \(\alpha _0 = 64^\circ ,~k = 0.22,~\xi =0.3\). The evolution of the flow topology is similar to the symmetrically pitching case until the primary LEV detaches (Figs. 10a–c vs 11a–c). In Fig. 11c, the eruption vortex near the leading-edge and the flow reversal at the trailing-edge lead to LEV detachment. Subsequently, the predicted lift deviates from the measured lift. The flow reversal at the trailing-edge induces a bluff body type vortex shedding (Fig. 11d, e). The TEV grows as large as the primary LEV. Consequently, a coherent LE-TE vortex pair is formed.

3.4 Vortex dynamics

Both Theodorsen’s theory and UTAT-H show reasonable agreement with the measured lift force even when an LEV is present at a large pitching amplitude. The unsteady lift prediction declines once the flow becomes vortex dominated (Fig. 9). To improve the predictions of the nonlinear unsteady load, we need to take into account the contribution of the coherent LE and TE vortices. In this section, we compare the same two cases as in the above section, the symmetric pitch at \(\alpha _0 = 64^\circ ,~k=0.22,~\xi =0.5\), and the asymmetric pitch at \(\alpha _0 = 64^\circ ,~k=0.22,~\xi =0.3\). We extract the trajectories and circulations of the identified LEVs and TEVs whose contours are presented in Figs. 4 and 5 for symmetric and asymmetric pitching cases.

Fig. 12
figure 12

Trajectories of a LEV and b TEV cores in streamwise direction of symmetric pitch at \(\alpha _0 = 64^\circ ,~k=0.22,~\xi =0.5\). Solid lines represent best fit curves

Full size image
Fig. 13
figure 13

Circulation of a a LEV, b TEVs, and c accumulative circulation of TEV 4 and TEV 5 of symmetric pitch at \(\alpha _0 = 64^\circ ,~k=0.22,~\xi =0.5\). Solid lines represent best fit curves. Dashed lines are extrapolated assuming circulation remains the same after leaving the PIV domain

Full size image
Fig. 14
figure 14

a Comparison of lift coefficients between measured, Theodorsen’s theory, and data-driven method of symmetric pitch at \(\alpha _0 = 64^\circ ,~k=0.22,~\xi =0.5\) and b vortex lift and contributions from circulation and relative velocity. Dashed part of the lines show extrapolated trends

Full size image

In the symmetric pitching case, multiple TEVs are identified (Fig. 4). Figure 12 shows the streamwise projections of the trajectories of these vortices. Solid lines represent best fit curves. The trajectories of the LEV and a sequence of small TEVs (TEV 1 to TEV 3) are fitted to linear curves, while TEV 4 and 5 are fitted to third order polynomials. The initial small TEVs (TEV 1 to TEV 3) are advected downstream with the freestream velocity \(U_\infty\). This behaviour is consistent with Theodorsen’s theory, which assumes that the wake advects at the freestream velocity. The later coherent TEVs (TEV 4 and TEV 5), grow much larger in size and strength (Fig. 13), and advected downstream slower than \(U_\infty\). Their combined circulation balances the circulation of the primary LEV (Fig. 13). Following Eq. 18, TEV 4 and TEV 5 contribute negatively to the lift because their advection velocity is lower than that of the LEV. Ol et al. (2009) and Ramesh et al. (2014) also observed that the measured lift was lower than the lift predicted by Theodorsen’s theory. Based on the present study, the discrepancies observed by these authors are likely to be due to the TEV being advected slower than the LEV.

We consider TEV 4 and TEV 5 and the primary LEV as a single vortex pair. The vortex lift is computed from Eq. 18. We found that the vortex growth term is small and it is neglected in the present work. The LEV and the TEV velocities (\(u_\text {LEV}\) and \(u_\text {TEV}\)) are computed from the slope of the best fit of \(x_\text {LEV}(t)\) and \(x_\text {TEV}(t)\), respectively. During the symmetric pitching motion, multiple TEVs form and the ensemble-averaged velocity of TEV 4 and TEV 5 is used as \(u_\text {TEV}\).

Figure 14a compares the measured lift, Theodorsen’s prediction (Eq. 7), and the improved prediction of Theodorsen’s theory coupled with the vortex lift (Eq. 19). Fig. 14b shows the vortex force \(C_\text {L}^\text {V}\) and the contribution from the LEV circulation \(\varGamma _\text {LEV}\) and the LEV-TEV relative velocity \(u_\text {LEV} - u_\text {TEV}\). The lines are solid where based on measured data and dashed when extrapolated. We do not have information for \(u_\text {TEV}\) after \(t U_\infty / c \approx 6.5\), when the TEV 5 leaves the PIV domain. Both \(u_\text {LEV}\) and \(u_\text {TEV}\) needs to reach the freestream velocity in the far field and thus the vortex force has to vanish, but we do not know how fast this asymptotic trend occurs. Hence, in Fig. 14a we do not extrapolate the trends of the vortex force for \(t U_\infty / c > 6.5\).

Fig. 15
figure 15

Trajectories of a LEV and b TEV cores in streamwise direction at \(\alpha _0 = 64^\circ ,~k=0.22,~\xi =0.3\). Solid lines represent best fit curves

Full size image
Fig. 16
figure 16

Circulation of a LEV and b TEVs at \(\alpha _0 = 64^\circ ,~k=0.22,~\xi =0.3\). Solid lines represent best fit curves. Dashed line are extrapolated assuming circulation remains the same after leaving the PIV domain

Full size image
Fig. 17
figure 17

a Comparison of lift coefficients between measured, Theodorsen’s theory, and data-driven method at \(\alpha _0 = 64^\circ ,~k=0.22,~\xi =0.3\) and b vortex lift and contributions from circulation and relative velocity. Dashed lines are extrapolated

Full size image

Figure 15 depicts streamwise projections of the trajectories of detected LEV and TEV cores for the asymmetric case. Solid lines represent best fit curves. The trajectories of the LEV and TEV 1 are fitted to linear curves, while the TEV 2 is fitted to third order polynomials for \(t U_\infty /c < 5.2\) and to a linear curve for \(t U_\infty /c > 5.2\). In order to overcome the non differentiability at \(t U_\infty / c = 5.2\) arising from the different fitting polynomials, the computed lift is smoothed by a moving average using a window size of 31 points. The LEV moves downstream with constant speed, whereas the large TEV stagnates and moves upstream for \({3< t U_\infty /c< 4}\). For \(t U_\infty /c > 5.2\), the TEV 2 advects downstream with a constant velocity similar to the LEV advection velocity (\(u_\text {TEV} \approx u_\text {LEV})\).

Figure 16 shows the circulation time history of (a) the LEV and (b) the TEVs. Both the LEV and the TEV 2 asymptotically reach their maximum circulation, but the asymptotic value of the TEV 2 is larger than that of the primary LEV (\(\varGamma _\text {TEV}/(U_\infty c) \approx 2.8\) vs \(\varGamma _\text {LEV}/(U_\infty c) \approx 2.3\)). To balance the difference, the secondary LEV emerges (Fig. 11e, f). This measured information is directly substituted into Eq. 18 to compute the vortex lift by the data-driven method.

Figure 17a compares the measured lift, Theodorsen’s prediction (Eq. 7), and the prediction of Theodorsen’s theory coupled with the vortex lift (Eq. 19). The contribution from the LEV circulation \(\varGamma _\text {LEV}\) and the LEV-TEV relative velocity \(u_\text {LEV} - u_\text {TEV}\) are also shown in Fig. 17b. The dashed part of the line show where the data is extrapolated. In the region where Theodorsen’s theory overpredicts the lift force due to the vortex interaction, \(t U_\infty /c > 2\), the lift computed by the impulse theory corrects that of Theodorsen’s theory, resulting in an improved agreement with the measured lift.

4 Concluding remarks

This study reports the unsteady lift force generation and flow development on a pitching aerofoil at \({\mathrm{{Re}}=32,000}\) through time-resolved force and velocity field measurements. We use two predictive lift models. The first model is the linear theory of Theodorsen, which we modified for large-amplitude, asymmetric kinematics. Lift is computed for 20 Fourier harmonics of symmetric and asymmetric smoothed triangular pitching kinematics to satisfy the sinusoidal oscillation assumption in Theodorsen’s theory. The second model is the unsteady thin-aerofoil theory modified for high angles of attack variations. Both models show a remarkable agreement even when there is a large LEV present at the largest pitching amplitude studied (\({\alpha _0 = 64\,^\circ }\)), but the agreement diminishes in some conditions when a coherent LEV-TEV vortex pair is formed.

We develop a data-driven method based on the impulse theory to estimate the vortex force associated with the LEV-TEV vortex pair. This lift force, which is the rate of change of the vortex pair’s impulse, increases linearly with the strength of vortex pair and the relative streamwise velocity of the TEV with respect to the LEV. This lifting mechanism is not accounted for in Theodorsen’s theory, where the bound circulation is fixed to the solid body and the shed circulation advects at the freestream velocity. When this force component is added to the force predicted by Theodorsen’s theory, the numerical-experimental agreement improves. We therefore conclude that the limiting criterion for Theodorsen’s theory validity is neither whether the boundary layer is attached or separated, nor the formation and separation of the LEV. Instead, for a pitching aerofoil, we find that the limiting criterion is whether the magnitude of the vortex force is significant compared to the force predicted by Theodorsen’s theory. In practice, we observe that the vortex force is significant when a coherent TEV is formed and it advects at a significantly slower streamwise velocity than the freestream velocity.

While these conclusions are based only on the conditions tested in this study, the underling theoretical foundation suggests that they should be applicable to any kinematics. Yet, future work should verify whether these conclusions hold also for plunging and a combination of pitching and plunging kinematics.

Overall, these results pave the way to the development of predictive low-order models for high-amplitude manoeuvres characterised by massive flow separation.