Abstract
Leading-edge separated flow field over a sharp flat plate is experimentally investigated in Reynolds numbers ranging from 6.2 × 103 to 4.1 × 104, using particle image velocimetry (PIV) and its statistics. It was observed that the average reattachment length is nearly independent of Reynolds number and the small secondary bubble observed near the leading edge was found to shrink with increasing Reynolds number. The wall-normal profiles of the statistical values of kinematic quantities such as the velocity components and their fluctuations scaled well with average reattachment length lR and freestream velocity U∞. Their magnitudes compare well with previous investigations even though the current triangular shaped sharp leading edge is different from previous flat-faced or semi-circular ones. The shear layer was observed to exhibit 2 different linear growth rates over 2 distinct regions. Instantaneous PIV realizations demonstrate unsteady nature of the separation bubble, whose origins in the upstream portion of the bubble are analysed. Bimodal nature of the probability density function (PDF) of fluctuating streamwise velocity at around x/lR = 0.08–0.15 indicates successive generation and passage of vortices in the region, which subsequently interact and evolve into multiscale turbulent field exhibiting nearly Gaussian PDF. Shedding of vortices with wide range of scales are apparent in most of the instantaneous realizations. Proper Orthogonal Decomposition (POD) of the velocity fluctuation magnitude field revealed that the flow structures of the dominant modes and their relative energies are independent of Reynolds number. In each of the dominant modes (first 3 modes), the length scales corresponding to the large scale structures and their spacing are the same for all Reynolds numbers, suggesting that their Strouhal number (observed to be ~ 0.09–0.2 at Reynolds number of 6.2 × 103) of unsteadiness should also be independent of Reynolds number. A single large structure- comparable in size to lR—was apparent well before reattachment in a few instantaneous realizations, as compared to multiple small-scale structures visible in most realizations; at Reynolds number of 6.2 × 103, realizations with such large-scale structures occurred approximately after every 20–30 realizations, corresponding to non-dimensional frequency of 0.4–0.6, which is identified to be the “regular shedding”. It was possible to reconstruct the large-scale structure during the instances from just the first 3 POD modes, indicating that the Strouhal number of regular shedding too is independent of Reynolds number.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Sharp edge of a plate leading-edge can result in leading-edge separation of the flow. While with incompressible and with compressible subsonic freestream, the sharp edge separation (over plates with rectangular leading edge, in most literature) can occur even with zero or small “favorable” angles of plate incidence (Ota and Kon 1974), in supersonic flows leading-edge separation can be also caused by shock wave interactions (Wang et al. 2017). It is both of theoretical significance, since the separation may occur at the location of vanishing boundary layer thickness (i.e. the leading edge), and of practical importance in airfoils, wings, and turbine blades for example whose aerodynamic performance are significantly affected by the separation phenomenon. Leading-edge separation on a sharp edge can also be expected in supersonic airfoils operating at low speeds (1958). The massively separated flow past sharp edges is an important issue in aerodynamics of vehicles such as buses and lorry trailers (Choi et al. 2014).
In the early work by Ota and Kon (1974), heat transfer measurements were conducted in a separated-reattached flow over a flat plate with flat forward-facing leading edge. It was reported in the work that the point of reattachment was about 4 times the plate thickness downstream away from the leading edge. Ota (1974) developed a free-streamline theory for the flow and the theoretically predicted value of reattachment length were found to agree well with experimental data. Further, Ota et al. (1981) investigated the effects of Reynolds number and shape of leading edge on reattachment length. Using flow visualization technique with Aluminum powders, it was discovered that starting from low Reynolds number, the reattachment length increased and reached a maximum at a specific Reynolds number which was dependent upon the shape of leading edge. They also categorized the flow around the plate into 3 regimes which were (i) laminar separation-laminar reattachment, (ii) laminar separation-turbulent reattachment, and (iii) turbulent separation-turbulent reattachment. In the last regime, reattachment length demonstrated little variation against Reynolds number.
The theoretical analysis of flow field with the simplification of “zero boundary layer thickness separation” at leading edge suggested a Reynolds number independent flow (Chapman et al. 1958). At low speeds, for zero or small “favorable” angles of incidence, the separation is caused since the stagnation point is not exactly at the sharp leading edge, due to plate thickness. Considering, for instance, a flat (rectangular) leading edge facing the freestream, the stagnation point will be at the middle of the flat-face; the streamlines above the stagnation streamline thus tend to have an upward velocity and acceleration, and are confronted by the sharp turning at the corner of the leading edge, which results in flow separation exactly at the corner. Although in such case, the theory of zero boundary layer thickness separation is not applicable, Reynolds number independence of the separation has been observed experimentally (Ota et al. 1981; Hiller and Cherry 1981), and is also evident from the reasonable comparison of data from different experimental (Kiya and Sasaki 1983; Djilali and Gartshore 1991) and computational (Tafti and Vanka 1994; Yang and Abdalla 2009) works at different Reynolds numbers.
The separation is, however, not a steady phenomenon and its dynamics is characterized by flapping and shedding of vortices. In the study by Kiya and Sasaki (1983), they conducted experiments on separated-reattached flow over a flat plate with a 90° blunt (rectangular) leading edge at the Reynolds number of Ret = 2.6 × 104 based on freestream velocity, plate thickness, and kinematic viscosity. A frequent shedding of vortices was observed and integral time scale along the edge of the separated shear layer had a linear increase indicating that rolled-up vortices coalesced successively upstream of the reattaching zone. The constant time scale after reattachment suggested these vortices travelled downstream without significant change in the structure. A large-scale structure was extracted and was found to be shed downstream from the bubble at a frequency around flR/U∞ = 0.6 which was interpreted as a regular vortex shedding. The distance between the large-scale vortices was estimated to be around 0.8lR where lR is reattachment length. On top of this regular frequency, a large-scale unsteadiness in the bubble whose frequency was about flR/U∞ = 0.12 was also discovered. Cherry et al. (1984) also made similar observations concerning the frequencies in the separated and reattaching flow over the rectangular leading-edged plate. Similar frequencies had been observed by Eaton and Johnston (1981) in the flow over a backward-facing step. The low-frequency unsteadiness was associated with a flapping motion of the shear layer near the separation line, which was related to the enlargement and shrinkage of the bubble. Numerical work by Tafti and Vank (1994) which overall had fair agreement with experimental work in other investigations also reported a similar low-frequency mode at flR/U∞ = 0.15 corresponding to the shear-layer flapping. Kiya and Sasaki (1985) further observed that the strength of the large-scale vortices in the reattaching zone appeared to be dependent on this low-frequency shrinkage and enlargement of the bubble.
With the recent advancements in flow diagnostics such as particle image velocimetry (PIV) and fast response sensors, as well as with the advances in computational techniques and facilities, the separated and reattaching flow over sharp edges has been resolved better. Large Eddy Simulations (LES) data by Yang and Abdalla (2009) compared well with the experimental data on the reattachment length. Surprisingly, the low-frequency shear layer flapping was observed to be absent in their LES results, and the shedding was the only unsteady mode in their simulations. The flapping mode was however observed in numerical results of Tenaud et al. (2011). The implementation of Proper Orthogonal Decomposition (POD) to analyze the extensive data using advanced diagnostics has provided valuable insights. POD analysis of Podvin et al. (2014) and Tenaud et al. (2016) showed that although the flow exhibited 2 characteristic frequencies corresponding to the flapping and shedding modes, the most energetic motions corresponded to the shedding of large-scale vortices. A quasi-invariance in the spanwise direction was also noted. Experimentally, Sicot et al. (2012) used fast response pressure sensors and PIV to study the flow structures downstream of reattachment region in a massively-separated flow. The pressure data was analyzed using extended POD technique. They identified the signature of the shedding mode of the shear layer on the pressure and the velocity spectra.
However, the focus of all recent studies has been made on the downstream region of the flow past the point of reattachment. The interest seems to be more on the fluctuations upstream of the reattachment and their causes. The application of advanced diagnostics and analytical techniques in the near field of flow separation (region near the leading edge) can better resolve the dynamics. In particular, given that the shedding mode constitutes the most energetic motions, their origins can be tracked. Further, on the Reynolds number independence of the reattachment length and the characteristic frequencies, a detailed statistical analysis of the spatially resolved PIV data could be illuminating. It is with this backdrop that the present study has been initiated. The massive separated flow over a flat plate with triangular sharp edge is experimentally investigated at different Reynolds numbers varying by an order of magnitude, by means of planer PIV. In the previous works reported in the literature, the leading edges were bluff, typically flat-faced or semi-circular, resulting in separation at corners. In the present study, triangular sharp edge was chosen to look for contrast with the bluff edges; however, the separation length scales (normalized by plate thickness) turned out to be comparable with those reported in the literature, as would be discussed later. Statistical quantities of the flow are analyzed from the PIV data. POD analysis of the PIV data is also used to study the behavior of the various modes in the separated region. With a reasonable temporal resolution of the lowest Reynolds number flow, the time series of the data for this case are also analyzed.
2 Experimental facility
2.1 Wind tunnel and test model
The experiments were conducted in the de Havilland Wind Tunnel Facility at the School of Engineering, the University of Glasgow. This is a closed-circuit facility with an octagonal cross-section of 2.66 m wide, 2.1 m high, and 5.4 m long. Prior to the test section, the tunnel has entry section with screens and contraction ratio of 5:1 to ensure uniform velocity increase and low turbulence level. The tunnel flow speed was monitored by a pitot tube installed in the tunnel and the freestream speed was controlled by a manual speed controller that drove the fan of the tunnel. In this experimental study, streamwise turbulence intensity of the freestream, defined as root mean square (RMS) of fluctuating streamwise velocity component divided by the speed of the freestream (i.e.\(\mathrm{Tu}=\sqrt{\stackrel{-}{{u}^{{{\prime}}2}}}/{U}_{\infty }\)), was measured to be 0.7–0.9% depending on the flow speed.
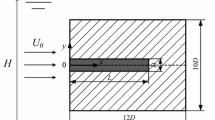
The experimental apparatus is illustrated in Fig. 1. A t = 30-mm thick flat Perspex plate of 800-mm length and 1600-mm width was mounted on 3 aluminum legs which were firmly fixed in the test section of the tunnel. The sharp triangular leading edge in the present study in in contrast with the rectangular leading edges used for the investigation of sharp-edge separation in the reported literature. Its detailed geometry is shown in Fig. 2. The total blockage ratio of the model was 3.2%. An inclinometer was used to ensure that the surface of the plate is horizontal.
2.2 Particle image velocimetry (PIV)
The planar velocity field of the separated flow at the spanwise-centered plane of the plate is visualized and quantified using PIV technique. The PIV set-up consisted of two Nd:YAG lasers (LPY-700, λ = 532 nm, 100 mJ/pulse), laser sheet optics, a high-speed CMOS camera (Phantom V341, Vision Research), and a synchronizer. The commercial software package (DaVis 8.0, LaVision) was used to control the image acquisition timing. The flow was seeded with atomized olive oil whose droplets had an average diameter of 1 μm, yielding the Stokes number of Sk = 0.002 << 1. The particles were scattered well downstream of the test section, so that that the seeding outlet did not interfere with the test section as well as the droplets were uniformly distributed in the flow when they circulate back to the upstream of the test section. By means of laser sheet optics, the laser sheet is directed along the center-line of the plate (defined as z/lR = 0) and the sheet had a thickness of 3 mm. The CMOS camera was equipped with a 300 mm focal length lens (Sigma 120–300 mm f2.8), and its aperture was opened to its maximum (f/2.8) to ensure strong signal intensity. The camera was placed outside the test section, aligned perpendicularly to the laser sheet. The streamwise and vertical position of the flow field are denoted by x and y (Fig. 1), where the origin of the field is defined at the very tip of the leading edge. The measurements were conducted from x = − 20 to 315 mm. Since the camera cannot capture such a wide domain in a single measurement, the measurements were conducted in 3 different zones which were x \(=\)− 20 to 95 mm, 90–205 mm, and 201– 315 mm. Each measurements were conducted at a full resolution of 2560 × 1600 pix2.
Shown in Table 1 are the freestream conditions under which the present experiments were performed. Reynolds number is defined by freestream velocity, plate thickness, and kinematic viscosity of the freestream, Ret = U∞t/ν. Based on the particle movement, the time delay was determined, so that the movement was less than 8 pixels or 1/4 of the size of the interrogation window. For every experiment, the laser was run at its maximum repetition rate of 200 Hz over 3 s to illuminate the particles, and 4 measurements were taken at one flow velocity at one camera position. Thus, each case has 2400 realizations with a time resolution of 200 Hz for the 600 realizations. Statistical quantities such as average and RMS are calculated from 2400 realizations. To ensure the convergence, the wall-normal profile of velocity in streamwise and wall-normal directions are compared in Figs. 3 and 4. The streamwise position x/lR = 0.25 is arbitrary. Above 1000 samples, the profiles overlap with each other therefore 2400 samples are considered ample for statistical convergence.
Particle images were processed by the LaVision DaVis 8.0 software. A pair of particle images is subdivided into smaller rectangular sub-region called interrogation window for planer cross-correlation and the spatial displacement of the particles in the window was quantified to calculate the velocity. The images were processed using multiple interrogation windows that decrease in size in successive iterations: 128 × 128 pixels with 50% overlap, 64 × 64 pixels with 50% overlap, and 32 × 32 pixels with 75% overlap. The 75% overlap at the final pass was implemented to increase the spatial resolution of the calculated vector field. With that final interrogation window, the acquired vector fields contain 64,000 vectors (320 × 200) and the final spatial resolution based on the final window size is approximately 0.36 mm/pixel in both streamwise and vertical directions. Uncertainty in velocity was also calculated in the process which was evaluated to be less than 2.0% of mainstream velocity.
3 Results and discussions
3.1 Mean quantities
One of the most important quantities in a separated-reattached flow is the average bubble length denoted by lR. Since velocity information was not available at the wall due to strong laser reflection, the length was determined visually by tracking the streamline so that the streamline before the re-attachment point circulates back to the bubble and the one after the point continues to flow downstream. This is illustrated in Fig. 5 by the red vectors and the dot in between. Figure 6 plots the average bubble length normalized by the plate thickness against the Reynolds number. As illustrated in the graph, the average bubble length slightly varies around lR/t = 5.8 in the range of Reynolds number investigated. Weak dependency of the average bubble length is experimentally observed by Hiller and Cherry (1981), and Cherry et al. (1984) who reported lR/t = 4.9 at Ret = 3.2 × 104, Kiya and Sasaki (1983) who reported lR/t = 5.05 at Ret = 2.6 × 104, and Djilali and Gartshore (1991) who reported lR/t = 4.7 at Ret = 5.6 × 104. Numerical investigation also suggested a weak dependency on Reynolds number: Yang and Abdalla (2009) reported lR/t = 6.5 at Ret = 6.5 × 103 for the case of no freestream turbulence and Tafti and Vanka (1994) reported lR/t = 6.36 at Ret = 1.0 × 103. The present values compare well with the previous experimental and numerical results. Hiller and Cherry (1981) remarked that the flow is essentially independent of Reynolds number in the range 3.4 × 104 < Ret < 8 × 104 and only a weak extension of the bubble was observed at Ret = 2.7 × 104.
The discrepancy in bubble length in the present experiments with those from previous investigations may be due to the geometry of the leading edge (45° angle in this investigation) whereas a blunt 90° edge or circular edge were used previously or other factors; differences in the blockage ratio of the apparatus, and turbulence intensity in freestream in different experiments can also contribute to the discrepancies in the observations. Of these factors, turbulence intensity is known to have an effect of reducing the separation length. In the present PIV measurement, turbulence intensity slightly increased from 0.7 to 0.9% with Reynolds number (i.e. freestream velocity). This could have contributed to the slight decrease of the separation length at higher Reynolds number, but considering all the differences from previous investigations, the present result strongly supports that the bubble length is weakly dependent on Reynolds number as far as the range of Reynolds number in the present investigation is concerned.
Figure 7 illustrates the average streamlines at the lowest and highest Reynolds number in the experiment. Note that the coordinates and velocity magnitude in the background are non-dimensionalized by the average separation length and freestream velocity respectively. In the figures, the air is directed upward as it approaches the leading edge and accelerates as it flows around the ovally-shaped bubble. Not only the bubble length, but also the bubble heights are nearly the same for both cases, which are approximately y/lR = 0.1. This was observed in the other flow conditions, too. Inside the bubble is a large zone of clockwise circulation. The center of the circulation slightly moves downstream with increasing Reynolds number. It is also discovered that the small secondary bubble which circulates counter-clockwise very near the leading edge exists in the case of low Reynolds number whereas it almost vanishes with slight expansion of the primary bubble towards leading edge in the case of high Reynolds number. It is likely that the secondary bubble will disappear at even higher Reynolds number which was not investigated in the present paper.
Figure 8 presents profiles (variation in the y-direction) of the horizontal and vertical components of the average velocities at different streamwise locations for all Reynolds number. The velocities are normalized by the freestream velocity U∞, and the profiles are taken at 8 different streamwise locations (x/lR = 0.05, 0.1, 0.2, 0.4, 0.6, 0.8, 1.0, 1.6). As presented in the graphs, both velocity profiles are well scaled using lR and U∞ and there is only little difference at different Reynolds numbers. The large region of reversed flow exists, and after re-attachment length, horizontal component especially near the wall increases in positive direction in any cases. The reversed velocity in the streamwise direction reached as large as − 0.3 U∞ around x/lR = 0.4–0.6 which compares well with that of Kiya and Sasaki (1983).
3.2 Turbulence quantities
Figure 9 presents profiles (variation in the y-direction) of normalized RMS values of the fluctuating velocity components and Reynolds stress respectively. The graphs are plotted at the same locations as the average velocities in Fig. 8. In Fig. 9, it may be seen that the scaled RMS velocity fluctuation profiles at any given streamwise location are generally the same for all the cases, except for the small discrepancies between them, particularly for v-fluctuations for x/lR = 0.05–0.2. Despite such small differences, the vertical position at which the RMS fluctuation attains maximum value is the same for all the cases at any given streamwise location. After x/lR = 0.6, the profiles of the RMS fluctuations appear to be similar.
The present results for the RMS fluctuations well compare with the results obtained by Kiya and Sasaki (1983) whose values were around u′ = 0.15–0.25U∞ and v′ = 0.1–0.2 U∞ in streamwise and vertical directions respectively at x/lR = 0.2–1.0 except for some points where the present results reached as high as u′ = 0.4U∞ and v′ = 0.3U∞ in streamwise and vertical direction respectively. The profiles appear sharper in the upstream location which was caused by a large velocity difference across a thin shear layer while the RMS inside the bubble is relatively small in contrast to the shear layer. Also, the peaks of the sharp profile were later found to be where vortices had been continuously being formed in the instantaneous realizations. The peak RMS fluctuation decreases and the profile widens downstream due to shear layer growth and turbulent mixing. It can be observed from Fig. 10 that Reynolds stress in each case has similar profiles as well with the exception in the upstream region, especially at x/lR = 0.1–0.2. Also, unlike the RMS of the fluctuating velocities, Reynolds stress profile widens without much decrease in the maximum value.
The growth in shear layer thickness with streamwise distance is plotted in Fig. 11. The thickness is the vorticity thickness based on Eq. (1), defined by Djilali and Gartshore (1991). The thickness is taken from averaged velocity field and normalized by the reattachment length as in the equation,
It can be observed that normalized shear layer thickness, too, is independent of Reynolds number, since the plot of all the cases almost overlap. Three separate regions having different linear slopes can be observed; very short smooth region (whose growth rate count not be ascertained) for 0.04 < x/lR < 0.1, dδω/dx \(\approx \) 0.23 for 0.1 < x/lR < 0.5, and dδω/dx \(\approx \) 0.06 for 0.5 < x/lR < 1.1 which correspond to stable region near the leading edge, the region of vortex generation, and turbulent reattachment region respectively (discussed in subsequent section). The trend of having separate regions of different growth rates were also observed by Djilali and Gartshore (1991) and they obtained the growth rates of 0.147 for x/lR < 0.65 and 0.1 for x/lR > 0.65. Similarly, Ruderich and Fernholtz (1986) obtained 0.148, and Brown and Roshko (1974) obtained 0.145–0.22 in the first half. The values from the present investigation are close to the previous values.
3.3 Dynamic structures
Figures 12 and 13 illustrate instantaneous distributions of fluctuating velocity vectors and vorticity in the upstream region at Ret = 6.2 × 103. Note that the vorticity is in z-direction, and the all physical quantities are normalized by U∞ and lR. The figures clearly illustrate how the separated shear layer, which is apparently steady (as seen from different instantaneous realizations) and laminar for up to x/lR = 0.1, breaks down into vortex structures whose details are captured well. As the flow approaches the leading edge, the flow is directed upwards and travels along the curvature of the primary bubble, and a smooth free shear is established at the very beginning of the curvature. However, around x/lR = 0.1–0.15, the inviscid instabilities due to inflectional profile seem to have grown rapidly and developed into Kelvin–Helmholtz type vortices, which are shed downstream. After around x/lR = 0.2, the vortices break down. Even though the separation is laminar, the initial development of instabilities in the shear layer of the leading-edge separation bubble cannot be compared with other laminar separation bubbles, for which the origin of inflectional instabilities has been traced back to the boundary layer upstream of separation (Diwan and Ramesh 2009). In the present case, the separation occurs right at the leading edge. The development of these instabilities into vortices, and the shedding of those vortices in the initial part of the bubble must significantly affect the unsteady aspects reported in the previous literature. It is for this reason that the present study especially focuses on the dynamics of the shear layer in the initial portion of the leading-edge separated bubble.
In the absence of sufficiently time-resolved data, it is useful to look at the probability density functions (PDF) of velocity fluctuations at various points on the shear layer. Figures 14, 15, 16, 17 are the PDF of the velocity fluctuations at (x/lR, y/lR) = (0.05, 0.01), (0.08, 0.055), (0.12, 0.06), (0.15, 0.08), (0.25, 0.10), (0.5, 0.12), (1.0, 0.02), and (1.6, 0.02) at Ret = 6.2 × 103 and 4.1 × 104. The points are taken arbitrarily along the streamline which divides the flow field into the bubble and external freestream. In the graphs, the PDF of streamwise velocity fluctuation at both Reynolds number are rather narrow (though apparently Gaussian) in the beginning of the separation around (x/lR, y/lR) = (0.05, 0.01) and becomes wider and clearly bi-modal as the flow progresses downstream, and become Gaussian-like further downstream. At lower Reynolds number for x/lR = 0.12–0.5, and at higher Reynolds number for x/lR = 0.08–0.25, the PDF is clearly bimodal; that is, two different values of velocity fluctuation tend to have locally high probability. Particularly, while one of the modes is at the positive side of the fluctuation the other is at the negative side. This suggest passage of successive vortices intermittently over those points, since each of the vortex has opposing sense of velocity on any two opposite sides about its axis. Further downstream, the PDF suggest a random velocity distribution, suggesting the flow becoming turbulent exhibiting multiple scales. In fact, it was observed from large numbers of instantaneous PIV realizations that it was always around x/lR = 0.1–0.2 along the dividing line, the shear layer rolls up and start producing vortices, which is supposedly contributing to the bimodal peaks in the streamwise direction. In contrast to the PDF of streamwise velocity fluctuation, the PDF of vertical velocity fluctuation do not exhibit bimodal behaviors, but appear to be Gaussian-like at all streamwise positions. However, the distributions do appear relatively wider in the middle locations, where the PDF of streamwise velocity fluctuations exhibit bimodal behavior.
Downstream of the region, the fluctuations become random (with unimodal Gaussian distribution) due to the non-linear evolution and interaction of vortices. From x/lR = 0.15–0.35, fairly large vortices are apparent in Fig. 12. The produced vortices travel downstream and break apart into smaller ones. Also, the region after this point occasionally experiences an emergence of one large structure, and one typical moment is illustrated in Fig. 18. In the figure, one can observe a large structure of high velocity fluctuation from x/lR = 0.25 to the end of the image, which is in contrast to Fig. 12 where one finds many smaller regions of high fluctuation. This was observed once in approximately 20–30 images, i.e. for every 100–150 ms. This large-scale structure continues downstream, too, and therefore were also captured in the region downstream. Using smoke visualization technique, Cherry et al. (1984), too, captured the large-scale structures which occurred occasionally and was shed downstream.
Shown in Fig. 19 is the fluctuating vectors around the average reattachment point. The PIV realization in this region illustrates a lot of smaller structures as well as the occasional passing-by of the large structures generated upstream, both of which contributing to variation in instantaneous re-attachment point. The fluctuating nature of reattachment length were illustrated in the detailed numerical work by Yang and Voke (2001) who reported that it varied about ± 25% of the average value. Although it was not possible to precisely identify the instantaneous re-attachment point in the present study, the variation is visually apparent from the realizations.
The maximum temporal resolution of the PIV system in the present study is 200 Hz, which does not help to study high-frequency phenomena. However, for the lowest Reynolds number case, the quantity U∞/lR ~ 18.2 Hz which is an order lower than the acquisition frequency, encouraged the analysis of temporal series of the velocity (fluctuations) data at different locations in the specific case. Figure 20 shows the power spectral density (PSD) functions of streamwise velocity at three different points, (x/lR, y/lR) = (0.01, 0.015), (0.1, 0.06), and (0.5, 0.12). At all points, it appears that a weak peak appears around low non-dimensional frequency of flR/U∞ = 0.09–0.2 where f is the dimensional frequency which turns out to be close to low-frequency mode discovered by previous investigations in literature. The present work could not resolve higher frequencies, however, since even the lower frequencies are not greatly lower than the acquisition rates in other cases, the temporal series studies are extremely limited by the PIV system. The large sample of data can however be resolved by means of the POD, which helps in revealing the dynamics of the flow field. This is discussed in the next subsection.
3.4 POD of flow field
Proper Orthogonal Decomposition (POD) is used to identify statistical coherent structures in the flow field. It was first introduced in fluid mechanics for the investigation of turbulence by Lumley (1967) in 1967, and a detailed review on the application of the technique in the analysis of turbulent flows was presented by Berkooz et al. (1993). Applying POD to the stereo-PIV data of turbulent jet in a crossflow, Meyer et al. (2007) found that the first 2 modes had significant energy to sufficiently approximate the flow, and could infer that the 2 modes were different phases in time of the same phenomena. Mandal et al. (2010) resolved bypass transition over a plate from the POD of planar PIV data. Thus, with the large amount of data that can be obtained from advanced diagnostics as well as computations, the dynamics of the flow can be resolved by studying the significant POD modes. POD method by Sirovich (1987) was employed in the present investigation. The POD is done on the fluctuating components of velocity. 2 separate eigenvalue problems are solved to find the eigenvectors, from which the POD modes are constructed; the formulations are elaborated by Pedersen (2003). The code distributed by Meyer (2008) was employed in the present investigation.
Comparisons of the first 7 decomposed orthogonal modes of the field of fluctuation of velocity magnitude in region near leading edge is shown in Fig. 21 for the 2 extreme Reynolds numbers of Ret = 6.2 × 103 and 4.1 × 104. It was apparent that for both Reynolds numbers, the first 3 modes generally have similar structures with nearly the same length scales as well as the spacing between them. Thus, the first 3 modes are Reynolds number independent. These modes have large length scales. The normalized length scales are thus the Reynolds number independent for each of the lower modes, since the separation length is observed to be Reynolds number independent. Since the length scales are the same, the time scale is inversely proportional to freestream velocity. Thus, the non-dimensional frequency (Strouhal number, St = flR/U∞) is expected to be Reynolds number independent with these lower modes.
Physically, the 1st and 3rd modes present shedding of structures shown in Fig. 21, with the regions of high energy one after another as one move along the shear layer, and the vector direction in one structure is nearly the opposite of the vector direction in the subsequent structures as shown in Fig. 22 for the 1st POD mode for Ret = 6.2 × 103. The 2nd mode corresponds to the shear mode, with one long high energy region along the shear layer and another inside the bubble. Even among these 2 structures, the vectors are observed to be opposite to each other in direction. The 3rd mode too displays shedding structures.
POD of the downstream region of the bubble (the reattachment region) is shown in Figs. 23 and 24. Shedding structures along the shear layer are apparent in both 1st and 2nd modes, in contrast to the shearing structures in the 2nd mode of the leading-edge region. The Reynolds number independence is also apparent in the first 2 modes. In the 3rd mode, qualitative differences with Reynolds number start to appear, though the length scales and the number of apparent structures is nearly same for different Reynolds numbers. The region is thus dominated by shedding structures. The coalescence of vortices to form large-scale structure upstream of the reattachment, and the injection of fluid into the bubble at the unsteady reattachment location make the picture complex, with all realizations displaying multiple flow scales. The evolution and coalescence of the vortices is non-linear phenomena, and hence it cannot be addressed from the present study with 2 separate sets of data for the leading edge and reattachment region which are not obtained simultaneously. The observation of regular shedding and flapping at reattachment are detailed in the literature as discussed in Section II. The subsequent discussions shall rather explore the origin of the regular shedding and flapping frequencies by inspecting the flow field near leading edge, without attempting to explain how the structures evolve downstream of this region (due to the limitation of spatial window of the PIV).
In order to be able to comment on the frequencies associated with the modes, a time series is formed from the temporal coefficients (Chronos) for different realizations corresponding to each mode. For the lowest Reynolds number of Ret = 6.2 × 103, the freestream velocity was 3 m/s, for which the PIV time resolution is reasonable: at 200 Hz, the PIV operating frequency is an order of magnitude higher than the phenomena with frequency of ~ 15 Hz based on characteristic flow time scale lR/U∞—corresponding to Strouhal number of 1- for 3 m/s flow velocity (it will be apparent subsequently that the second POD mode has significant energy at Strouhal number of ~ 1). At higher Reynolds numbers the frequencies corresponding to St = 1 is higher, and thus the time resolution of the PIV gets worse with the increasing freestream. The time series and FFT of the coefficients for different modes are shown in Figs. 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38 for the region near leading edge, are thus examined for the case of Ret = 6.2 × 103 having the best possible time resolution in the present study. The 1st and 3rd modes illustrate a clear peak at a non-dimensional frequency of flR/U∞ = 0.09 and 0.18 (harmonic of the frequency of 1st mode) respectively, which is roughly close to the low-frequency mode reported in the previous literatures. The peak is also close to the range of frequencies apparent in Fig. 20. The 1st and 3rd modes also have considerable energy for up to a non-dimensional frequency of around 0.8, which is close to that of the high-frequency mode (‘regular’ shedding) in previous reports in the literature. Particularly, the 3rd mode has prominent local peaks at flR/U∞ of 0.6 and 0.7. The power spectrum of the 2nd and 4th modes appears to be broad band, though with the 2nd mode considerable amplitudes are apparent for flR/U∞in the range 0.4–0.8.
With higher modes, the structures are found to become smaller, and the number of such structures increase with mode number. Significantly, from the 4th mode, the shapes and the length scales of the structures are different for different Reynolds numbers; the contrast in the mode shapes and scales in the 4th and 5th at different Reynolds numbers can be observed in Fig. 21. Thus, with the smaller scales, there is clear Reynolds number dependence in their dynamics, though it was not possible in the present investigation to establish trends for the higher modes. 5th and 6th mode appear to have a peak at flR/U∞ = 0.4, though this is specific to the case of Ret = 6.2 × 103, for which the PIV time resolution is reasonable to enable spectral analysis. It must be admitted that with limited time resolution, the higher frequencies, even those corresponding to the realizations showing the large structure for higher Reynolds number cases, may not have been resolved. Thus, it was not attempted to interpret the spectrum of higher modes having smaller high-frequency structures.
The reconstruction of the realizations using a few lower modes revealed an interesting pattern. A comparison of the reconstruction of velocity fluctuations fields using the first 3 modes, 5 modes, and up to 7 modes, of a realization typical of most instants (at \(t{U}_{\infty }/{l}_{R}\)=0.08), and the realization when a single large coherent structure was apparent (at \(t{U}_{\infty }/{l}_{R}\)=2.48), are shown in Figs. 39 and 40. It is only with first 7 modes that the structures start to appear in the reconstructed realization of most instants, and the first 3 modes did not result in any physically meaningful reconstruction. With the addition of further higher modes, the finer details of the field could be reconstructed. However, for the instance when a large-scale structure appears, the first 3 modes were sufficient to capture general structures, while finer structures emerge with the addition of higher modes. In fact, the mode coefficients (the Chronos) of 1st, 2nd, 3rd mode for most instances are low; for example, at \(t{U}_{\infty }/{l}_{R}\)=0.08 the coefficients are − 5.0, − 1.6, and − 2.7. However, during the instances when the one large-scale structure appears, the coefficients are large, especially those of the 1st and 3rd modes; for example, at \(t{U}_{\infty }/{l}_{R}\)=2.48 the coefficients are 33.5, − 1.1, and 11.2.
Thus, the most important aspect to be noted with the comparison is that, the reconstructions of these realizations tells the way the energy of the various modes are distributed temporally, through the POD temporal coefficient. The lower modes—the first 3—which have the highest energies (i.e. largest eigen values, since the modes are arranged in descending order of eigen values in POD analysis), and observed to be Reynolds number independent, do not contribute significantly in the reconstruction of most realizations involving multiple small-scale structures. The coefficients at those instances are very small. Meaningful reconstruction of those instances is possible only with inclusion of higher modes.
However, at a certain frequency, the coefficients of the lower modes take high values in those instances when the large structures appear, such that the Reynolds number independent lower modes play a significant role at those instances. For the lowest Reynolds number case (Ret = 6.2 × 103), these instances appear every 20–30 realizations as noted above. With the acquisition rate of 200 frames per second, this corresponds to 100–150 ms, and non-dimensional frequency of flR/U∞ = 0.4–0.6, which corresponds to the ‘regular shedding’ frequency of large-scale vortices reported in the literature (Kiya and Sasaki 1983). The formation of large-scale vortices that constitute ‘regular shedding’ are thus resolved to be formed in the earlier part of the separation bubble, from the small-scale vortices in preceding instances. This is not however the dominant frequency that is reflected in the power spectrum of the coefficients of 1st and 3rd modes whose peak is at flR/U∞~0.1 (though there is considerable energy for flR/U∞ in the range 0.4–0.6). Further, with very limited time resolution, the inferences regarding higher frequencies from the power spectrum could be misleading, although the low frequencies are apparent in the spectrum. The larger scale “flapping mode” at lower frequency of flR/U∞ ~ 0.1 cannot be isolated and explained from these reconstructions, though the frequency shows up in the power spectrum. Two of the dominant modes 1st and 3rd, which are Reynolds number independent, have clear peaks at this frequency range, with amplitudes well above the other peaks at higher frequencies. The ‘flapping’, being a phenomenon related to the enlargement and shrinking of bubble, cannot however be identified from the resolution of shedding structures in localized PIV window—the separation bubble was visually split into two in the current investigation. A larger window that can capture the entire bubble may resolve the mode, which cannot however be pursued in the present study. It is nonetheless evident from the POD analysis that both the “large-scale” phenomena—the flapping as well as the regular shedding—are Reynolds number independent phenomena since they are dominated by the lower modes.
4 Conclusions
Leading-edge separated flow field over a sharp flat plate is experimentally investigated at Reynolds number ranging from 6.2 × 103 to 4.1 × 104, using the statistics of the PIV data. It was observed that the average reattachment length is nearly independent of Reynolds number and a small secondary bubble near the leading edge was observed, which was found to shrink with increasing Reynolds number.
The profiles in wall-normal direction (along y/lR) of both streamwise and wall-normal (non-dimensional) velocity components, and their fluctuations, at all streamwise locations are found to be nearly Reynolds number independent. Shear layer thickness grew along streamwise distance with 3 distinct growth rates in 3 different regions, for all Reynolds numbers. The first region was very close to the leading edge, whose growth could not be resolved. In the subsequent regions, 2 distinct linear growth rates (slopes) of 0.23 and 0.06 respectively were noted, for the streamwise positions of 0.1 < x/lR < 0.5 (region of vortex generation) and 0.5 < x/lR < 1.1 (reattachment region).
The unsteady nature of the bubble was clearly apparent in from the different instantaneous realizations. It was observed that at x/lR = 0.1, the shear layer was rolling up into vortices, and after x/lR = 0.2, the field is dominated by many vortex structures of varying scales. There were however few odd instances when the structures seemed to occasionally become one large coherent structure of scale comparable to the separation length. At the lowest Reynolds number, for which the PIV frame rate provided reasonable time resolution, it was observed that these instance occurred every 20–30 frames (6.6–10 Hz), suggesting a non-dimensional frequency of flR/U∞ ~ 0.4–0.6.
Proper orthogonal decomposition of the flow field, especially in the region near the leading edge, helped in understanding the origins of the unsteadiness. While the 1st and 3rd mode shapes indicated shedding, it was shear flapping that corresponded to the 2nd mode shape in the region near the leading edge. The scales in the first 3 modes were found to be independent of Reynolds number. The higher modes were observed to have multiple smaller scales, and were found to be dependent on Reynolds number. Reconstruction of the realizations of most instants required at least 7 POD modes, suggesting the significance of higher modes during most instances. However, the Reynolds number independent first 3 high-energy modes sufficiently reconstructed the dominant structures at the instance when the large-scale coherent structure appeared. This suggests that most of the energy of the lower modes are manifested in those few instances when large-scale coherent structure appears. The scale of the structure, and the non-dimensional frequency (flR/U∞ = 0.4 ~ 0.6) of such instance corresponds to the regular shedding, which is traced to the upstream portion of the bubble. The low-frequency phenomena of flapping, associated with enlargement and shrinking of the bubble, cannot be identified by inspecting the snapshots in local PIV windows that visually split the bubble into two. However, the power spectrum of the velocity fluctuation time series at different positions on the shear layer, as well as the power spectrum of the POD coefficients of the 1st and the 3rd mode indicated the frequency of flR/U∞ ~ 0.1. Both large-scale phenomena—flapping and regular shedding- are therefore dominated by the first 3 modes, and thus are Reynolds number independent phenomena.
References
Berkooz G, Holmes P, Lumley JL (1993) The proper orthogonal decomposition in the analysis of turbulent flows. Annu Rev Fluid Mech 25:539–575
Brown GL, Roshko A (1974) On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 646:775–816
Chapman DR, Kuhen DM, Larson HK (1958) NACA Report No.1356
Chatterjee A (2000) An introduction to the proper orthogonal decomposition. Current Sci 78(8):808–817
Cherry NJ, Hiller R, Latour MEMP (1984) Unsteady measurements in a separated and reattaching flow. J Fluid Mech 144:13–46
Choi H, Lee J, Park H (2014) Aerodynamics of heavy vehicles. Annu Rev Fluid Mech 46:441–468
Diwan SS, Ramesh ON (2009) On the origin of the inflectional instability of a laminar separation bubble. J Fluid Mech 629:263–298
Djilali N, Gartshore IS (1991) Turbulent flow around a bluff rectangular plate Part II: numerical predictions. J Fluid Eng 113:60–67
Eaton JK, Johnston JP (1981) A review of research on subsonic turbulent flow reattachment. AIAA J 19(9):1093–1100
Henshall BD, Cash RF (1958) Observations of the flow over a two-dimensional 4 percent thick aerofoil at transonic speeds. In: Aeronautical Research Council Report and Memoranda: R&M No.3091
Hiller R, Cherry NJ (1981) The effect of stream turbulence on separation bubbles. J Wind Eng and Ind Aerodynamics 8:49–58
Kiya M, Sasaki K (1983) Structure of a turbulent separation bubble. J Fluid Mech 137:83–113
Kiya M, Sasaki K (1985) Structure of large-scale vortices and unsteady reverse flow in the reattaching zone of a turbulent separation bubble. J Fluid Mech 154:463–491
Lumley JL (1967) The structure of inhomogeneous turbulent flows. In: Yaglom AM, Tartarsky VI (eds) Atmospheric turbulence and radio wave propagation, pp 166–177
Mandal AC, Venkatakrishnan L, Dey J (2010) A study on boundary-layer transition induced by freestream turbulence. J Fluid Mech 660:114–146
Meyer KE (2008) Identify flow structures with Proper Orthogonal Decomposition. DANSIS seminar on Visualization. https://www.yumpu.com/en/document/view/5873898/identify-flow-structures-with-proper-orthogonal-dansis
Meyer KE, Pedersen JM, Ozcan O (2007) A turbulent jet in crossflow analysed with proper orthogonal decomposition. J Fluid Mech 583:199–227
Ota T (1974) A separated and reattached flow on a blunt flat plate in a tunnel. Quart J Mech Appl Math 27:379–386
Ota T, Kon N (1974) Heat transfer in the separated and reattached flow on a blunt flat plate. J Heat Transfer 96(4):459–462
Ota T, Asano Y, Okawa J (1981) Reattachment length and transition of the separated flow over blunt flat plates. J Bull JSME 192(24):941–947
Pedersen JM (2003) Analysis of planar measurements of turbulent flows. Denmark Technical University of Denmark: MEK-FM-PHD No.2003–01
Podvin B, Fraigneau Y, Tenaud C, Daru V (2014) Coherent structures in the boundary layer of a flat thick plate. Compt Rendus Mech 342:417–424
Ruderich R, Fernholz HH (1986) An experimental investigation of a turbulent shear flow with separation, reverse flow, and reattachment. J Fluid Mech 163:283–322
Sicot C, Perrin R, Tran TT, Boree J (2012) Wall pressure and conditional flow structures downstream of a reattaching flow region. Int J Heat Fluid Flow 35:119–129
Sirovich L (1987) Turbulence and the dynamics of coherent structures. Q Appl Maths 45(3):561–571
Tafti DK, Vanka SP (1994) A three-dimensional numerical study of flow separation and reattachment on a blunt plate. Phys Fluids A 3:12
Tenaud C, Podvin B, Fraigneau Y, Daru V (2011) Numerical simulation of the turbulent separation-reattachment flow around a thick flat plate. J. Physics 318:042059
Tenaud C, Podvin B, Fraigneau Y, Daru V (2016) On wall pressure fluctuations and their coupling with vortex dynamics in a separated-reattached turbulent flow over a blunt flat plate. Int J Heat Fluid Flow 61:730–748
Wang QC, Wang ZG, Zhao YX (2017) The impact of streamwise convex curvature on the supersonic turbulent boundary layer. Phys Fluids 29(11):116106
Yang Z, Abdalla IE (2009) Effects of free-stream turbulence on a transitional separated-reattached flow over a flat plate with a sharp leading edge. Int J Heat Fluid Flow 30:1026–1035
Yang Z, Voke PR (2001) Large-eddy simulation of boundary-layer separation and transition at a change of surface curvature. J Fluid Mech 439:305–333
Funding
Open access funding provided by University of Glasgow.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fujiwara, K., Sriram, R. & Kontis, K. Experimental investigations on the sharp leading-edge separation over a flat plate at zero incidence using particle image velocimetry. Exp Fluids 61, 205 (2020). https://doi.org/10.1007/s00348-020-03039-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-020-03039-w