Homogenization of streaks in a laminar boundary layer

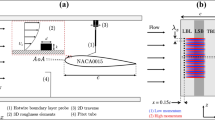
Abstract

The present work, based on experimental, numerical and theoretical investigations, introduces a method to homogenize streaks in the laminar boundary layer. The streaks are created by a spanwise array of roughness elements on the surface of a flat plate. A homogenization body in the form of a horizontal bar is added at a downstream location away from the roughness array to homogenize the velocity differences of the streaks in the laminar boundary layer. Measurements are done with hot-film anemometry and supported by numerical simulations and linear stability theory. The streak amplitude can be significantly reduced with the proposed homogenization body. Furthermore, the reduction in spanwise gradients of the mean velocity leads to a significant reduction in the sinuous instability of the streaky flow. The effects of the homogenization body on the displacement thickness and the observation of flow unsteadiness downstream of the homogenization body are discussed. The present work thus proposes and explores a passive technique to control undesired streaks in the laminar boundary layer.

Graphic abstract

1 Introduction

One of the first visualizations of streaks in a laminar boundary layer was done by Mochizuki (1961) downstream of a hemispherical roughness element. Depending on the Reynolds number, Mochizuki (1961) found either a steady wake, periodic vortex shedding or turbulent randomization of the smoke streaklines. Careful visualizations by Acarlar and Smith (1987) revealed the existence of a horseshoe vortex wrapping around the roughness and a recirculation zone emerging in the near wake of the roughness. Hairpin vortex shedding was observed beyond a Reynolds number of 120 based on the radius of the hemisphere and the tip velocity. Downstream of the recirculation zone, vorticity decays and velocity streaks rise and persist in the far wake. A sketch of these flow features is shown in Fig. 1. Numerous publications have dealt with the effects of streaks in laminar boundary layers since then.

Fig. 1

Roughness flow topology, sketch modified from Acarlar and Smith (1987)

Streaks can be created for example by roughness, screens, rods, flaps or freestream turbulence. In all cases, streamwise vorticity drives a wall-normal exchange of momentum that gives rise to streamwise elongated streaks. More descriptively, the process can be imagined as a scar being ripped into the boundary layer (Andersson et al. 2001). A theoretical discussion on this effect is provided by Landahl (1990), who introduced the term ”lift-up effect” to explain the exchange of high-speed and low-speed fluid due to streamwise vorticity in a shear layer. Mathematically speaking, streaks are a consequence of non-normality of the linear stability operator of the governing Navier–Stokes equations (Trefethen et al. 1993; Schmid 2007), leading to algebraic growth followed by viscous decay. This combination is also referred to as “transient growth.”

In many scientific and industrial applications, streaks originate particularly from high levels of freestream turbulence. In such situations, the boundary layer is receptive to low-frequency vorticity disturbances from the surrounding flow (Phani Kumar et al. 2015). If the spanwise amplitude of the streaks becomes too large, the flow may rapidly trip to turbulence and bypass the ’classical’ exponential growth of Tollmien–Schlichting (TS) waves (Durbin 2017). More precisely, sinuous-type secondary instabilities of the streaks may set in if their amplitude grows larger than 26 % of the freestream velocity while varicose-type instabilities set in at much higher streak amplitudes (Andersson et al. 2001). This can ultimately lead to the breakdown to turbulence (Brandt et al. 2004) and thus increase drag, cost and emission of a moving body.

A desirable effect of streaks is their ability to attenuate TS waves. This mechanism has already been observed by Kachanov and Tararyki (1987) and Boiko et al. (1994) and later by Fransson et al. (2005). If parameters are chosen correctly, the attenuation of TS waves can lead to a delay of laminar-to-turbulent transition as shown in numerous studies (Fransson et al. 2006; Fransson and Talamelli 2012; Sattarzadeh et al. 2014). The explanation for this observation is an additional Reynolds stress term which decreases the perturbation kinetic energy (Cossu and Brandt 2004) and thus attenuates TS waves. Another explanation was given more recently, namely the stabilizing effect of the mean-flow distortion, see Dörr and Kloker (2018). Transition delay could also be reproduced by Lemarechal et al. (2018) and Puckert (2019) in the same facility as in the present experiments; however, the transition delay was highly sensitive to parameter variations. If parameters are chosen wrong, premature transition is likely to be observed again. An overview of different effects of streaks on laminar boundary layers is sketched in Fig. 2 as a qualitative function of streak amplitude.

Fig. 2

Evolution of streaks in the laminar boundary layer

Streaks are important in both laminar-to-turbulent transition and in the turbulence regeneration cycle. Therefore, studies on streak reduction in both laminar and turbulent boundary layers are found in the literature. In turbulent flows, the primary goal is to reduce skin-friction drag. Suction and blowing, for instance, has often been used to control streamwise vorticity that would otherwise lead to the formation of streaks (Choi et al. 1994). In physical flows, the required control loop is difficult to install because of very small dimensions of sensors and actuators. To circumvent this difficulty, uncontrolled localized suction has successfully been used by Bakchinov et al. (1999). Later, a control logic for wall suction was implemented by Rathnasingham and Breuer (2003) and Lundell (2007). Another active method to reduce streaks without the need for feedback loops is the application of counter-rotating streamwise vortices or colliding spanwise wall jets. Schoppa and Hussain (1998) showed with DNS that these structures can reduce small-scale streamwise vorticity if they are larger than the size of natural streaks in the turbulent boundary layer. Moreover, oscillatory walls are also known to reduce streaks in turbulent boundary layers (Laadhari et al. 1994; Touber and Leschziner 2012). In hypersonic flows, Fasel (2017) presented a method to reduce hot-cold streaks for hypersonic applications with passive 2D and 3D elements. In subsonic flows, studies on passive methods to control streaks are not known to the authors.

The objective of this investigation is therefore to homogenize streaks in laminar boundary layers. This can ultimately lead to a control method to prevent the ’bypass’ path to turbulence. The paper is structured as follows. First, the set-up of the homogenization unit and the scientific methodology of both the experiment and the simulations are introduced. Second, a proof of concept is provided and followed by an analysis of different effects of the homogenization body on the laminar boundary layer. Last, a discussion on the applicability of the proposed method for passive flow control is given with conclusions and outlook for further research.

2 Set-up

The set-up of the physical experiments and the numerical simulations is illustrated here. The set-up is identical in both methods and can thus be compared well. The main purpose of the numerical simulation is to provide a base flow for linear stability analyses.

2.1 Experiment

The experiments in this work have been conducted in the Laminar Water Channel at the Institute of Aerodynamics and Gas Dynamics at the University of Stuttgart. It is a low-turbulence, closed-circuit water channel with a test section of dimensions $8 \times 1.2 \times 0.2 \, \text {m}^3$. The natural turbulence intensity of the facility is approximately 0.08 % of the freestream velocity in the frequency range of $0.1{-}10$ Hz (Puckert and Rist 2018). Even lower values were reported by Wiegand (1996). A laminar boundary layer of Blasius type forms in the test section on a flat plate with elliptical leading edge and side edge boundary-layer suction (Puckert 2019). The spanwise center of the leading edge is the origin of the xyz-coordinate system as shown in Fig. 3.

Fig. 3

Set-up of the roughness and horizontal bar embedded into a flat-plate boundary layer. Streaks indicated in the wake of the roughness

A spanwise array of 6 cylindrical roughness elements with height $k=10 \, \text {mm}$ and diameter $d=1.5\,k$ is placed at $x_k=87\,k$ from the leading edge of the flat plate to create streamwise streaks at a regular spacing. The choice of these parameters is based on preliminary work by Puckert (2019) and has to meet the constraints of the facility (Wiegand 1996). The chosen roughness height, for instance, allows to create both laminar and turbulent wakes, depending on the Reynolds number Re_k = kU_e / ν, where U_e is the boundary layer edge velocity and ν the kinematic viscosity of water. Re_k can be adjusted through the freestream velocity of the water channel. The relative height of the roughness to the boundary-layer thickness is similar to the literature (Klebanoff et al. 1992; Fransson et al. 2005). The spanwise center $z=0$ is located between the roughness and the dimensional parameters of this set-up have been determined in a preliminary study that was conducted both visually and quantitatively with hot-film to find an equal distribution of high-speed and low-speed streaks. The spanwise spacing ${\Delta} _z = 5\,k$ of the roughness array yields a non-dimensional spanwise wavenumber of

$$\begin{aligned} \beta = \frac{2 \pi }{{\Delta} _z / l} \sqrt{\frac{\nu }{U_{e} l}} = 0.53, \end{aligned}$$

(1)

with unit length l according to the normalization of Andersson et al. (1999). This wavenumber is close to $\beta =0.45$, where Andersson et al. (1999) predict streaks to act as optimal perturbations in bypass transition. This set-up thus provides streaks that could be the result of freestream turbulence diffusing naturally into the boundary layer at large levels of freestream turbulence (Brandt et al. 2004).

The centerpiece of the present study is the homogenization body downstream of the roughness array. It consists of a stainless steel bar of diameter $d_{\mathrm{hom}}=1.6$ mm and is supported by thin Plexiglas strips at both ends. The wall-normal distance of the bar is $y_\mathrm{hom}/k=1$ for Case I and $y_\mathrm{hom}/k=0.5$ for Case II, respectively. Case I and Case II are distinguished by the wall-normal spacing between the horizontal bar and the flat plate. Case III is identical to Case I with a higher Reynolds number and investigated numerically, where artificial damping of perturbations is possible, see Sect. 2.2. In all cases, the streamwise station of the bar is far enough behind the roughness at $x_\mathrm{hom}/k=130$ to allow transient effects to dissipate according to the studies of Puckert (2019). The purpose of the horizontal bar (“homogenization body”) is to reduce the streak amplitude and thus homogenize the streaks. The parameters of all available cases in this work are summarized in Table 1. A reference case without homogenization body is also provided in this study for comparison.

Table 1 Parameters of experimental set-up

The hot-film measurements have been acquired with Constant Temperature Anemometry (CTA), a hot-film probe Dantec 55R15 and a 16-bit A/D converter. The sampling rate was 100 Hz to satisfy the Nyquist criterion for the present frequency range. The sampling rate is sufficient considering that a typical Tollmien–Schlichting-wave frequency at our facility is in the order of 0.1-0.4 Hz, hairpin vortices of roughness wakes in the order of 1 Hz and late stages of transition also in the order of 1 Hz, see Puckert (2019). The calibration of the hot-film has been done in situ by moving the probe through resting water, see “Appendix 1”. An overheat ratio of 8 % is used as recommended by the manufacturer. No temperature compensation is needed due to the very small temperature drift of $< 0.05\,^\circ$C per day (Wiegand 1996). The bridge voltage of the CTA circuit is converted into velocity through King’s law and the velocity u in streamwise direction is decomposed into steady (${\bar{u}}$) and fluctuating ($u'$) components and filtered digitally between a bandwidth of 0.1-10 Hz (Puckert 2019). The complete set-up is sketched in Fig. 3, and the parameters are summarized in table 1.

2.2 Numerical simulations and linear stability theory

Numerical simulations are performed in OpenFOAM (Jasak 2009) with the steady-state solver simpleFoam for Case I and II. The governing equations in these cases are the incompressible Navier–Stokes equations which are solved with an iterative procedure until a residuum of $10^{-6}$ is reached. To obtain a laminar baseflow for Case III, the selective frequency damping (SFD) described in Åkervik et al. (2006) is implemented and used. The computational domain extends over $-50< x/k < 200$, $0 < z / {\Delta} _z < 1$ and $0< y/k < 30$ with periodic boundary conditions at the side walls and constant velocity at the inlet. The outlet condition is defined as constant pressure. The bottom, roughness and homogenization body are no-slip walls, whereas the top is a slip wall. The block-structured mesh has been generated in Pointwise, and a grid convergence study has been performed to determine a suitable cell number of 494,890. Refinements are done towards the flat plate, around the cylindrical roughness and the homogenization body, see Fig. 4.

Linear stability theory is applied to obtain a better understanding of the linear dynamics in selected cases. For this purpose, the 2D normal mode ansatz

$$\begin{aligned} \mathbf{q}' (y,z,t)=\hat{\mathbf{q }}(y,z) e^{i \alpha x - i \omega t} \; (+c.c.) \end{aligned}$$

(2)

is chosen to compute the eigenmodes from an operator-form of the incompressible, linearized Navier–Stokes equations. In Eq. (2), the state vector $\mathbf{q}'$ is expanded into the product of the eigenvector $\hat{\mathbf{q }}$ and exponential function of the mode, containing the streamwise wavenumber $\alpha$, complex frequency $\omega$, time t, imaginary unit i and complex conjugate c.c.. The two dimensions y and z of this analysis lead to the name bi-local or bi-global stability analysis, depending on the literature (Bucci 2017; Theofilis 2011). This 2D method is particularly suitable for quasi-parallel flows, i.e., with slow streamwise variation of the base flow such as in the present case with streaks. More details on LST and the code applied to this work can be found in Wu and Rist (2020).

Fig. 4

Computational mesh. Slices at $z=0$ of a roughness and b homogenization body. Every second line is shown

3 Results

3.1 Streak creation and homogenization

The introduction of streaks into the boundary layer, as well as the effects of the homogenization body, is evaluated in a slice perpendicular to the streamwise direction at $x/k=163$. This station is far enough downstream of the homogenization body for local effects to dissipate. The hot-film is traversed between 75 spanwise positions in the range of $-1.5< z/{\Delta} _z < 1.5$ and 14 wall-normal positions in the range of $0.1< y/k < 2.7$ to record the streamwise velocity component. The measurement duration at each position was 60 seconds, which is more than sufficient to capture the most important fluctuations of the flow. Figure 5 illustrates both mean and root-mean-squared (rms) values of the non-dimensional, streamwise velocity for the reference case without homogenization body, Case I, and Case II. Note that the spanwise origin is manually corrected to remove the effects of a very small crossflow in the laminar water channel (typically $<1^{\circ }$ deflection).

Fig. 5

Slice at $x/k=163$ showing isolines of ${\bar{u}}/U_e$ from 0.1 to 1 in increments of 0.1 as solid black lines. Pseudocolors represent $u'_{\mathrm{rms}}/U_e$. (top) reference, (middle) Case I, (bottom) Case II

Figure 5 (top) shows streaks with regular spacing in the mean flow. Low-speed streaks can be recognized by lifted velocity isolines at $z / {\Delta} _z =-\,1$, 0 and 1, whereas high-speed streaks are located at $z / {\Delta} _z=-\,0.5$ and 0.5, which is the spanwise position of the roughness. Whether the roughness far wake is of high or low velocity compared to the surrounding flow depends primarily on the thickness of the roughness and subsequent vortex system induced by the roughness. In case of a thin roughness, the horseshoe vortex system from the front side of the roughness dominates and creates a high-speed streak in the center. If the roughness is thick, the vortex system in the near wake of the roughness may introduce a low-speed streak in the centerline. The decision whether the centerline contains high-speed or low-speed fluid can depend on Reynolds number, roughness shape and spanwise spacing as shown in visualizations in Puckert et al. (2015). To explain the present results, a sketch of the flow topology is shown in Fig. 6. Arrows indicate the rotation direction of the horseshoe vortices that wrap around the roughness elements as known from Acarlar and Smith (1987). Driven by this vorticity, low-speed fluid is pushed up between the roughness wake and high-speed fluid is transported down behind the roughness at a sufficient distance from the recirculation zone. The vorticity then decays while streaks persist for a long streamwise distance. The vortex system in the near wake may be steady, periodic or chaotic, depending on the Reynolds number. These observations are documented in previous investigations, see for instance Puckert (2019), and the literature (Acarlar and Smith 1987; Klebanoff et al. 1992). The distribution of high-speed and low-speed fluid in Fig. 5 (top) forms a wavy pattern. The spanwise wavelength equals the spacing of the roughness ${\Delta} _z$, confirming that the streaks are controlled by the roughness.

Fig. 6

Flow topology from top view. Blue arrows indicate rotation. Base flow direction from top to bottom

When the homogenization body (Case I) is added, see Fig. 5 (middle), the spanwise gradients are reduced in comparison with Fig. 5 (top). The strongest homogenization effect can be found at $y/k=1$, which is at the height of the homogenization body. The same effect can be observed in Fig. 5 (bottom). The streak amplitude in the laminar boundary layer is qualitatively weaker in Case I and II compared to the reference case, which proves that the proposed method is effective. A more detailed discussion, including a quantitative definition of the streak amplitude, follows in the next section.

Fig. 7

Non-dimensional, streamwise velocity ${\bar{u}}/U_e$ from numerical simulations of (top) reference and (bottom) Case I at $y/k=1$ (for illustration purpose z stretched by factor 10)

Disturbances, marked by fluctuation level $u'_\mathrm{rms}$ in Fig. 5 (top), occur predominantly in regions of high spanwise velocity gradients with some outliers due to transient effects in the Laminar Water Channel. In Case I, the disturbance level is increased due to the homogenization body between $0.5<y/k<2$, see Fig. 5 (middle). If the homogenization body is installed at the lower wall-normal position in Case II, the disturbances are almost as low as in the reference case, see Fig. 5 (bottom). This can be explained by the low Reynolds number based on the diameter of the bar in Case II. At a spanwise average of $Re_d \approx 26$ in Case II, no significant vorticity can be expected. With $Re_d \approx 51$ in Case I, on the other hand, first laminar disturbances may occur like in a von-Kármán type of vortex street (Schlichting and Gersten 2005). It can be noted that preliminary visualizations with the homogenization body placed at $y/k=1.5$ (thus $Re_d \approx 70$) exhibited rapid breakdown to turbulence. Such ’trip wires’ have received considerable attention in the past and are not the goal of this investigation. Though Case II induces less disturbances into the flow, it is also less effective than Case I. Therefore, particular attention is given to Case II in the following investigations to understand the physics of this method in more detail.

Another perspective is provided with numerical results in Fig. 7 for Case I at $y/k=1$. The wake of the roughness forms a high-speed streak surrounded by low-speed streaks. Local effects of the roughness are confined to a short streamwise distance and vanish before reaching the horizontal bar. This figure confirms that the bar is in a region where the parallel-flow assumption for 2D linear stability theory is valid. The streaks behind the homogenization body at $x/k>130$ in Fig. 7 (bottom) are qualitatively much weaker than in Fig. 7 (top). This is in qualitative agreement with the physical experiments and substantiates successful streak homogenization.

The working principle of this method is based on two effects. First, the drag of the horizontal bar equalizes large-scale velocity inhomogeneities similar to screens in the settling chamber of a wind tunnel. Here, high-speed streaks are inhibited more than low-speed streaks because the drag increases with velocity. Second, small-scale vorticity disturbances induced locally behind the horizontal bar may enhance the exchange of momentum between neighboring high-speed and low-speed streaks, which leads to further homogenization. The risks of these effects are additional drag and unsteady disturbances in the laminar boundary layer. These effects are investigated in Sect. 3.3.

3.2 Streak amplitude

To evaluate the homogenization of streaks more quantitatively, the streak amplitude is defined as in Shahinfar et al. (2012):

$$\begin{aligned} A_\mathrm{st}(y)= & {} \frac{{\max }_z({{\bar{u}}})-\text {min}_z({{\bar{u}}})}{2U_e}\;, \end{aligned}$$

(3)

$$\begin{aligned} A_{\mathrm{st},{\max }}\,=\, {\max }_{y}(A_\mathrm{st}(y))\;. \end{aligned}$$

(4)

The maximum and minimum of ${\bar{u}}$ at $z=\text {const.}$ yields a streak amplitude $A_\mathrm{st}(y)$ that depends on the y-position. The maximum streak amplitude within a yz-plane is then defined by Eq. (4).

An exemplary velocity distribution for Case I at $(x,y)/k=(170,1)$ is shown in Fig. 8. The experimental data originate from measurements with spanwise increments $dz /{\Delta} _z= 0.02$ between each position and a measurement time of 120 s at each position. The experiments are further compared to numerical simulations and exhibit overall excellent agreement except for the low-speed region in Case I, where the simulation underestimates the flow velocity slightly. Applying Eq. (3) to the numerical values gives a streak amplitude of $A_\mathrm{st}=0.22$ for the reference case and $A_\mathrm{st}=0.15$ for Case I. In other words, the streak amplitude of Case I is reduced by 32 % compared to the reference case. It is reasonable to use numerical results in such comparisons because they exclude experimental outliers. For instance, the experiments in Fig. 8 yield a streak reduction of 35 %, which is very similar to the numerical result but slightly larger due to outliers. Error bars shown in Fig. 8 are calculated as described in “Appendix 2”. Keeping in mind the restrictive assumptions of the steady solver and experimental shortcomings, the agreement between experiment and simulation can still be considered excellent.

Fig. 8

Non-dimensional, streamwise velocity ${\bar{u}}/U_e$ for Case I at $(x,y)/k=(170,1)$

Figure 9 shows the streak amplitude in wall-normal direction at $x/k=163$ for the reference, Case I, and II, respectively. The experimental data originate from the same measurements as in Fig. 5. Numerical data are available for the reference case and Case I and have been added to the figure. Overall, there is good agreement between the experiment and the simulation. The streak amplitude grows with increasing wall-normal direction up to a maximum value between $1.1< y/k < 1.5$ and then drops back to zero further away from the wall. A good estimate of the location of the maximum is at or slightly above the wall-normal location of the homogenization body, which was further upstream at $y/k=1$. In Case I, the flow in the experiment seems strongly influenced by the homogenization bar and exhibits two maxima above and below $y/k=1$. Although the simulation does not represent this detail, it does not change the streak amplitude significantly and is therefore accepted.

In Andersson et al. (1999), the optimal perturbations from an optimization algorithm were reported to be streaks with a maximum amplitude at $y/k = 0.94$ (converted to our coordinate system). Considering the idealization of ’optimal’ streaks, the agreement to the location of our maximum in the reference case at $y/k = 1.1$ (experiment) and $y/k = 1.0$ (simulation), respectively, is good. It is known that experimentally created streaks are strongest further away from the wall than in optimal perturbation theory (White 2002; Fransson et al. 2004).

In this context, Fig. 9 also gives a hint on where in the boundary layer the homogenization body should be placed. The streak reduction is more effective in Case I than in Case II. This is most likely due to the wall-normal placement of the homogenization body close to the maximum streak amplitude and the higher diameter-based Reynolds number of Case I, which enhances the mixture of momentum. Visual attempts to place the homogenization body at $y/k=1.5$ resulted in immediate transition and were excluded from quantitative experiments. Thus, a low wall-normal position of the homogenization body leads to low homogeniztion performance while a too high position may trip the flow.

Fig. 9

Streak amplitude $A_\mathrm{st}$ versus wall-normal coordinate y/k at station $x = 163$

The downstream evolution of streak amplitudes is shown in Fig. 10 for the reference case and Case I. Figure 10 exhibits a rapid rise of $A_\mathrm{st}$ at $x/k=87$ as a result of local effects at the roughness array (dotted lines). The transient growth of streaks (Brandt et al. 2004) can be observed from $x/k \ge 95$ where local effects of the roughness vanish. After further growth of $A_\mathrm{st}$ in the downstream direction, the fate of $A_\mathrm{st}$ depends on the presence of the homogenization body (dashed line at $x/k=130$). If there is no homogenization body (reference case), the streak amplitude continues to grow until $x/k=144$ and decays thereafter. In Case I, on the other hand, a significant reduction in $A_\mathrm{st}$ can be observed downstream of the homogenization body. This observation is in agreement with the findings above. Furthermore, Fig. 10 reveals that the homogenization effect is particularly strong in the close vicinity of the homogenization unit between $130< x/k < 140$. Downstream of $x/k=140$, the streak amplitude evolves similar to the reference case with an almost constant offset.

Fig. 10

Downstream evolution of streak amplitude $A_\mathrm{st}$ from numerical simulations

3.3 Mechanisms of the homogenization unit

This section focuses on both steady and unsteady flow features induced by the homogenization unit to understand further effects of the horizontal bar in the boundary layer.

3.3.1 Displacement thickness

In contrast to the flow through screens in wind tunnels, the boundary layer is not bounded by a wall at the top. As a consequence, the adverse pressure gradient induced by the bar thickens the boundary layer. This can be quantified by the displacement thickness $\delta ^*$, which is linked to the boundary-layer thickness and momentum thickness in a Blasius flow. The displacement thickness is obtained by integration of the streamwise velocity (White 2006):

$$\begin{aligned} \delta ^* = \int _{0}^{\infty }\left( 1-\frac{{{\bar{u}}}(y)}{U_e}\right) \text {d}y. \end{aligned}$$

(5)

Equation (5) is evaluated with numerical data and averaged across the spanwise direction to obtain a representative value of $\delta ^*$ for each yz-slice. The results are shown in Fig. 11 for the reference case and Case I with homogenization body. The theoretical displacement thickness of the Blasius boundary layer,

$$\begin{aligned} \delta ^* = 1.7208 \sqrt{\frac{\nu x}{U_e}}, \end{aligned}$$

(6)

is also added to the figure for comparison.

The reference case and Case I in Fig. 11 are in good agreement to the theoretical Blasius solution upstream of the roughness at $x/k=87$ (dotted lines). This was expected and is another confirmation of a correct numerical simulation. Closer to the roughness, $\delta ^*$ rises in both reference case and Case I due to the blockage effect of the roughness. A local maximum appears at the roughness, exceeding the Blasius solution by up to 32 %. This difference decreases downstream of the roughness. In the proximity of the bar at $x/k=130$ (dashed lines), $\delta ^*$ increases in Case I and continues almost with a constant offset to the Blasius solution. Further downstream, the curve for Case I may eventually relax and return to the original Blasius solution, similar to the reference case. A larger value of $\delta ^*$ in Case I leads to a larger $Re_{\delta ^*}$, which can have negative effects on the stability and laminar state of the flow. The installation of the homogenization unit can thus be understood as a trade-off between spanwise gradients and wall-normal thickness. The stability of the homogenized flow will be investigated in more detail in Sect. 3.3.3.

Fig. 11

Non-dimensional displacement thickness $\delta ^{*}/k$ versus downstream coordinate x/k

3.3.2 Unsteadiness

To evaluate the velocity fluctuations downstream of the horizontal bar, another experiment has been performed. Figure 12 illustrates the non-dimensional fluctuations $u'_\mathrm{rms}/U_e$ versus x-direction for the reference case and for Case I and II. To acquire these data, the hot-film probe was positioned to five spanwise positions between $0 \le z/{\Delta} _z \le 0.8$ at different stations $140 \le x \le 390$. The results in Fig. 12 represent the averaged rms value of all spanwise measurements. This procedure ensures that the probe does not miss important features in spanwise location where both high-speed and low-speed streaks occur. The wall-normal position $y/\delta ^*$ with respect to the displacement thickness was kept constant at the height of the horizontal bar $k/\delta ^*|_\mathrm{bar}$ to compensate for the growth of the boundary layer. More precisely, for the reference and Case I it is $y = 1.191 \delta ^*$ and for Case II it is $y = 0.596 \delta ^*$, although the wall-normal position is not crucial for the detection of streak breakdown. Matsubara et al. (1998) showed that intermittency profiles, being a measure of turbulent parts in the flow, are almost constant inside a streaky, transitional boundary layer. This was confirmed in preliminary visual experiments at this facility (Lemarechal et al. 2019). The measurement time was 60 s at each position.

Figure 12 exhibits an increase in the fluctuations for Case I between $130< x/k < 200$ followed by a return to the reference case. In contrast, Case II remains at or below the reference case in the majority of measurements. Note that Case II was measured closer to the wall since the horizontal bar in this case is also installed closer to the wall. Most likely, the difference of wall-normal probe position explains the low fluctuation level of Case II.

Fig. 12

Disturbance root mean square $u'_{\mathrm{rms}}/U_e$ from experiments in streamwise direction

To clarify why the fluctuation level of Case I in Fig. 12 rises and then drops back to the reference level, four time traces of the same experiment are plotted in Fig. 13. Here, the spanwise position $z/{\Delta} _z = 0.2$ is chosen, while other positions yield similar results (not shown). The stations $x/k=140$ and 160 are located before the fluctuation peak of Fig. 12, $x/k=200$ at the peak and $x/k=300$ behind, respectively. The time traces at $x/k=140$ and 160 appear laminar with some disturbances. High-frequency disturbances in $x/k=140$ lead to an apparently thicker line than in $x/k=160$, see detail on top of the plot. This effect will be investigated in more detail in the next paragraph. Here, it is interesting to see chaotic motion in a part of the signal at $x/k=200$. This turbulent motion is intermittent in time, i.e., it emerges from and returns to the laminar state. The turbulent motion is one part of the explanation for the rise of fluctuation rms in Fig. 12 and can also be observed at other locations in the vicinity of $x/k=200$. Further downstream, at $y/k=300$, the signal looks smooth again. This can be explained by relaxation of the base flow as the distance to the homogenization body increases. The turbulence cannot self-sustain itself and returns to the laminar state similar to a turbulent spot in a favorable pressure gradient (Narasimha et al. 1984). The intermittent creation of turbulence may not be desirable in engineering applications; however, the lateral exchange of momentum can strongly assist in the extinction of the remaining streamwise streaks.

Fig. 13

Time traces of Case I at different stations. Offsets added for better readability

To understand the creation and amplification of instabilities behind the bar, Fourier transforms are performed on the experimental data closest to the bar at $x/k=140$. The Power Spectral Density (PSD) of the five available measurements at different spanwise positions are added, and the sum is shown in Fig. 14. The same procedure has been repeated for the signals at $x/k=160$, 200 and 300. The abscissa in Fig. 14 is the Strouhal number $\mathrm{St}=f d / u_{d,th}$, where f is the physical frequency in Hertz, d the diameter of the horizontal bar and $u_{d,th}$ the velocity at the center of the horizontal bar in the Blasius boundary layer. This type of non-dimensionalization enables a comparison with the literature. In the spectrum for $x/k=140$, there is a region of increased PSD between $0.1 \le \mathrm{St} \le 0.16$ and again at its higher harmonics. At low frequencies, the PSD increases naturally with another peak at $\mathrm{St}=0.011$, which is in the range of Tollmien–Schlichting waves for the present Reynolds number and streamwise location. For $x/k=160$, Tollmien–Schlichting-like disturbances contribute even more energy to the spectrum. These Tollmien–Schlichting waves can also be seen in temporal space in Fig. 13 and are another reason for the rise and fall of the fluctuation rms in Fig. 12.

Returning to Fig. 14, the curve for $x/k=200$ does not contain a clear peak but rather exhibits distributed high values of PSD. Again, this is a strong indication for random, turbulent motions within parts of the signal. This result substantiates the observation from Fig. 13. The spectrum for $x/k=300$ contains the smallest values of PSD compared to the other curves. No frequency peaks appear in this case. The flow becomes less energetic throughout the spectrum, which can be explained by the settling of turbulent events.

Fig. 14

Power spectral density (PSD) of streamwise velocity disturbances $u'$ at three stations x/k as described in legend

Vortex shedding behind the bar can be predicted by modeling a 2D cylinder in uniform crossflow. The dominant Strouhal number can be estimated with the empirical formula by Fey et al. (1998) using the diameter-based Reynolds number $\mathrm{Re}_d$:

$$\begin{aligned} \mathrm{St} = 0.2684-\frac{1.0356}{\sqrt{\mathrm{Re}_d}}. \end{aligned}$$

(7)

The Reynolds number provided in table 1 yields a Strouhal number of $\mathrm{St}=0.12$ for Case I. This result matches perfectly to the frequency peak of Case I in Fig. 14. Although Eq. (7) does not take the velocity gradients of the physical flow into consideration, it can be inferred that the horizontal bar induces vortices in the boundary layer.

This result can be substantiated with the flow visualization in Fig. 15. Potassium permanganate crystals were placed in the near wake of the roughness where they do not disturb the flow significantly. The parameters of this visualization are the same as in Case I. As the crystals dissolve in water, dye streaklines are drawn into the boundary layer. Due to the higher density of water compared to air, the mean free path length in water is much smaller than in air, leading to less diffusion. Therefore, dye streaklines persist for a much longer distance than smoke in air (Strunz 1987). The magenta dye streaklines in Fig. 15 reveal unsteady structures in the wake of the horizontal bar. These structures are aligned in the spanwise direction. The unsteadiness is formed in the near wake of the bar and dissipates viscously further downstream of the bar. This unsteady observation helps to understand the measurement in Fig. 14 and visualizes the Strouhal behavior predicted by Eq. (7).

Fig. 15

Experimental visualization of unsteady flow downstream of horizontal bar (Case I) visualized by dye streaklines from potassium permanganate crystals

3.3.3 Linear stability theory

Linear stability theory allows to determine the fate of an infinitesimal disturbance through linearized equations. Here, temporal theory has been performed, i.e., the wavenumber $\alpha$ is real, whereas the frequency $\omega = \omega _r + i \omega _i$ is complex. The imaginary part of the frequency $\omega _i$ can be understood as the growth rate: if $\omega _i<0$, the flow is linearly stable and it is unstable if $\omega _i>0$. Results from temporal theory can be converted into spatial theory with Gaster’s transformation (Gaster 1962). This is particularly useful for comparisons to experiments (White 2006).

Figure 16 is a result of a temporal computation combined with Gaster’s transformation. It shows the linear stability diagram in the near wake of the horizontal bar. Negative values of $\alpha _i$ indicate linear instability, and positive values represent stable eigenvalues. Combining $\omega _r=2 \pi f k / U_e$ with the definition of the Strouhal number yields the conversion identity

$$\begin{aligned} \omega _r = 2 \pi \frac{\bar{u_d}}{U_e} \frac{k}{d} \mathrm{St} = 2 \pi \frac{\mathrm{Re}_d}{\mathrm{Re}_k} \left( \frac{k}{d}\right) ^2 \mathrm{St} \end{aligned}$$

(8)

which allows to compare the experimental observations in Fig. 14 with LST in Fig. 16. The range of vortex shedding in the experiment was $0.1 \le \mathrm{St} \le 0.16$ in Fig. 14, which equals to $2.3 \le \omega _r \le 3.6$ in LST. This range compares very well to the most unstable frequencies in Fig. 16. Linear stability theory is therefore able to predict the experimentally observed vortex shedding accurately. It can also be inferred from Fig. 16 that the origin of the instabilities is very close to the roughness between $x/k=130$ and 133 and slowly vanishes further downstream. Furthermore, the low-frequency instability region below $\omega _r=1$ is qualitatively in agreement with the frequency peaks at $\mathrm{St}=0.011$ ($\omega _r = 0.25$) in Fig. 14. For the sake of completeness, it needs to be mentioned that, strictly speaking, bi-local theory loses validity when the flow is nonparallel (Huerre and Monkewitz 1990; Chomaz 2005). For this reason, Fig. 16 is to be read with care despite the good agreement with the experiment. In the following analyses, LST is performed further downstream in quasi-parallel flow where the 2D assumption is more valid.

Fig. 16

Stability diagram for Case I

Temporal theory is applied to a yz-slice at $x/k=170$ in Case I and Case III to investigate whether or not the streak reduction is able to reduce instabilities. The two most unstable modes from the stability spectrum are investigated with a procedure suggested by Piot et al. (2008) and Siconolfi et al. (2015). An artificial velocity field $\mathbf {U}$ is created as a linear combination of the velocity field without horizontal bar $\mathbf {U}_\mathrm{ref}$ and with horizontal bar $\mathbf {U}_\mathrm{bar}$. The combination is then created as

$$\begin{aligned} \mathbf {U} = \mathbf {U}_\mathrm{ref} + \gamma (\mathbf {U}_\mathrm{bar} - \mathbf {U}_\mathrm{ref}) \end{aligned}$$

(9)

with a control parameter $\gamma \in [0,1]$. The velocity field $\mathbf {U}$ is physically not meaningful except for $\gamma =0$ (reference) and $\gamma =1$ (with bar). It can be imagined as a continuous changeover from $\mathbf {U}_\mathrm{ref}$ to $\mathbf {U}_\mathrm{bar}$. As a result, the modes in the linear stability spectrum will move in trajectories as the base flow changes from $\mathbf {U}_\mathrm{ref}$ to $\mathbf {U}_\mathrm{bar}$.

The outcome of this procedure is shown in Fig. 17 (left) for the two most unstable modes of Case I. As will be shown later, one mode is symmetric (varicose) and the other is antisymmetric (sinuous) with respect to the spanwise center. Without horizontal bar ($\gamma =0$), both varicose and sinuous modes are linearly stable close to neutral stability. Most other modes in the spectrum are located in the lower part of the diagram (not shown). As the effect of the horizontal bar becomes stronger ($\gamma \ge 0$), the varicose mode travels to the upper half of the complex plane, whereas the sinuous mode descents to the lower part of the plane, thus becoming more stable.

The same technique is shown in Fig. 17 (right) for Case III. This case is identical to Case I except for a higher Reynolds number $\mathrm{Re}_k=700$. The purpose of this additional case is to determine whether the horizontal bar is able to stabilize the sinuous mode. Indeed, the sinuous mode is highly unstable in the reference case without bar ($\gamma =0$) and stabilizes with horizontal bar ($\gamma =1$). The varicose mode behaves similar to Case I in Fig. 17 (left).

Fig. 17

Least stable modes in linear stability spectrum as a function of $\gamma$ for (left) Case I and (right) Case III at $x/k=170$

Figure 18 illustrates the varicose mode of Case III without horizontal bar ($\gamma =0$) and with horizontal bar ($\gamma =1$). The data of this case originate from the same analysis as in Fig. 17. The base flow in Fig. 18, indicated by solid black lines, is strongly affected by the presence of the horizontal bar. Spanwise gradients are weaker at the cost of a slower velocity in major parts of the boundary layer. The mode shape changes significantly but is symmetric both without and with the horizontal bar.

Fig. 18

Real part of eigenvector at $x/k=170$ for varicose mode of Case III. Left: $\gamma =0$, right: $\gamma =1$

The dominant sinuous mode of the same case is presented in Fig. 19. It is interesting to see that the change of spanwise gradients from $\gamma =0$ to 1 reduces the extent of the color patches in Fig. 19 (right). Furthermore, small patches of opposite sign are created close to $z=0$. The energy of the mode may thus be split into more zones with opposite sign, which may further hinder a physical sinuous oscillation to ignite. This conclusion will, however, remain a hypothesis, because the experimental detection of sinuous instabilities at high Reynolds numbers is often overshadowed by varicose instabilities from the roughness (Bucci 2017).

Fig. 19

Real part of eigenvector at $x/k=170$ for sinuous mode of Case III. Left: $\gamma =0$, right: $\gamma =1$

3.3.4 Final remarks

The present study explores how boundary-layer streaks can be successfully damped, reduced or stabilized and further shows that the linear stability can be improved with respect to the sinuous mode. There are also adverse effects when applying this method. First, the horizontal bar leads to additional drag. Second, the drag of the bar leads to an increase in the boundary layer thickness which supports the growth of instability modes, in particular those of varicose type. Therefore, this method is recommended in flows where high streak amplitudes and sinuous instabilities are not desired. Environments with high freestream-turbulence seem appropriate for this method. These can be found for instance in the atmospheric boundary layer, turbine engines, wind turbines, process engineering or other applications in mechanical engineering. In future, it will be interesting to see if this method can also be used to delay laminar-to-turbulent transition.

4 Conclusions

In this investigation, a method is proposed to reduce streamwise streaks in the laminar boundary layer. The streaks are created by a spanwise array of cylindrical roughness elements. Further downstream, the streaks are homogenized by a horizontal bar that is aligned in the spanwise direction at a defined distance to the wall. Three cases have been investigated and compared to a reference without the horizontal bar. Both experiments and numerical simulations show that the streak amplitude is reduced successfully by the horizontal bar. The strongest effect can be achieved in a case when the bar is placed close to the maximum streak amplitude without the bar. The reduction in the streak amplitude is approximately 32 % in this case. Depending on the case, the Reynolds number of the bar is either above or below the ’critical’ threshold to vortex shedding. A stronger homogenization effect is observed beyond the critical threshold, however, Tollmien–Schlichting-wave-like disturbances and intermittent turbulence in parts of the measurement signals were also observed. Interestingly, the intermittent turbulence is not able to sustain itself when the flow relaxes and fades away further downstream.

Linear stability analyses have been performed and reveal that the sinuous mode, which is often considered most harmful in streaky flows, is reduced in one case and even stabilized in another case. On the contrary, the varicose instability becomes more unstable with the horizontal bar. This can be explained by the growth of the boundary-layer displacement thickness when the horizontal bar is installed. Overall, the presented method can reduce the streak amplitude in different conditions and stabilize the sinuous linear mode while destabilizing the varicose mode. In a follow-up investigation, it is to be shown that this method can delay streak-induced laminar-to-turbulent transition.

Appendices

Appendix 1: Hot-film calibration

The calibration of the hot-film probe is done prior to each experiment by traversing the probe through resting water in velocity increments of 0.005 ms$^{-1}$. The result of such a calibration is shown in Fig. 20. A correlation between traverse velocity U and probe voltage E can be obtained by nonlinear regression with King’s law $E = (A + BU^C)^{0.5}$ to determine the calibration coefficients A, B and C (King 1914). The proof-of-concept of this calibration method at the Laminar Water Channel was published in Subasi et al. (2015). When the calibration coefficients are known, the equation can be used inversely to calculate the velocity u of a flow from a given voltage E, see Puckert (2019).

The calibration of the hot-film in resting water is a special procedure and has been introduced at this facility after several attempts to calibrate against hydrogen bubble visualizations (see Fig. 21) and ultrasonic velocity measurements with equipment particularly suitable for low velocities. Note that the dynamic pressure is not sufficient to use a standard pitot pressure system for the calibration like in wind tunnels. A special arrangement with a high-precision scale is another solution to this problem that has been used earlier.

Fig. 20

Calibration of hot-film probe

Appendix 2: Uncertainty analysis

In the following analysis, a statistical evaluation of random errors and an estimation of systematic errors is performed to provide the uncertainty of the experiments.

The random error of a single measurement can be quantified by the standard deviation (Gränicher 1994)

$$\begin{aligned} \sigma _{} = \sqrt{ \frac{1}{n-1}\sum _{i=1}^{n} (x_{i} -{\bar{x}})^2 } \end{aligned}$$

(10)

with sample $x_i$, number of samples n and mean quantity ${\bar{x}}$. In contrast to the standard deviation of the mean for statistically independent quantities, this definition is a good indication for the degree of disturbances in a flow. Note that the standard deviation of the mean would yield a random error close to zero due to the high number of samples resulting from a long measurement duration. For the combined quantity $A_\mathrm{st}$ in Eq. (3), random error is propagated.

More importantly, the experiment is subject to systematic errors. In particular, the boundary layer edge velocity $U_e$ may deviate from the target value. This error may originate from the probe calibration, temperature effects, probe corrosion or other unknown factors. As already shown in Puckert (2019), a practical way to estimate the combination of these errors is by comparison with another method. Here, hydrogen bubble visualizations are used. The velocity is found by carefully introducing timelines at a given frequency, measure their distance and then calculate $U_e$ as distance divided by time. This method has also been used and described in detail by Shin (2014). Figure 21 compares the results of both methods. The deviation can be calculated with Eq. (10) and yields a systematic error estimate of $\sigma _{U_e} = 0.0013\,\text {ms}^{-1}$.

Fig. 21

Comparison of hot-film (CTA) and hydrogen bubble method (Puckert 2019)

Another source of systematic error is inaccurate knowledge of the Reynolds number, which depends on $U_e$, k and $\nu$. Taking into account manufacturing errors and possible dirt between the roughness and the flat plate, an estimate of the roughness-height error is $\sigma _k = 5\times 10^{-5}$ m. The kinematic viscosity of water is a function of the temperature, which is directly measured prior to the experiments with a mercury thermometer. The resulting error, including a factor of 1.5 for reading errors of the mercury thermometer and deviations from ideal water properties, is $\sigma _{\nu }=3\times 10^{-9}$ m$^2$s$^{-1}$. It was shown by Puckert (2019), appendix B, that the combination of $\sigma _k$ and $\sigma _{\nu }$ adds approximately the same uncertainty to the Reynolds number as $\sigma _{U_e}$. It is thus reasonable to estimate the overall systematic error as $2\, \sigma _{U_e} = 0.0026\,\text {ms}^{-1}$.

Both systematic and random errors contribute to the measurement uncertainty and can be added geometrically (Travoularis 2005):

$$\begin{aligned} \sigma _{{\bar{u}}/U_e}= & {} \sqrt{ \left( \sigma _{{\bar{u}}, \mathrm{rand}} \right) ^2 + \left( 2\sigma _{U_e} \right) ^2 } \quad \text {and} \end{aligned}$$

(11)

$$\begin{aligned} \sigma _{A_\mathrm{st}}= & {} \sqrt{ \left( \sigma _{A_\mathrm{st}, \mathrm{rand}} \right) ^2 + \left( 2\sigma _{U_e} \right) ^2}. \end{aligned}$$

(12)

The respective uncertainties are added in Figs. 8 and 9 to provide the reader an estimate of possible errors.