Laboratory investigations on the resonant feature of ‘dead water’ phenomenon

Abstract

Interfacial internal wave excitation in the wake of towed ships is studied experimentally in a quasi-two-layer fluid. At a critical ‘resonant’ towing velocity, whose value depends on the structure of the vertical density profile, the amplitude of the internal wave train following the ship reaches a maximum, in unison with the development of a drag force acting on the vessel, known in the maritime literature as ‘dead water’. The amplitudes and wavelengths of the emerging internal waves are evaluated for various ship speeds, ship lengths and stratification profiles. The results are compared to linear two- and three-layer theories of freely propagating waves and lee waves. We find that despite the fact that the observed internal waves can have considerable amplitudes, linear theories can still provide a surprisingly adequate description of subcritical-to-supercritical transition and the associated amplification of internal waves. We argue that the latter can be interpreted as a coalescence of frequencies of two fundamental stable wave motions, namely lee waves and propagating interfacial wave modes.

Graphic abstract

1 Introduction

When a ship is traveling through a strongly stratified water body, a certain amount of its kinetic energy is being used up for the excitation of internal waves in its wake, hardly noticeable from the surface, yet perceived as a drag force acting on the vessel. For centuries, the phenomenon has been known to Norwegian seamen as “dödvand” or dead water. In the fjords of the Scandinavian coastline, freshwater from slow glacier runoff gently sets on top of the saline seawater without substantial mixing and hence nearly jump-wise vertical density profiles can develop (Parsmar and Stigebrandt (1997)). These circumstances facilitate particularly strong dead water effect associated with large-amplitude wave activity along the internal density interface (pycnocline).

In the logbook of the 1893–1996 Norwegian Polar Expedition Arctic explorer, Fridtjöf Nansen reported experiencing marked dead water drag on board research vessel Fram that reduced the ship’s speed to a fifth part. Nansen’s original observations were further analyzed by (the then-PhD student) Ekman, who, to understand the phenomenon, has conducted laboratory experiments in a quasi-two-dimensional wave tank, filled up with a two-layer working fluid consisting of saline- and freshwater. In these measurements, a scale model of Fram was towed along the surface subjected to either constant or gradually changing force as control parameter, against which the model’s velocity U was measured (Ekman 1904). Ekman found that for smaller towing forces (and smaller U) dead water drag $F_{\mathrm{{dw}}}$ follows a quadratic scaling $F_{\mathrm{{dw}}} \approx \zeta U^2$ up to a certain threshold, where coefficient $\zeta$ is a function of the density profile $\rho (z)$ and the wetted area of the ship.

Fig. 1

Hysteresis of ship speed—as observed and discussed by Ekman in his original work—illustrated graphically as a function of changing towing force (decreasing branch: blue, increasing branch: red). The unstable branch is marked with a dashed line. The green curve represents the (inverse of) subcritical relationship $F_{\mathrm{{dw}}} \approx \zeta U^2$

However, when U reaches a critical value of $U\approx 0.8 \cdot c_0^{(2)}$, where $c_0^{(2)}$ denotes the long-wave velocity of interfacial waves on the pycnocline (to be discussed later) the corresponding $F_{\mathrm{{dw}}}$ starts to decrease significantly. At this domain, where the Froude number $Fr \equiv U/c_0^{(2)}$ is in the range of $0.8-1$, the drag acting on the ship reaches a maximum, coincidentally with the excitation of interfacial waves of the largest amplitude along the pycnocline.

Then in Ekman’s “changing force”-type experiments, a hysteresis was encountered, as sketched in Fig. 1. When the gradually increasing towing force reached a certain tipping point (the right end of the red branch in Fig. 1), the speed of the ship suddenly jumped to a higher value. An analogous drop of U could be observed when decreasing the towing force in time (blue branch of Fig. 1). The unstable branch (dashed line) is inaccessible to the system for any prescribed towing force. When initiating experiments with a constant force within this hysteretic regime, Ekman found that the ship’s velocity U exhibited large fluctuations, comparable to the mean value (Ekman 1904).

If one intends to explore the dynamics in this unstable branch it is, therefore, beneficial to conduct experiments in which, instead of the applied force, the towing velocity U is prescribed. Such settings are common in the laboratory modeling of lee-wave dynamics (see, e.g., Eiff and Bonneton 2000; Knigge et al. 2010; Gyure et al. 2003; Vosper et al. 1999), where obstacles of various shapes are being towed at the surface (or at the bottom) in a tank of stratified working fluid and the properties of the generated internal waves, hydraulic jumps and ‘wave rotors’ are evaluated (Vosper 2004; Sachsperger et al. 2015, 2017).

In the present experimental work, we follow a similar approach to address the dead water phenomenon, by pulling a ship model at a constant speed and—instead of the experienced drag—analyzing the properties of the excited interfacial waves on the pycnocline. Here the ‘critical regime’ is characterized by wave patterns whose vertical extent is comparable to the height of the upper layer. The fact that wave amplitudes show strong dependence on the wave velocity (that is set by ship speed U) implies that the waves are of nonlinear nature (Yuan et al. 2007). Even for velocities where no wave trains are observed, the localized bump following the ship at the pycnocline resembles the solitary wave solutions of the nonlinear Korteweg–de Vries equation (Apel 2003; Boschan et al. 2012).

A large pool of theoretical, numerical and experimental studies exists discussing the properties of internal waves emerging in the dead water problem addressing nonlinear wave excitation both in the subcritical (Grue 2015; Johnson and Vilenski 2004; Lacaze et al. 2013) and supercritical (Grue et al. 2016; Robey 1997) regimes, as well as the applicability of the theoretical findings to observational data, including the historical logs of Fram (Grue 2018).

The aforementioned characteristic feature of dead water phenomenon that internal wave drag (and amplitude) exhibits a peak at around $Fr \approx 0.8-1$ can already be explained in linearized finite-depth two-layer theories, as shown by, e.g., (Miloh et al. 1993; Yeung and Nguyen 1999). Despite of the obvious nonlinearity of the problem, as far as the large-amplitude interfacial wave forms are concerned when this peak is encountered, the effect of nonlinear corrections is often found to be surprisingly minor in this respect (see, e.g., Fig. 5 of Grue et al. 2016).

In a series of earlier laboratory experiments on topography-induced large-amplitude interfacial waves (Vincze and Bozoki 2017), we have also demonstrated that linear three-layer theories, e.g., the one of Fructus and Grue (2004) may yield remarkably good fits to experimental data. Therefore, in the present work, we focus on the applicability of linear theories to the dead water phenomenon in similarly stratified settings. Our aim here is to explore the U-dependence of the wavelength and amplitude of internal waves in the wake and contrast the results with predictions of the linear theory for lee waves and for freely propagating three-layer interfacial waves. These measurements supplement the ‘constant force’ experiments of Mercier et al. (2011) who have conducted state-of-the-art measurements with a prescribed towing force (utilizing a falling weight) to propel a ship model in a rather similar setup. It is to be emphasized that the difference between the ‘constant force’ and ‘constant velocity’ settings may be a crucial issue from the maritime applicability point of view (ships are driven at constant power usually), but is not an essential difference in the framework of the present study.

The main finding to be reported here is that the largest interfacial wave amplitudes emerge when the typical wavelength of the freely propagating interfacial wake waves (whose velocity is set by the speed of the ship model) is equal to the wavelength associated with ‘trapped’ lee waves (whose frequency is determined by the buoyancy frequency of the density profile) and thus a coalescence of frequencies and wave numbers develops between these two fundamental co-existing wave motions. Similar resonance-like amplification involving, e.g., vorticity waves and internal gravity waves has already been reported in stratified systems, see, e.g., (Carpenter et al. 2011). Yet, to the best of our knowledge, the present work is the first to interpret the problem of dead water phenomenon in this framework.

The paper is organized as follows. Section 2 describes the experimental setup and the applied data acquisition methods. Our results are presented in Sect. 3. The paper is then concluded with a brief discussion of the findings in Sect. 4.

2 Experimental setup and measurement methods

Fig. 2

The schematics of the setup. The geometrical parameters of the tank are $L=239$ cm (total length, not fully shown), $w = 8.8$ cm, and $H = 12$ cm

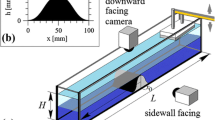
The experiments reported here have been carried out in a rectangular laboratory tank made of transparent plexiglass. Its length and width are $L = 239$ cm and $w = 8.8$ cm, respectively (see Fig. 2). The tank was filled up to level $H = 12$ cm with density-stratified water: the bottom domain contained saline water solution colored by red or blue food dye for the sake of visualization. Following the preparation of this layer, freshwater was poured through a sponge slowly onto the water surface to minimize mixing effects and to yield quasi-two-layer density profiles, characterized by an approximately 2-cm-thick region of steep density increase (see Fig. 3) or ‘gradient layer’. The temperature differences within the water body were negligible.

Fig. 3

Vertical density profiles of the experiments as measured with a conductivity probe. Three configurations of two-layer thicknesses were prepared with various bottom layer densities, as shown in the three panels (the dashed lines mark the theoretical interfaces of the two-layer approximation.) a $h_1^{(2)} = 7$ cm, $h_2^{(2)} = 5$ cm; b $h_1^{(2)} = 3$ cm, $h_2^{(2)} = 3$ cm; c $h_1^{(2)} = 5$ cm, $h_2^{(2)} = 7$ cm. The middle layer thicknesses $h_2^{(3)}$ of the three-layer approximations for the same profiles are also indicated by yellow coloring (cf. Table 1)

The properties of the 11 different stratification profiles are summarized in Table 1. $h_1^{(2)}$ and $h_2^{(2)}$ mark the effective thicknesses of the upper and bottom layers, respectively, using the two-layer approximation [hence, the upper index ‘(2)’], i.e., assigning a jump-wise effective density change to the mid-height of the gradient zone. As a characteristic vertical scale in the system a ‘reduced thickness’ $H_r$ can be introduced as the harmonic mean of $h_1^{(2)}$ and $h_2^{(2)}$, i.e., $H_r= \left( h_1^{(2)} h_2^{(2)})/ (h_1^{(2)}+ h_2^{(2)}\right)$. Table 1 also lists the values of the average density $\rho _2$ of the bottom layer and the corresponding two-layer linear interfacial wave velocity $c_0^{(2)}$ in the long-wave limit that reads as

$$\begin{aligned} c_0^{(2)}=\sqrt{g \frac{\rho _2-\rho _1}{\rho _1} H_r}, \end{aligned}$$

(1)

where g denotes the gravitational acceleration and $\rho _1 \approx 1$ kg/l is the average density in the top (freshwater) layer (Sutherland 2010).

For a more precise treatment of the density profiles, a three-layer approximation can also be applied (Fructus and Grue 2004), in which the top, gradient and bottom layers (indexed with $j = 1,2,3$, respectively) are characterized by their approximate thicknesses $h_j^{(3)}$ and density gradients, or equivalently, their buoyancy (or, Brunt–Väisälä) frequencies $N_j$ that take the form

$$\begin{aligned} N_j\equiv \sqrt{-\frac{g}{\rho _0} \frac{\mathrm{{d}}\rho }{\mathrm{{d}}z}\Big |_j}. \end{aligned}$$

(2)

The values of $h_j^{(3)}$ and $N_j$ are obtained via piecewise linear regression to a given profile by determining the intersection points and slopes of the fitted lines. In the three-layer theory of Fructus and Grue (2004) for ‘piecewise linear’ stratification, there is no such an explicit formula for the long-wave velocities $c_0^{(3)}$ as in the two-layer approximation (1), as will be addressed later. Hence, the $c_0^{(3)}$-values in Table 1 are numerical results.

Table 1 Geometrical and physical parameters of the experiments for the two- and three-layer approximations (above and below the double line, respectively)

Table 2 The lengths of the used ship configurations

To capture dead water phenomenon, we investigated the interfacial internal wave excitation behind towed $\mathrm{{LEGO}}^{\mathrm{{TM}}}$ ‘tug boat’ models (series 4005 and 4025) (1982). These toy ships have a modular design of a bow and a stern building block and four removable identical intermediate segments. Thus, five configurations ($S_1$–$S_5$) with different lengths d could be investigated, as listed in Table 2 and shown in Fig. 4. The width of the models was 5.9 cm, comparable to tank width w. The ship model was towed by a (nylon) fishing line spanned horizontally above the water surface by ca. 10 cm, as sketched in Fig. 2, and driven by a DC motor whose voltage (and hence, the towing speed) could be adjusted between the experiment runs. The ship models’ draught (i.e., the vertical distance between the waterline and the bottom of the hull) was found to be approximately 1 cm in all cases. It is to be noted that in such a narrow tank, the flow is practically two dimensional; therefore, we did not (and could not) investigate the three-dimensional structure of the wake.

Fig. 4

The five different ship configurations of increasing length d, marked S1–S5 (downward. cf. Table 2). The bottom layer is visualized using red food dye. The snapshots are organized such that the first wave trough locations behind the ship models are underneath each other

Each experiment was recorded with a HD video camera (at frame rate 50 fps and frame size $720\;\mathrm {px}\times 1280\;\mathrm {px}$) pointing perpendicularly to the sidewall close to the middle of the tank, yielding a spatial resolution of ca. 0.5 mm. To acquire the precise value of ship velocity U and to obtain time series of vertical motion of the interface, the video recordings were evaluated by Tracker, an open-source correlation-based feature tracking software (http://physlets.org/tracker/).

3 Results

3.1 Qualitative description of the flow

As a ship model moves along the tank in the studied velocity range $U\in (1.3 ; 12.2)$ cm/s, it generates pronounced waves on the internal interface, while the displacement of the free water surface remains negligible, as visible in Fig. 4. An important property of the observed dynamics is that the internal waves are following the ship and propagate at the same velocity as the ship itself. This is visualized in the space-time plots of Fig. 5 for three different constant towing speeds U (see caption). In these diagrams, the shading of a point at horizontal position x and time t is given by the sum darkness (i.e., number of black pixels in grayscale-converted frames) of the pixel column at x as calculated from the video frame at time t, e.g., the ones shown in Fig. 4. The interface displacement at each time instant is obtained via subtracting the aforementioned sum darkness from its initial value at rest (obtained before the towing has started) at the given position x. As the background of the tank is stationary throughout the videos, the spatial and temporal changes in darkness are attributed to internal waves. The trajectory of the bow of the ship is highlighted with solid black line in each panel.

Fig. 5

Space-time plots of interfacial wave propagation behind the ship model. (Stratification profile #11, ship configuration S2.) The towing speeds are $U = 4.40$ cm/s (a) $U = 4.82$ cm/s (b) $U = 6.31$ cm/s (c). Horizontal position x and time t are measured from the left edge of the image and from the start of the ship motion, respectively. The coloring in each panel is normalized to the respective minimum and maximum values; thus, amplitudes of the different cases cannot be compared to each other. The black lines represent the trajectories of the bow of the ship. The dark vertical lines are position markers on the tank itself, cf. Fig. 4

The typical wavelength $\lambda$ and the characteristic amplitude A of the internal waves are set by the towing speed U, the density profile $\rho (z)$, and the ship’s length d. The A(U) dependence is far from monotonous: for each stratification, there exists an intermediate velocity $U^*$ at which internal waves of the largest amplitude develop. This ‘resonant’ amplification is demonstrated with the video frames in Fig. 6 for three values of towing velocity U, listed on the panels (stratification #11, ship configuration S2). The snapshots are aligned such that the largest displacements of the density interface (marked with black vertical lines) are beneath each other for better comparability. The ship model’s direction of motion is leftward in all images.

Fig. 6

Interfacial wave excitation behind ship model S2 for different towing velocities U at stratification profile #11. The snapshots are organized such that the first wave trough locations behind the ship models, marked by black vertical lines, are underneath each other. The wave amplitude is largest at $U^*=5.3$ cm/s

At the smallest U (uppermost panel), a wave crest appears at the interface beneath the ship model. For larger Us, a train of waves form (cf. Fig. 5) and the first crest shifts towards the stern of the ship, while the characteristic horizontal size (peak-to-peak wavelength $\lambda$) of the interfacial disturbance increases. Coincidentally, its vertical size (or, amplitude A) also increases and reaches a maximum at $U^*$, as captured in the second panel of Fig. 6. In the $U>U^*$ regime, wavelength $\lambda (U)$ continues to increase, but amplitude A(U) starts to decrease, as seen in the two bottom panels in Fig. 6. In the following subsection, we explore the parameter dependence of $U^*$ and the associated internal wave dynamics.

3.2 Parameter dependence of the critical towing speed

The observed maximum vertical interface displacements A (hereafter referred to as amplitudes) against towing speed U are shown in Fig. 7a for four exemplary experiment series. The symbols correspond to different stratification profiles (namely #5, #8, #9, and #10, see legend and cf. Table 1 and Fig. 3). All four series were conducted using ship configuration S2 ($d = 16.2$ cm) and were selected for demonstrational purposes. The error bars represent the spatial resolution of the analyzed video records.

Apparently, critical towing speed $U^*$ markedly depends on the properties of density profile $\rho (z)$ with values ranging between 2.1 and 9.1 cm/s. Based on earlier results (Miloh et al. 1993; Motygin and Kuznetsov 1997), the relevant nondimensional velocity scale of the dead water problem is the internal Froude number Fr, i.e., the ratio of the ship speed U and the two-layer long-wave velocity $c_0^{(2)}$.

$U^*$ indeed scales linearly with $c_0^{(2)}$ as confirmed by the scatter plot of Fig. 7b. Here each data point represents the towing velocity maximizing amplitude A in the given series of experiments (the different symbols indicate the various ship configurations used, as indicated in the legend). The dashed line shows the linear fit of $U^* = 0.80\;(\pm 0.01)\,c_0^{(2)}$ to all data points.

Thus, Froude number $Fr \equiv U/c_0^{(2)}$ indeed appears to be an important parameter of the dynamics. However, as will be addressed in what follows, other physical parameters of the stratification profiles and even ship length d affect the occurrence of maximum interfacial wave amplitudes.

Fig. 7

a Interfacial wave amplitudes A as a function of towing velocity $c_0^{(2)}$ for exemplary stratification profiles #5, #8, #9, and #10 (cf. Table 1) obtained with ship configuration S2. b Critical towing speed $U^*$ as a function of two-layer long-wave velocity $c_0^{(2)}$. The different symbols denote different ship configurations (see legend). Error bars represent the sampling of the towing velocities. The dashed line shows the linear fit $U^* = 0.8 c_0^{(2)}$

3.3 Comparison with linear two- and three-layer theories

Here we compare the observed wave (and ship) speeds U and wave numbers k to the available theoretical predictions of linear two- and three-layer theories.

Assuming two homogeneous water layers of different densities separated by a sharp interface, the phase velocity reads as

$$\begin{aligned} c^{(2)}(k)=\sqrt{\frac{g}{k}\frac{\rho _2-\rho _1}{\rho _1\coth (h^{(2)}_1k) +\rho _2\coth (h^{(2)}_2k)}}, \end{aligned}$$

(3)

where the notations are as introduced in Sect. 2 (Pedlosky 2013). In the long-wave ($k \rightarrow 0$) limit, the relationship takes the form of equation (1); therefore, $c^{(2)}(0) \equiv c_0^{(2)}$. Expressing the velocities and wave numbers in the problem’s ‘natural’ nondimensional units, i.e., $U/c_0^{(2)}$ and $kH_r$ (hereafter referred to as $k'$), respectively, maps equation (3) to the same curve for all two-layer density profiles. This graph is shown with blue solid line in Fig. 8, alongside the measured data points. The symbol shapes mark different ship configurations (see legend) and the coloring represents nondimensional wave amplitude $A'$, i.e., the maximum vertical displacement A of the interface divided by the parameter a of the fitted resonance curve of the given ship configuration (cf. Fig. 7). $k'$ was calculated via measuring peak-to-peak wavelengths $\lambda = 2\pi /k$ between the second and third wave troughs. Note, that this method yields a considerable smaller value of $\lambda$ than the typical length of the first wave trough (cf. Fig. 5). Runs where no wave train developed were omitted from this analysis.

The linear two-layer theory systematically overestimates the wave speeds for larger values of $k'$; as the wavelength becomes comparable to the thickness of the pycnocline, the two-layer approximation—assuming step function-like density profiles—is not sufficient anymore. Interestingly, however, the best agreement between the data and the theory (in the $k' \approx 0.5$ domain) is observed at near-resonant wave speeds, i.e., where wave amplitudes $A'$ are large (see Fig. 8).

For larger towing speeds ($U/c_0^{(2)}\gtrsim 0.8$), the observed wave numbers remain larger than the predictions of the two-layer theory and exhibit a roughly inversely proportional scaling $U/c_0^{(2)}\propto k'^{-1}$ (see the gray hyperbolic guide curves in Fig. 8) the implications of which will be discussed in Sect. 3.4.

Fig. 8

Nondimensional towing (wave) speeds $U/c_0^{(2)}$ as a function of nondimensional wave number $k'=kH_r$. The symbol shapes mark different ship configurations (see legend), and the color scale marks nondimensional amplitude $A'$, rescaled by the (polynomial-)fitted maximum values of the corresponding resonance curves (cf. Fig. 7). The blue curve represents the invariant (with respect to the nondimensional units used here) two-dimensional velocity–wave number relation (3), the red curve denotes an exemplary three-layer relation, obtained for the parameters of experiment #5, based on the implicit formula (4) of Fructus and Grue 2004. The gray curves represent two hyperbolae,i.e., ‘iso-frequency curves’ in the corresponding nondimensional time units, $y = 0.5/x$ and $y = 1/x$, respectively.

The linear three-layer theory described in Fructus and Grue (2004) has provided a quite accurate description of the observed interfacial velocities and wave numbers in flow-topography interaction experiments (Vincze and Bozoki 2017). This approximation assumes rigid top surface, small-amplitude waves, and three layers with depths $h_j^{(3)}$ ($j = 1,2,3$) and piecewise linear stratification characterized by buoyancy frequencies $N_j$ (see Eq. 2 and Table 1). This model was chosen for our analysis as the simplest one in the literature that can properly treat the aforementioned ‘non-step function-like’ property of the density profiles.

The dispersion relation $c^{(3)}(k)$ can be derived numerically from the implicit equation

$$\begin{aligned} K_2^2-T_1 T_2 - T_1 T_3 - T_2 T_3 = 0, \end{aligned}$$

(4)

where $K_j = \sqrt{N_j^2/(c^{(3)})^2-k^2}$ is the vertical wave number in layer j and $T_j = K_j \cot (K_j h^{(3)}_j)$. The maximum wave speeds $c^{(3)}_0$ listed in Table 1 corresponding to the long-wave ($k\rightarrow 0$) limit are also derived numerically from the above formulae.

To demonstrate the difference between the predictions of the two- and three-layer theories, the rescaled $c^{(3)}(k)$ curve calculated with the parameters of stratification profile #5 (see Table 1) is added to Fig. 8 in the form of a red curve. Note that unlike the aforementioned two-layer curve (blue), the three-layer one is not invariant at all in the units used here. For instance, in this exemplary case $c_0^{(3)}>c_0^{(2)}$ holds, but for many other profiles, the sign would be reversed (cf. Table 1). Therefore, the red curve in Fig. 8 should not be compared with all the data points in the plot (only to those that are obtained for stratification profile #5, not highlighted in the figure).

Instead, for a meaningful presentation of the two models’ performance, we plot the theoretical phase velocities of the two- and three-layer models against the measured wave speeds U for each observed wave number k in the correlation diagrams of Fig. 9a and b, respectively. In both panels, the theoretical long-wave velocity ($c_0^{(3)}$ or $c_0^{(2)}$) was used as the unit for nondimensionalization. Symbol shapes denote different ship configurations and the coloring represents rescaled amplitude $A'$ as in Fig. 8. It to be remarked that with the particular density profiles applied here, where $N_2 \gg N_1, N_3$ holds, a further simplification of the model would be possible by setting $N_1=N_3=0$. We found that in this case, the numerical results of $c^{(3)}(k)$ remain the same within $\pm 5\%$.

As noted before, the two-layer theory systematically overestimates the speeds in the $U/c_0^{(2)}\lesssim 0.8$ range (i.e., when $U\lesssim U^*$), thus the vast majority of the data points scatter above the $y = x$ line (black) in panel a. The three-layer theory, however, yields a fairly good match with the observations in the same subcritical regime. In the supercritical range, however, both two- and three-layer approximations break down entirely, as indicated by the deviation of the data points from the $y = x$ line, implying that here another physical mechanism becomes relevant in the wave number selection.

Fig. 9

Two-layer (a) and three-layer (b) theoretical velocities as a function of the measured towing (and wave) speed U. The symbol shapes mark different ship configurations (see legend), and the color scale marks nondimensional amplitude $A'$, rescaled by the (polynomial-)fitted maximum values of the corresponding resonance curves (cf. Fig. 7). The values on both the horizontal and vertical axes are rescaled with respect to the long-wave limit velocities of the respective approximation (two layers for a, three layers for b). The black solid curves represent the $y = x$ line

3.4 Lee-wave dynamics

A hyperbola in a velocity–wave number (c(k)) dispersion plot marks a constant frequency $\omega$ (since $c=\omega /k$). For the nondimensional parameters of Fig. 8 the hyperbolic guide curves represent identical frequencies with respect to the stratification-dependent time unit $\sqrt{H_\mathrm{{r}}\rho _1/(g(\rho _2-\rho _1))}$. Thus, the fact that the data points appear to follow hyperbolic scaling when $U > U^*$ implies that a characteristic frequency associated with the given density stratification $\rho (z)$ determines the observed wave numbers.

Fig. 10

Correlation plot between the intermediate layer buoyancy frequency $N_2$ and fitting parameter $\alpha$, obtained by regression to the U(k) plots in the $U>U^*$ velocity range. The different symbols and colors represent different ship configurations (see legend). The error bars denote the fit errors (standard deviations) of $\alpha$. The slope of the black linear function is 0.48

Such physically meaningful ‘eigenfrequencies’ are the buoyancy frequencies $N_j$ of the layers (see Table 1), among which the mid-layer value $N_2$ is the largest in all cases. Fitting the function $\alpha /k$ to the dimensional U(k) data in the $U>U^*$ (supercritical) range yields the empirical frequency parameter $\alpha$ that is plotted against $N_2$ in Fig. 10. The error bars represent the regression errors and, as before, the different symbols mark various ship configurations. The scattering of the data points indicate a linear relationship $\alpha = 0.48\;(\pm\;0.01)N_2$. The result of the fit is shown with a black solid line.

The simplest (linear) theory that describes fixed frequency wave propagation behind an obstacle in a stratified fluid is that of lee waves emerging at the downstream sides of mountain (or seamount) ridges (Sachsperger et al. 2015, 2017). If the system is characterized by a single buoyancy frequency N (linear stratification) and the obstacle is moving at velocity U with respect to the medium then $U = N \cos (\phi )/k_{\mathrm{{lee}}}$ holds (Pedlosky 2013), where $\phi$ is the tilt of the wave number vector $\mathbf {k}_{\mathrm{{lee}}}$ from the horizontal ($|\mathbf {k}_{\mathrm{{lee}}}|= k_{\mathrm{{lee}}}$). Thus, the maximum achievable $k_{\mathrm{{lee}}}$ becomes $k_{\mathrm{{lee}}}=N/U$, corresponding to fully horizontal wave propagation. [$(N/U)^2$ is referred to as ‘Scorer parameter’ in lee wave theory (Sachsperger et al. 2015).]

As mentioned above, buoyancy frequencies $N_1$ and $N_3$ of the top and bottom layers are small in the studied density profiles, thus any lee wave activity is expected to be confined to the roughly 2-cm-thick intermediate layer which would then act as a ‘waveguide’ (Vincze and Bozoki 2017) for the observed oscillation frequencies (i.e., above $N_1$ and $N_3$) at the interface. Since the layer thickness is an order of magnitude smaller than the typical wavelengths in the $U>U^*$ regime, $\mathbf {k}_{\mathrm{{lee}}}$ is nearly horizontal here ($\phi \approx 0$).

The linear scaling presented in Fig. 10 appears to be consistent with the proposition that it is indeed lee wave-like dynamics that is observed in the supercritical regime, but—due to the peculiarities of the stratification profile—not in its ‘classical’ form. As an empirical correction we may, therefore, introduce an effective buoyancy frequency $N_{\mathrm{{eff}}}\approx 0.48 N_2$ to characterize the stratification, whose possible physical interpretation will be addressed in Sect. 4.

Fig. 11

Critical wavelength $\lambda ^*$ (corresponding to the maximum amplitude) as a function of ship length d. The different symbols mark different stratifications. The slopes of the black and gray linear guidelines are 1 and 0.5, respectively

Finally, we investigated the critical wavelength $\lambda ^* (\equiv 2\pi /k^*)$ corresponding to the maximum amplitude as a function of ship length d. The results are shown in Fig. 11 for seven different stratification profiles, marked by different colors and symbols. The solid black line marks $y = x$ and the gray guides are linear functions with a slope of 0.5 and a vertical offsets 10 cm and 27 cm. Apparently, the critical wavelength tends to increase with ship length that roughly follows the empirical formula $\lambda ^*\approx 0.5 d + f(\rho (z))$, implying that the ship configuration also plays a role in the wave number selection.

4 Discussion and conclusions

Inspired by the historical work of Ekman analyzing the ‘dead water’ phenomenon (Ekman 1904), we have conducted laboratory experiments on wave excitation by a ship model towed at a fixed speed over a salinity stratified water body. We have analyzed the dependence of the interfacial wave number k and peak-to-peak amplitude A on the towing speed U, the stratification profile $\rho (z)$ and ship length d.

Due to the fact that in this setting the observed amplitudes are comparable to the characteristic vertical length scale $H_\mathrm{{r}}$ of the problem, the excited waveforms can only be explained, if at all, by means of nonlinear wave theories (see, e.g., Grue 2015; Grue et al. 2016). Yet, we deliberately focused our analysis on linear approximations to explore to what extent can these account for the basics of the observed dynamics, most notably the resonance-like amplitude amplification around $U/c_0^{(2)} = 0.8$ and the associated transition in terms of the U(k) dependence.

From the findings reported in the previous section it appears that the observable characteristic wave number k at a given U is set by the larger one of the corresponding three-layer wave number $k^{(3)}(U)$ predicted by the linear approximation of Fructus and Grue (2004) and the lee wave number $k_{\mathrm{{lee}}}(U)$ derived using ‘effective buoyancy frequency’ $N_{\mathrm{{eff}}}\approx 0.48 N_2$. In other words, among the two competing mechanisms, the one yielding shorter waves generates the first trough behind the ship model and, hence, sets the characteristic wavelength in the system. The crossing point of the two dispersion relations, where $k_{\mathrm{{lee}}} = k^{(3)}$ holds is encountered around the critical towing speed $U^*$, as sketched in Fig. 12. At this resonant wave number, the two wave types would be superimposed onto each other resulting in an amplified interfacial wave excitation, that is confirmed by the observations. As a secondary effect, the selection of the resonant wavelength $\lambda ^*$ was also found to be influenced by the length d of the ship, as shown in Fig. 11.

The reason for the occurrence of the aforementioned factor of 0.48 in the effective buoyancy frequency $N_{\mathrm{{eff}}}$ is unclear. Comparing this value to the internal wave dispersion relation $\omega =N_2 \cos (\phi )$ within the intermediate layer we find that it would imply a wave propagation whose lines of constant phase lie at an angle $\phi \approx 61 ^{\circ }$ to the vertical. However, we were not able to identify any geometrical constraint (e.g., one associated with the depression at the interface behind the ship) that would necessitate the presence of such a limiting angle.

On the other hand, taking the total bottom-to-surface density difference $\Delta \rho$ and assuming linear stratification along the full depth H gives a certain ‘mean buoyancy frequency’ $N_{\mathrm{{m}}}=\sqrt{g/\rho _1\,(\Delta \rho /H)}$ which is found to follow the average scaling $N_{\mathrm{{m}}}\approx 0.46 (\pm\, 0.04) N_2$ for the profiles listed in Table 1, which is fairly close to $N_{\mathrm{{eff}}}$. Thus, the explanation may be that for long waves whose wavelength $\lambda$ exceeds H, the otherwise complex three-layer profile can be simply ‘averaged over’ in terms of density gradients.

It is to be noted that the co-existence of boundary-trapped lee waves and internal waves (behind a step-shaped obstacle) has been investigated experimentally in Sutherland (2002); there, however, the two wave types were propagating in a rather different manner, as the internal wave modes could freely enter the top domain of the tank due to the continuous linear stratification applied. (In the present case, these wave modes are also restricted to the vicinity of the pycnocline.)

Our results clearly demonstrate the somewhat surprising and unexpected message that linear theories can occasionally be applied to the description of interfacial waves in such velocity and amplitude ranges that otherwise belong to the domain of nonlinear wave dynamics. Future research is in preparation to investigate the transient temporal characteristics of the dead water phenomenon via linear stability analyses, similar to the stratified plane-Couette problem, where also a prominent peak of wave amplitudes has been described in terms of Fr, see (Facchini et al. 2018). It is clear, however, that linear models are insufficient to describe more complex features of the observed phenomena, e.g., waveforms, vorticity, etc. The authors also hope to increase awareness in the community about the dead water phenomenon, which—despite being discovered over a century ago—is still an interesting ground for theoretical, numerical, and experimental research.

Fig. 12

The schematic wave number velocity diagrams of the lee waves (red curve), the three-layer model of Fructus and Grue (2004) (black), and the actually observable U(k) domain (green) set by the maximum of the two competing U(k) functions at each k. The intersection point $U^*(k^*)$ (black filled circle) fairly corresponds to maximum amplitude internal wave excitation