1 Introduction

Aircraft noise has been recognised as an issue since commercial airliners were powered by turbojet engines in the late 1940s. Lighthill provided a theoretical framework for the problem of aerodynamic sound and pioneered the multidisciplinary subject of aeroacoustics (Lighthill 1952). The acoustics of jets have been studied extensively over the past 60 years leading to the development of more efficient and quieter aircraft systems (e.g. turbofan engines). Thus, an appreciable reduction in jet noise has been achieved. Jet noise, however, still remains one of the dominant sources of aircraft noise and it is estimated that jet noise is responsible for between a third and a half of the total acoustic energy generated during take-off (Bailly et al. 2016). Understanding and mitigating jet noise, therefore, remains crucial for achieving sideline and flyover aircraft noise certification levels.

As with any problem dealing with high Reynolds number flows, jet aeroacoustics is complex. The exact set of equations derived by Lighthill shows that the acoustic far pressure field of a high-speed, unheated jet can be predicted with knowledge of the instantaneous values of the Reynolds stress tensor in the jet turbulence field. Nowadays, large eddy simulation (LES) and direct numerical simulation (DNS) can provide direct prediction of aerodynamic noise. These techniques, however, are currently too time-consuming and costly for use in industry to quantify the noise risks of future aircraft designs. For this situation, Reynolds-averaged Navier–Stokes (RANS) simulations are more appropriate. The unsteady statistics of the problem, therefore, must be inferred by other means. The RANS solutions can be supplemented with model-scale experimental data to provide the stationary statistics of the jet noise source region. These data can also be used to validate and develop new LES and DNS methods.

The first documented work providing single- and two-point measurements of the turbulent velocity field of a jet was presented by Laurence (1956). Davies et al. (1963) then extended Laurence’s measurements to include more axial and radial distances between the reference probe (i.e. the stationary probe) and the moving probe. These, together with several other studies in the 1970s, provided the initial data for modelling the jet mixing noise source. Significant improvements in both constant temperature anemometry hardware and digital computing has led researchers to revisit these early hot-wire measurements. Among others, Harper-Bourne (1999, 2003) and Morris and Zaman (2010a, b) carried out two-point measurements of incompressible jets.

When compared to other experimental techniques, hot-wire anemometry has several advantages: (1) a high maximum frequency response; (2) a high signal-to-noise ratio; (3) a broad velocity range; (4) low cost; (5) easy to use, and (6) fast data post-processing. The main two disadvantages are that the probe intrudes into the flow and that point-wise data acquisition is time-consuming. Laser Doppler velocimetry (Kerhervé et al. 2006) and particle image velocimetry techniques (Bridges and Podboy 1999; Pokora and McGuirk 2015; Dahl 2015) have extended the number of reference probe locations; however, the maximum discernible frequency is limited (e.g. Strouhal number \(\mathrm {St}\le 1\)). Finally, while high-fidelity LES schemes have improved our ability to calculate the Reynolds stress tensor within the entire jet volume (Karabasov et al. 2010; Wang et al. 2017), such methods remain time-consuming, computationally expensive and frequency limited. As yet, the link between the stress tensor and the true source of jet noise still remains unclear.

The works by Harper-Bourne (1999, 2003) and Morris and Zaman (2010a, b) are frequently used to inform jet noise source models and to validate large eddy simulations. These works, however, are limited by both the jet exit Mach number (\(M_{\mathrm {j}}\le 0.25\)) and the number of reference probe locations—Harper-Bourne’s analysis incorporated one reference probe location and Morris and Zaman’s analysis contained two axial reference probe locations. Additionally, the separations used to calculate two-point statistics were carried out in only one direction along each axis. Therefore, jet mixing noise source models based on these databases are limited by the following two assumptions: (1) the compressibility effects on the jet statistics are negligible, and (2) the joint moment functions are even. Additionally, based on previous works, it is not clear which physical length should be used to scale the changes in the two-point statistics of a jet with axial location.

In order to use the turbulence statistics of incompressible jets to model the mixing noise of real jet flow applications, it is important to show that this data is valid at moderate and high subsonic speeds. This paper considers subsonic jets at Mach numbers 0.2, 0.4, 0.6 and 0.8. Two test campaigns were performed: (1) single-point tests and (2) two-point tests. Analysis of the axial component of the velocity field is reported in this paper. Data from the first test were used to provide information about the jet’s low-order statistics (i.e. autocorrelation coefficients, one-dimensional spectra and self-similarity parameters). A single-point survey of the flow field was carried out from the nozzle exit to 15 jet diameters \(D_{\mathrm {j}}\) downstream. In the second test, information concerning the joint moments (i.e. space–time cross-correlations, cross-power spectra and characteristic length-scales) was recorded. The two-point tests were performed over a broad range of reference probe locations—axial locations \(x/D_{\mathrm {j}}=2\), 4, 5 and 8, and radial locations \(y/D_{\mathrm {j}}=0.0\) and 0.5. The movable sensor was traversed in three orthogonal directions. Further extending previous work, tests were also performed with the moving sensor located both upstream and downstream of the reference probe location in order to show the symmetry of the joint moments (i.e. the anisotropy of the correlation volume).

Approximate scaling laws for the properties used to model the jet mixing noise source are also presented. These models extend other databases in the literature (Harper-Bourne 2003; Kerhervé et al. 2006; Morris and Zaman 2010b) by showing the effects of jet exit velocity and axial location, the non-evenness of the joint moment functions, and coherence decay for different probe separation directions.

The paper is structured as follows. In Sect. 2, the experimental facility and instrumentation used to perform the tests are presented. A discussion of the nominal jet flow conditions and probe locations follows. Then, in Sect. 3, the main results are discussed. First, low-order statistics are presented to validate the experiment and to provide the physical length-scales of the jet used in the following sub-sections. Secondly, the turbulence spectra distributed within the jet are analysed. Absolute values and normalisation with axial location and exit velocity are then proposed. Finally, the joint moments are considered both in the time and frequency domains. In the former, models for the decay of the correlation coefficients and pertinent length-scales are discussed. In the latter, the magnitude of the coherence function and frequency-dependent length-scales are investigated. Finally, the main conclusions are summarised in Sect. 4.

2 Methodology

2.1 Experimental facility

Experiments were carried out in the Doak Laboratory at the University of Southampton, UK. The Doak Laboratory is a small-scale 400-Hz anechoic open jet wind tunnel that exhausts into a quiescent atmosphere. The facility has dimensions of, approximately, 15-m long by 7-m wide by 5-m high. The air jet is supplied by a high-pressure compressor–reservoir system. Fine control of the reservoir pressure is obtained via an Emerson globe valve. The air is exhausted passively via a rectangular collector into a small secondary acoustic chamber before exiting the building (Fig. 1). Single-stream jet tests can be performed on flow regimes characteristic of civil aircraft and at 1/50th model-scale. The jet rig is capable of achieving a controlled exit Mach number range of between \(0.15\le M_{\mathrm {j}}\le 1\).

Fig. 1
figure 1

ISVR Doak Laboratory: setup used for single-point aerodynamic hot-wire measurements

Full size image

The jet nozzle used for the static measurements presented in this paper is a 38.1-mm-diameter, convergent nozzle. This nozzle has a high convergence angle of \(14^{\circ }\) and is a scaled version of a larger 86.1-mm nozzle used in the Noise Test Facility (NTF) at QinetiQ, Farnborough, UK. The jet boundary layer properties for this particular nozzle at several jet Mach numbers were presented in Section 3.2.1 of Proenca (2018). The boundary layer thickness estimated from the velocity profile is around 0.2 mm. Therefore, the hot-wire probe used (1.25 mm long, 0.005 mm diameter) was sensitive to the curvature of the nozzle. Consequently, whilst the flow is transitional, all statistics are measured downstream of any laminar section and well within the fully turbulent region.

The anechoic chamber was equipped with two ISEL traverse systems mounted adjacent to the jet nozzle exit. One system was configured with three motor power modules, allowing independent movement along the x, y and z planes. The maximum stroke along each axis was 610 mm (i.e. 16 jet nozzle diameters). The origin was defined as the centre of the jet nozzle exit, \(x = y = z = 0\). The traverse position resolution is 6.25 \(\upmu\)m, which is appropriate for the minimum required movements (100 \(\upmu\)m).

2.2 Instrumentation

A constant temperature anemometry (CTA) hot-wire system was used to measure the jet velocity fluctuations. Single normally oriented hot-wire probes were used in the experiments discussed herein. The probes consist of one cylindrical heat sensor element sensitive to both pitch and yaw. The probe, therefore, measures the resultant instantaneous mass flux, \(\rho \mathbf {u}\). However, since both the density variation and the transverse velocity components are typically at least one order of magnitude lower than the axial velocity component, it is common practice to assume that a single hot-wire measures the stream-wise component of an unheated flow when the probe stem axis is aligned with the jet axis (Laurence 1956; Davies et al. 1963; Harper-Bourne 2003; Morris and Zaman 2010b).

A preliminary test was carried out to select the most suitable hot-wire probe. The Dantec 55P11 miniature platinum-plated tungsten probe was selected because it produced similar root-mean-square velocity fluctuation levels to both the gold-plated and nickel film probes. A temperature probe was also mounted near the hot-wire sensor to account for any local temperature fluctuations. The hot-wire probes were calibrated in situ using a Dantec StreamLine Calibrator over the velocity range of interest (i.e. 1–300 m/s). The calibration coefficients were then extracted from a fourth-order polynomial curve-fit.

Other instruments were used to measure the nominal jet flow conditions. The jet exit aerodynamic Mach number was defined using the nozzle exit pressure ratio and isentropic flow equations. It was assumed that, for an isothermal subsonic jet, the static pressure at the nozzle exit was equal to the ambient chamber pressure. The total pressure was measured upstream of the nozzle exit using a flush-mounted surface transducer in the plenum. Temperature probes used to calculate the speed of sound were located both in the jet pipe and in the chamber.

2.3 Test definition and data acquisition

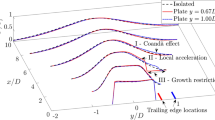
For the single-point measurements, the hot-wire probe was traversed radially across the jet at several axial stations downstream of the nozzle exit. Based on previous measurements (Almeida et al. 2017), a jet spreading half angle of \(7^{\circ }\) was used to define the nominal limits of each radial profile. Two-point measurements were then performed using a reference probe and a moving probe. The moving probe was traversed in the three orthogonal directions: axial, radial and azimuthal. Figure 2a shows a schematic of the jet region investigated together with a definition of the pertinent jet spreading angles and the locations of the reference probe for the two-point measurements (red squares). Figure 2b, c describes the coordinate system used for the jet, \(\mathbf {y}\left( x,y,z\right)\), and the separation vector, \(\zeta \left( \xi ,\eta ,\varphi \right)\).

Fig. 2
figure 2

Schematics showing the locations of the reference probe (red squares) used in the two-point test: a definitions of the three jet regions, spreading angles (\(\beta\) and \(\gamma\)) and lengths (\(\delta _{\beta }\), \(\delta _{\mathrm {pc}}\), \(X_{\mathrm {c}}\)); b–d show the coordinate systems of the reference probe (x, y, z) and the separation vector \(\zeta \left( \xi ,\eta ,\varphi \right)\)

Full size image

The definitions of the test set points are summarised in Tables 1 and 2. Table 1 shows the four jet exit Mach numbers and probe locations in the single-point test. Table 2 shows the three jet exit Mach numbers, the locations of the reference probe and the direction of the separations performed for the two-point test. Two-point measurements were also performed on the opposite shear layer (i.e. at \(y/D_{\mathrm {j}}=\pm 0.5\)) to check the symmetry of the joint moment statistics. Note that \(M_{\mathrm {j}}=0.8\) was not studied in this campaign. This jet speed proved to be a challenging test due to hot-wire probe breakage to one another.

Table 1 Domain of analysis: single-point measurements
Full size table
Table 2 Domain of analysis: two-point measurements
Full size table

All data were acquired using a 24-bit National Instruments dynamic signal acquisition system. An eight-channel NI PXI-4472 was used to acquire ambient chamber and mean rig flow data, sampled at 1 kHz. The analogue output of the CTA was connected to the National Instruments A/D converter. Hot-wire measurements were performed at a sampling rate of 50 kHz and each test point was acquired for 10 s.

3 Results and discussion

3.1 Single-point statistics

In this section, results obtained from single-point measurements are discussed. The mean velocity and turbulence intensity within the first 15 jet diameters downstream of the nozzle exit are investigated. In this region, it is shown that the low-order statistics collapse well using the vorticity thickness as a self-similar parameter. Finally, power spectral density and autocorrelation functions are presented.

3.1.1 Mean velocity and turbulence intensity

The mean velocity (\(\overline{U}\)) and turbulence intensity (\(\mathrm {TI}\)) distribution of a jet are well-known. The mean velocity across the shear layer at a specific axial location are typically modelled as a Gaussian function (Abramovich 1963). The authors have found that the following empirically derived formula most accurately determines the global behaviour of the Doak jet:

$$\begin{aligned} \overline{U}(x,y) = {\left\{ \begin{array}{ll} \overline{U}_{\mathrm {max}} \exp \left[ -\dfrac{(y \pm \delta _{\mathrm {pc}}/2)^2}{(\delta _{\beta }/2)^{2}} \right] &{}\text {if } \vert y \vert> \delta _{\mathrm {pc}}/2 \\ \overline{U}_{\mathrm {max}} &{}\text {if } \vert y \vert \le \delta _{\mathrm {pc}}/2, \end{array}\right. } \end{aligned}$$
(1)

where \(\overline{U}_{\mathrm {max}}\) is the mean velocity along the centreline, \(\delta _{\mathrm {pc}}\) is the length between the nominal edge of the potential core, and \(\delta _{\beta }\) is the shear layer half-width (see definitions in Fig. 2).

The velocity fluctuations, \(u^{\prime }\), are commonly represented by the turbulence intensity, defined as the ratio of the root-mean-square of the velocity fluctuation to the jet exit mean velocity, \(U_{\mathrm {j}}\). The turbulence intensity can be approximated as a function of the mean shear rate, \(\mathrm{d}\overline{U}/\mathrm{d}y\), as shown by Davies et al. (1963); however, calibration constants are required to correct the turbulence levels at different axial locations. The mean shear rate underestimates the turbulence intensity in the region around the jet centreline because the jet potential core is not strictly laminar. Nonetheless, the turbulence intensity peak and behaviour is well-established.

Experimental results for the distribution of \(\overline{U}\) and \(\mathrm {TI}\) are presented in Fig. 3. Equation (1) is illustrated by the solid black line in Fig. 3a. Blue dashed lines indicate the edge of the shear layer, where the mean local velocity is equal to 5% of the jet exit velocity.

Fig. 3
figure 3

a Jet mean velocity and b turbulence intensity profiles for a \(M_{\mathrm {j}}=0.6\) jet. Hot-wire data are shown by red dots and arrows. Results from Eq. (1) are shown as solid black lines in a. The edge of the shear layer is shown as the dashed blue line in a and is defined by the location where \(\overline{U}=0.05U_{\mathrm {j}}\)

Full size image

Note that the spreading rate, \(\beta\), is constant throughout the jet. This leads to the conclusion that two different shear layer growth rates exist: one ranging from the nozzle exit to the end of the jet potential core, and another from the end of the potential. Defining the correct spreading rate is important when attempting to scale the jet statistics, as we will see later. Furthermore, the fact that the shear layer half-width does not grow at the same rate in the initial and transitional regions suggests that the characteristic large scales of the jet also have different growth rates. Thus, an average of the upper and lower shear layer spreading angles was used to create the following expression to define the jet shear layer half-width:

$$\begin{aligned} \delta _{\beta } = {\left\{ \begin{array}{ll} \dfrac{x\sin (\beta +\gamma )}{\cos \beta \cos \gamma } &{}\text {if } x < X_{\mathrm {c}}\\ x\tan \beta +0.5D_{\mathrm {j}}&{}\text {if } x \ge X_{\mathrm {c}}. \end{array}\right. } \end{aligned}$$
(2)

Equation (2) will be useful when scaling the central and joint moment statistics presented in the subsequent sections.

In order to collapse the low-order statistics along each radial profile, another physical length-scale should be used to account for the presence of the potential core. Figure 4 shows the mean velocity and turbulence intensity profiles normalised by the velocity half-width, \(y_{0.5}\), and the vorticity thickness, \(\delta _{\omega }=U_{\mathrm {j}}/\vert \mathrm{d}\overline{U}/\mathrm{d}y\vert _{\mathrm {max}}\). Results for the local mean velocity (Fig. 4a) agree well with the incompressible jet studied by Morris and Zaman (2010b) and show that the local mean velocity of high subsonic jets can be collapsed onto an universal curve. The differences seen in the turbulence intensity profiles at different axial locations (see Fig. 4b in the region \(\left( y-y_{0.5}\right) /\delta _{\omega }<0\)) are due to the fact that the fluctuations near the potential core region are rapidly increasing as the potential core begins to break down (see Fig. 3b).

Fig. 4
figure 4

a Mean velocity distribution normalised by half-velocity width and vorticity thickness; data shown for four axial locations and for four jet exit velocities. b Turbulence intensity profiles; data taken from the same axial locations as in a; jet exit Mach number \(M_{\mathrm {j}}=0.6\)

Full size image

In summary, three main conclusions from the study of the Doak jet’s low-order statistics can be made. Firstly, the spreading rate of the jet is constant within the two first regions of the jet, which results in two linear shear layer half-width growth rates. Secondly, no appreciable effects of jet exit velocity are seen for high subsonic, compressible jets. Thirdly, the Doak jet is self-similar.

3.1.2 Power spectral density and autocorrelation functions

The power spectral density (PSD) forms a Fourier pair with the autocorrelation function. They are also specific cases of the cross-correlation and the cross-power spectral density (CPSD). Velocity fluctuations and the square of the velocity fluctuations are needed in jet noise modelling, so we consider both second and fourth-order joint moments. For second-order coefficients, cross-correlation and CPSD are defined as follows:

$$\begin{aligned}&R_{ij}(\mathbf {y},\varvec{\zeta },\tau )=\dfrac{ \overline{u'_i(\mathbf {y},t)u'_j(\mathbf {y}+\varvec{\zeta },t+\tau )}}{\sqrt{\overline{u_i'^2}(\mathbf {y})\overline{u_j'^2}(\mathbf {y}+\varvec{\zeta })}}, \end{aligned}$$
(3)
$$\begin{aligned}&S_{ijkl}(\mathbf {y},\zeta ,\omega )=\dfrac{1}{2\pi }\int _{-\infty }^{\infty } R_{ijkl}(\mathbf {y},\zeta ,\tau )\mathrm{e}^{-i\omega \tau }\text {d}\tau . \end{aligned}$$
(4)

As only the axial component of the velocity is considered in this paper, the PSD of the velocity fluctuations is written as \(S_{11}\) and the PSD of the square of the velocity fluctuations is represented by \(S_{1111}\). The PSD was calculated at each point in the jet using Welch’s method (Welch 1967). The velocity signal was split into 100 segments each with 50% overlap. The FFT of each segment was taken using a Hanning window. Results presented herein are the average taken over the estimates of each segment.

The PSD shows the same amplitude information as the root-mean-square of the velocity fluctuation. Thus, the highest PSD levels are seen along the lip-line, as shown in Fig. 3b. In this region, the jet’s spectral distribution is well-known: a flat profile in the energy producing region and a universally decaying \(f^{-5/3}\) slope in the high-frequency part of the spectrum. An example of the PSD in the high turbulence kinetic energy region is shown in Fig. 5a. Within the nominally laminar potential core region, however, the PSD shows a ‘hump’, often recognised as a signature of the coherent structures present on the edge of the potential core. Power spectral density data obtained inside the potential core of the jet are presented in Fig. 5b. Each graph shows data for four jet exit Mach numbers.

Fig. 5
figure 5

Results for the jet power spectral density on the lip-line and centreline. Data for four jet exit velocities are displayed in each sub-figure

Full size image

It is clear that, along the lip-line and at a fixed axial location, increasing the jet exit velocity both extends the flat energy region to higher frequencies and increases the PSD amplitude. This is expected because the Reynolds number increases, shifting the turbulence energy spectrum to higher wavenumbers. This increase in frequency is also consistent with points within the jet potential core, where the signature of the coherent structure is seen to move to higher frequencies.

In Fig. 5b, the broadband nature of the coherent structure signature changes and several tones appear at \(M_{\mathrm {j}}=0.8\). This tonal noise has been observed previously by Lawrence and Self (2015) and is currently explained by waves trapped within the potential core region (Towne et al. 2017; Jordan et al. 2018). As mentioned in Sect. 2.2, the hot-wire probe measures the contribution of density and velocity fluctuations. Within the potential core, the density fluctuations are no longer negligible when compared to the velocity fluctuations. The fact that the tones are seen only at the highest jet velocity studied is also in agreement with Towne et al. (2017).

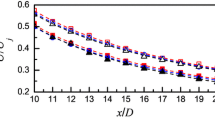
It is possible to establish self-similar parameters to collapse the jet PSD distribution. For a fixed jet exit velocity, the PSD amplitude increases and the frequency at which the energy begins to decay as \(f^{-5/3}\) decreases (Almeida et al. 2017). This is a direct effect of the shear layer growth downstream of the jet nozzle exit. The most appropriate non-dimensional parameter to scale both the PSD amplitude and the frequency, therefore, is the Strouhal number based on the jet exit velocity and the local shear layer half-width, \(\mathrm {St}_{\beta }\). Figure 6a shows an example of this normalisation along the lip-line for four jet exit velocities and at four axial locations. The same procedure is shown in Fig. 6b, where data along the centreline are shown at two axial locations.

Fig. 6
figure 6

Power spectral density normalised by the jet exit velocity and the shear layer half-width. Frequency is normalised by \(U_{\mathrm {j}}\) and \(\delta _{\beta }\)

Full size image

The data along the lip-line (Fig. 6a) collapse well with both frequency and amplitude. The Strouhal number based on the shear layer half-width does successfully collapse the data at the peak for different jet speeds measured inside the potential core (Fig. 6b). The amplitude, however, as suggested by Fig. 5b, is only weakly dependent on the jet exit velocity. This is related to the complex relationship between the velocity and density fluctuations in the potential core. On the centreline downstream of the potential core, the PSD begins to follow the same laws as the region of high turbulence kinetic energy (see \(x/D_{\mathrm {j}}=8\) data on Fig. 6b). Since the PSD based on the square of the velocity fluctuations is of particular interest to jet mixing noise models, the same scaling law was tested (using \(S_{1111}/{U_{\mathrm {j}}}^3\delta _{\beta }\) in order to maintain consistent units). The results are in good agreement to those presented in Fig. 6.

With the help of Fig. 5, it is possible to infer the shape of the autocorrelation at different locations in the jet turbulent flow field. In regions where the turbulence levels are high, the autocorrelation has an exponential-like decay from a maximum value equal to the root-mean-square of \({u'}^{2}\) or \({u'}^{4}\) (i.e. the second-order or fourth-order correlation, respectively). For points located inside the jet potential core, the autocorrelation of second-order coefficients is of exponential-cosine type. The hump characterising the trace of the Kelvin–Helmholtz instability is responsible for the wavelike component of this function, and the frequency of the peak found in the spectrum matches the period seen in the autocorrelation. Autocorrelation fourth-order coefficients do not present negative excursions because the velocity fluctuation at each location is squared. This results in higher amplitudes and a much slower decay of the coefficients.

It was found that the autocorrelation coefficients in the high turbulence kinetic energy region collapse well when the time delay is normalised by the jet exit velocity and the local shear layer half-width, as defined in Eq. (2). As expected, no simple scaling law was found for the autocorrelation coefficients measured at different points inside the jet potential core. Figure 7 shows a summary of the results found along the jet lip-line and centreline for the autocorrelation function. Several jet axial locations and Mach numbers are shown where the lip-line coefficients collapse onto a single curve and where the data weakly depend on the jet exit velocity. A one-term exponential fit was obtained from a non-linear least-squares model and is illustrated by the solid lines. The only region in which the jet time-scale, \(U_{\mathrm {j}}/\delta _{\beta }\), fails to collapse the data is along the centreline within the potential core, shown in Fig. 7b.

Fig. 7
figure 7

a Experimental data and empirical model for the autocorrelation coefficients in the region of high turbulence intensity and b autocorrelation coefficient experimental data measured along the centreline

Full size image

3.2 Two-point statistics: time domain

The data measured in the two-point test campaign, summarised in Table 2, are analysed in this section. Figure 8 illustrates the space–time cross-correlation coefficient results obtained for a Mach 0.6 jet with the reference sensor located at \(x/D_{\mathrm {j}}=8\) and \(y/D_{\mathrm {j}}=0.5\). Several axial separations, i.e. \(\zeta \left( \xi ,\mathbf {0,0}\right)\), are shown.

Fig. 8
figure 8

Sample of cross-correlation coefficient data for several axial separation distances. Reference sensor located at \(x/D_{\mathrm {j}}=8\) and \(y/D_{\mathrm {j}}=0.5\). Data for \(M_{\mathrm {j}}=0.6\)

Full size image

The line connecting the peaks of each data series (red diamond symbols) represents the autocorrelation moving frame. The area under this curve is frequently used to estimate the integral time-scales and length-scales of the jet flow field. Another length-scale can be obtained from the fixed frame or space correlation coefficients. These are obtained at \(\tau =0\), represented by the black circles in Fig. 8.

Transverse correlations differ from the axial separations shown in Fig. 8. For the transverse separations, the two sensors are supposedly located within the same coherent eddy. Convection, therefore, plays a negligible role and the correlation function is weakly time dependent. The reason the peak coefficient is found at a time delay different from zero is due to the velocity gradient between the two points. To illustrate these details, Fig. 9 shows radial and azimuthal cross-correlation coefficients. Results for several separations are shown and the peak coefficients are displayed as yellow circles (for the fixed frame of reference) and cyan diamonds (for the moving frame of reference).

Fig. 9
figure 9

Space–time cross-correlation coefficients of transverse separations on the lip-line. a \(x/D_{\mathrm {j}}=5\), \(M_{\mathrm {j}}=0.2\). b \(x/D_{\mathrm {j}}=8\), \(M_{\mathrm {j}}=0.4\). The peak coefficients are shown by cyan diamonds. Yellow circles show space correlation coefficients

Full size image

In Fig. 9a the mean shear between the two sensors is responsible for the peak location away from the fixed frame of reference. This data was obtained for a reference probe located on the lip-line, when the moving sensor is traversed towards the jet centreline. Since the local mean velocity measured by the moving sensor is higher, this probe sees each coherent structure before the reference sensor. Thus, the peak takes place at \(\tau <0\). When the moving sensor is traversed from the lip-line towards the edge of the shear layer, the peak consistently occurs at \(\tau>0\). Note, however, that the amplitudes of the coefficients recorded in both the fixed and moving frames of reference are similar. The decay of the space correlation coefficients, therefore, is similar in both frames of reference. Finally, when studying the azimuthal separations, Fig. 9b confirms that the peak coefficient occurs, as expected, at \(\tau =0\), where no convective effects or mean shear exist between the two sensors.

3.2.1 Effect of jet exit velocity

In this section, the effects of jet exit velocity on the two-point statistics are discussed. This is important for validating previous measurements performed at low subsonic speeds (Harper-Bourne 2003; Morris and Zaman 2010b). Figure 10 presents fourth-order cross-correlation coefficient data measured at three jet exit velocities. In both graphs, the reference sensor was located on the lip-line and near the end of the potential core. As the jet exit velocity increases, the correlation of the velocity signal at a fixed distance is seen to decay more rapidly. Physically, this represents a coherent structure moving at increased velocity. Figure 10a shows that the jet time scale (i.e. \(D_{\mathrm {j}}/U_{\mathrm {j}}\)) is a good parameter to capture this effect. When considering the space coefficients shown in Fig. 10b, the same conclusion can be drawn: the coefficients for both low subsonic, incompressible jets and high subsonic, compressible jets scale simply with jet exit velocity and nozzle exit diameter.

Fig. 10
figure 10

Space–time and space cross-correlation coefficients of three jet exit velocities. Reference sensor location is displayed in each sub-figure

Full size image

When the reference sensor is positioned at other axial locations on the lip-line, the results are in agreement with Fig. 10. The space–time and space correlation coefficients will collapse to a single curve when normalised by the jet time scale. This is also true for coefficients obtained from radial and azimuthal separations.

One main difference was found for measurements with the reference probe located inside the jet potential core. The amplitude of the coefficients at fixed separation distances are seen to decay with increasing jet exit velocity. It is believed the decrease in correlation level is caused by probe interference effects. The turbulence levels inside the jet potential core are low and the presence of one sensor upstream affects the measurements by the probe which is further downstream. The probe interference affects both space–time and space coefficients. Nonetheless, the low turbulence levels inside the potential core also define this region as of second importance to the modelling of jet noise sources based on the stress-tensor.

Now that the jet exit velocity effects were inspected, the several correlation coefficients are modelled from the data as follows: (1) coefficients measured along the lip-line or along the centreline and downstream the end of the potential core (i.e. \(x/D_{\mathrm {j}}=5\) and 8) are modelled based on all three jet exit velocities measured and (2) points located inside the potential core are analysed using only \(M_{\mathrm {j}}=0.2\).

3.2.2 Space correlation coefficients

As with the autocorrelation function, space correlation coefficients provide useful information about the flow physics of simple (e.g. homogeneous) flows. However, knowledge of these coefficients is crucial when modelling the autocorrelation moving frame curve for jet mixing noise source models. Additionally, if a relationship exists between the length-scale derived from the fixed and moving frames of reference, the former is usually preferable because there is a lesser effect of negative correlation coefficients. Two-point tests were examined: (1) to propose models for the decay of the space correlation coefficients; (2) to determine the characteristic length-scales of the flow, and (3) to investigate the evenness of the space correlation function.

An empirical model was obtained to describe the space correlation coefficients. The method used is similar to that performed for the autocorrelation in Sect. 3.1.2. The main difference is that the space correlation coefficient is not necessarily an even function. Axial separations performed upstream or downstream of the reference sensor will likely produce different decay rates in non-homogeneous flows. The final model is shown in Fig. 11. Data from all three Mach numbers studied are displayed as the different symbols. The reference sensor locations are illustrated by different colours and the exponential fit is shown by the solid line.

Fig. 11
figure 11

Experimental data and semi-empirical model for space correlation coefficients for points along the jet lip-line. All three graphs obtained from the square of the velocity fluctuations

Full size image

For all separations, the coefficients decay to values slightly below zero at large separations. The classical definition of the characteristic length-scale (i.e. the area beneath the correlation curve) could then produce very small lengths. Harper-Bourne (2003) and Morris and Zaman (2010b) propose that the length-scale should be defined as the separation distance to which the correlation coefficient is equals to 1/e. Note that this assumes that the correlation does not decay to values below zero and it can be modelled as a one-term exponential of the form \(\exp {\left( -A\zeta \right) }\), where A is a constant. A one-term exponential is expected to produce a good fit for correlation coefficients of a fully developed turbulent flow. However, in the nominally laminar potential core, the signature of a dominant instability, or coherent structure, produces the negative loops in the correlation curves. An exponential cosine model of the form \(\exp {\left( -A\zeta \right) }\cos \left( 2\pi f_{0}\right)\), where \(f_0\) is the instability dominant frequency, should then be used.

The authors found that the classical and 1/e approaches produce the same length-scale when the fourth-order correlation coefficients are interrogated. Two strategies were used to derive the length-scales based on second-order coefficients, namely, (1) integration of the correlation from the time delay in which \(R_{11}=1\) to the time where \(R_{11}=0\) and (2) use of the relationship between second and fourth-order coefficients valid for homogeneous flows, \(R_{iiii}=R_{ii}^2\) (Monin and Yaglom 1975; Batchelor 1982). Both strategies produced length-scales about the same size as those obtained from the 1/e method. The final model for the space correlation coefficients is

$$\begin{aligned} R_{11,1111}\left( \zeta \left( \xi ,\eta ,\varphi \right) \right) = \exp \left( -\dfrac{\zeta }{\mathscr {L}_{\zeta \left( \xi ,\eta , \varphi \right) }\delta _{\beta }}\right) , \end{aligned}$$
(5)

where \(\mathscr {L}_{\zeta \left( \xi ,\eta ,\varphi \right) }\) is the characteristic length-scale obtained from the 1/e method described above. A similar equation can be written for the autocorrelation coefficients. In that case, a characteristic time-scale is obtained. A summary of the time and length-scales found for each separation vector is summarised in Table 3.

Table 3 Characteristic time and length-scales proportional to the jet shear layer half-width obtained from autocorrelation and space correlation functions
Full size table

The three key points to note from this subsection are: (1) spatial correlation of the stream-wise component of the velocity is an even function in all three directions investigated; (2) coefficients based on the velocity fluctuations and square of the velocity fluctuations are related simply as for homogeneous flows, and (3) the jet exit velocity and shear layer half-width (as defined in Eq. 2) are the only parameters necessary to collapse data obtained at different locations and all subsonic jet velocities. All of these claims, however, are not valid inside the jet potential core, where the coherent structure dominates the fine-scale turbulence.

3.2.3 Space–time correlation coefficients

Previous experiments have suggested that a one-term exponential fails to fit the behaviour of the cross-correlation coefficients (Harper-Bourne 2003; Morris and Zaman 2010a, b). This failure has previously been attributed to a misalignment issue between the two probes, since the minimum distance is often set by eye. Furthermore, hot-wire measurements presented in the literature have only ever been performed in one direction (e.g. \(\xi>0\)).

Figure 12a shows an example of cross-correlation coefficients measured at axial separations in two opposing directions (i.e. \(\pm \xi\)). The peak coefficient for each separation is shown by a cyan diamond and it is evident that the coefficients measured for \(\xi <0\) decay faster when the separation distance increases upstream against the oncoming jet flow. In Fig. 12b, fourth-order coefficients measured at four reference sensor locations have been normalised by the shear layer half-width. Two exponential fits are shown, a one-term (black, solid line) and a two-term (pink, dashed line) function. Data in Fig. 12 were obtained from a \(M_{\mathrm {j}}=0.6\) jet, however, similar results are also seen for all other jet exit velocities.

Fig. 12
figure 12

a Example showing the non-evenness of the space–time cross-correlation coefficients (second-order, \(x/D_{\mathrm {j}}=8\), \(y/D_{\mathrm {j}}=0.5\)). b Fourth-order space–time cross-correlation coefficients measured at several axial locations (\(M_{\mathrm {j}}=0.6\)) with exponential best-fit curves

Full size image

It can be seen from Fig. 12b that the values at \(\tau =0\) from the one-term exponential fits calculated from \(\xi <0\) and \(\xi>0\) are similar. If the poor fit at \(\tau =0\) was caused only due to a misalignment of the probes, it could be easily corrected with the \(\pm \xi\) set of data by applying a small horizontal offset to the curves. This was not possible. The authors suggest that the reason a one-term exponential does not fit the data is the well-known fact that d\(R/\mathrm{d}\tau =0\) at the origin (Hinze 1975). Thus, the one-term exponential function does not capture well the coefficients of very small separations.

It would be interesting to further investigate the development of the correlation coefficients at small separation distances. The Taylor micro-scale could then be calculated and used to model the correlation decay more accurately. However, it is unfortunate that the spatial resolution of the hot-wire probes are not able to measure these features in small-scale nozzles.

The present database also suggests a different observation in comparison to the literature regarding the evenness of the space–time cross-correlation function. It is widely believed that the correlation coefficients decay faster than anisotropy effects, and that the cross-correlation, therefore, should be an even function (Harper-Bourne 2003; Morris and Zaman 2010a, b). The data presented here, however, appear to contradict this hypothesis. The non-evenness of the correlation function is noticeable only for the axial space–time cross-correlation coefficients (i.e. \(\zeta \left( \xi ,0,0\right)\)). This is due to the fact that the space–time correlation coefficients decay much faster (at least by a factor of four) compared to space correlation coefficients. As discussed before, transverse separations have no appreciable difference when fixed frame and moving frame coefficients are compared.

Second- and fourth-order space–time correlation coefficients for various separations are shown in Fig. 13a. The reference sensor is located at \(x/D_{\mathrm {j}}=4\), \(y/D_{\mathrm {j}}=0.5\) and data are shown for separations in both axial directions. The time axis is normalised by the jet exit velocity and the reference sensor shear layer half-width. The same data are then successfully collapsed in Fig. 13b with the time axis normalised by the shear layer half-width at the location of the moving sensor. Although only a few points are shown, the scaling holds true for the other jet locations and conditions.

Fig. 13
figure 13

Second-order and fourth-order cross-correlation coefficients normalised by a the shear layer half-width of the reference sensor and b the shear layer half-width at the location of the moving sensor. All data from \(M_{\mathrm {j}}=0.6\)

Full size image

It can be concluded that cross-correlation coefficients obtained for axial separations depend on the relative position of the moving probe to the reference probe. Normalising the time delay by the local shear layer half-width at the location of the moving probe appears to collapse all data onto a single exponential decay curve. The length-scale obtained from the axial space–time coefficients was found to be \(0.95\delta _{\beta ,\mathrm {local}}\), which is slightly more than three times the length-scale obtained from the space coefficients (\(0.31\delta _{\beta }\)). Regarding the transverse length-scales, the empirical curves presented in Sect. 3.2.2 for space correlations are also valid for the space cross-correlation coefficients.

3.3 Two-point statistics: frequency domain

In this section, results in the frequency domain are briefly discussed. The functions used herein are Fourier pairs of the time domain coefficients investigated in Sect. 3.2.3. A procedure to calculate the frequency-dependent length-scales and the decay of the coherence is presented and compared with literature.

3.3.1 Coherence and length-scales

The coherence function \(\gamma _{1111}\) is used to model the Reynolds stress tensor of turbulent flows. The coherence function can be used to determine the characteristic frequency-dependent length-scales in different regions of the flow. In the case of high subsonic jets, the length-scale is frequency dependent and avoids the issue of separating time and space variables as with the space–time cross-correlation function.

The coherence function is obtained from the CPSD of two unsteady velocity signals measured simultaneously at two different locations in the jet turbulence field. The mathematical definition of the coherence function is given below:

$$\begin{aligned} \gamma _{ijkl}(\mathbf {y},\varvec{\zeta },\omega ) = \dfrac{S_{ijkl}(\mathbf {y},\varvec{\zeta },\omega )}{\sqrt{S_{ij}^{2}(\mathbf {y}, \omega )S_{kl}^{2}(\mathbf {y}+\zeta ,\omega )}}. \end{aligned}$$
(6)

A sample of the magnitude of the coherence function results is shown in Fig. 14a for a Mach 0.6 jet. Several axial separations are illustrated. The reference sensor was located on the jet lip-line at the end of the potential core. Other locations along the lip-line show similar results.

The frequency-dependent length-scales are calculated using the amplitude of the coherence at different separation values. Figure 14b shows the decay of coherence with separation distance for several fixed frequencies (Strouhal number based on the jet diameter). A one-term exponential fit is shown by the solid lines. The length-scales for each frequency are determined either by integrating the exponential fit or by the separation distance at which \(\vert \gamma \vert =1/{e}\). Analyses of the frequency-dependent length-scales are presented in the next section. Experimental data indicate that the time- and length-scales at low frequency have an almost constant value and, at the other end of the spectrum, the high-frequency length-scales decay as \(f^{-1}\) (Fisher and Davies 1964; Self 2004; Morris and Zaman 2010b). Our interest now is to evaluate the effect of jet exit velocity and axial location on the frequency-dependent length-scales.

Fig. 14
figure 14

Example of a the magnitude of the coherence measured at a reference point \(x/D=4\), \(y/D=0.5\), \(M_{\mathrm {j}}=0.6\) and b one-term exponential curve fits to the coherence coefficients at fixed Strouhal numbers

Full size image

These questions were partially answered in the time domain results discussed in previous sections. Indeed, the coherence decay suggests that the jet exit velocity and length-scales are related linearly. When the frequency axis is normalised by the jet exit velocity and a fixed physical length, such as the nozzle exit diameter, all data from different jet speeds have been seen to collapse onto an universal curve. The development of the length-scales with increasing axial distance from the nozzle exit, however, shows an interesting behaviour. Consider the results shown in Fig. 15a. The length-scale and the Strouhal number are both normalised by the shear layer half-width measured at the reference sensor location. The frequency-dependent axial length-scales calculated downstream of the reference sensor (black circles) and upstream of the reference sensor (red crosses) produce different levels at the large scales. This is consistent with what was seen in the time domain analysis. Note, however, that the relatively small scales have a universal behaviour, decaying with the inverse of frequency. Furthermore, the frequency cut-off, or the location in which the transition between the flat profile and the inverse frequency decay, is not aligned (see Fig. 15a). As before, a good match is obtained if the frequency axis is normalised by the shear layer half-width at the location of the moving sensor.

An example of the local Strouhal number frequency normalisation is illustrated in Fig. 15b. The frequency cut-off of the axial separations upstream and downstream of the reference sensor are in better agreement. The frequency cut-off is around Strouhal number equals 0.2, which is similar to results presented by Morris and Zaman (2010b). We found that the shear layer half-width of the moving sensor is then the correct parameter to scale the frequency cut-off. Note, however, that the high-frequency content now appears to decay with two different gradients. This new information suggests that only the large-scale structures actually scale with the local shear layer width. The high-frequencies, therefore, are independent of the direction in which the separation occurs.

Finally, regarding the amplitude of the frequency-dependent axial length-scales, the physical length must account for the fact that the joint moment function will decay at a different rate if the moving probe traverses either upstream or downstream of the reference probe. The separation distance in which the space–time cross-correlation function peak decays as 1/e was used to normalise the frequency-dependent length-scales. An example of this procedure is shown in Fig. 15c, d. In Fig. 15c, the Strouhal number is normalised by the shear layer width measured at the reference probe location, while the location of the moving sensor was considered in Fig. 15d. The amplitudes collapse reasonably well using the 1/e length-scale. Results for the frequency cut-off and the decay of the length-scales in the high-frequency part of the spectrum are similar to what was discussed in Fig. 15a, b.

Fig. 15
figure 15

Frequency-dependent length-scales obtained from the coherence function. Reference sensor located at \(x/D_{\mathrm {j}}=4\), \(y/D_{\mathrm {j}}=0.5\), and jet exit Mach number \(M_{\mathrm {j}}=0.6\) for all graphs. y-axis: the shear layer half-width measured at the reference sensor location is used to normalise plots a, b; in c, d, the length-scale was normalised by the separation in which the space–time cross-correlation function decays to 1/e. x-axis: the Strouhal number of graphs a, c is defined as \(\mathrm {St}_{\beta ,\mathrm {ref}}=f\delta _{\beta ,\mathrm {ref}}/U_{\mathrm {j}}\); in plots b, d, the frequency was normalised using the location of the moving sensor, \(\mathrm {St}_{\beta ,\mathrm {local}}=f\delta _{\beta ,\mathrm {mov}}/U_{\mathrm {j}}\)

Full size image

As expected, the frequency-dependent length-scales obtained from the radial and azimuthal separations do not present any differences regarding the direction in which the separation is performed. Consistent with the axial coherence, the same flat profile was observed for the low frequencies and the inverse frequency decay was observed for the high frequencies.

3.3.2 Coherence decay model

In order to model the Reynolds stress-tensor in the frequency domain, it is important to know how the coherence function decays with separation distance. For jet mixing noise, the complete correlation, or coherence, volume must be modelled. Functions, therefore, are sought to describe the exponential decay at different jet locations and separation directions and at each frequency. The coherence results for all reference sensor locations and jet exit velocities studied were normalised by the frequency-dependent length-scale presented in the previous section and are presented in Fig. 16. The three plots show the absolute coherence decay for separations performed in the axial, radial and azimuthal directions. Data from all four reference sensor locations and for jet exit Mach number \(M_{\mathrm {j}}=0.2\) are presented. Six different frequencies were chosen and are plotted as a Strouhal number based on the jet diameter. Similar results were found for the other jet exit Mach numbers studied as well as for other Strouhal numbers up to 5. The length-scale used to normalise the separation distance is the value found at the frequency cut-off.

Firstly, regarding the coherence decay for the axial separations shown in Fig. 16a, a one-term exponential function adequately describes the behaviour of the coherence coefficients. This is in agreement with other results from the literature (Harper-Bourne 2003; Kerhervé et al. 2006; Morris and Zaman 2010b). The coherence coefficients of the smallest separations are also captured well by the exponential fit. There is a scatter of data as the separation distance increases.

An interesting observation relates to the transverse separation results. The coherence decay of radial and azimuthal separations is typically modelled as a Gaussian function. However, it is clear to see, from Fig. 16b, c, that such a profile is not necessarily the best fit for the data, particularly for small radial separations and both small and large azimuthal separations. In fact, the best-fit equations are shown in the legend of each figure. For the radial separations (see Fig. 16b), a value of \(n=1.4\) seems to be more appropriate than \(n=1\). For azimuthal separations, a Gaussian function fits the data relatively well at moderate separations, but fails to describe the behaviour properly at both small and large separation distances.

Fig. 16
figure 16

Variation of the magnitude of the coherence with separation distance. The separation distance is normalised by the frequency-dependent length-scales discussed in Sect. 3.3.1. All data from \(M_{\mathrm {j}}=0.2\)

Full size image

In summary, the correct scaling of the joint moment statistics in the frequency domain of subsonic jets has been presented and discussed. The magnitude of the coherence function was used to calculate the axial, radial and azimuthal length-scales, which were found to have a frequency dependence. It is shown that the larger coherent structures scale with the local shear layer half-width, while the small-scales have a universal behaviour. Thus, only the larger scales are affected by the direction in which the separation is performed. The length-scales obtained were used to normalise the separation distance and to scale the coherence data. As expected, the coherence function decays exponentially for axial separations, however, other exponents are seen to improve the fits for both the radial and azimuthal separations.

4 Conclusion

This paper presented an investigation into the jet turbulence statistics obtained via hot-wire anemometry measurements. The properties described are applicable to jet mixing noise modelling in the framework of an acoustic analogy. Tests were performed to extend well-known databases, including measurements of high-subsonic jets, multiple reference probe locations, and moving probe separations both upstream and downstream of the reference probe location.

By analysing space–time cross-correlation coefficients measured at different reference points along the lip-line, the decay of the correlation coefficients in both the frequency domain and the time domain were seen to scale well with the shear layer half-width and the jet exit velocity. It was also demonstrated that one should use the shear layer width at the location of the moving probe to collapse any two-point data and, thus, to develop any cross-correlation or coherence models.

Empirical models for the one-dimensional spectra, space and space–time correlation coefficients, coherence decay and characteristic length-scales were presented. These models improve on existing knowledge presented in the literature. Key findings provide insight into the physics of the jet stress-tensor. For example, it was shown that there is a direct link between the Taylor micro-scale and the contrasting decay rates for longitudinal and transverse separations. The belief that hot-wire misalignment explains the fact that one-term exponential models do not cross the point \(R_{ij}(0,0)=1\) has been shown rather to be a real feature of this micro-scale. Some differences with existing models provided by other databases are attributed to the different nozzle inlet boundary conditions. Clearly, further research should be carried out to investigate how the jet initial conditions affect the two-point statistics and also how the Taylor micro-scale should be used to model the entire jet correlation volume.

Experimental evidence has also shown that the jet turbulence is quasi-homogeneous and quasi-frozen in the region of high turbulence intensity. This claim is based on the following two observations. First, the second-order and fourth-order cross-correlation coefficients are related simply by a power of two. Thus, the longitudinal length-scales are shown to be about twice the size of the transverse length-scales. Secondly, in agreement with hypotheses proposed in the literature, it has now been evidenced that the two-point statistics can be recovered by using single-point measurements together with estimates of the local eddy convection velocity. These simplifying assumptions, however, cannot be used for modelling the highly intermittent region at the edge of the jet or inside the jet potential core.

Finally, it has been shown that low-order statistics and joint statistical moments at jet exit velocities in the range \(0.2\le M_{\mathrm {j}}\le 0.8\) are self-similar. This result gives confidence to existing jet mixing noise prediction methodologies based on turbulence models informed by low-speed, incompressible jet measurements.