Effect of Reynolds number on flow behavior and pressure drag of axisymmetric conical boattails at low speeds

Abstract

The effect of Reynolds number on flow behaviors and pressure drag around axisymmetric conical boattails was experimentally investigated at low-speed conditions. Four conical boattails with slant angles of 12°, 16°, 20°, and 22° were studied. The Reynolds number ranged from 4.34 × 10⁴ to 8.89 × 10⁴ based on the model diameter. The global-luminescent-oil-film skin-friction measurement was employed to analyze the surface skin-friction topology. Quantitative skin-friction values at the centerline were obtained in this study. The results show that a separation bubble can be formed on boattail surfaces at angles from 12° to 20°. However, at a boattail angle of 22°, flow is fully separated near the boattail shoulder. The integrated afterbody pressure drag indicated that, at angles of 12°, 16°, and 22°, the Reynolds number has very small effect on the afterbody drag, while, at 20° the drag coefficient decrease was relatively large with increasing Reynolds number. We believe that this study provided the first results for a boattail angle of 20° and we observed that the size of the separation bubble decreased as the Reynolds number increased. The effect of the separation bubble on the pressure distribution was also examined in detail.

Graphical abstract

Appendices

Appendix 1. Velocity fields in vertical symmetrical plane and boundary-layer measurement

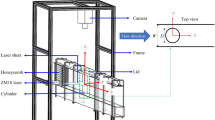
To examine the characteristics of velocity fields in a vertical symmetrical plane and boundary layer before the boattail shoulder, particle image velocimetry (PIV) tests were performed. The experimental setup for PIV measurement is shown in Fig. 13.

Fig. 13

Experimental setup for PIV measurement. a Side view and b back view

In this experiment, a smoke generator (LSG-500S) was placed before the inlet of the wind tunnel to realize a flow-containing particles with mean diameter of 1 µm. The flow-field illumination was provided by a double-pulsed Nd-YLF Laser (LDY-303, 527 nm, Litron Lasers). The thickness of the laser sheet was approximately 1 mm. The time interval between pulses was changed between 4 µs and 8 µs depending on the free-stream velocity. The movement of particles in wind-tunnel tests was captured by a high-speed camera with maximum resolution of 1,280 × 800 pixels (Phantom V611, Vision Research); the camera was equipped with a Nikon objective lens with 100 mm focal length and an extension tube of 36 mm. The sampling rate of the camera was 600 fps and the time length of measurement was approximately 9 s. The camera angle was 40 × 25 mm² to provide an image resolution of approximately 32 pixels/mm.

Experimental conditions were the same as skin-friction measurement. Velocity profiles of the boundary layer were measured for all boattail angles. At each boattail model, the experiment was performed for four Reynolds numbers from Re = 4.34 × 10⁴ to Re = 8.89 × 10⁴.

To obtain the average velocity field with high spatial resolution and detailed boundary layer profile, a single-pixel resolution ensemble correlation algorithm was applied. This algorithm was developed by Westerweel et al. (2004), and it provides a powerful tool for measuring the velocity profile with high spatial resolution. In the algorithm, the spatial correlation between a single pixel in the first frame and an interrogation window in the second frame is calculated for a set of double frames. This calculation of cross-correlation uses the time evolution of a single-pixel intensity instead of the spatial interrogation window. Therefore, only the averaged velocity fields can be available. To reach a satisfactory convergence of the calculation, a large number of images are required. In this study, 5,400 double-frame images which correspond to the 9 s were processed.

The streamwise velocity and flow field on the symmetric vertical plan at boattail angle of 20° and Reynolds numbers of Re = 4.34 × 10⁴ and Re = 8.89 × 10⁴ are shown in Fig. 14. The black lines show the position of the zero stream velocity. Clearly, a reversed flow region is observed near the shoulder for both Reynolds numbers. However, the separation bubble is much smaller and the streamlines above the bubble are more severely bent with the larger Reynolds number. The length of separation bubble at Re = 4.34 × 10⁴ determined by PIV measurement was longer than the result of GLOF measurement. It is probably because the amount of particles was not enough near the wall surface. In addition, the turbulent intensities are very high near the reattachment position, which could lead to some error in the measurement.

The boundary layer was examined at x/L_b = − 0.12 (2.52 mm before the shoulder) and was averaged by the surrounding 10 pixels (0.31 mm) in the streamwise direction. The mean boundary-layer profile is shown in Fig. 15. The thickness of the boundary layer was determined by the distance from the wall to a point where the flow velocity reached 99% of the free-stream velocity. The boundary-layer thickness δ, displacement thickness δ^*, momentum thickness θ, and shape factor H are listed in Table 3. The boundary-layer thickness was slightly changed at different boattail configurations. It should be noted that the shape of boundary layer does not monotonously change with boattail angle. In fact, the velocity profile is less steep at β = 22° due to the fully separated flow with the low-pressure gradient magnitude near the shoulder (Fig. 11d).

Fig. 14

Streamwise velocity fields on symmetrical vertical plane at boattail angle of 20°. a Re = 4.34 × 10⁴ and b Re = 8.89 × 10⁴

Fig. 15

Boundary-layer profile at x/L_b = − 0.12. a Re = 4.34 × 10⁴ and b β = 20°

Table 3 Characteristics of boundary layer at x/L_b = − 0.12 and Re = 4.34 × 10⁴

Table 4 Boundary-layer thickness at different Reynolds numbers (x/L_b = − 0.12, β = 20°)

Obviously, boattail angle has a very small effect on boundary-layer profile before the shoulder. The shape factor H was around 1.3, which indicates that the boundary layer before the shoulder was fully turbulent.

The boundary-layer thickness at a boattail angle of 20° changed slightly (δ/D = 0.095–0.109) with the Reynolds numbers tested in this study (Table 4). The change of boundary-layer thickness in this study was much smaller than it was in a previous study (δ/D = 0.132–0.395; Mair 1969). As reported by Mair (1969), the boundary-layer thickness has a small effect on the boattail pressure drag. Consequently, the effect of boundary-layer thickness on pressure distribution and pressure drag should be limited in this study.

Appendix 2. Wall shear stress estimation

In the turbulent boundary layer of a smooth wall, there is a region where the mean stream velocity is a logarithmic function of distance from that point to the wall. It is referred as log-law region and was first reported by Karman (1930). The relation between the mean velocity and the distance to the wall in the log-law region can be expressed as follows:

$${u^+}=\frac{1}{\kappa }\ln {z^+}+{C^+},$$

(6)

where ${u^+}=\frac{u}{{{u_\tau }}}$ is dimensionless velocity and ${z^+}=\frac{{z{u_\tau }}}{\nu }$is the wall coordinate. u is mean velocity, z is distance to the wall, ν is kinematic viscosity, and u_τ is shear velocity. The shear velocity is defined as${u_\tau }=\sqrt {\frac{{{\tau _{\text{w}}}}}{\rho }}$, where τ_w is wall shear stress and ρ is density of air. The empirical constants in Eq. 6 are called vor Karman constant κ and additive constant C⁺. In this study, they are assumed as κ = 0.41 and C⁺ = 5.0 (Kendall and Koochesfahani 2008).

When the boundary layer profile is given, the wall shear stress τ_w can be calculated to match with the Eq. 6. Consequently, the local skin coefficient C_fx can be calculated as ${C_{{\text{fx}}}}=2{\tau _{\text{w}}}/(\rho {u^2})$. To obtain the quantitative mean skin-friction values at the centerline of boattails, skin-friction coefficient C_fx at x/L_b = − 0.12 was calculated for all the testing cases. An example of logarithmic fitted line at boattail angle of 20° is shown in Fig. 16. At z⁺ < 20 and Re ≥ 5.92 × 10⁴, slight divergences of data occur. In addition, at z⁺ > 100, the experimental data begins to deviate from the log-law region. The reason for these trends is from favorable pressure gradient near the shoulder (Schloemer 1967; Bader et al. 2016). However, the experimental data were fitted well in the log-law region and the effect of pressure gradient on the wall flow can be neglected. Experimental results also showed that the skin-friction coefficient slightly decreases with increasing Reynolds number from Re = 4.34 × 10⁴ to Re = 8.89 × 10⁴ (Table 5).

Fig. 16

Velocity profiles and fitted line at β = 20°

Table 5 Skin-friction coefficient (x/L_b = − 0.12, β = 20°)