Measurements of near-wall pressure fluctuations for trailing-edge serrations and slits

Abstract

Pressure fluctuations on the suction side of a NACA 0018 with trailing-edge add-ons are obtained from integration of time-resolved stereoscopic and tomographic particle image velocimetry data and compared to the ones computed from Lattice–Boltzmann simulations. The airfoil is retrofitted with solid and slitted serrated trailing edges and measured at 0° and at 12° angles of attack. At 0° angle of attack, the boundary-layer thickness and the intensity of the pressure fluctuations are found to decrease along the edge of the serration from its root to its tip. The spectra of the pressure fluctuations additionally show a change of decay in frequency along the serration edge. This last finding has important repercussions for noise-prediction models, which usually assume the turbulence and the slope of the pressure spectra to be “frozen” in the streamwise direction. Results from this study also indicate that the pressure-fluctuation modification along the serrations scales with the local boundary-layer parameters, which can be obtained from experimental and numerical data. In particular, the pressure spectra collapse into a single profile when the local boundary-layer thickness and skin-friction coefficient is employed, instead of the parameters of the incoming flow. The analysis is further extended to flow fields at positive angle of attack, where serrations are known to exhibit lower performance in noise reduction. At incidence angle, the scaling with the local parameters shows that the spatial distribution of boundary-layer thickness and pressure fluctuations is uniform along the serration. This evidence might indicate a positive correlation between the noise-reduction performance of serrations and the spatial change of pressure spectra (and local boundary-layer thickness) along their edge.

Graphical abstract

1 Introduction

The intensity and the spanwise correlation of the surface-pressure fluctuations beneath a turbulent boundary layer at the trailing edge of an airfoil are the most relevant quantities for the estimation of turbulent boundary-layer trailing-edge noise [TBL–TEN (Brooks et al. 1989)]. This broadband component of airfoil self-noise is dominant in wind turbines (Williams and Hall 1970). Recent research focused on several passive noise-mitigation solutions, which could be easily installed in existing machines with relatively low modifications of the original aerodynamic performance (Oerlemans et al. 2009). For instance, sinusoidal and sawtooth geometries (Oerlemans et al. 2009; Moreau and Doolan 2013; Chong and Vathylakis 2015; Arce León et al. 2015, 2016a, b, c; Dassen et al. 1996; Oerlemans 2016) have already been manufactured and installed at the trailing edge of many wind turbines. More complicated geometries have been designed by employing slits (Arce León et al. 2015; Gruber 2012), brushes (Herr and Dobrzynski 2005), iron (Avallone et al. 2017), and randomly shaped trailing edges (Chong et al. 2013). Although these geometries have already proven to reduce noise with respect to a straight trailing edge, a huge difference is reported between their analytically predicted noise reduction (Howe 1991; Lyu et al. 2016) and the measured one (Oerlemans et al. 2009).

Most of the noise-prediction models available in the literature for trailing-edge noise [e.g., (Brooks et al. 1989)] require local information about the boundary-layer thickness and the pressure fluctuations at the trailing edge. The first analytical model found in the literature that estimates the broadband noise reduction due to the installation of serrated edges on a flat plate is the one of Howe (1991). Lyu et al. (2015, 2016) developed a semi-analytical approach applying the Schwarzschild method for the solution of the propagation of the pressure fluctuations [see also (Amiet 1976)]. The above-mentioned models are known to be able to predict how the pressure fluctuations are scattered and propagated to the far field. However, the sound-pressure levels at the receiver depend on the actual pressure spectra at the trailing edge. The analytical integration of the spectra of the pressure fluctuations into far-field noise requires the adoption of the frozen-turbulence assumption [e.g., (Lyu et al. 2015, 2016)]. This assumption allows writing the pressure spectra at each location along the edge as an exponential function of two wavenumber components k_x and k_y, respectively, in the chordwise and spanwise directions. The previous hypothesis is rather accurate for flows where the flow direction is perpendicular to the edge of the geometry, as, for example, in straight trailing edges, as shown from the works of Lyu et al. (2016) and Howe (1991a, b). Recent studies (Avallone et al. 2018) have measured instead a consistent change of the wavenumber vector and of the boundary-layer properties along serrations. This is due to the fact that the edge is inclined with respect to the main flow direction, entailing that the boundary layer is developing along the trailing-edge geometry (Avallone et al. 2016). Therefore, measurement and employment of the local properties of the boundary layer are necessary to accurately propagate the pressure fluctuations to the sound-pressure levels in the far field. Obtaining at the same time pressure spectra and velocity statistics beneath a turbulent boundary layer on a thin serration is a difficult task, due to the intrusive nature of available microphones, hot-wire probes, and high-frequency pressure sensors. The full thickness of conventional serrations is still a fraction of the size of common miniaturized microphones, fact that makes non-intrusive measurements extremely difficult. Therefore, recent works from the literature have tried to relate the change of the spectral content of the pressure fluctuations (Avallone et al. 2016, 2017) with the macroscopic flow properties of the incoming boundary layer (Moreau and Doolan 2013; Chong and Vathylakis 2015; Jones and Sandberg 2012). Several experimental (Oerlemans et al. 2009; Arce León et al. 2016a, b, c; Gruber et al. 2011) and numerical studies of the last decade (Jones and Sandberg 2012; Sanjosé et al. 2014; Liu et al. 2015; Sandberg and Jones 2011) have additionally shown that the size of typical microphone and pressure films is relatively large in comparison with the flow features associated with a turbulent boundary layer at the edge of a serration (Chong and Vathylakis 2015).

The evaluation of pressure from PIV is known as an alternative methodology for the indirect computation of pressure fluctuations. The use of the technique allows for a combined analysis of velocity and pressure fluctuations in turbulent boundary layers (Ghaemi et al. 2012a; van Oudheusden 2013; Schröder et al. 2011). In particular, by integration of the Navier-Stokes equations with the experimental velocity as input, a time-resolved series of pressure fields is generated. When compared to microphone measurements, the PIV-based pressure reconstruction allows obtaining a relatively higher spatial resolution (i.e., the resolution of the input PIV vector fields). On the other side, the state-of-the-art laser hardware rarely allows to match the much higher time resolution of a surface/far-field microphone, due to high-frequency limitations. Examples of recent experimental investigations have shown measurement rates achieved in tomo-PIV experiments which range from 2.7 kHz for airfoil trailing-edge applications (Ghaemi and Scarano 2011) and bluff body wakes (de Kat and van Oudheusden 2012) to 5–10 kHz for turbulent boundary layers (Ghaemi et al. 2012a; Schröder et al. 2008; Pröbsting et al. 2013). The substantial increase in acquisition frequency often comes at the expense of a further reduction either of the measurement volume or of the spatial dynamic range. Many studies have also focused on the implementation of the technique itself. With no claims to be exhaustive, later, in this manuscript, some details of the procedure will be briefly discussed, with the aim to allow the reviewer to get familiar with the methodology. These studies follow 2 decades of the literature on turbulent boundary-layer flows as reviewed in Marusic et al. (2010). As reviewed by van Oudheusden (2013), many improvements have been recently made on the technique to extend its range of applicability.

In the present work, a detailed analysis of the pressure fluctuations of serrated edges is obtained with results both from pressure reconstruction from time-resolved tomographic Particle Image Velocimetry (PIV) and from Lattice–Boltzmann numerical simulations (Succi 2001). The transition position in the numerical simulations is tuned to reproduce the experimental boundary-layer properties. In this way, all comparisons and observations can be extrapolated in those regions, where the PIV is deemed unreliable due to hardware limitations (Raffel et al. 2007). The aim of the study is to determine whether for serrated trailing edges, by measurement of the spatial variation of the boundary-layer characteristics, the pressure fluctuations can be still collapsed in a single profile. Therefore, the development of the pressure spectra subsequently along serrated trailing edges is also obtained from experimental results and compared to several analytical models of surface-pressure fluctuations found in the literature [e.g., (Goody 2004; Moreau et al. 2011)]. In Sect. 2, a description of the experimental setup and of the data-reduction techniques is presented. Section 3 focuses on the setup of the numerical simulations. Section 4 presents a detailed analysis of the experimental and numerical results. The presentation of results is carried out by first validating the tomographic and stereoscopic setup. Results are then briefly extended to the slitted serrations and to the analysis at positive incidence angle. The additional results are included to show that the scaling can be still used once the local parameters from the boundary layer are known. Section 5 concludes the discussion.

2 Experimental setup

2.1 Wind tunnel and wing model

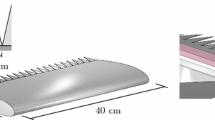
An un-tapered wing with aspect ratio AR = 2 and an NACA 0018 airfoil profile is employed for the study. The model with a chord length of c = 200 mm and a span s = 400 mm (Fig. 1) is installed in the low-speed V-tunnel of Delft University of Technology. In its original configuration, the open-jet wind tunnel was used with a contraction ratio of 60 and a test section of 400 mm × 400 mm with a free-stream turbulence intensity below 1%. The tunnel is operated at a free-stream velocity V_∞ = 20 m/s. In the current study, two angles of attack are presented: 0° and + 12°. Measurements are carried out at the suction side of the airfoil. Corrections for derivation of the actual flow angle due to the open jet can be found in Fuglsang et al. (1998). The correction factor to obtain the effective angle of attack is 0.55 (i.e., the actual angle of attack α* = 6.6° for a geometric one α = 12°).

Fig. 1

Wing, serrations, and slit dimensions

Boundary-layer transition to turbulent is forced by carborundum roughness elements of nominal grain size of 0.589 mm. The elements are randomly distributed over a 5 mm band extending along the entire span and located at x_tr = 0.2 c downstream of the leading edge (location in Fig. 1). The spanwise homogeneity of the turbulent transition front is verified with the broadband response of a removable microphone downstream of the roughness elements. The wing is manufactured using computer numerical-control machining (CNC) from an aluminum block with a surface roughness of less than 0.05 mm. Figure 1 shows the manufacturing of the modular trailing edge able to retrofit laser-cut solid and slitted serrations, as well as a straight trailing edge with minimum thickness of 1 mm. Serrations are characterized by their length 2 h and wavelength b, respectively, equal to 40 mm (2 h = 0.2 c) and 20 mm (b = 0.1 c). Slitted serrations are obtained with slots of 0.5 mm laser cut in the solid shape. The serration length is chosen to be equal to four times the length of the boundary-layer thickness based on 95% of the free-stream velocity [δ₉₅ based on XFOIL (Drela 1989) computations] for the tested chord-based Reynolds number of 270,000. A Cartesian coordinate system is defined in Fig. 2 with its origin chosen at the mid-plane location of the trailing edge. Its z-axis coincides with the trailing-edge direction, while the x-axis is aligned with the chord (i.e., aligned with the serration surface). It follows that the y-coordinate axis is orthogonal to the chord outward from the surface of the add-ons. A specific nomenclature is adopted for the entire study, as reported in Fig. 1: the straight trailing edge is referred to as “STE”, while “Sr20R21” and “Slit20R21” correspond to the serrated and slitted geometries with 2 h = 20% c and ratio (R) 2 h/b = 2/1.

Fig. 2

Schematic of the PIV setup with orientation of the Cartesian coordinate system

2.2 Stereoscopic particle image velocimetry setup

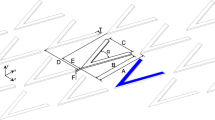
Time-resolved stereoscopic Particle Image Velocimetry (PIV) is employed to obtain time series of velocity fields at the trailing edge of the wing. A schematic of the PIV setup together with the Cartesian frame of reference is presented in Fig. 2.

A stereoscopic setup is realized by seeding the flow with tracer particles from an evaporated glycol-based SAFEX mixture with liquid droplets of about 1 µm. Illumination is provided by a Quantronix Darwin Duo laser (Nd:YLF, 2 × 25 mJ per pulse at 1 kHz). Laser optics form a light sheet with an approximate width of 80 mm and a thickness of 1.5 mm. Particle images are recorded by two Photron Fastcam CMOS cameras (1024 × 1024 pixels, 12 bit, 20 µm/px) equipped with a Nikon–Nikkor 105 mm focal-length macro-objective set at a diaphragm aperture f_# = 5.6. The stereoscopic setup features one camera orthogonal to the free-stream velocity direction and a second one at an angle of 35° with respect to the first one, in forward scattering with respect to the laser light. A Scheimpflug adaptor allows proper focusing of the camera that is inclined with respect to it. The final field of view (FOV) is obtained by de-warping the images acquired by both cameras into a single field, calibrated with a multi-plane target. With an overall distance of about 40 cm from the middle plane, the resulting magnification factor is about 0.23. An area of 2.8 × 5.5 cm² is imaged at a digital resolution of about 12 px/mm by combining the two sensors of 512 × 1024 px² (i.e., 1024 × 1024 px² reduced to 512 × 1024 px² for 10 kHz acquisition) to a 2D-3C stereoscopic plane of 340 × 660 px². The most relevant stereoscopic PIV parameters are summarized in Table 1.

Table 1 Experimental parameters for the 2D-3C stereoscopic PIV setup

Vector fields are acquired at three different z/b locations as indicated in the detail view of Fig. 2. The targets (red for the serrated case and black for the straight configuration) indicate the streamwise location at which the boundary-layer profiles are extracted in the results section. It has to be noted that the x coordinate of the red target varies together with the z one, following the serration edge. The minimum y-coordinate at which experimental data are available identifies the height at which statistics are extracted. Time-averaged flow fields and turbulent fluctuations are obtained from uncorrelated flow fields recorded with an acquisition frequency of 250 Hz. Time-resolved data are instead acquired at a frequency of 5 kHz (i.e., with a frame separation of 200 µs) with a pulse separation time of 100 µs, further rearranged in a 10 kHz sequence (free-stream particle displacement of 24 px at 20 m/s). Time-averaged flow fields and statistics from uncorrelated fields are recorded with a lower pulse separation time of 50 µs, with a maximum of 12 px in the free stream. Data ensembles of 2000 samples per test case are taken. Laser and cameras are synchronized by means of a LaVision HighSpeed Controller. The LaVision DaVis 8.1 software is used for acquisition and processing. A multi-pass algorithm (Soria 1996) with window deformation (Scarano 2002) is used to compute the velocity fields. Spurious vectors representing less than 5% of the total number are removed and linearly interpolated with the surrounding ones by use of a median filter (Westerweel and Scarano 2005) with a kernel of 5 × 5 vectors. A final interrogation window size of 16 × 16 px² with an overlap of 75% is employed, resulting in a final resolution of 1.1 × 1.1 mm² and a final vector spacing of 0.3 × 0.3 mm². A spatial dynamic range of SDR = 31 is computed by considering the largest measurable flow motion equal to the FOV length and the smallest resolvable spatial variation equal to twice the resolution (Ghaemi and Scarano 2011). Estimation of the smallest and largest scales of coherent structures within the turbulent boundary layer is carried out by evaluating those having a lifetime long enough to contribute to the statistics. The smallest ones are equal to about 20 viscous wall units y⁺ (Stanislas et al. 2008), approximately y⁺ = 20 (y = 0.830 mm), where y⁺ is estimated following Clauser and the more general Musker methodology (Clauser 1954). The largest structures of interest are large-scale motions (LSMs) with a typical streamwise extent of three times the boundary-layer thickness (Adrian 2007), the minimum size of which is 13.3 mm in this study. In this experimental investigation, the ratio between the LSMs and the smallest coherent structures is W_st = 48, corresponding to SDR/W_st = 0.65, comparable to similar experimental studies (Ghaemi et al. 2012a; Pröbsting et al. 2013).

2.3 Tomographic particle image velocimetry setup

A tomographic PIV setup (Elsinga et al. 2006) is built in a multi-pass light-amplification configuration (Schröder et al. 2008; Ghaemi and Scarano 2010) to allow for integration of the pressure fluctuations in 3D from the measurements of the three velocity components within the illuminated volume (Fig. 3). The setup is built from a similar equipment (laser and 4 cameras instead of 2) as detailed in the stereoscopic 2D-3C configuration in Sect. 2.2.

Fig. 3

Schematic of the Tomographic PIV setup with a multi-pass light-amplification approach (Schröder et al. 2008; Ghaemi and Scarano 2010)

The illumination of the volume is obtained with a multi-pass light-amplification approach to increase the signal-to-noise ratio in a volume of about 55 × 7 × 30 mm³ (streamwise, wall normal, and spanwise directions). The imaging system consists of 4 Photron Fast CAM cameras equipped with a Nikon Nikkor 105 mm focal-length macro-objective set at f_# = 11. The digital resolution in the domain is 15.5 voxel/mm. For each configuration, a sequence of 10,000 particle images was recorded at an effective acquisition frequency of 10 kHz (pairs of particle images were acquired at 5 kHz with ∆t = 100 µs). Illumination and imaging systems were synchronized and controlled by means of a LaVision HighSpeed Controller. The LaVision DaVis 8.1 software was used for data acquisition. The sequential motion-tracking enhancement algorithm [SMTE (Lynch and Scarano 2015)] was used for volume reconstruction and correlation. A final interrogation volume size of 20 × 20 × 20 voxels (0.9 × 0.9 × 0.9 mm³) with an overlap factor of 75% was employed, resulting in a spatial dynamic range SDR = 35, with the smallest resolvable spatial variation considered to be twice the interrogation volume size (Ghaemi and Scarano 2018). Relevant values of the experimental setup are summarized in Table 2. The same estimation carried out with the stereoscopic setup quantifies the size ratio of the LSMs to the smallest coherent structures to W_st = 48, corresponding to SDR/W_st = 0.70. This ratio is close to the one estimated for similar experimental studies (Pröbsting et al. 2013; Ghaemi and Scarano 2018).

Table 2 Experimental parameters for the 3D PIV setup

2.4 PIV velocity uncertainty quantification

The velocity fields used for statistics are derived from the stereoscopic PIV setup, while the pressure fields are integrated from the tomographic PIV results. Therefore, while in this section the velocity uncertainties from the stereoscopic velocity fields are discussed, the ones pertaining to the pressure reconstruction are presented in the next one. The main sources of uncertainty in the velocity, as obtained from the stereoscopic PIV setup of this study, are: peak locking, finite spatial resolution, stereoscopic calibration, and cross-correlation sampling uncertainties. Errors due to peak locking are quantified by comparing the size of the imaged particles with their actual size on the sensor. With a digital resolution of 12 px/mm, a magnification factor of 0.26, and a diaphragm aperture of 5.6, the imaged particle on the sensor is about 9 µm (Adrian and Yao 1985), way below the camera pixel pitch equal to 20 µm/px. To avoid peak-locking problems, a defocusing procedure is applied to the raw images by slightly displacing the focus plane from the laser one (Westerweel 1997). The previous method allows keeping the imaged particle on the sensor in the range between 1–1.5 px, thus obtaining a stochastic distribution of round-off errors in the computed velocity field. The absence of considerable peak-locking effects is a-posteriori verified by plotting the histogram of the round-off value of the particle vector displacements. Errors due to the modulation by finite spatial resolution of the resulting velocity fields may also influence the measured flow structures. With the multi-pass cross-correlation algorithm featuring window deformation, the length scale of flow structures measured with less than 5% modulation has to be larger than 1.7 times the window size (Schrijer and Scarano 2008). Having a window size of 1.3 × 1.3 mm², flow structures down to 1.5 mm can be measured with a 95% accuracy. Errors due to stereoscopic calibration are mitigated by an iterative self-calibration (Raffel et al. 2007) procedure and applied to further improve the fitting of the de-warped images from the calibration-target location to the laser one. By employment of a polynomial fitting for the mapping of the images in LaVision DaVis, residual disparity-vector fields after de-warping of the images of less than 0.10 px are achieved, which are considered satisfactory to carry out the stereo cross correlation (Raffel et al. 2007). Random errors are mainly due to the cross-correlation algorithm. Due to the large dynamic range of vector displacements, errors have been found to vary with respect to the region of interest in the boundary layer. With 2000 uncorrelated samples per test case, errors on the instantaneous fields amount to less than 1% V_∞ in the free-stream region and less than 3% V_∞ in the boundary layer. Quantification of the overall level of uncertainty when considering the size of the statistical sample assesses the final uncertainty on the mean velocity to 0.05% V_∞ and on the root-mean square to 2% V_σ (where V_σ are the velocity fluctuations as root-mean square of the instantaneous values). The method used to estimate the previous values is validated with the work of Wieneke (2015).

2.5 Evaluation of the pressure fluctuations

Before discussing the uncertainties in the pressure fluctuations, the methodology to retrieve the pressure information from the velocity one is here briefly explained. The flow pressure is obtained by means of a Poisson solver that integrates the pressure gradient computed from the Navier–Stokes momentum equation using the tomographic PIV velocity fields as input (Baur and Köngeter 1991). When considering a stationary orthonormal Cartesian frame of axis and the respective velocity vector $\vec {V}$, the pressure gradient reads (Anderson Jr 1985):

$$\nabla p= - \rho \frac{{{\text{D}}\vec {V}}}{{{\text{D}}t}}+\mu {\nabla ^2}\vec {V}= - \rho \left( {\frac{{\partial \vec {V}}}{{\partial t}}+\vec {V} \cdot \nabla \vec {V}} \right)+\mu {\nabla ^2}\vec {V},$$

(1)

where p, ρ, and µ are, respectively, the flow pressure, density, and dynamic viscosity, while $\partial$ and D represent the partial and material (or total) flow derivatives. The right-hand side of Eq. 1 can be implemented either in the Lagrangian or in the Eulerian form, respectively, adopting the material derivative or a combination of the temporal/spatial derivatives of the flow velocity (Fig. 4). Recent studies have shown that the particular choice of the discretization has a relevant effect on the accuracy of the reconstruction of the pressure from PIV (Charonko et al. 2010). In addition, it has been also reported that the Lagrangian approach is relatively more accurate with time-resolved data, mainly because seeding particles can be followed for a finite sequence of time instants (de Kat and van Oudheusden 2012; Liu and Katz 2006). In the present study, the material derivative of the velocity is estimated using a least-squares fit of the velocities along a reconstructed particle trajectory in a similar way as in Pröbsting et al. (2013).

Fig. 4

Schematic of the Eulerian discretization of the derivatives (left) and of the Lagrangian approach for the material derivative calculation (right)

The main changes with respect to the latter implementation are the employment of a stencil with n = 2 (i.e., 5 vector fields) and m = 2 (i.e., 2nd order approximation of the flow curvature), which has been found to give already converged results for the time spectra. Boundary conditions are set by computing the normal components of the pressure gradient and used as Neumann boundary conditions on the left (incoming boundary layer), right (wake flow), and bottom (serration surface or airfoil wake) boundaries (Anderson Jr 1985). A Dirichlet-type boundary condition is applied at the top of the boundary layer. For such a condition, a known pressure based on the average velocity field is obtained from Bernoulli’s equation:

$$p={p_\infty }+\frac{1}{2}\rho \left( {V_{\infty }^{2} - {{\left| {\vec {V}} \right|}^2}} \right),$$

(2)

where p_∞ and V_∞ correspond to the free-stream values. The Dirichlet condition is lowered down to the wall-normal location of 0.2 δ in a similar study as the one of Ghaemi et al. (2012a), which showed a negligible effect on the calculated wall pressure as well as a more accurate representation of the relatively larger velocity fluctuations. In the last 2 decades, several approaches have been proposed for the specific problem of the pressure integration. The pressure field can be calculated by a direct spatial-integration scheme starting from given values as boundary conditions [as, for example, in the work of Baur and Köngeter (1991) or Liu and Katz (2006)]. The present work follows a similar approach, but proposed by Gurka et al. (1999) and later by De Kat (2012), whereby the problem is formulated in terms of the Poisson pressure equation obtained by applying the divergence operator to Eq. 1. The solution of the Poisson equation is obtained by an additional discretization of the grid in a second-order accurate central-difference scheme (5-point stencil). The resulting system of linear equations is solved by a pre-conditioned iterative method (GMRES) as in a similar study from the authors (Ragni 2012).

2.6 Uncertainty on the pressure fluctuations

The uncertainty analysis for the measured tomographic PIV velocity fields is performed by taking into account the iterative approximation of the fluid-particle path (Ghaemi et al. 2012a). The main systematic error in the time-resolved evolution of the velocity fields used for the reconstruction of the flow pressure is caused by the particle acceleration between the multiple vector fields. Boillot and Prasad (1996) quantify this error as:

$${\epsilon _{u,{\text{sys}}}}[m]=\frac{1}{4}\Delta {t^2}\left| {\frac{{{\text{D}}\vec {V}}}{{{\text{D}}t}}} \right|,$$

(3)

where D$\vec {V}$/Dt is the measured particle acceleration obtained by processing multiple exposure arranged in the time sequence along t. With a typical measured particle acceleration in the boundary layer of about 1–3 × 10³ m/s² [larger than in the study of Ghaemi et al. (2012a) due to the local airfoil acceleration], the systematic error in the velocity fields is estimated to be about 7.5 µm (0.09 px). The final expression of the error on the pressure with the Lagrangian method is obtained from two components: the first due to the truncation of the derivative and the second due to random components on the velocity fields [cfr. studies of Ghaemi et al. (2012a) in boundary layers and Violato et al. (2011) in jets]:

$${\epsilon _{\text{p}}} \approx \rho ds\left( {{\epsilon _{{\text{Lag,tru}}}}\left[ {\frac{m}{{{s^2}}}} \right]+{\epsilon _{{\text{Lag,vel}}}}\left[ {\frac{m}{{{s^2}}}} \right]} \right) \approx \rho ds\left( {\frac{1}{2}{{\left( {n\Delta t} \right)}^2}\left| {\frac{{{\text{D}}\vec {V}}}{{{\text{D}}t}}} \right|~\frac{{\left| {\nabla \cdot \vec {V}} \right|}}{{\Delta t}}+\frac{{{\epsilon _V}}}{{2n\Delta t}}} \right),$$

(4)

where ds is the actual vector spacing and n is the stencil of the 2n vector field used for the material derivative computation. We hereby assume that the Poisson integration does not add significant error to the pressure evaluation (de Kat and van Oudheusden 2012). With a truncation error of about 120 m/s² with n = 2, an acceleration of 3 × 10³ m/s², and a typical random one of 90 m/s², the total error on the pressure results to about 0.08 Pa.

3 Computational setup

3.1 Flow solver

The intensity and spectra of the pressure fluctuations estimated from PIV data are compared to the ones obtained from 3D unsteady numerical simulations performed with a Lattice–Boltzmann method (LBM) solver. This particular method provides with an accurate representation of the aerodynamic and aeroacoustic fields when applied to complex flow problems (van der Velden et al. 2016a). The commercial software 3DS-Simulia PowerFLOW-Flow 5.4b is adopted in this study. The solver employs a discretization of the Lattice–Boltzmann equation with 19 degrees of freedom in 3 dimensions (D3Q19). The particular discretization is suitable for an accurate approximation of the Navier–Stokes equations for a perfect gas at low Mach number in isothermal conditions (Chen et al. 1992). A detailed description of the method together with the equations can be found in the work of Succi (2001). The algorithm solves the distribution of particles with the LB equation on a Cartesian mesh, known as lattice. A specific explicit time integration and a collision model are used for the particle distribution g_i along the ith lattice direction:

$${g_i}\left( {\vec {x}+{{\vec {c}}_i}\Delta t,t+\Delta t} \right) - {g_i}\left( {\vec {x},t} \right)={C_i}\left( {\vec {x},t} \right).$$

(5)

The distribution g_i describes the particle motion at position $\vec {x}$ with discrete (microscopic) velocity ${\vec {c}_i}$ in the lattice. ${C_i}\left( {\vec {x},t} \right)$ is the particle collision term for which the Bhatnagar–Gross–Krook (BGK) model (Chen et al. 1992; Bhatnagar et al. 1954) is adopted. The details of the approximation of the particle-collision term with a Maxwell–Boltzmann distribution approximated by a second-order expansion of the particle kinetic terms can be found in the study of Chen et al. (1992). The macroscopic flow quantities are derived from integration of the particle distribution function and from the microscopic velocities. This allows the solver to obtain both the flow density ρ and the velocity $\vec {V}$ from an integration procedure on the lattice points:

$$\rho \left( {\vec {x},t} \right)=\mathop \sum \limits_{i} {g_i}\left( {\vec {x},t} \right);~~~~~~~~~\rho \vec {V}\left( {\vec {x},t} \right)=\mathop \sum \limits_{i} {\vec {c}_i}{g_i}\left( {\vec {x},t} \right).$$

(6)

By integrating the flow variables on the lattice points, the procedure allows reducing many of the problems associated with the inaccuracies due to the differentiation on the mesh-grid points that typical finite-difference solvers possess. A Very Large Eddy Simulation (VLES) model is implemented to take into account effects of unresolved scales of turbulence in the lattice grid. Details on the specific model can be found in the work of Yakhot and Orszag (1986). To reduce the computational time of the solution, the resolution at the wall is kept at three viscous wall units and a wall model is used for the approximation of the no-slip boundary condition. Details on the formulation used for the boundary-layer approximation and on the generalized law-of-the-wall model (Launder and Spalding 1974) to take into account the local pressure gradient can be found in another study from the author (Avallone et al. 2018). The compressible and time-dependent nature of the transient CFD solution and the low dissipation properties of the LB scheme (Brès et al. 2010) allow extracting the sound pressure from the near field up to a cut-off frequency corresponding to approximately 15 voxels per acoustic wavelength. In the far field, noise is computed using the Ffowcs–Williams and Hawkings (FWH) equation. The formulation 1A, developed by Farassat and Succi (1980) and extended to a convective wave equation, is used in this study (Brès et al. 2010). Integrations are performed on the surface of the airfoil, where the unsteady pressure is recorded with the highest frequency rate available on the finest mesh resolution.

3.2 Computational test case

Numerical computations are performed for a clean and serrated NACA 0018 wing of chord c = 200 mm and span s_LBM = 80 mm (s_LBM/c = 0.4). The spanwise dimension of the mesh is chosen as a compromise between the computational costs associated with the simulations and the possibility to simulate as many serrations as possible. In the present study, a maximum of four serrations is achieved. Free-stream velocity and angle of attack are kept at 20 m/s and 0°, corresponding to the experimental free-stream Mach number of 0.06 and a chord-based Reynolds number of 270,000. The turbulence intensity of the free stream is set to 0.1%, slightly lower than the one of the experimental one, reported to be between 0.5 and 1%. The simulated trailing-edge thickness is kept equal to the experimental one (1 mm), originally chosen to avoid any tonal noise component due to vortex shedding (t_a/δ ≈ 0.1 < 0.3 critical value, where t_a is the airfoil thickness and δ is the expected boundary-layer one at the tested Reynolds, as verified in Table 2) (Bearman 1965). The boundary-layer transition is forced to turbulent by a zig–zag strip of height 3 × 10⁻³ c (0.6 mm), streamwise length of 15 × 10⁻³ c (3 mm), and wavelength of 15 × 10⁻³ c (3 mm) placed on both sides of the airfoil at 20% of the chord. The height of the serrated strip approximately corresponds to half of the incoming laminar boundary-layer thickness at the strip location. Serrations are exactly replicated as in the experiments (i.e., length 2 h = 0.2 c = 40 mm and wavelength b = 0.1 c = 20 mm).

A sketch of the geometry and of the adopted Cartesian coordinate system is shown in Fig. 5. The Cartesian frame is identical to the experimental one. The size of the simulated domain is 12 c in both streamwise/wall-normal directions and s in the spanwise one. Periodic boundary conditions are applied on the lateral faces of the domain. An anechoic outer layer is used to damp-out the outward radiating and the inward reflected acoustic waves outside a circular refinement zone of diameter equal to 10 c. A total of 10 mesh-refinement regions with a resolution-increase factor of 2 are employed. The refinements allow placing the first cell at the wall of the geometry in the viscous sub-layer at 3.9 × 10⁴ c = 0.078 mm above the trailing-edge location, corresponding to y⁺ = 3. The rest of the airfoil boundary is discretized with one coarser level of resolution. In total, approximately 150 million cubic cells (voxels) are used for the discretization of the domain. A mesh-resolution study has been carried out to assess the convergence of the boundary-layer characteristics at the trailing-edge location and the far-field noise with respect to the experiment of the same authors (Arce León et al. 2016). The accuracy of the discretization is also validated by comparing the results with experimental data. The flow simulation time is 0.3 s (30 flow passes) requiring 6,300 CPU hours on a Linux Xeon E5-2690 2.9 GHz platform. The physical time step corresponding to Courant–Friedrichs–Lewy (CFL) number of 1 in the finest mesh-resolution level is 1.3 × 10⁷ s. The unsteady pressure on the airfoil surface is sampled with a frequency of 30 kHz (St_a = f_ac/V_∞ = 300) for a physical time of 0.2 s (20 airfoil flow passes). The flow data are down-sampled in a uniform grid with 0.1 mm (i.e., more than 5 times the resolution obtained with the PIV setup) for visualization and comparison with the experimental measurements. The described methodology has been validated in a previous study by van der Velden et al. (2016a). Given the periodicity of the serrations, the computed fields are spatially averaged along the spanwise direction, as well as over their top and bottom sides. The average is carried out along points with the same relative location with respect to the serration root. This procedure reduces the uncertainty on the mean values as well as increases the number of samples available for the spectra evaluation (Jones and Sandberg 2012).

Fig. 5

Computational test case and schematics of the interpolation for visualization and PIV comparison

3.3 Grid-resolution study

A grid-resolution study is carried out to verify the convergence of the aerodynamic/aeroacoustic fields with respect to the grid spacing. Four grids are investigated by sequentially doubling the resolution in the whole domain: a coarse grid with minimum voxel size of y⁺ = 12, a medium one with y⁺ = 6, a fine one with y⁺ = 3, and a very fine one with y⁺ = 1.5. The boundary-layer thickness at the TE of the airfoil in its clean straight configuration is used as integral parameter for the grid-resolution study. The parameter is plotted versus the grid factor N^2/3 in Fig. 6, where N is the total number of voxels (i.e., consecutive N correspond sequential doublings of the domain resolution). Figure 6 shows that a converged boundary-layer thickness is obtained for the fine resolution case y⁺ = 3. The Richardson extrapolation (Richardson 1910) with a refinement ratio of r = 2 and order of convergence of p = 3, plotted as dashed line in Fig. 6, verifies the convergence of the hydrodynamic flow field. An additional verification of the convergence of the results with the grid spacing is carried out as indicated by Roache (1994) with the grid-convergence index GCI, function of the fractional variation of the consecutively computed boundary layers ϵ = (δ_N+1δ_N)/δ_N and of the parameter r^p, where r is the grid ratio and p is the order of the method. It is found that GCI_2,3 = 2.36% and GCI_1,2 = 0.30% for the fine and very fine grid resolutions, respectively. Their ratio approximate r^p with a 2% of accuracy, which is sufficient to ensure that both grids are in the asymptotic range of convergence (Roache 1994).

Fig. 6

Grid-resolution study: boundary-layer thickness at x/c = 0 for different lattices. The dashed line indicates the Richardson extrapolation (1910), while the square tick indicates the resolution adopted for the study in the manuscript

Based on the previous considerations, the fine grid resolution is used for the rest of the study. Boundary-layer parameters as extracted from the solution of the fine computation are summarized in Table 2.

4 Results and analysis

The presentation of results is carried out by first validating the stereoscopic and the tomographic PIV setups. In particular, given that the stereoscopic PIV setup has a relatively broader wall-normal elongation and a relatively higher resolution, its results are used as reference for velocity comparisons between the experimental and the numerical data. When extending the analysis to the pressure information instead, the 3D data from both experiments and simulations will be employed. The integral parameters of the turbulent boundary-layer convecting past the trailing edge of the NACA 0018 airfoil are additionally measured by PIV and compared to numerical simulations. In the first two paragraphs of this section, both repeatability and reproducibility of the results are, therefore, verified using the experimental data against computations. In the present study, it is also verified that at the root location, coherently with results from the literature (Arce León et al. 2016), the incoming boundary layer at the trailing edge at zero angle of attack is found comparable to the one with and without add-ons. However, due to reasons of conciseness, the additional evidence of the negligible upstream effect of the serrations is omitted in this paper.

4.1 Comparison of planar and tomographic PIV results

Although differences between stereoscopic and tomographic setups for studies of boundary layers have already been addressed in the literature [e.g., in Ghaemi et al. (2012b)], in the present section, a clear comparison between the planar and tomographic results is carried out to verify that both experimental realizations can be interchangeably compared with the numerical ones. Figure 7 shows a 3D visualization of the boundary layer on top of a single serration. Iso-surfaces of velocity magnitude normalized by the free-stream values show different layers of increasing velocity organized in streaks with hairpin-like structures visualized through iso-surfaces of Q-criterion in the main flow direction [similar to the previous studies (Stanislas et al. 2008; Ghaemi and Scarano 2018; Schröder et al. 2007)].

Fig. 7

Iso-surfaces of magnitude of velocity normalized by the free-stream one with iso-surface of q-criterion. The origin of the serration follows the origin of the Cartesian frame in Fig. 2

In Fig. 8, the reproducibility of the flow field in both 3D and 2D setups is assessed by comparing the tomographic results to the stereoscopic ones. Mean boundary-layer profiles of the streamwise velocity component and streamwise and wall-normal turbulent fluctuations of the streamwise and wall-normal velocity components are extracted at the serration origin (x/c = 0 and z/c = 0). A general good agreement is appreciated between the 2D and 3D PIV data. Turbulent fluctuations measured with the tomographic setup additionally indicate a small amplitude modulation due to a combined effect of the different spatial resolution and the use of a 3D correlation algorithm. The boundary layer is well represented in both realizations, even if the illuminated volume is in fact smaller than the full boundary-layer thickness for the 3D tomographic setup (due to hardware limitations). This will be considered in the evaluation of the pressure from the tomographic setup as explained in the following sections.

Fig. 8

Comparison of boundary-layer profiles and fluctuations of streamwise and wall-normal turbulent fluctuations $\overline {{uu}}$ and $\overline {{vv}}$ between 2D stereoscopic and 3D tomographic PIV setups for Sr20R21 at z/b = 0. Dashed lines indicate the boundary-layer fit with log law (L.L.) and with the viscous extrapolation to the wall (V. L.) with k = 0.40, B = 5, u_τ = 0.46 m/s (White 2006; Musker 1979)

4.2 Turbulent boundary-layer comparison, PIV results against LBM data

Once verified that the results between the stereoscopic and the tomographic PIV setups are reproducible and that the same boundary-layer shape can be obtained, a second comparison with the numerical results is carried out. In particular, given the slightly higher resolution of the stereoscopic data with respect to the tomographic one, the first ones are used as reference in the following velocity-based graphs. Contours of mean velocity and Reynolds stresses are compared for the airfoil with the straight trailing edge at 0° angle of attack in Fig. 9. In Fig. 9 (top row), contours of magnitude of the flow-velocity variation normalized with respect to the free-stream value are plotted at the trailing edge of the airfoil. Strong similarities are visible between experiments and computations. A slightly faster re-alignment of the flow to the free-stream direction is noted in the numerical results. This small imperfection could be due to the non-exact representation of the tunnel blockage in the computations, carried out without the side walls of the experiment. Boundary-layer profiles perpendicular to the serration surface are extracted at the location indicated with the solid line (x/c = 0) and plotted in Fig. 9. Boundary-layer integral parameters are obtained from the profiles in Fig. 9 and are presented in Table 3. From analysis of the u⁺ plots in Fig. 9, good agreement is found between the experimental boundary layer and the computational one.

Fig. 9

From top to bottom: normalized mean-velocity magnitude |V|/V_∞ − 1, mean streamwise velocity, and Reynolds stresses profiles from stereoscopic PIV (P) and LBM (L). At the bottom, comparison of the mean streamwise and Reynolds stresses for the clean trailing-edge STE

Table 3 Boundary-layer characteristics estimated from PIV and LBM for the STE case (x/c = 0), extracted at the black-line location of Fig. 9

In addition, turbulent fluctuations are further presented in Fig. 9. For the same reasons, due to the symmetry of the flow and the higher contribution of the in-plane components of the turbulent stresses for the noise (Arce León et al. 2016), the verification of the out-of-plane velocity component is still carried out in this study, but omitted from the plots. Intensities of $\overline {{uu}}$ and of $\overline {{vv}}$ are plotted as normalized by the square of the free-stream velocity in Fig. 9. Despite the difference in magnitude, similar profiles are found between the stereoscopic PIV and LBM Reynolds profiles. The first reliable vector from the PIV results is at y⁺ = 30, corresponding to about one window-size distance from the wall. Experimental results still show a clear spatial-resolution modulation of the maximum values of $\overline {{uu}}$ and $\overline {{vv}}$ profiles at y⁺ = 50,100—[already seen in a similar study (Van der Velden et al. 2016b)]. Boundary-layer parameters at the trailing-edge location (x/c = 0) are summarized in Table 3. Although not extremely relevant for the present study, information on the spanwise correlation length and on its role with respect to the prediction of the noise reduction can be found in a separate study from the authors (Avallone et al. 2018) (i.e., l_z/δ = {0.63–0.48} at St_c = {10–15} for serrated edges and l_z/δ = {0.5–0.43} at St_c = {10–15} for the straight configuration). It has to be noted that despite the efforts in measuring and simulating the flow field with the highest available resolution, still, a clear gap exists between the first point in the boundary layer and the y⁺ value. Therefore, an attempt is made to obtain the skin-friction coefficient via the formula of Spalding (1961): u_τ = V_e (C_f/2)^1/2, where the friction velocity u_τ is calculated from the full boundary-layer fit with the generalized log law from Musker (1979) and the edge velocity V_e.

Beside a reasonable agreement between PIV and LBM, major differences are found in the values of the edge velocity, which could confirm the non-exact representation of the blockage between experiments and simulations. In the present study, such a location is obtained as the one, where the boundary-layer spanwise vorticity becomes negligibly small [see Spalart and Watmuff (1993) and Balint et al. (1991)]. However, computations and experiments well agree on the displacement and momentum thickness of the boundary layer, respectively, equal to δ^* = 3.7 mm and θ = 1.7 mm. The shape factor H = δ^*/θ of approximately 2.1 is typical of turbulent boundary-layer applications (Green et al. 1973; Zarbi et al. 1990) and it is found similar to the experimental ones. The results additionally well compare with the predictions from XFOIL (Drela 1989), even though with a definitely higher displacement thickness than expected at the same conditions (δ^* ~ 2.5 mm). This is most probably caused by the experimental forcing of the transition obtained with scattered roughness elements of carborundum. The previous procedure, in fact, does not fully represent the ideal transition obtained by imposing a prescribed N-critical location in XFOIL. In a similar study from the authors (Avallone et al. 2018), the far-field acoustic spectra obtained from the numerical computations (FWH analogy described in Sect. 3.1) are additionally compared to the results from the microphone array from of Arce-Leόn et al. (Arce León et al. 2016), obtained with the same airfoil and serrations. The present verification is additionally carried out to verify the correct simulation of the serrated devices, producing a positive reduction of broadband noise (Avallone et al. 2018).

4.3 Mean surface-pressure distribution obtained from tomographic PIV and LBM

In this section, the mean velocity and surface pressure as obtained from tomographic PIV are presented and later compared to the results from LBM. The aim of the section is to show how a gradual change of pressure-fluctuation magnitude is built up, already at 0 angle of attack, along the edge of the serration. As already mentioned, in the remainder of the paper, velocity statistics will be plotted as obtained from the stereoscopic PIV results, while for the pressure profiles and contours, the tomographic results will be used (also indicated in the captions). PIV results are first presented in Fig. 10, in terms of normalized mean-velocity variation |V|/V_∞ − 1 and in terms of mean and fluctuating pressure coefficient, referred to as $\overline {{{c_{\text{p}}}}}$ and ${c_{{\text{p~rms}}}}~$, respectively. Masked regions correspond to areas, where the signal-to-noise ratio is too low for cross correlation (e.g., high reflections or serration shadows). To be noted that the integration mask of the pressure algorithm accounts for an additional point, due to the wrong gradient closed to the wall. The mean-velocity contours in Fig. 10 (first row) show flow features pertaining to a turbulent boundary layer developing at the trailing edge of the airfoil. A mild pressure recovery at the trailing edge with maximum intensity of approximately 0.10 is reported from the mean pressure coefficients of Fig. 10 (second row). Coherently with the formation of a viscous wake, the mean free-stream pressure coefficient is not recovered. Very small differences can be seen in the mean velocity and pressure fields when moving along the serration edge, i.e., by changing both spanwise and streamwise locations.

Fig. 10

Normalized mean-velocity magnitude |V|/V_∞ − 1, mean pressure coefficient $\overline {{{c_{\text{p}}}}}$ and its fluctuations ${c_{{\text{p~rms}}}}$ obtained from tomographic PIV. NACA 0018, Re = 270,000, α = 0°, V_∞ = 20 m/s

Similar conclusions can be drawn extending the comparison to the fluctuating pressure components in the third row of Fig. 10. The straight configuration shows larger fluctuations with respect to the serrated case in the wall-normal direction (e.g., Fig. 10 STE c_prms). The presence of the serration mitigates the magnitude of the pressure fluctuations at the root (Avallone et al. 2016). This is confirmed by results extracted at different spanwise locations along the serrations, indicating pressure fluctuations gradually decreasing in magnitude towards the tip of the geometry. An increase in fluctuations very near the edge (x/2h = 2) of the domain is reported due to the relatively stronger uncertainty of the velocity vectors and their derivatives in this outer part.

In Fig. 11, the stereoscopic PIV results are used for the extrapolation of the u⁺ and the profiles of turbulent fluctuations, respectively, normalized by the friction velocity and by the square of the free-stream one. Both $\overline {{uu}}$ and $\overline {{vv}}$ contributions show a boundary-layer profile which peaks at about y⁺ = 100 to further decrease down to the wall. Results from Fig. 11 also indicate a clear reduction of the boundary-layer thickness towards the tip of the serration (cfr. u⁺ profiles). Coherently with what remarked in the previous studies (Avallone et al. 2016; Arce León et al. 2016), the lowering of the fluctuations along the edge shown in Fig. 11 also suggests that the flow is subjected to a mild acceleration in the streamwise direction, due to the protruding add-on. Whether the remarked flow acceleration and change of the maximum turbulent fluctuations along the serration edge is associated with a change of surface-pressure fluctuations is an important question to be answered. As already anticipated in fact, a rapid change of the pressure fluctuations (i.e., mean values and spectra) along the serration edge is typically not taken into account in the state-of-the-art models for scattering of pressure fluctuations (Lyu et al. 2016).

Fig. 11

Mean streamwise velocity profile u⁺ and Reynolds stresses $\overline {{uu}}$, $\overline {{vv}}$ at three different spanwise locations along the serration edge. Stereoscopic PIV and numerical LBM results. Boundary-layer fit with k = 0.40, B = 5, u_τ = 0.46 m/s (White 2006)

The variation of the pressure fluctuations along the serration is analyzed in Fig. 12 by extracting the profiles at the same locations of Fig. 11. It has to be noted that in Fig. 12, the consistent gap in resolution between PIV and LBM is relevant. Bernoulli pressure fluctuations are also added, as obtained by converting the velocity fluctuations into pressure with the conventional expression p* = p_∞ + 1/2ρ_∞(V_∞² − |V|²) and compared to the static values. The latter represent the maximum pressure associated with the pure kinetic motion of the fluid with respect to the actual pressure that is exerting at that location. In Fig. 12, it can be seen that while the velocity fluctuations reduce (together with the dynamic pressure associated with it) close to the wall, static-pressure fluctuations maintain the same intensity as in the buffer layer. Most importantly, they peak at the same vertical location, as the presented turbulent fluctuations do in Fig. 11.

Fig. 12

Mean pressure coefficient $\overline {{{c_{\text{p}}}}}$ and pressure fluctuations ${p_{{\text{rms}}}}$ as obtained from tomographic PIV, normalized by free-stream dynamic pressure at three streamwise locations along the edge. The Bernoulli pressure is indicated with *. Dashed lines indicate $\overline {{{c_{\text{p}}}}}$ obtained using the boundary-layer fits from Fig. 11

A change of the maximum of the pressure fluctuations along the edge is additionally shown in Fig. 12 when moving across different spanwise locations. The previous observation is also in line with the previous velocity results showing a reduction of the boundary-layer thickness (Avallone et al. 2016; Arce León et al. 2016). A correspondence is also found for the maximum of pressure fluctuations decrease in the buffer layer with respect to the turbulent fluctuations $\overline {{uu}}$ and $\overline {{vv}}$ in Fig. 11 driven by the flow acceleration. Finally, as shown by the two rows of plots in Fig. 12, the decrease of the intensity of the pressure fluctuations is not due to the simple decrease of the kinetic energy in the flow (or equivalently of the velocity magnitude, cfr. Bernoulli pressure fluctuations). The decrease of the Bernoulli pressure-fluctuation profiles in Fig. 12 shows in fact a similar behavior in all cases from the root to the tip of the serration. In summary, results seem to point out that the main differences of the serration flow with respect to the previous analytical modeling can be summarized by:

• 1. A local change of the turbulent fluctuations driven by the flow acceleration dictated by the presence of the serrated geometry.

• 2. A gradual reduction of the amplitude of the maximum pressure fluctuations as well as of their values at the wall, along the edge of the serrations.

The previous two observations entail that the distribution of the pressure fluctuations statistically change along the serration. A factor of about 10 in $\overline {{{p^2}_{{{\text{rms}}}}}} /q_{\infty }^{2}$ is reported in this study in Fig. 13, well comparing to already similar results (Avallone et al. 2018) from numerical investigations. As a curiosity, it has to be noted that a similar gradual change of the pressure fluctuations has been reported by Chong and Vathylakis (2015), although with opposite sign due to their installation on a flat plate (in particular, without flow acceleration due to the airfoil shape and most importantly, due to the absence of flow on one of the two sides).

Fig. 13

Intensity of the mean pressure fluctuations $\overline {{p'p'}} /p_{0}^{2}$ as reported by the authors (Avallone et al. 2018) (corresponding to $\overline {{{p^2}_{{{\text{rms}}}}}} /q_{\infty }^{2}$ in this manuscript). Comparison between the results from the numerical study in the literature and the ones from tomographic PIV in this manuscript

4.4 Unsteady pressure-fluctuation analysis between tomographic PIV and LBM

The previous section has demonstrated a considerable change of the magnitude of pressure fluctuations along the serration. In the present section, the study is extended to the unsteady components, in particular to the spectra of the pressure fluctuations. The aim is to verify what the change along the edge is, and whether it can be accounted for by re-scaling the spectra with the local properties of the boundary layer. The gradual change of the mean pressure profiles shown in Sect. 4.2 could be in fact related to a change of the energy content associated with the flow structures convecting above the serration edge (Lyu et al. 2016). A comparison between experiments and numerical computations is plotted in Fig. 14, by means of surface spectra extracted along the edge of the serration. For clarity of visualization, the pressure spectra are plotted with respect to their frequency and normalized with respect to ρ²V_∞³δ^*. Spectra are evaluated using a periodogram approach with Hamming windows of 64 elements and 50% overlap. Fast Fourier Transform (FFT) is performed over 4096 elements, thus resulting in a frequency resolution of approximately 5 Hz. Figure 14 shows that both numerical and experimental spectra change along the spanwise direction in both magnitude and shape, rapidly decaying with frequency.

Fig. 14

Spectra of the pressure fluctuations, data from tomographic PIV, and numerical LBM results. NACA 0018, Re = 270,000, α = 0°, V_∞ = 20 m/s. Sr20R21 = serration with 2 h = 20%c, and ratio = 2 h/b = 2/1. PIV taken at the first y location

One of the most interesting finding of Fig. 14 is the fact that the pressure fluctuations also reduce in magnitude and frequency along the serrated edge. In particular, numerical simulations show that part of energy of the flow structures is shifted towards relatively higher frequencies (> 3 kHz in Fig. 14). However, below 2 kHz, a net spatial decrease of pressure fluctuations is reported from the root to the tip of the serration. It has to be noted that this spatial decrease might influence a rather larger frequency range when scattered to the far field, due to the particular geometry of the edge. Since the presented plots of Fig. 14 indicate that the frozen-turbulence hypothesis is not verified along the serrated edge, the main question to be answered is whether it is possible to model/re-scale such a change along the edge using the experimental parameters of the boundary layer as input. The verification of this approach would confirm the presence of a consistent boundary layer and pressure change through the serrated edge, contrarily to what assumed by previous literature. The numerical computations additionally show a cross-over frequency, corresponding to a point, where the pressure fluctuations at the serration edge become stronger (i.e., higher frequency content) than those ones from the straight trailing edge (or equivalently than the root ones). One of the main reasons of the difference is attributed to the limited frequency resolution of the PIV data.

The obtained spectral response of the pressure fluctuations for slitted serrations is also very similar to the solid ones. The spectral distribution of the pressure fluctuations as obtained from tomographic PIV is plotted in Fig. 15.

Fig. 15

Spectra of the pressure fluctuations at three locations along the edge. Experimental PIV data. NACA 0018, Re = 270,000, α = 0°, V_∞ = 20 m/s. Slits and Sr20R21 = serration both with 2h = 20%c, and ratio = 2h/b = 2/1

Two main observations can be drawn from a direct comparison of the solid and slitted serrations in Fig. 15:

• 1. The triangular porous surface of the slits still determines a variation of the pressure spectra along the streamwise direction.

• 2. Higher levels of pressure fluctuations at the root of the slitted sawtooth configuration with respect to the straight one are measured (in agreement with observation n.2).

When combining these two observations with measured results from the previous studies (Arce León et al. 2016a, b, c; Azarpeyvand et al. 2013), it becomes clear why this particular periodic slit configuration cannot reach the noise-reduction performance of the solid serrated counterpart in terms of far-field noise. In particular, the porous shape still presents a triangular shape which increases the amplitude of the pressure fluctuations at the root region, where the previous studies have demonstrated that the serrations are less effective (Avallone et al. 2017, 2018). Therefore, it becomes important to verify whether local information about the boundary-layer properties at the edge can be still used to scale (and later predict) the spectra of the pressure fluctuations.

The remainder of this section is left to this purpose, that is to find whether information of the local boundary-layer parameters along the serration could be sufficient to scale both magnitude and spectral distribution of the pressure fluctuations. If the previous hypothesis is proven to be verified, then it could be possible to implement such a streamwise modulation for a more accurate prediction of far-field noise. Different models are available in the literature for scaling of the surface-pressure fluctuations once known the characteristics of a particular turbulent boundary layer. Most of these models rely on the use of the initial boundary-layer thickness and skin-friction coefficient (i.e., free stream or the value at the TE). In Fig. 16, both experimental and numerical results are instead plotted along the serrated edge by scaling the pressure spectra with the local properties of the boundary layer, as summarized in Table 4. In this case, a clear collapse of the three profiles is found. Amongst edge velocity, boundary-layer momentum thickness, and skin-friction coefficient, the last two seem to play a dominant role in this study due to the higher relative variation, especially under mild pressure gradients. The skin-friction coefficient, extrapolated from the experiment and from the numerical simulations, shows in fact a constant increase until the tip of the serration (i.e., of a factor of less than 2 from the root one, corresponding to a thinner boundary layer). To compare the current collapse against assessed empirical models, Fig. 16 additionally includes four empirical models: respectively, the ones proposed by Smolyakov and Tkachenko (1991), Chase (1980) [formulation from Howe (1998)], Goody (2004), and the one of Moreau et al. (2011). Once comparing the results with respect to the behavior of the different models, it can be seen that most of them agree in the mid-range of frequency, while the models of Smolyakov and Tkachenko and Goody better maintain their agreement up to the highest investigated frequencies, respectively, for LBM and PIV results (about 1530 kHz, ω δ*/V_e ≈ 10¹ for numerical results and about 5 kHz, ω δ^*/V_e ≈ 10^0.5 from experimental ones). The better prediction from the two last models in turbulent boundary layers under a relatively low-pressure gradient is not new (Moreau et al. 2011); however, the particular collapse obtained by the current scaling has major repercussions for serrated devices. The change of pressure fluctuations along the edge [also confirmed by other studies from the same authors (Avallone et al. 2016)] follows from a linear increase of skin friction along the serration (cfr. Table 4 for scaling parameters), which can also be related to the thinner boundary layer at the edge of the serration with respect to the incoming one.

Fig. 16

Spectra of the pressure fluctuations obtained from experiments and computations compared with the model of Smolyakov and Tkachenko (1991), Howe (1998), Chase (1980), Goody (2004), and the one of Moreau et al. (2011) with linear change of the friction coefficient along the serration edge as in Table 4

Table 4 Boundary-layer parameters extracted from PIV and LBM: solid serrations

Table 5 Extrapolated parameters from PIV data, Re = 270,000, α = 12°

Analysis of the extrapolated parameters in Table 4 confirms that the skin-friction increase is proportional to the change in the boundary-layer displacement thickness for the solid serrations. Similar coefficients from Table 4 can be obtained for the slitted configuration z/b = [0, 0.25]; however, the obtained skin-friction coefficient (once calculated the effective boundary-layer thickness at z/b = 0.5) is indeed higher than the one for the solid configuration, confirming what already observed.

Although this could be caused by the relatively lower pressure gradient change along the serration, further investigations are needed to generalize such a statement. However, it is important to realize that the way the pressure spectra are modified by the change of skin friction along the serration has important repercussions on how the pressure fluctuations are scattered into pressure waves at the edge.

4.5 Pressure gradient effect on the pressure scaling

A last comparison is carried out for serrated configuration under positive angle of attack. Validation of the boundary layer as obtained from PIV and LBM is presented in the following figure; however, for reasons of conciseness, the remainder of the study will focus on the most important part of the paper, that is the scaling of the pressure fluctuations. Serrations are in fact known to be effective when aligned with the incoming flow streamlines; however, a lowering of the acoustic performance has additionally been reported when operating the entire airfoil at positive angle of attack (Arce León et al. 2016). The aim of the section is thus to verify that the local information on the boundary-layer properties at the trailing edge can be used for scaling of the pressure spectra under a considerable pressure gradient. To the purpose, the analysis is briefly extended to a α = 12°, corresponding to an effective angle of attack of 6.6° as discussed before. However, the study has been verified by the authors to other angles of attack tested and simulated, in the range between α = [0°, 12°]. For reasons of conciseness, the simulated data are analyzed, but omitted from further studies (the main discrepancies being about 0.5 mm in the prediction of δ*).

One of the main differences with respect to zero angle of attack that is noticed for both PIV and LBM data is that the flow is seeping through the teeth of the serrations at the root, while few changes are appreciated for z/b = 0 (Fig. 17). The boundary layer is relatively larger in both experimental and numerical results when compared to the previous realization and more uniform along the serration edge as the results from Fig. 17 indicate. When comparing the boundary-layer profiles and the pressure distribution altogether in Fig. 18 with respect to the ones at zero angle of attack, a factor of about two of increase in the pressure-fluctuation intensity is measured especially at the root. The u⁺ distribution of Fig. 18, left shows relatively higher velocities along the edge with respect to the straight configuration. At the same time, a lowering of the pressure fluctuations at the wall with respect to the straight configuration (Fig. 18-right) is also evident. Both $\overline {{uu}}$ and $\overline {{vv}}$ (for brevity not presented) have been found to reduce in the streamwise direction as seen for the zero angle of attack case.

Fig. 17

Contours of velocity variation along the three spanwise locations of Fig. 2 in the top row; bottom: experimental boundary-layer profiles of u⁺ as from experimental and numerical data. Boundary-layer fit with k = 0.40, B = 5, u_τ = 0.50 m/s (White 2006)

Fig. 18

Experimental boundary-layer profiles of u⁺, mean pressure coefficient $\overline {{{c_{\text{p}}}}}$, and pressure fluctuations ${p_{{\text{rms}}}}$ at three streamwise locations along the edge. Boundary-layer fit with k = 0.40, B = 5, u_τ = 0.50 m/s (White 2006)

Spectra of the pressure fluctuations at the same serration locations as before are plotted against the different models of Sect. 4.3 (with new parameters corresponding to α = 12°, V_∞ = 20 m/s, and δ* = 5.3 mm) and compared with the ones at zero angle of attack in Fig. 19. Interesting fact is that the obtained distribution of the pressure fluctuations, once the fitted parameters are extrapolated from the data, is more uniform along the spanwise direction when compared to the results at 0° angle of attack. Almost no-variation is seen along the streamwise direction (cfr. Table 4, coefficients for the boundary-layer local parameters) and higher pressure fluctuations are observed with respect to the reference case, confirming the observations in Sect. 4.1.4. This is due to the new characteristics of the boundary layer, which is thicker and, therefore, relatively less developing in space through the same trailing-edge length. It has to be noted that few of the previously presented prediction models [excluding Goody’s (2004) and the one of Moreau et al. (2011)] are evidently poorly performing due to the presence of a non-negligible pressure gradient at the edge. The previous models are still reported in Fig. 19 for clarity of the comparison with the others.

Fig. 19

Normalized spectra of the pressure fluctuations for different spanwise and streamwise locations. Models updated with local boundary-layer properties: Smolyakov and Tkachenko (1991), Howe (1998), Chase (1980), Goody (2004) and Moreau et al. (2011). Experimental values from PIV: NACA 0018, Re = 270,000, α = 12°, V_∞ = 20 m/s, δ* = 5.3 mm

Once interpreting the results from Sects. 4.3 to 4.5, few conclusions can be made, especially when considering the acoustic results already published by the authors (Arce León et al. 2016). In particular, it can be seen that scaling the spectra with the local flow parameters still conveys with a better collapse than with the incoming boundary-layer properties. In addition, results seem also to indicate that a lower noise reduction might be related to the impossibility of maintaining (due to boundary-layer size and skin-friction change) the beneficial change of the pressure spectrum along the serrated edge (Table 5).

5 Conclusions

A study about pressure-fluctuation changes along serrated and slitted trailing edges is carried out. The study is motivated by a possible improvement of the simplifying assumption of frozen turbulence, which is not able to correctly represent the correct pressure-fluctuation distribution along serrated geometries. If implemented, such correction could reduce the actual gap between the predicted and actual noise performance of serrations and slits. The work of this study is focused on a combined experimental and computational investigation of the TE flow of an NACA 0018 wing retrofitted with serrations and slits. Unsteady flow simulations are carried out to reproduce the same boundary-layer characteristics as measured by time-resolved stereoscopic and tomographic PIV at the edge of the serration. Tuning of the height and spanwise periodicity of the tripping device in the computations allows an accurate matching of the turbulent boundary layer experimentally obtained by forcing transition with distributed roughness of carborundum. Results show a relatively good agreement between the PIV data and the numerical ones. Once validated with the higher spatial and temporal resolution output of the numerical computations, results are employed to understand what the role of the pressure fluctuations in the noise-reduction mechanism of serrated devices is. One of the major differences, with respect to the analytical studies in the literature, is found to be the change in the pressure-fluctuation magnitude and spectra along the serration edge. This change is not predicted by the available turbulent boundary-layer models. However, the present study shows that using the locally obtained change of skin-friction coefficient along the geometry (linearly changing along the serration edge for small angles of attack), it is possible to describe the magnitude and spectra of the pressure fluctuations. Results including slitted geometries and higher angles of attack seem to point out that the observed change of pressure fluctuations is also beneficial for noise reduction. The present study also shows that for slitted configurations, particular attention has to be devoted to the increase of the pressure fluctuations at the root, justifying the development of new shapes, where the empty parts between the teeth are filled up. The analysis of the pressure fluctuation at positive angle of attack, where the authors showed that the serrations are less effective in reducing noise, confirms the previous conclusions. Due to a more pronounced flow separation at the edge, the pressure spectra are seen to vary less in magnitude and frequency content along the serration edge.